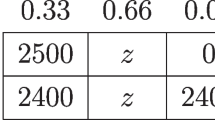
Abstract
The compromise effect arises when being close to the “middle” of a choice set makes an option more appealing. The compromise effect poses conceptual and practical problems for economic research: by influencing choices, it can bias researchers’ inferences about preference parameters. To study this bias, we conduct an experiment with 550 participants who made choices over lotteries from multiple price lists (MPLs). Following prior work, we manipulate the compromise effect to influence choices by varying the middle options of each MPL. We then estimate risk preferences using a discrete-choice model without a compromise effect embedded in the model. As anticipated, the resulting risk preference parameter estimates are not robust, changing as the compromise effect is manipulated. To disentangle risk preference parameters from the compromise effect and to measure the strength of the compromise effect, we augment our discrete-choice model with additional parameters that represent a rising penalty for expressing an indifference point further from the middle of the ordered MPL. Using this method, we estimate an economically significant magnitude for the compromise effect and generate robust estimates of risk preference parameters that are no longer sensitive to compromise-effect manipulations.











Similar content being viewed by others
Notes
We say that a participant is risk averse (risk seeking) when her certainty equivalent for a gamble is less (more) than the gamble’s expected value.
As we discuss below, we also find that the compromise effect influences the probability weighting function.
Our procedure differs from T&K’s in three ways. First, T&K do not report the actual values they used. Second, while their gambles were all hypothetical, our “Part A” gambles are incentivized. Third, for each screen, T&K implement a two-step procedure: after finding the point at which participants switch from preferring the alternative outcomes to preferring the fixed prospect, the participant make choices between the fixed prospect and a second set of seven alternative outcomes, linearly spaced between a value 25% higher than the lowest amount accepted in the first set and a value 25% lower than the highest amount rejected. We avoid this two-step procedure (which Harrison et al. 2007a call an “Iterative Multiple Price List”) to maintain incentive compatibility.
To mitigate this possible unintended effect, our experiment’s instructions avoid words like “switch” and “middle”. Instead, the instructions stated the following on a practice screen which the participants had to complete at the beginning of the experiment (see Online Appendix Section 12): “the site will automatically fill in the answers to certain questions based on the answers you have already provided. For instance, if you indicate that you would prefer to gain $126 over picking a ball from the bag, the site will assume that you would also prefer to gain $135 over picking a ball from the bag, and it will answer that question for you.” (By contrast, Andersen et al.’s (2006) Switching MPL asks subjects to choose which row they want to switch at.)
We use \(\gamma =0.99\) because \(\gamma =1\) corresponds to log utility and implies a certainty equivalent of $0 for any prospect with a chance of a $0 outcome.
As many researchers have shown (e.g., Harrison et al. 2005a; Holt and Laury 2002), real stakes sometimes change the results of an experiment, as compared with hypothetical stakes. We use real stakes in the gain domain (Part A). When we ask participants to make decisions that involve both the gain and the loss domain or just the loss domain in Parts B–D, we use hypothetical stakes because of the ethical problems associated with making experimental participants bear real losses (as opposed to the pseudo-loss of losing an experimental endowment). We emphasize that the main results are robust to using only Part A (gains) questions, where we do use real stakes.
Participants were allowed to complete the experiment in more than one session and some response times exceeded 24 h. Of the 497 participants for whom we have response time data, 405 took less than an hour.
In Part C, the alternative prospects are presented in increasing order of monetary payoff.
As discussed below, we excluded from the estimation participants for whom the MLE did not converge when estimated using only their data. This participant’s data were among the data that were excluded as a result of this.
For Part A we estimate a \(\sigma _{q}\) parameter for each of five groups of screens. Screens are grouped together based on the expected utility of their fixed prospects; the latter is calculated based on the parameter estimates reported by Fehr-Duda and Epper (2012, Table 3). We estimate \(\sigma _{A, 0-25}\), \(\sigma _{A, 25-50}\), \(\sigma _{A, 50-75}\), \(\sigma _{A, 75-100}\), \(\sigma _{A,100+}\), where \(\sigma _{A, L-H}\) is for screens with a fixed prospect whose expected value is between L and H. For Part B, we proceed analogously. We also estimate \(\sigma _{C,\text {small}}\) and \(\sigma _{C, \text {big}}\) for the two smaller and the two larger fixed prospects of Part C, respectively, and \(\sigma _{D}\) for the two fixed prospects of the two screens of Part D we use.
We drop the two screens of Part D that involve only positive outcomes (designed by T&K as placebo tests for loss aversion) so that Parts C and D primarily identify \(\hat{\lambda }\). When we refer to “all screens from Parts A–D,” we mean all screens excluding these two.
We note that in CPT, risk preferences are determined by a combination of the utility function and the probability weighting function, and therefore there is no one-to-one mapping from risk preferences to utility curvature. However, our ex ante hypotheses concerned utility curvature \(\gamma\) and loss aversion \(\lambda\) only (not the probability weighting function). As we discuss below in Sect. 6, we find in our data that the compromise effect also influences the probability weighting function.
Wakker (2010, section 9.6) highlights two concerns when \(u(\cdot )\) takes the CRRA form and \(\gamma ^{+}\ne \gamma ^{-}\). First, the ratio of disutility from a sure loss of x to utility from a sure gain of x, \(\frac{-\lambda u^{-}(-x)}{u^{+}(x)}\), is not uniformly equal to \(\lambda\) but instead depends on the value of x. Second, for any \(\lambda\) , there exists a range of x values for which this ratio is actually smaller than 1, which is the opposite of loss aversion. These problems make estimates of \(\lambda\) sensitive to exactly which prospects are used in the experiment. As previously mentioned, in the Online Appendix we report estimates of a robustness check where we assume CARA utility and different utility curvature parameters in the gain and loss domains.
The statistical power to test the pairwise differences in our parameter estimates (for each discrete step in the Pull treatment) is limited. Accordingly, we test Hypothesis 3.a and Hypothesis 3.b by estimating a linear model. Figures 9 and 10 imply that a linear specification is a good approximation.
In the model without the compromise effect, \(\hat{\beta }\) tends to increase in Pull. In the gain domain, this implies that Pull reduces the elevation of the probability weighting function, and thus lowers the probability weight assigned to the outcome with the higher payoff. In this way, Pull reduces the certainty equivalent for the gamble. As for \(\hat{ \alpha }\), it decreases in Pull. In the gain domain, a lower \(\alpha\) means a lower probability weight for the outcome with the higher payoff if that outcome’s probability exceeds \(1/e=0.368\). Since most gambles in the experiment satisfy that condition, Pull decreases \(\hat{\alpha }\), which in turn implies a lower certainty equivalent for most gambles. Online Appendix Section 4 reports the complete set of estimates of the parameterized model with and without the compromise effect.
In OLS regressions of \(\hat{\sigma }_{q}\) on a constant and \(\hat{E}_{\tilde{q }\in q}[|\hat{U}(P_{\tilde{q}f})|]\), the intercept is economically small in all cases. For the estimates of \(\hat{\Delta }\) reported here, we use a 0 intercept.
Sprenger (2015) assumes that the fixed prospect in each binary choice pins down a participant’s reference point. Because the fixed prospect was held constant across our scale manipulations, this approach can’t explain the effects we find.
References
Abdellaoui, M., Bleichrodt, H., & Paraschiv, C. (2007). Loss aversion under prospect theory: A parameter-free measurement. Management Science, 53(10), 1659–1674.
Andersen, S., Harrison, G. W., Lau, M. I., & Rutström, E. E. (2006). Elicitation using multiple price list formats. Experimental Economics, 9(4), 383–405.
Andersen, S., Harrison, G. W., Lau, M. I., & Rutström, E. E. (2008). Eliciting risk and time preferences. Econometrica, 76(3), 583–618.
Andersson, O., Holm, H. J., Tyran, J.-R., & Wengström, E. (2016). Risk aversion relates to cognitive ability: Preferences or noise? Journal of the European Economic Association, 14(5), 1129–1154.
Apesteguia, J., & Ballester, M. A. (2018). Monotone stochastic choice models: The case of risk and time preferences. Journal of Political Economy, 126(1), 74–106.
Beauchamp, J. P., Cesarini, D., & Johannesson, M. (2017). The psychometric and empirical properties of measures of risk preferences. Journal of Risk and Uncertainty, 54(3), 203–237.
Benjamin, D. J., Brown, S. A., & Shaprio, J. M. (2013). Who is ‘behavioral’? Cognitive ability and anomalous preferences. Journal of the European Economic Association, 11(6), 1231–1255.
Birnbaum, M. H. (1992). Violations of monotonicity and contextual effects in choice-based certainty equivalents. Psychological Science, 3(5), 310–314.
Booij, A. S., van Praag, B. M. S., & van de Kuilen, G. (2010). A parametric analysis of prospect theory’s functionals for the general population. Theory and Decision, 68, 115–148.
Bruhin, A., Fehr-Duda, H., & Epper, T. (2010). Risk and rationality: Uncovering heterogeneity in probability distortion. Econometrica, 78(4), 1375–1412.
Dohmen, T., Falk, A., Huffman, D., & Sunde, U. (2010). Are risk aversion and impatience related to cognitive ability? American Economic Review, 100(3), 1238–60.
Dohmen, T., Falk, A., Huffman, D., & Sunde, U. (2018). On the relationship between cognitive ability and risk preference. Journal of Economic Perspectives, 32(2), 115–34.
Fehr-Duda, H., & Epper, T. (2012). Probability and risk: Foundations and economic implications of probability-dependent risk preferences. Annual Review of Economics, 4, 567–593.
Fox, C. R., & Poldrack, R. A. (2014). Prospect theory and the brain. In P. W. Glimcher & E. Fehr (Eds.), Neuroeconomics: Decision making and the brain (2nd ed., pp. 533–567). Cambridge: Academic Press.
Freeman, D., Halevy, Y., & Kneeland, T. (2019). Eliciting risk preferences using choice lists. Quantitative Economics, 10, 217–237.
Gächter, S., Johnson, E., & Herrmann, A. (2007). Individual-level loss aversion in riskless and risky choices. IZA discussion paper no. 2961.
Harrison, G. W., Johnson, E., McInnes, M. M., & Rutström, E. E. (2005a). Risk aversion and incentive effects: Comment. American Economic Review, 95(3), 897–901.
Harrison, G. W., Lau, M. I., Rutström, E. E., & Sullivan, M. B. (2005b). Eliciting risk and time preferences using field experiments: Some methodological issues. In J. Carpenter, G. Harrison, & J. List (Eds.), Field experiments in economics (Research in experimental economics) (Vol. 10, pp. 125–218). Bingley: Emerald Group Publishing Limited.
Harrison, G. W., Lau, M. I., & Rutström, E. E. (2007). Estimating risk attitudes in Denmark: A field experiment. Scandinavian Journal of Economics, 109(2), 341–368.
Harrison, G. W., List, J. A., & Towe, C. (2007). Naturally occurring preferences and exogenous laboratory experiments: A case study of risk aversion. Econometrica, 75(2), 433–458.
Harrison, G. W., & Rutström, E. E. (2008). Risk aversion in the laboratory. In J. Cox & G. Harrison (Eds.), Risk aversion in experiments (Research in experimental economics) (Vol. 12, pp. 41–196). Bingley: Emerald Group Publishing Limited.
Hey, J. D., & Orme, C. (1994). Investigating generalizations of expected utility theory using experimental data. Econometrica, 62(6), 1291–1326.
Hjorth, K., & Fosgerau, M. (2011). Loss aversion and individual characteristics. Environmental and Resource Economics, 49(4), 573–596.
Holt, C. A., & Laury, S. K. (2002). Risk aversion and incentive effects. American Economic Review, 92(5), 1644–1655.
Kamenica, E. (2008). Contextual inference in markets: On the informational content of product lines. American Economic Review, 98(5), 2127–2149.
Köbberling, V., & Wakker, P. (2005). An index of loss aversion. Journal of Economic Theory, 122, 119–131.
Koppell, J. G. S., & Steen, J. A. (2004). The effects of ballot position on election outcomes. Journal of Politics, 66(1), 267–281.
Köszegi, B., & Rabin, M. (2006). A model of reference-dependent preferences. Quarterly Journal of Economics, 121(4), 1133–1165.
Köszegi, B., & Rabin, M. (2007). Reference-dependent risk attitudes. American Economic Review, 97(4), 1047–1073.
Lichtenstein, S., Slovic, P., & Zink, D. (1969). The effect of instruction in expected value optimality of gambling decisions. Journal of Experimental Psychology, 79(2), 236–240.
Montgomery, H., & Adelbratt, T. (1982). Gambling decisions and information about expected value. Organizational Behavior and Human Performance, 29, 39–57.
Prelec, D. (1998). The probability weighting function. Econometrica, 66(3), 497–527.
Saha, A. (1993). Expo-power utility: A ‘flexible’form for absolute and relative risk aversion. American Journal of Agricultural Economics, 75(4), 905–913.
Simonson, I. (1989). Choice based on reasons: The case of attraction and compromise effects. Journal of Consumer Research, 16(2), 158–174.
Sprenger, C. (2015). An endowment effect for risk: Experimental tests of stochastic reference points. Journal of Political Economy, 123(6), 1456–1499.
Tversky, A., & Kahneman, D. (1974). Judgment under uncertainty: Heuristics and biases. Science, 185(4157), 1124–1131.
Tversky, A., & Kahneman, D. (1992). Advances in prospect theory: Cumulative representation of uncertainty. Journal of Risk and uncertainty, 5(4), 297–323.
Wakker, P. P. (2010). Prospect theory: For risk and ambiguity. Cambridge: Cambridge University Press.
Wilcox, N. T. (2011). ‘Stochastically more risk averse:’ A contextual theory of stochastic discrete choice under risk. Journal of Econometrics, 162(1), 89–104.
Acknowledgements
We thank Helga Fehr-Duda, Philipp Koellinger, Kevin McCabe, Ted O’Donoghue, Matthew Rabin, Charlie Sprenger, as well as the Editor Charles Noussair and two anonymous referees, for helpful comments. For research assistance, we are grateful to Jonathan Cohen, Brice Cooke, Jaesun Lee, and especially Brendan Price, Alexandra Roulet, and Stephen Tino. Research reported in this publication was supported by the National Institute on Aging of the National Institutes of Health under Award Numbers R01AG021650 and P01AG005842 to the NBER and R21AG037741 to Cornell University. The content is the sole responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health. Beauchamp and Laibson thank the Pershing Square Fund for Research on the Foundations of Human Behavior for financial support.
Author information
Authors and Affiliations
Contributions
Beauchamp, Benjamin, Chabris, and Laibson designed the study; Beauchamp analyzed the data, and led the development of the model with inputs from Benjamin and Laibson; Beauchamp, Benjamin, and Laibson wrote the paper; Laibson obtained funding for the study.
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
About this article
Cite this article
Beauchamp, J.P., Benjamin, D.J., Laibson, D.I. et al. Measuring and controlling for the compromise effect when estimating risk preference parameters. Exp Econ 23, 1069–1099 (2020). https://doi.org/10.1007/s10683-019-09640-z
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10683-019-09640-z