Abstract
A rich history of theoretical models in finance shows that speculation can lead to overpricing and price bubbles. We provide evidence that, indeed, individual speculative behavior fuels overpricing in (experimental) asset markets. In a first step, we elicit individual speculative behavior in a one-shot setting with a novel speculation elicitation task (SET). In a second step, we use this measure of speculative behavior to compose dynamic, continuous double auction markets in line with Smith et al. (Econometrica 56(5):1119–1151, 1988). We find significant higher overpricing in markets with traders who exhibited more speculative behavior in the individual SET. However, we find no such differences in overpricing when we test for alternative explanations, using a market environment introduced by Lei, Noussair, and Plott (Econometrica 69(4):831–859, 2001) where speculation is impossible. Taken together, our results corroborate the notion that speculation is an important factor in overpricing and bubble formation if market environments allow for the pursuit of capital gains.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Res tantum valet quantum vendi potest. (A thing is worth only what it can be sold for.)
Glossa ordinaria by Accursius (c. 1183–c. 1260)
Price bubbles and crashes are prominent, recurring phenomena with famous examples reaching from the Dutch tulip mania (1634–1637) and the South Sea Bubble (1720) to the Dot-com Bubble (1995–2000) and the bursting of the U.S. housing bubble (2007–2008). Despite considerable literature on price bubbles (see, e.g., Brunnermeier 2008; Palan 2013; Scherbina and Schlusche 2014, for overviews), empirical evidence on their underlying mechanisms and drivers remains elusive. One of the alleged drivers that regularly captures the attention of the media is speculation, often defined as a trading strategy where investors seek capital gains by holding an asset above its fundamental value (a ‘bubble asset’), because they expect to sell it at an even higher price to another investor, often referred to as ‘greater fool’ (Kindleberger and Aliber 2005).Footnote 1 A rich history of theoretical models in finance (e.g., Brunnermeier 2008; Scherbina and Schlusche 2014) shows that speculation can be a rational strategy and fuel asset bubbles where “investors can rationally expect an asset price to move in one direction in the short run and in the opposite direction in the long run” (De Long et al. 1990b, p. 394). Empirically, however, it remains a challenge to identify and test for the influence of speculation—or speculators—on bubble formation. As fundamental values are generally not known in secondary data from financial markets, the joint-hypothesis problem (Fama 1970, 1991) creates a serious challenge to the empirical identification of price bubbles and hence the impact of speculation on the formation of bubbles.
To tackle this joint-hypothesis problem, many studies make use of experimental asset markets as here the fundamental value can be clearly defined (e.g., Bloomfield and Anderson 2010), and, thus, a price deviation from the fundamental value can be measured. For this reason the use of experiments as a test bed for financial theory in general (e.g., Bossaerts and Plott 2002, 2004) as well as speculation in particular (e.g., Plott and Agha 1983) has been well established. One approach to experimentally investigate the role of speculation in bubble formation is by exclusion. Do bubbles form even though speculation is excluded by design? In their seminal paper, Lei et al. (2001, LNP) reconstruct the market environment of Smith et al. (1988, SSW), in which subjects trade an asset that pays a stochastic dividend each round and which is well-known to produce bubbles, but remove the ability to speculate by limiting the role of each agent to be either a buyer or a seller. Surprisingly, despite the complete elimination of the possibility to resell at a higher price, LNP still observe large price deviations from fundamental prices and bubbles. Although LNP provide strong evidence, by falsification, that speculation is not essential to the formation of bubbles, they “do not claim that speculation does not occur in asset markets of this type […].” (LNP, p. 834) In fact, it is still unclear, whether and, if yes, how much speculation adds to bubble formation when trading is possible.
To answer this question, and in the wake of LNP, a number of studies attempt to identify specific trading patterns from experimental trading data ex-post (Haruvy and Noussair 2006; Caginalp and Ilieva 2008; Haruvy et al. 2014; Baghestanian et al. 2015). The model of De Long et al. (1990b) is commonly used to classify market subjects into three types: rational speculators (RAs) look forward and trade on (correctly) expected future price movements, while momentum traders (MMs) look back and chase recent trends by extrapolation. Both RAs and MMs ignore any differences between prices and fundamentals. In contrast, fundamental value traders (FVs) only trade on current prices and fundamentals.Footnote 2 Based on this classification, differences in mispricing are attributed—across markets—to differences in the distribution of traders’ types and—within markets—to the weight that different trading strategies have over time in a bubble-crash pattern.Footnote 3
Yet, it remains a challenge to identify the contribution of speculative behavior to bubble formation. First, both RAs and MMs are very similar in their observed trading behavior, because they only differ in their short-term, forward and backward looking time horizons. This similarity in observed behavior makes it difficult to disentangle the two trader types empirically. In fact, in a prototypical bubble-crash pattern, the behavioral difference between RA and MM can only be measured in the period at the peak of the bubble and one period thereafter.Footnote 4 If a speculator errs and exits the bubble only one or two periods before (or after) the peak, her trading behavior would be either indistinguishable or wrongly classified as MM. Most simulation models in the mentioned literature make sharp predictions based on RAs with identical and accurate beliefs about future prices, which leaves little room for error or for heterogeneity in the timing of a bubble exit. However, market timing is a difficult task and uncertainty about the exit of others has been shown to support bubbles even amongst speculators who are rational and collectively both well-informed and well-financed (Abreu and Brunnermeier 2003). Hence, we cannot rule out that at least some MMs are RAs in disguise. Ideally, we would want to identify speculative behavior in the absence of momentum trading. Second, most trader classification experiments administered the multi-period continuous double auction market environment of Smith et al. (1988), which comes with highly dynamic, endogenous, and path dependent price formation processes. There exists ample evidence for a multitude of effects related to market feedback and dynamics in the SSW design, which potentially confound speculative behavior in bubbles and thus complicate the ex-post separation of trading strategies that aim to outwit others (RA) from other rational (FV) and irrational (MM) approaches.Footnote 5
We aim to provide evidence that individual speculative behavior is one of the reasons why bubbles, or more precisely “overpricing”, occurs. Before we proceed, we would like to emphasize that the definition of a “bubble” is still controversially discussed and that the empirical detection of price bubbles, even ex-post, is very difficult as the exact fundamental value is unknown in archival data (e.g. Brunnermeier 2008). In the remainder of this paper we will therefore refer to overpricing, instead of bubbles, and to specific measures that describe fundamentally unjustified positive price deviations. However, whenever we refer to other studies on this topic, as in this introduction, we follow the nomenclature of the authors and refer to bubbles when they do.
To test whether individual speculative behavior is one of the reasons for overpricing, we isolate speculative behavior ex ante in a much simpler setting, at the individual level and without explicit market interaction in a novel speculation elicitation task (SET). The SET measures speculative behavior of individuals with a ‘SET-score’: the higher a subject’s SET-score, the higher a trader’s speculative behavior. Importantly, the SET-score cannot be influenced by momentum strategies using past prices, because it is based on a one-shot game. Moreover, as subjects take individual decisions in the SET, the SET-score excludes potentially confounding effects of market feedback and dynamics. In a second step, we compose markets along the previously elicited SET-score in order to analyze how markets with higher or lower average speculative behavior affect price formation in the SSW design. We observe greater positive price deviations from the fundamental value in high SET-score markets than in low SET-score markets. Finally, to exclude the possibility that non-speculative factors, which may be correlated with the SET-score, cause the observed overpricing, we administer the no-speculation environment of LNP (instead of the SSW design) as a robustness check. As expected, we find no difference in overpricing comparing the high SET-score to the low SET-score markets in the LNP sessions. This corroborates the notion that the SET indeed captures individual speculative behavior, and that this behavior at least partly creates overpricing in the SSW design. By linking individual speculation with overpricing, this paper mainly contributes to the extensive literature on bubbles in experimental asset markets (Palan 2013), but also to empirical studies in financial economics that focus on overpricing and price bubbles with archival data. It also has a methodological contribution by providing the SET as a simple and quick-to-administer task for measuring speculative behavior.
The SET is based on the ‘bubble game’ introduced by Moinas and Pouget (2013). In the bubble game, three traders consecutively buy and sell an asset to each other that is commonly known to have zero fundamental value. At each point in the sequence, an incoming trader chooses between either (1) accepting a buy offer at a given price and offering it to the next trader in line at a higher price, or (2) rejecting the buy offer, effectively leaving the current owner stuck with a worthless asset. The last trader in the sequence cannot sell the asset anymore. Thus, when buying the asset, traders speculate on being able to sell it to a next trader at a higher price. Traders do not know their position in the market sequence but the price at which they are offered the asset serves as a signal on their position; the higher the offer price, the higher the probability of being last in the sequence.
Under common rationality, backward induction shows that no trader should buy the asset and hence a positive price—or bubble—should never form. Moinas and Pouget (2013), however, find substantial trading in their experiments and show that buying into the bubble game solves an individual rationality condition: the utility of buying is larger or equal to the utility of not buying, as long as the believed probability of someone next in line buying is large enough. In fact, Moinas and Pouget (2013) find support for a subjective Quantal Response Equilibrium model (QRE, McKelvey and Palfrey 1995; Rogers et al. 2009) where traders depart from the no-bubble Nash equilibrium based on the assumption of a less than perfect payoff responsiveness of other traders. Hence, Moinas and Pouget (2013) claim that “quantal responses […] are important drivers of speculation” (abstract) and that the bubble game provides “an experimental study of speculation” (title), where traders buy bubble assets, because they believe that subsequent traders make mistakes.Footnote 6 This finding is in line with the noise trader theory by De Long et al. (1990a), in which traders buy bubble assets expecting to resell them to noise traders, and with the simulation models used in the above mentioned experimental literature to identify speculative trading patterns. Importantly, this rationale translates to speculation in the SSW design, where “bubbles can occur when traders are uncertain that future prices will track the fundamental value, because they doubt the rationality of the other traders, and therefore speculate in the belief that there are opportunities for future capital gains.” (Lei et al. 2001, p. 832)Footnote 7 Hence, with regard to speculative rationale, there exists a direct link between bubbles in the SSW design and in the bubble game (also see Moinas and Pouget (2013), e.g., on p. 1515).Footnote 8
With the SET we provide an experimental design that elicits the highest price a trader is willing to buy for in the bubble game. The SET elicits buy decisions for all possible prices and can therefore be seen as an extended, price-list version of the original bubble game. In our experimental setting, every subject goes through a list of all seven potential prices, starting at the highest possible price, and decides whether to buy (and offer to sell for a higher price) or not. At the highest price a subject is sure to be the last in line and cannot resell. Moving down the list, the first price at which a subject is willing to buy the asset determines the SET-score. This score can be interpreted as a measure for speculative behavior: following QRE-logic, the higher the buying price, the higher the assumed error rates of others must be for a trader’s individual rationality condition to be satisfied, or, in noise trader terms, the higher the SET-score the more a trader is willing to speculate on the existence of noise traders down the line.
To answer our main research question, we test whether the individual propensity to speculate, as measured by the SET-score, affects overpricing in asset markets—in particular, in the SSW design. Specifically, in each session we split the subject population in SET-score tertiles and assign each tertile to one of three independent but otherwise similar SSW markets.Footnote 9 If individual speculative behavior affects overpricing, we expect systematically higher overpricing in markets with high SET-scores than in markets with low SET-scores. Note that subjects receive no information about other traders’ SET-scores nor about the market composition process. In doing so, we prevent any influence of the market composition on subjects’ beliefs, which would confound our results. Note that this lack of information about other trader types does not affect our predictions on overpricing, because for speculative bubbles “it need not to be the case that irrational traders actually exist, but only that their existence is believed to be possible” (LNP, p. 834). Hence, in markets with many speculators (high SET markets) we expect traders to feed on each other as they receive price signals that confirm their assumption of a high resale value, while in markets with few or no speculators (low SET markets) such a positive feedback loop will be less likely.Footnote 10
We find our main research question to be confirmed. First, we detect speculative behavior in the SET; in particular, the SET-scores are sufficiently heterogeneous to compose distinctly different markets. Second, markets with speculative traders fuel overpricing; we find positive price deviations from the fundamental value to be statistically and economically significantly higher in high SET-score markets than in low SET-score markets. Third, we test whether our results are not driven by other, non-speculative factors by administering the no-speculation environment of LNP. As expected, the SET-scores have no influence on overpricing in LNP markets. Hence, the SET does not elicit behavior that survives in the non-speculative environment of LNP, such as risk-loving preferences or violation of dominance (Moinas and Pouget 2013), but it does seem to measure some speculative rationale (in line with, e.g., the QRE) that adds to overpricing in the SSW design. Overall, our results corroborate the notion that speculation is an important factor in overpricing and bubble formation if market environments allow for the realization of capital gains.
The rest of the paper is organized as follows. In Sect. 2 we discuss the experimental design. In Sect. 3 we present the main results, which we then discuss conclusively in Sect. 4.
2 Experimental design
2.1 General setup and implementation
Each session consisted of three parts: in part one we elicited the SET-score, in part two subjects participated in an asset market, and in part three we elicited demographics, CRT (incentivized: Frederick 2005), and risk attitudes (incentivized: Holt and Laury 2002; not incentivized: Dohmen et al. 2005).Footnote 11 In Sessions S1–S6 (SSW sessions), subjects participated in the SSW design while in Sessions S7–S9 (LNP sessions) students participated in a no-speculation market environment in line with LNP.
A total of 178 students participated in the SSW sessions and an additional 86 subjects participated in the LNP sessions making for a total of 264 subjects over all nine sessions. Each session lasted about 1 h and 45 min and the average earnings per subject were 22.27 euros (SD 4.94). All payments were made in cash and in private at the very end of the experiment. All tasks were computerized using z-Tree (Fischbacher 2007) and subjects were recruited using ORSEE (Greiner 2004). SSW sessions were conducted in the period from March to May 2014 and June 2017 and LNP sessions were conducted from December to March 2015–2016. All sessions were run at the NSM Decision Lab at Radboud University (Nijmegen, The Netherlands).Footnote 12
2.2 Speculation elicitation task (SET)
The SET is based on the bubble game introduced by Moinas and Pouget (2013) and consists of a sequential market of three traders. Starting with a one euro initial capital endowment, each trader can either accept or reject to buy an asset with a fundamental value equal to zero for the price offered (see Fig. 1). If a trader accepts to buy at a price P, she invests one euro initial capital—the remaining amount is financed by an external financier—and automatically offers the asset to the next trader in the sequence for a price that is ten times higher, \(10\times P\). The trader earns ten euro if the next trader decides to buy and loses her investment if the next trader rejects to buy or if no next trader exists. If a trader rejects to buy, she and all subsequent traders keep their one euro initial capital.
For example, the first trader in line decides to buy the asset for \(P=1000\) paying the one euro initial capital. Then, she offers the asset to the second trader in the sequence for \(P=(10\times 1000=)10{,}000\) who decides to buy as well paying her one euro initial capital. As an immediate consequence, the first trader earns ten euro. The second trader now offers the asset for \(P=(10\times 10\times 1000=)100{,}000\) to the third trader. The third trader however rejects the offer. Hence, the second trader holds a worthless asset and lost her investment while the third trader keeps her initial capital. To summarize, the payoffs are ten euro for the first trader, zero euro for the second trader and one euro for the third trader.
Sequence of the SET. Notes The first trader in line is offered to buy the asset at a randomly drawn price \(P_{1}\in \{10^{0},10^{1},10^{2},10^{3},10^{4}\}\). When the first trader rejects, the game ends and all traders earn their one euro initial capital. When the first trader accepts, the asset is offered to the second trader in the sequence at a price \(P_{2}=10\times P_{1}\), i.e., \(P_{2}\in \{10^{1},10^{2},10^{3},10^{4},10^{5}\}\). When the second trader rejects, the game ends, the first trader earns zero, and the second and the third trader earn the one euro initial capital. When the second trader accepts, the first trader sells the asset and earns ten euros. The asset is then offered to the third trader in the sequence at a price \(P_{3}=10\times P_{2}\), i.e., \(P_{3}\in \{10^{2},10^{3},10^{4},10^{5},10^{6}\}\). When the third trader rejects, the game ends, the second trader earns zero, and the third trader earns the one euro initial capital. When the third trader accepts, the second trader sells the asset and earns ten euros. The third trader buys the asset even though being last in the sequence and is unable to resell. Thus, the third trader loses the one euro initial capital and earns zero
Traders have no information about their position in the sequence, i.e., each trader has an equal chance of being either first, second or third in the sequence. The price reveals information about a trader’s position in the sequence though. The price offered to the trader in the first position is randomly drawn from a set \(P_{1}\in \{10^{0},10^{1},10^{2},10^{3},10^{4}\}\) with a known triangular distribution.Footnote 13 The price offered to the second trader in the sequence is then \(P_{2}=P_{1}\times 10\), and the price offered to the third trader is \(P_{3}=P_{2}\times 10=P_{1}\times 100\). Thus, for any price offered, Bayes’ rule provides the probabilities of being first, second or third in the trading sequence. Note that for an offer \(P=10^{6}\) the probability of being last is equal to one. Under common rationality, backward induction rules out a Nash equilibrium with positive prices (see Moinas and Pouget 2013). Hence, independent of whether the traders know their position in the sequence, neither trader accepts an offer to buy. Note that buy decisions are made simultaneously and independently in a one-shot setting. Hence, subjects have no further information on the actions of other traders in their sequence.
To develop the SET design, we modified the bubble game of Moinas and Pouget (2013) in two ways. First, instead of presenting the subjects with one buy decision at a particular price, we elicited subjects’ buy decision for each price possible given the set of initial prices equal to \(P_{1}\in \{10^{0},10^{1},10^{2},10^{3},10^{4}\}\). This implies a set of offered prices equal to \(P\in \{10^{0},10^{1},10^{2},10^{3},10^{4},10^{5},10^{6}\}\). To elicit a buy decision at each price in this set we asked each subject “Do you want to buy the asset at 1,000,000?,” “Do you want to buy the asset at 100,000?,”…, “Do you want to buy the asset at 1?”Footnote 14 Note that in order to facilitate backward induction we started with the highest possible price for which a buy decision immediately leads to zero payoff. The SET therefore provides a clear switching price \(P^{S}\) for which a subject rejects to buy at prices \(P>P^{S}\) and accepts to buy at prices \(P\le P^{S}\). Our SET-score is defined by the rank of the switching price \(P^{S}\) as shown in Table 1. A low SET-score reflects a low propensity to speculate while a high SET-score indicates a high propensity to speculate.Footnote 15
As a second change we tripled the opportunity costs for speculation, i.e. the starting capital, to three euro. In pilot tests with the original payment scheme we found that the distribution of SET-scores had a strong negative skew toward higher values, indicating a generally high propensity to speculate. Subjects needed to presume only a small winning probability to let the expected earnings from buying exceed one euro. With our calibration of the starting capital to three euro, subjects have to presume a winning probability of at least 3/10, which provides more heterogeneity in SET-scores and therefore allows us to better differentiate between speculative behavior for the composition of markets (see below).Footnote 16
After subjects entered the lab, we first explained the basics of the SET by reading the instructions for the one shot game aloud (see online appendix A.1), followed by on-screen comprehension questions (see online appendix A.2). We allowed several attempts to answer each question, but a subject could only move on to the next question once the current question had been answered correctly. Then the correct answers were publicly announced and thoroughly explained. After having explained the basics of the SET, we provided the procedural instructions on the subjects’ screen (see online appendix A.3). These instructions made clear that the game had to be played not for one but for all possible prices, and that one price would be randomly chosen to calculate their earnings. We clearly indicated that these on-screen instructions were the same for all subjects. To get a consistent buy decision for the whole list of prices, we clearly communicated that if subjects decide to buy at a certain price \(P^{S}\), they are assumed to also buy for each price below \(P^{S}\). We allowed subjects to check and revise their decisions before confirming their final decision. The final payoff for a subject i was calculated as follows. First, one of the seven prices was randomly drawn with equal probability to be the price the trader faced. Second, subject i’s position was randomly drawn. Third, the remaining two positions were filled with two randomly drawn subjects j and k from the subjects in the room. Subject i’s payoff was calculated on the basis of all the three subjects’ decisions.Footnote 17 Finally, after the SET task was administered, we asked subjects to estimate how many subjects in their session buy for a particular price (or lower). This belief elicitation task was incentivized (see online appendix A.4). Note that the subjects received information about their payoff from the SET at the end of the experiment, i.e. after the asset market and after the questionnaire. Hence, the subjects did not know that the other subjects in a market had similar SET-scores.
2.3 Asset markets (SSW sessions and LNP sessions)
To consider the effect of speculation on overpricing, we make use of the asset market design introduced in SSW. We chose the SSW design for several reasons. First, the SSW is known to produce overpricing and price bubbles (Palan 2013), which provides room for speculation and hence scope for different market compositions to take effect. Second, as explained in Sect. 1, the speculative rationale in the SET and the SSW is similar (see also Moinas and Pouget 2013), which allows for inference on the role of speculation in overpricing. Third, the SSW design has a long tradition in experimental finance and remains the most commonly employed market environment (Haruvy et al. 2014), which facilitates comparison to earlier studies and placement in the literature. Fourth, the market environment by LNP is based on the SSW.
We compare markets composed of subjects with high speculative behavior, i.e. subjects who scored high in the SET, to markets composed of subjects with low speculative behavior, i.e. subjects who scored low in the SET. In each session, we compose markets as follows. We ranked the elicited SET-scores, split them in three groups and assigned them to three markets. The 10 subjects with the highest SET-scores, representing those subjects within the session population with the highest propensity to speculate, were assigned to one market, henceforth “H-market”. The 10 subjects with the lowest SET-scores, representing the subjects within the session population with the lowest propensity to speculate, were assigned to another market, henceforth “L-market”. The remaining subjects were assigned to a third market with medium SET-scores, henceforth “M-market”. Due to no-shows, the M-markets of Sessions S1 and S7 contained 8 subjects while the M-markets of Sessions S5 and S6 contained 9 subjects. Tied SET-scores were randomly assigned to one of either markets. Subjects did not know how markets were composed.Footnote 18 Hence, we are able to compare the performance of three asset markets using the SSW design, differentiated by the population’s individual speculation behavior into L-, M- and H-markets, leaving all other parameters constant.
The average (median) SET-scores in SSW sessions for the L-, M-, and H-markets are 2.2 (2), 3.4 (3), and 4.3 (4) respectively while for LNP sessions the SET-scores were 1.5 (2), 3.1 (3) and 4.2 (4) respectively. Using Cuzick’s trend tests to test for a trend in SET-scores from the L- (through the M-) to the H-markets, we can reject the Null that no trend from L to H exists in each session in favor of the alternative that SET-scores increases from L to H (\(p<.001\)). Comparing only the L-markets to the H-markets, a Mann Whitney U test confirms statistically significant differences in SET-scores for each individual session as well (\(p<.001\)). Figure 2 shows the distribution of SET-scores in the three market environments over all nine sessions. Due to the experimental implementation of the market allocation facility we could not guarantee an overlap of SET-scores across markets, in particular between market L and M, and M and L. However, there is a clear difference between market L and H as the highest SET-score in the L-markets is 4 with only 1% of the distribution while the lowest SET-score in the H-market is 3 with only 2% of the distribution.
Before trading, subjects had a neutral trial period of 5 min to get used to the trading platform.Footnote 19 After the trial period subjects entered the market. Endowed with 2500 francs and two shares, subjects were able to trade shares in 15 double-auction trading periods. Each period lasted 3 min, and francs and shares carried over from period to period. At the end of every period, each share paid a dividend of 0, 8, 28, or 60 francs with equal probability; note that in each of the three markets in the same session the shares pay the same dividends. Since the expected dividend equals 24 francs in every period, the fundamental value in period t equals \(24\times (16 - t)\), i.e. 360 francs in period 1, 336 francs in period 2, … and 24 francs in period 15. After period 15, the shares remain worthless and the francs were transferred to euros at a rate of one euro for 300 francs.
In SSW sessions, traders were able to buy AND sell shares (see online appendix B.1). In LNP sessions we prohibited speculation as traders were either able to buy OR to sell shares in line with LNP’s NoSpec treatments (see online appendix B.2). As instructions were almost similar to SSW, overpricing can only be explained by expectations about the dividend draws but not by speculation. To assign a trader his or her role as either buyer or seller we ranked subjects within each market on their SET-score. Subjects with uneven ranks were assigned the role of buyer while subjects with even ranks were assigned the role of seller.Footnote 20
In the LNP market environment, we expect to see no differences between markets and hence the Null hypothesis (no speculation) is that prices do not systematically differ comparing H-, M-, and L-markets. In the original the SSW design, however, we expect support for the alternative hypothesis (speculation), which implies higher overpricing in the H-market than in the M-market and in the L-market.
3 Experimental results
We present our results in the order of implementation of the tasks, starting with the SET (Sect. 3.1), proceeding with the trading in the SSW sessions S1–S6 (Sect. 3.2), and ending with the LNP sessions S7–S9 (Sect. 3.3).
3.1 SET
As shown in Table 1, the SET-score distribution shows that 5% of all subjects chose not to buy at all while the remaining 95% of participants did buy and thus speculated on the next trader in line buying as well. Most subjects chose to buy at prices at or below 1000 yielding an average SET-score of 3.22 (SD 1.25). None of the subjects chose to buy at the highest possible price \(P=10^{6}\) and only two subjects chose to buy the asset for a price of 100,000. These results suggest that subjects understood the game quite well. The average earnings for each SET-score are shown in the last row of Table 1. The results indicate that speculation pays off in the SET as earnings are on average higher for speculators.
To investigate whether individual measures explain speculative behavior, we run an OLS regression with the log SET-scores as dependent variable and demographic variables together with CRT scores, risk attitudes and beliefs as independent variables. Specification (1) and (2) in Table 2 show that none of the control variables is significant.Footnote 21 The subject’s belief on the buying behavior of fellow subjects, however, is significantly and positively correlated with a subject’s own SET-score. Hence, on average, and in accordance with the greater fool theory, subjects who believe that others choose a higher \(P^{S}\) also choose a higher \(P^{S}\) themselves. When a subject believes the subsequent trader to buy at \(P\le P'\), then his buy price should be at most \(P^{S}=P'/10\), i.e., a subjects SET-score should be lower than the expected SET-score of others. Overall, we find that about 85% of all subjects are within one price step of that optimal response. We discuss this relationship in more detail in the online appendix, section F.
3.2 Speculation and overpricing in SSW sessions
Figure 3 depicts the median price path for the L-, M-, and H-markets in all SSW sessions. While some markets trade along the fundamental value, in particular the L-markets, other markets show severe overpricing, mostly H-markets. Figure 4 provides a clearer picture with respect to the differences between L- and H-markets. It shows the per-period median price difference for each session (grey line) together with the average of all such differences in each period (black line). Positive differences indicate higher prices for H-markets. As can be seen, almost all differences are positive. Hence, the two figures clearly show the differences between L- and H-markets supporting the alternative hypothesis from Sect. 2.3.
We measure the magnitude of overpricing in line with the recent literature using two measures; geometric deviation (GD), introduced by Powell (2016) and positive deviation (PD), introduced by Eckel and Füllbrunn (2015). We decided to report results on GD and PD, because they provide information about overpricing of markets; we are less interested in measures of mis-pricing like for example the geometric absolute deviation (GAD). For the interested reader we also provide further “bubble measures” considered in the literature—GAD, RD, RAD, AB, TD, boom, turnover—in the online appendix. GD measures the geometric deviation from the fundamental value defined as \(GD=\left( \prod _t \frac{P_{t}}{FV_{t}} \right) ^{1/15}-1\) with \(P_{t}\) being the median price and \(FV_{t}\) being the fundamental value in period t. With a GD of 10 (\(-\) 10)% prices are on average 10% higher (lower) than the average fundamental value. PD simply measures the sum of all positive per-period deviations of the median price from the fundamental value, i.e. \(PD=\sum _{i=1}^{15}\left( P_{t}-FV_{t}\right) _{P_{t}>FV_{t}}\). This measure looks at the area between the fundamental value and the median price.Footnote 22
Table 3 reports GD and PD for each market together with the average SET-score. In each session, overpricing is lower in the L-market than in the H-market. To put the results into perspective, overpricing is on average about 14% in the L-markets, while in H-markets overpricing is on average about 82%, i.e., overpricing is almost six times higher in H-markets than in L-markets. When looking at PD we can also see that the area in the average H-market is about five times greater than in the L-market (524 vs. 2570). We moreover find a significant correlation of 72% (\(p<.001\)) and 77% (\(p<.001\)) between the average market SET-score and GD and PD, respectively—neglecting potential session effects.Footnote 23
To statistically compare the L- and the H-markets, i.e. the markets with the highest difference in terms of SET-scores, we use a Mann–Whitney U test comparing six L-markets and six H-markets. We find a significant difference for GD (\(p=.006\)) and PD (\(p=.006\)), and for almost all additional bubble measures (see online appendix). Hence, overpricing is significantly higher in the H-markets than in the L-markets. Further on, Table 3 suggests a clear trend from the L-, through the M-, to the H-markets. In some sessions the differences in SET-scores between markets are quite small. For these sessions it is not surprising that the overpricing measures are quite close to each other. We therefore use the combined data from the SSW sessions to evaluate the Null that \(GD_{L}\ge GD_{M} \ge GD_{H}\) against the alternative that \(GD_{L}<GD_{M}<GD_{H}\). Using Cuzick’s trend test we can reject the Null indicating a significant trend in overpricing (\(p=0.003\)). The same holds for using similar tests for PD (\(p=0.002\)) and for most of the other measures (see online appendix). Hence, overpricing is increasing in the average propensity to speculate.
To understand whether subjects’ beliefs can explain price patterns and whether differences between market types exist, we asked the subjects to predict the average price for the upcoming period.Footnote 24 For the first period prediction we find no evidence for a relationship with the SET-score: the Spearman coefficient between SET-score and first period prediction equals 0.061 (\(n=177\), \(p=0.413\)). Consequently, we also do not find a treatment effect comparing L-, M-, and H-markets (Kruskal–Wallis, \(p=0.582\), corrected for ties).Footnote 25
We can also look at the prediction errors of subjects, i.e. how well the subjects predict the price in a period. Therefore, we first derive the subject prediction error measured as the sum of distances between the prediction and the average period price for each subject. We then use the median of all subject prediction errors in a market, the ‘market prediction error’ (MPE), as the relevant unit of observation. To compare the MPE across market types, we test whether the MPE in the L-markets equals the MPE in the H-markets. Using a Wilcoxon signed rank test, we can reject this hypothesis indicating that the prediction errors are higher in H-markets than in L-markets (\(p=0.046\)). However, if subjects follow an adaptive learning model in such market environments, as suggested by Haruvy et al. (2007), then the prediction errors should be higher in markets with overpricing and a crash. And indeed this is what we find: the correlation coefficient between market prediction error and GD equals 0.746 (\(p<0.001\), \(n=18\)).
Finally, we look at the predictions over time. It seems that the subjects’ predictions can best be modeled by an adaptive learning model. We find that in the L-, M- and H-markets both adaptive beliefs and anchoring on the fundamental value can explain price predictions. However, the relative importance of anchoring on the fundamental value decreases in the average market SET-score, i.e. anchoring on the fundamental value seems more important in the L-markets than in the H-markets. In particular, we find that subjects fail to correctly predict the market crash. Section F in the online appendix provides details on the analysis on beliefs.
To summarize, as predictions seem to follow lagged prices, prediction errors are higher in markets with overpricing than in markets without overpricing. This complicates a comparison of treatments with regard to beliefs, because we cannot disentangle price trajectories and the market type.
3.3 No speculation treatment in LNP sessions
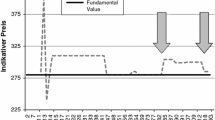
LNP made an interesting observation; they report that even in asset markets in which speculation is excluded by design—subjects in the role of buyers can only buy and subjects in the role of sellers can only sell—overpricing does occur. Hence, speculative motives cannot drive overpricing in such markets. As a consequence, market compositions with respect to SET-scores should have no effect. If we would find such an effect, however, the SET-score would also measure something other than purely speculative behavior. To test this, we run three additional sessions with the same protocol as in the SSW sessions but with the only exception that traders were allowed to either only buy or only sell assets, similar to the NoSpec treatment in LNP. Figure 5 shows the median prices and the the fundamental value in LNP sessions. We can see that prices are almost all above or close to the fundamental value which is in line with LNP; however, the effect is smaller than in LNP. Overall, Fig. 5 shows no relationship between SET-scores and overpricing—in particular, we do not find the same relationship as in the SSW session. However, in comparison to SSW sessions the overpricing measures are less reliable, because the number of trades is relatively low (the number of trades is quite high at the beginning, but becomes small after some periods). There are also some periods without trading. Hence, the trading measures should be treated with caution.
In many dimensions our results are close to the original findings. For example, prices are mostly above fundamental values. In terms of trading volume, the results from our LNP sessions are relatively close to those found in the LNP article. We find that in those sessions on average 86% of possible trades are executed whereas LNP find that between 80 and 90% of trades are executed. However, we also see less overpricing in our LNP sessions in comparison to the observations from LNP. We think that this is due to a different parametrization. Our LNP sessions are designed to be close to our SSW sessions. LNP have less traders (n = 7/8 vs. n = 9/10), more shares (total 80 vs. 20), different endowments (either cash or shares vs. cash and shares), less periods (12 vs. 15), and different dividend payments ({20,40} vs {0, 8, 28, 60}).
One reason for lower overpricing in our LNP sessions might be that LNP had thicker markets (more shares), which allowed for more trading opportunities. Furthermore, if traders have a preference for a balanced portfolio, then traders in LNP aim to either buy shares, when they were endowed with cash only or aim to get cash by selling shares, when they were endowed with shares only. In our LNP sessions, traders were endowed with both and have thus less motivation to trade. Another explanation might be that the SET was administered at the beginning of the experimental sessions, which could have made backward induction more salient in our LNP sessions. This, however, would also apply to the SSW sessions, where we see strong overpricing. Moreover, administering the SET at the beginning of the session applies to all treatments. The crucial result is that we see no systematic difference between the L-, M- and H-markets which supports the notion that speculative tendencies do not drive overpricing in LNP sessions.
4 Discussion and conclusion
Our results seem to indicate that indeed the speculative trading behavior of market subjects plays a role in overpricing and the formation of price bubbles. Of course, this is not to say that other factors might not play a role as well. We readily acknowledge the existence of many determinants for overpricing, many of which are unrelated to speculative behavior. Moreover, our definition of speculative behavior, namely a trader’s SET-score, hinges on the assumption that the speculative reasoning in the SET (along the lines of the QRE and noise trader theory) also applies to trading in asset markets based on the SSW design. Although a full investigation is beyond the scope of our paper (and might be addressed in future work), many aspects of our results lend credibility to this assumption.
Firstly, as shown in table A.3 in the online appendix, we see an increasing importance of market pressure (defined as the number of bids minus the number of asks in a period) on price changes moving from the L- to the H-markets. In other words, the higher one’s SET-score, the more likely one deems future capital gains, which translates to excess market pressure. As the QRE predicts, high SET-score individuals assume higher error rates among fellow traders leading to higher expected capital gains; this finding is consistent with similar arguments offered for speculation in the SSW design by LNP and Plott (1991). Moreover, this rationale directly translates to simulation models used in the experimental literature to identify speculative trading patterns in the SSW design (e.g. Baghestanian et al. 2015), which are based on noise trader theory (De Long et al. 1990a).
The bubble game is based on the centipede game, where players are able to extract higher rents from the experimenter through coordination. Although this is not an equilibrium strategy one could argue that the SET measures coordination rather than speculation. Specifically, when all subjects in the SET buy the asset at all prices, the expected average payoff is higher than not buying at all, namely 6.36 versus 3 euro in the Nash equilibrium. However, if the SET measures a tendency to coordinate, then this should have no effect on overpricing or on bubble formation in the SSW design, because in SSW markets traders trade against each other: if one traders wins, another trader automatically loses; a feature that is not present in the SET. Hence, as coordination cannot explain overpricing or bubble formation in both the SET and the SSW design, we do not think that coordination drives our results.
Another alternative explanation for our results might be that the SET captures a failure to backward induct rather than speculative trading strategies. However, we do not think this is the case in our experiment. Firstly, we have made backward induction salient in our test questions as well as by starting the price list in the SET elicitation procedure at the highest possible price. Moreover, as the results in section F in the online appendix suggest, subjects seem to make a conscious decision regarding their best possible action given their beliefs about the SET-scores of others. Specifically, about 85% of subjects buy at most one step away from their optimal buying price given their beliefs about the SET-score of the other subjects in their session. Finally, not a single subject bought the asset for the highest possible price—at which one is sure to be last in the trading sequence—in the SET which clearly points towards an understanding of the mechanics behind the game.
LNP found overpricing even when buying for resale is not possible (their non-speculation treatment) meaning that this overpricing must be driven by either risk-loving preferences or irrationality in the sense of a violation of dominance (Moinas and Pouget 2013). Following this result it could be argued that our results, too, might be the result of irrationality that is correlated with SET-scores. In our final three ‘robustness check’ sessions in line with LNP, however, we find no correlation between SET-scores and overpricing. Overall, we can conclude that irrational behavior is not likely to be the driving force behind our main result. We do not claim, however, that the speculative behavior measured in the SET is the only driving force of overpricing in the SSW design. It is well-known that many other factors might play a role as well (Palan 2013). In that sense our conclusion does not clash with that of LNP, who write: “We do not claim that speculation does not occur in asset markets of this type, merely that speculation is not necessary to cause departures from fundamental values.” Paraphrasing LNP, we do not claim that speculation is necessary to cause departures from fundamental values, merely that it does occur in asset markets of this type.
We also observe differences between our results and the SSW price patterns in the literature; in particular, we find prices to be at or above fundamental value right from the beginning in almost all markets. One possible explanation for this could be that administering the SET at the beginning of the session positively affected subsequent trading behaviour. (Note that our results relating to treatment effects still hold, because all subjects in all treatments were exposed to the same sequence.) An at least equally likely explanation for the early overpricing in our experiment is our choice of endowment in the SSW design. We opted for a high cash to asset ratio to give speculation a good chance to produce overpricing, as shown by, e.g., Haruvy and Noussair (2006) and also Kirchler et al. (2012). The high initial prices in our SSW sessions are therefore expected and in line with the above mentioned studies that also implemented high cash to asset ratios.
As Gill et al. (2017) show, it is important whether someone is ranked highest or lowest in a group. In principle, our SET-score ranking procedure would allow us to compare the behavior of similar subjects in different setups. For example, subjects with a SET-score of three might be placed in the M-market or in the H-market. However, in the M-market such traders would have the highest SET-score, while in the H-market they have the lowest score. It would be interesting to see if and how subjects with the same SET-score adjust their trading behaviour to their relative position in a market.Footnote 26 Unfortunately, in this paper the number of subjects with similar SET-scores in both market types is too small to draw reliable conclusions. We therefore have to leave this interesting aspect for future research.
In this paper, we test whether speculative behavior of traders affects overpricing in experimental asset markets. To capture speculative behavior at the individual level, we introduced a new measure—the SET-score derived from the speculation elicitation task (SET)—based on the bubble game (Moinas and Pouget 2013). The SET can be easily implemented in the laboratory (in about 15–20 min) and provides a simple and easy-to-interpret score.Footnote 27
We find that overpricing is higher in markets composed of traders with a high individual propensity to speculate than in markets composed of traders with a low propensity to speculate (provided the possibility of speculation is not excluded by design as in one of our robustness checks). Hence, we were able to provide evidence that individual speculative trading behavior adds to overpricing and the formation of asset market bubbles.
Notes
Analogously, speculation also applies to shorting assets below fundamentals and to the emergence of negative bubbles. For simplicity we focus on speculation in positive bubbles and on going long. Note that this definition of speculation is less strict than ‘speculative overpricing’, which refers to prices that exceed the most optimistic belief about the real value of the asset with prices even above the highest possible cash flow of an asset. The latter is often used in rational bubble models with heterogeneous beliefs about the fundamental value of an asset (e.g. Palfrey and Wang 2012). In both of our experimental settings, however, the (sum of) expected dividends of the asset is known at all points in time; so there is no possibility for heterogeneous beliefs on cash flows or fundamental values.
Here we refer to the terminology and adaptation by Haruvy et al. (2014). Specifically, RAs anticipate the next period’s price and increase (decrease) holdings if the price moves upwards (downwards). MMs buy (sell) when the last two prices show an upward (downward) movement. FVs purchase (sell) when today’s market prices are below (above) the fundamental value of the asset.
Assume, for example, a bubble market where prices start at the fundamental value in Period 1, then increase continuously until Period 14, where they peak and then monotonously decrease to the fundamental value at the end of trading in Period 20. We start to categorize trading strategies in Period 3, because we require two past prices, \(p_{t-1}\) and \(p_{t-2}\), to define the demand for MMs. Following, e.g., Haruvy and Noussair (2006) and Haruvy et al. (2014) any stock purchases in this period equally count toward MM and RA, because \(p_{t-1}-p_{t-2}>0\) and \(p_{t+1}-p_{t}>0\). All other behavior is either FV or remains unclassified. This continues until Period 14 where RAs for the first time show a different behavior than MMs: RAs start selling their stock in (correct) anticipation of lower prices in Period 15 and in Period 16, while MMs continue buying. However, after Period 16 both RAs and MMs sell into the crash until Period 19, where classification ends because of missing expected prices (to define RAs) in Period 20. Hence, given sufficient trading data, the classification of RAs versus MMs is based on a behavioral difference of only 2 out of 17 periods.
For example, LNP report that a lack of activity and boredom trades can play a role in the SSW design. See Palan (2013) and Powell and Shestakova (2016) for comprehensive overviews of studies that identify other factors, e.g., wealth changes, experience effects, and misinterpretations of past dividend draws (e.g., gambler’s fallacy).
A similar argument was offered by Plott (1991).
In both settings, backward induction coupled with full information on the fundamental value leads to a no-bubble Nash equilibrium with prices at the fundamental value. Specifically, as in the SET, buying an asset above the fundamental value in the SSW design should only be considered when the assumed probability of reselling for a higher price in one of the subsequent periods is high enough to satisfy a trader’s individual rationality condition. Accordingly, the thought process captured by the QRE can not only be applied to the bubble game and the SET but also to speculative trading behavior in the SSW design (and asset markets in general).
See online appendix, section A, B and C for detailed instructions.
Table A.1 in the online appendix provides descriptive statistics of the subjects in the experiment.
For higher prices an external financial investor pays the difference. Earnings are divided between the financial investor and the participant such that the participant always earns 10 euro. See Moinas and Pouget (2013) for details.
See online appendix A for the exact SET instructions and a screenshot of the task.
Finer SET-score scales can easily be created by increasing the cap on \(P_{1}\), but doing so is a two-edged sword. On the one hand, more levels allow for a more elaborate scale as more decisions are made and more heterogeneity in speculation becomes possible. On the other hand, a design with many levels might include superfluous decisions and would take up too much time.
In fact, with opportunity costs of three euro the distribution of SET-scores shifted more toward the center. The results from the pilot with one euro starting capital are available upon request.
Example: Suppose \(P=1000\) was drawn for subject i (suppose i chose to buy), and suppose i is drawn to be number 2 in line. Then we look at the decision of subject j for \(P=100\) (suppose j chose to buy) and of subject k for \(P=10{,}000\) (suppose k chose not to buy). Now the payoff for subject i is calculated according the decisions of all three (which is zero as k rejected to buy and i purchased from j).
In line with previous studies, e.g., Cheung et al. (2014) and Levine et al. (2014), subgroups are composed without public knowledge on the determinants of selection. This ensures that our treatment variable, the degree of speculative behavior, constitutes the only difference between markets without influencing the subjects’ beliefs.
For instructions see online appendix B.
All L-markets and H-markets contained 5 buyers and 5 sellers while the M-markets of Session S5 and S6 (with 9 traders each) contained 5 buyers and 4 sellers and the M-market of Session S7 (with 8 traders) contained 4 buyers and 4 sellers.
Due to technical difficulties with a computer at the end of Session 1, one subject was unable start the questionnaire. This student is therefore excluded from the regression analysis presented in Table 2.
The literature sometimes uses the average and sometimes the median period price as the relevant unit to calculate the bubble measures. We chose the median period price to reduce the influence of outliers. However, our results do not qualitatively change when using mean transaction prices instead of median transaction prices.
To test whether CRT (among others Bosch-Rosa et al. 2015) or risk preferences (among others Eckel and Füllbrunn 2015) play a role in overpricing we also look at correlations between CRT and GD (PD) and general risk and GD (PD). The four correlations are all below 18% and not significant. Hence, CRT and general risk are barely correlated with overpricing.
We applied the protocol from Eckel and Füllbrunn (2015) but asked for the next period only, in line with SSW. Find the instructions in the online appendix.
Median predictions for the first period transaction price were 379, 421 and 373 for the L-, M- and H-markets respectively.
We thank one of the reviewers for bringing up this idea.
We provide instructions and z-Tree code as supplementary material at the publishers webpage.
References
Abreu, D., & Brunnermeier, M. K. (2003). Bubbles and crashes. Econometrica, 71(1), 173–204.
Baghestanian, S., Lugovskyy, V., & Puzzello, D. (2015). Traders heterogeneity and bubble-crash patterns in experimental asset markets. Journal of Economic Behavior & Organization, 117, 82–101.
Bloomfield, R., & Anderson, A. (2010). Behavioral finance: Investors, corporations, and markets. New York: Wiley.
Bosch-Rosa, C., Meissner, T., & Bosch i Domènech, A. (2015). Cognitive bubbles. Working paper.
Bossaerts, P., & Plott, C. (2002). The CAPM in thin experimental financial markets. Journal of Economic Dynamics and Control, 26(7–8), 1093–1112.
Bossaerts, P., & Plott, C. (2004). Basic principles of asset pricing theory: Evidence from large-scale experimental financial markets. Review of Finance, 8(2), 135–169.
Brunnermeier, M. K. (2008). Bubbles. In S. N. Durlauf & L. E. Blume (Eds.), The New Palgrave Dictonary of Economics (pp. 1221–1288). Elsevier.
Caginalp, G., & Ilieva, V. (2008). The dynamics of trader motivations in asset bubbles. Journal of Economic Behavior & Organization, 66(3), 641–656.
Camerer, C. F., Ho, T.-H., & Chong, J.-K. (2004). A cognitive hierarchy model of games. The Quarterly Journal of Economics, 119(3), 861–898.
Cheung, S. L., Hedegaard, M., & Palan, S. (2014). To see is to believe: Common expectations in experimental asset markets. European Economic Review, 66, 84–96.
De Long, J. B., Shleifer, A., Summers, L. H., & Waldmann, R. J. (1990a). Noise trader risk in financial markets. Journal of Political Economy, 98, 703–738.
De Long, J. B., Shleifer, A., Summers, L. H., & Waldmann, R. J. (1990b). Positive feedback investment strategies and destabilizing rational speculation. The Journal of Finance, 45(2), 379–395.
Dohmen, T., Falk, A., Huffman, D., Sunde, U., Schupp, J., & Wagner, W. (2007). Individual risk attitudes: New evidence from a large, representative, experimentally-validated survey (p. 1730). IZA Discussion Paper.
Dufwenberg, M., Lindqvist, T., & Moore, E. (2005). Bubbles and experience: An experiment. American Economic Review, 95, 1731–1737.
Eckel, C. C., & Füllbrunn, S. (2015). Thar SHE blows? Gender, competition, and bubbles in experimental asset markets. The American Economic Review, 105(2), 1–16.
Fama, E. F. (1970). Efficient capital markets: A review of theory and empirical work. The Journal of Finance, 25(2), 383–417.
Fama, E. F. (1991). Efficient capital markets: II. The Journal of Finance, 46(5), 1575–1617.
Fischbacher, U. (2007). z-Tree: Zurich toolbox for ready-made economic experiments. Experimental Economics, 10(2), 171–178.
Frederick, S. (2005). Cognitive reflection and decision making. Journal of Economic Perspectives, 19, 25–42.
Gill, D., Kissová, Z., Lee, J., & Prowse, V. (2017). First-place loving and last-place loathing: How rank in the distribution of performance affects effort provision. Management Science. https://doi.org/10.1287/mnsc.2017.2907
Greiner, B. (2004). The online recruitment system orsee 2.0-a guide for the organization of experiments in economics. Working Paper Series Economics, 10(23), 63–104.
Haruvy, E., & Noussair, C. N. (2006). The effect of short selling on bubbles and crashes in experimental spot asset markets. The Journal of Finance, 61(3), 1119–1157.
Haruvy, E., Lahav, Y., & Noussair, C. N. (2007). Traders’ expectations in asset markets: Experimental evidence. The American Economic Review, 97(5), 1901–1920.
Haruvy, E., Noussair, C. N., & Powell, O. (2014). The impact of asset repurchases and issues in an experimental market. Review of Finance, 18(2), 681–713.
Holt, C. A., & Laury, S. K. (2002). Risk aversion and incentive effects. American economic review, 92(5), 1644–1655.
Jehiel, P. (2005). Analogy-based expectation equilibrium. Journal of Economic Theory, 123(2), 81–104.
Kindleberger, C. P., & Aliber, R. Z. (2005). Manias, panics and crashes: A history of financial crises. New York: Wiley.
Kirchler, M., Huber, J., & Stöckl, T. (2012). Thar she bursts: Reducing confusion reduces bubbles. The American Economic Review, 102(2), 865–883.
Lei, V., Noussair, C. N., & Plott, C. R. (2001). Nonspeculative bubbles in experimental asset markets: Lack of common knowledge of rationality vs. actual irrationality. Econometrica, 69(4), 831–859.
Levine, S. S., Apfelbaum, E. P., Bernard, M., Bartelt, V. L., Zajac, E. J., & Stark, D. (2014). Ethnic diversity deflates price bubbles. Proceedings of the National Academy of Sciences, 111(52), 18524–18529.
McKelvey, R. D., & Palfrey, T. R. (1995). Quantal response equilibria for normal form games. Games and Economic Behavior, 10(1), 6–38.
Moinas, S., & Pouget, S. (2013). The bubble game: An experimental study of speculation. Econometrica, 81(4), 1507–1539.
Palan, S. (2013). A review of bubbles and crashes in experimental asset markets. Journal of Economic Surveys, 27(3), 570–588.
Palfrey, T. R., & Wang, S. W. (2012). Speculative overpricing in asset markets with information flows. Econometrica, 80(5), 1937–1976.
Plott, C. R. (1991). Will economics become an experimental science? Southern Economic Journal, 57, 901–919.
Plott, C. R., & Agha, G. (1983). Intertemporal speculation with a random demand in an experimental market. In R. Tietz (Ed.), Aspiration levels in bargaining and economic decision making. Lecture Notes in Economics and Mathematical Systems (No. 213, pp. 201–216). Berlin: Springer.
Powell, O., & Shestakova, N. (2016). Experimental asset markets: A survey of recent developments. Journal of Behavioral and Experimental Finance, 12, 14–22.
Powell, O. (2016). Numeraire independence and the measurement of mispricing in experimental asset markets. Journal of Behavioral and Experimental Finance, 9, 56–62.
Rogers, B. W., Palfrey, T. R., & Camerer, C. F. (2009). Heterogeneous quantal response equilibrium and cognitive hierarchies. Journal of Economic Theory, 144(4), 1440–1467.
Scherbina, A., & Schlusche, B. (2014). Asset price bubbles: A survey. Quantitative Finance, 14(4), 589–604.
Smith, V. L., Suchanek, G. L., & Williams, A. W. (1988). Bubbles, crashes, and endogenous expectations in experimental spot asset markets. Econometrica, 56(5), 1119–1151.
Stracca, L. (2004). Behavioral finance and asset prices: Where do we stand? Journal of Economic Psychology, 25(3), 373–405.
Acknowledgements
We thank Te Bao, Han Bleichrodt, Oege Dijk, Zhenxing Huang, Jürgen Huber, Michael Kirchler, Charles Noussair, Sophie Moinas, Stefan Palan, Jianying Qiu, Stephanie Rosenkranz, Stefan Trautmann, Stefan Zeisberger, seminar participants at the Radboud University, Universities of Utrecht, Innsbruck, as well as conference participants at the Experimental Finance Conference 2014 in Zurich and at the ESA Meeting 2014 in Fort Lauderdale for valuable comments. We are grateful to Achiel Fenneman for excellent research assistance. Financial support from the Institute for Management Research at Radboud University is gratefully acknowledged.
Author information
Authors and Affiliations
Corresponding author
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Janssen, DJ., Füllbrunn, S. & Weitzel, U. Individual speculative behavior and overpricing in experimental asset markets. Exp Econ 22, 653–675 (2019). https://doi.org/10.1007/s10683-018-9565-4
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10683-018-9565-4