Introduction

Population dynamics is directly related to the long-term persistence of species on all trophic levels (Inchausti and Halley 2003). Therefore, understanding the role and relative impact of various extrinsic and intrinsic factors in population regulation has been in the focus of population ecology for many decades (Bjørnstad and Grenfell 2001; Myers et al. 2018). Seminal papers in the early Twenteeth century (Lotka 1925; Volterra 1926; Nicholson and Bailey 1935) have shown that predator–prey systems have an inherent tendency to oscillate and ever since numerous studies have scrutinized the possible causes and consequences of both cyclic and non-cyclic fluctuations in the abundance of prey and predator species (Millon and Bretagnolle 2008; Row et al. 2014; Myers et al. 2018; Oli 2019). While predation is the most supported extrinsic factor to explain characteristic features of prey population cycles by both field experiments and modelling studies (e.g., Hanski et al. 2001; Gilg et al. 2003; Krebs et al. 2018), evidence suggests that in many cases a single factor, such as predation alone, cannot generate the observed fluctuating patterns in prey population size (e.g., Moss and Watson 2001; Oli 2003; Andreassen et al. 2020). By synthetizing empirical data on small mammals, for instance, Andreassen et al. (2013) proposed that vole population cycles are likely to be shaped by the joint effects of predation, dispersal behaviour and social organization. In line with that, mathematical simulations described cycle lengths, amplitudes and autumn population sizes closest to what can be observed in nature when all three parameters were included into the model (Radchuk et al. 2016). Although the ‘behavioural polymorphism hypothesis’ (Chitty 1967) has been rejected as a sole explanation for the emergence of population cycles (Krebs 2013), social interactions among prey individuals have been proposed to shape cyclic population dynamics in other taxa as well (e.g., Martínez-Padilla et al. 2014). As inducing delay in population cycles experimentally or stopping cyclic fluctuations in natural populations of most study species is unfeasible (but attempted in the past; e.g., Myers 1990; Myers and Cory 2016), adopting a relevant modelling approach may give the necessary insight about the role of specific individual-level interactions and variation within those interactions in the emergence and persistence of population fluctuations.

Inadvertent social information and population dynamics

The presence, behaviour or product of the behaviour of other organisms often serve as social cues to conspecific or heterospecific observers, conveying inadvertent social information (ISI) that may be utilized adaptively during decision-making (Danchin et al. 2004). Our understanding of how social information can modulate population growth and influence species interactions has greatly increased in recent years (Parejo and Avilés 2016; Kane and Kendall 2017; Gil et al. 2017, 2018, 2019). As a result, predator avoidance is now considered one of those ecological contexts in which individuals are expected to generally respond to social cues produced by others in many terrestrial and aquatic systems (Gil et al. 2017). Building on the classical logistic growth model, Gil et al. (2018) showed that social information use could alter both quantitative and qualitative dynamics of populations, affecting realized carrying capacity and population persistence when predation rate is high relative to population growth. Gil et al. (2019) also proved that the simple use of social information by individuals (e.g., originating either from evolved signals or inadvertently produced cues) can have positive effects on per capita population growth, raising equilibrium population sizes and allowing persistence of populations (with Allee effects) when predation or interspecific competition would otherwise drive the population to extinction. Furthermore, the authors proved that social information use has the potential to facilitate the coexistence of competing populations or species, depending on the relative strength of the production of social information and competition between interacting individuals. However, none of these theoretical studies accounted for the stochastic variation among individuals in the acquisition and use of social information, important features that are expected to be prevalent in many animal species, or investigated how characteristics of population fluctuations may change due to ISI use.

Inadvertent social information use in non-grouping animals

Recent evidence challenges the view that ISI use is confined to animals living in cohesive groups (i.e. permanent or periodical group formations, in which animals exhibit social attraction toward other group-members, thus actively seek and maintain close spatial proximity) and indicate that non-grouping organisms (individuals that may aggregate or form temporary groups under specific abiotic environmental conditions, but do not show attraction to conspecifics) can respond (and thus might benefit by paying attention) to inadvertent social information as well. In the context of predator avoidance, for instance, Coolen et al. (2005) studied the use and diffusion of ISI in wild-caught wood crickets (Nemobius sylvestris). The authors showed that naïve individuals adjusted their behaviour to the presence of wolf spiders after having observed the predator avoidance behaviour of knowledgeable conspecifics. These changes were also found to last even after the removal of demonstrators and could modify the behaviour of other naïve crickets, too. In several non-social mammals, individuals were also shown to use the alarm calls of sympatric species as social cues to adjust their behaviour to predation risk (e.g. Randler 2006; Lea et al. 2008; Trefry & Hik 2009). Such findings, in line with the predictions of the above models, also imply that responding adaptively to social stimuli about predation risk, i.e. behavioural or positional cues originating from conspecific or heterospecific individuals, may be taxonomically widespread and, similarly to the utilization of other biotic or abiotic cues in the environment, not strongly associated with sociality or living in cohesive groups.

Despite the growing number of studies providing evidence for ISI use in non-grouping animals (also in foraging context; e.g. Webster and Laland 2017; Gil and Hein 2017; Martinez et al. 2018), its occurrence is generally thought to be incidental and thus its potential effect on population dynamics and species interactions remained unexplored. However, many non-grouping animals are likely to be exposed to social stimuli (e.g. at patchily distributed resources) at certain times (Krause and Ruxton 2002) and may interact not only via direct encounters, but also indirectly in a variety of ways (e.g. auditory, chemosensory, electrosensory, etc.), all of which may facilitate the acquisition of social information. Recent findings also suggest that those species that are capable of detecting predictive relationships between events in their environment are capable of using socially acquired information as well (Heyes 2012, 2016; Heyes and Pearce 2015). If social cues are as any other predictive environmental cues, all observers present within the range of the relevant sensory perception can have the opportunity to exploit those cues (although might not necessarily do so). Simple mechanisms, e.g. relative differences in activity and associated conspicuousness among aggregating individuals or spatial changes in acoustic cues over time may then provide dynamic information about predation threat for nearby conspecifics (as implied in Chivers and Ferrari 2014; Magrath et al. 2014). Such behavioural adjustments to social cues, coupled with the sufficiently high local or temporary population density (e.g. the natural density of wood crickets is estimated to be 120 individuals per m2; Coolen et al. 2005), may exert a yet unrecognized effect on population dynamics of non-grouping animals as well.

Testing the effect of ISI use on predator–prey dynamics: a simulation study

To illustrate what population-level behaviours may emerge from the interactions among non-grouping prey individuals with each other and with their biotic and abiotic environment, I built individual-based models in a factorial design yielding four model types: no predation, predation only, predation and predator detection ability in prey and predation and both predator detection ability and ISI use in prey. While the constructed models are tentative, they generated projections that closely mirror self-limited population growth in the absence of predators (M1; model 1) and were in line with the expectations of oscillating predator–prey dynamics when predators are present but prey do not exhibit predator avoidance behaviour (M2; model 2). Because of that, they have the potential to provide important first insights about how incorporating relevant extrinsic and/or intrinsic factors alters the predictions of classical population models.

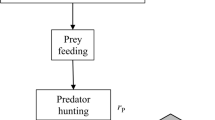
During simulations, both predator and prey moved randomly on a landscape consisting of 30 × 30 grid cells. At the landscape edge, individuals changed their movement direction and moved back toward the centre by one cell in the case of prey and by either one or two cells in the case of predators (randomly chosen for each predator that would have crossed the edge). At the start of a simulation cycle, 200 prey and 50 predators were randomly placed on the grid and then individuals performed a given set of behaviours depending on the model type in each cycle. The order of appearance within a cycle and a detailed description of these behaviours are shown in Fig. 1 and Table 1. The models assumed that only one individual could survive per cell (both prey and predators) at the end of a cycle, introducing density-dependent mortality to their population dynamics, thus landscape cells represented the carrying capacity of the environment. In M1, predators were absent, only prey moved, fed, reproduced and competed in the simulated landscape. In M2, predators were present and could consume any prey (maximum two preys per predator) within their detection range (i.e. at a one-step distance from the predator’s position in any direction). In M3 (model 3), prey had the ability to detect predators in adjacent grid cells with a 50% success rate. Prey feeding always occurred once per time step as long as the prey was not alarmed. Alarmed prey were immune to predation, but did not feed and consequently lost their opportunity to reproduce in that cycle. In M4 (model 4), prey could detect predators either directly (as in M3) or by observing alarmed conspecifics nearby with a 50% success rate; both had the same negative consequence on reproduction and positive effect on predator avoidance. Extinction events occurred only in M2 models (1.5% of iterations; these time series were discarded from later comparisons), while none were observed in other model types with the applied parameter settings (Table 1).

Fig. 1
figure 1

A flow diagram depicting sequential prey and predator behaviour during a simulation cycle in the four model types. Description of each behaviour is shown in Table 1

Full size image
Table 1 Parameters of the constructed models in the order as they appeared in the simulation cycles. M1 (model 1) is the model in which no predators were present (i.e. prey abundance fluctuating around carrying capacity imposed by competition-related mortality). M2 (model 2) denotes the model in which predation occurred without the prey being able to detect predators. M3 (model 3) is the model in which prey could detect predators and avoid predation, whereas in M4 (model 4) prey could both detect predators and use inadvertent social information from nearby conspecifics to avoid predation. “X” indicates those behaviours that were included into simulations for a given model type. Detection range was defined as a one-step distance from an individual’s position in any direction (in both predator and prey)
Full size table

I run the population simulations for each model type 200 times (iterations) for 350 cycles. The first 100 simulation cycles were discarded as burn-in. Overall predator and prey population sizes were characterized by calculating the mean, standard deviation, minimum and maximum values from the remaining simulation cycles for each time series. Periodicity was determined by spectral analysis using the ‘peacots’ R package (Louca and Doebeli 2015). The Lomb-Scargle periodogram of each time series was calculated to determine period length and the statistical significance of the periodogram maximum was estimated based on the null hypothesis of an Ornstein–Uhlenbeck state space (OUSS) process. The OUSS model is regarded as a more adequate null hypothesis than white noise for cycle detection in ecosystems with non-negligible correlation times. Amplitude was calculated as the maximum difference between local maxima and subsequent local minima (i.e. the highest and the lowest population size within a 6-cycle moving window) in each time series. Partial autocorrelation function (PACF; Box and Jenkins 1976) was used to investigate if there was a negative feedback of the second order that would imply interaction between the predator and prey populations (in either direction). Significance of PACF [2] coefficients was assessed by Bartlett’s criterion (Berryman and Turchin 2001; Berryman and Lima 2007). All simulations and calculations were performed in R 3.6.1 (R Core Team 2019). R script for model construction and simulation outputs are available at Figshare (https://doi.org/10.6084/m9.figshare.13013306.v1).

Simulation results and discussion

In the lack of predation model (M1), prey populations were characterized by high mean population size with low-variation random fluctuations around the realized carrying capacity of the simulated landscape (Table 2, Fig. 2a). This realized carrying capacity was lower than the total number of grid cells, however, since the maximum number of individuals (778.9 ± 4.34) never reached that theoretical plateau value. As expected, periodicity and second-order density dependence were detected only in 3.5 and 4% of these populations, respectively. When predators were added to the model (M2), predation-induced mortality generated high-amplitude cyclic fluctuations in the prey populations (i.e., periodicity was significant in 99% of the simulation runs), which, in turn, caused a similar pattern in the predator populations as well (Table 2, Fig. 2b). Due to effective hunting (i.e., hunting was always successful if any prey was located within the detection range of predators), the mean population size of prey nearly halved compared to the previous scenario (387.35 ± 14.6 vs. 749.84 ± 0. 94). Second order density dependence was detected in both directions, indicating that predators and prey were involved in feedback control of each other’s population density (Fig. 3). Thus, the trophic interaction between predator and prey individuals generated cyclic patterns that closely resemble the classical Lotka-Volterra predator–prey dynamics and are similar to some examples of cyclic population fluctuations observed in nature (e.g., Millon and Bretagnolle 2008). When the ability of predator detection was also included into the model (M3), periodicity in prey populations became less pronounced (but 81.5% of prey populations could still be characterized by a typical period length), while amplitude decreased and minimum prey population size increased drastically compared to the previous scenario (292.94 ± 52.58 vs. 499.36 ± 66.49 and 276.29 ± 26.36 vs. 103.05 ± 29.17, respectively; Fig. 2c). As the predator detection ability was not perfect and successful detection was directly linked to a fitness cost (i.e., missed opportunity of reproduction), mean prey population size did not increase substantially in comparison to the M2 outputs (451.55 ± 7.8 vs. 387.35 ± 14.6). On the other hand, mean predator population size decreased remarkably due to lower hunting success (and consequently higher starvation-related mortality), but the extent of fluctuation in predator population size was also considerably lower than in the previous scenario. Nevertheless, second-order density dependence was still detectable in both directions resulting from the trophic interaction between the two species (Fig. 3). When ISI use in prey was also added to the model (M4), fluctuations in population sizes became non-cyclic in 75% and 84% of simulation runs in prey and predator populations, respectively (Fig. 2d). Mean population size decreased further in the predator populations, while standard deviation in population sizes diminished further in both prey and predator populations compared to the M3 outputs. This finding indicates that ISI use in prey stabilized the investigated predator–prey dynamics at lower predator population sizes compared to previous scenarios with the presence of predators (Fig. 3). In previous works, social information was already shown to contribute to the persistence of prey populations in the face of high predation risk (e.g., Gil et al. 2018). The above results complement these predictions by indicating that ISI use related to predator avoidance may also alter temporal fluctuations in prey populations and disrupt cyclic patterns even if information diffusion takes place at a moderate rate. While second-order density dependence in prey was still present in 100% of the simulated populations, the strength of correlation between predator and prey population sizes decreased further compared to the M3 scenario. Moreover, prey did not play a role in the population regulation of predators in 16% of the simulation runs. These results suggest that ISI use in prey may alter the strength of dependence between predator and prey populations, too.

Table 2 Descriptive metrics (mean ± SD) in the four model types. Statistical significance of the period length reflects the probability that the estimated OUSS process would generate a periodogram with global maximum at least as “extreme” as the observed peak in given time series. I used Bartlett’s criterion (± 2/√n, where n is the number of observations) to assess the significance of PACF [2] correlation coefficients (Berryman and Turchin 2001; Berryman and Lima 2007)
Full size table
Fig. 2
figure 2

Temporal fluctuations in the abundance of a randomly chosen replicate population for each model type (a: M1, b: M2, c: M3, d: M4). Black lines in all panels indicate prey population sizes, while red lines in the b, c and d panels show corresponding predator population sizes. The first 100 iterations were discarded as burn-in from the calculation of descriptive metrics

Full size image
Fig. 3
figure 3

Three types of predator–prey dynamics superimposed on one another as coordinates in phase-space. Green circles represent large-amplitude cycles from a M2 time series, where predation occurred without the prey being able to detect predators. Blue circles denotes mid-amplitude fluctuations from a M3 time series, where prey could detect nearby predators and modify their behaviour accordingly. Orange circles represent small-amplitude cycles from a M4 time series, where both predator detection and ISI use related to predation threat in prey were incorporated into the model

Full size image

Simulations clearly showed that the ability of predator detection and exhibition of adaptive predator avoidance behaviour led to reduced predator population sizes, most probably due to a substantial decrease in predation success (predators died due to starvation if hunting was unsuccessful in the models). ISI use was found to further strengthen this effect, because even if it occurred only with a 50% success rate, the probability of encountering another prey individual from which social information could be acquired was higher (due to the higher abundance of prey) than the chance of encountering a predator and detecting its presence with a similar 50% success rate. The imperfect detection of predators and ISI use together increased prey survival and reduced predation-induced fluctuations in population size. Alarmed prey individuals forfeited reproduction in a given simulation cycle and retained the opportunity to reproduce subsequently in the absence of (detected) predation threat. Because of that, these model parameters only moderately affected mean prey population size, but contributed to the stabilization of predator populations at lower mean population sizes (compared to those of the M2 models). It is important to note that this effect of ISI use was observed despite the stochastic variation in prey movement and the lack of social attraction toward conspecifics; high mortality due to competition also prevented the formation of stable aggregations that could have facilitated social information use. In recent studies, either the possibility of group formation was incorporated into the modelling framework (e.g., Gil et al. 2017) or the spatial distribution of individuals was not taken explicitly into account (e.g., Gil et al. 2018, 2019). The presented results thus supplement the findings of previous works by confirming that prey individuals may facilitate predator avoidance in their population through the provision of social information even if that information is incidentally acquired from randomly moving conspecifics. Consequently, ISI use can have an influential role in shaping predator–prey dynamics in non-grouping species as well.

I made several simplifying assumptions that potentially limit the generality of the above findings. Model assumptions included the presence of reflecting landscape edges, which is appropriate in species that cannot leave their habitat patch easily or at will, e.g. many pond-living aquatic organisms or terrestrial species that live in spatially or temporarily isolated habitat patches. When simulations were run on a landscape with wrapped edges (i.e., individuals moved to the opposite side of the landscape when crossing a boundary and continued moving), however, I obtained results qualitatively identical to the presented ones. This indicates that the simulation outcomes were robust against this parameter setting (Table S1). The assumption of forfeited feeding in alarmed prey was incorporated into the models based on the phenomena of non-consumptive effects (NCE) of predators, i.e. costly consequences of antipredator behaviour in prey (Preisser et al. 2007), which can take, among others, the form of reduced feeding rates. Such effects are known to shape prey population dynamics in a wide range of taxa and may have ultimately greater impact on prey populations than consumption itself (Peckarsky et al. 2008). The quantification of NCEs in most predator–prey system is still lacking, however (Gehr et al. 2018), so more exact parametrization in this regard is possible only for a limited number of cases. If ISI use decreases predation success, one may also expect the counter-evolution of behavioural (e.g., Falk et al. 2015), morphological (e.g., Wilson et al. 2018) and/or physiological changes (e.g., Brodie et al. 2005) in predators that oppose ISI use in prey in natural predator–prey systems. The possibility of predator evolutionary response was not incorporated into the models, but considering such predator–prey coevolution might have profound effects on the dynamics of simulated populations like reversing of the ordering of peaks in the predator–prey cycles (Cortez and Weitz 2014). Parameter values of movement distances, predation success, predator detection rate and its fitness cost and acquisition rate of ISI were also specified arbitrary in this study. In future works, fine-tuning these parameters will help to test the extent of deviations in the applied parameter settings that could invalidate the conclusions drawn.

Conclusion

The main purpose of this study was to draw attention to the possibility that (1) ISI use have the potential to alter predator–prey population dynamics and (2) such effects may be prevalent in non-grouping species as well. Although the influence of the included model parameters were not tested here (i.e., how the outcomes of these models change in response to changes in the parameters), simulation results proved that ISI use may disrupt population cycles and stabilize predator–prey dynamics, facilitating their long-term coexistence (similarly to the findings of previous models; e.g., Gil et al. 2017, 2018, 2019). While encounter rate of social cues may be limited in some non-grouping animals, temporary abundance may be sufficiently high in others for effective information diffusion at high value resource locations or in densely populated habitats. Moreover, social cues are not limited to originating from conspecific individuals of the same population, but heterospecifics can also provide relevant social information for non-grouping observers if they exploit the same resources or are threatened by the same predators (Goodale et al. 2010; Magrath et al. 2015; Sridhar and Guttal 2018). I do not propose that predator avoidance behaviour and associated ISI use could explain the generality of non-cyclic fluctuations in animal populations (e.g., Louca and Doebeli 2015). However, if social cues are indeed used as common source of information in animals (independently of the existence or complexity of a prevalent social structure), then similar social information-mediated effects on interspecific interactions and population dynamics may be more general in natural communities than we previously thought.