Introduction

Hulled emmer (Triticum turgidum subsp. dicoccum) was the main wheat of Old World agriculture in the Neolithic and early Bronze Age. The tetraploid (2n = 4x = 28 chromosomes) emmer wheat is a descendant of subsp. dicoccoides, the wild emmer wheat (Weiss and Zohary 2011). According to archaeological evidence, wild emmer was one of the first crops cultivated in the southern Levant (10,300–9,500 BP; uncalibrated) (Feldman and Kislev 2007). Domesticated emmer characterised by non-brittle ears appeared several hundred years later (9,500–9,000 BP), and was grown mixed with wild emmer in many Levantine sites for a millennium or more. This paved the way for spontaneous hybridizations resulting in a high phenotypic variation of this crop. Due to this wide genetic base and the large geographical area of cultivation in the Fertile Crescent (Levant, SE Turkey, Iraq, Iran), many tolerances to biotic and abiotic stresses can be expected in emmer wheat.

Among the worldwide most important pathogens in wheat are the biotrophic fungi yellow rust (YR) or stripe rust (Puccinia striiformis f.sp. tritici), powdery mildew (PM) (Blumeria graminis f.sp. tritici), and the hemi-biotrophic fungus Zymoseptoria tritici (teleomorph: Mycosphaerella graminicola) causing Septoria tritici blotch (STB). According to a recent review, these three diseases cause 2.1%, 1.1%, and 2.4% yield reduction in wheat globally (Savary et al. 2019). Only leaf rust and Fusarium head blight cause higher losses.

YR was in previous times only episodically a problem for wheat, but became increasingly important in Europe since 2011 due to the wide distribution of the aggressive Warrior race originating from the Himalayan region (Hovmøller et al. 2016). The Warrior race (named PstS7) took over the European YR population within the year 2012 and has more virulence genes than previous European races. Two years later, a descendant of the Warrior race (namely PstS10, Warrior (–)) got predominant in Europe (see SFig. 1, GRRC 2023). Race composition of PM has not been analysed in the last decades, but the pathogen is ubiquitous in all major wheat growing areas. Similarly, STB is now reported in most wheat-growing regions and causes significant damage. Approximately 70% of the fungicides used in Europe are sprayed for preventing Z. tritici epidemics (Torriani et al. 2015).

The situation of variety resistance for YR and PM is similar. Mainly race-specific resistances are used that are acting during the whole lifetime of the plant (all-stage resistances, ASR), but are not durable in most instances. A few genes are restricted in their action to adult plants conferring a partially expressed, non-race specific resistance with higher durability (adult-plant resistance, APR). More than 100 PM resistance genes or alleles mapping to 63 different loci (Pm1-Pm68) have been identified from common wheat and its relatives (Mapuranga et al. 2022). Accordingly, 84 permanently and 100 temporarily designated stripe rust resistance genes have been reported in different hexaploid bread wheat, durum wheat, and wild species backgrounds (McIntosh et al. 2022). For STB, 22 major genes (named Stb) have been mapped that contribute to qualitative resistance (Saintenac et al. 2021).

Additionally, quantitative resistances are available for all three diseases that are non-race specific conferring a reduced pathogen development but are prone to high environmental variation and comprise mainly adult-plant resistances. To date, 363 quantitative trait loci (QTLs) with different names are known for YR (McIntosh et al. 2022) and over 100 QTLs for PM (Rana et al. 2022). Also, for STB, 126 QTLs were described in a meta-analysis (Saini et al. 2022). Typically, these QTLs have a minor to moderate effect on resistance and are scattered across the whole genome.

YR and PM have evolved as primary plant pathogens in Southwest Asia in the same region where the diploid and tetraploid wheats developed (Nevo et al. 2013). In Iran, a sister species of Z. tritici has been found infecting wild grasses (Stukenbrock et al. 2007). The timing and similar geographical origin of the three pathogens and wild wheats strongly suggest a common co-evolution resulting in resistance mechanisms on host side. Indeed, wild emmer harbors many resistance genes against PM and the three wheat rusts including YR (for review see Nevo 2014). Several major genes for stripe rust resistance were recently detected in wild emmer wheat (Tene et al. 2022), some of them were already transferred into domesticated wheat, including Yr15, Yr35, Yr36, Yr-SM139, and additional ASR and APR genes (Elkot et al. 2021). Because cultivated emmer is a direct descendant of wild emmer, many resistance genes and QTLs should also be present in the cultivated species (Liu et al. 2017a), but studies investigating larger sets of domesticated emmer cultivars are yet lacking. A large genetic variation for YR resistance was uncovered by molecular means in the closely-related durum wheats of European (Liu et al. 2017b; Miedaner et al. 2019), Canadian (Singh et al. 2013), and Ethiopian (Alemu et al. 2021; Liu et al. 2017c) origin. Because monogenic resistances for all three diseases are notoriously instable due to the highly flexible adaptation of the pathogen populations, the use of quantitative resistance in breeding is recommended (Miedaner et al. 2013). This strategy involves many genes (QTLs) and is best followed by genomic selection. This method applies high-density marker chips to large breeding populations with the aim to predict the phenotype by its genomic composition and to test only the genomically selected entries in the field (Poland and Rutkoski 2016). In contrast to marker-assisted selection (MAS), where each QTL is selected independently, the use of whole-genome prediction has a greater power to capture small-effect loci that would be missed by MAS. Because we have no possibility in this project for a selection experiment, we performed genomic prediction with the available data, instead.

Therefore, our main objectives were (1) to analyze the phenotypic variation for resistances to YR, PM, and STB, (2) to perform a genome-wide association study (GWAS) to uncover the inheritance of these resistances, (3) to evaluate the prospects of genomic prediction, and (4) to search for QTLs controlling multiple disease resistances among 143 emmer genotypes.

Materials and methods

Plant material and field trials

The plant material consisted of 143 genotypes of winter emmer, two bread wheat (Julius, Genius), two spelt (Franckenkorn, Zollernspelz), two winter durum (Wintergold, Sambadur), and one einkorn genotype (Terzino). All genotypes were evaluated in growing seasons 2018/19 and 2019/20 in Germany at up to five environments (year x location combinations) (Table 1): Hohenheim (HOH) near Stuttgart in 2019 and 2020, Oberer Lindenhof (OLI) near Reutlingen in 2019 and 2020, and Rosenthal (ROS) near Peine in 2020. Growth regulators and fungicides were not used. Trials were laid in an alpha-lattice design with two replicates as double rows in plots of 1m2 size. Yield data were available from trials at five environments: HOH 2019 and 2020, OLI in 2020 and in 2019 additionally Schwäbisch Hall and Rastatt. Yield trials were laid in an augmented design in plots of > 5m2 size. Herbicides, growth regulator and fungicides were here used as locally recommended. Nitrogen fertilization was 65% lower than in bread wheat. Sowing was done mechanically in all trials.

Table 1 Mean disease severity scorings (BLUEs, 1–9) in individual environments with natural infection
Full size table

No artificial inoculation to induce diseases was done. Therefore, data on disease severity were recorded based on the natural occurrence of diseases in four environments for YR, two environments for PM, and five environments for STB. The race composition of YR in Germany was analysed by checking 50 and 59 isolates in the experimental years 2019 and 2020, respectively, at the Julius-Kühn-Institute, Federal Research Centre for Cultivated Plants, Institute for Plant Protection in Field Crops and Grassland in Kleinmachnow (GRRC 2023, SFig. 1). In 2019, Warrior(–), Triticale2015, and Warrior were the most frequently detected races, where Warrior(–) accounted for 60% of the samples, while in 2020, for the first time, Warrior(–) could be distinguished into the subraces Kalmar, Amboise, and Benchmark, which together increased to a frequency of 77%. The occurrence of Triticale2015 remained relatively constant, the original Warrior race was not detected any more. The race composition of PM is unknown. The scores for disease resistances were measured on a scale ranging from 1 to 9, where 1 denotes no visible disease and 9 the highest susceptibility to disease. Heading date was evaluated as the number of days from Jan. 1, when 50% of the heads of a plot were visible. Plant height (cm) was measured from the soil surface to the end of the spike of the main tillers once per plot. Heading date and plant height were recorded at four environments namely HOH19, OLI19, HOH20, and ROS20. Raw yield is the total yield including hulls, grain yield is from the de-hulled crop.

Phenotypic data analysis

For all traits except STB, a classical single-stage analysis was performed. Since, STB was recorded at environments with different experimental designs, a two-stage procedure was adapted for its phenotypic analysis.

On the first stage, used only for STB, evaluation of the single locations was performed. The mixed models given in Eqs. 1a and 1b were used for augmented design and alpha design, respectively:

$${\text{y}}_{{{\text{ik}}}} = {\text{u}} + {\text{g}}_{{\text{i}}} + {\text{b}}_{{\text{k}}} + {e }_{{{\text{ik}}}} ,$$
(1a)

where \(y_{ik}\) is the phenotypic observation for the ith genotype in the kth incomplete block, \(u\) is the general mean, \(g_{i}\) the genotypic effect of the ith genotype, \(b_{k}\) is the effect of the kth incomplete block, and \(e_{ik}\) is the residual.

$${\text{y}}_{{{\text{ijk}}}} = {\text{u}} + {\text{g}}_{{\text{i}}} + {\text{rep}}_{{\text{j}}} + {\text{b}}_{{{\text{jk}}}} + {e }_{{{\text{ijk}}}}$$
(1b)

where \(y_{ijk}\) is the phenotypic observation for the ith genotype in the jth replicate in the kth incomplete block, \(u\) is the general mean, \(g_{i}\) the genotypic effect of the ith genotype, \(rep_{j}\) the effect of the jth replicate, \(b_{jk}\) is the effect of the kth incomplete block of the jth replicate, and \(e_{ijk}\) is the residual.

For the estimates for the second stage of a two-stage analysis, the genotype main effect \(g_{i}\) was assumed as fixed effect to obtain best linear unbiased estimates (BLUEs) (\(\overline{y}_{i}\)) and their approximated variance–covariance matrix (\(\hat{V}\)) in models 1a and 1b. Thus, separate analyses and separate effect estimates were obtained for each environment. Finally, estimates forwarded to the second stage were indexed by environment \(k\) (\(\overline{y}_{ik} , \hat{V}_{k} )\).

A weighting method in the context of two-stage analysis can be useful to approximate the variance–covariance structure of adjusted means and hence slightly improve the analysis (Möhring and Piepho 2009). We used Smith’s weights (Damesa et al. 2017; Smith et al. 2001, 2005) obtained as the diagonal elements of the inverse of \(\hat{V}_{k}\), which is the variance–covariance matrix of adjusted means of the genotypes from first stage.

For the serial of trials, the mixed model given in Eq. (2a) was implemented in the second stage for STB:

$$\overline{y}_{ik} = \mu + g_{i} + env_{k} + g_{i} :env_{k} + \overline{e}_{ik} ,$$
(2a)

where \(\overline{y}_{ik}\) is the BLUE of the \(i\) th genotype in the \(k\) th environment obtained in the first stage, \(\mu\) is the general mean, \(g_{i}\) is the main effect of the \(i\) th genotype, \(env_{k}\) is the main effect of the \(k\) th environment, \(g_{i} :env_{k}\) is the genotype-by-environment interaction, and \(\overline{e}_{ik}\) is the error of the mean \(\overline{y}_{ik}\) obtained in the first stage.

For all traits except STB, the series of trials was analysed, according to the mixed model given in Eq. (2b):

$$y_{ikno} = u + g_{i} + env_{k} + g_{i} :env_{k} + rep_{kn} + b_{kno} + e_{ikno} ,$$
(2b)

where \(y_{ikno}\) is the phenotypic observation for the ith genotype tested in the kth environment in the nth replication in the oth incomplete block, \(u\) is the general mean, \(g_{i}\) the genotypic effect of the ith genotype, \(env_{k}\) the effect of the kth environment, \(g_{i} :env_{k}\) was the genotype-by-environment interaction, \(rep_{kn}\) is the effect of the nth replication in the kth environment, \(b_{kno}\) is the effect of the oth incomplete block of the nth replication in the kth environment, and \(e_{ikno}\) was the residual.

In models 2a and 2b, for estimating BLUEs, all effects except \(g_{i}\) were assumed as random and for obtaining variance components, all effects were assumed as random. Variance components were estimated using the restricted maximum likelihood (REML) method assuming a random model (Cochran and Cox 1957). A likelihood ratio test with model comparisons was performed to test the significance of the variance components (Stram and Lee 1994).

For all traits, the broad sense heritability (h2) across the series of trials was estimated as given in Eq. (3):

$$h^{2} = 1 - \frac{\vartheta }{{2\sigma_{G}^{2} }} ,$$
(3)

where ϑ is the mean variance of a difference of two best linear unbiased predictors (BLUPs) and \(\sigma_{G}^{2}\) the genotypic variance (Piepho and Möhring 2007). Pearson’s correlation coefficients (\(r_{p}\)) were estimated among BLUEs of the examined traits. All analyses were performed utilizing the statistical software R (R Core Team 2018) and the software ASReml 3.0 (Gilmour et al. 2009).

Genotypic and molecular analysis

Molecular markers

The diversity panel containing 143 emmer genotypes was genotyped by genotyping-by-sequencing (GBS) at Diversity Arrays Technology (Yarraluma, Australia) (Li et al. 2015). The dominant silico-DArTs and the co-dominant single nucleotide polymorphism (SNP) markers were denoted by their clone ID with a suffix ‘D’ or ‘S’ corresponding to the marker type – DArTs or SNPs, respectively. Markers with more than 20% missing data across the diversity panel or a minor allele frequency (MAF) lower than 5% were removed from the initial marker set using PLINK (Purcell et al. 2007). Separately for DArTs and SNPs, the missing values were imputed using LinkImpute, a software package based on a k-nearest neighbor genotype imputation method, LD-kNNi (Money et al. 2015). The PLINK and LinkImpute were executed using statistical software R (R Core Team 2018). The imputation accuracy was 97% and 95% for DArTs and SNPs, respectively. The accuracy of imputation is the proportion of masked known genotypes (default = 10,000) that were correctly imputed (Money et al. 2015). Both types of markers were combined into one dataset. Markers with MAF lower than 5% were discarded again after the imputation, resulting in 67,605 markers. Of them 35,747 markers had a known map position on the reference genome assembly of Triticum dicoccoides—Wild Emmer Wheat Zavitan WEWSeq v2.1 (Zhu et al. 2019).

Population structure

Relationships among the 143 genotypes were analyzed by implementing principal coordinate analysis based on the Rogers distance (Rogers 1972), which was computed using genome-wide markers in R package “poppr”. The function cmdscale of base R was used to calculate principal coordinates based on Rogers distance (SFig. 2). The principal coordinate analysis revealed two major groups, i.e., one group consisted of 24 genotypes where 20 genotypes originated from the German gene bank in Gatersleben (Leibniz Institute of Plant Genetics and Crop Plant Research, IPK, 06466 Seeland, OT Gatersleben, Germany) while the other group consisted of all other genotypes including genotypes from the German gene bank. This grouping has been considered in this study by fitting the first and second principal coordinates as covariate variables in the model.

Association mapping

Association mapping was conducted by using “Bayesian-information and Linkage-disequilibrium Iteratively Nested Keyway (BLINK)” method (Huang et al. 2019) implemented in the GAPIT R package (Lipka et al. 2012; Wang and Zhang 2021). BLINK is a statistically powerful and computationally efficient algorithm, which produces fewer false positives and identifies more true positives than the most recently developed GWAS method, FarmCPU (Liu et al. 2016). In addition, BLINK does not require quantitative trait nucleotides (QTNs) to be evenly distributed throughout the genome, whereas FarmCPU does, thus BLINK eliminates the unrealistic assumption (Huang et al. 2019). The first two principal coordinates were fitted as covariate variables to reduce the false positives due to population stratification. For association mapping, we used BLUEs of traits calculated across all environments, and 35,747 markers with known map coordinates on WEWSeq v2.1.

A P value < 0.05 corrected according to Hochberg and Benjamini was considered as the significance threshold and was used to identify significant marker-trait associations (MTAs). The sequences of the significant MTAs for YR, PM, and STB are provided in Supplementary Table S1. The proportion of phenotypic variance explained by the QTLs was estimated by fitting the significant markers in linear models jointly in the order of strength of their association (lower the P value, higher the strength of association) (Würschum et al. 2015). For additive genetic model, marker information was coded as 0, 1, 2, where 0 and 2 are the two homozygous (DArTs and SNPs) and 1 the heterozygous genotypes (SNPs). The total proportion of explained phenotypic variance (R2) was calculated as:

$$R_{adj}^{2} = R_{adj}^{2} \times 100,$$

where \(R_{adj}^{2}\) is the adjusted coefficient of determination of the linear model (Würschum et al. 2015). The phenotypic variance explained by individual significant markers (\(R_{m}^{2}\)) was calculated as:

$$R_{m}^{2} = \left( { \frac{{SS_{m} }}{{ss_{total} }} } \right) \times 100,$$

where \(SS_{m}\) is the sum of squares for the marker m and \(s{s}_{total}\) is total sum of squares of all markers fitted in a linear model. The allele substitution effect of each significant marker was derived as the regression coefficient from the linear model with only the respective marker under consideration.

To visualize the differences in disease severity between different groups of genotypes based on the allelic state of a given molecular marker, we produced the box plots. Due to the unequal number of genotypes in different groups, we opted to use the ad-hoc method of notches, which displays the confidence interval around the median. If the notches of two boxes do not overlap, there is a strong evidence (95% confidence) that their medians differ (Chambers et al. 1985).

Candidate gene identification

The genes possibly controlling the phenotype were searched in the publicly available gene files for reference genome WEWseq_PGSB_v1 of Triticum dicoccoides—Wild Emmer Wheat Zavitan (https://wheat.pw.usda.gov/GG3/node/909). Using customized R script, only high-confidence genes were retrieved for the markers that explained ≥ 5% phenotypic variance. Descriptions and IDs of genes within 3 Mbp up or downstream of the marker position were searched for genes with relevance to disease resistances.

Genomic prediction

The potential of the application of genomic selection for YR, PM, and STB was explored using two genomic prediction models – ridge regression best linear unbiased prediction (rrBLUP) and weighted ridge regression best linear unbiased prediction (w-rrBLUP), implemented using R package rrBLUP (Endelman 2011; Endelman and Jannink 2012). In w-rrBLUP approach, the QTLs, which individually explained ≥ 9% of the phenotypic variance were fitted as fixed effect and all other markers as random effect (Spindel et al. 2016; Zhao et al. 2014). In addition, we compared the prediction ability of marker-assisted selection (MAS) with rrBLUP and w-rrBLUP. For MAS, only significant markers from GWAS explaining ≥ 9% phenotypic variance were used.

The genomic prediction methods were implemented using five-fold cross validation using 80% of the data as training set (TS) and the remaining 20% as prediction set (PS) with 1000 runs (Würschum and Kraft 2014). In addition, the genomic prediction was performed using 80% of the data from one year as training set (TS) and 20% of the data from the second year as prediction set (PS) with 1000 runs. The prediction ability (\(\rho\)) of a given prediction method was estimated as Pearson’s correlation coefficient between the observed and the predicted trait values.

The models used for MAS, rrBLUP and w-rrBLUP are given in Eq. (4), (5) and (6), respectively.

$$Y = X\beta + e$$
(4)
$$Y = Zu + e$$
(5)
$$Y = X\beta + Zu + e ,$$
(6)

where Y is the vector of phenotypic observations (BLUEs), β the vector of fixed marker effects, u the vector of random marker effects, X and Z the design matrices related to β and u, respectively, and e the error (residual).

Results

Naturally occurring YR was observed in four, PM in two, and STB in five environments (Table 1). The mean disease severities were low for PM, but moderate for the two other diseases ranging from 2.00 to 4.91. The large-plot yield trials had similar mean ratings for STB like the disease trials with microplots.

The magnitude of the three disease severities across genotypes was quite similar that ranged from 0.94 to 6.89 (Table 2) showing a large variation from highly resistant to rather susceptible. Accordingly, the genotypic variances were significant (P < 0.001), but also the genotype x environment (G x E) interaction variances. The resulting entry-mean heritabilities were high for YR, PM and plant height, but moderate only for STB and heading date. This was mainly caused by the very high G x E variance of both traits surpassing the genotypic variance two- and fourfold, respectively.

Table 2 Summary of the phenotypic analysis
Full size table

Nineteen emmer genotypes (equaling 13.3%) demonstrated resistance to all three diseases with ratings < 3 (Table 3). Therefore, they exhibit higher resistance than four of the five variety-protected cultivars with names. Roter Heidfelder, Ramses, Saphir and Osiris exhibited a high susceptibility to YR, whilst Osiris additionally was highly susceptible to PM and STB. Thus, the new emmer genotypes detected in this study represent significant breeding progress for multiple disease resistances. Interestingly, there are some multiple-resistant genotypes from the gene banks with appreciable raw and grain yields which are comparable or even better than the standard varieties. The new breeding line E-14005–303/40/3–423/3/3 was outstanding in grain yield, but highly susceptible to YR.

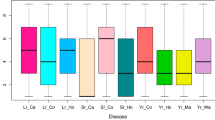
Table 3 Emmer genotypes that show multiple resistances to three diseases compared to the most susceptible emmer genotypes, emmer standards/cultivars, and other wheats; for comparison also the lodging tolerance and the yield is given
Full size table

Low, but significant correlations occurred between YR and PM/STB (Fig. 1). YR and PM also significantly correlated with heading date, while plant height showed significant correlations with YR and STB. The distributions showed a normal distribution for all traits, for PM it was shifted to the resistant ratings. Grain yield was not closely correlated with YR, PM, and STB severities with coefficients of correlation 0.25 (p = 0.002), 0.20 (p = 0.02), and –0.29 (p = 0.0004), respectively. Correlations among YR, PM, STB severities and heading date or plant height were low to moderate (Fig. 1).

Fig. 1
figure 1

Correlation between BLUES of 143 emmer genotypes calculated across multiple locations (observation trials) for different traits. The correlation was calculated based on the BLUEs of 143 emmer genotypes

Full size image

For YR, PM, and STB severity nine, three, and seven significant MTAs, respectively, were detected in a calculation across all environments simultaneously (Table 4, Fig. 2). Their effects were low to moderate, only the 7A QTL for PM seems to be a major gene. The QTLs on chromosomes 1B, 3A, and 4B for YR resistance and on chromosomes 1B and 2A for STB resistance also explained a rather high proportion of the phenotypic variance. The total phenotypic variance explained by a combination of all markers was rather high ranging from 59 to 79%. The disease scores at these loci showed large differences between the resistant and the susceptible allele (Figs. 3, 4, 5). To achieve the lowest disease severities, the combination of two or three QTLs appears necessary.

Table 4 Marker trait associations (MTAs) identified using BLINK model; in bold are markers with moderate to large effects (≥ 15% R2)
Full size table
Fig. 2
figure 2

Manhattan plots for a yellow rust, b powdery mildew, and c septoria tritici blotch. The solid red horizontal line indicates Bonferroni-corrected p value threshold of 0.05. The dashed red horizontal line corresponds to the highest HB-corrected p value of significant MTAs. Any marker falling on or above this line is significant according to the HB-corrected p value of 0.05. HB-corrected p value = p value corrected according to Hochberg and Benjamini

Full size image
Fig. 3
figure 3

Boxplots showing comparisons for yellow rust (1–9) between genotypes having different alleles for significant markers identified in GWAS. n on the x-axis denotes the number of genotypes in a group. For panels with single markers, the title of the x-axis contains name of the chromosome followed by position (bp), marker name and phenotypic variance explained by the marker. For the panel with combination of markers: title of the x-axis contains names of the markers combined followed by sum of the explained phenotypic variance by combined markers; R and S denote resistant and susceptible allele of a marker, respectively. Boxplots of only those markers that explained > 5% of the phenotypic variance are shown. For combination of multiple markers, only the haplotypes with n > 5 are shown

Full size image
Fig. 4
figure 4

Boxplots showing comparisons for powdery mildew (1–9) between genotypes having different alleles for significant markers identified in GWAS. n on the x-axis denotes the number of genotypes in a group. For panels with single markers, the title of the x-axis contains name of the chromosome followed by position (bp), marker name and phenotypic variance explained by the marker. For the panel with combination of markers: title of the x-axis contains names of the markers combined followed by sum of the explained phenotypic variance by combined markers; R and S denote resistant and susceptible allele of a marker, respectively, while H denotes heterozygous genotype (AG). Boxplots of only those markers that explained > 5% of the phenotypic variance are shown. For combination of multiple markers, only the haplotypes with n > 5 are shown

Full size image
Fig. 5
figure 5

Boxplots showing comparisons for septoria tritici blotch (1–9) between genotypes having different alleles for significant markers identified in GWAS. n on the x-axis denotes the number of genotypes in a group. For panels with single markers, the title of the x-axis contains name of the chromosome followed by position (bp), marker name and phenotypic variance explained by the marker. For the panel with combination of markers: title of the x-axis contains names of the markers combined followed by sum of the explained phenotypic variance by combined markers; R and S denote resistant and susceptible allele of a marker, respectively. Boxplots of only those markers that explained > 5% of the phenotypic variance are shown. For combination of multiple markers, only the haplotypes with n > 5 are shown

Full size image

From the three methods used for genomic prediction in this study, the w-rrBLUP showed higher prediction abilities than rr-BLUP or MAS for YR, PM, and STB (SFig. 3). When the five-fold cross validation was performed within the GWAS population, prediction abilities ≥ 0.8 were achieved for all three resistances (Fig. 6). When, however, cross validation was performed with the data from 2020 only using the data from 2019 as training set, prediction abilities dropped to about 0.7 for YR and PM resistances and even to 0.4 for STB resistance.

Fig. 6
figure 6

Prediction ability of the weighted ridge regression BLUP (w-rrBLUP) model for yellow rust, powdery mildew, and septoria tritici blotch, under a five-fold cross validation using BLUEs across all locations in two years, and b cross validation using BLUEs across locations in 2019 as training set and BLUEs across locations in 2020 as validation set

Full size image

A possible candidate gene located within a 3 Mbp interval around the nearest marker was detected for the 3A-m1687611D marker linked with YR resistance and described as "leucine-rich repeat receptor-like protein kinase family protein" (TRIDC3AG055380). For the PM resistance gene linked with the 7A-m1109265D marker, five genes were available that were described either as "WRKY DNA-binding protein 61" (TRIDC7AG011340), "WRKY transcription factor 72 family protein" (TRIDC7AG011350), "disease resistance protein RGA2" (TRIDC7AG012090, TRIDC7AG012040) or "disease resistance protein RPM1" (TRIDC7AG011800). For STB resistance, a total of 702 high-confidence genes were found in a 3 Mbp interval up or down of each significant QTL. None of these, however, showed a specific resistance motif.

Discussion

Emmer cultivation is a small niche, but in Germany the crop is attracting renewed interest as a food cereal (Longin et al. 2016). For that reason, we sampled a large collection of emmer lines from gene banks and our breeding program and investigated 143 emmer lines thereof in multiple location trials on important agronomic and quality traits for the market. In this study, we focus on disease resistance against YR, PM and STB.

A large genetic variation was found among 143 emmer accessions ranging from almost disease free with a rating of 1 up to a rating of 7 on the 1–9 scale (Table 2). This resulted in high heritabilities for PM and YR resistances. The only moderate heritability for STB resistance was caused by the high genotype x environment interaction that exceeded the genotypic variation as already described in literature (Dreisigacker et al. 2015; Risser et al. 2011). The shape of the distribution for PM and STB severity approximated a normal distribution (Fig. 1), indicating that several genes are responsible for these phenotypes. YR resistance showed a more bimodal distribution, but this was attenuated by the segregation of further genes. Heading date had moderate correlations to YR and PM resistances, while plant height correlated with YR and STB resistances. The latter is known from literature (Miedaner et al. 2013) and might be related to plant architecture. Tallness of the emmer wheat might be a passive resistance mechanism to STB. Accordingly, the correlation between plant height and STB resistance was negative with tall genotypes having lower STB ratings. There was a small, but significantly positive correlation between YR and PM resistance and a significantly negative correlation between YR and STB resistances. Despite weak to moderate phenotypic correlations to heading date and plant height we did not detect matching QTL with the three disease resistances.

We found a total of 19 significant MTAs for the three disease resistances, with widely varying proportions of explained phenotypic variation (R2). This may seem like a small number of MTAs for using BLINK in GWAS, but we only report those associations that were significant across all environments, where the respective disease could be scored, because we believe that only these QTLs are of interest for practical breeding. The restricted population size also may have played a role concerning the number of detected MTAs, nevertheless it is still the largest diversity panel in cultivated emmer investigated on these diseases to our knowledge. Many of the QTLs had small contributions of 0–10% and do not appear to be worth pursuing, but some had larger effects.

For YR resistance, three QTLs on chromosomes 1B, 3A, and 4B had R2 values ranging from 15 to 28% and might comprise individual genes (Table 4). For each of these positions, QTLs have been reported previously (Alemu et al. 2021; Liu et al. 2017a, b, c; Miedaner et al. 2019; Singh et al. 2013; Tene et al. 2022), but the comparison is difficult, because older papers lack physical positions of the QTLs, therefore hampering the one-to-one comparison with our study. Moreover, the QTLs mostly have large confidence intervals covering sometimes substantial parts of the chromosome arm. Chromosome 1B seems to be a hotspot for YR resistance because at least eight Yr genes are located here: Yr9, Yr10, Yr15, Yr24, Yr26, Yr29, Yr64, Yr65 as reported by Tene et al. (2022, rf. to their Fig. S9). Yr29 is a known pleiotropic adult-plant resistance gene with moderate effect also designated as Lr46/Yr29/Sr58/Pm39, and located on chromsome 1BL at 669–673 Mbp in the Chinese Spring map of bread wheat (Yuan et al. 2020) and was also detected in durum wheat (Lan et al. 2019; Zhou et al. 2021). Our locus was mapped with the nearest marker at 692 Mbp.

On chromosome 3A, the only previously cataloged Yr gene is Yr76 (Xiang et al. 2016). Our locus with major contribution, however, is located on the same reference genome at 635 Mbp. Tene et al. (2022) described two QTLs for YR resistance on chromosome 3A at positions 680 Mbp, and 720 Mbp that are, however, not closely linked to our locus. Other temporarily designated Yr genes on chromosome 3A include YrTr2 with no known exact localisation (Aoun et al. 2021). Also the three QTLs detected in Aoun et al. (2021)were on the short arm of chromosome 3A. On chromosome 3B, Tene et al. (2022) detected three QTLs for YR resistance in the positions 550 Mbp, 708 Mbp, and 886 Mbp. Our identified Yr locus m4003911D at that chromosome was at 860 Mbp, thus possibly being linked to the latter reported locus of Tene et al. (2022).

STB resistance was caused by two major-effect QTLs on chromosomes 1B and 2A explaining 17 and 24% of phenotypic variation, respectively. On chromosome 1B, two Stb genes are located (Stb2, Stb11), but their physical position is not known, while on chromosome 2A, no Stb gene is yet known. Mekonnen et al. (2021) detected a QTL for STB resistance on this chromosome but it had only a low contribution (R2 = 10.6%) and extends physically over a wide interval from 22 to 513 Mbp that is far away from our locus (779 Mbp).

On chromosome 7AS, monogenic PM resistance was found explaining 67% of phenotypic variation in our study. Korchanova et al. (2022) and Ouyang et al. (2014) both found a monogenic, full resistance gene on the same chromosome in an emmer landrace (QPm.GZ1-7A) and a wild emmer accession (MlIW172), however, both genes were located on the long arm together with about 20 other Pm genes, while the gene in our study was clearly detected on the short arm. It confers in some genotypes a full resistance and had already a very high allele frequency in our population of about 90%. This could be responsible for the narrow phenotypic distribution skewed to resistance (Fig. 1). The high effect and near-fixation rate in emmer illustrates that this gene has already recognized by early breeder’s or natural selection. A search in the database resulted in six genes with four resistance motifs within a 3 Mbp interval, but none codes for the nucleotide-binding site-leucine-rich repeat (NBS-LRR) protein family what makes it even more interesting.

To the best of our knowledge, only one QTL (QPm.caas.7A) was previously detected on chromosome 7AS that is closely linked to the microsatellite Xbarc174 (ca. 90 cM, Lan et al. 2009). Unfortunately, also here no physical position is given. This QTL was detected over two environments, but explained only 6.7% of phenotypic variance (R2) in the previous mapping study of biparental populations. So, it is not likely that this QTL is identical with our major gene.

Three pairs of overlapping QTLs were found (Table 4), two between YR and STB resistances and one between YR and PM resistances. Marker m1692044D on chromosome 1B overlapped with m5577224D and marker m3533508D on chromosome 2A overlapped with m3024004D. Both STB markers were considered as major, also the YR marker on chromosome 1B. For the QTL on chromosome 1B the distance between the physical position was 6.9 Mbp, for the second on chromosome, however, 52 Mbp. Because there is in parallel a significant negative correlation between YR and STB resistances (r = ─ 0.23, P < 0.01) this might be a hint for multi-disease resistance, that would, however, be linked in repulsion. A third QTL on chromosome 2B overlapped between YR (m2260988S) and PM (m5567903D) resistance in a 16 Mbp interval, having, however, only a small contribution to resistance to both YR and PM. Between both disease resistances a moderate positive correlation (r = 0.35) was found. Interestingly, no overlapping QTL were found for PM and STB resistances and accordingly no significant correlation (Fig. 1).

The main purpose of this study was to detect resistance within the cultivated emmer gene pool and to use the more resistant materials for further improvement of emmer. In practice, emmer has been found to be highly susceptible to YR. This may be due to the high susceptibility of the older variety-protected cultivars, which had YR scores of 4.5 to 5.6 in our study (Table 3). Indeed, 19 emmer genotypes had quite good YR scores in our trial, but they did not reach the bread wheat cultivar 'Genius' (Table 3). This difference is caused by the long selection of bread wheat breeders for YR resistance, which could not compete with the short time in which modern emmer is bred. For powdery mildew resistance, the emmer accessions were similar or even better than 'Genius', which is rated 2 on a scale of 1–9 in the list of recommended cultivars (BSL 2022). Rather good accessions were also found for STB resistance. More importantly, the 19 selected genotypes had good scores for all three diseases, which is particularly valuable. For yield, some of these gene bank accessions were even competitive with (older) recommended varieties. From the point of view of multiple disease resistance, the einkorn cultivar 'Terzino' was by far the best, but its grain yield is very low.

The main challenge for the future is to combine these multiple-disease resistances with the lodging tolerance of the tall emmer. None of the emmer accessions could match the low lodging tolerance scores of the two bread wheat cultivars. This clearly shows that even small crops require intensive breeding efforts to reintroduce them into agricultural practice. And being an old and traditional crop is no value in itself.

From the three methods used for genomic prediction in this study (MAS, rrBLUP, w-rrBLUP), the differences between MAS and w-rrBLUP were marginal (SFig. S3), most probably because of the fact that we used the same markers for MAS and for the weighting procedure of w-rrBLUP. The difference in prediction ability of MAS and w-rrBLUP is especially minimal for YR and PM possibly because of large total phenotypic variance explained by markers used for prediction. Whereas, the markers for STB used for MAS or w-rrBLUP explained relatively low total phenotypic variance compared with markers for YR or PM, and hence the difference in prediction abilities between MAS and w-rrBLUP for STB is larger (0.17) than for YR (0.03) or PM (0.02) (SFig. 3).

When comparing w-rrBLUP, the prediction abilities were very high for YR and PM resistances with 0.82 and 0.86 in the five-fold cross validation dropping only to 0.71 and 0.75 when the data from 2019 were used as training set to predict data from 2020 (Fig. 6). This shows that genotype x environment interaction for these resistances should be rather small as already illustrated by their high heritabilities. This was opposite to STB resistance, where also a high prediction ability was found (0.79) that dropped, however, to 0.4 in the second scenario (Fig. 6). Accordingly, heritability estimate was much smaller. This confirms the well-known fact that STB resistance is inherited in a much more complex way than resistance to biotrophic diseases and even Fusarium head blight (Mirdita et al. 2015a). Also, the prediction ability of rrBLUP or w-rrBLUP was considerably higher than MAS for STB. Therefore, genomic selection can be considered as a promising way to improve STB resistance (Mirdita et al. 2015b) alongside phenotypic recurrent selection. The latter would increase allele frequency in the breeding population and circumvent the problem of low prediction ability, when resources should be used that are non-related to the training population. For YR and PM, the w-rrBLUP performed slightly better than MAS and for YR considerably better than rrBLUP, hence hinting at the usefulness of using detected MTAs explaining large phenotypic variation for prediction. Consequently, w-rrBLUP seems to be the method of choice for YR. Finally, pretty similar prediction abilities of three methods for PM are highly likely due to the two markers m3022383S and m1109265D explaining 9% and 67% of the phenotypic variation, respectively. For PM, any of the three methods can achieve the similar gains.

In conclusion, the set of 143 emmer genotypes provided resistances to YR, STB, and PM. Of these, four QTLs with major effects (R2 > 10%) for YR and STB resistances stand out. For PM resistance even a major gene on chromosome 7AS was detected which may be novel. Cross-validation combined with association mapping revealed the absence of large-effect QTLs for YR and STB resistances, preventing efficient pyramiding of different resistance loci by marker-assisted selection. For example, for the YR resistance, even the combination of three resistance QTLs only gave a median of 2.24 on a scale of 1–9, with only a few progenies showing complete resistance, i.e. a rating of 1. For STB resistance, the best rating was 1.33, but this was, on average, even not reached by the combination of three resistance QTLs. For all three resistances, genomic selection seems to be a better option to improve the resistances within the emmer genepool than marker-assisted selection. Notably, also marker-assisted selection can be considered for improving YR and PM resistances owing to the large-effect QTLs discovered in this study.