Introduction

Barley (Hordeum vulgare L.) is one of the founder crops of Old-World agriculture. It is likely the first cereal that was domesticated in the Middle East, about 8000 BC, from the wild species Hordeum vulgare ssp. spontaneum as suggested by archaeological remains of barley grains found at various sites in the Fertile Crescent (Zohary and Hopf 1993). Badr et al. (2000) demonstrated the monophyletic nature of barley domestication.

The wild progenitor (H. vulgare ssp. spontaneum) has a two-rowed phenotype, with strictly rudimentary, lateral rows. It is likely that Neolithic cultivators of barley selected a phenotype with a six-rowed spike, in order to increase grain number and thereby grain yield. The gene responsible for the six-rowed spike in barley vrs1 (six-rowed spike 1), was isolated by positional cloning (Komatsuda et al. 2007).

Six-rowed barley is thus usually preferred for feed production, as higher yielding, while two-rowed barley is more often used for malting and beer-making. Malt is dried germinated barley grain. Malting quality depends on grain size homogeneity, friability and diastatic power of the malt, that is its ability to digest starch into fermentable sugar, which is later converted into ethanol in the brewing process. Malting barley possesses usually a lower protein content, since an excess of protein in the extract can make beer cloudy. Two-rowed barley, which has higher average and more homogeneous grain size, is traditionally preferred by the malting and brewing industry in Europe, e.g. in English ale-style beers or traditional German beers. France, which ranks first in Europe for malting barley production and first worldwide for malt export (1.2 Mt annually, 80% of French production), also uses six-rowed malting barley, which is the second grown small grain cereal behind bread wheat. That is why French breeders have specifically developed breeding programmes of six-rowed barley for malting quality. Most breeding schemes rely on doubled haploid production as a faster breeding method. However, the evaluation of yield, agronomic traits and malting quality requires seed increase and multi-environment trials, which takes 6–8 years after primary crosses.

In particular, the evaluation of malting quality is achieved by a micro-malting test (e.g. Haslemore et al. 1982), which requires a lot of grains and is time consuming (usually > 4 days). Such tests are usually applied on a limited number of lines that have already been screened for agronomic traits such as yield or disease tolerance, just before official registration trials. The selection pressure is therefore quite low, thereby leading to slow genetic gain.

Genomic selection (GS) was first proposed by Meuwissen et al. (2001) who applied ridge and Bayesian regression models to animal populations for predicting breeding values. Appropriate methods such as ridge regression or Bayesian approaches must be used in the usual case where the marker number is higher than the number of observations (phenotypes). Marker effects are first estimated from the genotypic and phenotypic data in a training population. Then marker effects are used to calculate breeding values in the target population with only genotypic data, and selections are based on these Genomic Estimates of Breeding Values (GEBV). This method has been used successfully for dairy cow breeding (Goddard and Hayes 2007). Indeed, in the case of dairy cow breeding (and particularly for bulls), the advantages of GS over classical breeding are obvious, with genotyping being much cheaper than progeny testing and GS being applicable at birth time, while progeny testing requires > 7–8 years. Therefore, GS of dairy bulls allowed early selection on a larger population, thus leading to nearly doubling the genetic gain per unit of time while the costs of proving bulls were reduced by 92% (Shaeffer, 2006). Although less obvious than in dairy cows, plant breeding could benefit from GS, provided that 1) genotyping cost is lower than phenotyping cost and/or can be applied at an earlier stage on a larger set of candidates and 2) prediction accuracy of GS is similar to that of phenotypic selection (Bernardo & Yu 2007; Crossa et al. 2010; Heffner et al. 2009; Jannink et al. 2010; De los Campos et al. 2013).

Condition 1 can be applied to cereal quality traits such as breadmaking in wheat or malting traits in barley, which are relatively expensive. In this manuscript, we analysed agronomic traits and malting-related traits in a set of registered varieties and breeding lines of six-rowed winter barley, with a focus on genomic prediction ability of malting quality traits, as a feasibility study of GS implementation in malting barley breeding.

The objective of this study was 1) to assess the feasibility of genomic selection in real barley breeding programmes, 2) to compare GS predictive abilities obtained either within a single breeder’s material, or on a larger set when merging two breeder’s lines and available registered varieties and 3) to compare the predictive ability of 4 genomic models, each being more adapted to a specific genetic architecture (polygenic vs oligogenic, epistasis or not),

Materials and methods

Plant material

Two French breeders, here named as Breeder1 and Breeder2, provided a set of proprietary doubled haploid breeding lines (DH) of six-rowed winter barley, that had already been screened for adaptative traits such as plant height, flowering, lodging or disease resistance. For competition issues, each set of proprietary lines was evaluated separately by each breeder in 2–3 locations during two growing seasons, 2017/2018 and 2018/2019. To allow connectivity in the whole data, a set of registered varieties, here named as “founders” (since often used as parents of the breeder’s DH lines) were evaluated in common by the two breeders. Breeder1 provided 259 proprietary DH breeding lines and Breeder2, 315 DH breeding lines.

One hundred and five « founder lines», i.e. registered pure lines varieties (hybrids were discarded) freely available under UPOV agreement were used to enable main location effect correction.

Genotyping data

The barley 50 K iSelect SNP Array (Bayer et al. 2017) was used for whole genome polymorphism assessment of the 679 breeding lines and cultivars. From the initial 44,040 SNP, quality control and filtering for missing data (< 20% per SNP), heterozygous SNP (< 5%) and minor allele frequency (> 1%) lead to a subset of 24,945 SNP, among which 24,101 were mapped on the barley physical map (Ariyadasa et al. 2014) and further used in statistical analyses.

Missing data were imputed using an EM algorithm (Poland et al. 2012) implemented in the A.mat function of the rrBLUP package (Endelman 2011).

A genomic relationship matrix K was computed using the 24 K markers according to the van Raden (2008) equation using the A.mat function from the rrBLUP package:

$${\text{K}} = \frac{{WW^{T} }}{{2\sum \left( {p_{k} - 1} \right)p_{k} }}$$

where W is a centered N × M marker matrix of the i lines with Wik = Xik + 1 − 2pk with Xik the genotype of the i-th individual for the k-th marker as {− 1,0,1} and pk the allele frequency at the k-th marker.

A principal coordinate analysis (PCoA, with the “cmdscale” command in R)) was applied to Rogers’ distance matrix (Rogers 1972) computed with the “dist” command in R, to illustrate the additive relationships among the breeding lines and registered varieties studied.

Phenotypic data

Breeder1 evaluated his 259 DH lines and the 105) founder lines in three locations in France, namely Thoiry, Auffay, Warmeriville, in two growing seasons, i.e. harvest years 2018 (1872 plots) and 2019 (1327 plots). An unbalanced trial was carried out at each location with most breeding lines being unreplicated, and a few control lines being replicated 15–20 times (cvs Etincel, Pixel and Visuel), and up to 50–60 times (cv KWS-Tonic) in 2018. In 2019, a simpler design was used with a single control (cv Pixel) being replicated 42–50 times and all tested lines randomly distributed.pline spatial models were used to correct for field heterogeneity using the SpATS R-package (see below). All trial plots (10–12 m2) were managed according to local farmer practice for malting barley, including fungicide treatment.

Breeder2 evaluated its 315 DH lines and 95 of the 105 founder lines in two locations in France, Cupperly and Presmesque, in the same two growing seasons, i.e. harvest years 2018 and 2019. Each location carried out unbalanced trial with most breeding lines unreplicated, a few control lines being replicated 10 times (cv Amistar) or 20–50 times (cvs Casino and Etincel) in 2018. As for breeder 1 trials, spline spatial models were used to correct for field heterogeneity.

The common set of variables available for all plots in every location included: Yield (dt/ha), protein content (%), thousand grains weight (g), test weight (Kg/hl), Calibration (% kernels > 2.5 mm) and heading date (days from January 1st), later named agronomic traits.

In addition, the following traits related to malting ability (later named malting traits) were evaluated after micro-malting tests, on grain from a single plot of two locations each year (Cupperly and Warmeriville in 2018, Premesque and Warmeriville in 2019). Since the replicated control plots were not evaluated, spatial correction was not possible for those traits, namely friability, extract, viscosity and beta-glucan content.

Malt friability was assessed according to the EBC (European Brewery Convention) 4.15 method (Friability, glassy corns and unmodified grains of malt by friabilimeter—International method): whole malt corns were fragmented by the mechanical action of the friabilimeter’s drum and small fragments of physically modified material were passed through the mesh of the drum whereas larger, unmodified, fragments were retained. Friability is defined as the % of fragments that passed through the sieve.

Extract of malt was determined according to the EBC 4.5.1 method (Extract of malt): fine malt grind is mashed and filtered after a standard procedure. Extract was defined by the determination of the specific density of the wort using a pyknometer or a density meter. It defines the potential of malt for producing wort solubles by a standard mashing program. This procedure was also used for the determination of viscosity of wort, and soluble beta-glucans content.

Wort viscosity is an important parameter to estimate the quality of malt. The lower the viscosity, the better the modification of grains during germination. After malt extract, wort viscosity at 20 °C is determined using a calibrated viscometer according EBC 8.4 method (Viscosity of laboratory wort from malt).

The content of soluble beta-glucans is the main cause of wort viscosityA high-quality malt should then contain a limited quantity of these soluble polysaccharides. Theese were determined according to the EBC 4.16.2 method (High molecular weight β-glucan content of malt and malt wort: fluorimetric method). The fluorochrome Calcofluor binds with high molecular weight β-glucan above MW 10,000 in solution (in malt wort). The monitoring apparatus was calibrated against standards made of purified barley β-glucan.

Statistical analysis of phenotypic data

Within each trial (i.e. site x location combination), the randomly replicated controls were used to correct agronomic traits for field spatial heterogeneity using the SpATS R-package, which allows the use of two-dimensional (2D) penalized splines (P-splines) to adjust spatial data (Rodriguez-Alverez et al., 2018). Then spatially adjusted plot values were used in a linear mixed model (LMM) using the lme4 library (Bates et al 2015) in R (R core team 2020), with genotype and its interactions considered as random. For quality traits, no spatial correction was possible, due to the lack of replicated controls, and raw data were used instead in the LMM of the incomplete block design. Indeed, in the case of a highly unbalanced design as we have, the conditional modes of the random effects are known to be better corrected for fixed effects (environments) than the adjusted means in fixed effects models

$${\text{Y}}_{{{\text{ijk}}}} = {\upmu } + {\text{y}}_{{\text{j}}} + {\text{y}}:{\text{s}}_{{{\text{jk}}}} + {\text{g}}_{{\text{i}}} + {\text{gy}}_{{{\text{ij}}}} + {\text{gs}}_{{{\text{ik}}}} + {\upvarepsilon }_{{{\text{ijk}}}}$$
(1)

where Yijkl is the phenotypic value of the i-th genotype in j-th year and the k-th site μ is the overall mean, gi is the random effect of the i-th genotype, yj is the fixed effect of j-th year, y:sk is the fixed effect of the k-th location, nested within the j-th year, gyij is the random interaction between the i-th genotype and the j-th year, gsik the random interaction between the i-th genotype and the k-th location and εijk is the residual error, i.e. the three way interaction, since most genotypes were not replicated.

Equation (1) with gi and its interactions with y and s as random effect was used (command VarComp in R lme4 library) to estimate variance components σ2g, σ2gy, σ2gs and σ2e, and their confidence intervals (command confint in R).

Since the experimental design was highly unbalanced, classical heritability formulae based on variance component ratios are poorly suited, and we rather used formula (20) in Piepho et al. (2007)

$$h^{2} = 1 - \left( {v\left( {{\text{BLUP}}} \right)/2\sigma^{2}_{g} } \right)$$

where v(BLUP) is the mean variance of a difference of two BLUPs (Cullis et al. 2006).

Heritability of each trait was estimated either using the full dataset, or separately for each breeder’s set or the set of founders.

The conditional modes (i.e. corrected for environment main effects) of each genotype were then extracted from the LMM (command ranef in the lme4 R package) and further used to show the trait distribution, and pairwise correlations.

Since the genotype variance component was generally higher than its interaction variances, these genotypic conditional modes were further used to test the predictive ability of genomic selection models.

Genomic prediction models

The BWGS R software was used in this study (Charmet et al. 2020) to estimate the predictive ability of four genomic selection models, namely GBLUP, Bayes Cpi (Habier et al., 2011), LASSO (Park & Casella 2008), and EGBLUP (Jiang and Reif 2015). GBLUP assumes an infinitesimal model, with every marker having a small effect drawn from a single Gaussian distribution, while Bayes Cpi assumes a proportion of markers having zero-effects and others with non-zero effects from a scaled t-distribution. LASSO also assumes a narrower distribution, with fewer QTLs having large effects, compared to a Gaussian distribution. EGBLUP is an extension of GBLUP with a “squared” relationship matrix to model epistatic additive by additive QTL interactions, as described by Jiang and Reif (2015).

Model validation

To compare the models and estimate their predictive ability, different strategies were used:

  1. 1.

    Cross validation with tenfold random, i.e. both training and validation sets sampled from a common population consisting of:

    1. a.

      Breeder1 + Breeder2 + founder lines (N = 679)

    2. b.

      Breeder1 lines + founder lines evaluated in the same locations (N = 364, i.e. 259 + 105)

    3. c.

      Breeder2 lines + founder lines evaluated in the same locations (N = 410, i.e. 315 + 95)

    4. d.

      Founder lines only (N = 105)

Each cross-validation was replicated 50-times, i.e. with 50 different tenfold divisions.

Strategies b. and c. give an estimate of what each breeder can expect from his own and publicly available material, while strategy a. measures the advantage of merging data sets from different breeders to train prediction models. Strategy d. was used to assess the robustness of genomic prediction when training size decreases dramatically and what could be achieved using publicly available material only.

To assess whether the lower predictive ability obtained in strategies b–d. compared to strategy a. can be attributed to training size only, we carried out random subsampling from the full data to achieve training size N in {50, 100, 200, 300, 400, 500}, with 50 replicates each. To illustrate, we show results on yield and friability, the traits with most contrasting predictive abilities.

  1. 2.

    Across-population validation, using either:

    1. a.

      Breeder1 + founder lines as training set and Breeder2 lines as validation set

    2. b.

      Breeder2 + founder lines as training set and Breeder1 lines as validation set

    3. c.

      Breeder1 + Breeder2 lines as training set and founder lines as validation set

The predictive ability was calculated as the Pearson’s correlation between predicted values and adjusted means from the LMM. To obtain confidence intervals of predictive ability in across-population prediction, we used a bootstrap method as described in Rutkoski et al. (2012).

Results

Trait variation and summary statistics

An example of spatial adjustment of yield in the trial “Cupperly 2018” is illustrated in supplementary Fig. 1. Although the differences between raw and fitted plot data seem to be small at a first glance, the spatial spline model did correct for a spatial trend. To assess whether this correction was desirable or not, we compared predictive abilities of the GBLUP model on either raw data or adjusted data. An improvement of 5% and 7.5% of the predictive ability was observed for yield and protein content, respectively, the traits that are most likely to be affected by field heterogeneity.

The genotype variance component σ2g appears to be larger than the interaction variance components σ2gs and σ2gy (Table 1). This allowed us to use adjusted genotypic means (i.e. conditional mode from the LMM) in further genomic prediction models.The single trait distributions of conditional modes of genotypic effects of the ten traits studied are all continuous, with a single mode and a gausssian-like belle shape (Fig. 1). Among the agronomic traits, the highest pairwise correlation (0.77) is between average grain weight TGW and calibration which is quite obvious.

Table 1 Variance components [confidence interval] of the 10 traits
Full size table
Fig. 1
figure 1

2D plots (lower triangle), distribution histograms (diagonal) and Pearson’s correlation (upper triangle) of the 10 variables

Full size image

Among malting related traits, the highest correlation (0.90) is found between viscosity and β-Glucan content, and another (0.64) between friability and extract. Both correlations were expected from causal reasons. Viscosity and β-Glucan are negatively correlated with extract, which is favorable to breeding objectives, since extract is to be enhanced while viscosity is to be reduced. Malting traits are weakly correlated to agronomic traits, the highest (in absolute value) negative correlation being between extract and protein content (− 0.42). This suggests s that genetic improvement of agronomic traits and malting traits can be achieved independently.

The first two axes of a principal component analysis (supplementary Fig. 2) clearly shows the two groups of tightly correlated malting traits, which are in opposite directions along axis 1, while the agronomic traits are mostly located along axis 2, particularly TGW and calibration, thus independent from malting traits, and protein content being poorly represented, as less correlated to all other variables in this two-dimensional plane. Heading date, poorly represented on axes 1–2, is not correlated with agronomic or quality traits.

Molecular Data

In the whole set of 44,040 markers from the barley 50 K iSelect SNP Array, there were only 0.73% of missing Data. In the 24,101 markers that remain after filtering as explained in the MM section, the average rate of missing data was 0.65%, with 85% of markers having less than 1% missing data. The proportion of missing data per genotype ranged from 0 to 10%, with 94% of lines having less than 5%, and 80% less than 1% missing data, that were imputed as described above.

The average rate of heterozygosity was very low (1.76%), either by marker or by barley line. Moreover, 80% of the barley lines had less than 1% heterozygous markers, as expected for DH lines. Some lines were more heterozygous, likely due to cross-pollination during seed multiplication, but were kept in the analysis, since removing them did not change the results.

The distribution of the 24,101 filtered markers was fairly homogeneous over chromosomes, ranging from 2505 on chromosome 4H to 4604 on chromosome 3H. The scatter plot of the 679 breeding lines and cultivars on the first two axes of the principal coordinate analyses of the Roger’s distance matrix is shown in Fig. 2.

Fig. 2
figure 2

Scatter plot of the breeding lines (blue & green symbols) and registered varieties (red symbols) on the first two axes of the principal coordinate analysis of the Rogers distance matrix from the 24,201 SNPs

Full size image

The clouds of the two breeders’ lines are only partly overlapping. Cultivars are more spread out on the whole graph, with a higher density in the middle zone where the two breeder’s lines overlap. This overlap is likelydue to the use of cultivars as parents of crosses by both breeders (personal communication), while the starting divergence among the two sets of breeding lines could be explained by the fact that each breeder has his own source of parental lines. However, the overlap seems to be large enough to anticipate the possibility of successful cross-prediction between the two breeders, i.e. one breeder set used for training and the other set used for validation.

Genomic prediction

Cross validation using the whole set of lines (N = 679) shows moderate predictive ability for yield and protein content (0.45–0.50), and good to very good ones for all quality and malting-related traits (Table 2). In particular, predictive abilities of traits measured by the micro-malting test (last four rows) are all larger than 0.65, and up to 0.80 for friability.

Table 2 Predictive abilities, i.e. Pearson’s correlation between observed phenotypes (conditional mode from LMM) and genomic estimates of breeding values obtained by GBLUP for the 10 traits, using several validation methods; mean/standard deviation from50 replications of tenfold random sampling
Full size table

Columns 2 and 3 show predictive abilities in random cross-validation using lines from a single breeder + founder lines, i.e. what a single breeder can hope to achieve alone, without sharing data with another breeder.

Column 4 shows predictive abilities obtained by cross-validation within a very small training set (N = 105), made of the founder lines. Although these PA are more variable than using the largest training set (standard deviation of PA are 2–4 times larger), they are unexpectedly large, particularly for malting traits.

To assess whether predictive ability of smallerspecific subsets is due to training size, we used random sampling within the whole dataset.

As expected from the theory, predictive ability decreases with sample size when sampling is random, while the variation in predictive ability among validation sets increases. Predictive abilities obtained for yield (Fig. 3a) and friability (Fig. 3b) using specifically selected subsets are higher than (founders and breeder1) or equal to (breeder2) those obtained using random samples of the same size.

Fig. 3
figure 3

Predictive abilities for yield (Fig. 3a) and friability (Fig. 3b) obtained by either random sampling (green) or determined subsets according to the origin of the lines (founders only, breeder1 + founders, breeder2 + founders)

Full size image

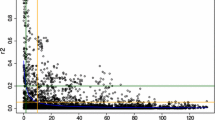
As expected, predictive ability increases and its standard error decreases as marker number increases, up to a plateau that is reached with as few as 2000 markers, which are enough to achieve predictive abilities that are close to and as reliable as those obtained with the full marker data (Fig. 4). The most likely explanation is that the extent of linkage disequilibrium is large enough between any of the 2000 markers and its neighbors, so that they are able to capture the effect of any QTL lying between them. To test this hypothesis, we estimated the decay of linkage disequilibrium with physical distance between markers (Supplementary Fig. 4).

Fig. 4
figure 4

predictive abilities for yield (orange boxes) and friability (green boxes) of GBLUP according to marker number randomly sampled from 24,101 SNP

Full size image

The predictive abilities obtained with across-population validation, i.e. using pre-defined subsets for training and validation, are generally lower than those obtained by CV.

The size of the training set is roughly decreasing from left to right. As expected, PA decreases with the size of the training set, more rapidly than using random cross validation (Table 2), particularly for Yield and protein content. However, they remain within the range of practical usefulness for malting quality traits.

Values in column 1 of Table 3 are close to those of column 1 in Table 2, with similar size of training sets (N = 612 in random tenfold CV, N = 569 in BRE1 + BRE2 subset). This is illustrated in Fig. 5, which shows the predictive abilities for the 10 traits in the first columns in Table 2 (random cross validation) and Table 3 (across population validation), i.e. with the largest possible size of the training set. Across population validation gives predictive abilities that are slightly lower for agronomic traits, except Test weight, but very similar ones for malting traits, and even higher for extract rate.

Table 3 predictive abilities (PA) obtained by GBLUP for the 10 traits using across-population validation. Mean/standard deviations estimated from1000 bootstrap resampling of both adjusted phenotypes and GEBV vectors
Full size table
Fig. 5
figure 5

barplot of the predictive abilities of random CV (red boxes) and across population validation using the founders as the validation set (green boxes) for the 10 traits. (Color figure online)

Full size image

To explore why malting related traits are more precisely and more robustly predicted by molecular markers than agronomic traits, we tried genomic predictions with models which depart from the infinitesimal one used in GBLUP (Table 4). Indeed, LASSO and Bayes Cpi both estimate additive effects, but allow some markers to have null or very small values, while a few ones have larger effects, while EGBLUPs includes additive-by-additive pairwise interaction betenne markers.

Table 4 square root of heritability estimated in the full experiment, i.e. 2 years × 5 locations (2 for the malting-related traits), and predictive abilities (mean/standard deviation from 50 replicates) of 4 statistical models (see MM) obtained by random cross validation in the whole dataset
Full size table

As expected, given the limits of the design, Yield and protein content show moderate heritabilities. This is also the case for heading date, a trait that is most often considered as being highly heritable. This is likely due to the relatively narrow range of variation in our studied material, made only of six-rowed winter barley adapted to western Europe. The square root of this heritability is assumed to be the theoretical upper limit of the predictive ability of any model.

The traits with a high heritability also have high predictive abilities. Globally, there are very few differences in predictive abilities among the 4 models, although LASSO shows lower PA, particularly for the least heritable traits, namely yield and protein content, Bayes Cpi gives PA very similar to those of GBLUP, sometimes slightly, but not significantly higher, the difference being often in the third digit, i.e. within the range of 2 standard deviations. Comparatively, EGBLUP, which aims to model first order epistatic interactions, has higher PA than GBLUP, which only accounts for addictive marker effects. EGBLUP sometimes gives significant improvement (second digit), particularly for yield.

Discussion

Trait correlations

Both agronomic traits and malt-related traits show continuous, unimodal distributions, as expected for traits under polygenic control. It is worth noticing that the correlations we found in our six-rowed winter barley panel are all favorable to breeding goals. As seen in the figure of PCA 1–2 axes, agronomic traits and malt quality traits are brought by different axes, which means that there is no trade-off to be expected on yield when selecting for malt quality. Moreover, malt quality traits show favorable correlations, since extract and friability, that are to be augmented, are positively correlated to each other, and negatively correlated to wort viscosity and β-glucans, that are to be reduced. Protein content is negatively correlated to yield (− 0.32), which may appear as unfavorable to breeding objectives, but not as tightly as reported in bread wheat, e.g. − 0.82 in French registration trials 1991–1999 (Oury et al. 2003). Moreover, a high protein content is not looked for in malting barley, since too much protein causes problems in the filtration process, as illustrated by the negative correlation between protein content and extract rate (− 0.35). Thus, a stabilization of protein content, which is necessary to correctly feed yeast, is desired rather than a continuous enrichment. Finally, all traits are independent to heading date, which makes it possible to select high malting quality in both early and late flowering material to better fit local climates. As a whole, we could say that six-rowed malting barley breeders are lucky, compared to high quality wheat breeders.

Genomic prediction: cross validation

Although marker-assisted selection in barley was proposed more than 20 years ago (e.g. Han et al. 1997), this method can only be applied to some traits controlled by a few QTL with large effects, such as diastatic power of β-glucan content(Li et al. 2009; Fang et al. 2019). The development of high-density marker systems based on SNPs in barley is about ten years old, and have paved the way to an efficient use of modern quantitative genetic approaches such as genomic selection. Considering this relatively recent development and the secondary importance of barley as a field crop, reports on GS in barley are even more recent. Given its cost and resources-demanding aspect, malting quality has been a major objective of such studies. One of the first reports was Schmidt et al. (2016), who explored the applicability of GS for malting quality in two practical breeding programs, namely spring and winter barley. They studied more traits than we did, including enzymatic activities (α-amylase and β-glucanase), but our four malting traits were also included in their report. Using an Illumina-9 K SNP tool, they kept 4359 markers in winter barley, which allowed them to achieve predictive abilities ranging from 0.625 (Extract) to 0.798 (β-glucan content), i.e. values very close to our results, despite a very small training population (N = 102). It is noticeable that in Schmidt et al. (2016), GS predictive ability was lower in spring barley compared to winter barley, by 0.16 on average, despite larger training populations. They explained this result by a more homogeneous population structure of their winter barley panel, as we also reported in the present study.

Nielsen et al. (2016) reported predictive abilities of G-BLUP model in a little-structured population of 309 spring barley lines using 3540 SNP markers. With random leave-one-out, they obtained PA ranging from 0.40 (protein content) to 0.68 (seed weight), and even 0.83 for ergosterol, which was not measured in our study, but whose PA was similar to what we observed for β-glucan.

It is generally acknowledged that increasing training population size increases predictive ability, as expected from the theory (e.g. Daetwyler et al. 2008; Goddard 2009) or simulation studies (e.g. Iwata and Jannink, 2011). Our results fit the theory when subsampling at random from the original set of barley accessions (Fig. 3). Similar results were also reported by Nielsen et al. (2016). However, this relationship is far from being a fixed rule. For example, Edwards et al. (2019), recently showed that, for a fixed size, it is better to increase the number of crosses (progenies) rather than the number of lines per cross.

In our study, cross-validation within each breeder’s material or founders only does not always give lower predictive abilities than those obtained in the whole set of lines. This may be due to a higher kinship among a single breeder’s lines than within the whole set of 679 lines. Indeed, the average additive relationships in the whole set is 0.373, while they are 0.391, 0.388 and 0.399 in breeder1’, breeder2’ and founders’ lines, respectively. Moreover, only 12.4% of the line pairs are related by more than 0.5 when considering the whole set of 679 lines, while the proportions are 16.5%, 16.3% and 22% in breeder1’, breeder 2’ and founders, respectively. These higher relationships within a specific set may counterbalance the effect of the smaller size of training population and explain why the PA obtained with specific training sets is higher than those obtained by random sampling in the whole subset (Fig. 3).

Another explanation could be that founder lines were evaluated by both breeders, therefore in 5 locations each year, instead of only two or three locations for breeder’s own lines, thereby achieving a higher heritability of the phenotypic traits. This should be visible through the broad sense heritability when estimated from a single subset of lines, that are shown in Supplementary Table 1. Heritabilities estimated on founder lines only are always higher than when estimated on the whole dataset. This may partly explain the higher predictive ability shown in Fig. 3a. Moreover, heritabilities estimated in Breeder 2’s materials are always lower than those estimated from Breeder 1’s lines, which is consistent with the lower predictive abilities obtained (Fig. 3).

Genomic prediction: across population validation

In Nielsen et al (2016), predictive abilities of their “leave set out” method, which can be compared to what we get when testing on material from the other breeder, gives lower predictive ability, ranging from 0.31 (protein) to 0.52 (seed weight), and 0.72 for ergosterol. This was also observed in our study (Tables 2 and 3). Again, this result may be explained by a lower average relationship between breeder’s sets (Breeders1-founders: 0.376, Breeder2-founders 0.365, breeders1 + breeder2-founders 0.368), than within breeder’s set (0.399 within founders). The same figure is observed for the percent of line pairs which are related by more than 0.5 (11% between breeders1 + breeder2’ lines and founders, half the value of 22% within founders). The advantage of using lines from two breeders to get a larger training population (Table 3, column 1) did not always translate into a higher predictive ability, particularly for malting related traits. This could also be explained by an average relationship between breeder1’ and breeder2’ lines of 0.35, lower than those observed between breeder’ lines and founders, and also a smaller proportion of highly (> 0.5) related pairs (8% vs 11%). A similar result was already reported, by Lorenz & Smith (2015). Using barley lines from two university breeding programs (MN and ND), they showed that adding genetically distant individuals from another breeding program to training population does not improve, and even reduces genomic prediction accuracy in barley. The breeding materials of those two US programs were really distinct. A clear-cut clustering is obvious in their Fig. 1 (heatmap) as well as in our supplementary Fig. 3, although less obvious. Although their scale of genomic relationships was different from ours (not normalized), the mean relationships between programs was significantly lower than within each program, which is also the case in our material. When tested using an independent set of lines (founders as validation set, Table 3), predictive abilities obtained using breeder 1 + breeder 2 lines as training set are higher than those obtained using a single breeder’s material, likely due to a larger size of the training set and similar average relationships with the validation set (0.109 for breeder1’, 0.111 for breeder2’ and 0.110 for breeder1 + breeder2 combined). From a practical point of view, this means that, when their breeding populations do not show too much genetic divergence, there is something to be gained by merging materials from different breeders in order to obtain a larger training set.

Genomic prediction: effect of marker number

Nielsen et al. (2016), already reported that as few as 2000 markers were enough to attain maximum predictive ability. This fits to our empirical finding of prediction accuracy being nearly optimal with M = 2000 markers. Although linkage disequilibrium (LD) seems to decay quite rapidly at the scale of a whole chromosome, on average (supplementary Fig. 4, green curve), it remains greater than 0.3 up to # 2 Mb. Given the size of the barley genome, 4250 Mb in our data, # 2100 markers (4200/2) regularly spaced is expected to achieve a complete coverage of the full genome at LD-threshold = 0.3.

. This extend of LD over large distance likely reflects a limited effective population size in this particular breeding material of 6-rowed winter barley, as also illustrated by relatively high pairwise kinship, either within or between breeder sets of lines.

Genomic prediction: statistical model

As already often reported (e.g. Heslot et al. 2012), we did not find huge differences between statistical models in terms of predictive ability, and this applies to all studied traits. Often the “old” GBLUP method, based on genomic estimates of Kinship, which is equivalent to the ridge regression BLUP, appears to be one of the best methods. Although it relies to the unrealistic assumptions of an infinite number of QTL with very small effects drawn from the same distribution, it does not significantly differ from other methods that allow QTL effects to come from various zero or non-zero distributions. Similar results were reported by Wang et al. (2015). Using simulated data, they showed that Bayes Cpi had higher predictive ability only with the scenario with the lowest number of 20 QTL. For all other genetic architectures, from either simulated or real data with true polygenic traits, RR-BLUP slightly outperformed the other methods.

As in our previous report on bread wheat (Charmet et al. 2020), the method which is supposed to capture non-additive marker effects (EGBLUP), shows slightly higher predictive ability than GBLUP, although the differences are not statistically significant. Indeed, the larger improvement brought by EGBLUP was 3.8%, observed for grain yield. This is much lower than those reported by Raffo et al (2022) for wheat grain yield in Denmark. However, Raffo et al (2022) observed a 16.5% improvement of genomic prediction models with epistasis, compared to additive models, but only in the leave-one-out validation (an extreme case of cross validation). This improvement was not observed in the leave-one-breeding-cycle out validation (equivalent to our across population validation).

In our study, we only considered single trait genomic prediction. Although a recent study (Bhatta et al. 2020) reported significantly higher predictive abilities of multitrait Genomic prediction over single trait methods, we do not think this will be the case in our material. Indeed, the PA of the single-trait models in Bhatta et al. (2020) are generally lower than those reported in our study. In particular, malt-related traits already show very high predictive abilities (0.6–0.8), which are thus less likely to be much improved by multitrait models.

Conclusion

The present study, based on representative material from applied breeding programs of six-rowed winter barley, showed highly encouraging results in the perspective of using genomic prediction to accelerate breeding progress for malting traits. Predictive abilities of maltingbtraits are very highand would allow an efficient use of genomic prediction to replace phenotyping in an early generation, thereby increasing selection intensity and reducing cycle length. Genetic resources from a single breeder and publicly available materials (varieties) are enough to achieve useful predictive abilities, but merging material and data from competing companies may allow some improvement in predictive ability of GS models.

This is very encouraging with respect to the possibility to efficiently screen more candidates (at cheaper cost) and/or at earlier stage in the breeding scheme, thereby enabling a faster genetic gain for malting quality traits.