Grain yield and stability of tropical maize hybrids developed from elite cultivars in contrasting environments under a rainforest agro-ecology

Abstract

In the maize producing regions of Sub-Saharan Africa (SSA), compounding effects of genotype-by-environment interaction have necessitated breeding maize for outstanding performance and stability across varying environments. This study was conducted to assess the performance and stability of late-maturing cultivars and their respective hybrids evaluated under contrasting environments in the tropical rainforest region. We evaluated 108 genotypes in field trials under three different growing conditions in 2018 involving 14 open-pollinated parents and their hybrids derived from a diallel mating design. The genotypes were evaluated under field conditions using 9 × 12 alpha lattice design with three replications in six environments. The genotypes were divided into three groups, containing either the parents, hybrids or checks, for estimating the stability variance and grain yield. The difference between the lowest and highest yielding environment was 3.9 t ha⁻¹, while the repeatability of the grain yield trials ranged from 39 to 80%. The average grain yield of the hybrids (2.33 t ha⁻¹) was significantly higher than that of the parents (2.19 t ha⁻¹) and the check varieties (2.03 t ha⁻¹). The hybrids were more stable than both the parents and the checks. They also showed a higher stability against a common group of the parents and checks. The results of this study suggest that high yielding and stable population hybrids can be utilized in breeding programmes aiming to provide improved varieties for the large number of rural maize farmers in the SSA zone, who often lack access or the capacity to purchase commercial hybrids.

Introduction

Maize is a major food security crop supporting millions of people in Sub-Saharan Africa (SSA) and further regions of the developing world. The low maize yield in SSA (1.5–2.0 t ha⁻¹) in comparison to developed countries is primarily attributed to production constraints, which include several abiotic stress factors and low adaptation of exotic germplasm to target environments in the major maize production agro-ecological regions of the SSA Savannahs (Badu-Apraku et al. 2011c; Adebayo et al. 2017). Strong effects of genotype-by-environment interaction as well as a general scarcity of improved cultivars (Abakemal et al. 2016) furthermore impair the yield potential of maize in these regions. These dynamic environmental conditions are particularly evident in Nigeria, where small-scale farmers who largely lack the capacity to influence the plant production environments with inputs like synthetic fertilizers and pesticides (Oluwatusin et al. 2017) are cultivating the majority of the country´s maize acreage. Hence, there is a considerable need for the development of high yielding and stable genotypes that are accepted by farmers which are exposed to a diverse range of growing conditions. In the recent years, plant breeders in this region have concentrated on yield stability of individual maize genotypes across few locations with none or little interest on the particular variety type (Badu-Apraku et al. 2015b; Meseka et al. 2016; Nyombayire et al. 2018; Setimela et al. 2018; Seyoum et al. 2019).

In developing countries, open pollinated (OP) maize cultivars have been used for providing low-priced farm-saved seeds and dependable yields to farmers, although they generally produce lower grain yield compared to well adapted single cross hybrid cultivars. However, hybrid seed is comparably expensive and therefore not easily accessible to small-scale famers. The qualities of improved maize populations and population-derived hybrids makes them both interesting alternatives to commercial single-cross hybrids as well as valuable sources for developing novel inbred lines (Carena 2005; Kutka 2011). Although rarely used, several studies have shown that population hybrids show some heterotic increase or panmictic mid-parent heterosis in productivity across stressed and non-stressed environments when exploiting heterotic patterns among them (Carena 2005, 2007; Gabriel et al. 2009). Future climate scenarios suggest that maize yields in some regions will decline by up to 10% by 2050 (Tesfaye et al. 2015). Therefore, exploiting the putative higher yield stability of such heterogeneous and heterozygous variety types would moreover represent a significant step in coping with the increasing abiotic stress factors expected from climate change.

However, the concept of yield stability of a genotype in an evaluation and breeding programme is ambiguous, often used in quite different senses and based on different statistical determinations and analyses (Purchase et al. 2000). Several stability parameters have been proposed to characterize yield stability when genotypes are tested across multiple environments, with each parameter giving different results (Temesgen et al. 2015). Becker and Léon (1988) distinguished between two different concepts of stability; static stability and dynamic stability. A genotype is said to exhibit static stability when its performance is unchanged with respect to varying environments, thus implying that the variance of yield or other relevant traits over environments is low. Dynamic stability has on the other hand to do with a genotype showing predictable response to environments, and thus showing small deviations from its expected response in the testing environments. Becker and Léon (1988) stated that all stability procedures based on quantifying G × E interaction effects belong to the dynamic stability concept. These include procedures partitioning G × E interaction, such as Wricke’s ecovalance (Wricke 1962) and Shukla’s stability variance (Shukla 1972), various nonparametric stability statistics as well as procedures using regression approaches such as that proposed by Finlay and Wilkinson (1963), Eberhart and Russell (1966) and Perkins and Jinks (1968) that might be extended by including molecular marker data and environmental covariates (Lian and de los Campos 2016; Millet et al. 2019).

Although yield per se can readily assessed in series of unbalanced multi-environment trials (Rivière et al, 2015; Rattunde et al. 2016), the minimum number of locations needed to assess yield stability of single genotypes can however be high. Piepho (1998) recommended, based on theoretical considerations, 50–200 environments to accurately estimate yield stability. Empirical studies suggested on the other hand that ten or more environments are advisable for obtaining reliable estimates (Becker 1987), and it has e.g. been reported for wheat that at least 40 environments are required to obtain a heritability of h² = 0.7 for grain yield stability (Liu et al. 2017). These requirements are however difficult or even impossible to meet if large numbers of genotypes are to be tested. Mühleisen et al. (2014a) suggested thus to divide genotypes into several groups and assess the yield stability of the latter, which requires testing in fewer environments to precisely assess their yield stability, compared to studies focusing on the yield stability of single genotypes. Hence, the yield stability of groups comprising either parental lines or hybrids can e.g. be compared in a reduced number of environments as these groups consist of a larger number of genotypes, and thus yield a large sample of genotype–environment effects resulting in a higher precision of the corresponding variance component estimation than for individual genotypes. The use of diverse environments and the comparison of groups rather than individual genotypes implies consequently that despite a relatively smaller number of environments, substantial and significant difference in yield stability might be established between genotype groups (Mühleisen et al. 2014a). The primary objectives of this study were to thus (1) to evaluate the yield performance and stability of 14 open-pollinated varieties and their hybrids under optimal and sub-optimal growing environments and (2) assess relationships among test environments under the rainforest agro-ecology of Nigeria.

Materials and methods

Field trials were conducted in 2017 and 2018 at the Teaching and Research Farms of Obafemi Awolowo University (OAU), Ile-Ife (7°31′N, 4°31′E, 256 m asl, and 1000–1250 mm annual rainfall) and Michael Okpara University of Agriculture, Umudike (05º29′N, 07º33′E; 122 m asl, and 2177 mm annual rainfall) in Nigeria. Elite open-pollinated maize varieties (14) derived from late-maturing maize germplasm sources were drawn from the drought-tolerant and pro-vitamin A breeding populations of the International Institute of Tropical Agriculture (IITA), Ibadan, Nigeria (Table 1). All possible crosses were made in a diallel fashion without reciprocal among the 14 varieties to produce 91 population hybrids during the growing season of 2017. All possible 91 crosses were made in both directions using bulked pollen of each parent population. Seeds from each cross and its reciprocal were bulked to represent a particular varietal hybrid (Table 1). The parental varieties, the hybrids, and three check cultivars were evaluated for their grain yield performance in six environments under both optimal and sub-optimal growing conditions in 2018 (Table 2). The group of checks comprised two improved OPVs obtained from IITA and a local variety commonly grown by rural farmers in the test locations. The growing conditions, which formed six environments, were based on the total amount of rainfall and the time of planting. Under the optimal growing conditions, the trials were established during the main planting season of maize with optimum amount of rainfall. Under the marginal conditions, the trials were planted at the onset of rainfall when the frequency of rain is erratic and soil moisture is sub-optimal for maize cultivation and towards the end of the rainy season, when flowering is targeted to coincide with drought spell. The environments were thus diverse with respect to the growing conditions and water availability, while drought stress experienced by the genotypes during the flowering stage in the marginal growing condition (late planting) also contributed to the differences between the locations. The general strategy of the conducted trial series was thus to replace testing in multiple year-by location combinations by testing in a number of extreme environments that were representative for agro-ecological conditions that might otherwise only been observed over a longer time period. The National Root Crops Research Institute agrometeorological unit (https://nrcri.gov.ng/index.php/agro-meteorology/) provided meteorological data for the location Umudike, whereas that of the Ile-Ife location was provided by the Micrometeorology Unit, Physics Department, OAU, being the closest weather stations to the experimental sites. The experiment was laid as a randomized incomplete block design (9 × 12 alpha lattice) with three replications in each environment. Experimental units consisted of two-row plots, each 5 m in length with a spacing of 0.75 m. The distance between two adjacent plants within a row was 0.50 m in all trials. Three seeds were planted, and the seedlings later thinned to two per hill approximately 2 weeks after emergence to achieve a final plant population density of about 53,333 plants ha⁻¹. The number of ears per plant (EPP) was estimated as the ratio of the number of harvested ears per plot to the number of harvested plants per plot. Grain yield was computed from the ear weight and converted to kg ha⁻¹. A shelling percentage of 80% was assumed for all cultivars and the grain yield was adjusted to 15% moisture using the following formula:

$$\upgamma = \varepsilon \times \frac{{\left( {100 - n} \right)}}{85} \times \frac{{\left( {10000} \right)}}{\varphi } \times 0.80$$

where γ = grain yield (kg ha⁻¹), ϵ = ear weight (kg m⁻²), n = moisture at harvest, φ = plot area (m²).

Table 1 Characteristics of the three check varieties as well as the 14 parents used for the diallel crosses that were tested in the rainforest agro-ecology of Nigeria in 2018

Table 2 Characteristics of the test environments used for the evaluation of the genotypes in 2018

Statistical analysis of the individual trials

The phenotypic data of each individual environment were analysed by a linear mixed model of the form:

$${\text{y}}_{\text{jkl}} = {{\upmu }} + {{\upalpha }} \cdot {\text{x}}_{\text{jkl}} + {\text{g}}_{\text{j}} + {\text{r}}_{\text{k}} + {\text{b}}_{\text{kl}} + {\text{e}}_{\text{jkl}}$$

(1)

where ${\text{y}}_{\text{jkl}}$ are the phenotypic observations of grain yield, ${{\upmu }}$ is the grand mean, ${\text{r}}_{\text{k}}$ the fixed effect of the kth replicate, ${\text{b}}_{\text{kl}}$ the random effect of the lth block nested within the kth replicate, and ${\text{e}}_{\text{jkl}}$ the residual effect. The effect ${\text{g}}_{\text{j}}$ of the jth genotype was firstly modelled as random to estimate the genotypic variance ${{\upsigma }}_{\text{g}}^{2}$ and subsequently fixed to derive Best Linear Unbiased Estimates (BLUEs). When considered as fixed, the genotypic effect was further partitioned into parent, hybrid, check and their orthogonal contrasts in order to explain the proportion and significance of variation of each components of the genotype. The number of ears per plant ${\text{x}}_{\text{jkl}}$ and the corresponding regression coefficient ${{\upalpha }}$ served as a covariate in order to compensate for an unequal plant stand between plots. Broad-sense heritability of an individual environment, henceforth denoted as repeatability, was calculated with the following formula (Piepho and Mohring 2007):

$${\text{h}}^{2} = \frac{{{{\upsigma }}_{\text{g}}^{2} }}{{{{\upsigma }}_{\text{g}}^{2} + \frac{{{{\upsigma }}_{\text{e}}^{2} }}{\text{r}}}}$$

(2)

where ${{\upsigma }}_{\text{e}}^{2}$ is the residual variance and r is the number of replications.

Two-stage analysis across trials

Following a two-stage analysis, the BLUEs of the individual environments were subsequently used for an across environment analysis with the linear mixed model:

$${\text{y}}_{\text{ij}} = {{\mu }} + {\text{u}}_{\text{i}} + {\text{g}}_{\text{j}} + {\text{e}}_{\text{ij}}$$

(3)

where ${\text{y}}_{\text{ij}}$ are the BLUEs of grain yield derived from the analysis of the individual environments, ${{\mu }}$ the grand mean, and ${\text{g}}_{\text{j}}$ the effect of the jth genotype that was modelled as fixed to derive BLUEs and subsequently as random to estimate variance components. The fixed effect ${\text{u}}_{\text{i}}$ designated the ith environment and the residual effect ${\text{e}}_{\text{ij}}$ that was in this case confounded with the genotype-by-environment interaction effect followed a normal distribution with ${\mathbf{e}} \sim {\text{N}}\left( {0, {{\upsigma }}_{\text{e}}^{2} } \right)$. The genotypes were subsequently divided into three genotypic groups comprising the parents, hybrids and checks for assessing the stability variance. The statistical model for the analysis can be described with the following mixed model (Mühleisen et al., 2014b):

$${\text{y}}_{\text{hij}} = {{\mu }} + {\text{q}}_{\text{h}} + {\text{u}}_{\text{i}} + {\text{g}}_{\text{hj}} + {\text{qu}}_{\text{hi}} + {\text{f}}_{\text{hij}}$$

(4)

where ${{\mu }}$ is the grand mean, ${\text{q}}_{\text{h}}$ is the fixed effect of the h^th group, and ${\text{g}}_{\text{hj}}$ the fixed effect of j^th genotype within the h^th group. The effect ${\text{qu}}_{\text{hi}}$ of the group-by-environment interaction as well as the group-by-genotype-by-environment interaction ${\text{f}}_{\text{hij}}$ were modelled as random. Group specific estimates of the stability variance were obtained modelling heterogeneous genotype-by-environment interaction variances for each group following the suggestion by Mühleisen et al. (2014b) with a variance–covariance matrix of the form:

$$\left( {\begin{array}{*{20}c} {{{\upsigma }}_{{{\text{f}}_{{{\text{g}}\left( 1 \right)}} }}^{2} } & 0 & 0 \\ 0 & {{{\upsigma }}_{{{\text{f}}_{{{\text{g}}\left( 2 \right)}} }}^{2} } & 0 \\ 0 & 0 & {{{\upsigma }}_{{{\text{f}}_{{{\text{g}}\left( 3 \right)}} }}^{2} } \\ \end{array} } \right)$$

(5)

where ${{\upsigma }}_{{{\text{f}}_{{{\text{g}}\left( 1 \right)}} }}^{2}$, ${{\upsigma }}_{{{\text{f}}_{{{\text{g}}\left( 2 \right)}} }}^{2}$, and ${{\upsigma }}_{{{\text{f}}_{{{\text{g}}\left( 3 \right)}} }}^{2}$ designate the residual variance, henceforth called the stability variance, of the three groups with ${\mathbf{f}}_{{\mathbf{h}}} \sim {\text{N}}\left( {0, {{\upsigma }}_{{{\text{f}}_{{{\text{g}}\left( {\text{h}} \right)}} }}^{2} } \right)$. The stability variance of a group was thus defined as its genotype-by-environment interaction analogues to the stability variance of individual genotypes described by Shukla (1972).

One-stage analysis across trials

The two-stage analysis was subsequently compared with a one-stage analysis that was conducted by employing a mixed model of the form:

$${\text{y}}_{\text{ijkl}} = {{\mu }} + {{\upalpha }}_{\text{i}} \cdot {\text{x}}_{\text{ijkl}} + {\text{u}}_{\text{i}} + {\text{g}}_{\text{j}} + {\text{gu}}_{\text{ij}} + {\text{r}}_{\text{ik}} + {\text{b}}_{\text{ikl}} + {\text{e}}_{\text{ijkl}}$$

(6)

where ${\text{y}}_{\text{ijkl}}$ are the phenotypic observations of grain yield, ${{\mu }}$ the grand mean, and ${\text{g}}_{\text{j}}$ the effect of the jth genotype that was modelled as fixed to derive BLUEs and subsequently as random to estimate variance components as beforehand. The fixed effect ${\text{u}}_{\text{i}}$ designated the ith environment and ${\text{gu}}_{\text{ij}}$ the random genotype-by-environment interaction effect. The number of ears per plant ${\text{x}}_{\text{ijkl}}$ served again as a covariate, though this time with an environment specific regression coefficient ${{\upalpha }}_{\text{i}}$. The effects ${\text{r}}_{\text{ik}}$ and ${\text{b}}_{\text{ikl}}$ designated again the replicate and block effect, while the residual effect ${\text{e}}_{\text{ijkl}}$ followed a normal distribution with ${\mathbf{e}} \sim {\text{N}}\left( {0, {{\upsigma }}_{\text{e}}^{2} } \right)$. The stability variance was likewise assessed by dividing the genotypes into three groups of parents, hybrids, and checks. The statistical model for the analysis can be described with the following mixed model (Mühleisen et al. 2014a):

$${\text{y}}_{\text{hijkl}} = {{\mu }} + {{\upalpha }}_{\text{i}} \cdot {\text{x}}_{\text{hijkl}} + {\text{q}}_{\text{h}} + {\text{u}}_{\text{i}} + {\text{g}}_{\text{hj}} + {\text{qu}}_{\text{hi}} + {\text{f}}_{\text{hij}} + {\text{r}}_{\text{ik}} + {\text{b}}_{\text{ikl}} + {\text{e}}_{\text{hijkl}}$$

(7)

where the designation of all previous described effect was retained, while the additional effects ${\text{qu}}_{\text{hi}}$ of the group-by-environment interaction as well as the group-by-genotype-by-environment interaction ${\text{f}}_{\text{hij}}$ were modelled random. Group specific estimates of the stability variance were again obtained modelling heterogeneous genotype-by-environment interaction that were in the case of the one-stage analysis not confounded with the residual variance.

Computation of the panmictic mid-parent and commercial heterosis

Heterosis was finally computed with BLUEs derived from the single-step model [6] by:

$${\text{Het}}_{\text{MP}} = 100 \cdot \left( {{\hat{\text{H}}} - \overline{\text{MP}} } \right)/\overline{\text{MP}}$$

([8])

and

$${\text{Het}}_{\text{C}} = 100 \cdot \left( {{\hat{\text{H}}} - \hbox{max} \left[ {{\hat{\text{C}}}} \right]} \right)/\hbox{max} \left[ {{\hat{\text{C}}}} \right]$$

([9])

where the panmictic mid-parent heterosis was expressed as the relative difference between the estimated hybrid performance ${\hat{\text{H}}}$ and the mid-parent value $\overline{\text{MP}}$, whereas the commercial heterosis ${\text{Het}}_{\text{C}}$ was computed as the difference between the hybrid performance and the estimated performance of the best check variety $\hbox{max} \left[ {{\hat{\text{C}}}} \right]$. Statistical analyses were performed using the statistical package sommer for the R programming environment (R Development Core Team 2016). A combined ANOVA across the six test environments was performed using SAS PROC GLM (SAS Institute 2012). The variation due to the genotype was further partitioned into components due to the parents, hybrids, checks and their interactions. Lastly, a GGE biplot analysis of the selected genotypes was conducted using the GGEBiplots (Frutos et al. 2014) package for R.

Results

Results of the combined analysis of variance revealed significant mean squares (P < 0.01) for environment, genotype and genotype-by-environment interaction effects for grain yield (Table 3). The test environments contributed 68.2% of the total variation in the sum of squares; genotypes accounted for 3.6% and the genotype-by-environment interaction source for 10.3% of the total variation. When the genotype effect was partitioned into its components, hybrids accounted for the largest proportion of variation (91.8%), followed by parent (4.3%) and hybrid vs parent (3.0%). Although hybrid vs check and check vs hybrid and parent had significant contributions to the genotypic effect, their percentage contribution to variation is considerably small (< 1%).

Table 3 Percentage sum of squares from the combined ANOVA of grain yield (t ha⁻¹) of the 108 maize genotypes evaluated at six environments in Nigeria

The repeatability of the grain yield trials ranged from 39% to 80%, and the broad sense heritability across environments in the one-stage and two-stage analyses were estimated as 50% and 42% respectively (Table 4), underlying the high quality of the assessed phenotypic data for all subsequent analysis. Grain yield was on average 265% higher in Ile-Ife than the location Umudike. At location Ile-Ife, the average yield during the optimal growing condition was slightly lower than that of the early growing condition but 72% higher in comparison to the late growing condition. The average yield during the optimal growing condition was on the other hand higher in Umudike than that of the two marginal growing conditions. The variation in environmental conditions was reflected by large differences in the average grain yield observed across the growing conditions. The difference between the lowest and the highest yielding environment was 3.9 t ha⁻¹. The correlations among and across the environments are shown in Table 5. Among the environments, there were generally weak associations, which depicted independencies and distinctiveness of these environments with respect to the yield potential of the tested genotypes, while environments with a similar planting date showed a comparably higher correlation even when they were located at different sites and the total amount of rainfall differed substantially (Table 2).

Table 4 Summary statistics for the tested check varieties, open-pollinated parental varieties and population hybrids within each location-by-growing condition combinations as well as across all environments

Table 5 Pearson correlation of the average grain yield performance among the different environments and across environments for all 108 tested genotypes

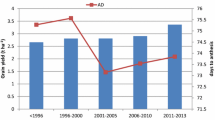
The stability variances and the average grain yield of the different genotype groups in both the one-stage and two-stage analyses are presented in Fig. 1. In the one-stage analysis, the average grain yield of the hybrids (2.33 t ha⁻¹) was higher than that of the parents as well as the checks i.e. the hybrids out-yielded the parents by 5.4% and the checks by 15.9%. In a similar trend, the average grain yield of the hybrids (2.32 t ha⁻¹) was higher than that of the parents (2.19 t ha⁻¹) and checks (2.16 t ha⁻¹) in the two-stage analysis. The stability analysis of the individual genotype groups revealed furthermore that the grain yield performance of the hybrids was much more stable than both the parents and the check varieties in either one of the analyses, while the checks were the least stable according to their estimated stability variance. When the parents and the checks were moreover combined to form a common group, the hybrids were still superior in terms of both grain yield and stability (Supplementary Fig. S1).

Fig. 1

Stability variances (a) and average grain yield (t ha⁻¹) of parents, hybrids and checks (b) tested in six environments with their corresponding standard errors using either a one-stage or two-stage analysis

Notwithstanding, several hybrids out-yielded the parental populations and the check varieties (Fig. 2). Approximately 54% of the hybrids yielded above average, in contrast to 36% of the parental populations and the average grain yield across the environments was 2.18 t ha⁻¹ and 2.33 t ha⁻¹ for the parental populations and their hybrids, respectively (Fig. 2a). The panmictic mid-parent heterosis ranged from  − 29.31% for entry H65 (a cross between parent 7 and parent 9) to 72.69% for entry H28 (a cross between parent 3 and parent 6) with an average of 5.86% (Fig. 2a). The commercial heterosis varied from − 35.43% for the cross between parent 3 and parent 13 to 53.38% for the cross between parent 4 and parent 6 with an average of 0.84% (Fig. 2c). Markedly, out of the 91 hybrids, 48 showed a positive commercial heterosis.

Fig. 2

Violin plot of the average yield distribution of the population hybrids (blue), the performance of the 14 parental populations (red horizontal bars), and the three check varieties (green horizontal bars) (a) as well as the relative mid-parent (b) and commercial heterosis (c) of the 91 population hybrids. (Color figure online)

Additional details of the individual grain yield of all the genotypes in each environment and their average performance across the environments can be found in Supplementary Table S1. In summary, hybrid H38 (STR SYN - Y2 x TZL Comp - 3 C3 DT) had the highest average grain yield across the environments (3.38 t ha⁻¹), while check 1 (DT STR SYN 2–7) showed the lowest grain yield with 1.55 t ha⁻¹ (Table 6). Approximately 10% of the best yielding parental populations and the hybrids were plotted alongside the three check varieties to show their “mean vs stability” estimates (Fig. 3). The GGE biplot analysis indicated furthermore that entry H38 was the highest yielding genotype but relatively unstable when compared to most of the tested entries as well as the check varieties. The hybrids H15, H39, and H69 combined on the other hand a high grain yield with a relative stable performance across environments making them interesting candidates for further studies.

Table 6 The yield of 10% best performing maize hybrids, parents and the checks within and across the environments using a single-step analysis

Fig. 3

Mean vs stability display of the GGE biplot showing the performance (the blue horizontal line or abscissa points to higher mean yield across environments) and stability (the blue vertical line or ordinate points to poorer stability in either direction) of 10% best yielding population hybrids and parents, alongside the three check varieties across the test environments as reported in Table 6. I-Early = Early planting at Ile-Ife; I-Opt = Planting under optimal growing conditions at Ile-Ife; I-Late = Planting late season at Ile-Ife; U-Early = Early planting at Umudike; U- Opt = Planting under optimal growing conditions at Umudike; U-Late = Planting late season at Umudike. (Color figure online)

Discussion

Like in other SSA countries, the average grain yield of maize in Nigeria is with approximately 1.7 t ha⁻¹ generally low when e.g. compared to the average yield in United States (9.3 t ha⁻¹) over the same time period (1986–2011) (Olaniyan 2015). In recent years, this has culminated into breeding for high-yielding cultivars, as maize is a major staple food for about 50% of the Sub-Saharan African population (IITA 2009) and its vast majority is grown on small-scale rural farms. The current study aimed therefore to evaluate the genetic potential of maize population hybrids, which are a promising alternative due to low priced and more accessible improved seed for small-scale subsistence farmers.

The vulnerability of agroecosystems in which small scale-famers in SSA cultivate maize to variations in weather is currently of increasing concern, as optimal production scenarios associated with unpredictable changes in climate may become more common (Gaudin et al. 2015). The environments used in this study were diverse with respect to the growing conditions and geographic locations. The agronomic practices were the same for all the environments and these represent the recommended practices adopted by maize farmers in the locations. Mühleisen et al. (2014a) emphasized the importance of diverse agroecosystems for assessing yield stability of crops with high accuracy in such scenarios. Result from correlation revealed that there was no significant relationship among the three growing conditions at Ile-Ife, indicating that the growing conditions are unique and distinct. It may also imply that different cultivar must be recommended for the different growing conditions. The significant relationship between late planting and optimal growing conditions (r = 0.37**) suggest that there can be common cultivars that will perform well under both growing conditions at Umudike. However, caution must be exercised because the correlation coefficient is small and the coefficient of determination (R² = 13.69%) indicate that the relationship is not reliable. From the result of correlation analysis of the individual environments with the across environment analysis, it was observed that although all the individual environments had a significant correlation with the trial series, optimal growing conditions at Ile-Ife had the highest correlation coefficient and by implication highest R² followed by optimal growing conditions at Umudike. This implies that optimal condition at Ile-Ife were on average the most representative of all environments for evaluating the maize genotypes.

Different maize genotypes typically display differential responses to varying environmental conditions. As a result, the major challenge for maize breeders has always been the selection of superior genotypes for narrow or wide adaptation and the identification of the best testing sites that could be used to identify superior and stable genotypes (Badu-Apraku et al. 2015a). The significant mean squares detected in the present study for the 108 genotypes indicated accordingly differential responses of the genotypes to environments and the need to identify high-yielding and stable genotypes across different test environments (Badu-Apraku et al. 2013). The presence of a highly significant genotype-by-environment interaction for grain yield of the cultivars is a confirmation of the need for the extensive testing of these cultivars in multiple environments and/or over several years before a particular cultivar can be recommended to farmers. This also confirms the need for breeders in the region to take genotype-by-environment interaction into serious consideration in evaluating cultivars, and to estimate its magnitude, relative to the magnitude of the genotypic and environmental main effects affecting grain yield. Assessment of the total sum of squares revealed that the environmental sums of squares accounted for 68.2% of the variation for grain yield with the genotype contributing only 3.6%, reflecting a much wider range of environmental main effects over genotypic main effects. This finding is in agreement with the results of several multi-environment trials already conducted in SSA (Haussmann et al. 2001; Badu-Apraku et al. 2011a, b, 2013; Sserumaga et al. 2018).

The result of partitioning the variation in the genotypic effect revealed that hybrids accounted for over 90% of the variation among the 108 evaluated genotypes. Although the parents accounted for 4% of the variation in genotype, the variation was not significant. It is therefore striking to note that even though there is no significant phenotypic variation among the 14 parents used, their hybrids exhibited a wide variability. The significant difference in the hybrid vs parent orthogonal contrast is a strong indication of heterosis in the maize germplasm evaluated. It further implies that the varieties used as parents can be classified into heterotic groups and through reciprocal recurrent selection, inbred lines can be extracted from each heterotic group and better hybrids can be developed from such inbreds. Heterosis in maize has been associated with increase in yield potential and adaptation to stress (Araus et al. 2010). The estimation of heterosis in this study revealed that the population hybrids exhibited both mid-parent and commercial heterosis for grain yield similar to the results reported by Ali et al. (2012).

Aside for grain yield, yield stability was compared for different genotype groups in the study at hand rather than individual genotypes in order to obtain more precise estimates of the stability variance in comparison to the latter approach. It was evident that the population-hybrids exhibited the highest level of stability followed by the parental populations. At the same time, the hybrids gave the highest average grain yield across all test environments. The high and stable performance of these population hybrids underlines their improved genetic constitution, potentially making them a highly useful and promising cultivar type for small-scale farmers in SSA, while the objective to create specific varieties adopted by farmers might be reached by following a participatory breeding or variety selection approach. Some previous studies also reported higher yield stability for hybrids than that of their parents when measuring the yield stability based on the stability variance (Oury et al. 2000; Gowda et al. 2010; Mühleisen et al. 2014a). However, a study by Koemel et al. (2004) using the regression approach as suggested by Eberhart and Russell (1966) observed no differences between hybrids and lines for wheat. In a similar work on sorghum by Haussmann et al. (2000), the hybrids out-yielded their parent lines with an average relative hybrid superiority of 54%. Wide ranges of stability variance were recorded within the genotype groups, with hybrids as well as line blends having slightly higher stability than pure stands of inbred lines. The authors speculated that improvements in yield stability might have been associated with an increase in heterozygosity and heterogeneity. According to Léon (1994), this effect of heterozygosity on grain yield stability varies among crop species depending on their reproductive system suggesting that in an outcrossing species like maize, heterozygosity has a strong positive effect on grain yield stability. Developing variety types with high degrees of heterozygosity and genetic heterogeneity for adaptation traits can additionally help in achieving better individual and population buffering capacity (Haussmann et al, 2012). This point was further buttressed in a study carried out in winter wheat by Döring et al. (2015), where the stability also increased with an increase in the heterogeneity of the studied wheat cultivar groups.

Conclusion

It is concluded from this study that there is wide genetic variability among the 108 evaluated genotypes with the widest variation being exhibited among the population hybrids. They showed furthermore large potential to deliver higher grain yield and stability than their parents as well as the farmer-grown check varieties. The study revealed moreover a significant panmictic mid-parent and commercial heterosis indicating that some of the evaluated superior hybrids can be recommended for further testing and ultimate release for resource-poor farmers in the rainforest agro-ecological zones of Nigeria since their development and production are easier and cheaper in comparison to conventional single-cross hybrids.