Abstract
Defenders of deontological constraints in normative ethics face a challenge: how should an agent decide what to do when she is uncertain whether some course of action would violate a constraint? One common response to this challenge proposes a threshold principle on which it is subjectively permissible to act iff the agent’s credence that her action would be constraint-violating is below some threshold t. But the threshold approach seems arbitrary and unmotivated: where does the threshold come from, and why should it take any one value rather than another? Threshold views also seem to violate “ought” agglomeration, since a pair of actions each of which is below the threshold for acceptable moral risk can, in combination, exceed that threshold. In this paper, I argue that stochastic dominance reasoning can vindicate and lend rigor to the threshold approach: given characteristically deontological assumptions about the moral value of acts, it turns out that morally safe options will stochastically dominate morally risky alternatives when and only when the likelihood that the risky option violates a moral constraint is greater than some precisely definable threshold (in the simplest case, .5). The stochastic dominance approach also allows a principled, albeit intuitively imperfect, response to the agglomeration problem. Thus, I argue, deontologists are better equipped than many critics have supposed to address the problems of decision-making under uncertainty.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
We are often uncertain about what we morally ought to do. Such uncertainty can arise from uncertainty about the empirical facts: for instance, is this substance that I am about to put in my friend’s coffee sweetener, or is it arsenic (Weatherson 2014)? It can also arise from uncertainty about basic moral principles—what we might call “purely moral” uncertainty: for instance, given some specification of all the relevant empirical facts, is it permissible to tell my friend a white lie about his new haircut?
Consequentialists have traditionally had the most to say about both kinds of uncertainty. With respect to empirically-based moral uncertainty, consequentialists standardly claim that we should maximize expected value—i.e., a probability-weighted sum of the values of each possible outcome of an option. The study of purely moral uncertainty is still in its infancy, but the dominant approaches in this literature to date have shared an almost exclusively consequentialist, expectational flavor: Lockhart (2000), Ross (2006), Sepielli (2009), and MacAskill (2014), for instance, all defend expectational approaches to decision-making under purely moral uncertainty.Footnote 1
Expectational reasoning, however, seems ill-suited to—if not actively incompatible with—non-consequentialist moral theories like Kantian deontology, most obviously because (unlike, say, classical utilitarianism) these theories are not naturally interpreted as assigning finite cardinal degrees of rightness and wrongness to options that can be multiplied by probabilities and summed to yield expectations. For this reason among others, several philosophers have doubted whether Kantians et al. can provide any plausible decision rule for epistemically imperfect agents.
The purpose of this paper, however, is to show one way in which deontologists can say something plausible, precise, and well-motivated about decision-making under uncertainty, of both the empirical and purely moral varieties. I will propose that stochastic dominance reasoning provides powerful motivation for a threshold principle of choice under uncertainty, which implies inter alia that when an agent A faces a choice between options O and P, where P is certainly morally permissible and the status of O is uncertain, A subjectively ought not choose O if her credence that O is objectively prohibited is greater than or equal to .5.
In the next section, I describe in more detail the challenge to deontology posed by both kinds of moral uncertainty. §3 introduces stochastic dominance and motivates it as a requirement of rationality. In §4, I show that stochastic dominance reasoning yields substantive and plausible conclusions for agents making decisions under uncertainty about deontological constraints, which at least in the simplest cases take the form of a straightforward threshold principle. Finally, §5 addresses an objection to threshold principles raised by Jackson and Smith (2006), that such principles seem to violate “ought” agglomeration. I suggest a solution to this problem that follows naturally from the approach developed in preceding sections and which, though intuitively imperfect, strikes me as an improvement over other extant solutions.
2 Absolutist Deontology and Uncertainty
Deontological moral theories, as I will stipulatively define them for purpose of this paper, are those that endorse constraints: option types, characterized non-relationally (and more particularly, without reference to the consequences of alternative options), whose tokens are prima facie prohibited, and for which the presumptive prohibition cannot be rebutted merely by the fact that all alternative options would have worse consequences.Footnote 2 A simple test for whether a theory endorses a constraint against options of type X is whether it holds that one ought to perform a single token of X, in order to prevent multiple future tokens of X—if tokens of X are bad in isolation, a characteristically consequentialist theory will endorse X-minimizing tokens of X, while a deontological theory that endorses a constraint against X will not. An absolutist deontological theory, then, is one that endorses absolute constraints—option types whose tokens are always prohibited (e.g., intentionally killing an innocent person) or always obligatory (e.g., keeping a valid promise). In what follows, I will focus mostly (though not exclusively) on absolutist deontological theories.Footnote 3
The problem of uncertainty for deontologists, then, is this: How should an agent decide what to do when she’s unsure whether a some option would violate a constraint? For instance, consider the following case.
Possible Promise I have unexpectedly found myself in possession of tickets to the Big Game this afternoon. But as I am celebrating my good fortune, it occurs to me that I may have promised my friend Petunia that I would help her paint her house later today, just when the game is being played. I vaguely remembering making such a promise, but I’m not sure. I have no way to contact Petunia and must decide, here and now, whether to go to the game and risk breaking a promise, or go to Petunia’s house, avoiding the moral risk but missing the game.
Possible Promise is an instance of empirically-based moral uncertainty, but there are nearly identical cases of purely moral uncertainty. For instance:
Dubious Promise A week ago, Petunia sent me a text message asking if I would help paint her house today. I replied that I would. Unbeknownst to Petunia, however, I was in the hospital at the time, recovering from a minor operation and under the influence of a strong narcotic painkiller. By the time the influence of the painkiller subsided, I had completely forgotten my conversation with Petunia, and only just remembered it a moment ago, while planning my trip to the game.
I take it that, under these circumstances, I may reasonably be uncertain whether I am obligated to skip the game and help Petunia, even if I am certain of a background deontological conception of morality on which an ordinary, fully capacitated promise would have been morally binding. (If you don’t immediately feel any uncertainty about this case, adjust the strength of the painkillers as needed.) Because my moral uncertainty does not trace back to any empirical uncertainty (e.g. about what I said to Petunia, my mental state at the time, or her expectations of my future behavior), it is purely moral uncertainty, uncertainty about the content of a basic moral principle.
In either of these cases, the question is what to do given my uncertainty about what morality requires of me—that is, what ought I do, in the subjective or belief-relative sense of “ought,” given that I’m unsure what I ought to do, in the objective or fact-relative sense of ought?Footnote 4 There are various answers the deontologist might give, but it is generally agreed that she should not give any of the following: (1) It’s subjectively permissible to go to the game iff I’m certain that I did not make a binding promise to Petunia, and hence that going to the game is objectively permissible. (By this standard, all or nearly all options are subjectively prohibited.) (2) It’s subjectively permissible to go to the same iff I same some positive credence that I did not make a binding promise, and hence that it’s objectively permissible. (By this standard, deontological constraints would never or almost never generate subjective prohibitions, and hence would be in effect practically inert.) (3) It’s subjectively permissible to go to the game iff I did not in fact make a binding promise to Petunia. (This standard does not amount to a decision rule that’s usable by ordinary human agents.)
Absent a better decision theory than these, deontology is in trouble. Though various theories are conceivable, a major focus of the recent literature has been on threshold views, according to which, for any objectively prohibited option type X there is some threshold t ∈ (0,1) such that one subjectively ought not choose a practical option O if the probability that O is an instance of X is greater than t.Footnote 5
The threshold view faces an important technical objection, which we will address in §5. But it also faces much simpler worries about motivation that have yet to be seriously addressed. First, why should there be any credal threshold at which options abruptly switch status, from subjectively permissible to subjectively prohibited? What plausibility can there be, say, in the idea that if I have .27 credence that going to the game would break a promise to my friend, there is nothing at all wrong with going, but if I have .28 credence, I am strictly prohibited from going? Second, and closely related, what could serve to make any particular credal threshold the right one? Why should the threshold be set here rather than there? And how can we ever hope to know where it has been set?Footnote 6 The apparent inadequacies of the threshold view lead Jackson and Smith (2006, 2016) and Huemer (2010), inter alia, to conclude that the problem of uncertainty poses a fatal objection at least to absolutist forms of deontology.
In the next two sections, however, I will suggest a way of justifying threshold principles that can assuage these worries.
3 Stochastic Dominance
The idea of dominance reasoning is familiar from game-theoretic contexts like the prisoner’s dilemma: If I am uncertain about the state of the world, but certain that, given any possible state of the world, option O is more choiceworthy than option P, then O is said to strictly dominate P.Footnote 7 If I am certain (i) that, given any possible state of the world, O is at least as choiceworthy as P, and (ii) that given some state(s) of the world O is more choiceworthy, then O is said to weakly dominate P.
Stochastic dominance generalizes these statewise dominance relations as follows: Option O stochastically dominates option P iff, relative to the agent’s subjective or epistemic probabilitiesFootnote 8:
-
1.
For any degree of choiceworthiness x, the probability that O has a choiceworthiness of at least x is equal to or greater than the probability that P has a choiceworthiness of at least x, and
-
2.
For some x, the probability that O has a choiceworthiness of at least x is strictly greater than the probability that P has a choiceworthiness of at least x.Footnote 9
An illustration: Suppose that I am going to flip a fair coin, and I offer you a choice of two tickets. The Heads ticket will pay $1 for heads and nothing for tails, while the Tails ticket will pay $2 for tails and nothing for heads. Assume that the choiceworthiness of these options is simply determined by your monetary reward. The Tails ticket neither strictly nor weakly dominates the Heads ticket because, if the coin lands Heads, the Heads ticket will yield a better payoff. But the Tails ticket does stochastically dominate the Heads ticket. There are three possible payoffs, which in ascending order of desirability are: winning $0, winning $1, and winning $2. The two tickets offer the same probability of a payoff at least as good as $0, namely 1. Likewise, they offer the same probability of an outcome at least as good as $1, namely .5. But the Tails ticket offers a greater probability of a payoff at least as good as $2, namely .5 rather than 0.
The principle that agents subjectively ought not choose stochastically dominated options is on an extremely strong a priori footing. Formally, a stochastically dominant option will be preferred to a dominated alternative by any agent whose preferences are monotonically increasing with respect to objective choiceworthiness, i.e. for whom a given probability of a higher degree of choiceworthiness is always preferred to the same probability of a lower degree of choiceworthiness, all else being equal (Hadar and Russell 1969, p. 28).
More informally, it is unclear how one could ever reason one’s way to choosing a stochastically dominated option O over an option P that dominates it. For any feature of O that one might point to as grounds for choosing it, there is a persuasive reply: However choiceworthy O might be in virtue of possessing that feature, P is at least as likely to be at least that choiceworthy. And conversely, for any feature of P one might point to as grounds for rejecting it, there is a persuasive reply: However unchoiceworthy P might be in virtue of that feature, O is at least as likely to be at least that unchoiceworthy. To say that P stochastically dominates O is in effect to say that there is no feature of O that can provide a unique justification for choosing it over P.
4 Stochastic Dominance and Deontological Uncertainty
Let’s return now to the pair of cases from §2, in which I am unsure whether I am obligated to skip the Big Game to help Petunia paint her house, either because I am empirically uncertain whether I made a promise or because I am purely-morally uncertain whether some past act constituted a morally binding promise.
Let’s assume, for the moment, that I believe with certainty in an absolute obligation to keep one’s valid promises, if one can. Being absolute, this obligation is lexically stronger than any non-moral reason (like the reasons stemming from my desire to see the game). An act of promise-keeping, therefore, is more choiceworthy (supported by stronger all-things-considered objective reasons) than any option that violates a moral obligation or is morally neutral, and an act of promise-breaking is less choiceworthy (opposed by stronger all-things-considered objective reasons) than any option that fulfills a moral obligation or is morally indifferent.
Given these assumptions, we can construct a decision-theoretic representation of cases like Possible/Dubious Promise, along lines suggested by Colyvan et al. (2010). In their model, absolutist deontology is characterized by the following axiomatic extension of standard decision theory:
-
D1* If [outcome] Oij is the result of an (absolutely) prohibited act, then any admissible utility function u must be such that u(Oij) = −∞.
-
D2* If [outcome] Oij is the result of an (absolutely) obligatory act, then any admissible utility function u must be such that u(Oij) = +∞. (Colyvan et al. 2010, p. 512)Footnote 10
On this model, while absolutely obligatory options have “infinite” positive choiceworthiness and absolutely prohibited options have “infinite” negative choiceworthiness, options that neither violate nor fulfill absolute duties have finite choiceworthiness determined, presumably, by prudential reasons and perhaps by other sorts of moral reasons (e.g., consequentialist reasons of benevolence).
The idea of infinite positive or negative choiceworthiness need not be taken too literally. As Colyvan et al. point out (pp. 521ff), decision-theoretic models may be descriptively adequate without being explanatory: A Kantian does not avoid lying, for instance, because she believes that acts of lying possess an infinite negative quantity of some normative property. Nevertheless, the fact that, for a Kantian, moral obligations and prohibitions are lexically stronger than prudential reasons can be accurately represented by treating the choiceworthiness of an action from duty as the upper bound on the scale of reason strength, and the choiceworthiness of an action against duty as the lower bound.
This representation in hand, we can employ stochastic dominance reasoning to draw conclusions about how a committed deontologist should respond to moral uncertainty. Suppose that, in the cases from §2, the prudential choiceworthiness of seeing the Big Game is +20, while the prudential choiceworthiness of helping Petunia paint is +5 (and that I know these prudential facts with certainty). It follows that the option of helping Petunia will stochastically dominate the option of going to the game if and only if the probability that I made a binding promise to Petunia is greater than or equal to .5.
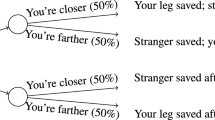
My decision has four possible outcomes (Table 1), which in order from best to worst are: (i) I did make a promise to Petunia, but I go to the game, violating that promise (−∞). (ii) I did not make a promise to Petunia, but skip the game to help her paint anyway (+5). (iii) I did not make a promise to Petunia, and go to the game, violating no obligation (+20). (iv) I did make a promise to Petunia, and I skip the game to help her paint, thereby fulfilling that obligation (+∞).Footnote 11 To check for stochastic dominance, we can consider, for each of these outcomes, the probability that either option will yield an outcome at least that choiceworthy.
Suppose, then, that the probability that I made a binding promise to Petunia is exactly .5. In this case, helping Petunia paint (option P) stochastically dominates going to the game (option G): P and G have the same probability of choiceworthiness equal to or greater than −∞ (namely, probability 1); P has a greater probability of choiceworthiness equal to or greater than +5 (1 vs. .5); P and G have the same probability of choiceworthiness equal to or greater than +20 (.5); and P has a greater probability of choiceworthiness equal to or greater than +∞ (.5 vs. 0) (Table 2). Thus, P stochastically dominates G.
On the other hand, suppose the probability that I made a binding promise to Petunia is only .49. In that case, G has a greater probability than P of choiceworthiness equal to or greater than +20 (.51 vs. .49), so P does not stochastically dominate G (Tables 3 and 4).
Notice that this reasoning applies to Dubious Promise, the case of purely moral uncertainty, no differently than it applies to Possible Promise, the case of empirically-based moral uncertainty. In either case, helping Petunia will stochastically dominate going to the game iff my credence that I am objectively obligated to help Petunia is greater than or equal to .5.Footnote 12 Thus, it seems, stochastic dominance reasoning gives the deontologist something definite, precise, and well-motivated to say about both kinds of uncertainty.Footnote 13
So far I have assumed that the background deontological theory I accept is absolutist. But none of the preceding arguments depend on this assumption. The same reasoning applies to a non-absolutist version of deontology on which (again following Colyvan et al. (2010, pp. 515–8)) the choiceworthiness of fulfilling/violating an obligation is represented, not by ± ∞, but merely by very large finite values—i.e., on which our reasons to meet our moral obligations are not lexically stronger than other sorts of reasons, but are nevertheless very strong compared to ordinary prudential reasons. Suppose, for instance, that promise-keeping has a choiceworthiness of +9001 and promise-breaking has a choiceworthiness of −9001. It is easy to see that the stochastic dominance argument for helping Petunia paint, when my credence that I made a binding promise is greater than or equal to .5, will go through mutatis mutandis.
Note, moreover, that the appeal to stochastic dominance rather than expectational reasoning gives us a principled way of avoiding one of the chief pitfalls of absolutism, namely, the risk of “Pascalian paralysis”: If violating a moral obligation is treated as an outcome with choiceworthiness −∞, then options that are almost certainly morally permissible but carry even a vanishingly small risk of violating a moral obligation will carry an expected choiceworthiness of −∞—the same expected choiceworthiness, in fact, as options that are certain to violate a moral obligation.Footnote 14 Worse still, if (as seems plausible) every possible option has some non-zero probability of fulfilling a moral obligation and some non-zero probability of violating a moral obligation, then the expected choiceworthiness of every possible option is undefined (∞ + (−∞)).
One way to avoid these Pascalian difficulties is to hold that a rational agent may never have non-zero credence in any outcome with infinite positive or negative choiceworthiness. But this seems implausible and has only ad hoc motivation. The better response is to modify our decision theory, either weakening or amending expectational decision theory in a way that allows an agent with modest credence in infinite positive and negative choiceworthiness values to nevertheless remain responsive to finitary considerations. Stochastic dominance is one such weakening of expectational decision theory: As far as stochastic dominance principles are concerned, it is rationally permissible for me to go to the game, despite the risk of infinite moral turpitude, so long as that risk has a probability less than .5.Footnote 15
The .5 probability threshold for subjective permissibility follows from stochastic dominance when an agent is certain of all her non-moral reasons. But when she is uncertain which option her non-moral reasons favor, stochastic dominance may become more demanding. Suppose, for instance, that I am uncertain whether I would have a better time at the game or painting with Petunia. Perhaps I believe there is a one-in-three probability that my team will lose, and I know that while seeing my team win would have a prudential choiceworthiness of +20, seeing them lose would have a choiceworthiness of −10. Simply ignoring the game and helping Petunia paint, on the other hand, is guaranteed a choiceworthiness of +5. In this case, the probability of objective obligation at which stochastic dominance will require that I help Petunia is reduced—specifically, to .4 rather than .5 (Tables 5 and 6 illustrate the threshold case; if the probability of a binding promise were any less than .4, then G would have a greater probability than P of choiceworthiness greater than or equal to +20). But in simplest cases of moral-prudential conflict—where I am certain that option O is morally permissible but prudentially inferior to option P, and certain that P is prudentially superior to O but uncertain whether it is morally permissible—we may say that stochastic dominance requires me to choose O iff the probability that P is objectively prohibited is greater than or equal to .5.Footnote 16
Of course, even with the addition of prudential uncertainty, the requirements of stochastic dominance appear to fall short of the practical stringency we intuitively expect at least some deontological constraints to possess. In the cases we have examined, stochastic dominance makes no distinction between “weaker” constraints (like the constraint against telling white lies) and “stronger” constraints (like the constraint against killing the innocent). And while thresholds like .5 or .4 may seem plausible for weaker constraints, they seem much less plausible when we think about stronger constraints—surely a deontologist should not conclude, for instance, that a judge need not worry about the constraint against punishing the innocent so long as the probability that her sentencing decision violates that constraint is a only .49, rather than .51.
The relatively generous threshold for acceptable risk of violating a deontological constraint need not strike everyone as so implausible: If we conclude that, when deontological risk is below the prohibitive threshold (e.g., .5), consequentialist moral reasoning takes over, then the practical implications in these cases can be no worse than the implications of our most preferred form of consequentialism. But moreover, I have only argued that rejecting stochastically dominated options is a requirement of rational choice under uncertainty, not that it is the only such requirement. Everything I have said so far leaves it open to the deontologist to argue for more demanding principles of moral caution, at least with respect to some constraints, on grounds other than stochastic dominance. And even if one takes the laxity of the stochastic dominance threshold to be intuitively unacceptable with respect to any deontological constraint, we have still made progress by establishing a kind of lower bound on deontological principles of choice under uncertainty: An agent must at least believe it to be more likely than not that some morally risky option violates no constraint, for that option to be subjectively permissible.
Still, it seems to me that this objection from the variable stringency of constraints represents a residual difficulty that it will be hard for deontologists to fully overcome. It is intuitive to hold that the practical force of deontological constraints must be sensitive to both (i) the probability of a constraint being violated by a given option and also (ii) the seriousness, importance, or stringency of the constraint in question. But taken together, these intuitions push us in the direction of an expectational view that, while it may still incorporate agent-centered normative considerations, has lost much of its distinctively deontological character (see note 3 supra). The deontologist may resist this pressure, but she must then be prepared to bite some intuitive bullets.Footnote 17
5 Option Individuation and Ought Agglomeration
So far I have argued that stochastic dominance provides a principled foundation for a threshold view, which can rebut the accusation that such views are unmotivated and arbitrary. But threshold views face another important difficulty, which we have yet to confront. This difficulty was first noted by Jackson and Smith (2006), who illustrate it with the following thought experiment.
Two Skiers Two skiers are headed down a mountain slope, along different paths. Each, if allowed to continue, will trigger an avalanche that will kill different groups of ten innocent people. The only way to save each group is to shoot the corresponding skier dead with your sniper rifle. The moral theory you accept (with certainty) tells you that you ought to kill culpable aggressors in other-defense, but are absolutely prohibited from killing innocent threats. Unfortunately, you are uncertain whether the skiers know what they’re doing—they may be trying to kill their respective groups, or they may just be oblivious. Specifically, you assign each skier the same probability p of acting innocently, and the probabilities for the two skiers are independent.
Suppose you accept a threshold view on which you are subjectively prohibited from killing a potential aggressor iff your credence that he is an innocent threat is greater than t. And suppose that in this case, p is just slightly less than t. It seems, then, that you ought to shoot Skier 1, and you ought to shoot Skier 2 (since in each case the probability of shooting an innocent threat is less than t). If you shoot both skiers, however, the probability that one of them is innocent and hence that you will have violated a deontological constraint is greater than t. So, it seems, you ought not perform the compound option: shoot Skier 1 and shoot Skier 2. This means, apparently, that threshold views violate the intuitively compelling principle of “ought” agglomeration: ought(P) ∧ ought(Q) ⊢ ought(P ∧ Q).
The problem goes deeper than this, as we’ll see, but before introducing further difficulties, I’ll describe my solution to this initial difficulty. I suggest that deontologists should endorse the following claim:
Minimalism The subjective deontic status of a simple option O in choice situation S is determined by the choiceworthiness prospects of the options in S. The subjective deontic status of compound options (sets or sequences of simple options belonging to different choice situations), if they have such statuses at all, is determined by the subjective deontic status of the simple options they comprise, plus principles of deontic logic.
Why should deontologists endorse Minimalism? Here’s a very rough argument: In just the same way that deontological assessment is agent-relative, it is also choice situation-relative. Just as deontological theories characteristically tell me not to violate a constraint even to prevent five other people from violating the same constraint, so they tell me not to violate a constraint even to prevent myself from violating the same constraint in five future choice situations. For instance, even if telling a lie now is the only way to extricate myself from a situation in which I would certainly end up telling five equally wrong lies, I still ought not lie. This unwillingness to countenance tradeoffs between constraint violations is, it seems to me, one of the central characteristic features of deontology.
If deontological moral assessment is always relativized to particular choice situations, then deontological theories simply don’t assign degrees of choiceworthiness to compound options that span multiple choice situations. Therefore, the subjective deontic status of compound options can’t be determined by their choiceworthiness prospects, since they don’t have such prospects in the first place. Insofar as deontological theories assign deontic statuses to compound options at all, then, it can only be based on the status of the simple options they comprise.
Minimalism lets us trivially avoid violations of “ought” agglomeration: Since the deontic status of S1 ∧ S2 is not determined by its choiceworthiness prospect, stochastic dominance reasoning and hence the threshold view are inapplicable. To say that ¬S1 ∧ ¬S2 stochastically dominates S1 ∧ S2 is either a conceptual mistake (if, as I have suggested, these compound options simply have no choiceworthiness prospects to compare for stochastic dominance) or simply irrelevant to the deontic status of S1 ∧ S2. If S1 ∧ S2 has a deontic status at all, this is determined by the statuses of S1 and S2 and the truths of deontic logic. Thus, if S1 and S2 each have a given status, and our preferred deontic logic implies that that status agglomerates, we may conclude that S1 ∧ S2 has that status as well.
Unfortunately, there’s more to the agglomeration problem. Suppose, Jackson and Smith say, that you are such a crack shot with your rifle that you could, if you wished, shoot both skiers with a single bullet, rather than shooting each skier individually. Here, surely, is a single option, whose total probability of violating a constraint (the probability that at least one skier is an innocent threat) exceeds the threshold of permissible moral risk. Should deontological theories say that you are permitted to shoot both skiers, but only so long as you use separate bullets (thereby making two choices, each of which involves an acceptable level of moral risk)?
The right thing to say about this case, it seems to me, is that the agent still faces two choices (whether to shoot Skier 1, and whether to shoot Skier 2), and that shooting both skiers with a single bullet, though it is only a single physical motion, nevertheless is the output of a compound option that involves two separate choices. Consider, for comparison, the following case:
The Buttons of Wrongness A mad ethicist has rigged a contraption that will test your judgments about two ethical dilemmas at once. You may press one of four buttons, colored red, green, yellow, and blue. If you press the red button, a message will be sent from your phone to one of your friends, telling him a white lie about his new haircut. If you press the green button, $1000 will be stolen from the accounts of a large corporation and donated to GiveDirectly. If you press the yellow button, both these things will happen. If you press the blue button, neither will happen. Pressing any of the buttons will deactivate the rest.
There is a sense, clearly, in which you make only one choice in this scenario, namely which button to press. But in what seems like a more normatively significant sense, you make two choices, namely whether to tell a white lie and whether to steal money for GiveDirectly—even though you will put both of these choices into effect by means of a single motion, namely, pressing a button. If this is right, then we need make no normative distinction between shooting the two skiers individually and shooting them both with a single bullet. In either case, the shooting represents two separate choices/simple options, each of which should be evaluated on its own terms.Footnote 18
There’s one more wrinkle, though: Consider a variant of Two Skiers where you can’t shoot each skier individually, but can only shoot them both with a single bullet—or leave them both unharmed, allowing their twenty victims to die. Here it is no longer plausible to claim that you face two separate choices. We seem forced to conclude, therefore, that you are subjectively permitted to shoot both skiers with a single bullet if and only if you also have the ability to shoot them each separately.Footnote 19 We can still satisfy agglomeration (since the options whose status failed to agglomerate in the original Two Skiers case now no longer exist), but we are left with an extremely counterintuitive practical conclusion.
This is undoubtedly a cost of the Minimalist solution to the agglomeration problem. But there is a principled reason to think that the absolutist, at least, must pay at least this great a cost to respond to the problem of uncertainty. I’ll close this section, and the paper, by describing what I take to be the basic dilemma (or rather, polylemma) for absolutists, of which the agglomeration problem is only a symptom. The problem is that, in order to hold that one may sometimes choose options that carry some non-zero probability of violating a constraint, while also holding that one may never choose options that certainly violate a constraint, the absolutist must make some counterintuitive normative distinctions between very similar cases. This can be illustrated by a “sorites of cases,” leading from the permissibility of action under uncertainty to overrideability of constraints. There are probably many different ways to construct such a sorites, but here’s one:
-
The Anti-Absolutist Sorites
-
P1.
It’s subjectively permissible for an agent A1 to run a .01 risk of killing an innocent person, in order to save ten innocent people (with probability 1).Footnote 20
-
P2.
If P1, then it’s permissible for a thousand agents A1–1000 to each (at different times and places, without any coordination) take separate actions that run independent .01 risks of killing (different) innocent people, in order to save (different) groups of ten innocent people. [Since the risks are independent, the probability that at least one innocent person will be killed by these actions is approximately .99996.]
-
P3.
If P2, then it’s permissible for A1 to take actions that run .01 risks of killing (different) innocent people, in order to save (different) groups of ten innocent people, 1000 times in the course of her life, at different times and places and based on separate practical deliberations.
-
P4.
If P3, then it’s permissible for A1 to take those same thousand actions all at the same time, or arbitrarily closely together in time. (Suppose that the actions each involve killing a potentially-innocent person with a weapon that’s triggered by pressing a button, and that A1 is a thousand-fingered alien who can, if she wishes, press all thousand buttons at once, or in an arbitrarily short period of time.)
-
P5.
If P4, then it’s permissible for A1 to make 1000 separate choices to run independent .01 risks of killing different innocent people, to save different groups of ten innocent people, while putting those choices into affect by a single physical motion. (Suppose that in addition to the thousand individual buttons, A1 also has a master button that has the same effect as pressing all 1000 individual buttons.)
-
P6.
If P5, then it’s permissible for A1 to perform that same physical motion, with the same beliefs about its possible consequences, as the result of a single choice rather than a thousand individual choices. (Suppose now that there is only the master button, and not the thousand individual buttons that give her the choice of killing each potentially-innocent person individually.)
-
P7.
If P6, then it’s permissible for A1 to make the same choice even if the probabilities that each of the 1000 targets is innocent are not independent, but perfectly anti-correlated in such a way that she is guaranteed to kill exactly ten innocent people.
-
P8.
If P7, then it’s permissible for A1 to make the same choice even if she has identifying information about the ten innocent people who will be killed, e.g., even if she knows their names.
-
C.
It’s permissible to kill ten innocent people with probability 1, in order to save 10,000 innocent people with probability 1. So, absolutism is false.
This is, I think, a fairly compelling argument against absolutism—none of the premises is easy to deny. Denying P1 means either embracing an utterly paralyzing practical conclusion, or simply refusing to entertain subjective normative notions at all and hence refusing to provide a decision rule for epistemically imperfect agents. Both of these strategies seem like non-starters. I cannot think of any reasonable way to deny P2. Denying P3 has the implausible implication that one agent can be permitted to take a risk that another agent is not, simply because the second agent has used up more of her lifetime “moral risk budget” on other choices. Denying P4, P5, or P6 would each likewise make important moral questions turn on seemingly irrelevant empirical features of choice situations (how close together a series of actions is in time, whether the same risks are brought about by one physical motion or many, or whether that motion is the result of one choice or many). Some absolutists, I suspect, will be tempted to deny P7 or P8, but both these moves strike me as extremely implausible. To deny P7 is to claim that it’s permissible to act in a way that will kill at least one innocent person with probability ~.99996, exactly ten innocent people in expectation, and potentially as many as 1000—but not permissible to kill exactly ten innocent people for sure, under the same circumstances and to prevent the same catastrophe. To deny P8 is to hold that I may permissibility kill some innocent people to save many, but only so long as I carefully shield myself from any identifying information about the people I’m killing.
There’s a great deal to be said, potentially, about each of these options.Footnote 21 But my own judgment is that P6 is the least-implausible place for the absolutist to make her stand, and therefore that Minimalism is the least-implausible response to the agglomeration problem.
6 Conclusion
Uncertainty, whether empirical or purely moral, presents a challenge for deontological absolutists. They must give an account of how agents should deliberate and act in the face of uncertainty, ideally an account that is as precise and intuitively well-motivated as the expectational account available to consequentialists. I have suggested that a threshold view grounded in stochastic dominance reasoning can at least partially meet this need. The agglomeration problem, and the broader difficulty of which it’s symptomatic, remain a serious challenge, but the cost of overcoming that challenge, though serious, is not necessarily prohibitive. I conclude, then, that deontologists in general and absolutists in particular are somewhat better equipped to respond to uncertainty than their critics have alleged.
Notes
The critics of this approach, on the other hand, have predominantly been those who deny that we need a theory of decision-making under purely moral uncertainty in the first place, because they deny that what an agent subjectively ought to do depends on her purely moral beliefs (e.g. Weatherson (2014), Harman (2015), Hedden (2016)).
It is standard in this literature to reserve the term “moral uncertainty” for what I am calling purely moral uncertainty. I use the term more broadly in this paper both to avoid repeated inelegant references to “morally relevant empirical uncertainty” and because one of my aims will be to emphasize the continuity between empirically-based and purely moral uncertainty, so it’s helpful to have an umbrella term that refers to both.
I focus on negative constraints for simplicity, but of course constraints can be positive as well—i.e., requirements rather than prohibitions.
I adopt this focus for two reasons: First, it’s quite a bit easier to characterize absolutism, and to say what it’s committed to, than to characterize non-absolutist deontology (and distinguish it from agent-relative consequentialism). Second, focusing on absolutism makes the problem of uncertainty much more straightforward. This is because non-absolutists have an option for dealing with uncertainty that absolutists do not, namely, to represent their theory’s moral verdicts with finite cardinal values and embrace a broadly expectational decision theory. (This is the approach taken by Seth Lazar, e.g. in Lazar (2017a, b).) My own view is that this expectational approach gives up most of what was distinctive about deontology in the first place (and results in a view that is less theoretically appealing than either classical utilitarianism or absolutist deontological views like Kantianism, since it must sacrifice a great deal of simplicity for the sake of fitting some very dubious intuitive data). But any serious discussion of this approach would take us too far afield.
Aboodi et al. (2008) criticize Jackson and Smith (2006) for focusing on absolutism, on the grounds that “hardly any (secular) contemporary deontologist is an absolutist” (p. 261, n5). But see Huemer (2010, p. 348, n3), who marshals a credible array of apparent (contemporary or near-contemporary) absolutists.
I will use objectively/subjective “oughts” interchangeably with objective/subjective obligations, permissions, and prohibitions.
Jackson and Smith (2006, 2016) and Huemer (2010) focus on threshold views as the natural deontological response to uncertainty, and conclude from the failure of those views that deontologists lack an adequate response to uncertainty. Hawley (2008) and Aboodi et al. (2008) both defend versions of the threshold view against Jackson and Smith’s objections. Isaacs (2014) suggests that it is subjectively permissible for an agent to choose a morally risky option only if she knows that that option would not be an instance of a deontologically prohibited type, which is a close cousin of the threshold view provided one accepts that belief above some credal threshold is a necessary condition for knowledge.
The choiceworthiness of an option is the strength of an agent’s all-things-considered objective reasons to choose that option. To say that O is more choiceworthy than P, then, is just to say that there is more all-things-considered objective reason to choose O.
I remain neutral on which sort of probability is relevant.
This relation is sometimes called first-order stochastic dominance, to distinguish it from higher-order relations that place increasingly tight constraints on an agent’s risk attitudes. Since we won’t have reason to consider these higher-order relations, I omit the qualifier.
There are other ways of representing deontological choiceworthiness that arguably better capture the structure of some deontological theories—e.g., with a bounded or unbounded ordinal scale, or with vector-valued choiceworthiness. I adopt Colyvan et al.’s representation for convenience, but the arguments in this section would go no differently if we adopted an ordinal or vector representation instead (cf. §6 of Tarsney (2018a)).
The talk of “outcomes” should not be seen as illicitly consequentialist. Violating or fulfilling a deontological obligation is an “outcome” only in the formal sense of being a distinct option-state combination valued differently than other option-state combinations. Calling these “outcomes” does not imply, for instance, that the wrongness of breaking a promise has anything to do with its causal consequences.
Interestingly, the view that it is subjectively permissible to take a morally risky act only when the probability of objective wrongdoing is less than .5 has a history in the Catholic moral theology literature, under the name “probabiliorism” (Sepielli 2010, pp. 51–2). Stochastic dominance, then, implies that a deontological absolutist must adopt a position at least as rigorous as probabiliorism in the cases of “asymmetrical” moral risk with which this literature is chiefly concerned.
The apparent continuity between these two kinds of cases casts doubt on the idea that subjective normative principles should make a basic distinction between uncertainty about empirical facts and uncertainty about basic normative principles, an idea that has recently been advanced by Weatherson (2014), Harman (2015), and Hedden (2016), inter alia. I elaborate this point in Tarsney (2018b).
This problem is especially acute in the literature on purely moral uncertainty, where some have worried that “fanatical” moral theories may hijack expectational reasoning—i.e., moral theories that attribute infinite positive or negative choiceworthiness to options, perhaps in very strange or counterintuitive ways, will take precedence over all finitary moral theories, so long as one assigns them any non-zero probability (Ross 2006, pp. 765–7).
Of course, stochastic dominance need not be understood as the only or the strongest principle of rational choice under uncertainty (cf. the last three paragraphs of this section). Various principles are possible that occupy an intermediate position between stochastic dominance and expectation-maximizing and that might impose a more rigorous form of moral caution on agents acting under uncertainty while still avoiding Pascalian paralysis. My own tentative view is that rejecting stochastically dominated options is in fact the only requirement of rational choice under uncertainty, but this claim is prima facie implausible, and I don’t have space to plausibilify it here. I attempt to do so in Tarsney (2018a).
Cases of this sort have been a major focus of the recent literature on purely moral uncertainty, in particular the cases of abortion and vegetarianism, both of which seem to present agents (at least in many cases) with a conflict of prudential reasons on one side and uncertain moral reasons on the other. See Guerrero (2007), Moller (2011), and Weatherson (2014), inter alia, for discussion of these cases.
In this section I have focused on a few artificially simple cases, where each option has only a few possible degrees of choiceworthiness. Under these circumstances, stochastic dominance delivers useful but relatively weak conclusions. In circumstances of greater uncertainty, however, stochastic dominance reasoning can become much more powerful. In particular, I show in Tarsney (2018a) that when an agent is in a state of “background uncertainty” about the choiceworthiness of her options (such that the choiceworthiness of each option can be represented as the sum of a “simple payoff” given by that option’s prospect, plus a “background payoff” determined by a probability density function that is the same for all options in the choice situation), many option-pairs that would not exhibit stochastic dominance in the absence of background uncertainty can come to exhibit stochastic dominance in virtue of that background uncertainty. I don’t have space to explore the implications of these results for deontological uncertainty (or to argue for the appropriateness of the requisite sort of background uncertainty in the deontological context) but in brief, under these conditions: (i) Stochastic dominance reasoning under deontological uncertainty no longer requires us to assume, for a given constraint, that violating the constraint has negative choiceworthiness and that complying with the constraint has positive choiceworthiness—each of these assumptions becomes individually sufficient to generate stochastic dominance relations. (ii) The threshold of moral risk at which morally safe options become stochastically dominant can be arbitrarily close to zero, depending on the agent’s degree of background uncertainty. (iii) The threshold will also be sensitive to the cost of satisfying a constraint and, insofar as the choiceworthiness function distinguishes between more and less stringent constraints, to the severity of the potential constraint violation (with effects going in the intuitive directions—a higher threshold of acceptable risk when the morally safe option is more costly, and a lower threshold when the potential violation is more serious).
This of course invites the question how we should individuate choice situations. I don’t have a worked-out answer to this problem, and it may ultimately be fatal to the suggestion I’m developing. But it seems to me that the best answer is something like this: Choices correspond to degrees of freedom in the space of possibilities that an agent has the ability to bring about. In Two Skiers, for instance, the space of available possibilities has two degrees of freedom: (i) Skier 1 is/isn’t killed and (ii) Skier 2 is/isn’t killed. It’s natural to say that the agent has two choices, since she exerts independent control over both of those variables—even though she might exercise that control by a single motion.
We are assuming that, although it is objectively obligatory to kill an aggressor in defense of innocent lives, an act that kills one aggressor and one innocent threat in order to save twenty innocent lives is still constraint-violating and objectively prohibited, just like an act that kills only the innocent threat. Hence the probability that shooting both skiers is objectively prohibited is the probability that at least of them is an innocent threat.
I choose these numbers for illustrative convenience. None of the other premises will be made less plausible, I think, if we adjust the numbers to involve a smaller probability of killing an innocent person, to save a larger number of innocent people.
In the extant literature: Aboodi et al. (2008) are most naturally read as rejecting P8. I read Black (forthcoming) as rejecting P3, though the view he develops is not committed to this answer. (Notably, both Aboodi et al. and Black defend absolutism against Jackson and Smith’s objections while explicitly declining to endorse absolutism.) Hawley (2008) is open to various interpretations, but seems committed to denying one of P1–4.
References
Aboodi R, Borer A, Enoch D (2008) Deontology, individualism, and uncertainty: a reply to Jackson and Smith. J Philos 105(5):259–272
Black, D (forthcoming) Absolute prohibitions under risk. Philosophers’ Imprint
Colyvan M, Cox D, Steele K (2010) Modelling the moral dimension of decisions. Noûs 44(3):503–529
Guerrero AA (2007) Don’t know, don’t kill: moral ignorance, culpability, and caution. Philos Stud 136(1):59–97
Hadar J, Russell WR (1969) Rules for ordering uncertain prospects. Am Econ Rev 59(1):25–34
Harman E (2015) The irrelevance of moral uncertainty. In: Shafer-Landau R (ed) Oxford studies in Metaethics, vol 10. Oxford University Press, Oxford, pp 53–79
Hawley P (2008) Moral absolutism defended. J Philos 105(5):273–275
Hedden B (2016) Does MITE make right? On decision-making under normative uncertainty. In: Shafer-Landau R (ed) Oxford studies in Metaethics, vol 11. Oxford University Press, Oxford, pp 102–128
Huemer M (2010) Lexical priority and the problem of risk. Pac Philos Q 91(3):332–351
Isaacs Y (2014) Duty and knowledge. Philos Perspect 28(1):95–110
Jackson F, Smith M (2006) Absolutist moral theories and uncertainty. J Philos 103(6):267–283
Jackson F, Smith M (2016) The implementation problem for deontology. In: Lord E, Maguire B (eds) Weighing reasons. Oxford University Press, Oxford, pp 279–291
Lazar S (2017a) Anton’s game: deontological decision theory for an iterated decision problem. Utilitas 29(1):88–109
Lazar S (2017b) Deontological decision theory and agent-centered options. Ethics 127(3):579–609
Lockhart T (2000) Moral uncertainty and its consequences. Oxford University Press, Oxford
MacAskill W (2014) Normative uncertainty. PhD thesis, University of Oxford
Moller D (2011) Abortion and moral risk. Philosophy 86(03):425–443
Portmore DW (2017) Uncertainty, indeterminacy, and agent-centered constraints. Australas J Philos 95(2):284–298
Ross J (2006) Rejecting ethical deflationism. Ethics 116(4):742–768
Sepielli A (2009) What to do when you don’t know what to do. Oxford Studies in Metaethics 4:5–28
Sepielli A (2010) ‘Along an imperfectly-lighted path’: Practical rationality and normative uncertainty. PhD thesis, Rutgers University Graduate School - New Brunswick
Tarsney C (2018a) Can first-order stochastic dominance constrain risk attitudes? arXiv:1807.10895
Tarsney C (2018b) Intertheoretic value comparison: a modest proposal. J Moral Philos 15(3):324–344
Weatherson B (2014) Running risks morally. Philos Stud 167(1):141–163
Acknowledgements
For helpful discussion and/or feedback on earlier drafts of this paper, I am grateful to Ron Aboodi, Krister Bykvist, Samuel Kerstein, William MacAskill, Dan Moller, Toby Ord, Julius Schönherr, Sergio Tennenbaum, and audiences at the Uehiro Centre for Practical Ethics, the Columbia-NYU Graduate Philosophy Conference, the University of Maryland, the British Society for Ethical Theory, the European Congress of Analytic Philosophy, and the Young Philosophers Lecture Series at Depauw.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Tarsney, C. Moral Uncertainty for Deontologists. Ethic Theory Moral Prac 21, 505–520 (2018). https://doi.org/10.1007/s10677-018-9924-4
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10677-018-9924-4