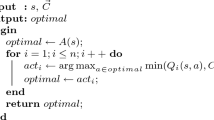Abstract
Recent years have yielded many discussions on how to endow autonomous agents with the ability to make ethical decisions, and the need for explicit ethical reasoning and transparency is a persistent theme in this literature. We present a modular and transparent approach to equip autonomous agents with the ability to comply with ethical prescriptions, while still enacting pre-learned optimal behaviour. Our approach relies on a normative supervisor module, that integrates a theorem prover for defeasible deontic logic within the control loop of a reinforcement learning agent. The supervisor operates as both an event recorder and an on-the-fly compliance checker w.r.t. an external norm base. We successfully evaluated our approach with several tests using variations of the game Pac-Man, subject to a variety of “ethical” constraints.
Similar content being viewed by others
Introduction
From self-driving cars to unmanned aerial vehicles, autonomous agents are becoming increasingly ubiquitous in many facets of contemporary life. Participation in activities formerly reserved for human operators requires such agents to adapt to (potentially unpredictable) changes in their environment; reinforcement learning (RL) has been demonstrated to be an effective tool for teaching agents such behaviour (e.g. Levine et al., 2016; Silver et al., 2017).
Contributing to human activities, however, elicits the further requirement that agents constrain their behaviour according to the ethical standards their human counterparts are subject to. This introduces the additional challenge of establishing boundaries for the behaviour of autonomous agents—and in some cases, making some form of ethical reasoning available to these agents. RL agents can be trained—via the assignment of rewards/penalties by an ethical utility function—to avoid unethical behaviour and pursue ethical compliance, see e.g. Noothigattu et al. (2019), Abel et al. (2016), Wu and Lin (2018), and Rodriguez-Soto et al. (2021). However, in many cases, this approach offers limited guarantees of the desired behaviour. Furthermore, such techniques can be cumbersome when dealing with the complexity of ethical reasoning; the presence of conflicting norms with different priorities, exceptions to norms, or contrary-to-duty obligations (i.e., obligations which are only applicable in case of violations), introduce subtleties not easily captured by learned policies. An additional challenge arises when we embed ethical principles in the learning process; doing so requires us to retrain the policy from scratch each time we wish to modify the adopted norms.
Similar to other black-box machine learning methods, RL lacks transparency in explaining why certain policies are compliant or not. Meanwhile, transparency is frequently adopted as a key requirement in work on machine ethics (e.g. in Dignum, 2017); the works (Aler Tubella & Dignum, 2019; Aler Tubella et al., 2019), for instance, deliberately address the problem of transparency. Despite the thoroughness of their approach, it has not been implemented and tested yet.
Our approach
We aim to integrate ethical reasoning into learning agents to accommodate changing values, cope with apparent contradictions in ethical requirements, handle situations where no compliance is possible, and facilitate the transparent justification of judgments made—without sacrificing the optimal behaviour the agent has learned. Our approach integrates RL with Deontic Logic, the branch of logic concerned with the formal specification of normative statements. Ethical norms can be modeled using Deontic Logic (von Wright, 1968; Nowell-Smith & Lemmon, 1960); the difference between ethical and legal norms is found in how they originate, not in what normative consequences they imply.
We introduce a logic-based normative supervisor module which we integrate into an RL agent. The supervisor advises the agent on courses of action that comply with the normative (e.g., ethical) requirements in force in a given situation. The supervisor can function as both an on-the-fly compliance checker and an event recorder; it will correct the action selected by the agent’s policy only when it violates a norm, and as an event logger, it will identify the specifics of these violations and record the conditions under which they occur (thereby informing further analysis and possible modifications to the agent or the norms it is subject to). The supervisor addresses what we see as important challenges in implementing ethical AI, especially the accommodation of changing values, the explicit justification of actions, and the selection of the ‘lesser evil’ when no compliant action is possible.
Among the various alternative formalisms proposed within the field of Normative Multi-Agent Systems (NorMAS) (Andrighetto et al., 2013), we have chosen defeasible deontic logic (Governatori et al., 2013; Governatori & Rotolo, 2008) to implement our normative supervisor. This is a simple and computationally feasible, yet expressive logic which allows for defeasible reasoning, handles contrary-to-duty norms, and can easily accommodate changes to the norm base. Moreover, the constructive nature of this logic allows us to determine how a given conclusion has been reached (Governatori, 2018).
Ethical Pac-Man
We demonstrate the functionalities of our approach on an RL agent that plays variations of the game Pac-Man. This game is a closed environment with clearly defined game mechanics and parameters which are easy to isolate, manipulate, and extend with variably intricate rule sets that can simulate normative conflicts and dilemmas. Pac-Man has already been used as a case study in Noothigattu et al. (2019) and Hasanbeig et al. (2019), both using a bottom-up approach to learn to act according to implicit behavioral constraints on the RL agent borne out in the environment, as opposed to top-down approaches that explicitly enforce imperatives on the agent’s actions. The work in Noothigattu et al. (2019) employs multi-objective RL with policy orchestration to impose constraints on a version of Pac-Man for which it is unethical to eat ghosts (“vegan” Pac-Man). It seamlessly combines ethically compliant behaviour and learned optimal behaviour; however, the ethical reasoning performed is still to a degree implicit, and it does not provide justifications for the choices made, nor is it clear how the approach would remain effectively transparent with more complex norm sets. Hasanbeig et al. (2019) integrates more complex constraints in a RL agent, but seeing as they are are embedded in the learned policy, it still lacks the transparency of a logic-based implementation.
We successfully demonstrated the effectiveness of our approach with a series of tests subject to a “vegan” norm base (Noothigattu et al., 2019), a “vegetarian” norm base (where Pac-Man is allowed to eat only one of the ghosts), and two norm bases that compromise Pac-Man’s ability to win the game. We then expanded the vegan norm base by adding permissive norms, leading to two new variants of the game; furthermore, we have experimented with a contrary-to-duty obligation that regulates the agent’s behaviour when it violates its norm base. Our framework facilitates such revisions to the norm base; records of violations that occur allowed us to confirm the nature of each violation as necessary, and were used to formulate additional norms for preventing violations. These tests allowed us to evaluate both the strengths and limitations of our approach.
Related work
The field of NorMAS studies the use of norms and normative systems to regulate the behavior of agents and to determine if the agent’s behavior complies with a set of norms (Andrighetto et al., 2013). Among the different proposals for NorMAS are non-monotonic approaches that extend the BDI (belief-desire-intention) architecture with a normative component to ensure that an agent’s plans comply with a set of norms or, alternatively, to select plans that do not violate the given norms, see e.g. Broersen et al. (2001) and Governatori and Rotolo (2008).
Our approach can be seen as an extension of Lam and Governatori (2013), with our plans being limited to single actions that do not result in a violation. Here, however, the agent is equipped with a RL module to learn the behaviours involved in pursuing non-ethical goals, in which our logical framework intervenes only if necessary. In addition, based on the log of the events (and the relevant normative states) we progressively expand the norm base to reduce the incidence of negative effects.
More formalisms and tools have been proposed to regulate the normative behavior of agents; these include logic programming (e.g. Sergot et al., 1986; Pereira & Saptawijaya, 2009; Berreby et al., 2017), argumentation (e.g. Prakken & Sartor, 2015), Input/Output logic (Makinson & Van Der Torre, 2007), and the agent model in Sadri et al. (2006), but to the best of our knowledge they have not yet been used in combination with RL.
Our work complements other approaches that equip an RL agent with potentially unsafe behaviour with a safe wrapper component limiting its actions. Shielding (Alshiekh et al., 2018; Jansen et al., 2020), for example, employs a linear temporal logic (LTL) (Pnueli, 1977) constraint for defining safe behaviour for the agent. Starting from this specification, they automatically synthesize a ‘shield’ component to prevent the agent from moving into unsafe states; this shield is computed before the RL agent begins operation. Our approach differs in that we compute the compliance of actions dynamically (allowing for changes in regulation during operation), and employ defeasible deontic logic, which is tailored to normative reasoning. In contrast with LTL, defeasible deontic logic is capable, for instance, of properly handling obligations and permissions in force after another obligation has been violated; a violation is represented by the conjunction \(Op\wedge \lnot p\) (where O is the deontic obligation operator) and LTL cannot accommodate a contrary-to-duty obligation Oq logically depending (as compensation) on a violation (Governatori, 2015).
This paper expands extensively upon the results presented in our preliminary work (Neufeld et al., 2021), which introduces the normative supervisor we use to regulate the agent’s behaviour in this work. In comparison to Neufeld et al. (2021), we delve into some of the supervisor’s internal mechanisms with more depth, and more expansively test its capabilities; we work through a thorough analysis of violations that occur in the “vegan” and “vegetarian” norm bases, and introduce norm bases that compromise Pac-Man’s ability to win the game, as well as norm bases that include reasoning about permissions and contrary-to-duty obligations. This extended battery of tests allows us a much more thorough discussion of the normative supervisor’s strengths and weaknesses in imposing ethical behaviour on an agent.
Paper organization
Section "Background" introduces some of the background concepts needed to discuss our work, including defeasible deontic logic. Section "The normative supervisor" provides a thorough breakdown of our normative supervisor’s architecture in the context of our case study, while Sect. "Variations and experimental results" presents the variants of the game and the corresponding tests. In Sect. "Conclusion and future work" we draw our conclusions and discuss future research directions.
Background
Below, we briefly contextualize our work in the field of machine ethics, introduce the necessary background on normative reasoning and defeasible deontic logic, review the topic of reinforcement learning, and describe (vegan) Pac-Man—the agent and environment utilized in our case study.
Machine ethics
Our work arises in the greater context of the field of machine ethics. Machine ethics, it might be argued, centres on the project of creating Artificial Moral Agents (AMAs). Autonomous systems may never be capable of moral agency in the same sense that humans are, but many believe that making them behave like moral agents remains a feasible challenge (Wallach & Allen, 2008). Autonomous agents that can shape their behaviour in response to the (ethical) norms humans impose on society may become an important part of the smooth integration of new technologies in everyday life. In particular, they may prove useful in the avoidance of harms (both direct and indirect) arising from this integration, and augment our ability to enforce ethical or legal standards on the design and use of these technologies. It should be noted that research into AMAs should not preclude the urgent need for responsible regulation and oversight of technologies old and new; instead, AMAs can and should complement these efforts. However, the development of (useful) AMAs comes with substantial difficulties.
In Moor (2006), a taxonomy of ethical agents is provided, with specific focus on explicit ethical agents, which are autonomous agents that reason explicitly about ethical values and/or norms (as opposed to having their actions constrained to avoid unethical outcomes, or functioning as full ethical agents, as a human might). Even these limited ethical agents come with serious challenges that must be bridged. Explicit representation of ethics requires ethical notions to be represented and reasoned about precisely and effectively; this must involve some kind of formalization of ethical principles. And once we are able to do that, there are a plethora of ethical principles to choose from, support for which varies with application domain or cultural context. How should we choose what kind of ethics we implement? Do machine ethicists and engineers have the right to make any such design decisions? Additionally, social and ethical norms change over time (IEEE, 2019), introducing a need for mechanisms for updating the AMA’s understanding of what is moral in the current context. More issues arise when we consider how to assign moral accountability for the actions of an AMA; this is part of the more general pursuit of imbuing autonomous agents with transparent and understandable reasoning skills, which becomes all the more important when ethical decisions must be justified.
In this paper we discuss a framework for integrating explicitly represented norms into the behaviour of certain learning agents. The normative supervisor we introduce does not serve as an architecture for an AMA; however, it enables us to modify the behaviour of artificial amoral agents, forcing them to act in such a way that matches how an AMA might in certain contexts. This framework was designed to introduce a high degree of configurability; the decoupling of the learning agent and the supervisor allows us to seamlessly switch between the normative systems we wish to enforce (whether these are ethical, legal, or social norms), accommodating the natural evolution of such systems. Moreover, it includes as a feature event recording, which allows us to retain records of the agent’s knowledge and the norms it is compelled to obey when, for example, a violation is incurred. At the core of this framework is a logic for normative reasoning (after all, ethical norms are unique only in how they emerge, not what normative consequences are entailed by them) which we introduce in the next subsection.
Normative reasoning and defeasible deontic logic
Normative reasoning diverges from the reasoning captured by classical logic in that it must deal with not only statements that are true or false, but also the imposition of norms on to such statements. This demands the use of deontic logic (a class of logics that deal with obligations, permissions and related notions), sometimes with the additional feature of defeasibility, which is the capability to weaken or overturn inferences in light of additional information (see, e.g., Prakken & Sartor, 2015).
To develop our logic-based normative supervisor we employed defeasible deontic (propositional) logic (DDPL for short) (Governatori et al., 2013) and its theorem prover SPINdle.
With this logic we can represent literals—atomic propositions and their negations—and modal literals (that is, literals subject to a modal operator), as well as rules built from them. For the purposes of this paper we only consider explicitly one deontic modality (obligation, \({\textbf {O}}\)) and use the standard equivalences to define prohibition and (weak) permission, namely: \({\textbf {F}}(p) \equiv {\textbf {O}}(\lnot p)\) (that is, p is forbidden) and \({\textbf {P}}(p) \equiv \lnot {\textbf {O}}(\lnot p)\) (p is weakly permitted) respectively. DDPL also gives us the option to define strong permissions, with rules that explicitly state that something is permitted as an exception to a prohibition (or obligation to the contrary) (Governatori et al., 2013); strong permissions will be used in Sect. "Introducing permissive norms".
In this paper we handle two types of norms: constitutive and regulative norms (see e.g. Boella et al. (2004) for the terminology). Regulative norms consist of obligations, prohibitions and permissions. On the other hand, constitutive norms regulate instead the creation of institutional facts as well as the modification of the normative system itself; their content is a relation between two conceptual entities, and they will typically take the form “concept x counts as concept y”, where x refers to a more concrete concept (e.g., walking) and y to a more abstract one (e.g., moving). We say that concept x is at a lower level of abstraction than concept y if there is a constitutive norm asserting that x counts as y (which will be denoted as \({\textbf {C}}(x, y)\)). Below we give the formal definition for rules (constitutive or regulative) in DDPL:
Definition 1
(Rules (Governatori et al., 2013)) Let r be a label that designates a rule:
where \(A(r)=\{a_{1}, ..., a_{n}\}\) is the antecedent, N(r) is the consequent, \(\hookrightarrow _{*}\in \{\rightarrow _{*}, \Rightarrow _{*}, \rightsquigarrow _{*}\}\) is a generic rule symbol, and \(*\in \{C, O\}\) designates the mode of each rule.
Rules labelled by C are constitutive rules and rules labelled by O are regulative rules, where the consequent of the rule is derived in the scope of a deontic operator. Strict rules (\(\rightarrow _*\)) are rules where the consequent strictly follows from the antecedent without exception. Defeasible rules (\(\Rightarrow _*\)) are rules where the consequent typically follows from the antecedent, unless there is evidence to the contrary. Defeaters (\(\rightsquigarrow _*\)) are rules that only prevent a conclusion from being reached by a defeasible rule; regulative defeaters are used to encode permissive rules (see Governatori et al., 2013). DDPL is furthermore equipped with a superiority relation > to resolve conflicts between rules.
Example 1
Consider the rule \(r_{0}:\ a\Rightarrow _{O}\lnot c\) that forbids c when a holds. In case a does not hold, then (assuming there are no other rules forbidding c), we have no way to conclude that c is forbidden, and hence we can say that c is weakly permitted. Assume we have in addition the defeater \(r_{1}:\ b\rightsquigarrow _{O} c\). When b holds, the defeater prevents the prohibition of c to hold making thus c (strongly) permitted. If \(r_{0}\) was a strict rule, c would remain forbidden. If we want to oblige c instead, we could define a defeasible rule \(r_{2}:\ b\Rightarrow _{O} c\) along with the superiority relation \(r_{2}>r_{0}\).
The central concept of DDPL is the defeasible theory (Governatori et al., 2013).
Definition 2
(Defeasible Theory (Governatori et al., 2013)) A defeasible theory D is a tuple \(\langle F, R_{O}, R_{C}, >\rangle\), where F is a set of literals (facts), \(R_{O}\) and \(R_{C}\) are sets of regulative and constitutive rules respectively, and > is a superiority relation over rules.
We will typically want to work with defeasible theories that are consistent.
Definition 3
(Consistent Defeasible Theory (Governatori et al., 2013)) A Defeasible Theory is consistent iff it does not prove any pair of literals of the form \({\textbf {O}}(l)\) and \(\lnot {\textbf {O}}(l)\), or l and \(\lnot l\). D is O-consistent iff the theory does not prove any of the pairs \({\textbf {O}}(l)\) and \({\textbf {O}}(\lnot l)\).
A defeasible theory is consistent (or O-consistent) if (1) the superiority relation is acyclic and (2) the sub-theory consisting of the set of facts and strict rules is consistent (or O-consistent).
From such defeasible theories we can derive conclusions. Conclusions in DDPL are established over proofs and can be classified as defeasible or definite, and positive or negative. A positive conclusion indicates that the referenced literal holds, while a negative indicates that this literal has been refuted. A definite conclusion is obtained by using only strict rules and facts using forward chaining of rules. A conclusion holds defeasibly (denoted by \(+\partial _C\) for a factual conclusion and \(+\partial _O\) for a regulative conclusion) if there is an applicable rule for it and the rules for the opposite cannot be applied or are defeated.
Over the course of a proof, each rule will be classified as either applicable (i.e., the antecedent holds and the consequent follows), discarded (i.e., the rule is not applied because the antecedent does not hold), or defeated by a defeater or higher priority rule. The definition of provability for defeasible obligations (Governatori et al., 2013) is (for a set of rules R, R[p] denotes the set of rules with p in the consequent, \(R_O\) is the set of regulative rules in R, an d \(R^{sd}\) is the set of strict or defeasible rule in R):
Definition 4
(Defeasible Provability (Governatori et al., 2013)) Given a defeasible theory D, if \(D\vdash +\partial _{O}\ p\), then:
-
1.
\(\exists r\in R^{sd}_{O}[p]\) that is applicable defeasible, and
-
2.
\(\forall s\in R_O[\lnot p]\) either:
-
3.
s is discarded, or
-
4.
\(s\in R^{sd}\) and \(\exists t\in R_O[p]\) which is applicable s.t. \(t>s\), or
-
5.
s is a defeater, \(\exists t\in R^{sd}_{O}[p]\) which is applicable s.t. \(t>s\)
A derivation in DDPL has an argumentation structure and consists of three phases. In the first phase we need an argument for the conclusion we want to prove. In the second phase, we analyse all possible counter-arguments, and in the third and final phase, we rebut the counter-arguments. An argument is simply an applicable rule. There are two ways to rebut an argument: undercut it, meaning that the argument is not applicable; or defeat the argument by proposing a stronger applicable argument. If we exclude the undercut case, in every phase the arguments attack the arguments in the previous phase. A rule attacks another rule if the conclusions of the two rules are contradictory. The pairs “\({\textbf {O}}(q)\) and \({\textbf {O}}(\lnot q)\)”, and “\({\textbf {O}}(q)\) and \({\textbf {P}}(\lnot q)\)” are deontic contradictions but \({\textbf {P}}(q)\) and \({\textbf {P}}(\lnot q)\) are not contradictory. Accordingly, any regulative rule for q attacks a strict or defeasible regulative rule for \(\lnot q\). However, a regulative defeater for q is not attacked by a regulative defeater for \(\lnot q\) (condition 2(c) above), since regulative defeaters are rules to conclude permissions.
Reinforcement learning
Reinforcement Learning (RL) is a subfield of machine learning that investigates efficient and effective algorithms for learning how an agent should behave in specific environments to maximize its expected cumulative reward. RL algorithms leverage utility functions that assign rewards/costs to each state-action pair to learn an optimal policy that prescribes to each state an action, thereby governing the agent’s behaviour in such a way that maximizes rewards earned over time.
In our case study, we use Q-learning (Watkins, 1989) with linear function approximation as our RL algorithm. This technique learns a function Q(s, a) to predict the expected cumulative reward (Q-value) for the agent in a state s if it takes action a. The function Q is approximated as a linear function which is the weighted sum of features describing some elements of the environment (e.g., the distance between the agent and object X); the features which are most relevant to predicting the agent’s success are weighted most heavily. The learned policy selects the action \(argmax_{a\in possible} \ Q(s, a)\) with the highest Q-value over a list of possible actions possible.
Vegan Pac-Man
The arcade game Pac-Man is played by controlling an eponymous agent located in a maze. Pac-Man must navigate the maze with the goal of entering cells containing a ‘food pellet’, so it can eat them for 10 points. The game is won when Pac-Man has eaten all the food pellets in the maze, receiving 500 points. The goal is to win the game while collecting the maximum number of points and minimizing time taken; each move of Pac-Man costs a time penalty of \(-1\) point. There are also two ghosts wandering around the maze. In order to avoid being eaten by ghosts, Pac-Man must avoid collisions with the ghosts—unless they enter a ‘scared’ state, which is triggered when Pac-Man eats a special “power” pellet. When the ghosts are scared, Pac-Man can eat them, and is rewarded with 200 points if it does so.
Similar to Noothigattu et al. (2019), we consider a variation of the UC Berkeley AI Pac-Man implementation (DeNero & Klein, 2014), where Pac-Man is ethically forbidden from eating ghosts. We call this variation “Vegan Pac-Man”; we also experiment with “Vegetarian Pac-Man”, where only blue ghosts are off-limits.
Our Pac-Man agent utilizes a Q-learning policy that selects the argmax of an approximated Q-function (as described above); as the utility function we use the game’s score, and game states are taken to be states. We use a game layout identical to that in Noothigattu et al. (2019); this is a \(20\times 11\) maze populated with 97 food pellets and two ghosts (blue and orange) which move randomly. The highest score that can be achieved is in general 2170. When eating ghosts is forbidden the maximum score is 1370.
The normative supervisor
We introduce a normative supervisor that functions as an on-the-fly compliance checker with the ability to identify courses of action that are compliant with an externally supplied norm base; when no such action exists, the supervisor determines which action will result in the least number of violations with respect to this norm base. Our architecture is highly modular, which contributes to the ease with which we can independently adjust the agent, the reasoner at the core of the normative supervisor, and the applicable norm base consisting of regulative norms and any relevant constitutive norms.
Architecture
The centerpiece of our approach is the normative supervisor whose main architecture is illustrated in Fig. 1. This module consists of a normative reasoning engine (we use the SPINdle theorem prover for defeasible deontic logic (Lam & Governatori, 2009)), and additional components that encode applicable norms and environmental data into a defeasible deontic logic theory, and translate the conclusions of the reasoning engine into instructions the agent can interpret.
We integrate the normative supervisor into the agent’s control loop between the localization and policy modules, as is depicted in Fig. 1. The localization module identifies the current agent’s state with respect to its environment and passes the current state and a list of possible actions to the normative supervisor. In simple environments (like the one we will deal with in this paper), the state representation passed to the normative supervisor will closely resemble the state the agent observes. In our case study, for example, the normative supervisor only receives information on (1) the agent’s position, (2) the other agents’ (ghosts’) positions, (3) the other agents’ state (whether or not the ghosts are scared), and (4) what actions are available to the agent. However, in more complex applications, the normative supervisor’s ability to accurately reason about a set of norms will depend on the accuracy with which the agent can approximate the relevant features of its environment.
The normative supervisor module filters out any action that is not compliant with the norm base. The policy will then identify from the remaining compliant actions the action optimal for generating the best outcome. If there are no available compliant actions then the normative supervisor will provide a list of ‘lesser evil’ actions. This module also enables us to log all the conclusions of the reasoning engine during the game for later scrutiny.
Configuring the norm base
We start with a simple norm base, consisting only of the behavioral constraint proposed in Noothigattu et al. (2019) that “Pac-Man must not eat ghosts”Footnote 1, represented as:
If this norm base is to constrain our agent’s actions, it needs to reference concepts processed by the agent, which is limited to the locations of game entities and the actions that Pac-Man can perform, which are North, South, East, West, and Stop. How do we get from the comparably abstract norm above to these lower-level state and action descriptions? We need to fill in the gaps, exercising our knowledge of the game mechanics to do so.
The only way eat(pacman, ghost) can be done is if (a) the ghost is in a ‘scared’ state, and (b) Pac-Man and the ghost move into the same cell. We can express these concepts as predicates over game objects, specifically as (a) scared(ghost) and (b) inRange(pacman, ghost). Pac-Man does not know which direction the ghost will move in, but we will assume a “cautious” model of action where Pac-Man should not perform any action that could constitute eating a ghost; that is, if Pac-Man takes an action that could reasonably lead to him violating a norm, we will consider that norm violated. Since Pac-Man’s next action determines what is in range, we in fact need five entities to express inRange(pacman, ghost), one corresponding to each action. These conceptual entities are used to construct a constitutive norm, or a kind of strategy, regarding the action of eating. For example:
which applies in the context \(\{scared (ghost),\ in North Range (pacman, ghost)\}\).
To define in North Range (pacman, ghost), we note that we have access to the positions of Pac-Man and the ghosts, so we can create another set of constitutive norms which are applicable in the context \(\{pacman(i,j)\}\):
where (k, l) has a Manhattan distance of 1 from \((i, j+1)\).
Automating translation
We now must amalgamate our informal representation of the norm base and the input and output to the agent into the formal language of the reasoner (DDPL and its theorem prover SPINdle (Lam & Governatori, 2009)). If we frame the reasoner as a central reasoning facility, the agent as a front-end, and the norm base as a back-end, we can implement this dynamic as a translator with two faces, one front-facing and one back-facing, feeding information into the reasoner from the agent and the norm base respectively. On both ends, the translations will be performed dynamically; the current state of the game will change at every time step, and in order to minimize the amount of data passed to the reasoner, there are elements of the norm base—namely constitutive norms—that will be generated only for the current context.
Front end translation
The front-end translator is in perpetual use, processing new data and proposed actions as the environment changes. It amounts to an algorithm that transforms input data from the agent into propositions which assert facts about the agent or the environment. Every cell of the Pac-Man grid contains characters (Pac-Man or one of the ghosts), an object (a wall or a food pellet), or nothing at all. Walls are accounted for during the localization stage of Pac-Man’s algorithm and norms regarding food pellets are not found in the norm base, so we will need to reason only about the characters. Hence we have two sets of variables in each game: \(pacman_{i,j}\) and \(ghost_{i,j}\) for each coordinate (i, j) on the grid, asserting the locations of Pac-Man and each ghost. These variables can be generated as SPINdle literals at the beginning of the game, and then used to generate a set of facts, Facts, for a defeasible theory:
where the set Facts of facts contains literals representing the locations of Pac-Man and the ghosts. It may also contain other facts about the game; e.g., if there is a scared ghost, both its location and scared(ghost) will be included in Facts.
Actions will be represented as literals, in the set
Summarily, a query from Pac-Man to the reasoner will be accompanied by a representation of the current game state, along with a list of possible actions possible, which will be translated to the corresponding literals in Actions.
Back end translation
In this crucial task we must ensure that norms dictate the same behaviour once translated into to the language of the reasoner; that is, that each component of the norm base is represented by the language.
We represent the regulative norm of Vegan Pac-Man as:
where defeasibility is given as a precautionary measure, just in case we want to add (potentially conflicting) norms later, as it gives us the option of leveraging the superiority relation or defeaters.
Some additional reasoning has to be performed to translate constitutive norms; we will in general translate the constitutive norms (over states) discussed in Sect. "Configuring the norm base" in the following way. If we have a constitutive norm \({\textbf {C}}(x, y)\) that applies in context \(\{a, b\}\), this is expressed in DDPL as
We have found that it is more time-efficient to generate these constitutive norms anew whenever the fact set changes, instead of generating every possible constitutive norm ahead of time, and having SPINdle deal with them all at once; we will define these norms dynamically, and only norms whose applicable context currently holds will be added to \(R_{C}\) in GameState. Thus, these norms will be generated w.r.t. the input from the agent; for example, if the context is \(\{pacman_{2,3}\}\), the rule(s) defining \(inNorthRange_{pacman,ghost}\) will include:
The translation of constitutive norms over actions will be a more complex matter. Firstly, since DDPL is a language with a single variable type, we chose to distinguish actions and states by applying deontic modalities to actions at all times, and never to states. So we can reformulate the relation \({\textbf {C}}(North, eat(pacman, ghost))\) as \({\textbf {C}}( {\textbf {O}}(North), {\textbf {O}}(eat(pacman, ghost)) )\), assuming the same context. Note that if moving North counts as eating a ghost, a prohibition to eat a ghost implies a prohibition to move North. So we can rewrite the above norm as
or with the applicable context in DDPL as:
Note that though this a constitutive rule, in DDPL it will be in \(R_{O}\). This will work for all of the constitutive norms attached to a prohibited action, where we place the context and the prohibition in question in the antecedent, and the prohibition of the concrete action in the strategy is the consequent.
We can be assured that this formalization yields a consistent theory.
Lemma 1
The defeasible theory GameState is consistent and \({\textbf {O}}\)-consistent.
Proof
Since Facts contains only the locations of Pac-Man and the two ghosts, as well as scared(ghost) if a ghost is scared, there can be no pairs of complementary literals. There are no rules in \(R_{C}\) with conflicting consequents, so the superiority relation is empty, and trivially acyclic. Moreover, since GameState only contains prohibitions, \(R_{O}\) likewise does not contain any rules with complementary consequents, and the superiority relation is again trivially acyclic. So GameState is both consistent and O-consistent. \(\square\)
Parsing conclusions
The last task that remains is the transformation the reasoner’s output into indicators communicating which actions in the agent’s arsenal are compliant and which are not. If no compliant action is available, we will need to provide a criterion to identify the “lesser evil” action.
Compliant solutions
We consider a compliant solution to be a possible course of action for the agent that does not violate any norms. If possible, this is what we would like to extract from the reasoner.
Definition 5
A set of compliant solutions is: (a) non-empty, and consisting only of (b) solutions composed of possible actions, (c) solutions that do not violate any norms, and (d) solutions that are internally consistent.
Our method for constructing such a set is heavily influenced by the output (conclusions) yielded by SPINdle. Recall from Definition 3 and the surrounding discussion that we can prove certain conclusions from a defeasible theory; each type of conclusion corresponds to an assertion we can make about the GameState. We are specifically interested in defeasible conclusions, because in our formalization regulative norms were expressed as defeasible rules. Thus for \(a\in Actions\), if we have a conclusion \(+\partial _{O} a\), a is obligatory; if we have a conclusion \(+\partial _{O} \lnot a\), a is forbidden. When we have a negative conclusion \(-\partial _{O} a\) or \(-\partial _{O} \lnot a\) we can assume that a is neither obliged nor forbidden, and is therefore weakly permitted. Finally, if for some a we can prove both \(+\partial _O\ a\) and \(+\partial _O \lnot a\), we can assume that GameState is not internally consistent and no defeasible mechanism has been employed to resolve the internal conflicts (Governatori et al., 2013).
We parse out a solution set by implementing the following steps:
-
1.
if we do not receive a full set of conclusions from SPINdle, we return an empty set;
-
2.
we remove all conclusions that do not reference a literal in possible;
-
3.
any action corresponding to a defeasibly proved positive literal occurs in every solution;
-
4.
any action corresponding to a defeasibly proved negative literal is discarded from every solution.
Proposition 1
The procedure yields either an empty set or a compliant solution.
Proof
If our solution is not internally consistent, we can prove both \(+\partial _O\ a\) and \(+\partial _O \lnot a\) for some action a. In this case SPINdle will return neither, and the above procedure yields an empty set in step (1); this will rule out any solutions that violate condition (d) in Definition 5. Only possible actions will occur in a solution as per step (2), so condition (b) from Definition 5 is met. As for condition (c): step (3) mandates that any obligatory actions are present in each solution, and step (4) excludes any forbidden actions. Thus, if the solution set is not empty, it is a set of compliant solutions. \(\square\)
The fact that Pac-Man can only execute one action at a time allowed us to simplify the above procedure when we implemented a conclusion parser for our normative supervisor. This simplified algorithm is given below.
Algorithm 1
ParseCompliant

‘Lesser of two Evils’ solutions
If there are no compliant solutions (i.e., the procedure defined in Sect. "Compliant solutions" results in an empty solution set), we want to identify which non-compliant actions constitute a “lesser of two evils” choice. This requires us to specify criteria for identifying degrees of non-compliance and a metric for expressing them. Beyond the conclusions yielded by SPINdle, the theorem prover also has an inference logger that classifies every rule in the theory as discarded, applicable, or defeated; we employ SPINdle in an unconventional way, and use these logs to construct such a metric.
Inspired by the economy principleFootnote 2, postulated by an ancient Indian philosophical school, the criterion chosen for our Pac-Man agent is a score derived from the norms that have been applied versus those that have been defeated (discarded norms are ignored). As described in Algorithm 2 below, this score is computed through the theory \(GameState_{act}\), which is constructed by adding a fact \({\textbf {O}}(act)\) to GameState. Recall that a rule will be defeated when its defeasible theory includes a fact that conflicts with the head of this rule. So when adding \({\textbf {O}}(act)\) to GameState, all non-discarded norms that prescribed \({\textbf {F}}(act)={\textbf {O}}(\lnot act)\) for GameState are defeated and any prescribing \({\textbf {O}}(act)\) is applied. To compute the score, we ignore the conclusions yielded by SPINdle and check the inference log to count which rules have been applied during reasoning (\(\# applied\)) and which were defeated (\(\# defeated\)) and set
This procedure is completed for every action in possible, and we select the action(s) with the highest score. If there are multiple actions with a highest score, we send multiple solutions to the agent and it will pick the best action according to its policy.
Algorithm 2
LesserEvil

Since Pac-Man will only have up to 5 possible actions available to him in any given state, Algorithm 2 can be computed in polynomial time.
Proposition 2
Selecting a best action according to the procedure above can be completed in polynomial time with respect to the size of the theory.
Proof sketch: As shown in Governatori et al. (2013), conclusions in DDPL can be computed in linear time with respect to the size of the theory, which is the number of literal occurrences plus the number of the rules in the theory. The claim holds since every action in possible is a literal, and the above procedure is completed |possible| times.
Variations and experimental results
We performed several tests that demonstrated the capabilities of our normative supervisor’s design and its efficacy as an event recorder, without hampering our agent’s ability to perform the behaviour it has learned.
As case study we use the “vegan” version of the game Pac-Man, and variations of it obtained by adding/removing norms from its norm base. We ran several testsFootnote 3 as batches of 1000 games, played by an agent trained on 250 episodes; initially, we trained the agent on 100 episodes and measured the agent’s performance over 100 games, before increasing the number of training episodes to optimize the RL policy w.r.t. average score and games won, and the number of test games in order to better understand the agent’s behaviour.
To compare the RL agent’s performance of the game with and without the normative supervisor, we ran three baseline tests using a random agent and two different (ethically agnostic) RL policies. The results of these baseline tests are given below. We refer to the first RL policy as safe because the algorithm used to train it does not differentiate between regular ghosts and scared ghosts, causing the agent to avoid ghosts altogether. We refer to the other RL policy as hungry because the corresponding algorithm differentiates between regular ghosts and scared ghosts, and the agent learns to optimize its score by eating the scared ghosts.
Norm base | Policy | % Games | Game score | Avg ghosts eaten |
|---|---|---|---|---|
Won | (Avg[Max]) | (Blue / Orange) | ||
N/A | random | 0 | − 445.44 [− 111] | 0.008 / 0.006 |
N/A | safe | 90.5 | 1208.11 [1544] | 0.007 / 0.06 |
N/A | hungry | 90.9 | 1607.6 [2141] | 0.87/ 0.87 |
We will use similar tables to represent all of our test results, indicating: the norm base in force, the policy run by the agent, the percentage of games which the agent won over all played (that is, where Pac-Man ate all the food pellets), the average and maximum score over all games, and the average number of blue and orange ghosts eaten per game. When not explicitly indicated, it should be assumed that the agent was trained on 250 games and tested with 1000.
In the below sections, we experiment with eight norm bases: the vegan and vegetarian norm bases (and a variation of the vegetarian norm base with an added rule avoid), the cautious and over-cautious norm bases (which compromise Pac-Man’s ability to win the game), the all-or-nothing and switch norm bases (which introduce permissive norms), and a norm base that contains a contrary-to-duty obligation (referred to as passive vegan).
Vegan Pac-Man
The Vegan Pac-Man is subject to a single regulative norm, vegan, stating that “Pac-Man must not eat ghosts”; the configuration and implementation of this norm base is discussed in detail in Sects. "Configuring the norm base", "Automating translation", and "Parsing conclusions".
We ran three sets of tests on Vegan Pac-Man, on a random agent, one with the safe policy, and one with the hungry policy. The results are given below.
Norm base | Policy | % Games | Game score | Avg ghosts eaten |
|---|---|---|---|---|
Won | (Avg[Max]) | (Blue/Orange) | ||
Vegan | random | 0 | − 449.13 [− 166] | 0 / 0.003 |
Vegan | safe | 91.4 | 1216.67 [1547] | 0.005 / 0.015 |
Vegan | hungry | 90.7 | 1209.86 [1708] | 0.023 / 0.02 |
The results of the tests with RL agents are comparable to Noothigattu et al. (2019), where Pac-Man was trained to behave in compliance with the vegan norm; in that paper the authors ran 100 games, obtaining an average of 0.03 ghosts eaten per game, while our approach averaged at 0.02 or 0.043 depending on the policy; similarly, their score averaged at 1268.5, while ours averaged 1216.67 and 1209.86. With respect to our baseline tests, the performance of Pac-Man—with respect to % games won and score—did not suffer; there was of course a decrease in score for the hungry policy Pac-Man, since the up to 800 points it could win by eating ghosts are no long available to it The score for the safe policy with and without the normative supervisor did not meaningfully change, and % games won actually increased by nearly an entire percentage point.
Remark 1
Due to the low complexity of the logic used and the modest size of our GameState theory—which rarely exceeded 50 rules—SPINdle took on average 1.1 ms (max 97 ms) in generating conclusions during the Vegan Pac-Man tests. The evaluation of non-compliant solutions, in the rare cases where it was required, took 45.6 ms on average (min 15 ms, max 114 ms). For a detailed analysis on the performance of SPINdle, see Lam and Governatori (2009).
Analysing violations
Inherent to Pac-Man’s environment is the possibility of encountering a state where no compliant action is possible; if Pac-Man encounters such a state, it is forced to violate the norm base. When the normative supervisor identifies these situations—that is, Algorithm 1 returns an empty solution set—we have configured it to store a description of them. Included in this description is a list of possible actions and the positions of all agents in the game; from this information we can reconstruct the circumstances in which Pac-Man took a non-compliant action. For vegan Pac-Man in particular, our examination of these records made it clear that the vast majority of violations took the form described in Fig. 2a below,
where every direction Pac-Man is able to move in is in the trajectory of a nearby scared ghost. The only exception we saw is depicted in Fig. 2b; this situation was rare, only occurring once in two thousand games. We can, in fact, prove that these two types of scenario are the only cases where Pac-Man will be forced to violate vegan.
Proposition 3
The cases depicted in Fig. 2 are the only cases in the Vegan Pac-Man game where no compliant solution is possible.
Proof
From Definition 5, we know that if there are no compliant solutions, either: the solution set (a) is empty, (b) contains only impossible actions, (c) contains solutions that violate at least one norm, or (d) contains solutions that are inconsistent. From Lemma 1, and Propositions 13 and 14 from Governatori et al. (2013), we know (d) is not a possibility; likewise, we will not encounter (b), because we construct a solution set only from possible actions. With respect to (c), prohibitions are identified as positive conclusions of negative rules, which are removed as in Algorithm 1, and since there are no positive obligations in GameState, Pac-Man will not fail to act in compliance with one; that is, the yielded solution will not violate any norms. This leaves only one possibility: (a), where the solution set is empty. This can only occur if every possible action is removed in Algorithm 1 because it is subject to a prohibition.
Note that Pac-Man always has the action Stop available to it, but there are no game states in which its set of possible actions is [Stop]—this would imply that Pac-Man is closed in on all sides by walls. However, we can have the set of possible actions [Stop, Dir] where \(Dir\in \{North, South, East, West\}\). This would imply that there are walls on all sides of Pac-Man, aside from the cell it can move to in taking action Dir. This is the exact scenario depicted in Fig. 2b.
A second possibility is that the set of possible actions is [Stop, Dir1, Dir2]; Dir1 and Dir2 can be any pair of directions. This can describe corners in the maze (of which there are 16), or the the “tunnel”-like portions on of the maze. In all of these cases, it is possible for one ghost to occupy one of the two spaces Pac-Man is free to move into, which is described in Fig. 2a.
For the remaining two possibilities, where Pac-Man has a list of possible actions of the form [Stop, Dir1, Dir2, Dir3] or [Stop, Dir1, Dir2, Dir3, Dir4], at least one direction in which it is possible to move will not be blocked by a ghost, since there are only 2 ghosts. As Pac-Man will be permitted to move in this direction, we cannot have a case where no compliance is possible. \(\square\)
Revising the norm base: vegetarian Pac-Man
Until now, we have not been differentiating between ghosts in our discussion; in reality, the rule vegan is actually two rules (\(X \in \{blue,orange\}\)):
We can contract the norm base by removing \(vegan_{orange}\), leaving \(vegan_{blue}\) as our only regulative norm. We called the Pac-Man that adheres to this norm base vegetarian. Our preliminary results—based on 100 games and trained over 100 episodes—are given below.
Norm base | Policy | % Games | Game score | Avg ghosts eaten |
|---|---|---|---|---|
Won | (Avg[Max]) | (Blue / Orange) | ||
Vegetarian (100 games) | hungry | 94 | 1413.8 [1742] | 0.01 / 0.79 |
For Vegetarian Pac-Man, the scenario in Fig. 2a cannot occur, but one blue ghost was still eaten. Proposition 3 tells us that there is exactly one other case where Pac-Man can be forced into non-compliance, but our investigation of the records capturing the above test yielded a second way in which Vegetarian Pac-Man can end up eating a blue ghost—without directly or knowingly violating its norm base. That is, Pac-Man (see Fig. 3) is put in a situation where there is at least one available action that will not result in it eating the blue ghost, but taking the action that results in eating the ghost does not, strictly speaking, violate any norms in Pac-Man’s norm base.
When both Pac-Man and the blue ghost move into the power pellet’s cell at the same time, Pac-Man ends up eating it. The result is a quirk in the game implementation; when generating the next state, the game changes the ghost’s state to ‘scared’ immediately after Pac-Man moves, but before it is determined whether Pac-Man eats the ghost or the ghost eats Pac-Man. This is roughly analogous to an agent committing to an action it believes is ethically compliant, which nevertheless ends up having morally negative consequences because the agent’s circumstances changed after they had already committed to the action.
For Vegetarian Pac-Man, the cases depicted in Figs. 2b and 3 represent the scenarios where it ends up eating blue ghosts. If we want avoid such cases, however, we can expand our norm base to prevent Pac-Man from entering such “dangerous” situations. To do that we introduce a number of constitutive rules defining the concept of “danger” for each coordinate (x, y) within range of a hazardous area, for example:
We will also need to indicate whether there is a ghost within range of this “danger zone”, as avoiding them is only necessary if there is a ghost nearby:
The regulative norm we impose on Pac-Man prevents it from “entering danger”:
What does it mean to “enter danger”? As we did previously, we can define strategies (constitutive norms) that describe what constitutes entering danger. Namely, for context \(\{inNorthRange_{pacman,danger}, inRange_{ghost, danger}\}\), the following constitutive norm holds: \({\textbf {C}}(North, enter_{pacman, danger})\). So we can define the rule:
We designate the version of Pac-Man subjected to these additional norms with the tag “avoid”. A summary of the performance of vegan Pac-Man during preliminary tests with this addition is given below; notice that the additional norms led to full compliance.
Norm base | Policy | % Games | Game score | Avg ghosts eaten |
|---|---|---|---|---|
Won | (Avg [Max]) | (Blue / Orange) | ||
Vegetarian—avoid (100 games) | hungry | 87 | 1336.2 [1747] | 0.00 / 0.88 |
Remark 2
Governatori and Rotolo (2008) discusses situations where the combination of the (ethical) norms and a particular factual situation results in breaches even for agents designed to comply with the norms at the cost of giving up their goals. There it is proved that sometimes the only way to comply with the norms is to prevent a situation from happening, and the agents have to modify their plans accordingly. The solution adopted in the current paper is to introduce new norms that render a position in the game, that unavoidably results in a violation, forbidden. This is not a comprehensive solution; we might not always be able to design coherent or feasible rules that can avoid such dangerous situations; for this reason, an additional mechanism for planning ahead to avoid violations would be desirable—albeit outside the scope of this paper.
When we moved on to running our batches of 1000 games, we found that neither the scenarios in Fig. 2 nor the one in Fig. 3 occur, and we have full compliance even without implementing the avoid rules:
Norm base | Policy | % Games | Game score | Avg ghosts eaten |
|---|---|---|---|---|
Won | (Avg [Max]) | (Blue/Orange) | ||
Vegetarian | random | 0 | − 446.96 [− 111] | 0.00 / 0.008 |
vegetarian | hungry | 89.3 | 1343.8 [1750] | 0.00 / 0.79 |
Vegetarian—avoid | hungry | 90.1 | 1361.06 [1751] | 0.00 / 0.81 |
These relatively identical results are likely due to Pac-Man’s additional training for these tests; for example, the region of the maze depicted in Fig. 2b contains no food pellets, and it is not necessary to enter it in order to win the game. We therefore found running preliminary tests with a more poorly performing agent a useful tool for better understanding how the norm base, the agent, and its environment interact.
Nevertheless, the additional rule avoid does not hamper performance and supplies an additional degree of security, and in certain applications of ethical AI, we might be interested in having a guarantee that a “negative” scenario, however rare, will not be allowed to occur.
Revising the norm base: cautious and over-cautious Pac-Man
Returning to the Vegan norm base, we can use the avoid rule (see Sect. "Revising the norm base: vegetarian Pac-Man") to help Pac-Man avoid eating ghosts altogether: by not eating the power pellet which makes the ghosts scared in the first place. For this norm base, we will have the avoid rule:
along with the constitutive norms:
where (x, y) is one step away from the area defined as dangerous, and
for all actions \(\in Actions\).
We designed two different norm bases; in one (denoted as cautious in the below table of results), we define the cells holding the power pellets as dangerous. In the other, we take a deliberately over-cautious approach, and define entering a dangerous area as entering an entire region of the maze; in particular, we define as dangerous certain \(3\times 4\) regions of the maze in which Pac-Man can find the power pellets. However, this makes the food pellets in these regions also inaccessible, and as a result, Pac-Man cannot win the game if it obeys avoid. The results of testing the vegan norm base with these cautious and over-cautious modifications of the avoid rule are given below.
Norm base | Policy | % Games | Game score | Avg ghosts eaten |
|---|---|---|---|---|
Won | (Avg[Max]) | (Blue / Orange) | ||
Vegan—over-cautious | hungry | 0% | − 174.95 [176] | 0.00 / 0.00 |
Vegan—cautious | hungry | 13.9% | 28.36 [1340] | 0.00 / 0.00 |
As we might expect from the over-cautious norm base, Pac-Man is compelled to obey the norm base at the expense of winning the game, and loses every game it plays. The fact that the normative supervisor will not allow an agent non-compliant actions (unless they cannot be avoided) even at the expense of failing to fulfil its primary function will be desirable quality in some cases, but this might not always be the case.
In the case of the cautious norm base, Pac-Man can, in theory, win the game (the power pellets—which are not technically food pellets—do not need to be eaten to win the game), but fails to do so in most cases. There are two reasons for this: the first is that this creates four additional places in the maze where a scenario like that depicted in Fig. 2b can occur. This leads to additional opportunities for Pac-Man to become trapped by the ghosts, and since obeying the norm base takes precedence over the policy, Pac-Man will choose not to eat the power pellet even if it will lose the game as a result. The second reason why Pac-Man’s success rate is so low is due to a shortcoming of our decoupled approach; Pac-Man’s policy does not take into account the fact that Pac-Man cannot continue moving in that direction. In this case, the supervisor filters out the best choice available, and Pac-Man has to go with the second best action—which, in some cases, might be Stop. In this case, Pac-Man will remain stuck in place until conditions in the game change enough for the policy to start recommending another action, and this may never get the chance to happen, if Pac-Man is trapped and eaten first. This particular scenario represents a good argument for combining the normative supervisor with additional methods for synthesizing goal-directed behaviour and ethical behaviour, for example by learning both simultaneously.
Introducing permissive norms
Thus far, we have only dealt with an implicit (weak) idea of permission; compliant solutions as defined in Definition 3 are permissible courses of action in this sense. However, we can also define a notion of strong permission, which gives an agent explicit permission to perform an otherwise forbidden action.
In this phase of our case study, we introduce two new norm bases. The first uses an “all-or-nothing” heuristic; Pac-Man attempts to adhere to the norm vegan, but as soon as it violates the norm by eating a ghost, it gives up and is permitted to eat any ghost therefrom. For the second we “merge” the vegetarian and the vegan norm bases, by implementing the following norm: if Pac-Man violates the norm vegan, it is therefrom permitted to eat another ghost, so long as the ghost is of the same colour of the one it just ate. In other words, this Pac-Man will attempt to adhere to the Vegan norm base, but if it fails to do so, it will switch to the Vegetarian norm base instead.
To implement these norm bases, we introduce two new components: persistent facts (facts that persist throughout the game despite state changes) and exceptions.
In order to comply with this norm base, Pac-Man needs to know if it has violated any norms over the course of the game, and which one it has violated. Hence it needs to have access to information about its hitherto performance. In building the translators, we constructed a programmatic representation of the agent’s current state; instead of overwriting this completely with each new time step, we can maintain attributes that record facts that persist over time. We implement the above caveat to the vegan norm base by adding to GameState a fact \(violated_{blue}\) (\(violated_{orange}\) resp.) if the supervisor has recorded Pac-Man eating a blue (orange resp.) ghost. We can add a third fact defined as \(violated\equiv violated_{blue}\vee violated_{orange}\).
In order to implement the above norm bases, we make use of defeaters to define an exception to the rule vegan. For the all-or-nothing norm base, these rules can be expressed as (\(X \in \{blue,orange\}\)):
And for the second norm base, where we switch from Vegan to Vegetarian, these rules can be expressed as (\(X \in \{blue,orange\}\)):
If we include these defeater rules in the norm base, Pac-Man will attempt to avoid eating ghosts, but as soon as it eats a XGhost, the fact \(violated_{X}\) begins to persistently appear in GameState, and the defeater will be triggered and void the prohibition from \(vegan_{X}\). The results of testing these norm bases are given in the table below.
Norm base | Policy | % Games | Game Score | Avg ghosts eaten | Tot.# Violat. |
|---|---|---|---|---|---|
Won | (Avg[Max]) | (Blue / Orange) | 1000 Games | ||
Vegan | hungry | 91.4 | 1231.7 [1937] | 0.048 / 0.049 | 55 |
(all-or-nothing) | |||||
Vegan (switch) | hungry | 90.6 | 1215.83 [1733] | 0.025 / 0.043 | 57 |
We have added a column supplying the number of violations incurred over 1000 games; since eating a ghost after Pac-Man has already eaten one does not necessarily violate the norm base, we cannot know from the number of ghosts eaten how many times Pac-Man violated its norm base. For the all-or-nothing Pac-Man, there can be at most one violation per game, after which Pac-Man may eat between 0 and 3 more ghosts. As we can see from the results, Pac-Man violated the norm base 55 times, but consumed 97 ghosts. For the Vegan/Vegetarian switch norm base, Pac-Man can violate the norm base at most twice, and if there is one violation, only one other ghost can be eaten. Here, Pac-Man violated the norm base 57 times but ate 68 ghosts. We checked the logs and confirmed that in every game there was at most one violation. Hence, in 11 of the 57 games in which there was a violation, Pac-Man ate a ghost twice, exploiting the permission triggered by the violation of the vegan norm. There were no cases of two violations per game, since it is unlikely to encounter situations like that depicted in Fig. 2b.
These tests yielded several further insights. Pac-Man violated the norm base at a significantly higher rate than we saw in the hungry policy Vegan Pac-Man test. Why was this? In the previous tests Pac-Man’s violations of the norm base (and therefore eating of ghosts it was forbidden from eating) were very infrequent, and the rare in-game reward it received from such a violation had little impact on the learning module. However, when Pac-Man was allowed to continue eating ghosts (incurring more rewards) after violating the norm base a first time, the learner was more affected by this higher reception of rewards; as a result, Pac-Man was placed in more and more situations where eating a ghost was unavoidable. This is a strong indication that when implementing more complex normative reasoning, we should consider integrating the reasoner not just into the real-time control facilities, but also into the learner—for example, preventing the agent from collecting rewards for outcomes resulting from a violation of the norm base.
Contrary-to-duty obligations: passive vegan Pac-Man
We explore one final norm base for Pac-Man, which utilizes a specific type of obligation called a contrary-to-duty obligation (CTD). An obligation is considered contrary-to-duty if it comes into force when another obligation is violated. A classic example of CTD is known as Forrester’s paradox (Forrester, 1984):
-
1.
It is obligatory that Smith not murder Jones.
-
2.
It is obligatory that, if Smith murders Jones, Smith murder Jones gently.
-
3.
Smith murders Jones.
The desired conclusion from the above propositions is that Smith murders Jones gently; though he is not supposed to murder Jones in the first place, since it is a fact that he does, he ought to do it in a certain way.
We will address a similar line of reasoning in this section; that is, we modify the norm base of Vegan Pac-Man by adding the following rule (we will call this Passive Vegan Pac-Man): “If Pac-Man does eat a ghost, it must do so while standing still.” The intricacies of this dynamic are not easy to demonstrate with the kinds of test results with which we have hitherto summarized Pac-Man’s behaviour. Thus, we will here walk through a kind of case-study-within-a-case-study, illustrating how the addition of this rule changes the results output by Algorithm 3 in a non-compliant scenario. In particular, we take a real example of a non-compliant scenario from a violation report from one of the Vegan Pac-Man tests (depicted in Fig. 4).
In this scenario, there is one ghost directly to the east of Pac-Man, and one just around the corner to the northwest. The output of Algorithm 3 for the scenario outlined in Fig. 4, under the Vegan norm base, is shown in Fig. 5:
As for the construction of the Passive Vegan norm base, recall that we interpreted \({\textbf {C}}(North, eat(pacman,ghost))\) as \({\textbf {C}}({\textbf {O}}(\lnot eat(pacman,ghost)),{\textbf {O}}(\lnot North) )\); this was convenient because earlier, we were dealing specifically with prohibitions. However, we are now interested in representing a different dynamic, and we will interpret this relation between the action of moving North to a new cell and eating a ghost as \({\textbf {C}}({\textbf {O}}(North), {\textbf {O}}(eat(pacman,ghost)))\). What we want to express here is that an obligation to move North will constitute eating the ghost in Pac-Man’s next turn (if Pac-Man is within range of a scared ghost to the north, of course). We can formalize this in DDPL as:
Note also that for these constitutive norms, we will need to add a superiority relation \(r_{act}>vegan\) for all \(act\in Actions\). This is so that in the case of a violation, vegan is defeated by assuming \({\textbf {O}}(North)\) (note that the superiority relation remain acyclic, so Lemma 1 still holds).
Finally, we can add our new contrary-to-duty obligation:
After the addition of the rule ctd, the output of Algorithm 3 changes, as shown in Fig. 6.
Now, the only action recommended is Stop—in compliance with the contrary to duty obligation ctd. This change occurs because now, in addition to violating vegan, the choices of West and East violate ctd as well. Thus, while the scenario is still non-compliant (and therefore a violation report would be generated), the agent receives an instruction in line with its contrary-to-duty obligation.
Conclusion and future work
We have presented a modular and transparent approach for enabling autonomous agents to operate within the bounds of ethical compliance, while still following RL policies that allow them to effectively pursue other goals. This approach, while designed with ethics in mind, is grounded more generally in the logic of normative reasoning, and could be applied to a much broader range of requirements, such as legality or safety.
The normative supervisor consists of modules that dynamically translate environmental data from the agent and norms from an extraneous norm base into a formal language, and a central reasoner—a theorem prover for defeasible deontic logic. From the translated data and the norms, the theorem prover extracts compliant actions and, in the absence of them, actions meant to minimize violations of the norm base. Our supervisor has the additional advantage of providing event recording facilities to log actions taken by the agent and their compliance to the norm base, while running in parallel with the agent.
We explored the functionalities of this normative supervisor and its interactions with an RL agent through a case study which demonstrated the module’s ability to transparently enforce norms on the agent’s behaviour, its facilitation of revisions to the ethical values the agent is subject to, and its ability to provide useful explanations of any violations that occurred during operation, informing our revisions of the norm base. Additionally, in our experiments we observed that the agent’s performance did not suffer with the introduction of the module into its architecture; while the average score dropped—a necessary result of the restrictions on its behaviour—the number of games won did not.
This case study also demonstrated possible shortcomings of our approach; the absence of faculties for planning and the complete decoupling of the agent’s policy from its ethical reasoning prevented it from thinking ahead and taking steps to avoid undesirable situations.
The fact that the supervisor’s performance was impacted by the policy used and the number of episodes upon which the RL agent was trained also introduces the question of how, from the RL side, we can maximize the supervisor’s effectiveness; a larger number of episodes led indeed to better performances by the agent, while a smaller number allowed us to detect an edge case.
Additionally, even though the introduced computational overhead was not prohibitive, it was still substantive, and will be a more prominent factor in larger environments or norm bases. The agent queries the normative supervisor each time it takes an action, and in agents with more time-sensitive functions, this may be problematic. We were able to alleviate the cost of these queries somewhat by choosing a very computationally feasible logic and dynamically translating norms and adding them to the theory as they became relevant (cutting down on the size of the theory and therefore computation time). Nonetheless, the scalability to applications that must process large amounts of data extremely quickly will be limited. We aim to develop techniques to mitigate and predict such overhead, but our approach certainly prioritizes transparency and oversight over time-efficiency, and will likely remain most effective for applications that do the same.
As future workFootnote 4 we plan to experiment with alternative reasoning engines, more complex norm bases, and possibly more sophisticated games. For example, the use of norm bases that require more elaborate conflict resolution mechanisms would allow us to explore the pursuit of multiple (and at times opposing) ethical goals.
Additionally, as we saw in Sect. "Introducing permissive norms", more investigation on how normative reasoning can be integrated into an agent’s learning process is warranted; the ‘lesser evil’ module gives us a framework for evaluating and measuring the moral worth (or rather, detriment) of actions, which could prove a useful tool for an agent trying to learn ethical behaviour. Another motivation for pursuing this integration is the matter of policy optimization; the normative supervisor sometimes dictates that the agent stray from its optimal policy, and it might be the case that a better, compliant policy could be discovered if the normative reasoning was incorporated into training.
Moving forward, we also hope to explore the use of the supervisor in conjunction with other approaches to eliciting ethical compliance; we could, for example, use the event recorder capabilities with the agent in Noothigattu et al. (2019), or as a last minute compliance checker for an agent with an ethical planner as described in Bremner et al. (2019).
We are interested in extending our approach with methods for determining which norms govern an agent’s behaviour from logs of its actions and the environment in which these actions were performed (for first steps see, e.g., Savarimuthu and Cranefield (2011) and Haynes et al. (2017).
In our case study, we manually identified and integrated revisions to our norm base meant to minimize violations, and automating this process would be a challenging, but potentially rewarding research direction.
Notes
For simplicity, we will not differentiate between the blue and the orange ghost for the time being.
This principle was discussed by the Mīmāṃsā author Kumārila (7th c. CE), in the context of solving potential conflicts among the commands in the Vedas—the Indian sacred texts. The principle says that a norm that conflicts with the minimum number possible of other norms should be preferred.
We use a laptop with Intel i5-8250U CPU (4 cores, 1.60 GHz) and 8GB RAM, running Ubuntu 18.04, Java Ver. 8, Python Ver. 2.7. An implementation of the normative supervisor and the Pac-Man game can be found at https://github.com/lexeree/normative-player-characters.
An implementation of the normative supervisor is under active development at: https://github.com/lexeree/normative-player-characters.
References
Abel, D., MacGlashan, J., & Littman, M. L. (2016). Reinforcement learning as a framework for ethical decision making. In AAAI workshop: AI, ethics, and society (Vol. 16, p. 02). http://www.aaai.org/ocs/index.php/WS/AAAIW16/paper/view/12582
Aler Tubella, A., & Dignum, V. (2019). The glass box approach: Verifying contextual adherence to values. In Proceedings of the AISafety@IJCAI 2019, CEUR workshop proceedings (Vol. 2419). http://ceur-ws.org/Vol-2419/paper_18.pdf
Aler Tubella, A., Theodorou, A., Dignum, F., & Dignum, V. (2019). Governance by glass-box: Implementing transparent moral bounds for AI behaviour. In Proc. of IJCAI: The twenty-eighth international joint conference on artificial intelligence (pp. 5787–5793). ijcai.org. https://doi.org/10.24963/ijcai.2019/802
Alshiekh, M., Bloem, R., Ehlers, R., Könighofer, B., Niekum, S., & Topcu, U (2018) Safe reinforcement learning via shielding. In Proceedings of the thirty-second AAAI conference on artificial intelligence (pp. 2669–2678). https://www.aaai.org/ocs/index.php/AAAI/AAAI18/paper/view/17211
Andrighetto, G., Governatori, G., Noriega, P., & van der Torre, L. W. N. (eds.) (2013). Normative multi-agent systems, Dagstuhl follow-ups (Vol. 4). Schloss Dagstuhl - Leibniz-Zentrum fuer Informatik. http://drops.dagstuhl.de/opus/portals/dfu/index.php?semnr=13003
Berreby, F., Bourgne, G., & Ganascia, J. G. (2017). A declarative modular framework for representing and applying ethical principles. In Proc. of AAMAS 2017: The 16th conference on autonomous agents and multiagent systems (pp. 96–104). ACM. http://dl.acm.org/citation.cfm?id=3091125
Boella, G., & van der Torre, L. (2004). Regulative and constitutive norms in normative multiagent systems. In Proc. of KR 2004: The 9th intern. conf. on principles of knowledge representation and reasoning (pp. 255–266). AAAI Press. http://www.aaai.org/Library/KR/2004/kr04-028.php
Bremner, P., Dennis, L., Fisher, M., & Winfield, A. (2019). On proactive, transparent, and verifiable ethical reasoning for robots. Proceedings of the IEEE, 107(3), 541–561. https://doi.org/10.1109/JPROC.2019.2898267
Broersen, J., Dastani, M., Hulstijn, J., Huang, Z., & van der Torre, L. (2001). The boid architecture: Conflicts between beliefs, obligations, intentions and desires. In Proc. of AGENTS 2001: The fifth international conference on Autonomous agents (pp. 9–16). ACM. https://doi.org/10.1145/375735
DeNero, J., & Klein, D. (2014). UC Berkeley CS188 intro to AI—Course materials
Dignum, V (2017) Responsible autonomy. In Proc. of IJCAI 2017: The twenty-sixth international joint conference on artificial intelligence (pp. 4698–4704). ijcai.org. https://doi.org/10.24963/ijcai.2017/655
Forrester, J. W. (1984). Gentle murder, or the adverbial samaritan. The Journal of Philosophy, 81(4), 193–197. https://doi.org/10.2307/2026120
Governatori, G. (2015). Thou shalt is not you will. In K. Atkinson (Ed.), Proceedings of the fifteenth international conference on artificial intelligence and law (pp. 63–68). ACM https://doi.org/10.1145/2746090.2746105
Governatori, G. (2018). Practical normative reasoning with defeasible deontic logic. In Reasoning web international summer school, Lecture notes in computer science (Vol. 11078, pp. 1–25). Springer. https://doi.org/10.1007/978-3-030-00338-8_1
Governatori, G., Olivieri, F., Rotolo, A., & Scannapieco, S. (2013). Computing strong and weak permissions in defeasible logic. Journal of Philosophical Logic, 42(6), 799–829. https://doi.org/10.1007/s10992-013-9295-1
Governatori, G., & Rotolo, A. (2008). BIO logical agents: Norms, beliefs, intentions in defeasible logic. Journal of Autonomous Agents and Multi Agent Systems, 17(1), 36–69. https://doi.org/10.1007/s10458-008-9030-4
Hasanbeig, M., Kantaros, Y., Abate, A., Kroening, D., Pappas, G. J., & Lee, I. (2019). Reinforcement learning for temporal logic control synthesis with probabilistic satisfaction guarantees. In Proc. of CDC 2019: The IEEE 58th conference on decision and control (pp. 5338–5343). IEEE . https://doi.org/10.1109/CDC40024.2019.9028919
Haynes, C., Luck, M., McBurney, P., Mahmoud, S., Vítek, T., & Miles, S. (2017). Engineering the emergence of norms: A review. Knowledge Engineering Review, 32, e18. https://doi.org/10.1017/S0269888917000169
Jansen, N., Könighofer, B., Junges, S., Serban, A., & Bloem, R. (2020). Safe reinforcement learning using probabilistic shields (invited paper). In Proc. of CONCUR 2020: The 31st international conference on concurrency theory, Leibniz international proceedings in informatics (LIPIcs) (Vol. 171, pp. 3:1–3:16). https://doi.org/10.4230/LIPIcs.CONCUR.2020.3
Lam, H. P., & Governatori, G. (2009). The making of SPINdle. In Proc. of RuleML 2009: The international symposium of rule interchange and applications, LNCS (Vol. 5858, pp. 315–322). Springer. https://doi.org/10.1007/978-3-642-04985-9
Lam, H. P., & Governatori, G. (2013). Towards a model of UAVs navigation in urban canyon through defeasible logic. Journal of Logic and Computation, 23(2), 373–395. https://doi.org/10.1007/978-3-642-04985-9_29
Levine, S., Finn, C., Darrell, T., & Abbeel, P. (2016). End-to-end training of deep visuomotor policies. The Journal of Machine Learning Research, 17, 39:1–39:40
Makinson, D., & Van Der Torre, L. (2007). What is input/output logic? Input/output logic, constraints, permissions. In Dagstuhl seminar proceedings (Vol. 07122). Schloss Dagstuhl-Leibniz-Zentrum für Informatik, Internationales Begegnungs- und Forschungszentrum für Informatik (IBFI), Schloss Dagstuhl, Germany. http://drops.dagstuhl.de/opus/volltexte/2007/928
Moor, J. (2006). The nature, importance, and difficulty of machine ethics. IEEE Intelligent Systems, 21, 18–21. https://doi.org/10.1109/MIS.2006.80
Neufeld, E., Bartocci, E., Ciabattoni, A., & Governatori, G. (2021). A normative supervisor for reinforcement learning agents. In A. Platzer, & G. Sutcliffe (Eds.), Proc. of CADE 28: The 28th international conference on automated deduction, LNCS (Vol. 12699, pp. 565–576). Springer. https://doi.org/10.1007/978-3-030-72019-3_18
Noothigattu, R., Bouneffouf, D., Mattei, N., Chandra, R., Madan, P., Varshney, K. R., Campbell, M., Singh, M., & Rossi, F. (2019). Teaching AI agents ethical values using reinforcement learning and policy orchestration. In Proc. of IJCAI 2019: The twenty-eighth international joint conference on artificial intelligence (pp. 6377–6381). https://doi.org/10.24963/ijcai.2019/891
Nowell-Smith, P. H., & Lemmon, E. J. (1960). Escapism: The logical basis of ethics. Mind, 69(275), 289–300.
Pereira, L. M., & Saptawijaya, A. (2009). Modelling morality with prospective logic. International Journal of Reasoning-based Intelligent Systems, 1(3/4), 209–221. https://doi.org/10.1504/IJRIS.2009.028020
Pnueli, A. (1977). The temporal logic of programs. In Proc. of the 18th annual symposium on foundations of computer science (pp. 46–57). IEEE Computer Society. https://doi.org/10.1109/SFCS.1977.32
Prakken, H., & Sartor, G. (2015). Law and logic: A review from an argumentation perspective. Artificial Intelligence, 227, 214–245. https://doi.org/10.1016/j.artint.2015.06.005
Rodriguez-Soto, M., López-Sánchez, M., & Rodríguez-Aguilar, J. A. (2021). Multi-objective reinforcement learning for designing ethical environments. In Proc. of IJCAI 2021: The thirtieth international joint conference on artificial intelligence (pp. 545–551). https://doi.org/10.24963/ijcai.2021/76
Sadri, F., Stathis, K., & Toni, F. (2006). Normative KGP agents. Computational and Mathematical Organization Theory, 12(2–3), 101–126. https://doi.org/10.1007/s10588-006-9539-5
Savarimuthu, B. T. R., & Cranefield, S. (2011). Norm creation, spreading and emergence: A survey of simulation models of norms in multi-agent systems. Multiagent and Grid Systems, 7(1), 21–54. https://doi.org/10.3233/MGS-2011-0167
Sergot, M. J., Sadri, F., Kowalski, R. A., Kriwaczek, F., Hammond, P., & Cory, H. T. (1986). The british nationality act as a logic program. Communications of the ACM, 29(5), 370–386. https://doi.org/10.1145/5689.5920
Silver, D., Schrittwieser, J., Simonyan, K., Antonoglou, I., Huang, A., Guez, A., Hubert, T., Baker, L., Lai, M., Bolton, A., Chen, Y., Lillicrap, T. P., Hui, F., Sifre, L., van den Driessche, G., Graepel, T., & Hassabis, D. (2017). Mastering the game of go without human knowledge. Nature, 550(7676), 354–359. https://doi.org/10.1038/nature24270
The IEEE Global Initiative on Ethics of Autonomous and Intelligent Systems: IEEE standard review—Ethically aligned design: A vision for prioritizing human wellbeing with artificial intelligence and autonomous systems (1st ed.). IEEE (2019)
von Wright, G. H. (1968). An essay in deontic logic and the general theory of action: With a bibliography of deontic and imperative logic. Co: North-Holland Pub.
Wallach, W., & Allen, C. (2008). Moral machines: Teaching robots right from wrong. Oxford University Press. https://doi.org/10.1093/acprof:oso/9780195374049.001.0001
Watkins, C. J. C. H.: Learning from delayed rewards. Ph.D. thesis, King’s College, Cambridge, UK (1989). http://www.cs.rhul.ac.uk/~chrisw/new_thesis.pdf
Wu, Y. H., & Lin, S. D. (2018). A low-cost ethics shaping approach for designing reinforcement learning agents. In Proc. AAAI 2018: The thirty-second AAAI conference on artificial intelligence (pp. 1687–1694). AAAI Press. https://www.aaai.org/ocs/index.php/AAAI/AAAI18/paper/view/16195
Acknowledgements
This work was partially supported by WWTF project MA16-28 and the DC-RES run by the TU Wien’s Faculty of Informatics and the FH-Technikum Wien.
Funding
Open access funding provided by TU Wien (TUW).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Neufeld, E.A., Bartocci, E., Ciabattoni, A. et al. Enforcing ethical goals over reinforcement-learning policies. Ethics Inf Technol 24, 43 (2022). https://doi.org/10.1007/s10676-022-09665-8
Accepted:
Published:
DOI: https://doi.org/10.1007/s10676-022-09665-8