1 Introduction

The notion of group selection has been controversial for at least fifty years (Williams, 1966; Okasha, 2006, 2016; West et al., 2007; Wilson & Wilson, 2007; Wynne-Edwards, 1962; Sober & Wilson, 1998; Lloyd, 2017). Selective explanations regarding groups of individuals as the target of selection can be re-described from the point of view of the individuals or even the genes of individuals forming those groups. This has led many authors to become skeptical about the value of group-level explanations. In the last thirty years or so, scholars have progressively realized that the distinction between multilevel selection and individual-level selection—under the guise of kin selection and inclusive fitness (West et al., 2007)—is a matter of perspective or convention rather than fact.Footnote 1 That is, any multilevel setting can be adequately described from the lower-level or the higher-level perspective. Such claims have been made both informally (e.g., Dawkins, 1982; Kitcher et al., 1990; Sterelny & Kitcher, 1988; Maynard Smith, 1987; Waters, 1991) and formally (e.g., Queller, 1992; Dugatkin & Reeves, 1994; Kerr & Godfrey-Smith, 2002; West et al., 2007). Although some diverge from this conventionalist position (see e.g., van Veelen et al., 2012; Lloyd et al., 2008; Wade et al., 2010; Bijma & Wade, 2008), it is now considered orthodox by many evolutionary biologists (for a philosophical analysis, see Okasha, 2016).

Despite this, the distinction between individual and group selection is still considered significant by some biologists and philosophers, especially in the context of evolutionary transitions in individuality (see e.g., Bouchard & Huneman, 2013; Calcott & Sterelny, 2011; Okasha, 2006; Michod, 1999; Bourrat, 2022b, 2022c; Black et al., 2020). Why is this the case? In this paper, I argue that it is partly because the idea of ‘group selection’ or, more generally, multilevel selection can be understood in two different ways. One way to understand the distinction relies on the conventionalist position that they are formally equivalent at the level of the equations used to describe evolutionary change. I call this sense mlsc, for ‘multilevel selection qua conventional.’ However, in a different sense, which I put forward here, the distinction is factual if one attends to whether the putative interactions between the individuals of a population factually delimit subentities containing multiple individuals (groups). In other words, under this second sense, whether a setting involves multilevel selection hinges on whether groups of individuals can be delineated in a principled and empirical way, independently from an observer. I call this second sense mlsf for ‘multilevel selection qua factual.’ I argue that mlsc and mlsf have not been clearly distinguished in the literature. Note here that these two senses are not mutually exclusive so that a particular setting could be considered as exhibiting multilevel selection under both the mlsc and mlsf senses, or come apart so that it is only considered as exhibiting multilevel selection under the mlsc but not the mlsf sense.

The paper will run as follows. In the next section, I show the limitations of treating the multilevel selection question purely as mlsc and argue that both the Price equation and contextual analysis—classical approaches to multilevel selection—fall short of distinguishing genuine levels of selection if it is understood as mlsf. In the third section, I deploy and elaborate an approach based on Wimsatt’s (Wimsatt, 2007) distinction between aggregative and non-aggregative characters to distinguish genuine from arbitrary groups that address multilevel selection understood as mlsf.

2 Limits to the Price Equation and Contextual Analysis

One motivation for understanding the distinction between multilevel and individual-level selection under the mlsf rather than solely the mlsc sense is that if it is purely understood as a matter of convention, this leads to a paradox. We know, for instance, that multicellular organisms are the outcome of evolutionary processes, referred to as ‘evolutionary transitions in individuality,’ that led unicellular organisms to form collectives of cells and, ultimately, multicellular organisms (Buss, 1987; Maynard Smith & Szathmary, 1995; Michod, 1999; Okasha, 2006). Yet, despite multicellular organisms being groups, they have been treated as individuals by standard evolutionary biology. The transition from unicellular to multicellular organisms is only one such evolutionary transition—many others have occurred during evolution, such as the transition from prokaryotic to eukaryotic cells (see Bourke, 2011).

Although a full description of evolutionary transitions in individuality from the point of view of lower-level individuals could, in principle, be given, most evolutionary biologists would argue that events of evolutionary transitions in individuality and the higher-level individuals they produced—such as eukaryotic cells or multicellular organisms—are factual rather than result from mere definitional fiat.Footnote 2 If so, this implies that the mlsc perspective does not capture fully what can be meant by ‘group selection’ or, more generally, ‘collective-level selection.’Footnote 3 Since multilevel selection is now regarded by many as a genuine evolutionary process, it is a matter of some urgency to determine a theoretical basis to distinguish selection processes occurring at different levels of organization in a factual rather than conventional manner. This point can be more thoroughly appreciated if one understands that the formalism underlying the conventionalist approach can be applied regardless of whether collectives genuinely exist (Glymour, 2017). Following this formalism, one can, in principle, take any population of particles and organize them in collectives however one wants. So long as the so-formed ‘collectives’ exhibit variation in character that leads to differences in fitness at that level, there is some collective-level selection, which vindicates the mlsc position. However, in and of themselves, these approaches do not permit us to adequately understand the notion of collective-level selection under a mlsf sense—that is, where collectives are biologically relevant.Footnote 4

To see this, let us start with the Price equation (Price, 1970), the most common formalism used in this literature (see Okasha, 2006). This equation, which is a mathematical identity, tells us that the evolutionary change of a character z over a period of time (\(\Delta {\overline{z}}\)) of a population of particles reproducing asexually, perfectly, in discrete generations, and in which there is no drift, is equal to:

$$\begin{aligned} \Delta {\overline{z}}={\text {Cov}}(\omega _i,z_i), \end{aligned}$$
(1)

where \({\text {Cov}}(\omega _i,z_i)\) represents the covariance between the character z of the particles i (\(z_i\)) and its relative fitness (\(\omega _i\)). If we assume, for simplicity, that this covariance represents a linear causal relationship between z and \(\omega\) such that, following the interventionist framework (Woodward, 2003), intervening on z would produce a change in \(\omega\), it represents the evolutionary change attributable to natural selection (Frank, 1998, 2012). Equation (1) seems to vindicate the idea that only particle-level selection occurs in this scenario.

Yet, suppose now that one decides to group particles in collectives on purely arbitrary grounds. One can now define the character and actual relative fitness of a particle, respectively, as:

$$\begin{aligned} z_{kj}= Z_k + \Delta z_{kj}, \end{aligned}$$
(2)

and

$$\begin{aligned} \omega _{kj}= \Omega _k + \Delta \omega _{kj}, \end{aligned}$$
(3)

where \(Z_k\) and \(\Omega _k\) represent the character and actual relative fitness of the collective k defined by an observer (measured as the average character and actual relative fitness of its constituent particles), respectively, and \(\Delta z_{kj}\) and \(\Delta \omega _{kj}\) represent the character and actual relative fitness deviation, respectively, of the particle j from that of collective k. With this in place, following Queller (1992), one can rewrite Eq. (1) as:

$$\begin{aligned} \Delta {\overline{z}}=\underbrace{{\text {Cov}}(\Omega _k,Z_k)}_{\begin{array}{c} \text {Collective-level}\\ \text {selection} \end{array}}+ \underbrace{{\text {E}}[{\text {Cov}}(\Delta \omega _{kj},\Delta z_{kj})]}_{\text {Particle-level selection}}, \end{aligned}$$
(4)

where \({\text {Cov}}(\Omega _k,Z_k)\) represents the covariance between collective character and collective fitness—classically interpreted as collective-level selection—and \({\text {E}}[{\text {Cov}}(\Delta \omega _{kj},\Delta z_{kj})]\) represents the expected (i.e., weighted average across all collectives) within-collective covariance between particle character and particle fitness, classically interpreted as particle-level selection.

Equation (4) is a version of the classical multilevel Price equation (Poincaré, 1972; Okasha, 2006), which has been used to rehabilitate the idea of group selection (see e.g., Hamilton, 1975; Sober & Wilson, 1998, pp. 71–76). If the two terms are nonzero, the classical interpretation is that selection operates at both the particle and collective levels. Yet, recall that the grouping of particles in collectives in this case was made on purely arbitrary grounds. Other groupings could have led to different conclusions about the existence and magnitude of selection at the two levels.

The perfect equivalence between Eqs. (1) and (4) means that one can decide to see the average change in z as one resulting from selection occurring only at the particle level, or as the result of multilevel selection. Note additionally that assuming an infinite population size—that is, there is no drift—there are infinite ways that one can partition particles into collectives (which are not even required to have the same size).

Before moving further, an important remark should be made—namely, that the information contained in the lower-level description (used for Eq. (1)) and the multilevel description (used for Eq. (4)) is identical. This assumption is standard in this literature (see e.g., Kerr & Godfrey-Smith, 2002, where the authors are very explicit about it). The two ways to describe the system only represent different ways of ‘packaging’ the information about the setting. If this assumption were violated, the conclusions reached in this manuscript would not be valid. In many cases, different descriptions at different levels provide different bits of information about a given system. It is a very likely and worthwhile hypothesis that evolutionary biologists switch to different levels in their explanations because they provide overlapping but also different pieces of information. Elsewhere, I explore this question (Bourrat, 2021a, 2023a, 2023b); however, in this manuscript, following others, I will assume a perfect informational overlap between the two descriptions.

It follows from these remarks that if the Price equation is the only tool used to answer whether the evolutionary change for a trait occurs as a result of collective-level selection in a given setting, the conventionalist position—that is, mlsc—seems to be vindicated. This is so because it would be equally correct to provide a description of this change at the particle level only or one that would involve collectives delineated following particular rules (e.g., spatial rules).

A realist using this tool—that is, following a mlsf approach to multilevel selection—might nevertheless respond that a biologist will know how to partition a population of particles into collectives in a way that renders the notion of selection at the collective level factual. Although this might be correct in some situations, genuine collective boundaries will not always be easy to discern. Further, the project of providing an explicit criterion or set of criteria—perhaps implicitly grounding the intuition of the biologist making the partitioning—enabling the distinction between genuine and arbitrary collectives is a worthwhile enterprise in and of itself. Crucially, please note that I make no assumptions about whether particles interact and influence one another’s fitness in Eqs. (1) or (4). Whether interactions occur would not change the conclusion reached here. In fact, it has been shown by Queller (1992) that a partitioning based on inclusive fitness, a particle-level perspective where the fitness of a focal particle is modulated by its (social) interaction(s) with other particles of the population, can equally be derived from Eq. (1).

Starting from the conclusion that the Price equation is insufficient to flesh out the idea of multilevel selection in the mlsf sense, several authors have proposed that collective-level selection occurs only when the fitness of a particle is the outcome of two causal factors: namely, its character and the character of its collective. This approach is known as contextual analysis, a form of multiple linear regression analysis (see Heisler & Damuth, 1987; Goodnight et al., 1992; Okasha, 2006).Footnote 5 Formally, we define the fitness of a particle j in a collective k as:

$$\begin{aligned} \omega _{kj}= \beta _{wz}z_{kj} + \beta _{wZ}Z_k + e_{kj}, \end{aligned}$$
(5)

where \(\beta _{wz}\) represents the partial linear regression coefficient of particle actual relative fitness on particle character, \(\beta _{wZ}\) represents the partial linear regression coefficient of particle actual relative fitness on collective character, and \(e_{kj}\) is the residual. Replacing Eq. (5) in Eq. (1), applying the distributive properties of variance and covariance, the property that a covariance between a variable and itself is its variance, and assuming there is no correlation between the residuals and particle character, we obtain:

$$\begin{aligned} \Delta {\overline{z}}=\underbrace{\beta _{wz}{\text {Var}}(z_{kj})}_{\begin{array}{c} \text {Particle-level}\\ \text {selection} \end{array}} +\underbrace{\beta _{wZ}{\text {Var}}(Z_k)}_{\begin{array}{c} \text {Collective-level}\\ \text {selection} \end{array}}. \end{aligned}$$
(6)

Following contextual analysis, \(\beta _{wz}{\text {Var}}(z_{kj})\) represents the particle-selection term, and \(\beta _{wZ}{\text {Var}}(Z_k)\) the collective-selection term. For details, see Okasha (2006, pp. 86–93).

Equation (6) is an improvement over Eq. (4) for the purpose of understanding multilevel selection under the mlsf sense. This is so because it discards cases where there are no interactions between the particles of a population—cross-level by-products, to use Okasha’s (2006) terminology—as representing cases where there can be collective-level selection. In a population where particles are not interacting with one another, the collective-level character is always nil, leaving only the particle-level selection term potentially different from zero. Although being able to distinguish clear cases where there are no interactions between the particles of a population from cases where there are interactions is a significant achievement, contextual analysis does not permit rejecting the conventionalist position entirely—for two reasons. First, the existence of between-particle interactions with fitness effects does not mean that these interactions delineate collectives with boundaries. Second, even if one could, in principle, delineate clear collectives in the population, it does not follow that the partitioning made by the observer delineates those collectives.Footnote 6 For convergent ideas, see Godfrey-Smith (2008).

To understand this, let us start with the first point and imagine a population where particles are interacting with one another, but where there are no genuine collectives, just a global population. Having partitioned the population arbitrarily into collectives could lead to a situation where \(\beta _{wZ}{\text {Var}}(Z_k)\) is different from zero. Yet, because the collectives have no reality other than in the mind of the observed, this would yield a notion of multilevel selection under the mlsc sense. Second, suppose now that there are genuine collectives in the population, so that particles of one collective interact with one another during their lifetime but do not interact with members of any other collective. In this setting, the population could still be portioned into arbitrary collectives, such as two halves of genuine collectives so that, again, \(\beta _{wZ}{\text {Var}}(Z_k)\) is different from zero. This situation would also be consistent with contextual analysis and only yield mlsc, not mlsf.

All this shows is that neither Price’s partitioning nor contextual analysis, in and of themselves, permits us to escape the conventionalist position on multilevel selection (see Bourrat, 2021a, 2022a, 2021b, for further thoughts on this). As such, they provide no account to understand multilevel selection under the mlsf sense. The first step to flesh out an mlsf account requires placing constraints on the notion of what a collective-level entity can be that will ground the distinction between genuine and arbitrary collectives—which both Price’s partitioning and contextual analysis fail to do adequately. Only in a population composed of genuine collectives is there some potential for collective-level selection to be present. Without genuine collectives, the possibility of mlsf does not even exist. Of course, one might still want to say that multilevel selection occurs under the mlsc sense, but this way of answering the question will not address, for instance, the question of the origins of new units of selection in evolution. It should not be denied that the question of the existence of collective-level selection, assuming collective entities are taken for granted, is an important one to address. However, it does not supersede the question of the existence of genuine collectives if multilevel selection is regarded as factual. In the next section, I provide an account that integrates both questions and yields an mlsf account of multilevel selection.

3 Functional Non-aggregativity and Multilevel Selection

If the foregoing reasoning is correct, to address multilevel selection under the mlsc sense, we require a method to distinguish real collectives from those that result from unprincipled choices made by an observer. This project can be regarded equivalently as providing a way to assess whether a type of entity in a hierarchy is the target of selection or an interactor, which is one of the realists’ main projects regarding units of selection (e.g., Hull, 1980; Lloyd, 1988, 2005, 2017; Brandon, 1982, 1990; Sober, 1990). To do so, inspired by Wimsatt’s work on non-aggregativity (see Wimsatt, 2007), I propose that the notion of aggregativity can be the basis for this distinction. I argue that a ‘functional aggregative collective character’ refers to a collective that is not genuine and, consequently, cannot be a target of selection at the collective level. In contrast, a ‘functional non-aggregative collective character’ refers to a genuine collective.

One way to way to approach the distinction between functional aggregativity and non-aggregativity in the context of the levels of selection problem is the following:

Functional aggregate collective. A collective delineated by an observer is a functional aggregate for a character if measuring the character of each of its particles independently and aggregating those measures into a collective character results in the same value as the collective character measured in situ. Conversely, a collective delimited by the observer is not a functional aggregate when the values obtained for these two measures differ.Footnote 7

To illustrate the idea of failure in aggregativity, suppose a setting where a population of bacteria (in the form of a biofilm) is able to resist the presence of an antibiotic by producing an extracellular material. Antibiotic resistance is a very common trait of biofilms (see Costerton, 2007). Classically, a single bacterium has, proportionally, much less resistance to antibiotics than an entire biofilm. Suppose for simplicity that the biofilm comprises three cells, a, b, and c. For the biofilm to exhibit non-aggregativity, the resistance to the antibiotic when measured independently (symbolized with indep()) must be different from a measure of resistance measured in the context of the collective (symbolized with context()), so that:

$$\begin{aligned} context(a+b+c) \ne indep(a)+indep(b)+indep(c). \end{aligned}$$

In the case of the biofilm, this inequality would be verified as the sum of the resistance to antibiotics for each cell measured independently being lower than when measured in the context of the biofilm.

What should be understood here by ‘independently’ is that the measures of particle characters are performed in a context where the particles have no means to interact with other particles while remaining in conditions otherwise identical to the in situ conditions. In other words, this would be equivalent to performing an ideal intervention on a particle following the interventionist account (Pearl, 2009; Woodward, 2003), with the causal variable being the presence or absence of interactions with other particles. Note here that intervening solely on the interactions with particles with no other changes will often be impossible in practice unless the interactions are not vital for the survival of the particles or for characters that can change rapidly. It should be stressed that these practical difficulties do not undermine the conceptual point that one step in assessing whether collectives drawn by an observer are genuine involves measuring the extent to which the particles within this collective interact.

When interactions are vital or the characters are developmental ones, ‘independent measures’ can nevertheless be operationalized as the closest possible setting (counterfactual) in which such measures could be made. The closest setting could, for instance, be particles from the closest taxa (or, in the case of experiments, the closest ancestors) with the same (or closest) allele (assuming a monogenic character) living solitarily rather than in groups (for more on this point, see Bourrat, 2021a, Appendix, box 9). This type of operationalization has been explored in experimental evolution (see Hammerschmidt et al., 2014; Rose et al., 2020) where growth rate comparisons are made between ancestors—assumed to be living more independently—and evolved lineages of the SBW25 strain of the bacteria Pseudomonas fluorescens. In these experiments, the evolved lineages underwent a selective regime at the collective level that enforces particular interactions between the bacterial cells of a collective imposed by the experimenter. This type of operationalization has also been used in the volvocine algae taxon in which species with different levels of multicellularity are found, from unicelled organisms to organisms that can be made of thousands of cells (see Kirk, 1998). In this taxon, trait comparisons between unicells (ancestor-like) and cells of multicell organisms have been performed to specifically understand evolutionary transitions in individuality (see Michod, 2005).

However, the existence of interactions between particles in a collective drawn by the observer—that is, a failure in functional aggregativity—is insufficient to establish functional non-aggregativity and, consequently, insufficient to delimit a genuine collective. It only provides evidence that the collectives delimited by the observer exhibit some non-aggregativity, not that they exhibit functional non-aggregativity, by which I mean that they would refer to bounded collectives. The example of bacterial biofilms taken above represents a case in point. They are typically not regarded as individuals in their own right in the same way that mammals, for instance, are (but, see Ereshefsky & Makmiller, 2013; Clarke, 2016, who present opposing views on this question). Instead, they exemplify cases where local interactions between particles without them forming groups, such as when there is a global population with a ‘viscous’ population structure (see Godfrey-Smith, 2008, for a discussion of the different notions of population structure). Other cases in which a failure of aggregativity would not imply functional non-aggregativity would be situations where the collectives drawn by the observers are gerrymandered: collectives exist but the boundaries drawn by the observer do not correspond to those collectives.

To demarcate a genuine collective from a gerrymandered one or one where the population structure is viscous, and thus discriminate functional non-aggregativity as opposed to a mere failure in aggregativity, the following condition should be met. To be counted as genuine, a given collective delimited by the observer with a given particle composition should exhibit the same collective character even if the composition of the particle particles in its neighborhood changes, assuming otherwise a constant environment. Once operationalized, this condition implies that two or more collectives with the same particle composition in terms of characters measured independently should exhibit the same collective character. If this second condition is met, the way the particles within a collective with a given composition interact is always the same (assuming here that non-particle environmental conditions are controlled for). Consequently, the boundaries of the collectives delimited by the observer are genuine. However, when this condition is violated, this constitutes evidence that the interactions between the particles of a collective with a given composition are different and, consequently, the boundaries delimited by the observer are arbitrary.

To illustrate further how functional non-aggregativity plays out in levels of selection, take the famous example from Sober (1984) of groups of individuals with different heights living in collectives. Suppose you observe collectives and want to know whether there is collective-level selection for height mlsf or whether these collectives are simply spatial aggregations of organisms. In other words, you want to know whether there is selection at the collective or particle (i.e., individual) level for height. To answer this question, you choose one of the delimited collectives and measure the average height in this collective, which represents the in situ measure of the collective character. Then, you take each individual of this collective and measure its height independently from any other individual. Finally, you compute the functional aggregative character of the collective—that is, the height the collective would have if it was a functional aggregate. To do so, you take the average individual’s height in the collective when measured independently from one another. If the average height of a delimited collective when measured in situ deviates from the average height computed when the individuals are taken independently, this provides evidence that the collective is not a functional aggregate. These operations are then repeated for each collective you delimited.

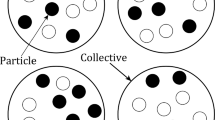
Yet, as mentioned earlier, the presence of non-aggregativity in a collective is not the demonstration that it is functional—that is, that the delimited collectives are genuine units. To show this, a collective composed of particles with the same character composition (i.e., the character is measured in isolation) should exhibit the same collective character, so that the collective corresponds to a genuine, as opposed to an arbitrary, collective. I assume here that each measure made is perfect. Of course, in any real situation, there would be some uncertainty for each one of these measures. Thus, answering the question of whether there is a failure in functional aggregativity, in addition to the question of whether there occurs the same failure in collectives with the same composition, is only possible with some confidence, provided the results of the relevant statistical tests used to ensure the different comparisons are significant. A numerical example illustrating the procedure just described is presented in Fig. 1.

Fig. 1
figure 1

Illustration of differences between arbitrary and genuine collective-level characters. Full lines indicate that the units are genuine, and dotted lines indicate that they are partitioned by the observer. The character value of each constituent particle (small full circles) measured independently is given inside each small circle. The character value of collectives (large dotted circles)—measured as the average of the constituent particles in the context of a collective—is given underneath each circle. In a, the collective character value is 2. When its particles are measured independently and an average is computed, the value obtained is the same as the character value of the collective: namely, 2. Because there is no difference between the collective-character value measured in situ and when it is computed with particles independently, we can conclude that the collective-level character is functionally aggregative. The in situ and independent values of the collective character being the same indicates that no interactions between the particles occur in the collective—thus, the collective is an arbitrary one. In contrast, in b, since the in situ collective-character value (4) is different from that taken when computed from the particle-character values measured in isolation from the collective (2), we can conclude that the collective-level character is non-aggregative. Yet, this does not permit one to establish that this character is functionally non-aggregative. For instance, in c, the collective-character values of two collectives with the same particle composition (when the particle characters are measured independently) are different: namely, 4 and 5. This indicates that the boundaries drawn by the observer are not genuine—either the collectives are gerrymandered or there are no genuine collectives in this population, just a viscous population structure. In other words, the constituent particles in the two collectives drawn by the observer interact differently. For a collective-level character to be genuine, constituent particles should behave in the same way, given they are in collectives of identical compositions—that is, leading to the same collective-level character value, a case illustrated in d where both collectives have a character value of 4

Full size image

The procedure described thus far permits us to delineate collective-level entities in a population of particles based on the conditions for functional-aggregativity that speaks to the mlsf way of understanding the multilevel selection question. We can now integrate it into a formalism based on the Price equation to assess, given a population in which collectives are factual as opposed to conventional, whether selection occurs at that level. To do so, we start by decomposing the character z of a particle j in the collective delimited by the observer k as:

$$\begin{aligned} z_{kj}= \alpha _{kj}+ \gamma _{kj}, \end{aligned}$$
(7)

where \(\alpha _{kj}\) is the character of the particle j of k measured independently, and \(\gamma _{kj}\) is the difference between the character of the particle j of k measured in the collective context (\(z_{kj}\)) and \(\alpha _{kj}\). We assume that \(\alpha _{kj}\) and \(\gamma _{kj}\) are independent because there is no particular biological reason to assume they are not. However, a more general approach could be developed to account for settings in which the two components are not independent. We choose to partition the particles into collectives so that, for any particle j of k, \(\gamma _{kj}=\gamma _{lm}\) if \(\alpha _{kj}=\alpha _{lm}\) and \(Z_k=Z_m\), where l is the l-th particle of the m-th collective. This last condition ensures that collectives are delimited in such a way as to capture genuine boundaries as opposed to arbitrary ones or, in other words, functional non-aggregativity as opposed to non-aggregativity simpliciter.

With this in place, we plug Eq. (7) into Eq. (1) so that:

$$\begin{aligned} \Delta {\overline{z}}={\text {Cov}}(\omega _{kj},\alpha _{kj}+ \gamma _{kj}). \end{aligned}$$
(8)

Using the distributive property of covariance, this can be rewritten as:

$$\begin{aligned} \Delta {\overline{z}}={\text {Cov}}(\omega _{kj},\alpha _{kj})+ {\text {Cov}}(\omega _{kj}, \gamma _{kj}). \end{aligned}$$
(9)

By definition, \({\text {Cov}}(y,x)=\beta _{yx}{\text {Var}}(x)\) (see Lynch & Walsh, 1998), so that we can rewrite Eq. (9) as:

$$\begin{aligned} \Delta {\overline{z}}=\underbrace{\beta _{\omega \alpha }{\text {Var}}(\alpha _{kj})}_{\begin{array}{c} \text {Particle-level}\\ \text {selection} \end{array}}+\underbrace{\beta _{\omega \gamma } {\text {Var}}(\gamma _{kj})}_{\begin{array}{c} \text {Collective-level}\\ \text {selection} \end{array}}. \end{aligned}$$
(10)

Following the distinction made earlier wherein functional aggregativity refers to particle-level selection and functional non-aggregativity refers to collective-level selection, the first term on the right-hand side of Eq. (10), (\(\beta _{w\alpha }{\text {Var}}(\alpha _{kj})\)), represents the evolutionary change due to particle-level selection, while the second term on the right-hand side, \(\beta _{w\gamma } {\text {Var}}(\gamma _{kj})\), represents the evolutionary change due to collective-level selection.

It should be stressed that finding that there is no collective-level selection following Eq. (10) does not invalidate the possibility of the existence of collective-level selection under an mlsc understanding. Equation (10) is, indeed, an alternative statistical decomposition of total evolutionary change \(\Delta {\overline{z}}\) and, consequently, fully compatible with Eq. (1), which is true by definition under the assumptions made. Yet, it puts adequate constraints on how to carve selection across levels of organization, which both Price’s partitioning—for which there is no constraint—and contextual analysis fail to do. Because these constraints are empirical and independent of an observer’s choices, the notion of collective-level selection it yields is of the mlsf sort. Although a re-description from the particle level is always possible, some ways of grouping particles into collectives are more biologically relevant than others. I have argued that the same failure of functional aggregativity across collectives with the same composition permits capturing this biological relevance.

4 Conclusion

In this paper, I have provided a novel way to address formally the tension between the idea that group selection (as opposed to individual selection) can occur and the idea that this distinction is a matter of conventions. Considered on purely statistical and compositional grounds, the conventionalists are correct that an individual-level description is equivalent to a multilevel description. However, this is no longer the case once a functional perspective is used. In that sense, the distinction is factual. Although I do not pretend to have solved all the problems and ambiguities surrounding multilevel selection—for instance, I have said nothing about group reproduction, which is seen by some as a significant feature of multilevel selection (e.g., Griesemer, 2000; Godfrey-Smith, 2009)—my analysis, particularly the partitioning used in Eq. (10), provides a starting point to flesh out this factual distinction.