A Theory of Marginal and Large Difference

Abstract

We propose a new theory based on the notions of marginal and large difference which has natural models in the context of nonstandard mathematics. We introduce the notion of finite marginality and show a representation result which ensures, for finitely marginal countable models, the existence of a homomorphism of the structure of marginal and large difference into a nonstandard model of the natural numbers, and show the extent to which any such homomorphism is unique. Finally, we show that our theory constitutes part of the underlying abstract structure of three distinct philosophical theories of vagueness: Dean’s neofeasibilism, Itzhaki’s theory of nonstandard heuristics, and our own initial sketch of a nonstandard primitivism about vagueness.

1 Introduction

1.1 Vagueness and Soritical Reasoning

One of the distinctive features of vague predicates is that they give rise to Soritical reasoning. The following ingredients are thought to yield instances of the Sorites paradox:

• (A) A strict weak order R;

• (B) A set A of objects such that

  • (1) R is a linear order on A;

  • (2) There are elements b and e of A such that R(b, e), b (evidently) has property T and e (evidently) fails to have property T;

  • (3) The inductive premise is plausible

    Inductive premise:

    $$\begin{aligned} \forall x,y\in A((T(x)\wedge S(x,y))\Rightarrow T(y)) \end{aligned}$$

    For every member x in A, if x has property T then x’s R-successor in A also has property T.

  • (4) A is finite.

From the inductive premise and the fact that b, the first member of A relative to R, has property T one reaches the conclusion that the second member of A relative to R also has property T. Via a novel application of the inductive premise one reaches the conclusion that the third member of A relative to R has property T. And so on, until one reaches the absurd conclusion that e, the last member of A relative to R, both has and lacks property T.

A typical example of a Soritical scenario consists of a finite sequence of people such that i) its first member is clearly not bald, ii) its last member is clearly bald, and iii) if y is the successor of x in the series, then x has 1 hair more than y. In this example, the weak order R consists in the balder than relation and the property T is the property of not being bald. Since the first member of the series isn’t bald, the second member of the series also isn’t bald, by the inductive premise. And so on, until one reaches the absurd conclusion that the last member of the sequence is both bald and not bald.

Recently, some philosophers (e.g., Dean 2018, Itzhaki 2021) have argued that a satisfactory resolution of the Sorites paradox, or at least satisfactory answers to some of the intriguing questions that it raises, requires an appeal to the idea that an infinite structure—akin to the order structure of nonstandard models of arithmetic and analysis—is, in some way or the other, present in Soritical scenarios (see also Dinis, 2018; Dinis & van den Berg, 2019; Dinis & Jacinto, 2021). The present paper offers one particular way of developing this thought.

One of our aims is to formulate and motivate what we call the ${{\textsf{ML}}}$ theory (of marginal and large difference). In our view, part of the puzzlement underlying the phenomenon of vagueness concerns the absence of a theory articulating the principles governing these notions.

A second aim of the paper is to offer a measurement theory for the notions of marginal and large difference as these are axiomatised by the ${{\textsf{ML}}}$ theory. Our results reveal that the ${{\textsf{ML}}}$ theory determines a rich structure of what might be called vague degrees. Significantly, this structure is akin to the order structure of models of nonstandard arithmetic and analysis. Accordingly, vague degrees turn out to be be representable, in a measurement-theoretic sense, by those models’ elements.

Our final aim is to show how the ${{\textsf{ML}}}$ theory constitutes part of the abstract structure which underlies recently proposed “nonstandard” theories of vagueness—in particular, Dean’s neofeasibilism, Itzhaki’s theory of nonstandard heuristics, and our own nonstandard primitivism.¹ A defense of any one of these theories is, however, outside the scope of the present paper.

The paper is structured as follows. In Sect. 2 we offer a formal characterisation of the ${{\textsf{ML}}}$ theory. Specifically, we present the theory’s axioms and gloss on their intuitive character. We also present a result showing that the ${{\textsf{ML}}}$ theory is not interpretable by the order relation of (standard) arithmetic or analysis. In Sect. 3 we show the theory’s consistency by providing models in the context of nonstandard arithmetic and analysis. We offer our measurement theory for the ${{\textsf{ML}}}$ theory in Sect. 4. In particular, we prove both a representation theorem and a uniqueness theorem with respect to a special class of so called “empirical models”. Finally, in Sects. 5, 6, 7, we briefly show how the ${{\textsf{ML}}}$ theory affords part of the abstract structure of the neofeasibilist, nonstandard heuristics and nonstandard primitivist theories of vagueness.

2 The ${\textsf{ML}}$ Theory

A strict weak order is a binary relation which satisfies the following conditions:

• (1) Irreflexivity: $\forall x \left( \lnot R(x,x)\right)$

• (2) Transitivity: $\forall x,y,z \left( (R(x,y) \wedge R(y,z)) \rightarrow R(x,z) \right)$

• (3) Almost connectedness: $\forall x,y,z \left( R(x,y) \rightarrow (R(x,z) \vee R(z,y)\right)$.

As mentioned, the ${\textsf{ML}}$ theory axiomatises the relations of both marginal and large difference with respect to an underlying strict weak order R. Accordingly, we assume the existence of two binary relations—denoted by, respectively, M and L. Their intended interpretation is the following: M(x, y) states that x is marginally smaller than y with respect to the order R, while L(x, y) states that x is largely smaller (i.e., much smaller) than y with respect to R. As such, the ${\textsf{ML}}$ theory is a theory of “marginal” and “large” difference.

The ${\textsf{ML}}$ theory’s first axiom postulates that the theory is not trivial: there are objects which are “largely different” with respect to the weak order R. The existence of “marginally different” objects is a direct consequence of Axiom 2.1 together with decomposition (Axiom 2.10 stated below).

Axiom 2.1

$\exists x,y\, L(x,y)$

The second and third axioms postulate that whenever x is marginally/largely smaller than y, then these objects are ordered by R.

Axiom 2.2

$\forall x,y \,(M(x,y)\Rightarrow R(x,y))$

Axiom 2.3

$\forall x,y \,(L(x,y)\Rightarrow R(x,y))$

We assume that marginal differences are transitive. This is in line with one of the so-called Leibniz rules (on which, see Dinis & van den Berg, 2019, Chapter 1), corresponding to the intuition that the sum of two infinitesimals is still infinitesimal, but in contrast with other approaches e.g. approaches using semi-orders such as Luce (1956) and Cobreros et al. (2012) (see also van Rooij, 2011, in which three objects a, b, c can be such that a is noticeably smaller than c, but b located between them is unnoticeably larger than a, and unnoticeably smaller than c).

Axiom 2.4

$\forall x,y,z \,(M(x,y) \wedge M(y,z)\Rightarrow M(x,z))$

The next axiom states that marginal differences are not large.

Axiom 2.5

$\forall x,y \,(M(x,y) \Rightarrow \lnot L(x,y))$

Axiom 2.6 captures the idea that marginal differences can be neglected with respect to large differences—an idea commonly associated with vague phenomena. Together with Axiom 2.4, this entails that large differences can never be decomposed merely into marginal differences. As such, our theory embraces transitivity principles in what regards the Sorites paradox.

Axiom 2.6

$\forall x,y,z \,(M(x,y) \Rightarrow ((L(z,y) \Rightarrow L(z,x)) \wedge (L(x,z) \Rightarrow L(y,z))))$

The next two axioms capture the intuition that increasing large differences only results in large differences.

Axiom 2.7

$\forall x,y,z\,((R(x,y)\wedge L(y,z))\Rightarrow L(x,z))$

Axiom 2.8

$\forall x,y,z\,((L(x,y)\wedge R(y,z))\Rightarrow L(x,z))$

Axiom 2.9 rules out differences which are neither marginal nor large.²

Axiom 2.9

$\forall x,y\,(R(x,y)\Rightarrow (M(x,y)\vee L(x,y)))$

Any large difference can be decomposed into a marginal difference and a large difference. This is of course another salient feature of vague phenomena: removing a grain of sand from a heap still leaves a heap.³

Axiom 2.10

(decomposition)

$$\begin{aligned} \forall x,y\,(L(x,y)\Rightarrow (\exists z(M(x,z)\wedge L(z,y)) \wedge \exists w(M(w,y)\wedge L(x,w)) )) \end{aligned}$$

Finally, we have an axiom of “density” for marginal differences: if x is marginally smaller than y then, for every z between x and y, it must be the case that x is marginally smaller than z and z is marginally smaller than y.

Axiom 2.11

$\forall x,y(M(x,y)\Rightarrow \forall z((R(x,z)\wedge R(z,y)) \Rightarrow (M(x,z)\wedge M(z,y)) ))$

This concludes our presentation of the ${\textsf{ML}}$ theory’s axioms. Before proceeding, we should make it clear that we do not claim it to be an exhaustive theory of the notions of marginal and large difference. Nor do we think that it captures all the different uses of ‘marginal difference’ and ‘large difference’, as these notions are commonly used. Rather, we take our axiomatisation to capture theoretically significant uses of these notions as they are employed in describing and reasoning about paradigmatic cases of “vague phenomena”.

A significant consequence of the ${\textsf{ML}}$ theory is that there are infinitely many objects. Axiom 2.1 entails that there are objects x and y such that y is largely greater than x. So, it follows from decomposition that there is some object $x_1$ which is marginally greater than x. By Axiom 2.6 we obtain that $x_1$ is largely greater than y. So, again by decomposition, there is some object $x_2$ which is marginally greater than $x_1$. And so on, so that we get an infinite sequence of objects $x_{1},x_{2},x_{3},\ldots$ such that no two elements of the sequence are identical, by Axiom 2.2 and the fact that R is a strict weak order.⁴

A commitment to an infinitude of objects is a common idealisation of several theories of measurement. For this and related reasons some authors (see e.g. Mundy, 1987 and Swoyer, 1987) have proposed that theories of measurement should be formulated as theories about relations between magnitudes (i.e. about relations between particular properties of objects) rather than about relations between objects.

We are sympathetic to this “higher-order” view on measurement theories, and ${\textsf{ML}}$’s quantifiers may be conceived as ranging over magnitudes rather than objects. Notwithstanding, and for the sake of familiarity, for the moment we will follow the more common practice of conceiving the quantifiers of the ${\textsf{ML}}$ theory as ranging over objects rather than properties.

Let us illustrate the theory with an example. Consider the relation R defined as being balder than. Then the relations of marginally balder than and largely balder than can be represented as follows (Fig. 1):

Fig. 1

‘Marginally balder than’ and ‘largely balder than’

Circles in the figure represent individuals. If a point has another one to its left, then the former is balder than the latter (e.g. R(m, n) and R(n, q)—n is balder than m and q is balder than n). Ellipsis, ‘$\ldots$’, indicate an infinite sequence of individuals, and vertical bars indicate that all the individuals to its right are largely balder than all the individuals to its left (e.g. L (m, p) and L(m, q)—p and q are both largely balder than m). Points which are not separated by vertical bars differ only marginally (e.g. M(m, n)—n is marginally balder than m).

We finish this section by presenting a result that points out the need to consider nonstandard structures.

Theorem 2.12

In the context of the ${\textsf{ML}}$ theory, the relation R is not interpretable as the usual less than ordering < on the reals or on the naturals.

Proof

We start by proving the result for the reals. Suppose towards a contradiction that R is interpretable as < on the reals. Using Axiom 2.1 we let x, y be such that L(x, y) and define

$$\begin{aligned} S:=\{z:L(z,y)\;\wedge \;x<z\}. \end{aligned}$$

Clearly, y is an upper bound of S, by Axiom 2.3. Moreover, S is nonempty. Indeed, by decomposition, there exists $z_0$ such that $M(x,z_0)$. We have that $z_0 \in S$ since $L(z_0,y)$, by Axiom 2.6, and $x<z_0$, by Axiom 2.2. Let $\ell$ be the least upper bound of S. Clearly, $x<a \le \ell$ for every $a \in S$.

It must be the case that $\lnot L(\ell ,y)$. Otherwise, there exists w such that $M(\ell ,w)$ and L(w, y), by decomposition. Since $M(\ell ,w)$, we have that $\ell <w$, by Axiom 2.2. But then $x< \ell <w$ and so $w\in S$. Hence $w \le \ell$ because $\ell$ is an upper bound of S, a contradiction.

Since y is an upper bound of S, we have that $\ell \le y$. So, either $\ell =y$ or $M(\ell ,y)$, by Axiom 2.9. In both cases, $L(x,\ell )$, by Axiom 2.6. Then there exists $w_0$ such that $M(w_0,\ell )$ and $L(x,w_0)$, by decomposition. So, $w_0<\ell$, by Axiom 2.2. Let $a\in S$. Then, by Axiom 2.6, we obtain $L(a,\ell )$ and $L(a,w_0)$. Hence $a<w_0$, for all $a\in S$, by Axiom 2.3. This means that $w_0$ is an upper bound of S and $w_0 < \ell$, in contradiction with the fact that $\ell$ is the least upper bound of S.

Therefore, R is not interpretable as < on the reals. The proof for the naturals is similar but appealing to the well-ordering principle instead of working with least upper bounds. $\square$

In Sect. 3—in particular in Sect. 3.2—we show that the ${\textsf{ML}}$ theory indeed has models in nonstandard arithmetic and nonstandard analysis.

3 Nonstandard Models

3.1 Nonstandard Analysis

‘Nonstandard analysis’ was the name given by Abraham Robinson (1961; 1966) to any theory giving a formal and consistent treatment of infinitesimals. There are many such theories (cf. e.g. di Nasso, 1999; Dinis & van den Berg, 2019; Kanovei & Reeken, 2014). For the purposes of this paper a very “economical” version due to Edward Nelson (1987, Chapter 4), which we shall denote by $\textsf{ENA}$ (for Elementary Nonstandard Analysis), is sufficient.⁵ Indeed, the main requirement that we need from nonstandard analysis is the possibility of defining different orders of magnitude, which can be achieved in virtually any theory that permits the existence of infinitesimals.

The axioms of Zermelo-Fraenkel Set Theory (with or without the Axiom of Choice) are the most common foundation of mathematics. These are written in a language which only contains one undefined non-logical symbol, ‘$\in$’, for set membership (cf. e.g. Kunen, 1980; Potter, 2004). The theory $\textsf{ENA}$ (cf. Figure 2) is a conservative extension of Zermelo-Fraenkel Set Theory which is governed by a simple set of extra axioms after adding to the language a new predicate, ‘${\textrm{st}}$’.⁶ One should read ${\textrm{st}}(x)$ as ‘x is standard’. Formulas which involve the predicate ‘${\textrm{st}}$’ are called external and those that do not, i.e. formulas in the language of classical mathematics, are called internal.

Fig. 2

The axioms of $\textsf{ENA}$

Let us briefly comment on the axioms of $\textsf{ENA}$. The first two axioms state that the usual natural numbers are standard. The third axiom postulates the existence of nonstandard natural numbers. Finally, we have as an axiom scheme a form of induction that allows us to conclude that a property is true of all standard natural numbers given that it is true of zero and that whenever it is true of some standard n, then it is also true of its successor $n+1$. Since $\textsf{ENA}$ is a conservative extension of classical mathematics, the usual form of induction is still valid, albeit only for internal properties. To see why such restriction is required, consider the formula $\Phi (n):\equiv {\textrm{st}}(n)$. If one could apply internal induction to $\Phi$ the conclusion would be that every natural number is standard, in contradiction with the third axiom.

One defines different orders of magnitude as follows. A real number x is said to be infinitesimal if its absolute value is smaller than the inverse of any positive standard natural number; limited, if it is, in absolute value, bounded by some standard natural number and unlimited, or infinitely large if it is not limited.

3.2 Nonstandard Models

In the following we show the ${\textsf{ML}}$ theory’s consistency by providing two different instantiations, ${\mathfrak {I}}_1$ and ${\mathfrak {I}}_2$, of the predicates R, M and L, such that all the axioms of the ${\textsf{ML}}$ theory are satisfied in the context of $\textsf{ENA}$. The choice of nonstandard models is guided by the observation that the simplest standard structures are not models of our theory, as revealed by Theorem 2.12. We will return to this point in Sect. 4.4.

The instantiation ${\mathfrak {I}}_1$ is arithmetical in nature because it only involves (both standard and nonstandard) natural numbers:

• (1) $R(x,y) := x <y$, where < is the usual order in the natural numbers

• (2) $M(x,y):= \exists n\, ( {\textrm{st}}(n) \wedge y= x+n)$

• (3) $L(x,y):=x \le y \wedge \lnot \textrm{st}(y-x)$

Instantiation ${\mathfrak {I}}_2$ is analytic in nature as it requires (nonstandard) real numbers:

• (1) $R(x,y) := x <y$, where < is the usual order in the real numbers

• (2) $M(x,y):=$ “$x < y$ and their difference is infinitesimal”

• (3) $L(x,y):=$ “$x < y$ and their difference is not infinitesimal”

Theorem 3.1

Given any of the instantiations ${\mathfrak {I}}_1$ and ${\mathfrak {I}}_2$, the ${\textsf{ML}}$ axioms are satisfied in $\textsf{ENA}$.

The verifications of the previous theorem are all immediate, so we omit its proof.

The following is a straightforward corollary of Theorem 3.1.

Corollary 3.2

The ${\textsf{ML}}$ theory is consistent, if $\textsf{ZF}$ is consistent.

4 Measurement

4.1 Ingredients of Measurement

Roughly, mathematical theories of measurement reveal the conditions under which relations between “concrete” entities are appropriately represented by mathematical relations. It is the fact that “concrete” relations—e.g. being more massive than, having a greater difference in temperature than – can be appropriately represented by mathematical relations that makes it possible to refer to those concrete relations by speaking about mathematical relations.

Representing concrete relations by mathematical relations allows to perform surrogative reasoning about them by reasoning about their mathematical representations. Relatedly, the mathematical representations of concrete relations afford further insight into their structure, since typically the mathematical models in which those concrete entities are represented are well-known.

A representational theory of measurement investigates the conditions under which particular concrete relations are representable by mathematical relations. The task of offering a representational theory of measurement for a certain phenomenon involves the following ingredients: (i) a theory of the phenomenon in question; (ii) a representation theorem showing that any model of this theory—here we follow the common practice of referring to such models as ‘empirical models’ – can be represented by a particular mathematical model ${\mathfrak {M}}$; and (iii) a uniqueness theorem characterising all the ways in which each empirical model may be represented by the mathematical model ${\mathfrak {M}}$.

Let us be more precise on the sort of results that are delivered by representation and uniqueness theorems. Consider first the notion of an homomorphism.

Definition 4.1

(Homomorphism) Let ${\mathfrak {M}}$ and ${\mathfrak {N}}$ be models in a common signature. Then, a homomorphism from ${\mathfrak {M}}$ to ${\mathfrak {N}}$ is a function f such that, for all objects $o_{1},\ldots ,o_{n}$ in the domain $D_{{\mathfrak {M}}}$ of model ${\mathfrak {M}}$,

$$\begin{aligned} o_1,\ldots ,o_n\text { stand in relation }(R)^{{\mathfrak {M}}}\text { iff } f(o_1),\ldots ,f(o_n)\text { stand in relation }(R)^{{\mathfrak {N}}}, \end{aligned}$$

for all n-ary predicates R of ${\mathfrak {M}}$ and ${\mathfrak {N}}$’s common signature.

When a homomorphism maps an empirical model to a mathematical model, it is said to be a representation of the empirical model in the mathematical model. Then, the measurement-theoretic notion of a scale is defined in the following way.

Definition 4.2

(Scale) A measurement scale is a triple $\langle {\mathfrak {M}},{\mathfrak {N}},f\rangle$ such that:

(i):

${\mathfrak {M}}$ is an empirical model;

(ii):

${\mathfrak {N}}$ is a mathematical model;

(iii):

f is a homomorphism from ${\mathfrak {M}}$ to ${\mathfrak {N}}$.

A representation theorem establishes, for a chosen mathematical model, that every empirical model can be represented in it. That is, a representation theorem establishes, for a chosen mathematical model ${\mathfrak {N}}$, that every empirical model has a scale containing ${\mathfrak {N}}$. Given any scale $\langle {\mathfrak {M}},{\mathfrak {N}},h\rangle$, surrogative reasoning about ${\mathfrak {M}}$ can then be performed by reasoning about the mathematical relations that obtain between the images of ${\mathfrak {M}}$ under h.

A uniqueness theorem offers a characterisation of how unique a scale is. It does so in terms of a distinguished class of transformations of the domain of the numerical model. Thus, a uniqueness theorem consists of a result to the effect that a specific class C of transformations of the domain of a chosen mathematical model is such that, for every empirical model and every homomorphism h from the empirical model to the numerical model: (i) the result of composing h with any transformation in C yields a novel homomorphism from the empirical model to the numerical model; and (ii) every homomorphism f from the empirical model to the chosen numerical model is identical to the result of composing h with some transformation c in C.

Given such a class C of transformations of the domain of the numerical model, it is possible to discern the limits of surrogative reasoning performed in terms of a scale $\langle {\mathfrak {M}},{\mathfrak {N}},h\rangle$. Only the mathematical relations which are invariant under all transformations in such a class C are meaningful irrespective of the choice of scale.

4.2 A Measurement Theory for ${\textsf{ML}}$

We now offer a measurement theory for the ${\textsf{ML}}$ theory by proving both a representation theorem and a uniqueness theorem in the context of $\textsf{ZFC}$.

The mathematical model which will be used to represent facts about marginal and large difference—the representative model – exhibits, in a sense to be explained below, a structure akin to the structure of countable nonstandard models of arithmetic. Given a scale $\langle {\mathfrak {M}},{\mathfrak {N}},h\rangle$ with ${\mathfrak {M}}$ a model of ${\textsf{ML}}$, h(x) may be described as the degree of $R_{{\mathfrak {M}}}$-ness of x in $\langle {\mathfrak {M}},{\mathfrak {N}},h\rangle$, for each $x\in D_{{\mathfrak {M}}}$. For instance, when T stands for the taller than relation, h(x) is the degree of tallness of x in the scale $\langle {\mathfrak {M}},{\mathfrak {N}},h\rangle$, for each $x\in D_{{\mathfrak {M}}}$.

We start by defining our representative mathematical model for the ${\textsf{ML}}$ theory.

Definition 4.3

(Representative model) The representative model $\mathfrak {R^{*}}$ is a quadruple $\mathfrak {R^{*}}=\langle D_{\mathfrak {R^{*}}},R_{\mathfrak {R^{*}}},M_{\mathfrak {R^{*}}},L_{\mathfrak {R^{*}}}\rangle$ where:

(i):

$D_{\mathfrak {R^{*}}}=\{\langle i,j\rangle :i\in {\mathbb {Q}}\; \text {and} \;j\in {\mathbb {Z}}\}$;

(ii):

$R_{\mathfrak {R^{*}}}(\langle a,b\rangle ,\langle c,d\rangle )$ iff $a<c$, or $a=c$ and $b<d$;

(iii):

$M_{\mathfrak {R^{*}}}(\langle a,b\rangle ,\langle c,d\rangle )$ iff $a=c$ and $b<d$;

(iv):

$L_{\mathfrak {R^{*}}}(\langle a,b\rangle ,\langle c,d\rangle )$ iff $a<c$.

The representative model may be conceptualised as divided into countably many blocks, arranged as the rational numbers, each of which composed of countable many elements, arranged as the integers. That is, a pair of a rational number and an integer may be understood as a coordinate; the rational number singles out a block in $\mathfrak {R^{*}}$ and the integer singles out a location within that block.

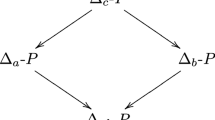
This structure is very close to the structure of countable nonstandard models of arithmetic. For our purposes, the main difference between the two structures is that in (countable) nonstandard models of arithmetic the previously mentioned blocks have appended to them a first block consisting of countably many locations arranged as the natural numbers (Fig. 3).

Fig. 3

Representative model

In Figure 3 we have that m and n share the same first coordinate and so $M_{\mathfrak {R^{*}}}(m,n)$, while we have both $L_{\mathfrak {R^{*}}}(m,p)$ and $L_{\mathfrak {R^{*}}}(n,p)$.

As should be clear, the representative model $\mathfrak {R^{*}}$ has the same signature as that of any model of the ${\textsf{ML}}$ theory. Observe also that $\mathfrak {R^{*}}$ is countable. Accordingly, our representation theorem will only concern countable models of ${\textsf{ML}}$.⁷

For the purposes of our representation theorem, we will impose a further restriction on models of ${\textsf{ML}}$. In order to introduce this restriction, we will first define (relative to models in the signature of ${\textsf{ML}}$) the notion of weakly marginal succession.

Definition 4.4

(Weakly marginal succession) For every model ${\mathfrak {M}}=\langle D_{{\mathfrak {M}}}, R_{{\mathfrak {M}}}$, $M_{{\mathfrak {M}}},L_{{\mathfrak {M}}}\rangle$ and all $x,y\in D_{{\mathfrak {M}}}$, y is a weakly marginal successor of x in ${\mathfrak {M}}$, denoted $S_{{\mathfrak {M}}}(x,y)$, if and only if both

(i):

$M_{{\mathfrak {M}}}(x,y)$;

(ii):

$\forall z\in D_{{\mathfrak {M}}}(M_{{\mathfrak {M}}}(x,z)\Rightarrow \lnot M_{{\mathfrak {M}}}(z,y))$.

That is, for y to be a weakly marginal successor of x it must be the case that x is marginally smaller than y and that if x is marginally smaller than some z, then z is not marginally smaller than y.

The extra restriction on models of ${\textsf{ML}}$ that we will impose is that they be finitely marginal.

Definition 4.5

(Finite marginality) A model ${\mathfrak {M}}=\langle D_{{\mathfrak {M}}}, R_{{\mathfrak {M}}},M_{{\mathfrak {M}}},L_{{\mathfrak {M}}}\rangle$ is finitely marginal if and only if:

$$\begin{aligned} \begin{aligned} \forall x,y\in D_{{\mathfrak {M}}}&(M_{{\mathfrak {M}}}(x,y)\Rightarrow \exists n\in {\mathbb {Z}}^{+}\exists z_1\ldots z_n\\&(x=z_1\wedge S_{{\mathfrak {M}}}(z_1,z_2)\wedge \ldots \wedge S_{{\mathfrak {M}}}(z_{n-1},z_{n})\wedge z_n=y)). \end{aligned} \end{aligned}$$

That is, a model is finitely marginal just in case, whenever x is marginally smaller than y, there is a finite chain of weakly marginal succession between x and y.

On the condition that the models of ${\textsf{ML}}$ are both countable and finitely marginal, our representation theorem ensures the existence of a homomorphism h yielding a representation, in $\mathfrak {R^{*}}$, of the structure of marginal and large difference, as these notions are axiomatised by the ${\textsf{ML}}$ theory.

Specifically, an object x is marginally smaller than an object y if and only if their images under h belong to the same block and the location of h(x) in that block comes before the location of h(y) in that block—i.e. if and only if $h(x)=\langle a,b\rangle$, $h(y)=\langle c,d\rangle$, $a=c$, and $b<d$, for some a, b, c, d. Moreover, an object x is largely smaller than y if and only if h(x) belongs to a block which comes before the block to which h(y) belongs—i.e. if and only if $h(x)=\langle a,b\rangle$, $h(y)=\langle c,d\rangle$, and $a<c$, for some a, b, c, d. In this way, blocks are arranged in a sort of 2-dimensional lattice where “horizontal” differences (i.e. differences along the first coordinate) are large and fixing a “column” (i.e. an element in the first coordinate) the “vertical” differences (i.e. differences along the second coordinate) are marginal.

The proof of the representation theorem appeals to the following notion of indiscernibility.

Definition 4.6

(Indiscernibility) For every model ${\mathfrak {M}}=\langle D_{{\mathfrak {M}}},R_{{\mathfrak {M}}},M_{{\mathfrak {M}}},L_{{\mathfrak {M}}}\rangle$, and all $x,y\in D_{{\mathfrak {M}}}$, x and y are indiscernible in ${\mathfrak {M}}$, denoted $x\sim _{{\mathfrak {M}}}y$, if and only if $\lnot (x R_{{\mathfrak {M}}}y)$ and $\lnot (y R_{{\mathfrak {M}}}x)$.

That is, x and y are indiscernible just in case none of them is $R_{{\mathfrak {M}}}$-related to the other.

Theorem 4.7

(Representation theorem) For every countable and finitely marginal ${\textsf{ML}}$-model ${\mathfrak {M}}=\langle D_{{\mathfrak {M}}},R_{{\mathfrak {M}}},M_{{\mathfrak {M}}},L_{{\mathfrak {M}}}\rangle$, there is a homomorphism h from ${\mathfrak {M}}$ to $\mathfrak {R^{*}}$.

Proof

Assume that ${\mathfrak {M}}$ is a countable and finitely marginal model of ${\textsf{ML}}$. Since ${\mathfrak {M}}$ is countable, let $o_1,o_2,o_3\ldots$ be a list of its elements. We will now inductively define a function h mapping each element o of $D_{{\mathfrak {M}}}$ to some element $h(o_j)$ of $D_{\mathfrak {R^{*}}}$. We let $h(o_1)=\langle 0,0\rangle$. Now, assume $h(o_j)$ is already defined, for all $j<k$. We will now define $h(o_k)$. There are four cases to consider:⁸

• (1) There is some $j<k$ such that $o_k\sim _{{\mathfrak {M}}}o_j$;

  • In such case, let $h(o_k)=h(o_j)$.

• (2) Either a) $M_{{\mathfrak {M}}}(o_j, o_k)$ or b) $M_{{\mathfrak {M}}}(o_k, o_j)$, for some $j<k$;

  • 2a): Pick the biggest $j<k$ such that $M_{{\mathfrak {M}}}(o_j, o_k)$. Then, let $h(o_k)=\langle \pi _{1}(h(o_j)),\pi _{2}(h(o_j))+n\rangle$, where n is the number of marginal difference-steps that it takes to get from $o_j$ to $o_k$—we know that there is such a number, since ${\mathfrak {M}}$ is finitely marginal.

  • 2b): $h(o_k)$ is defined in the obvious dual manner.

• (3) Either a) $L_{{\mathfrak {M}}}(o_k,o_j)$ for all $j<k$; or b) $L_{{\mathfrak {M}}}(o_j,o_k)$, for all $j<k$;

  • 3a): Pick the biggest $j<k$ such that $R_{{\mathfrak {M}}}(o_j,o_i)$, for all $i<k$. Let $h(o_k)=\langle \pi _{1}(h(o_j))-1,0\rangle$.

  • 3b): $h(o_k)$ is defined in the obvious dual manner.

• (4) We have that, for all $j<k$, $o_{j}\in \{u:L_{{\mathfrak {M}}}(u,o_k)\}$, or $\{u:L_{{\mathfrak {M}}}(o_k,u)\}$, with both sets finite and nonempty.

  • Pick the biggest $j<k$ such that $\pi _{1}(o_i)<\pi _{1}(o_j)$, for all $i<k$ such that $o_i,o_j\in \{u:L_{{\mathfrak {M}}}(u,o_k)\}$. Similarly, pick the biggest $l<k$ such that $\pi _{1}(o_l)<\pi _{1}(o_i)$, for all $i<k$ such that $o_l,o_i\in \{u:L_{{\mathfrak {M}}}(o_k,u)\}$. Then, let $h(o_k)=\langle \frac{\pi _{1}(h(o_j))+\pi _1(h(o_l))}{2},0\rangle$.

We now need to show that h is a homomorphism from ${\mathfrak {M}}$ into $\mathfrak {R^{*}}$. But it should be clear that it is, as the construction of h guarantees that the function h preserves all of $R_{{\mathfrak {M}}}$, $M_{{\mathfrak {M}}}$ and $L_{{\mathfrak {M}}}$. $\square$

So far, we have established that there is a representation, in $\mathfrak {R^{*}}$, of any (countable and finitely marginal) model of ${\textsf{ML}}$. Our next result clarifies to what extent such a representation is unique.

First consider the following class of transformations of $\mathfrak {R^{*}}$.

Definition 4.8

(Cautiously monotone-increasing transformation) For every subset X of ${\mathbb {Q}}\times {\mathbb {Z}}$, a function $\tau :X\rightarrow {\mathbb {Q}}\times {\mathbb {Z}}$ is a cautiously monotone-increasing transformation if and only if, for all $x\in {\mathbb {Q}}$ and all $y\in {\mathbb {Z}}$ such that $\langle x,y\rangle \in X$:

$$\begin{aligned} \tau (\langle x,y\rangle )=\langle f(x),g_x(y)\rangle , \end{aligned}$$

where:

(i):

$f:\{\pi _{1}(x):x\in X\}\rightarrow {\mathbb {Q}}$ is a monotone-increasing transformation (i.e. $\forall x,y\in \{\pi _{1}(x):x\in X\}(x<y\Leftrightarrow f(x)<f(y))$)

(ii):

g is a function with domain $\{\pi _{1}(x):x\in X\}$ such that, for every $x\in \{\pi _{1}(x):x\in X\}$, $g_{x}:\{y:\langle x,y\rangle \in X\}\rightarrow {\mathbb {Z}}$ is a monotone-increasing transformation.

Cautiously monotone-increasing transformations may thus be conceived as pairs of a monotone-increasing function f on the rational numbers and a collection G of monotone-increasing functions on the integers, with each member y of G being indexed by a rational. That is, $y=g_x$, for some rational x. Accordingly, a cautiously monotone-increasing transformation is a function mapping a pair $\langle a,b\rangle$ to a pair $\langle f(a),g_{a}(b)\rangle$, where, for all rationals a and c, $a<c$ iff $f(a)<f(c)$, and for all integers b and d, $b<d$ iff $g_{a}(b)<g_{a}(d)$, for all rational numbers a.

To understand what cautiously monotone-increasing transformations do, f may be conceptualised as a function mapping a block to a different block, with the proviso that a block x comes before a block y if and only if block f(x) comes before block f(y). Moreover, g may be conceptualised as a function mapping a location l (in block x) to a location $g_{x}(l)$ (in block f(x)), with the proviso that a location l in a block x comes before another location j in x if and only if location $g_{x}(l)$ (in block f(x)) comes before location $g_{x}(j)$ (in block f(x)).

By indexing the monotone-increasing functions on the integers with rational numbers it is guaranteed that, if $a\ne c$, then the only differences between $\langle a,b\rangle$ and $\langle c,d\rangle$ which matter are precisely those between a and c. Differences between b and d are spurious. That is, when blocks are distinct, specific differences having to do with the locations within each block are spurious.

We now have all the ingredients needed for our uniqueness theorem. The first part of the theorem states that the class of homomorphisms by which a given model ${\mathfrak {M}}$ of the ${\textsf{ML}}$ theory may be represented in $\mathfrak {R^{*}}$ is closed under cautiously monotone-increasing functions. The theorem’s second part ensures that this closure exhausts the ways of representing ${\mathfrak {M}}$ in $\mathfrak {R^{*}}$.

Theorem 4.9

For every model ${\mathfrak {M}}$ of the ${\textsf{ML}}$ theory, and every homomorphism h from ${\mathfrak {M}}$ to $\mathfrak {R^{*}}$

• (i) if $\tau$ is a cautiously monotone-increasing transformation, then $\tau \circ h$ is a homomorphism from ${\mathfrak {M}}$ to $\mathfrak {R^{*}}$;

• (ii) if u is a homomorphism from ${\mathfrak {M}}$ to $\mathfrak {R^{*}}$, then there is a cautiously monotone-increasing transformation $\tau$ such that $u=\tau \circ h$.

Proof

(i):

Suppose that $\tau$ is a cautiously monotone-increasing transformation. Using Theorem 4.7 and the fact that $\tau$ is cautiously monotone-increasing we derive that

$$\begin{aligned}&M_{{\mathfrak {M}}}(a,b) \text { iff } M_{\mathfrak {R^{*}}}(h(a),h(b)) \\ \text {iff }&\pi _{1}(h(a))=\pi _{1}(h(b)) \text { and } \pi _{2}(h(a))<\pi _{2}(h(b)) \\ \text {iff }&f(\pi _{1}(h(a)))=f(\pi _{1}(h(b))) \text { and } g_{\pi _1(h(a))}(\pi _{2}(h(a)))<g_{\pi _1(h(b))}\pi _{2}(h(b)) \\ \text {iff }&\pi _1(\tau (h(a)))=\pi _1(\tau (h(b))) \text { and } \pi _{2}(\tau (h(a)))<\pi _{2}(\tau (h(b)))\\ \text {iff }&M_{\mathfrak {R^{*}}}(\tau (h(a)),\tau (h(b)))\\ \text {iff }&M_{\mathfrak {R^{*}}}((\tau \circ h)(a),(\tau \circ h)(b)). \end{aligned}$$

Hence $M_{{\mathfrak {M}}}(a,b) \text { iff } M_{\mathfrak {R^{*}}}((\tau \circ h)(a),(\tau \circ h)(b)).$

Similarly,

$$\begin{aligned} L_{{\mathfrak {M}}}(a,b) \text { iff }&L_{\mathfrak {R^{*}}}(h(a),h(b)) \\ \text { iff }&\pi _{1}(h(a))<\pi _{1}(h(b)) \\ \text { iff }&f(\pi _{1}(h(a)))<f(\pi _{1}(h(b))) \\ \text { iff }&\pi _{1}(\tau (h(a)))<\pi _{1}(\tau (h(b)))\\ \text { iff }&L_{\mathfrak {R^{*}}}((\tau \circ h)(a),(\tau \circ h)(b)). \end{aligned}$$

Hence

$$\begin{aligned} L_{{\mathfrak {M}}}(a,b) \text { iff } L_{\mathfrak {R^{*}}}(\tau \circ h(a),\tau \circ h(b)). \end{aligned}$$

Finally,

$$\begin{aligned} R_{{\mathfrak {M}}}(a,b) \text { iff }&M_{{\mathfrak {M}}}(a,b) \text { or } L_{{\mathfrak {M}}}(a,b) \\ \text {iff }&M_{\mathfrak {R^{*}}}((\tau \circ h)(a),(\tau \circ h)(b)) \text { or } L_{\mathfrak {R^{*}}}((\tau \circ h)(a),(\tau \circ h)(b)) \\ \text {iff }&R_{\mathfrak {R^{*}}}(\tau \circ h(a),\tau \circ h(b)). \end{aligned}$$

Hence $R_{{\mathfrak {M}}}(a,b)$ iff $R_{\mathfrak {R^{*}}}(\tau \circ h(a),\tau \circ h(b))$, and we conclude that $\tau \circ h$ is a homomorphism from ${\mathfrak {M}}$ to $\mathfrak {R^{*}}$.

(ii):

Suppose that u is a homomorphism from ${\mathfrak {M}}$ to $\mathfrak {R^{*}}$. We define a function $\tau :\{h(x):x\in D_{{\mathfrak {M}}}\}\rightarrow D_{\mathfrak {R^{*}}}$ in the natural manner:

$$\begin{aligned} \forall x\in \{h(x):x\in D_{{\mathfrak {M}}}\}( \tau (h(x))=u(x)). \end{aligned}$$

Observe that $\tau$ is well-defined. For suppose that $\tau (x)\ne \tau (y)$. Then, $\tau (h(z))\ne \tau (h(w))$, for some z such that $h(z)=x$ and w such that $h(w)=y$. So, $u(z)\ne u(w)$. Hence, $z\ne w$, since u is a homomorphism $R_{\mathfrak {R^{*}}}(u(z),u(w))$ and $\lnot R_{{\mathfrak {M}}}(z,w)$ or $R_{\mathfrak {R^{*}}}(u(w),u(z))$ and $\lnot R_{{\mathfrak {M}}}(w,z)$. So, $x=h(z)\ne h(w)=y$, since h is a homomorphism.

We show that $\tau$ is cautiously monotone-increasing. For each $x\in D_{{\mathfrak {M}}}$, let

$$\begin{aligned} f(\pi _1(h(x)))=\pi _{1}(\tau (h(x)))=\pi _{1}(u(x)) \end{aligned}$$

and

$$\begin{aligned} g_{\pi _1(h(x))}(\pi _{2}(h(x)))=\pi _{2}(u(x)) \end{aligned}$$

We have that

$$\begin{aligned} \pi _1(h(x))<\pi _1(h(y)) \text { iff }&L_{\mathfrak {R^{*}}}(h(x),h(y)) \\ \text { iff }&L_{{\mathfrak {M}}}(x,y) \\ \text { iff }&L_{\mathfrak {R^{*}}}(u(x),u(y))\\ \text { iff }&\pi _1(u(x))<\pi _1(u(y))\\ \text { iff }&\pi _1(\tau (h(x)))<\pi _1(\tau (h(y)))\\ \text { iff }&f(\pi _1(h(x)))<f(\pi _1(h(y))), \end{aligned}$$

which shows that f is monotone-increasing. The fact that $g_{\pi _{1}(h(x))}$ is monotone-increasing is shown in an analogous way.

$\square$

4.3 Nonstandard Representation

Let us now return to the relationship between $\mathfrak {R^{*}}$ and nonstandard models of arithmetic. Observe that any countable nonstandard model of arithmetic ${\mathfrak {N}}=\langle D_{{\mathfrak {N}}},\textrm{st}_{{\mathfrak {N}}},<_{{\mathfrak {N}}},+_{{\mathfrak {N}}},\cdot _{{\mathfrak {N}}}\rangle$ is of order type $\omega +(\omega ^{*}+\omega )\times \eta$, where $\omega$ is the order type of the natural numbers, $\omega ^{*}$ is the dual order of $\omega$ and $\eta$ is the order type of the rationals. Now, let ${\mathfrak {N}}^{\ddagger }=\langle D_{{\mathfrak {N}}^{\ddagger }},<_{{\mathfrak {N}}^{\ddagger }},\prec _{{\mathfrak {N}}^{\ddagger }},\sqsubset _{{\mathfrak {N}}^{\ddagger }}\rangle$, where:

• (1) ${\mathfrak {N}}$ is a nonstandard model of arithmetic such that $D_{{\mathfrak {N}}^{\ddagger }}=D_{{\mathfrak {N}}}$ ;

• (2) $<_{{\mathfrak {N}}^{\ddagger }}=<_{{\mathfrak {N}}}$;

• (3) $\prec _{{\mathfrak {N}}^{\ddagger }}(x,y)$ iff ${\mathfrak {N}}\vDash \exists n(\textrm{st}(n)\wedge y=x+n)$, and

• (4) $\sqsubset _{{\mathfrak {N}}^{\ddagger }}(x,y)$ iff $x<_{{\mathfrak {N}}}y$ and ${\mathfrak {N}}\vDash \lnot \exists n(\textrm{st}(n)\wedge y=x+n)$.

A routine proof reveals that, for every nonstandard model ${\mathfrak {N}}$ of arithmetic, we have ${\mathfrak {N}}^{\ddagger }\cong {\mathfrak {R}}=\langle D_{{\mathfrak {R}}},R_{{\mathfrak {R}}}, M_{{\mathfrak {R}}},L_{{\mathfrak {R}}}\rangle$, where:

• (1) $D_{{\mathfrak {R}}}=(\{-\infty \}\times {\mathbb {N}})\cup ({\mathbb {Q}}\times {\mathbb {Z}})$

• (2) $M_{{\mathfrak {R}}}(\langle x,y\rangle ,\langle z,u\rangle )$ iff $x=z$ and $y<u$;

• (3) $L_{{\mathfrak {R}}}(\langle x,y\rangle ,\langle z,u\rangle )$ iff $x<z$;

• (4) $R_{{\mathfrak {R}}}(\langle x,y\rangle ,\langle z,u\rangle )$ iff $M_{{\mathfrak {R}}}(\langle x,y\rangle ,\langle z,u\rangle )$ or $L_{{\mathfrak {R}}}(\langle x,y\rangle ,\langle z,u\rangle )$.

It should be clear that ${\mathfrak {R}}$ is a model just like $\mathfrak {R^{*}}$ except for one single difference, specifically, that ${\mathfrak {R}}$ appends to the blocks of $\mathfrak {R^{*}}$ an initial block, indexed by $-\infty$, whose elements are arranged as the natural numbers. That is, it should be clear that ${\mathfrak {R}}^{*}$ is nothing but the model ${\mathfrak {R}}|_{{\mathbb {Q}}\times {\mathbb {Z}}}$—the restriction of the model ${\mathfrak {R}}$ to ${\mathbb {Q}}\times {\mathbb {Z}}$.

The following is an immediate corollary of our representation theorem:

Corollary 4.10

(Representation) For every countable and finitely marginal model ${\mathfrak {M}}$ of the ${\textsf{ML}}$ theory, there is a homomorphism from ${\mathfrak {M}}$ to ${\mathfrak {R}}$, and so also to ${\mathfrak {N}}^{\ddagger }$, for every countable nonstandard model ${\mathfrak {N}}$ of arithmetic.

The following uniqueness theorem, similar to Theorem 4.9—except that now the notion of a cautiously monotone-increasing transformation is expanded to arbitrary subsets of $(\{-\infty \}\times {\mathbb {N}})\cup ({\mathbb {Q}}\times {\mathbb {Z}})$ in the natural way –, is also available.

Theorem 4.11

For every model ${\mathfrak {M}}$ of the ${\textsf{ML}}$ theory, and every homomorphism h from ${\mathfrak {M}}$ to ${\mathfrak {R}}$

• (i) if $\tau$ is a cautiously monotone-increasing transformation, then $\tau \circ h$ is a homomorphism from ${\mathfrak {M}}$ to ${\mathfrak {R}}$;

• (ii) if u is a homomorphism from ${\mathfrak {M}}$ to ${\mathfrak {R}}$, then there is a cautiously monotone-increasing transformation $\tau$ such that $u=\tau \circ h$.

We spare the reader with the details, since the proof of Theorem 4.11 adds nothing to that of Theorem 4.9.

Finally, consider the expansion of the notion of a cautiously monotone-increasing transformation to nonstandard arithmetical models:

Definition 4.12

(Nonstandard cautiously monotone increasing transformation) For every countable nonstandard model of arithmetic ${\mathfrak {N}}$, and every subset X of $D_{{\mathfrak {N}}}$, a function $\tau :X\rightarrow D_{{\mathfrak {N}}}$ is a cautiously monotone-increasing transformation if and only if both

(i):

$\exists n({\textrm{st}}(n)\wedge y=x+n)$ if and only if $\exists n({\textrm{st}}(n)\wedge \tau (y)=\tau (x)+n)$;

(ii):

$x\le y\wedge \lnot {\textrm{st}}(y-x)$ if and only if $f(x)\le f(y)\wedge \lnot {\textrm{st}}(f(y)-f(x))$.

Then, we have the following corollary of Theorem 4.11.

Corollary 4.13

For every countable nonstandard arithmetical model ${\mathfrak {N}}$, every model ${\mathfrak {M}}$ of the ${\textsf{ML}}$ theory, and every homomorphism h from ${\mathfrak {M}}$ to ${\mathfrak {N}}^{\ddagger }$

• (i) if $\tau$ is a cautiously monotone-increasing transformation, then $\tau \circ h$ is a homomorphism from ${\mathfrak {M}}$ to ${\mathfrak {N}}^{\ddagger }$;

• (ii) if u is a homomorphism from ${\mathfrak {M}}$ to ${\mathfrak {N}}^{\ddagger }$, then there is a cautiously monotone-increasing transformation $\tau$ such that $u=\tau \circ h$.

4.4 Spurious Structure

As is revealed by Theorem 4.7, the initial blocks of ${\mathfrak {R}}$ and of countable nonstandard arithmetical models bring with them spurious structure vis-à-vis the representation of the facts about marginal and large difference captured by the ${\textsf{ML}}$ theory (even when only countable and finitely marginal models of the theory are considered). It was for this reason that we began by offering representation and uniqueness theorems with respect to ${\mathfrak {R}}^*$ rather than with respect to ${\mathfrak {R}}$, or to a countable nonstandard arithmetical model.

Still, nonstandard arithmetical models are better equipped than their standard counterparts for representing in a natural manner the facts about marginal and large difference captured by the ${\textsf{ML}}$ theory. Specifically, given the natural interpretation of the weak order R as less than, standard arithmetical models are incapable of representing the existence of an omega-sequence of individuals each of which is marginally greater than the one before it, with further (largely) greater individuals coming after all those individuals in the omega-sequence. By contrast the existence of an omega-sequence of individuals followed by largely greater individuals can be represented in nonstandard models via those models’ less than and existence of a nonstandard difference relations.

The less than and existence of a nonstandard difference relations of nonstandard arithmetical models are also capable of representing a dense structure of large differences. By contrast, the relation of existence of a standard difference is incapable of representing a dense structure of marginal differences. Accordingly, ${\mathfrak {R}}^*$ itself possesses spurious structure, even disregarding its countable character.

It is because nonstandard arithmetical models and the model ${\mathfrak {R}}^*$ all possess this spurious structure that we restricted our attention to finitely marginal models of ${\textsf{ML}}$. The representation of a dense structure of marginal difference thus requires models other than ${\mathfrak {R}}^*$. One natural option would be to further exploit the dense structure of the rationals by considering a model ${\mathfrak {M}}$ just like ${\mathfrak {R}}^{*}$ except that the domain of this new model consists of ${\mathbb {Q}}\times {\mathbb {Q}}$, rather than of ${\mathbb {Q}}\times {\mathbb {Z}}$.

It should be easy to see that our construction of a homomorphism mapping any countable and finitely marginal model of ${\textsf{ML}}$ to ${\mathfrak {R}}^*$ could then be adapted to construct a homomorphism mapping any given countable (and possibly not finitely marginal) model of ${\textsf{ML}}$ to this new model ${\mathfrak {M}}$. The proof of the uniqueness theorem would be left unchanged.

We will spare the reader with the details. We do wish to point that while we have not considered uncountable models of ${\textsf{ML}}$, we conjecture that the structure of marginal and large differences of at least some such models is representable in nonstandard analytical models. We leave investigation of this issue for future work.

5 Infinite Soritical Series and Dean’s NeoFeasibilism

So far, we have formulated the ${\textsf{ML}}$ theory of marginal and large difference, and shown that it can be represented in rich mathematical models with a structure akin to the order structure of nonstandard models. In the next sections we will consider three philosophical theories on vagueness and the Sorites—and show how the ${\textsf{ML}}$ theory constitutes part of their underlying abstract structure.

We will start with Dean’s (2018) neofeasibilism about vagueness. Before doing so, and because it will be relevant to the discussion in this section, we want to start by pointing out one way of making the assumptions of the Sorites paradox jointly consistent, while formulating it in a manner congenial to—but not mandated by—the ${\textsf{ML}}$ theory. For concreteness, we will continue to focus on a Soritical paradox for ‘bald’.

Some natural assumptions, given the resources of the ${\textsf{ML}}$ theory, concerning the version of the Sorites paradox which concerns ‘bald’ are the following:

Largely balder::

The last element of the Soritical series, ${\textbf{e}}$, is largely balder than ${\textbf{b}}$, the series’ first element.

baldness::

For every x, x is bald if and only if ${\textbf{e}}$ is not largely balder than x.

Then, it is a straightforward consequence of the ${\textsf{ML}}$ theory that everything balder than ${\textbf{e}}$ will count as bald. More interestingly, the following tolerance principles for baldness are straightforward consequences of the ${\textsf{ML}}$ theory and baldness.

Tolerance::

(i):

$\forall x, y((\lnot B(x)\wedge M(x,y))\Rightarrow \lnot B(y))$

If x isn’t bald and y is marginally balder than x, then y isn’t bald.

(ii):

$\forall x, y((B(x)\wedge M(y,x))\Rightarrow B(y))$

If x is bald and x is marginally balder than y, then y is bald.

Relatedly, it is prima facie reasonable to offer the following characterisation of succession in a Soritical series A.

Succession::

y succeeds x in series A if and only if

(i):

y is marginally greater than x with respect to order R;

(ii):

For every element z in series A such that R(x, z), R(y, z) or else $y=z$.

succession implies, in the context of our Soritical series for ‘bald’, the following fact about marginality:

Not bald enough::

If x has only 1 hair less than y, then x is marginally balder than y.

not bald enough presumably underlies our support for the inductive premise. Indeed, the inductive premise for ‘bald’ is a joint consequence of not bald enough, tolerance and baldness. Now, given an infinite Soritical series, the assumptions that (i) ${\textbf{b}}$ isn’t bald, (ii) ${\textbf{e}}$ is bald, and (iii) the inductive premise is true are jointly consistent. So, Soritical reasoning is not fallacious provided that the Soritical series for ‘bald’ is infinite.

The following picture (Fig. 4) might be helpful, where the conventions in place are the same as those in Figure 1:

Fig. 4

Soritical series for ‘bald’

In this picture ${\textbf{b}}$ represents the first element in the Soritical series for ‘bald’, ${\textbf{e}}$ its last element, with every element between ${\textbf{b}}$ and ${\textbf{e}}$ also being a member of the series. By baldness: ${\textbf{b}}$, m and n are all not bald, since ${\textbf{e}}$ is largely balder than each one of them; and o, p and ${\textbf{e}}$ are all bald, since none is largely balder than ${\textbf{e}}$. As the picture reveals, each one of the nonbalds is “infinitely distant” from each bald.

The observation that the premises of the Sorites paradox are jointly satisfiable provided that the soritical series is infinite will be key in Dean’s (2018) neofeasibilist theory of vagueness. In order to understand Dean’s neofeasibilism it will be helpful to start by briefly presenting the feasibilist theory of vagueness.

According to feasibilists the premises of the conditional sorites paradox are almost consistent: even if inconsistent, no derivation of a contradiction from those premises is feasible. By ‘the conditional Sorites’ is meant that version of the Sorites paradox which has among its premises conditionals asserting, for each member of the Soritical series except the last one, that if it has the relevant vague property, then its successor also has it. According to feasibilists, no derivation of a contradiction from the conditional form of the sorites paradox is feasible owing to the paradox involving too many premises. To give just one example, it is not uncommon for 1, 000, 000 to be given as the number of hairs of the first element of a Soritical series for ‘bald’ (its last element having 0 hairs).

For reasons that we will not revisit here, Dean finds feasibilism about vagueness unsatisfactory. In its place he proposes the neofeasibilist theory of vagueness.⁹ Dean’s feasibilism consists of (at least) the following three components:¹⁰

(i):

A reductionist view on vague predicates according to which satisfaction of any vague predicate supervenes on wholly precise matters. For instance, satisfaction of the predicate ‘is bald’ supervenes on hair number.

(ii):

The view that the numbers used to give extremal values in the Sorites paradox actually denote infinite numbers. For instance, ‘1, 000, 000’, as used to denote the number of hairs of the first element of the Soritical sequence for ‘bald’, actually denotes, according to Dean, an infinite number in a nonstandard arithmetical model. Without going into the details, Dean’s reasoning is that the extremal values for a number of predicates are offered without any empirical corroboration or consideration of their numerical properties. Rather, they have been chosen because they are safe—likely to be agreed upon. But it is their safety which turns out to suggest, by Dean’s lights, that they are infinite. They are safe precisely because they are “infinitely distant” from the other extreme. For instance, the denotation of ‘1, 000, 000’ would be “infinitely distant” from 0, a safe number of hairs for counting as bald.

(iii):

The view that the premises of the Sorites paradox are jointly consistent, even though adjacent members in a Soritical series differ by some fixed precise amount (e.g., exactly one hair, in the case of ‘bald’)—since the first and last elements of a Soritical series are “infinitely distant”.¹¹

As should be clear, the ${\textsf{ML}}$ theory constitutes part of the underlying abstract structure of the neofeasilibist theory of vagueness. For concreteness, let us focus on the predicate ‘is bald’. Then: (i) the partial order relation R may be interpreted as ‘balder than’; (ii) marginally smaller may be interpreted as having a finite positive difference in number of hairs; and (iii) largely smaller may be interpreted has having an infinite positive difference in number of hairs. This interpretation of the ${\textsf{ML}}$ theory fits with the one mentioned at the beginning of this section. Indeed, under the interpretation just given, neofeasibilists would not be opposed to the theses largely balder, baldness and not bald enough. And, as shown before, in the context of the ${\textsf{ML}}$ theory, these principles imply both tolerance and the inductive premise—principles to whose truth neofeasibilists are committed.

Furthermore, our representation theorem (or a generalization of this result) can presumably be deployed to show that vague predicates are appropriately represented by structures of the sort Dean appeals to, and a generalization of our uniqueness theorem can be deployed to show the extent to which such representations are unique. So, the ${\textsf{ML}}$ theory can indeed be seen as constituting part of the abstract structure underlying Dean’s theory.

While the underlying abstract structure of Dean’s theory is given, at least in part, by the ${\textsf{ML}}$ theory, it is not the only theory of vagueness for which this is the case. In particular, such a theory need not be committed to soritical series having infinitely many elements. In the next couple of sections we consider two theories which differ from neofeasibilism in this and other respects, and whose underlying abstract structure is also given by the ${\textsf{ML}}$ theory.

6 Itzhaki’s Theory of Nonstandard Heuristics

As we have just seen, tallness and succession yield a consistent set of premises when Soritical series consisting of infinitely many objects are considered. Notwithstanding, tallness and succession fail to yield a consistent set of premises when Soritical series consisting of only finitely many objects are considered. Given this observation, what resolutions of the more standard, finite versions of the Sorites fit with the ${\textsf{ML}}$ theory?

The resolutions of the paradox that we will consider involve rejecting the truth of the inductive premise in Soritical scenarios. Since rejecting the inductive premise arguably amounts to accepting the prima facie implausible claim that there is a sharp boundary between those objects in the series that fall under a vague predicate T and those that do not, four questions naturally arise:¹²

• The semantic question: How is the claim that there are sharp boundaries consistent with the existence of borderline cases? What is a borderline case, given that there are sharp boundaries?

• The epistemological question: If there is a sharp boundary, why are we unable to identify the point at which that boundary is located even when the relevant facts all seem to be known?

• The psychological question: Why are we inclined to accept the inductive premise, if it is false? Why are we inclined to think that the cut-off point between the Ts and the not-Ts is not at any particular point in the series?

• The metaphysical question: If there is a cut-off point, what are the facts about the use of the vague predicate T, or about the things to which T is applied, that ground the fact that the cutoff point is where it is?

While an all-encompassing theory of vague phenomena will have satisfactory answers to all these questions, our present focus will mainly be on the psychological question. One available approach is the one suggested in Itzhaki, (2021, Sect. 6). Itzhaki’s resolution is based on the idea that we heuristically attribute to objects fictional magnitudes with a nonstandard structure in order to ‘omit irrelevant information’. According to him Itzhaki, (2021, p. 24):

Every forest has an exact number of trees. The fact that our mental representation of a forest is that of an arbitrarily large number of trees, is just a cognitive tool to help us reason about concepts of varying or unknown size without having to refer to their actual size.

Similarly, there are no perfectly negligible quantities. The representation of small quantities as negligible is a tool for alleviating cognitive load by omitting information that is judged irrelevant in the context.

$\ldots$ That is, if one takes the induction premise as referring to actual individuals, rather than to ideal representations, then one must relate the idealised representation to actual individuals according to some heuristic principle. But a heuristic principle is not universally true, and therefore certain conditions must exist for it to apply. To accept this interpretation of the induction premise is to deny its validity as a logical principle, because it does not hold universally.

Just as Dean’s neofeasibilism, Itzhaki’s nonstandard heuristics theory is reductionist about vagueness, in that satisfaction of a vague predicate supervenes on wholly precise matters. In addition, it is composed of the following elements:

(i):

The view that vague properties have as correlates idealized cognitive representations;

(ii):

The view that idealized representations of vague properties satisfy an idealized version of the inductive premise;

(iii):

The view that representations of vague properties are related to their nonidealized correlates via heuristic principles.

Itzhaki’s account appeals to hyperreal numbers, a proper extension of the real numbers that includes nonstandard elements, in particular infinitesimals and infinite numbers.¹³ To give an example (one going beyond what Itzhaki was able to offer by way of clarifying his theory of nonstandard heuristics), Itzhaki takes satisfaction of ‘bald’ to supervene on a person’s number of hairs.¹⁴ He furthermore seemingly takes baldness to have a cognitive correlate, baldness$^{*}$. Not to be bald$^{*}$ is to be assigned—by a cognitively real number-of-hairs$^{*}$ function $\#^{*}(\cdot )$ mapping people to hyperreal numbers—$H\pm n$ hairs, for some finite positive integer n, and where H is a chosen infinite number. Itzhaki takes the function $\#^{*}(\cdot )$ to behave as follows. It maps a person to the number of hairs it really has if that person is known to be bald. It maps a person to H if the person isn’t bald but not known not to be bald, and maps the person to $H+m$, where m is its real number of hairs, if the person is known not to be bald.

While Itzhaki offers no remarks on what is the exact form of the principle by which idealized representations are related to actual individuals, it is reasonable to think that it involves replacing thought about baldness by thought about baldness$^{*}$. And indeed, the inductive premise is true if understood as concerning baldness$^{*}$ rather than baldness. So, Itzhaki’s answer to the psychological question is that the inductive premise (about baldness) seems true because the inductive premise (about baldness$^{*}$) is true, and we heuristically reason about baldness in terms of baldness$^{*}$. Further, and just as it was the case with Dean’s neofeasibilism, all premises of the Sorites paradox are jointly satisfiable on Itzhaki’s theory provided that the Soritical series is infinite and that the paradox is understood as concerning baldness$^{*}$ rather than baldness. The picture we get is thus the following (Fig. 5):

Fig. 5

Soritical series for baldness$^{*}$

It should be clear that the ${\textsf{ML}}$ theory also constitutes part of the abstract structure of Itzhaki’s theory of nonstandard heuristics. It suffices to interpret (i) the partial order relation as the relation in which x and y stand when $\#^{*}(x)>\#^{*}(y)$, (ii) marginally smaller than as the relation in which x and y stand when $\#^{*}(x)-\#^{*}(y)$ is a finite positive integer; and (iii) largely smaller than as the relation in which x and y stand when $\#^{*}(x)-\#^{*}(y)$ is an infinite positive integer. ‘Bald’ is then satisfied by all and only those people who are not largely smaller than any clear case of being bald—such as someone without any hairs.

Relatedly, our representation theorem (or a generalization theoreof) may presumably be deployed in a defence of the claim that hyperreal numbers are indeed appropriate for representing the structure of Itzhaki’s fictional magnitudes; and a generalization of our uniqueness theorem may presumably be appealed to in order to reveal the extent to which a representation of fictional magnitudes by hyperreal numbers is unique. For, as Itzhaki himself points out (Itzhaki, 2021, fn. 4), the hyperreal numbers constitute just one of a number of mathematical structures which may be used to account for our heuristic reasoning involving vague predicates.

7 Nonstandard Primitivism

As previously mentioned, Dean and Itzhaki are reductionists about the satisfaction of vague predicates, in that they take their satisfaction to supervene on precise matters. But one need not be a reductionist about vagueness.¹⁵ Furthermore, the availability of a theory of the relations of marginal and large difference—the ${\textsf{ML}}$ theory – affords the means for a preliminary sketch of an alternative primitivist theory of vagueness.

According to our proposed view, nonstandard primitivism, there are vague quantities out there in the world, over and above precise quantities. Their degrees are vague in that the having of such a degree by an entity is neither reducible to nor supervenient on the having of a precise degree by that entity. Further, there are marginally smaller than and largely smaller than relations between degrees of vague quantities. The obtaining of either one of these relations is also not reducible to nor supervenient on the obtaining of precise relations between precise degrees. Finally, according to nonstandard primitivism, marginally smaller and largely smaller than are appropriately axiomatized by the ${\textsf{ML}}$ theory.

For instance, on the nonstandard primitivist theory in question, it is held that we have a hold on the relations of largely balder than and marginally balder than, and that these relations obey the principles of the ${\textsf{ML}}$ theory. To be bald is not to be largely balder than some person with zero hairs.

To be sure, this primitivist theory need not be primitivist about balder than. It can still be that y is balder than x if and only if x has more hairs than y. What the theory is nonreductionist about are the notions largely balder than and marginally balder than, and the baldness degrees that these relate. Consequently, it is also nonreductionist about the satisfaction of ‘bald’: its satisfaction supervenes not on the precise, but rather on facts concerning what is largely balder than anyone with zero hairs.

As should be clear, nonstandard primitivism immediately implies tolerance, and largely balder than. Yet, and by contrast with neofeasibilism, the nonstandard primitivist theory now being sketched rejects succession and not bald enough. Indeed, this theory accepts the existence of versions of the Sorites paradox based on soritical series with finitely many elements, and advocates that in those cases the inductive premise is false.

While Itzhaki’s theory of nonstandard heuristics accounted for the inductive premise’s appeal by taking it to be confused with a true principle about our representations, rather than about degrees that objects might really have, according to nonstandard primitivism the inductive premise’s appeal is explained not by a feature of our representations but by the fact that we are prone to confuse (really existing) marginal differences between (really existing) degrees of objects with difference by a fixed small precise amount. From the standpoint of nonstandard primitivists, these are not to be confused: marginal difference does not supervene on difference by any fixed precise amount.

It is true that the inductive premise is true of Itzhaki’s representations as well as of the vague degrees postulated by nonstandard primitivism. However, according to Itzhaki’s nonstandard heuristics, it is not the case that objects really have the degrees that we take them to have via our vague representations. By contrast, according to nonstandard primitivism, objects really have vague degrees over and above precise degrees. So, in our view, neofeasibilism, nonstandard heuristics and nonstandard primitivism are indeed three distinct nonstandard approaches to vagueness.

Relevantly, nonstandard primitivism affords the resources for conceiving of baldness degrees in two distinct ways. The first is the familiar one of taking baldness degrees to be 1-1 correlated with hair number. The baldness degree of x is greater than that of y just in case x’s number of hairs is less than y’s.

The other way of conceiving of baldness degrees is afforded by the ${\textsf{ML}}$ theory—and complemented by our representation and uniqueness theorems. We might think of the quantifiers in terms of which the axioms of the ${\textsf{ML}}$ theory are formulated as ranging, in the first instance over baldness degrees (now not to be explained in terms of precise properties), rather than as ranging over individuals. It is these baldness degrees which, in the first instance, stand in relations of marginal and large difference. The relations marginally balder than and largely balder than then obtain between individuals x and y if and only if x’s degree of baldness is marginally (respectively, largely) greater than y’s. Indeed, this is the nonstandard primitivist’s preferred way of conceiving the axioms of the ${\textsf{ML}}$ theory, since it allows the theory not to be committed to there being infinitely many individuals in the first place.

Nonstandard primitivism thus affords the following picture of baldness and baldness degrees (Fig. 6):

Fig. 6

Soritical series for baldness, and baldness degrees

In this figure circles represent baldness degrees rather than individuals. Squares represent individuals and arrows map individuals to their baldness degrees. It can easily be appreciated that, according to nonstandard primitivism, if a baldness degree is a degree of a nonbald individual, then whatever baldness degree is marginally greater than it will itself be a baldness degree of a nonbald individual. But adjacent individuals in a Soritical series will not always both be bald or both be not bald. In the case of n and o, being one hair shorter does imply being largely balder. Accordingly, while n isn’t bald, o is.

The representation and uniqueness theorems then make it possible to use rational number-integer pairs to speak of particular baldness magnitudes. From a nonstandard primitivist standpoint, and while we will not develop this view here, it is scales for baldness degrees understood in this nonreductionist manner that should be adopted in formulating degree-based semantics for gradable adjectives, not scales given in terms of precise magnitudes such as hair number.

This is not the place to compare the relative merits of neofeasibilism, the theory of nonstandard heuristics, and nonstandard primitivism. For the present purposes, what is important to note is that the ${\textsf{ML}}$ theory also constitutes part of the abstract structure of nonstandard primitivism. Thus, the ${\textsf{ML}}$ theory is of wide applicability and explanatory power. As should be clear, at the moment our inclination is towards nonstandard primitivism. Yet, a case in its favour will have to wait for another occasion.

8 Conclusion

Alongside the work in Dean (2018) and Itzhaki (2021), our paper constitutes a further attempt at clarifying in what way, and to what extent, reasoning with vague predicates resembles reasoning about nonstandard arithmetical and analytical structures. Our first contribution has been to propose the ${\textsf{ML}}$ theory of marginal and large difference. Our second contribution has been a study of the mathematical structures capable of representing it. In particular, we have demonstrated representation and uniqueness theorems revealing that specific mathematical structures are capable of representing the ${\textsf{ML}}$ theory, and how unique that representation is. These results have shown that the structures capable of representing the ${\textsf{ML}}$ theory are akin to the order structures of nonstandard models. A further result revealed that neither the (standard) natural numbers nor the (standard) real numbers are capable of representing the ${\textsf{ML}}$ theory. Our third contribution has been to show how the ${\textsf{ML}}$ theory provides part of the abstract structure of three philosophical theories of vagueness. Two of these consisted of theories already present in the literature: Dean’s neofeasibilist and Itzhaki’s theory of nonstandard heuristics. The third theory – or a preliminary sketch thereof—was our own nonstandard primitivism about vagueness. This third contribution has revealed the ${\textsf{ML}}$ theory’s wide applicability and explanatory power. In future work we plan to further develop the nonstandard primitivist theory, of which the ${\textsf{ML}}$ theory is a central component.