Abstract
Aggregative moral theories face a series of devastating problems when we apply them in a physically realistic setting. According to current physics, our universe is likely infinitely large, and will contain infinitely many morally valuable events. But standard aggregative theories are ill-equipped to compare outcomes containing infinite total value. So, applied in a realistic setting, they cannot compare any outcomes a real-world agent must ever choose between. This problem has been discussed extensively, and non-standard aggregative theories proposed to overcome it. This paper addresses a further problem of similar severity. Physics tells us that, in our universe, how remotely in time an event occurs is relative. But our most promising aggregative theories, designed to compare outcomes containing infinitely many valuable events, are sensitive to how remote in time those events are. As I show, the evaluations of those theories are then relative too. But this is absurd; evaluations of outcomes must be absolute! So we must reject such theories. Is this objection fatal for all aggregative theories, at least in a relativistic universe like ours? I demonstrate here that, by further modifying these theories to fit with the physics, we can overcome it.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Determining the correct moral theory is not just a normative matter but also, in part, an empirical one. Suppose that we have a candidate moral theory that delivers plausible verdicts in some highly idealised cases. But once you apply that theory under realistic empirical assumptions, quite inconveniently, it delivers absurd verdicts in almost every decision that moral agents ever face. No matter your metaethics, you must agree that the theory should be rejected. In this manner, the moral theories we accept or reject can depend on empirical facts about the world.
In just this manner, empirical lessons from physics appear to undermine a swathe of leading moral theories: any and all theories that are aggregative with respect to value. These include not only classical utilitarianism but, rather, all theories that rank outcomes according to total aggregate of all of the value in each (no matter where in space or time that value arises).Footnote 1 Such theories appear to deliver absurd verdicts, in almost every practical case we might consider, if the universe is infinitely populous.
Current physics predicts that our universe will span an infinite volume over space and time, and that within this volume will occur infinitely many tokens of every physically possible discrete event.Footnote 2 Some of those events are morally valuable, e.g.: a human brain processing a sensation of pleasure, perhaps. Our universe will contain infinitely many such pleased brains, and so infinitely many instances of value (of value at least some \(\varepsilon >0\), on any given cardinal scale).Footnote 3 Similarly, our universe will contain infinitely many displeased brains, and so infinitely many instances of disvalue (of value below \(-\varepsilon <0\)). If we sum up the total value across any possible outcome—in effect, summing a positively infinite value with a negatively infinite one—then the total sum is undefined. And one undefined sum is no greater than another. With total aggregates like these for every outcome ever available to us, it seems that aggregative moral theories cannot say that any outcome is better than any other—they are incomparable. In many cases, this is deeply implausible. Thus we seem to have reason to reject aggregative theories en masse, thanks to empirical findings.Footnote 4
Fortunately for the project of aggregation, philosophers have proposed aggregative theories that avoid this problem (one of which is demonstrated below). These proposals do not rely on simple sums of value; they aggregate value differently, and represent the resulting aggregates using slightly more complicated mathematical objects (see, e.g., Vallentyne, 1993; Vallentyne and Kagan, 1997; Bostrom, 2011; Arntzenius, 2014; Jonsson and Voorneveld, 2018; Wilkinson, 2021a,2021b; Clark, n.d.). . Many of those proposals do this by taking advantage of the physical structure of our universe, whereby valuable events are positioned in time and space. Where simple aggregation delivered incomparability in infinite worlds, these proposals are thought to deliver just the verdicts the aggregationist wanted (see Sect. 3).
But physics has further surprises in store for us, much to the woe of aggregative theories. A century of work in physics, both theoretical and experimental, tells us that time in our universe is relative: the duration observed between one event and another varies with the velocity of whoever does the observing (Cohn, 1904). So too, whether two events are simultaneous or not can depend on that velocity (see Comstock, 1910, for an illustration of this phenomenon). If you were to simply speed up, the set of events that are happening ‘now’ for you would shift; it would include events that, for a slower observer, lie in the distant past or future. That isn’t to say that fast-moving observers are wrong—one observer’s perspective is no less legitimate than another, since we have no scientific experiment that distinguishes one constant velocity over any other as ‘at rest’. There simply is no absolute perspective—no absolute time—by which we can measure the duration between any two events, nor by which we can judge which events are simultaneous (Einstein, 1905).Footnote 5
This is a further blow to aggregative moral theories, as I demonstrate in this paper. Many of our proposals for aggregative theories that still work in an infinitely populous universe are time-sensitive—sensitive to when in time valuable events occur. But when those events occur is, in some sense, relative. And it turns out that so too the moral evaluations of those time-sensitive aggregative theories are relative. As I show in Sect. 4 below, none of our extant time-sensitive proposals can provide absolute moral evaluations. They all fail, in almost every decision moral agents ever face. And, as I show in Sect. 5, the same goes for such proposals designed specifically to avoid this relativistic problem.
But this problem bears not only on the plausibility of some narrow selection of views, which happen to be time-sensitive. If time-sensitive theories of aggregation fail, then all aggregative theories fail in an infinite universe. As shown elsewhere, any aggregative theory that is not time-sensitive will, in the infinite context, fail to compare any of the outcomes between which we might ever need to choose in practice (see Wilkinson, n.d.(a); Jonsson and Peterson, 2020). Given this, if problems of relativity undermine time-sensitive theories, then they undermine aggregative theories in general.
Aggregative theories thus face another problem akin to that posed by an infinitely populous universe. Based on empirical findings, our existing versions of those theories deliver absurd verdicts on a vast scale. Does this mean we must abandon all aggregative theories, just because our universe has these peculiar characteristics? Thankfully, no. Despite the failure of existing proposals, I demonstrate in this paper that a satisfactory solution does exist (see Sect. 6). By drawing on tools from physics, we can concoct a method of aggregation that indeed allows absolute moral evaluations, that avoids the flaws of previous solutions, and that even succeeds in the trickier setting of general relativity (see Sect. 7). Aggregationists need not abandon their theories just yet—this peculiar problem can be solved, and we can indeed make moral judgements based on what will promote the good.
2 Preliminaries
In what is to come, we will need to compare outcomes, or worlds. In particular, to give moral verdicts, we need only compare worlds that have a great deal in common—worlds that share exactly the same events everywhere except the causal futureFootnote 6 of the agent who is choosing which world to bring about. We can ignore worlds that do not share a common history. After all, we necessarily cannot change the past.Footnote 7
To compare such worlds, we want an ‘at least as good as’ relation \(\succcurlyeq\) on the set of all possibleFootnote 8 worlds \({\mathcal {W}}\). This relation \(\succcurlyeq\) will be a binary relation: it compares two worlds. It will be reflexive: each world must be at least as good as itself. It will be transitiveFootnote 9: if a world \(W_a\) is at least as good as \(W_b\), and \(W_b\) is at least as good as \(W_c\), then \(W_a\) is at least as good as \(W_c\). And it will have an asymmetric component (\(\succ\)) that holds between worlds of which the first is strictly better, as well as a symmetric component (\(\simeq\)) that holds between worlds that are equally good.
The goal is an aggregative theory. So whether \(\succcurlyeq\) holds between two worlds must be determined by the total aggregateFootnote 10 of value in each—some impartialFootnote 11 combination of the values of every individual valuable event. In the finite setting, this aggregate might be represented by a finite number on some cardinal scale. In the infinite setting, it can only be represented by more complicated mathematical objects. For instance, under the method described in the next section, the aggregate can be represented as a set of cumulative sums.
I will focus on time-sensitive \(\succcurlyeq\) relations. Such relations take advantage of the fact that each valuable event occupies some position in space and time (or so I will assume) so we can associate each such event with a discrete spacetime point.Footnote 12 For example, the event of a human stubbing their toe might be associated with the time and place of the stubbing. Or we might treat an entire human life as a single event, associated with the time and place of their birth, or perhaps the midpoint of all positions they ever occupy. However we select that point and however fine-grained we make each event—and nothing below hangs on how we do so—each valuable event will be associated with some point \({\textbf {x}}\) in spacetime.
Conversely, we can associate each point in spacetime with the value of all events associated with it. For each world \(W_a\), a corresponding value function \(V_a\) maps each spacetime point to some real number, a cardinal representation of the moral value at that point. Where there is no valuable event at \({\textbf {x}}\), we can let \(V_a ({\textbf {x}})\) be 0 or indeed any finite value, as long as that value is consistent.
To compare worlds \(W_a\) and \(W_b\) in the ways described below, we will need to evaluate \(V_a({\textbf {x}})\) and \(V_b({\textbf {x}})\) for particular points \({\textbf {x}}\)—to identify the value at the same point across worlds. But how do we identify that same point (or, if you prefer, its counterpart) across worlds?Footnote 13 This is fairly easy, given that the worlds we compare will be identical everywhere except the causal future of the decision-maker. So they will always share at least some of the same events. It is then natural to associate each of those events with the same point \({\textbf {x}}\) in both worlds. And we can extend this mapping of points into our causal future, simply by identifying each point \({\textbf {x}}\) across worlds by its position relative to those past points that the worlds have in common. For instance, the point 1 metre in front of me and at 1 second in the future in one world is the same point as that which is 1 metre in front of me and 1 second in the future in another world (provided that I am in the same position, relative to past events, in both worlds). This will (usually)Footnote 14 allow us to specify, for each point in one world, a unique spacetime point to map it to in the other world.
3 Expansionism
To demonstrate the relativistic objection, I will focus on one plausible method of aggregation that can compare infinite worlds: expansionism. By way of example, it goes like this.
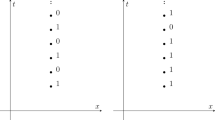
Take two worlds, such as \(W_{\text {recurring}}\) and \(W_{\text {once}}\) in Figs. 1 and 2, displayed on spacetime diagrams with matching coordinates.Footnote 15 Each world contains infinitely many valuable events—perhaps each is a human living a happy life. In \(W_{\text {recurring}}\), there is such a happy life lived at every grid-point in space and time from \(t=1\) onwards. In \(W_{\text {once}}\), there are happy lives lived at \(t=0\) but at no other time.
How might we compare these worlds? If we simply summed up the value in each, we could not say either is better—both contain infinitely many happy lives, so both sums are positively infinite.
Instead, we could sum the value in each world in a particular order, and consider their cumulative sum as we go. For instance, start at the point \({\textbf {p}}\) illustrated below. And sum the value of events in order of how far they are from \({\textbf {p}}\) on the diagram. Events that are one unit in length from \({\textbf {p}}\) get counted before those at two units in length, and so on. We sum value moving outwards from \({\textbf {p}}\), effectively expanding the circular region around \({\textbf {p}}\), letting the radius approach infinity (see Figs. 3 and 4).
Summing in this order, we obtain cumulative sums of the value within radius r of \({\textbf {p}}\), for each real r. Those cumulative sums are shown in Fig. 5.
A clear winner emerges: \(W_{\text {recurring}}\). Even though both worlds have the same total sum of value—both sums are positively infinite—\(W_{\text {recurring}}\)’s sum approaches infinity a lot faster when we sum over uniformly-expanding regions of space and time. In fact, for any sufficiently large circular region centred at \({\textbf {p}}\), \(W_{\text {recurring}}\) will have a greater cumulative sum. And, for these two worlds, we can replace \({\textbf {p}}\) with any point and a large enough circular region around it will contain more value in \(W_{\text {recurring}}\) than in \(W_{\text {once}}\). This is because value is far more densely packed into \(W_{\text {recurring}}\); in an important sense, it contains more of it. So we might judge that \(W_{\text {recurring}}\) is better than \(W_{\text {once}}\).
This method can be stated more precisely as Spatiotemporal Expansionism (or SE), which is adapted from Wilkinson (2021b, p. 19-20) and Vallentyne and Kagan (1997, p. 17).Footnote 16
SE: For worlds \(W_a\) and \(W_b\) with the same spacetime points, \(W_a \succ W_b\) if, for all starting points \({\textbf {p}}\), there exists \(r^\prime \in {\mathbb {R}}\) such that for all \(r>r^\prime\),
$$\begin{aligned} \sum _{\{{\textbf {x}}\, | \, d({\textbf {x}},{\textbf {p}})\le r\}} \Big ( V_a({\textbf {x}})-V_b({\textbf {x}}) \Big )> 0 \end{aligned}$$And \(W_a \simeq W_b\) if, for all \({\textbf {p}}\) and all \(r>r'\) the sum equals 0.
As described above, SE says the following. Take any starting point \({\textbf {p}}\). For each world, take the sum of all value within distance \(r^\prime\) of \({\textbf {p}}\). Take the difference between the sums for the two worlds. Is one greater, such that the difference between them is greater than 0? Will it still be greater if you expand the distance to even greater distances r? And will the same hold for any \({\textbf {p}}\) you choose? If so, you can say that one world is strictly better. If instead the difference remains 0, for all large r, then the worlds are equally good.
Note that here the measure of distance \(d({\textbf {x}},{\textbf {p}})\) between two points \({\textbf {x}}\) and \({\textbf {p}}\) is distance in the standard Euclidean sense: \(d^2=\Delta x^2+\Delta y^2+\Delta z^2+\Delta t^2\) (where \(\Delta x,\Delta y,\) and \(\Delta z\) are differences in spatial coordinates along three dimensions and \(\Delta t\) is the difference in time)Footnote 17 or, when the points differ in just one spatial dimension x as above, \(d^2=\Delta x^2+\Delta t^2\). This matches the distance obtained by placing a ruler on the page in the above diagrams. And this needs to be our distance metric for us to obtain the nice, bounded, circular regions we saw above.Footnote 18
With SE in hand, we seem to have a plausible method for comparing infinite worlds. It deals neatly with \(W_{\text {recurring}}\) and \(W_{\text {once}}\) above, even though both worlds contain infinitely many valuable events. And it happens to satisfy a variety of desirable conditions. For one, it delivers a \(\succcurlyeq\) relation which is reflexive and transitive. For another, it aggregates value over different points in an impartial manner, in that no point (and no person) is favoured over another—indeed, we could swap the value at one point with the value at any other, and SE would confirm that the world remains equally good.Footnote 19 So, even though the positioning of value in spacetime helps to compare worlds under SE, we need not discount nor ignore value based on its position (see Wilkinson 2021b: 12-15; contra Koopmans 1972).
4 Problems
But SE faces a serious problems, as do other time-sensitive methods of aggregation: it depends on an impoverished understanding of time.Footnote 20
Note that, in what follows, I demonstrate these problems for SE specifically. But analogous problems emerge, and can be demonstrated with similar examples, for the proposals of Vallentyne (1993), Bostrom (2011, p. 16), Arntzenius (2014, p. 56), and Jonsson and Voorneveld (2018).Footnote 21
4.1 Galilean Relativity
Problems emerge even without relativity in the Einsteinian sense. They arise even in the simpler setting of Newtonian physics.
Consider a seemingly straightforward case: Erid.
Erid
A civilisation based on the planet Erid is fortunate that it will last forever. Eridians are born at regular intervals and all have happy, identical lives. So constant amounts of moral value arises on Erid at regular intervals of time. You can choose to visit Erid and see the sights, or to pass by. If you do visit, your spacecraft will slightly disturb the motion of Erid’s star and surrounding planets, setting it moving at a tiny speed relative to where it would otherwise be, producing \(W_{\text {moving}}\). Pass by and the system remains undisturbed, producing \(W_{\text {stationary}}\). Either way, the same values will arise at the same times; your visit would make no one better or worse off.
Figure 6 represents the difference between the two worlds, \(W_{\text {moving}}-W_{\text {stationary}}\).Footnote 22 This world of differences has positive values at the positions the Eridians would occupy in \(W_{\text {moving}}\) and negative values where they would have been left in place in \(W_{\text {stationary}}\) (since \(W_{\text {moving}}\) has that much less value at those positions than does \(W_{\text {stationary}}\)). This diagram contains all of the information necessary to compare \(W_{\text {moving}}\) and \(W_{\text {stationary}}\). Since SE’s verdicts depend only on the differences between the two worlds, \(W_{\text {moving}}\) will be at least as good as \(W_{\text {stationary}}\) if and only if \(W_{\text {moving}}-W_{\text {stationary}}\) is at least as good as the world with value 0 at every point.
Intuition suggests that \(W_{\text {moving}}\) and \(W_{\text {stationary}}\) should be equally good. After all, they differ only by how fast the Eridians are travelling, and in that respect only slightly. But SE says otherwise: that \(W_{\text {moving}}-W_{\text {stationary}}\) is worse than the zero-world; so \(W_{\text {moving}}\) is worse than \(W_{\text {stationary}}\). To see why, expand from starting point \({\textbf {p}}\); and (naively) use the distance metric d based on the coordinate representation used above. We obtain the cumulative sum plotted in Fig. 7, which soon falls below 0, never to return.
The same holds no matter which starting point we choose. So SE seems to judge \(W_{\text {stationary}}\) as better than \(W_{\text {moving}}\). But this verdict is counterintuitive. Surely, setting the planet ever so slightly in motion should not make the lives of the Eridians, in effect, worth less. Intuition suggests that it should make no moral difference at all.
SE’s implications get all the more counterintuitive if we recognise that, under the laws of Newtonian mechanics, it will appear to any observer travelling at a constant velocity that they are at rest; they will be unable to detect their movement with any mechanical experiment. (This is known as Galilean relativity.) So, in \(W_{\text {stationary}}\) and \(W_{\text {moving}}\), there is a symmetry between the two outcomes—in each, the Eridians may consider themselves at rest, and that it’s the other outcome in which they would be in motion.
In fact, if \(W_{\text {moving}}\) occurred and the Eridians looked back on your decision from their own perspective, with themselves at rest, the regions used in the comparison above would appear as in Fig. 8.
Those regions around \({\textbf {p}}\) now look awfully peculiar—far from the most natural shape we might choose. From the Eridians’ perspective in \(W_{\text {moving}}\) they aren’t circles of fixed radius, but instead these peculiar skewed ellipses. Were they to compare the worlds themselves , and treated their own velocity as the one at absolute rest , they would draw those regions quite differently (as circles rather than ellipses in Fig. 8). Applying SE using those regions, they would reach the opposite verdict: that \(W_{\text {moving}}\) is the better outcome.
So we have a problem. The distance measure d, the regions of fixed distance around a given \({\textbf {p}}\) and, it seems, the verdicts of SE all depend on which velocity counts as being at absolute rest. Earlier, I assumed it was that of the Eridians in \(W_{\text {stationary}}\). But they themselves may not know that—there’s no mechanical experiment they could perform that would distinguish their own velocity as any more ‘at rest’ than another. Indeed, modern physics now tells us that there is no experiment at all which would distinguish one velocity over another (Einstein, 1905; Michelson & Morley, 1887)—there is no non-arbitrary way to specify absolute rest. So we have no reason to think there is such a thing.
What does this mean for SE? It seems that there can be no absolute distance metric d, that we cannot construct absolute regions of distance d around a point, and that SE cannot give absolute judgements. It seems we must abandon SE as well as, it seems, any aggregative moral theory.
4.2 Special Relativity
Although this problem arises in Newtonian physics, that isn’t the full story. Our understanding of space and time did not stop with Newton. We now know that observers at different velocities disagree about much more than what counts as at rest; they also disagree about measurements of spatial distance, measurements of time, and even whether events are simultaneous. Their perspectives differ far more than they would under Galilean relativity. (Surprisingly, this greater difference will help later in developing solutions).
To see such disagreement in action, consider worlds analogous to those above: in \(W_{\text {stationary}}\), Erid stays ‘at rest’ and produces moral value at regular intervals; and, in \(W_{\text {moving}}^\prime\), Erid is instead set in motion. These are illustrated in Fig. 9. (On this diagram, its relative speed is \(\frac{4}{5}\) of the speed of light, but the same result arises with even minuscule speeds.)
In both outcomes, the Eridians produce the same value per unit of time, according to their own experience of time. But, as shown in Fig. 9, they would disagree with their counterparts in the other outcome about which outcome produces value more quickly. If we treat Erid as at rest in \(W_{\text {stationary}}\), as this diagram does, the events in \(W_{\text {moving}}^\prime\) occur more slowly. But from the perspective by which \(W_{\text {moving}}^\prime\) is at rest, we would observe the exact opposite: that events in \(W_{\text {stationary}}\) occur more slowly!
This is due to time dilation, a consequence of the special theory of relativity. If one observer watches t seconds tick by on their own wristwatch, any observer moving at speed v (as a fraction of the speed of light) relative to them sees that ticking take \(t^\prime\) seconds, where \(t^\prime =\frac{t}{\sqrt{1-v^2}}\).
Since no velocity is any more at rest than another, the reverse holds as well: the first observer will also see the ‘moving’ observer’s wristwatch tick more slowly. So of course the Eridians \(W_{\text {moving}}^\prime\) and \(W_{\text {stationary}}\) would disagree about which outcome produces value more quickly. So too, they would disagree about the order of events: those in \(W_{\text {stationary}}\) would observe their first valuable event occurring before the first such event would occur in \(W_{\text {moving}}^\prime\); those in \(W_{\text {moving}}^\prime\) would observe the reverse.
From the perspective of the Eridians in \(W_{\text {moving}}^\prime\), the regions used in Fig. 9 above would now appear as in Fig. 10—no longer based on a sequence of nice concentric circles, but instead a sequence of ellipses skewed even more than before.
As before, these regions look awfully peculiar. And again, if the Eridians in \(W_{\text {moving}}^\prime\) drew the regions of fixed distance d from their own perspective, they would do so very differently. This is because the measure d between any (non-identical) points \({\textbf {x}}\) and \({\textbf {p}}\) is not absolute; it varies with the velocity at which it is measured.
But the deeper problem is that the definition \(d^2=\Delta x^2+\Delta t^2\) makes no mention of perspective or velocity; instead, it assumes that there were some such absolute quantities \(\Delta t\) and \(\Delta x\). But there aren’t—any such measurements are relative to the velocity of the observer, by special relativity. So we have no measure d with which to construct regions of fixed distance, we have no such regions, and we have no verdicts at all from SE. The principle is silent in all cases—all pairs of outcomes are incomparable.
But before we abandon SE entirely, perhaps we can modify it or the definition of d ever so slightly to still deliver some judgements. Here is one way we might do that. Define \(\Delta t\) and \(\Delta x\) as those quantities that would be measured at the velocity of the agent making the evaluation. They and d are then relative to that velocity. And let SE use this relativised version of d. Then SE’s verdicts will be relative too—in the case above, an agent travelling at one velocity would judge \(W_{\text {moving}}^\prime\) as the better outcome, and an agent travelling at another velocity would judge \(W_{\text {stationary}}\) as better. Both would be right, since SE’s verdicts are relative to the velocity of the judge.
But this modification is implausible. Our moral judgements must be absolute—when evaluating outcomes (rather than judging acts, where agent-relative considerations might be relevant) we are interested only in goodness simpliciter. And when evaluating outcomes based on their goodness simpliciter, we usually think that there can be only one correct evaluation for any pair of outcomes. But even for those who deny this and endorse moral relativism (such as relativism to the cultural setting in which a judgement is made), relativism to the agent’s speed seems particularly absurd. An otherwise worse outcome can be made better if the agent simply speeds up? This seems absurd to me.
And it is all the more absurd given that it can result from even arbitrarily small changes in velocity—the same disagreement arises in the case above when the civilisations in \(W_{\text {moving}}^\prime\) and \(W_{\text {stationary}}\) differ by any non-zero velocity. So this modification is a non-starter.Footnote 23
Here is an alternative modification. Again, let the metric d be relative to the velocity of the agent. But, for SE to compare two outcomes, don’t just require that all starting points \({\textbf {p}}\) agree. Also require that agents at all velocities agree—supervaluate over all perspectives. If they disagree, let SE remain silent: the two worlds under consideration are simply incomparable. But this approach is implausible too. The example above was a mundane one: you can either leave be or set future events (ever so slightly) in motion. If a method of aggregation cannot compare these outcomes, it seems seriously inadequate. And SE cannot, if modified in this way—it falls silent, even in cases as mundane as this. So, again, we must abandon SE.
5 Existing Solutions (and their Problems)
Must we abandon the expansionist approach entirely, and moral aggregation along with it? I hope not. Here are two other proposals for salvaging it, both from Arntzenius (2014). Unfortunately, each faces further problems, and serious ones at that.
5.1 Double Lightcones
Here is one suggested solution, described by Arntzenius (ibid.: 44) and credited to Cian Dorr.
In the definition of SE, forget about any distance measure d. All we need is a sequence of expanding regions of spacetime, each compact and containing the regions that come before it. And, to overcome the relativistic problem, those regions must not vary with the perspective of the observer.
We can obtain such regions as follows. Select two points, one earlier in time than the other, according to all observers—perhaps two points with the same spatial position, as illustrated below. For the earlier point, draw its future lightcone: the region of points you could reach from that point by travelling at or below the speed of light in any direction. And, for the later point, draw its past lightcone: the region of points from which you could reach the later point by travelling at or below light speed. The intersection of those two regions—their ‘double lightcone’—forms a diamond-shaped region with both endpoints as vertices. Repeat this process with further pairs of points to obtain your expanding regions. One such sequence of regions is illustrated in Fig. 11, expanding around \({\textbf {p}}\), applied to \(W_{\text {moving}}^\prime - W_{\text {stationary}}\) from above.
We could sum value over this sequence of regions instead of SE’s expanding circles. If we did, we would sum the \(-1\)s faster than the \(+1\)s, so our cumulative sum would approach \(-\infty\). We would be led to the verdict that \(W_{\text {moving}}^\prime\) is worse than \(W_{\text {stationary}}\). But is this verdict absolute, no matter the observer’s velocity?
Indeed, these regions would be constructed the same way by observers moving at any velocity, as long as they use the same pairs of endpoints to construct them. But the challenge lies in selecting those endpoints. To get a sense of why different observers or agents might disagree about which endpoints to use—and hence which double lightcones to use—consider that same sequence of regions from the perspective of the Eridians in \(W_{\text {moving}}^\prime\), as illustrated in Fig. 12.
As in the previous section, these regions now look awfully peculiar. They seem no more appropriate than, say, if we constructed the regions by setting endpoints at the same spatial position as \({\textbf {p}}\), but did so from the perspective of \(W_{\text {moving}}^\prime\). We would generate very different regions which, from this perspective, would have the same nice diamond shape we saw above. But they would give us a different verdict: summing over such a sequence of regions we would sum the \(+1\)s much faster than the \(-1\)s; our cumulative sum would approach \(+\infty\); so we would conclude that \(W_{\text {moving}}^\prime\) is better than \(W_{\text {stationary}}\).
In short, there is no non-arbitrary way to select the endpoints from which we construct these double lightcones. Simply placing them at some particular position relative to your starting point \({\textbf {p}}\) will always result in different regions for agents travelling at different velocities. And different selections can deliver different verdicts, as demonstrated above. So the problem remains.
5.2 The Spacetime Metric
Here is another proposal, also from Arntzenius (ibid.: 43).
In the definition of SE, simply replace the d with a better measure of 4-dimensional distance—one that is invariant across changes in velocity. In the standard, flat spacetime of special relativity we have one such metric: the spacetime metric, s, given by
When \(\Delta y\) and \(\Delta z\) are 0, as in my examples below, we have \(s^2=\Delta x^2 - \Delta t^2\).
What does s represent? It actually measures ‘proper time’, or ‘proper distance’. The proper time between two points is the duration of time we’d record on a clock travelling from one to the other at constant velocity. (Note that this only exists if you could reach one from the other by travelling below light speed.) Meanwhile, the proper distance is the spatial distance that you’d measure between them if you were travelling at just the right velocity to see those points as simultaneous. (And this only exists if there is such a velocity—if neither lies in the other’s future lightcone.)
If we replace d with s in the definition of SE, the regions we generate around \({\textbf {p}}\) will look like those shown in Fig. 13 below.Footnote 24 Each of these hyperbola-shaped regions corresponds to the set of all points within some constant proper time (or distance) of \({\textbf {p}}\). Effectively, each region is the set of points that you could reach from \({\textbf {p}}\) within some time \(|s^2 |\) (from your own perspective) by travelling at a constant speed, or that would look like they were within distance \(|s^2|\) of \({\textbf {p}}\) from some perspective. But recall that time passes more slowly for fast-moving observers, and lengths appear shorter. So, for two future points which seem to you to lie at the same time, the one further from you in space would actually be the smaller proper time from your position. Likewise, for two points which seem to you to lie at the same spatial position but at different times, the one further from you in time would be the smaller proper distance from you.
Crucially, the proper time/distance measured between any two points will be the same no matter the velocity at which it is measured. So too, any two observers would draw precisely the same regions no matter their velocity. They would draw specific points in different places on the graph, but they would still draw them within precisely the same regions. So we have a sequence of expanding regions on which everyone can agree, and over which we can apply SE absolutely and without controversy.
In the problem case of \(W_{\text {moving}}^\prime\) versus \(W_{\text {stationary}}\) from above, we would construct the regions in Fig. 14. And as you can see, each \(-1\) and its corresponding \(+1\) lie on the boundary of the same region—they lie at the same proper time/distance from \({\textbf {p}}\), and this would be the case from any perspective.
If we applied SE using these regions instead of the circles from earlier, each \(-1\) would cancel out the corresponding \(+1\). Our cumulative sum would be 0 at all stages (and, if we started from a point other than \({\textbf {p}}\), it would be 0 beyond some stage). So we would judge \(W_{\text {moving}}^\prime\) and \(W_{\text {stationary}}\) as equally good. Not only do we have a verdict, but we have the intuitively correct one: that the world is equally good whether we set the civilisation in motion or leave it be.
But this supposed solution faces its own serious problem: any of those regions can contain infinite value (or undefined total value). For instance, consider the worlds: \(W_{\text {right}}\), which contains a sequence of valuable events extending off towards the right; and \(W_{\text {left}}\), which contains a sequence extending off towards the left. These events are arranged such that \(W_{\text {right}}-W_{\text {left}}\) is as illustrated in Fig. 15.
In \(W_{\text {right}}-W_{\text {left}}\), all of those events with value \(+1\) or \(-1\) lie at \(s=0\) from \({\textbf {p}}\). Suppose we tried to take a cumulative sum, starting from \({\textbf {p}}\). That cumulative sum will break down immediately: we cannot assign a finite value to the region within proper time/distance 1 of \({\textbf {p}}\) (or even that within distance 0.000001); the sum of value in each such region is undefined.
So this proposal puts us in a position similar to where we started: we wanted to compare worlds containing infinite value, but standard addition on the real numbers does not allow us to do so. For the same reason, we cannot compare worlds like these.Footnote 25 So the proposal is inadequate.
6 A Better Solution
Despite the problems with that last solution, there is a promising solution in its vicinity.
As Arntzenius diagnoses it, the key problem with that solution was that each of the regions it uses has infinite 4-dimensional volume.Footnote 26 Thanks to this infinite volume and their shape, we can arrange infinitely many valuable events within each of them, as we saw above.
We could avoid that problem if only we had a similar sequence of regions but each with only finite volume. Why? I assume—quite plausibly, I think—that a (compact) region of finite volume can only ever fit finite total value. On standard accounts of value, a collection of events with infinite total value would require infinite volume. For instance, to produce a given quantity of pleasure within a human brain would require some minimum spatial volume and duration of time; to scale up this quantity ever more would require an ever greater duration (to extend the experience longer) and/or ever greater volume (to fit additional brains). You cannot scale up the quantity of pleasure to be infinite without scaling up the volume of spacetime involved to be infinite as well, and likewise if value takes on some plausible form other than pleasure. So you cannot fit infinite value into a (compact) region of finite volume.Footnote 27
In fact, we can avoid the problem even more easily. The regions in our sequence need not have finite volume. They need only have a finite portion of their volume lying within the agent’s future lightcone—in the agent’s causal future. As noted earlier, in practice, we do not need to ever compare worlds that differ anywhere except the agent’s causal future. So we can safely assume that, at any point \({\textbf {x}}\) outside the lightcone, the local values in any worlds \(W_a\) and \(W_b\) under comparison will be such that \(V_a({\textbf {x}})-V_b({\textbf {x}})=0\). So any region of spacetime with only finite volume within the agent’s future lightcone will only contain a finite difference in value between outcomes.
With this knowledge in hand, we can solve the problem faced earlier when comparing \(W_{\text {right}}\) and \(W_{\text {left}}\). As before (and as depicted by the dotted lines in Fig. 16), we can construct sequences of regions using proper time/distance, each containing points within some fixed \(|s^2|\) from starting point \({\textbf {p}}\). But we can restrict our attention to only some of those sequences: those in which each region contains only finite value. And we know that there will always be some sequences like this: just let \({\textbf {p}}\) be in the agent’s past; then each region will only have finite volume within the agent’s future lightcone, and so only finite value.Footnote 28 In \(W_{\text {right}}-W_{\text {left}}\) here, starting from one such \({\textbf {p}}\), the cumulative sum would be 0 at every stage (see Fig. 16). Likewise for any \({\textbf {p}}\) in the agent’s past lightcone.Footnote 29 And likewise for any \({\textbf {p}}\) we might choose here that gives regions each containing finite value. If we consider only such regions, then we can judge \(W_{\text {right}}\) and \(W_{\text {left}}\) as equally good, as intuition suggests they are!
That is just what I propose, with Relativistic Spatiotemporal Expansionism (RSE).Footnote 30
RSE: Let \(W_a\) and \(W_b\) be any worlds with the same spacetime points. Then \(W_a\succ W_b\) if there is some starting point \({\textbf {p}}\) and some distance \(r^\prime\) such that the following sum is finite and positive for all \(r>r^\prime\), and for no starting point \({\textbf {p}}\) is the sum finite and negative for all \(r>r^\prime\).
$$\begin{aligned} \sum _{\{{\textbf {x}}\, | \, |s({\textbf {x}},{\textbf {p}})^2|\le r\}} \Big ( V_a({\textbf {x}})-V_b({\textbf {x}}) \Big ) \end{aligned}$$And \(W_a \simeq W_b\) if for there is some starting point \({\textbf {p}}\) and some distance \(r^\prime\) such that the sum is equal to 0, and no starting point \({\textbf {p}}\) for which it is positive (or negative) for all \(r>r^\prime\).
RSE has us follow much the same procedure as SE: sum the values in \(W_a\) and \(W_b\) in order of their distance from \({\textbf {p}}\); if \(W_a\)’s sum takes the lead and keeps it beyond some distance \(r^\prime\), then \(W_a\) is better; and, if instead the sums are equal and stay equal beyond \(r^\prime\), then the worlds are equally good. The only differences from SE are: we use the distance given by proper time/distance (via \(|s^2|\)), to avoid problems with relativity; and, crucially, we don’t need all starting points \({\textbf {p}}\) to agree. To say that \(W_a\) is better, it’s enough to have just one \({\textbf {p}}\) that gives \(W_a\) the winning sum, as long as there is no other starting point \({\textbf {p}}^\prime\) that disagrees. Similarly, to say that the worlds are equally good, it’s enough to have just one \({\textbf {p}}\) that says that the sums become equal, as long as there is no \({\textbf {p}}^\prime\) that disagrees.
And RSE succeeds in comparing \(W_{\text {left}}\) and \(W_{\text {right}}\), as illustrated above. We have some point \({\textbf {p}}\) that generates a sequence of expanding regions over which the differences between worlds sum to 0 no matter how far we expand. And it so happens that no other starting point says otherwise, that the sum is strictly positive or strictly negative (and finite)Footnote 31 beyond some distance \(r^\prime\). So RSE judges \(W_{\text {left}}\) and \(W_{\text {left}}\) as equally good. And, intuitively, so they should be! One world involved sending off some sequence of value into space in one direction; the other involved sending it off in another, precisely mirrored direction at the same speed; so neither world should be any better than the other.
So RSE delivers the intuitively correct verdict in this problem case. And, since it uses a distance metric on which all observers agree, its verdicts are absolute. So we avoid the problems encountered earlier (and, indeed, can judge \(W_{\text {moving}}^\prime\) and \(W_{\text {stationary}}\) as equally good). The relativistic problem is solved.
7 General Relativity
This new aggregation method, RSE, delivers plausible and absolute verdicts in a universe governed by the special theory of relativity. But special relativity only approximates the spacetime structure of our universe. Does RSE succeed in an even more realistic setting—a universe governed by the general theory of relativity?
Under special relativity alone, spacetime is flat: objects not subject to any force travel in straight lines, which respect the properties of Euclidean geometry. But under general relativity, depending on the matter and radiation present, spacetime may be curved. This curvature corresponds to what we might think of as a gravitational ‘field’—massive objects appear to accelerate towards one another. But, given the discrepancies we observe in measuring distance and time (e.g. Hafele and Keating, 1972), we know that this is not due simply to a field of force; it is due to curvature of spacetime itself.
In a curved spacetime, the spacetime metric s no longer applies universally. Over any large interval, measurements of s will no longer be agreed upon by all observers, nor will it correspond to the proper time and distance between points. So we have a problem: where spacetime is curved, RSE as defined above will fail to deliver verdicts on which all observers agree.
But this problem is easily solved. Every curved spacetime has a near-analogue of s, often simply called its metric, or g. This metric depends on the distribution of matter and radiation across spacetime. So the measurements it produces between two points may depend on the absolute position of those points. But this is fitting, since the proper times (or proper distances) between those points depend on curvature, so on absolute position, as well.
One simple example of a curved spacetime is Schwarzschild spacetime, in which there is just one massive objectFootnote 32 and nothing else. This closely approximates the shape of spacetime close to the Earth. And it comes with a metric g, measurements of which match those of proper time and distance, and with which we can construct expanding regions.Footnote 33 We can use g to construct expanding regions around a point \({\textbf {p}}\) in some agent’s past lightcone, each region containing those points within fixed distance g of \({\textbf {p}}\). Those regions will be as illustrated in Fig. 17.
These regions allow us to apply a version of RSE in curved spacetime. They regions are similar to those generated by s, just skewed a bit by gravitational curvature—as we approach the massive body at \(r=0\), they tend towards being perfectly vertical on the diagram, matching that body’s path. And, as we see here, only a finite portion of each region lies within the agent’s future lightcone.Footnote 34 So, with the right choice of \({\textbf {p}}\), these regions will each only contain finite value, as we need them to. On top of that, these regions will be constructed the same way by all observers, regardless of their velocity, since g is a distance measure independent of the observer’s velocity (as it measures proper time and proper distance). And so, by switching our distance metric from \(|s^2|\) to g, it seems that we can easily modify RSE to work in curved spacetime.
In how broad a range of curved spacetimes does this strategy work? It is hard to say for sure (and far beyond the scope of a single paper), but I would speculate that RSE is likely to work in almost all spacetimes we might face in practice. After all, every possible spacetime will come with some distance metric g on which all observers agree. And, upon examination, a broad range of other realistic spacetimes seem to preserve the key property that: for any point \({\textbf {p}}\) in the agent’s past lightcone, the regions within proper time g of \({\textbf {p}}\) will overlap with the agent’s future lightcone for only a finite volume. For instance, this holds if we move from a Schwarzschild spacetime, with just one massive body, to a more realistic spacetime with many such bodies—such a spacetime becomes warped (as on the left side of the above figure) at many positions rather than just one. But that warping didn’t stop the overlap of the agent’s future lightcone and regions around \({\textbf {p}}\) from having finite volume; nor would having similar warping occur elsewhere stop it. And it seems that other realistic spacetimes will not prevent this either—whether we face a spacetime under which the universe is expanding or contracting (e.g., a Friedmann-Lemaître-Robertson-Walker spacetime), or in which massive bodies are rotating (as approximated by, e.g., Kerr spacetime) or have charge (as approximated by, e.g., a Reissner-Nordström spacetime), or even in which entropy is so great that curvature is approximately constant (e.g., a de Sitter or anti-de Sitter spacetime, as is predicted to characterise the far future of our universe according to versions of the flat-\(\lambda\) model—see Carroll,, 2020).Footnote 35 At least over a wide range of plausible spacetimes our future might resemble, it seems likely that a form of RSE (with the appropriate metric g) will still be able to deliver comparisons.Footnote 36
General relativity also presents a second problem. Recall the method I suggested in Sect. 2 for identifying the ‘same’ (or counterpart) spacetime points across worlds: first, identify events outside the agent’s future lightcone with the same points in each outcome, since those events are fixed; then, for each point \({\textbf {p}}\) within the future lightcone in some outcome, map it to whichever point \({\textbf {q}}\) in another outcome is the same distances in space and time from every points outside the lightcone as \({\textbf {p}}\) was. But it is now abundantly clear that this relation fails—distances in space and time are not absolute but instead differ with the velocity of the observer. So we might reformulate the relation: instead, map each such \({\textbf {p}}\) in one outcome to the \({\textbf {q}}\) in another outcome that is positioned at the same distances from each point outside the future lightcone, where distance is measured with \(|s^2 |\) (or, in curved spacetime, g). All observers agree on those measures, so they can agree on which points are the same under this relation.
But this reformulation can still break down in curved spacetimes. Agents will sometimes choose between outcomes with different curvature if their actions affect the distribution of matter in the universe. And it is possible that the curvature in those outcomes—and so the distances between points—is such that the point \({\textbf {p}}\) in one outcome maps to multiple points in the other (or none at all). This is an odd implication for an identity (or counterpart) relation to have!
Fortunately, this problem does not affect RSE. There are two places where the identity/counterpart relation can affect RSE’s verdicts. The first: we need to be able to expand our regions around the same point \({\textbf {p}}\) in each world. But we can do this even with a relation that misbehaves within our future lightcone—simply pick a point \({\textbf {p}}\) outside the agent’s future lightcone, which will always map to a unique and plausible point in every world. The second: for each point \({\textbf {x}}\), we want to identify the same point across worlds to take the difference in value at that point, which we will then sum up over all such points within each region. But nothing much hangs on whether some value lies at \({\textbf {x}}\) or at another point in the region; we really just need the (difference in) value across the whole region. So we can avoid any problem here by simply assigning \(V_a({\textbf {x}})=0\) (on whichever cardinal representation we are using for local values) whenever \({\textbf {x}}\) is absent from world \(W_a\); and, when \({\textbf {x}}\) has multiple counterparts in \(W_a\), simply let \(V_a\) be the sum of their values. This allows us to sum the differences in value across each region without needing to worry whether each point has a unique identity/counterpoint in every world. RSE works just fine despite this.
8 Conclusion
Above, we saw a potentially devastating problem for aggregative moral theories: thanks to special relativity, many such theories either cannot compare any outcomes at all, or else they must allow their comparisons to be dependent on the velocity of whoever is doing the comparing.
Many of our existing proposals for how to aggregate value in a physically realistic, infinitely large universe are time-sensitive. Indeed, Jonsson and Peterson (2020) and Wilkinson (n.d.(a)) argue that the only plausible aggregative theories in such a setting are time-sensitive. But often these time-sensitive theories only work under unrealistic assumptions about time. For example, in Sect. 3, we saw that to evaluate outcomes using the standard version of the ‘expansionist’ approach (from Vallentyne and Kagan, 1997; Arntzenius, 2014; Wilkinson, 2021b), we need standard Euclidean distance over four dimensions to be absolute and observer-independent. But it isn’t. So that approach cannot make any judgements at all. Even if we let that measure depend on the velocity of the observer, this approach leads to an absurd form of moral relativism—the correct judgement may differ if you change your speed enough.
Similar problems can be demonstrated for other theories—the proposals of Vallentyne (1993), Bostrom (2011, p. 16), and Jonsson and Voorneveld (2018) all face analogous problems, arising in analogous cases. So it seems we must reject all such proposals; it seems we must reject aggregative moral theories entirely.
But, as I’ve demonstrated, this problem can be overcome. With careful consideration of the geometry of spacetime, we can modify aggregative theories to still deliver judgements, and plausible ones at that, even in a relativistic universe. We can even do so in a universe in which spacetime is curved (depending, perhaps, on the exact nature of that curvature). We can still compare outcomes based on their total aggregate of value, even under the demands of a universe as peculiar as ours.
Notes
These include all theories that endorse a total utilitarian, total prioritarian, or critical level view of value, regardless of what other considerations those theories might recognise.
This is implied by the widely accepted flat-\(\lambda\) model of cosmology (see Wald, 1983; de Simone et al., 2010; Carroll, 2020, for discussion). It is also implied by the inflationary view (see Guth, 2007; Garriga and Vilenkin, 2001). But, by the latter theory, the universe as a whole may have infinite volume but only a finite volume of it within our causal future. If so, it may be physically impossible to cause changes in value at infinitely many different locations, and so the problems raised below may not arise. (But they may still arise if we adopt an evidential decision theory for moral decision-making—see MacAskill et al. (2021).)
Specifically, we will have a countably infinite number of them. Why? Because they are each positioned in a four-dimensional spacetime. They’ll also each occupy some (exclusive) finite region of spacetime—e.g., for a human brain to experience some amount of pleasure, it requires some non-zero spatial volume and some non-zero, finite duration. So we can only fit a countably infinite number of those token events into the world.
For readers unfamiliar with special relativity and seeking more explanation than I give here, I recommend Resnick (1979).
Despite the relativistic nature of spacetime, at least some points are observed as occurring in our future (or our past) no matter our velocity: those within our future (past) lightcone. That is our causal future (past).
This is somewhat controversial as, under evidential decision theory, we may often need to compare lotteries containing outcomes that differ in some past events. But this controversy is avoided if we are simply comparing the outcomes of our actions ex post, as I do here.
Possible in what sense? This could be the set of all epistemically possible worlds, or metaphysically possible worlds, or logically possible worlds. What follows can be read in terms of any of these.
Transitivity of moral betterness has its critics, e.g., Temkin (2014). It has also received compelling defences from, e.g., Broome (2004); Nebel (2018); Dreier (2019). I find it overwhelmingly plausible and, in keeping with the infinite aggregation literature to date, will assume without argument that it holds.
This aggregate may be the total sum of all instances of value, represented on a cardinal scale. Or it may be some other mathematical object which represents some combination of the values of all individual events. For example, the method described in Sect. 3 represents total value as a set of functions.
Impartiality here can be interpreted in any of several senses: 1) that \(\succcurlyeq\) must be a qualitative relation; 2) that \(\succcurlyeq\) must be a qualitative internal relation, and so entirely independent of the identities of which persons obtain value; 3) that, in addition to (1) and (2), \(\succcurlyeq\) must be invariant under any changes in some chosen class of qualitative properties of the persons obtaining value (e.g., their positions in space and time). I take \(\succcurlyeq\) as a qualitative internal relation but not independent of where persons are positioned in space and time. For discussion of whether this counts as impartial, see Wilkinson (2021a,2021b, §3).
Alternatively, we could associate each event with a region of points. This is compatible with what follows, so long as we replace the value function \(V_i({\textbf {x}})\) with a value density function \(v_i({\textbf {x}})\) and sum value over a region using a (Lebesgue) integral rather than a discrete sum.
Note that I do not rely on such points having essential properties (as under spacetime substantivalism)—points may just be artefacts of the relational properties of physical events. Nor am I committed to a particular view on whether such points are identical across worlds or merely counterparts—nothing below hangs on this.
This relation sometimes cannot give unique counterparts when outcomes differ in their spatiotemporal structure. More on this in Sect. 7.
This example hails from Vallentyne and Kagan (1997, p. 15).
Wilkinson (2021b) demonstrates several problems for SE, and proposes that we instead adopt the slightly stronger SE2.
SE2: Let \(W_a\) and \(W_b\) be worlds with the same spacetime points. For any starting point \({\textbf {p}}\), let \(\{r_1,r_2,r_3,...\}\) be the strictly increasing sequence of distances between \({\textbf {p}}\) and each \({\textbf {x}}\) such that \(V_a ({\textbf {x}}) - V_b ({\textbf {x}}) \ne 0\).
Then \(W_a\succ W_b\) if the following sum diverges unconditionally to \(+\infty\).
$$\begin{aligned} \lim _{r \rightarrow \infty } \sum _{i=1}^{r} (r_{i+1} - r_i) \sum _{\{{\textbf {x}}\, | \, d({\textbf {x}},{\textbf {p}})\le r\}} \Big ( V_a({\textbf {x}})-V_b({\textbf {x}}) \Big ) \end{aligned}$$And \(W_a \simeq W_b\) if the sum is bounded both above and below.
The problems and solutions described below apply in much the same way to both SE and SE2. For simplicity, I focus on the former.
We use different units for spatial distance (e.g., metres) and time (e.g., seconds), so how should we weigh these against each other when summing \(\Delta x^2\) and \(\Delta t^2\)? We could select any weighting we like but, fortunately, all possible weightings produce the same results in the examples below. (See the next footnote.) For simplicity of notation, I will weigh the two quantities such that 1 metre is equivalent to \(\frac{1\text { metre}}{c}\) seconds, where c is the speed of light in a vacuum in metres per second.
We might instead adopt any distance metric which satisfies \(d^p=|\frac{\Delta x}{a}|^p+|\frac{\Delta y}{a}|^p+|\frac{\Delta z}{a}|^p+|\frac{\Delta t}{b}|^p\), for some real p, a, b. But alternative values of p, a, and b would give us regions of more arbitrary shape. And they wouldn’t make any difference to problems we encounter in the next section so, for brevity’s sake, I will ignore them (see Wilkinson, 2021b, p. 19 for further discussion).
This is the condition of Finite Anonymity (over points in time and space) which is a common desideratum in the literature (e.g. Lauwers, 2010).
This is the world given by value function \(V_{\text {m}-\text {s}}({\textbf {x}})=V_\text {moving}({\textbf {x}})-V_\text {stationary}({\textbf {x}})\).
This modification faces a further problem. In practice, agents are often accelerating. If we allowed the verdicts of SE to be relative to not just the velocity but also the acceleration of an agent, the regions we obtain (such as those in Fig. 10) would no longer strictly contain one another—they would only partially overlap. Nor would they eventually cover all of spacetime, so SE would ignore value in some parts of the world!
Unlike d, s sometimes takes on imaginary values (whenever \(\Delta t > \Delta x\)). So \(|s^2|\) serves as the better replacement for d.
Why not just accept that worlds like this are exotic enough that we need not compare them? My main reason is that I suspect that, as argued in Wilkinson (n.d.(a)), almost every practical moral decision we face will resemble this case—the available outcomes will differ by infinite or undefined value over any region of our future lightcone that has infinite volume.
There are two notions of volume we might use here. The first is standard Euclidean volume, extended to four dimensions—a region with constant spatial volume V and duration in time t simply has 4-dimensional volume \(V\times t\). The alternative is ‘Riemannian volume’, which is generated from the metric s. Fortunately, in flat spacetime, the Riemannian volume of any given region will simply be \(-1\) times its Euclidean volume. So, if one is finite, so will be the other. And, given that Riemannian volume is the same for all observers, so will be the Euclidean volume.
The Euclidean volume of the region of all points within \(|s^2|=k\) of \({\textbf {p}}\) is given by:
$$\begin{aligned} \text {volume}= \int _{-\infty }^{+\infty } \frac{4\pi }{3}\Delta x^3 dt \\ = 2 \int _{0}^{1} \frac{4\pi }{3}\sqrt{t^2+k}^3 dt+2 \int _{1}^{+\infty } \frac{4\pi }{3}\left( \sqrt{t^2+k}^3-\sqrt{t^2-k}^3\right) dt \end{aligned}$$One benign exception is this. Suppose a person lives a life of infinite duration, containing infinite value. If we treat their entire life as a single event and associate it with a single point, then any region containing that point will contain infinite value, even if the region has only finite volume.
But this exception only arises due to the simplicity of how I have so far modelled the world. Lives need not be treated as single events; we could instead decompose them into smaller events. Nor must we associate events with discrete points in spacetime, rather than with the entire densely-packed regions of spacetime they occupy. (See Footnote 12.)
This can be shown in general. Let \({\textbf {p}}\) and \({\textbf {a}}\) (the position of the agent) be any two points such that \({\textbf {p}}\) is in \({\textbf {a}}\)’s past lightcone. (We can assume that both points have the same spatial position since there will always be some velocity such that, for observers travelling at that velocity, they are at the same spatial position.) Take any value of \(s^\prime\) such that \({\textbf {a}}\) is proper time less than \(s^\prime\) from \({\textbf {p}}\). And take the region of points in \({\textbf {p}}\)’s future lightcone that are proper time exactly \(s^\prime\) from \({\textbf {p}}\), corresponding to the curve given by \(s({\textbf {x}},{\textbf {p}})=s^\prime\). This region—call it R—is asymptotic to the edge of \({\textbf {p}}\)’s future lightcone (given by \(s({\textbf {x}},{\textbf {p}})=0\)). So we can take any ray starting at \({\textbf {a}}\) along the edge of its future lightcone, which will be parallel to some ray along the edge of \({\textbf {p}}\)’s future lightcone, and the ray will intersect R within finite time. The same goes for every ray from \({\textbf {a}}\) along the edge of its future lightcone so, by symmetry, the edge of \({\textbf {a}}\)’s future lightcone will intersect R in a sphere. As a result, the region bordered by the edge of \({\textbf {a}}\)’s future lightcone and R will be compact and have finite Riemannian volume (see Footnote 26). I thank an anonymous reviewer for suggesting this proof.
Strictly speaking, for \({\textbf {p}}\) not centred between the two sequences, each valuable event would not immediately be cancelled out by the corresponding event in the other sequence—the cumulative sum would still deviate from 0 (though for shorter and shorter intervals). So SE would still fail to say that \(W_{\text {right}}\) and \(W_{\text {left}}\) are equally good. But that is no great problem—the strengthened principle SE2 (from Wilkinson, 2021b) deals neatly with situations like this and judges the worlds as equally good. (See Footnote 16.)
This definition of RSE generates a sometimes intransitive \(\succcurlyeq\) relation (see Footnote 31 of Wilkinson, 2021b). But this is easily remedied, by modifying RSE in line with Wilkinson’s (ibid.: 30) later proposal (see Footnote 16). To avoid complicating RSE even further, without much gain, I will stick with the simpler definition used here.
There are some points we might choose that give an infinite value at every single stage of the sum: those precisely in line with either of the two sequences of value (but not both). This is why RSE specifies that starting points are only allowable if they give finite sums.
By assumption, this body has no electric charge nor angular momentum, and the cosmological constant is 0.
The Schwarzschild metric \(g^\prime\) is given by the equation(Schwarzschild, 1916):
$$\begin{aligned} g^\prime =\frac{r}{r-k}dr^2+r^2 d\theta ^2+r^2 \sin ^2 \theta d\phi ^2 - (1-\frac{k}{r})dt^2 \end{aligned}$$Here, spatial coordinates x, y, and z are replaced with polar spherical coordinates r, \(\theta\), and \(\phi\). And \(\Delta r\), \(\Delta t\), and so on are replaced by dr and so on, because \(g^\prime\) only gives the rate of change of the measure at each point—since curvature varies across spacetime, any equation in terms of \(\Delta t\) will vary as well. Given this, to obtain the distance between two points, we need to take the integral of \(g^\prime\) along a straight line between the points, and take the lowest such value—call it g.
This can be shown by a method similar to, but more complicated than, that of Footnote 28 above.
A full discussion of each of these spacetimes is beyond the scope of this paper, but I would refer interested readers to Carroll (2004) for detailed descriptions of each.
I suspect that this strategy will not always work in Gödel spacetime or other spacetimes that involve closed timelike curves. But these seem exotic enough to set aside for present purposes.
References
Arntzenius, F. (2014). Utilitarianism, decision theory and eternity. Philosophical Perspectives, 28(1), 31–58.
Arrow, K. (1999). Discounting, morality, and gaming. Discounting and Intergenerational Equity (pp. 13–21). Cambridge: Cambridge University Press.
Askell, A. (2019). Pareto principles in infinite ethics. In PhD dissertation, New York University.
Bostrom, N. (2011). Infinite ethics. Analysis and Metaphysics, 10(2011), 9–59.
Broome, J. (2004). Weighing lives. Oxford: Oxford University Press.
Cain, J. (1995). Infinite utility. Australasian Journal of Philosophy, 1995, 401–4.
Carroll, S. M. (2020). Why Boltzmann brains are bad. In S. Dasgupta, R. Dotan, & B. Weslake (Eds.), Current controversies in philosophy of science. (pp.7–20) Taylor & Francis.
Carroll, S. (2004). Spacetime and geometry: An introduction to general relativity. San Francisco: Addison Wesley.
Clark, M., (n.d). Infinite ethics, intrinsic value and the Pareto principle. Unpublished manuscript.
Cohn, E. (1904). Zur elektrodynamik bewegter systeme ii [On the electrodynamics of moving systems ii]. Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften, 43(2), 1404–16.
Comstock, D. (1910). The principle of relativity. Science, 31(803), 767–72.
de Simone, A., Guth, A., Linde, A., Noorbala, M., Salem, M., & Vilenkin, A. (2010). Boltzmann brains and the scale-factor cutoff measure of the multiverse. Physical Review D, 82(6), 063520.
Dreier, J. (2019). World-centered value. In C. Seidel (Ed.), Consequentialism: New Directions and Problems (pp. 31–50). Oxford: Oxford University Press.
Einstein, A. (1905). Zur elektrodynamik bewegter körper [On the electrodynamics of moving bodies]. Annalen der Physik, 322(10), 891–921.
Garriga, J., & Vilenkin, A. (2001). Many worlds in one. Physical Review D, 64(4), 043511.
Guth, A. (2007). Eternal inflation and its implications. Journal of Physics A: Mathematical and Theoretical, 40(25), 6811.
Hafele, J., & Keating, R. (1972). Around-the-world atomic clocks: Observed relativistic time gains. Science, 177(4044), 168–70.
Jonsson, A., & Peterson, M. (2020). Consequentialism in infinite worlds. Analysis, 80(2), 240–8.
Jonsson, A., & Voorneveld, M. (2018). The limit of discounted utilitarianism. Theoretical Economics, 13(1), 19–37.
Koopmans, T. (1972). Representation of preference orderings over time. Decision & Organization,57.
Lauwers, L. (2010). Ordering infinite utility streams comes at the cost of a non-Ramsey set. Journal of Mathematical Economics, 46(1), 32–7.
MacAskill, W., Vallinder, A., Shulman, C., Österheld, C., & Treutlein, J. (2021). The evidentialist’s wager. Journal of Philosophy, 118(6), 320–42.
Michelson, A. A., & Morley, E. W. (1887). On the relative motion of the earth and of the luminiferous ether. Sidereal Messenger, 6(1887), 306–10.
Nebel, J. (2018). The good, the bad, and the transitivity of better than. Noûs, 52(4), 874–99.
Nelson, M. (1991). Utilitarian eschatology. American Philosophical Quarterly, 28(4), 339–47.
Resnick, R. (1979). Introduction to Special Relativity. New York: Wiley.
Schwarzschild, K. (1916). Uber das gravitationsfeld eines massenpunktes nach der Einstein’schen theorie [On the gravitational field of a mass point according to Einstein’s theory]. Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften, 1916, 189–96.
Temkin, L. (2014). Rethinking the Good. Oxford: Oxford University Press.
Temkin, L. (2015). Rationality with respect to people, places, and times. Canadian Journal of Philosophy, 45(5–6), 576–608.
Vallentyne, P. (1993). Utilitarianism and infinite utility. Australasian Journal of Philosophy, 71(2), 212–7.
Vallentyne, P., & Kagan, S. (1997). Infinite value and finitely additive value theory. Journal of Philosophy, 94(1), 5–26.
Wald, R. (1983). Asymptotic behavior of homogeneous cosmological models in the presence of a positive cosmological constant. Physical Review D, 28(8), 2118.
Wilkinson, H. (2021a). Infinite Aggregation. PhD dissertation, Australian National University.
Wilkinson, H. (n.d.(a)). Chaos, ad infinitum. Unpublished manuscript.
Wilkinson, H. (2021). Infinite aggregation: Expanded addition. Philosophical Studies, 178(6), 1917–49.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Were it not for the assistance of many wonderful colleagues, this paper would hold far less value (no matter the velocity at which it is read). For detailed comments on various drafts, I thank Al Hájek, Brian Hedden, Dominic Hyde, Chris Meacham, H. Orri Stefánsson, Christian Tarsney, Teru Thomas, and three anonymous reviewers. For helpful discussion, I thank Heather Browning, Frank Jackson, Andreas Mogensen, Anders Sandberg, Toby Solomon, Larry Temkin, Dayal Wickramasinghe, and Timothy L. Williamson, as well as audiences at the Australian National University, Vilnius University, the 2017 Australasian Association of Philosophy Conference, the 2018 International Economic Philosophy Conference, and the 2018 conference of the International Society for Utilitarian Studies. And, for their financial support, I thank the Forethought Foundation for Global Priorities Research, the Australian-American Fulbright Commission, and the Australian Research Training Program.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Wilkinson, H. Aggregation in an Infinite, Relativistic Universe. Erkenn (2022). https://doi.org/10.1007/s10670-022-00650-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10670-022-00650-7