Abstract
This paper focuses on radical pooling, or the question of how to aggregate credences when there is a fundamental disagreement about which is the relevant logical space for inquiry. The solution advanced is based on the notion of consensus as common ground (Levi in Synthese 62:3–11, 1985), where agents can find it by suspending judgment on logical possibilities. This is exemplified with cases of scientific revolution. On a formal level, the proposal uses algebraic joins and imprecise probabilities; which is shown to be compatible with the principles of marginalization, rigidity, reverse bayesianism, and minimum divergence commonly endorsed in these contexts. Furthermore, I extend results from previous work by (Stewart & Ojea Quintana in J Philos Logic 47:17–45, 2016; Erkenntnis 83:369–389, 2018) to show that pooling sets of imprecise probabilities can satisfy important pooling axioms.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
There are various candidate interpretations of an opinion pool in the epistemological literature: a rational consensus; a compromise adopted for the purpose of group decision making; the opinion a group member adopts after learning the opinion of her ‘epistemic peers’; the opinion an external agent adopts upon being informed of the n expert opinions, etc. (Genest & Zidek, 1986; Wagner, 2009). The interpretative line endorsed in this essay is the first one: pooling considered as a form of consensus for the sake of the argument. Following the literature on pooling, agents’ attitudes are modeled by probability functions over an algebra of events. Much of the literature (Dietrich & List, 2014; Genest & Zidek, 1986; Wagner, 2009) focused on a constrained form of disagreement among the parties, namely when they disagree solely on the degree of belief assigned to events on a shared outcome and event space. The purpose of this paper is to generalize the question of pooling to cover cases when agents disagree radically; not only on their probabilistic judgments but also on the logical space over which those judgments are made.
Imprecise probabilities allow for an interesting and philosophically well-motivated account of consensus (Levi, 1985; Seidenfeld et al., 1989): consensus as common ground. Consider first the case of full or plain belief. (Konieczny & Pino Pérez, 2011) provides a good survey of the literature on belief merging of propositional bases. For each of the propositions in the doxastic space of possibilities, agents are said to have three attitudes: acceptance, rejection, or suspension of judgment. At the outset of inquiry, inquirers may seek consensus as shared agreement in their beliefs. This could be achieved by retaining whatever beliefs are accepted by all parties and suspending judgment on those that are not shared. Inquiry starting from the consensus view can proceed without begging questions against parties in the consensus, allowing various hypotheses of concern to receive a fair hearing. Such a consensus constitutes a neutral starting point for subsequent inquiry.
The idea that parties joining their efforts in inquiry or decision making should restrict themselves to their shared agreements can be extended to judgments of probability in the imprecise probabilities setting. In this setting agents credal attitudes are modeled by sets of probabilities \(\{{\varvec{p}}_i\}_{i\in I}\). To suspend judgment among some number of probability distributions is to use them for the purposes of inference and decision making. If the parties seeking consensus all agree that a distribution \({\varvec{p}}\) is not permissible, then the consensus position reflects that agreement and rules it out. A set of probability functions represents the shared agreements among the group concerning which probability functions are permissible to use in inference and decision making. This avenue was explored by (Stewart & Ojea Quintana, 2016, 2018). The purpose of this essay is to extend this approach to the case of radical pooling.
In this setup, a well informed modeler or arbiter is given a group of agents who disagree radically, with each agent i having an event space, a \(\sigma\)-algebra of propositions \(<{\mathcal {A}}_i>\), and a distribution \(<{\varvec{p}}_i>\) on that. Their task is to aggregate or pool the information in those profiles in a way that reflects the consensus as common ground. In the disagreement literature (Elga, 2007), and in the pooling literature (Dietrich & List, 2014), it is usually assumed that agents agree on the event space, but not on the probability distribution. I here relax that assumption; agents can be in disagreement about the event space. Intuitively, the event space constitutes the logical space of propositions over which our agents have probabilistic attitudes.Footnote 1 Agents are said to disagree radically if their event spaces are different. Other forms of disagreement are non-radical. The task here is to find a consensus position among parties, a sort of pooling operation over the logical spaces and their credal attitudes towards them. Furthermore, this is a third person perspective project, which is distinct but related to the first person question of (un)awareness in epistemology. In cases of (un)awareness a single agent grows or contracts their set of possibilities to form a new set of possibilities. These types of belief changes have been explored by Bradley (2017), and more recently by Steele and Stefánsson (2021a) and Mahtani (2021) in the probabilistic case; by Cresto (2008) in an AGM-style belief revision, and within game theory in the literature by Fagin and Halpern (1987), Halpern (2001), Dekel et al. (1998), Modica and Rustichini (1999). Section 3 elaborates on the relations between the project here and issues of awareness growth.
The guiding idea defended here is that the common ground consensus involves a sort of suspension of judgment on what is logically possible. Similar to the case of plain belief, the common ground is strongest position that is weak enough to be compatible with everyone’s views, and therefore constitutes a good non-question begging starting point for inquiry.
The paper has six sections. The next section motivates the view with an example from the history of science. The third one presents the view of consensus as common ground in detail, acknowledges certain assumptions, justifies the third person perspective, and argues for taking the join of the algebras as the logical pool. Section 4 argues that (i) marginalization, (ii) rigidity and reverse bayesianism, and (iii) divergence lead to the adoption of imprecise probabilities when agents expand their probabilistic judgments to larger algebras. The following section extends results from previous work by (Stewart & Ojea Quintana, 2016, 2018) to show that pooling sets of imprecise probabilities can satisfy important pooling axioms. The final section is conclusive.
2 A Motivating Example
2.1 The Priestley-Lavoisier Debate
Finding consensus in the presence of radical disagreement resembles questions about (revolutionary) theory change in philosophy of science. Central to the revolutionary view of science advanced by (Kuhn, 1970; Thomas, 2000) and (Feyerabend, 1962) is the claim that language used in a field of science changes so radically during a revolution that the old language and the new one are not inter-translatable. More generally, they espoused the idea that in those situations opposing theories are incommensurable. Similarly, agents disagreeing about the logical space of possibilities over which they make their probabilistic judgments might share no common basis on which to measure their divergence.
The resemblance has its limits. Here pooling is about finding rational consensus between parties. But according to the mainstream reading of Kuhn, in scientific revolutions parties do not have a recourse to a common theoretical language, body of observational evidence, or methodological rules. Despite the differences, the analogy is helpful. I am here concerned with Kuhn’s taxonomic or conceptual incommesurability. During periods of scientific revolution, existing concepts are replaced with new concepts that are at odds with the old ones because they do not share the same “lexical taxonomy”, they cross-classify objects according to different sets of kinds.
In order to illustrate the kind of conceptual tool developed here, I will build on the Priestley-Lavoisier debate around Phlogiston Theory. I will present and formalize the debate in Bayesian terms, and articulate a kind of consensual resolution of the disagreement that does not pretend to be historically accurate of what happened, but that I hope the reader finds sensible.
Priestley advocated the Phlogiston Theory, which attempted to give an account of combustion. Its basic explanatory hypothesis (H) was that there is a substance which is emitted in combustion, namely phlogiston. For example, when a metal is heated, phlogiston is emitted, and the calx of the metal is obtained. Furthermore, the process is sometimes reversible. By heating the red calx of mercury, Priestley found that he could obtain the metal mercury, and a new kind of air which he called “dephlogisticated air”. In contrast, Lavoisier’s theory of combustion is akin to our modern theory.
Phlogiston theory (PT) | Modern Theory (MT) | ||
|---|---|---|---|
Input | Output | Input | Output |
Metal + air + heat | Calx of metal + phlogisticated air | Metal + air + heat | Metal oxide + air which is poor in oxygen |
Red calx (oxide) of mercury + heat | Mercury + dephlogisticated air | Oxide of mercury + heat | Mercury + oxygen |
It seems easy to attain consensus. After all, identifying “dephlogisticated air” with “oxygen” (and “calx of metal” with “metal oxide”) seems to provide a good mapping for these experiments. But not all experimental outcomes of dephlogisticated air correspond to experimental outcomes of oxygen, albeit some do. Phlogiston theory departs from the false presupposition (H) that there is a unique substance which is always emitted in combustion, and this premise contaminates its terminology and carving of the logical space. This is Kuhn’s and Feyerabend’s point, that terms of phlogiston theory are theory-laden: “phlogiston” refers to that which is emitted in all cases of combustion. For Lavoisier, H is false and therefore “phlogiston” fails to refer.
Although they recognize that Phlogiston Theory is incorrect, historians of science might want to explain it’s success and acknowledge some of their truths. But such a revolutionary theory change from Phlogiston Theory to Modern Theory seems to leave no room for continuity or consensus. Kitcher’s (1978) analysis of this case can save us here. Kitcher explains how Priestley’s use of “dephlogisticated air” is theory-laden. Priestley’s early utterances of the expression, driven by the hypothesis H, correspond to “the substance obtained by removing from air the substance which is emitted in combustion”. Those token expressions of “dephlogisticated air” corresponded to a set of referents different from posterior token expressions. Some of the later utterances, after his isolation yet misidentification of oxygen through the heating of a red calx (oxide) of mercury, correspond to “the gas obtained by heating the red calx of mercury”. Hence those tokens of “dephlogisticated air” refer to oxygen. Lavoisier found a way to interpret the different tokens Priestley used, and therefore carve the space in a more refined way. Furthermore, in so far as Lavoisier et al. used the term “oxygen” to refer to those tokens of “dephlogisticated air”, there was room for communication between theoretical rivals.
2.2 Representing the Debate and Finding Consensus
The problem of theory change is being reconceptualized here as one of radical disagreement. Two tasks remain in this introduction: to represent this case in the language of Bayesianism, and to articulate a resolution on the basis of consensus as common ground.
From the perspective of a well informed historian, Priestley and Lavoisier came to the table with different probabilistic attitudes \({\varvec{p}}_P, {\varvec{p}}_L\) and algebras of propositions \({\mathscr {A}}_P,{\mathscr {A}}_L\). In our example, driven by hypothesis H, Priestley can be reconstructed as partitioning his event space so that there is an event P that represents the proposition that the output of the experiment includes phlogisticated air; \(P=\{w_i: w_i\) s.t. the experiment results in the release of phlogiston into the air\(\}\). After heating of a red calx (oxide) of mercury, Priestley is represented as discovering a gas that had a great capacity for absorbing phlogiston, and called it “dephlogisticated air”; \(DP=\{w_i: w_i\) s.t. the experiment results in the removal of phlogiston from the air\(\}\). What matters is that propositions and events like P and DP were at the core of phlogiston theory. As such, both P and DP are taken to be basic, maximally specific, propositions in \({\mathscr {A}}_P\).Footnote 2
The difference, from our modeler’s perspective, is that Lavoisier’s logical carving \({\mathscr {A}}_L\) was more refined. Where Priestley saw a gas without phlogiston, Lavoisier sometimes saw oxygen, but not always. Lavoisier understood that “dephlogisticated air” was a misnomer. The proposition DP includes instances of oxygen release but also others. The proposition O that the outcome of the experiment is the release of oxygen entails but it is not entailed by DP, \(O\subset DP\). Given H, the absence of phlogiston in the air was at the core of the theory and DP was basic. By rejecting H, Lavoisier could refine the space. In other words, let \(DP=\{w_1,w_2\}\in {\mathscr {A}}_P\). If \(\{w_1\}\) corresponds to an instance with oxygen and \(\{w_2\}\) without, then \(\{w_1\},\{w_2\}\notin {\mathscr {A}}_P\). For Lavoisier, \(\{w_1\},\{w_2\}\in {\mathscr {A}}_L\), so that at least with respect to this issue he made more relevant distinctions.
Phlogiston Theory | Modern Theory | Consensus |
|---|---|---|
\(A_P\) | \({\mathscr {A}}_L\) | \({\mathscr {A}}_P\vee {\mathscr {A}}_L\) |
\(DP=\{w_1,w_2\}\in {\mathscr {A}}_P\) | \(\{w_1,w_2\}\in {\mathscr {A}}_L\) | \(\{w_1,w_2\}\in {\mathscr {A}}_P\vee {\mathscr {A}}_L\) |
\(O=\{w_1\}\not \in {\mathscr {A}}_P\) | \(\{w_1\}\in {\mathscr {A}}_L\) | \(\{w_1\}\in {\mathscr {A}}_P\vee {\mathscr {A}}_L\) |
One initial way of finding consensus would be for our modeler to represent consensus as the more refined logical space \({\mathscr {A}}_L\) on the grounds that logical refinement constitutes an epistemic improvement. But it is not in general true that a more refined space is an indication of epistemic improvement; including irrelevant distinctions can make a space more convoluted without any epistemic gain. Also, in many interesting circumstances it is not the case that one space is a refinement of the other.
In other words, Priestley may rationally reject Lavoisier’s logical space as the right one on the basis that it is more refined. What would then be a reasonable consensus? The adoption of an initial common ground with further investigation in the future. This means retreating to a position that is compatible with all of the individual positions, but that still contains the shared agreement. In the case of algebras, there is a formalism that captures this: the join, \({\mathscr {A}}_L\vee {\mathscr {A}}_P\), the coarsest algebra that is finer than those two. In detail, its the algebra \({\mathscr {A}}_*\) such that (i) \({\mathscr {A}}_L\subseteq {\mathscr {A}}_*\) and \({\mathscr {A}}_P\subseteq {\mathscr {A}}_*\), and (ii) for any \({\mathscr {A}}^*\) with \({\mathscr {A}}_L\subseteq {\mathscr {A}}^*\) and \({\mathscr {A}}_P\subseteq {\mathscr {A}}^*\), \({\mathscr {A}}_*\subseteq {\mathscr {A}}^*\). Since \({\mathscr {A}}_P\subset {\mathscr {A}}_L\), we have that \({\mathscr {A}}_L\vee {\mathscr {A}}_P={\mathscr {A}}_L\), so Priestley might be convinced to accept Lavoisier’s carving as an initial space, not because it is more refined, but because it constitutes a fair, non question begging, starting point.
The rest of the essay will be devoted to developing and generalizing this notion of consensus for all the relevant cases. Although it is clear that this is not how Lavoisier and Priestley actually resolved their disagreements, it is felicitous that the scientific community adopted \({\mathscr {A}}_L\).
3 Finding a Logical Common Ground
3.1 Consensus as Common Ground
For each agent \(i\in I\), we, the modelers, consider an agenda \({\mathscr {A}}_i\), the propositions an agent \(i\in I\) regards possible, and a probability function \({\varvec{p}}_i: {\mathscr {A}}_i \rightarrow [0,1]\) satisfying the Kolmogorov axioms. Propositions in \({\mathscr {A}}_i\) are the objects of credal and plain belief attitudes. In the plain belief case, consensus as common ground amounts to retaining all of the propositions that are accepted by all of the agents, and suspending judgment on any other proposition. In the probabilistic case, to suspend judgment among some number of distributions is to regard them permissible for the purposes of inference and decision making, and this is captured by a set representation, as studied by (Stewart & Ojea Quintana, 2016, 2018).
There is an important difference between the case of radical disagreement and that of probabilistic (or for that matter, full belief) disagreement. In the latter, there is agreement on which are the objects of the epistemic attitudes. In other words, there is agreement on which are the relevant propositions of concern, but there might be disagreement about what credal or full belief judgment to have on them. In contrast, in the case of radical disagreement, there is no consensus on what is the relevant set of propositions - i.e. the objects of epistemic attitudes. Or more seriously, there might not be agreement about the identity of propositions across logical spaces, following Mahtani (2021).
Part of Kitcher’s (1978) contribution in the debate about theory change was to point out that (provided we make certain assumptions about the references of terms) we can offer some continuity in cases of scientific revolution (Kuhn, 1970; Thomas, 2000, Feyerabend, 1962). A well-informed modeler or historian of science might want to explain the success of phlogiston theory, acknowledge some of their truths, and regard its advocates as rational; even in light of the fact that the theory proved to be false. The situation in our case is similar. In order to provide a consensus view we assume that a well-informed modeler can identify propositions across logical spaces; that some propositions share the same truth-conditions.
This assumption is somewhat warranted by the idea that our arbiter is trying to model rational consensus as common ground. Without assuming any identities of possibilities across parties there is not enough room for any form of comparison, much less finding common ground. Arguably, there can be cases like that.Footnote 3 That does not preclude other forms of consensus to be attainable without that assumption. Consensus can be reached through revolution, conversion, voting, bargaining, or some other psychological, institutional, social, or political process. But that is not finding a common ground, and in many cases it might not be rational consensus. It is on the basis of the recognition of identities across spaces that finding common ground is at all possible. This is the main reason the present proposal is that of a third person well-informed modeler trying to find consensus, in contrast first person individuals finding consensus among themselves. Individuals might fail or be unwilling to cross-identify propositions.
Nevertheless, in most of the scenarios we care about, individual agents agree on the meaning of at least some propositions. Suppose two agents share a propositional variable \(Q_j\) and agree on its truth conditions. They can begin by agreeing on the same set of possible worlds to assign a reference to it. In our semi-formal example of the Priestley-Lavoisier debate, and in so far as Lavoisier was more refined than Priestley, they then shared the meaning of a significant part of the terminology (but not all). In natural languages this also occurs frequently. Sentences involving general nouns like ‘X is a tenant’ can be recognized as having the same truth-conditions, although different agents might be aware of different ways in which it can be made true. In other words, one agent could point to a way the world might be, which the other agent was not aware of, and they would both agree whether that possibility makes the proposition true or not.
This speaks to the connection between the current third person account of consensus with the first person accounts of awareness. In so far as there is agreement about the meaning of certain propositions between parties, the approach presented here can be proved useful. Furthermore, a well-informed modeler can be viewed as an arbiter or judge mediating disagreement between parties. By first retreating to a position that is non-question begging, this ideal arbiter can later settle the dispute through inquiry. Since the common ground is not at stake, and if the rules of inquiry are agreed upon parties, the disagreement can be in principle resolved. In cases of awareness growth, a single individual becomes aware of new possibilities, and the guiding question is whether there are rational rules for incorporating them to their current logical space. In some cases, but arguably not all, this process can be represented as a disagreement between temporal slices of a single individual. In some other cases, as a disagreement between alternative updates after awareness growth. In addition, a well-informed and neutral (third person) arbiter serves as a regulative idea for a rational first person individual. In the face of disagreement with someone else, or in general confronted with an alternative carving of the logical space, our agent can ask themselves what would an ideal neutral arbiter do. The thought of having an ideal neutral arbiter working as a regulative concept famously appears in Adam Smith’s (Smith & Haakonssen, 2002) notion of an impartial spectator, although in this case it concerns the appropriateness of actions and behaviors, and not what is the relevant logical carving.
3.2 Joins as Common Ground
Let us assume then that we are given a set of agents each with their respective language \({\mathcal {L}}_i\), corresponding to their respective algebras \({\mathscr {A}}_i\) in a way that some of the terminology shared in the languages has the same truth-conditions. Furthermore, each agent has a subjective probability distribution \({\varvec{p}}_i\) on their algebra \({\mathscr {A}}_i\), but that will be the subject of the next section. The guiding goal in this section is to provide a common ground logical space.
The suggestion here is to take the join of the \({\mathscr {A}}_i\). The join of a set of algebras is the coarsest algebra that is finer than all of the individual ones in the set.Footnote 4 By taking the join as the shared event space agents are precisely following the heuristic defended here: taking as common ground the coarsest space that is compatible with everyone’s original position. Taking any reduced algebra would imply excluding events deemed possible by some agent. Taking any finer algebra would be rationally unjustified.
The analogy with full belief is helpful here. Following the semantic interpretation of Belief Revision Logic AGM, the belief state of an agent can be identified with the (logical clousure) of the strongest proposition P in the algebra that is believed by that agent. Given two agents with belief states \(P_1\) and \(P_2\), finding a common ground means contracting to a state \(P^*\) that is weaker than \(P_1\) and \(P_2\); this is (i) \(P_1\subseteq P^*\) and \(P_2\subseteq P^*\). But ideally, \(P^*\) should also be as strong as possible to preserve the largest common ground, hence for any \(P_*\) satisfying (i) it should be the case that \(P^*\subseteq P_*\). This is precisely the join. In this analogy, having a stand about which propositions are true is akin to having a stand about which event space is the relevant, they are both intentional attitudes about how the world is. Before, a belief state \(P^*\) was stronger than another belief state \(P_*\) just in case \(P^*\subseteq P_*\). In our jargon here, an algebra \({\mathscr {A}}_*\) is stronger than another algebra \({\mathscr {A}}^*\) just in case \({\mathscr {A}}_*\subseteq {\mathscr {A}}^*\). Moving from \({\mathscr {A}}_*\) to \({\mathscr {A}}^*\) is an epistemic weakening, since it involves bringing into consideration more possibilities as relevant. Finally, finding a common ground is analogous in both cases: fall back to the strongest position compatible with the parties.
Furthermore, the proposed solution aligns with the scientific consensus that resulted from the Priestley-Lavoisier dispute. By rejecting the hypothesis phlogiston is released in combustion, Lavoisier studied the properties of the gas resulting from heating a red calx of (oxide of) mercury as properties of a new substance, oxygen. Priestley studied them as properties of a gas depleted from phlogiston and started with a coarser algebra. But then the join \({\mathscr {A}}_P\vee {\mathscr {A}}_L\) is just \({\mathscr {A}}_L\) and the proposed common ground is precisely Lavoisier’s carving. In this we follow Steele and Stefánsson (2021a) and Mahtani (2021), where awareness growth by refinement corresponds to comparing two algebras, one more refined than the other. But comparing one algebra to a more refined one is just one form algebraic disagreement, it is also possible for i to be more refined in some respects, but more coarse in others.Footnote 5
Nothing precludes the alternative that all of the parties involved considered possibilities that none of the other did. For example, for two agents A and B we could reasonably have \(\Omega ^*=\Omega _A=\Omega _B=\{w_1,w_2,w_3,w_4\}\), \({\mathscr {A}}_A\) is generated by \(\{\{w_1\},\{w_2\},\{w_3,w_4\}\}\), while \({\mathscr {A}}_B\) is generated by \(\{\{w_1,w_2\},\{w_3\},\{w_4\}\}\). Here A distinguishes between \(\{w_1\}\) and \(\{w_2\}\) while B does not, and conversely for \(\{w_3\}\) and \(\{w_4\}\). Importantly, the consensus position acknowledges as doxastically possible events that no one considered possible before. \({\mathscr {A}}_A\vee {\mathscr {A}}_B ={\mathscr {A}}^*={\mathscr {P}}(\Omega ^*)\), and in particular \(\{w_2,w_3\}\in {\mathscr {A}}^*\) but \(\{w_2,w_3\}\notin {\mathscr {A}}_A\) and \(\{w_2,w_3\}\notin {\mathscr {A}}_B\).Footnote 6 I take this to be a positive feature of the proposal. It shows that seeking consensus in one of its weakest forms, as common ground and at the outset of inquiry, already can lead to conceptual refinement and innovation.
4 Radical Pooling and Imprecision
Recall that in this setup a well informed modeler or historian of science is given a group of agents who disagree radically (like Priestley and Lavoisier did), with each agent i having an event space \(<{\mathcal {A}}_i>\), and a distribution \(<{\varvec{p}}_i>\) on that. The arbiter’s task is to aggregate or pool the information in those profiles in a way that reflects the consensus as common ground. The aggregation procedure in the previous section dealt with the \(\sigma\)-algebra of propositions \(<{\mathcal {A}}_i>\) by taking the join. This section will deal with the probabilities \(<{\varvec{p}}_i>\) by using imprecise pooling, interpreted here as a form of rational consensus.
4.1 A case for imprecision
The moves so far were the following:

How should the agent extend their subjective probability, originally defined over \({\mathscr {A}}_i\) to the new common ground logical space \({\mathscr {A}}^*\)?
The rest of this section will provide arguments for imprecision. I will show that imprecision is compatible with principles of rationality that some argue can be appealed to in these types of cases: marginalization, rigidity, reverse bayesianism, and divergence measures. The present account remains in principle neutral with respect to the issue whether those constraints are rationally required. The purpose is to show how coherent imprecision is with other principles.
The use of imprecise probabilities in the context of disagreement has well known downsides. For example, as (Elkin and Wheeler, 2018) explain, taking convex sets of probability functions may lead to failures of probabilistic independence. Take probability functions \(p_1\) and \(p_2\) such that \(p_1(A\cap B)=p_1(A)p_1(B)\) and \(p_2(A\cap B)=p_2(A)p_2(B)\). A convex combination \(p^*=\alpha p_1 + (1-\alpha )p_2\) with \(0\lneq \alpha \lneq 1\), might fail to preserve independence: \(p^*(A\cap B)\ne p^*(A)p^*(B)\). A defense against this objection was given in Stewart and Ojea Quintana (2016). Furthermore, the source of imprecision here is not due to pooling but due to awareness growth. Agents will extend their probabilities to posterior algebras that are in general richer than the prior ones. As the discussion on rigidity will reveal, in this case judgments of independence are preserved at this stage.
The proposal endorsed here will be to extend precise probabilities defined on \({\mathscr {A}}_i\) to sets of probabilities defined on \({\mathscr {A}}^*\) by taking natural extensions. This is an old and familiar move in the Imprecise Pooling literature. This is usually done in the more general language of gambles and previsions. (De Cooman & Troffaes, 2004) present a helpful introduction, plus some interesting results on prevision aggregation. Troffaes & Cooman’s book (Troffaes & De Cooman, 2014) develops extensively the theory of (lower) previsions. It is well known since de Finetti that in general (except degenerate cases) a linear prevision (i.e. a precise probability) on a strict subset of the set of all gambles has no unique natural extension to the larger set: natural extensions are generally imprecise.
The contribution for the rest of the section is to motivate the use of natural extensions on the basis of principles that have been endorsed in the unawareness literature, bridging imprecision and unawareness. Furthermore, natural extensions are usually interpreted as the most conservative correction of the original prevision to a coherent one over the larger set of gambles. This suits well the dialectic endorsed here; when expanding to new algebras agents should be as conservative as they can while still trying to accommodate for the new information.
4.2 Marginalization Leads to Imprecision
Given three \(\sigma\)-algebras \({\mathcal {A}}_1\subseteq {\mathcal {A}}_2\subseteq {\mathcal {A}}_3\) a probability function \({\varvec{p}}\) defined over \({\mathcal {A}}_2\), the marginalization of \({\varvec{p}}\) on \({\mathcal {A}}_1\) (\({\varvec{p}}\restriction _{{\mathcal {A}}_1}\)) is the unique \({\varvec{p}}_*\) defined over \({\mathcal {A}}_1\) such that for all elements \(E\in {\mathcal {A}}_1\), \({\varvec{p}}(E)={\varvec{p}}_*(E)\).Footnote 7 Conversely, we can look at all of the probabilities \({\varvec{p}}^*\) defined on \({\mathcal {A}}_3\) such that restricted or marginalized to \({\mathcal {A}}_2\) is equal to \({\varvec{p}}\), i.e. \({\varvec{p}}^*\restriction _{{\mathcal {A}}_2}={\varvec{p}}\). That is what we do here.
In our setup, each probability measure \({\varvec{p}}_i\) is defined over \({\mathscr {A}}_i\), and the task is to extend that measure to \({\mathscr {A}}^*\). We will use imprecise probabilities. In particular, there are several admissible extensions of \({\varvec{p}}_i\) to \({\mathscr {A}}^*\) and there is no reason for i to prefer one over the other. In our notation, \({\varvec{p}}_i^*\) refers to distributions defined over \({\mathscr {A}}^*\), the richer algebra.
So \({\mathbb {P}}_i\) is the set of all probability measures that extend \({\varvec{p}}_i\) - i.e. all the \({\varvec{p}}_i^*\) defined over \({\mathscr {A}}^*\) such that restricted to \({\mathscr {A}}_i\) gives back \({\varvec{p}}_i\). More precisely: \({\varvec{p}}_i^*\restriction _{{\mathscr {A}}_i}={\varvec{p}}_i\) if and only if for each \(H\in {\mathscr {A}}_i\), \({\varvec{p}}_i^*(H)={\varvec{p}}_i(H)\).Footnote 8
Proposition 1
\({\mathbb {P}}_i\) is convex for all i.
New events will have non-null probability weight only if they have old events as subsets. Completely new events will have null probabilistic weight. In the imagined scenario, Priestley would assign zero probability to Lavoisier’s alleged observation.
4.3 Rigidity (or Reverse Bayesianism) and Conservatism Lead to Imprecision
A standard, yet contested, principle of Bayesian epistemology is rigidity: conditional probabilities are kept fixed throughout updating. Let \({\varvec{p}}(\cdot )\) be defined over some algebra \({\mathscr {A}}\) of events be a representation of some agent’s (coherent) credal state. Suppose now the agent learns an event E and updates their credal state to \({\varvec{q}}(\cdot )={\varvec{p}}(\cdot |E)\) according to Bayesian standards. For all events \(H\in {\mathscr {A}}\) we have:
-
Rigidity: \({\varvec{q}}(H|E)={\varvec{p}}(H|E\cap E)={\varvec{p}}(H|E)\)
Jeffrey (1990) famously argued against this form of rigidity. I do not intend to discuss this form of rigidity, but one relevant for the radical disagreement case.
Intuitions are not clear on whether rigidity is an acceptable rationality constraints in the context of awareness growth. Nevertheless, there are defenses of rigidity-like principles in the literature, in particular in (Bradley, 2017) and Steele and Stefánsson (2021a). As explained before, although the approach defended here sympathizes with rigidity, the central purpose is to show that it is compatible with it.
The idea behind this principle is that we should extend our relational attitudes to the new set in such a way as to conserve all prior relational credences. Becoming aware of the new events should not affect the relative credibility of previously considered events. For all \(E,H\in {\mathscr {A}}_i\) with \({\varvec{p}}_i(E)\ne 0\ne {\varvec{p}}_i^*(E)\):
-
Strong Radical Rigidity [SRR]: \({\varvec{p}}_i^*(H|E)={\varvec{p}}_i(H|E)\)
SRR can arguably be regarded as too strong of a requirement. If so, consider the principle that demands that the strengthened conditional probabilities of old events given the old set of possibilities should be kept the same. Namely, for all \(H\in {\mathscr {A}}_i\):
-
Weak Radical Rigidity [WRR]: \({\varvec{p}}_i^*(H|\Omega _i)={\varvec{p}}_i(H|\Omega _i)={\varvec{p}}_i(H)\)
The following observation holds trivially, provided that \({\varvec{p}}^*_i(\Omega _i)\ne 0\).
Proposition 2
Strong Radical Rigidity and Weak Radical Rigidity are equivalent.
Related with rigidity is the principle of Reverse Bayesianism introduced by (Karni et al., 2018; Karni & Viero, 2011). More precisely, they extend the Savage framework by introducing extra axioms regulating awareness and they show that the collection of those axioms admit an expected utility representation in which the probability at hand obeys reverse bayesianism. A natural way to translate such property from the Savage framework to the present is the following:
-
Reverse Bayesianism [RB]: For all \(A, B\in {\mathscr {A}}_i\) non-null with respect to \({\varvec{p}}_i\) and \({\varvec{p}}_i^*\):
$$\begin{aligned} \frac{{\varvec{p}}_i(A)}{{\varvec{p}}_i(B)}=\frac{{\varvec{p}}_i^*(A)}{{\varvec{p}}_i^*(B)} \end{aligned}$$
The property states that the likelihood ratios of events in the original space remains intact after the expansion to the new space. Importantly, (Karni et al., 2018; Karni & Viero, 2011) results show that the probabilistic representation has the property for non-null [non zero probability] events in both \({\varvec{p}}_i\) and \({\varvec{p}}_i^*\) and for both A and B (not just the denominator).
Proposition 3
Strong Radical Rigidity implies Reverse Bayesianism.
Proposition 4
Reverse Bayesianism does not imply Strong Radical Rigidity in general.
Proposition 5
Reverse Bayesianism implies Strong Radical Rigidity, for all \(E, H, E\cap H\in {\mathscr {A}}_i\) non-null with respect to \({\varvec{p}}_i\) and \({\varvec{p}}_i^*\).
Proposition 6
Unconstrained Reverse BayesianismFootnote 9 is equivalent to Strong Radical Rigidity.
Hence for our purposes here, accounts compatible with rigidity will also be compatible with Reverse Bayesianism.
Several authors, in particular Steele and Stefánsson (2021a, b) argue that Reverse Bayesianism is not an acceptable general principle for awareness change. In particular, they offer counter examples in which the principle fails with common sense intuitions. These objections are fair for RB as a general principle, but are not particularly harmful to the argument made here. First, I am not arguing that RB is a good general principle for radical revisions, but a reasonable one in the context of opinion pooling. Second, as with marginalization, the argument is meant to show that the use of imprecise probabilities is compatible with RB [SRR, WRR].Footnote 10
Going back to imprecision, it is easy to observe that all the \({\varvec{p}}_i^*\in {\mathbb {P}}_i=\{{\varvec{p}}_i^*: {\varvec{p}}_i^*\restriction _{{\mathscr {A}}_i}={\varvec{p}}_i\}\) satisfy SRR,Footnote 11 yet the set of all \({\varvec{p}}_i^*\) satisfying SRR is strictly larger than \({\mathbb {P}}_i\).Footnote 12 The following condition suffices to make the two sets coextentional.
-
Radical Conservatism: \({\varvec{p}}_i^*(\Omega _i)={\varvec{p}}_i(\Omega _i)=1\).
Proposition 7
The set of all \({\varvec{p}}_i^*\) defined over \({\mathscr {A}}^*\) satisfying SRR [equivalently, unconstrained RB] and Radical Conservatism is just \({\mathbb {P}}_i=\{{\varvec{p}}_i^*: {\varvec{p}}_i^*\restriction _{{\mathscr {A}}_i}={\varvec{p}}_i\}\).
Radical Conservatism requires that outcomes originally inaccessible to the agent will get null probability, which requires some justification in this context.
First, this is not yet the output of a pooling function. Our modeler is not taking into account the credences of the agents but only their algebras. No (probabilistically representable) evidence in support of the new possibilities is being considered, and probabilistic consensus is not being sought. This will be done at the next stage.
Second, the guiding notion of consensus is one in which agents minimally weaken their credal positions so as to accommodate those of other agents. But an agent i did not originally acknowledged all the \(w\in \Omega ^*\) but \(w\not \in \Omega _i\) as relevant doxastic possibilities, so there seems to be no reason to give them any probabilistic weight. Also, as pointed before, giving them positive probabilistic weight implies reducing the probabilistic weight of doxastic possibilities they originally considered relevant; which is not a conservative operation.
4.4 Divergence Measures lead to Imprecision
Another way of understanding the question on how to extend \({\varvec{p}}_i\) from \({\mathscr {A}}_i\) to \({\mathscr {A}}^*\) is by taking \({\varvec{p}}_i\) to be a partial credence function over \({\mathscr {A}}^*\), one in which there are no values assigned for some elements of the algebra. A partial function can be considered incoherent if it assigns values to some elements but not their unions, intersections or complements.Footnote 13 Hence the question of how to structurally strengthen \({\varvec{p}}_i\) to \({\mathscr {A}}^*\) is akin to the issue of how to fix incoherent credences, a topic extensively developed by (Pettigrew, 2017) and (Predd et al., 2009). Their solution involves using divergence measures.
The argument here is not that using divergence is a rational requirement, but that imprecision is compatible with it. In most cases divergence measures, or more generally different forms of loss functions, are warranted on the basis that we are trying to better estimate some value like truth (in the accuracy first literature) or some target function (in function approximation in supervised and unsupervised learning). The problem here is not of estimation but rather of coherence (Pettigrew, 2017) and conservatism: among the coherent distributions over the richer algebra, which is the set of closest to the original distribution over the prior algebra.
In this section, \({\mathbb {P}}\) is the set of credence functions defined on \({\mathscr {A}}\) (rather than \({\mathscr {A}}^*\)).Footnote 14 A divergence is a function \({\mathscr {D}}_{{\mathscr {A}}}:{\mathbb {P}}\times {\mathbb {P}}\rightarrow [0,\infty ]\) such that for all credences \({\varvec{p}},{\varvec{p}}'\in {\mathbb {P}}\), (i) \({\mathscr {D}}_{{\mathscr {A}}}({\varvec{p}},{\varvec{p}})=0\), and (ii) \({\mathscr {D}}_{{\mathscr {A}}}({\varvec{p}},{\varvec{p}}')>0\) if \({\varvec{p}}\ne {\varvec{p}}'\). In general, neither symmetry nor the satisfaction of triangle inequality are required. The following are two classical examples:
Squared Euclidean Distance [SED]
Generalized Kullback-Leibler [GKL]
Divergence measures are generally used under the methodological assumption of minimal mutilation, which states that any shift from a prior to a posterior credal states should accommodate the posterior condition by minimally changing the prior. For example, Bayesian conditionalization satisfies the minimal mutilation principle according to GKL: \({\varvec{p}}(\cdot |E)={\varvec{p}}'\) minimizes \(GKL_{{\mathscr {A}}}({\varvec{p}},{\varvec{p}}')\) on the condition that the \({\varvec{p}}'\) is a probability function (i.e. coherent credal functions) that assigns value 1 to E. Similarly, Kullback-Leibler divergence generalizes Jeffrey conditionalization (Diaconis and Zabell, 1982). GKL is also a generalization of Jaynes’ Maximum Entropy formalism (Williams, 1980).
To “fix” \({\varvec{p}}_i\) amounts then to finding the (set of) coherent \({\varvec{p}}_i^*\) defined over \({\mathscr {A}}^*\) that minimizes some appropriate divergence measure. We can avoid the question on whether to use SED or GKL by looking at a generalization of both:
Additive Bregman Divergence [ABD]
Suppose \(\phi :[0,1]\rightarrow {\mathbb {R}}\) is a strictly convex function that is twice differentiable on (0,1) with a continuous second derivative. Suppose \({\mathscr {D}}:{\mathbb {P}}\times {\mathbb {P}}\rightarrow [0,\infty ]\). Then \({\mathscr {D}}\) is the additive Bregman divergence generated by \(\phi\) if, for any \({\varvec{p}},{\varvec{p}}'\in {\mathbb {P}}\),
SED is the ABD generated by \(\phi (x)=x^2\), and GKL is the ABD generated by \(\phi (x)=xlogx-x\). The additive Bregman divergence can also be justified on accuracy-first grounds. (Predd et al., 2009) show that if \({\varvec{p}}\) is an incoherent credence function, then the coherent credence function \({\varvec{p}}'\) that minimizes ABD with respect to it is more accurate than \({\varvec{p}}\) at all possible worlds. Therefore “fixing” incoherent credence functions using ABD increases accuracy. The following observation is important for our purposes:
Proposition 8
For all \({\varvec{p}}_i^*\) coherent credence functions defined over \({\mathscr {A}}^*\):
\({\varvec{p}}_i^*\in {\mathbb {P}}_i=\{{\varvec{p}}_i^*: {\varvec{p}}_i^*\restriction _{{\mathscr {A}}_i}={\varvec{p}}_i\}\) iff \({\mathscr {D}}_{{\mathscr {A}}_i}({\varvec{p}}_i,{\varvec{p}}_i^*)=0={\mathscr {D}}_{{\mathscr {A}}_i}({\varvec{p}}_i^*,{\varvec{p}}_i)\)
This section explored the structural strengthening of \({\varvec{p}}_i\) to \({\mathscr {A}}^*\) by extending it to \({\mathbb {P}}_i=\{{\varvec{p}}_i^*: {\varvec{p}}_i^*\restriction _{{\mathscr {A}}_i}={\varvec{p}}_i\}\). This was shown to be compatible with marginalization, the principle of minimal mutilation expressed by divergence measures, and some conservative constrains involving rigidity and reverse bayesianism. Any of the \({\varvec{p}}_i^*\in {\mathbb {P}}_i\) will satisfy those principles. Furthermore, excluding any of the \({\varvec{p}}_i^*\) satisfying the conditions would be arbitrary and unjustified. If we take any or all of those conditions to be exhaustive principles for structural strengthening, then we would be required to adopt \({\mathbb {P}}_i=\{{\varvec{p}}_i^*: {\varvec{p}}_i^*\restriction _{{\mathscr {A}}_i}={\varvec{p}}_i\}\).
4.5 Extending Imprecise Sets of Probability Functions
The previous sections focused on extending probability measures \({\varvec{p}}_i\) defined over \({\mathscr {A}}_i\) to \({\mathscr {A}}^*\). But the reader might endorse the view according to which subjective individual credal states should be represented by sets of probability functions - in particular convex sets. So suppose we start with a convex set of probabilities \(P_i\) representing agent i’s credences over \({\mathscr {A}}_i\) and we would like to extend it to \({\mathscr {A}}^*\). The proposed extension is:
\({\mathbb {P}}_i=\{{\varvec{p}}_i^*: {\varvec{p}}_i^*\restriction _{{\mathscr {A}}_i}={\varvec{p}}_i\) for some \({\varvec{p}}_i\in P_i\}\)
The following proposition is helpful:
Proposition 9
Provided that \(P_i\) is convex, \({\mathbb {P}}_i\) is convex.
5 Imprecise Pooling
So far, each agent has a convex set of probability functions \({\mathbb {P}}_i\) defined over a common algebra \({\mathscr {A}}^*\). Say \({\mathscr {P}}(P)\) is the power set of the set of all probability functions defined on an algebra \({\mathscr {A}}^*\). A generalized imprecise pooling function is defined as:
Our goal in this section is to find the appropriate pooling function \({\mathcal {F}}\) to conclude the aggregation process:

The next section provides an introduction to pooling, enumerating some well know results and principles adopted in the literature. Importantly, much of the literature assumes that the input of the pooling function is a precise profile of probabilities. We here have imprecise inputs. The sections following will develop the account for doing this, concluding with some generalized results.
5.1 Pooling Basics
Say P is the set of probability functions defined over a common algebra \({\mathscr {A}}\). Formally, a precise pooling method for a group of n individuals is a function:
mapping profiles of probability functions for the n agents \(({\varvec{p}}_1, ..., {\varvec{p}}_n)\), to single probability functions \(F({\varvec{p}}_1, ..., {\varvec{p}}_n)\). The probabilities are assigned to events, represented by a common algebra \({\mathscr {A}}\) defined over a shared sample space \(\Omega\).
Various concrete pooling functions have been studied. Linear pooling functions may be the most common and obvious proposal (Stone, 1961; McConway, 1981; Lehrer & Wagner, 1981).
Linear Opinion Pools \(F({\varvec{p}}_1, ..., {\varvec{p}}_n) = \sum _{i=1}^n w_i{\varvec{p}}_i\), where \(w_i \ge 0\) and \(\sum _{i=1}^n w_i = 1\).
Another proposal is to take a weighted geometric instead of a weighted arithmetic average of the n probability functions (Madansky, 1964; Bacharach, 1972; Genest et al., 1986).Footnote 15
Geometric Opinion Pools \(F({\varvec{p}}_1, ..., {\varvec{p}}_n) = c \prod _{i=1}^n{\varvec{p}}_i^{w_i}\), where \(w_i \ge 0\) and \(\sum _{i=1}^n w_i = 1\), and \(c = \frac{1}{\sum _{\omega ' \in \Omega }[{\varvec{p}}_1(\omega ')]^{w_1} \cdot \cdot \cdot [{\varvec{p}}_n(\omega ')]^{w_n}}\) is a normalization factor.Footnote 16
A third, more recent proposal from (Dietrich, 2010) is given by the following formula.
Multiplicative Opinion Pools \(F({\varvec{p}}_1, ..., {\varvec{p}}_n)(\omega ) = c \prod _{i=0}^n{\varvec{p}}_i\), where \({\varvec{p}}_0\) is a fixed “calibrating” probability function, and \(c = \frac{1}{\sum _{\omega ' \in \Omega }[{\varvec{p}}_0(\omega )] \cdot [{\varvec{p}}_1(\omega ')] \cdot \cdot \cdot [{\varvec{p}}_n(\omega ')]}\) is a normalization factor.Footnote 17
On the other hand, several principles have been suggested:
-
Strong Setwise Function Property (SSFP): There exists a function \(G: [0,1]^n \rightarrow [0,1]\) such that, for every event A, \(F({\varvec{p}}_1, ..., {\varvec{p}}_n)(A) = G({\varvec{p}}_1(A), ..., {\varvec{p}}_n(A))\).
-
Weak Setwise Function Property (WSFP): There exists a function \(G: {\mathscr {A}} \times [0,1]^n \rightarrow [0,1]\) such that, for every event A, \(F({\varvec{p}}_1, ..., {\varvec{p}}_n)(A) = G(A,{\varvec{p}}_1(A), ..., {\varvec{p}}_n(A))\).
-
Zero Preservation Property (ZPP): For any event A, if \({\varvec{p}}_i(A) = 0\) for \(i = 1, ..., n\), then \(F({\varvec{p}}_1, ..., {\varvec{p}}_n)(A)\) \(= 0\).
-
Marginalization Property (MP): Let \({\mathscr {A}}'\) be a sub-\(\sigma\)-algebra of \({\mathscr {A}}\). For any \(A \in {\mathscr {A}}'\), \(F({\varvec{p}}_1, ..., {\varvec{p}}_n)(A) = F([{\varvec{p}}_1\restriction _{{\mathscr {A}}'}], ..., [{\varvec{p}}_n\restriction _{{\mathscr {A}}'}])(A)\).
-
Probabilistic Irrelevance Preservation (IP): If \({\varvec{p}}_i(A|B) ={\varvec{p}}_i(A)\) for \(i = 1, ..., n,\) then \(F^B({\varvec{p}}_1, ..., {\varvec{p}}_n)(A\)) \(=\) \(F({\varvec{p}}_1, ..., {\varvec{p}}_n)(A).\)Footnote 18
-
Unanimity Preservation (UP): For all \(({\mathbb {P}}_1, ..., {\mathbb {P}}_n) \in {\mathbb {P}}^n\), if \({\mathbb {P}}_i = {\mathbb {P}}_j\) for all \(i, j = 1, ..., n\), then \({\mathcal {F}}({\mathbb {P}}_1, ..., {\mathbb {P}}_n) = {\mathbb {P}}_i\).
-
External Bayesianity (EB): For every profile \(({\varvec{p}}_1, ..., {\varvec{p}}_n)\) in the domain of F and every likelihood function \(\uplambda\) such that \(({\varvec{p}}^\uplambda, ..., {\varvec{p}}_n^\uplambda )\) remains in the domain of F, \(F({\varvec{p}}_1^\uplambda, ..., {\varvec{p}}_n^\uplambda ) = F^\uplambda ({\varvec{p}}_1, ..., {\varvec{p}}_n)\).Footnote 19
There is a large literature justifying these principles, and studying the interaction between them and the different forms of precise pooling. Surveys of the literature include (French, 1985), (Genest & Zidek, 1986), and (Dietrich & List, 2014). This is not the place to cover that material. The reason to invoke the principles is that there are limitative results showing that the axioms can not be jointly satisfied by precise pooling functions.
Theorem 1
McConway (1981), Theorem 3.3; Lehrer and Wagner (1981), Theorem 6.7 Given that the algebra contains at least three disjoint events, a pooling function satisfies SSFP iff it is a linear pooling function.
Theorem 2
( McConway, 1981, Corollary 3.4) Given that the algebra contains at least three disjoint events, F satisfies WSFP and ZPP iff F is a linear pooling function.
McConway has shown that a pooling function has the WSFP iff it has the MP. So linear pooling functions satisfy MP and ZPP.
Theorem 3
(Genest, 1984, p. 1104) The geometric pooling functions are externally Bayesian and preserve unanimity.
Part of the appeal of using imprecise probabilities, as shown by (Stewart & Ojea Quintana, 2016), is that they can jointly satisfy (an appropriate translation of) criteria that precise pooling cannot:
Theorem 4
(Stewart & Ojea Quintana, 2016, Propositions 2,3,5)
Convex IP pooling functions satisfy SWFP, WSFP, MP, ZPP, and unanimity preservation.
Convex IP pooling functions are externally Bayesian.
Convex IP pooling functions satisfy irrelevance preservation.Footnote 20
The same strategy will be used in Sect. 5.3, when considering how to aggregate sets of precise probabilities.
5.2 Pooling Imprecise Probabilities
We can now move to our problem at hand. Now we are given a profile of sets of probabilities functions \({\mathbb {P}}_i\) defined over a common algebra \({\mathscr {A}}^*\). This problem has been explored in the literature, but not particularly in the current setting.
In an unpublished research note (Walley, 1982), Walley provides an account of information fusion and presents fifteen criteria for the aggregation of opinions represented as sets of probabilities. The report is very hard to get, but both (Dubois et al., 2016) and (Bradley, 2019) provide a summary of it, together with general setup for information fusion. None of them present the problem as one of finding consensus, and they are also not focused on finding it in the context of radical disagreement. Furthermore, they are not in direct dialogue with the literature on pooling and disagreement presented in the previous section. Nevertheless, and maybe unsurprisingly, some of the criteria coincide with those in pooling; we will get into that in short. (Walley, 1982) comes up with a number of merging rules that result from the fifteen criteria. Some of them, the most tractable ones in the pooling setting, are:
-
Proposal 1: \({\mathcal {F}}({\mathbb {P}}_1, ..., {\mathbb {P}}_n) = \bigcap _{i = 1}^n {\mathbb {P}}_i\).
-
Proposal 2 \({\mathcal {F}}({\mathbb {P}}_1, ..., {\mathbb {P}}_n) = \bigcup _{i = 1}^n {\mathbb {P}}_i\).
-
Proposal 3 \({\mathcal {F}}({\mathbb {P}}_1, ..., {\mathbb {P}}_n) = H(\bigcup _{i=1}^n{\mathbb {P}}_i)\).Footnote 21
Moral and Sagrado (1998) also consider postulates for merging credal sets inspired by Walley. Their proposal is too involved to elaborate here, but two contrasting points are in place. First, their setup is one of expert opinion merging, and they adopt Dempster-Shafer theory of evidence in order to weight each agent according to their expertise. The approach here is one in which agents are all taken into account fairly and equally, and not given different weights. The second point is that they consider postulates that will fail here. For example, they postulate that if \({\mathbb {P}}^*\) is the set of all probabilities over \({\mathscr {A}}^*\), then \({\mathcal {F}}({\mathbb {P}}_1, ..., {\mathbb {P}}_n,{\mathbb {P}}^*)={\mathcal {F}}({\mathbb {P}}_1, ..., {\mathbb {P}}_n)\). The idea is that \({\mathbb {P}}^*\) represents complete ignorance and therefore should be ignored in merging. (Walley, 1982) and (Dubois et al., 2016) consider versions of this principle. Proposals 2 and 3 clearly fail at this.
In the present interpretation of the operator as one of consensus, even an ignorant (or possibly skeptical) agent with credal state \({\mathbb {P}}^*\) should be given a fair hearing. Taking unions (Proposal 2) ensures this. Taking the convex set of unions (Proposal 3) might lead to greater imprecision, but this might be warranted if all potential resolutions are to be preserved at the outset. The next few sections will be a defense of Proposals 2 and 3 on the basis of pooling axioms.
5.3 The Pooling Axioms Reformulated
As mentioned before, (Walley, 1982) offered several criteria for aggregating imprecise probabilities, as do Moral and Sagrado (1998) and Bradley (2019). We are here going to follow the pooling framework, and reformulate the axioms presented in Sect. 5.1 for aggregating sets of probabilities:
-
Strong Setwise Function Property (SSFP): There exists a function \(G: {\mathscr {P}}([0, 1])^n \rightarrow {\mathscr {P}}([0,1])\) such that for any \(A \in {\mathscr {A}}^*\), \({\mathcal {F}}({\mathbb {P}}_1, ..., {\mathbb {P}}_n)(A) = G({\mathbb {P}}_1(A), ..., {\mathbb {P}}_n(A))\).
-
Weak Setwise Function Property (WSFP): There exists a function \(G: {\mathscr {A}}^* \times {\mathscr {P}}([0,1])^n \rightarrow {\mathscr {P}}([0,1])\) such that, for any \(A \in {\mathscr {A}}^*\), \({\mathcal {F}}({\mathbb {P}}_1, ..., {\mathbb {P}}_n)(A) = G(A,{\mathbb {P}}_1(A), ..., {\mathbb {P}}_n(A))\).
-
Zero Preservation Property (ZPP): For any \(A \in {\mathscr {A}}^*\), if \({\mathbb {P}}_i(A) = \{0\}\) for all \(i = 1, ..., n\), then \({\mathcal {F}}({\mathbb {P}}_1, ..., {\mathbb {P}}_n)(A) = \{0\}\).
-
Marginalization Property (MP): Let \({\mathscr {A}}'^*\) be a sub-\(\sigma\)-algebra of \({\mathscr {A}}^*\). For any \(A \in {\mathscr {A}}'^*\), \({\mathcal {F}}({\mathbb {P}}_1, ..., {\mathbb {P}}_n)(A) = {\mathcal {F}}([{\mathbb {P}}_1\restriction _{{\mathscr {A}}'^*}], ..., [{\mathbb {P}}_n\restriction _{{\mathscr {A}}'^*}])(A)\).Footnote 22
-
Irrelevance Preservation (IP): If \({\varvec{p}}(A|B)={\varvec{p}}(A)\) for all \({\varvec{p}}\in \bigcup _{i=1}^n{\mathbb {P}}_i\), then \({\mathcal {F}}({\mathbb {P}}_1, ..., {\mathbb {P}}_n)(A) = {\mathcal {F}}^B({\mathbb {P}}_1, ...,{\mathbb {P}}_n)(A)\).
-
Unanimity Preservation (UP): For all \(({\mathbb {P}}_1, ..., {\mathbb {P}}_n) \in {\mathbb {P}}^n\), if \({\mathbb {P}}_i = {\mathbb {P}}_j\) for all \(i, j = 1, ..., n\), then \({\mathcal {F}}({\mathbb {P}}_1, ..., {\mathbb {P}}_n) = {\mathbb {P}}_i\).
-
External Bayesianity (EB): For every profile \(({\mathbb {P}}_1, ..., {\mathbb {P}}_n)\) in the domain of \({\mathcal {F}}\) and every likelihood function \(\uplambda\) such that \(({\mathbb {P}}_1^\uplambda, ..., {\mathbb {P}}_n^\uplambda )\) remains in the domain of \({\mathcal {F}}\), \({\mathcal {F}}({\mathbb {P}}_1^\uplambda, ..., {\mathbb {P}}_n^\uplambda ) = {\mathcal {F}}^\uplambda ({\mathbb {P}}_1, ..., {\mathbb {P}}_n)\).Footnote 23
Some of the principles considered by (Walley, 1982) coincide, most notably commutativity with updating (External Bayesianity here). Some other are not explicit but still hold for our cases, like Symmetry (the order of the input does not affect the output). And some others are in Walley but not in pooling or vice versa. The argument for Proposals 2 and 3 will be that they both satisfy all of the pooling axioms reformulated.
5.4 Some Results
Most of these results are extensions of the ones present in (Stewart & Ojea Quintana, 2016).
Proposition 10
Let \({\mathcal {F}}: ({\mathscr {P}}(P))^n \rightarrow {\mathscr {P}}(P)\) be an IP pooling function (not necessarily convex). \({\mathcal {F}}\) satisfies WSFP iff \({\mathcal {F}}\) satisfies MP.
Proposition 11
Convex IP pooling functions (Proposal 3) satisfy SSFP, WSFP, MP, ZPP, and unanimity preservation.
Lemma 1
(Cf. Levi, 1978; Girón & Ríos, 1980) Convexity is preserved under updating on a likelihood function, i.e., \({\mathcal {F}}^\uplambda ({\mathbb {P}}_1, ..., {\mathbb {P}}_n)\) is convex.
Proposition 12
Convex IP pooling functions (Proposal 3) are externally Bayesian.
Proposition 13
Convex IP pooling functions (Proposal 3) satisfy irrelevance preservation.
Proposition 14
Let \({\mathcal {F}}({\mathbb {P}}_1, ..., {\mathbb {P}}_n) = \bigcup _{i = 1}^n {\mathbb {P}}_i\) (Proposal 2). Then, \({\mathcal {F}}\) satisfies SSFP, WSFP, ZPP, MP, unanimity preservation, external Bayesianity, and confirmational irrelevance preservation.Footnote 24
It is trivial to observe that Proposal 1 fails to satisfy some of the axioms.
The question of how to aggregate sets of probabilities in general is still open in the literature. There are open problems about the interpretation of the operation and about which are the adequate axioms or principles for it. The strategy in this section was to defend Proposals 2 and 3 on the basis that they satisfy reasonable criteria for pooling, and an interpretation of pooling in terms of consensus as common ground. Taking unions and convex hulls of unions represents taking the strongest position compatible with all of the individual ones.
6 Conclusion
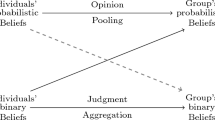
The general procedure can be visualized in the following diagram:

The nature of this essay is programmatic. It is focused in assessing a form of disagreement that has been neglected in the literature, disagreement about which is the relevant logical space of possibilities. The position defended here is that pooling can be interpreted as a technical and philosophical characterization of a form of consensus, namely consensus as common ground at the outset of inquiry.
This view was exemplified with the Priestley and Lavoisier debate in Sect. 2. Section 3 presents the view of consensus as common ground in detail, acknowledges certain assumptions, justifies the third person perspective, and argues for taking the join of the algebras as the logical pool. Section 4 argues that (i) marginalization, (ii) rigidity and reverse bayesianism, and (iii) divergence lead to the adoption of imprecise probabilities when agents expand their probabilistic judgments to larger algebras. The previous section extends results from previous work by (Stewart & Ojea Quintana, 2016, 2018) to show that pooling sets of imprecise probabilities can satisfy important pooling axioms.
As explained in Sect. 3, the proposal assumed the perspective of a third person well-informed modeler that was capable of identifying propositions and their truth conditions across different logical spaces. As discussed there, this is a necessary conditions in order to attain consensus of the form we are interested here. Assumptions of this form, discovered by Mahtani (2021), are still being discussed in the literature and may have further philosophical consequences.
It is important to remark that taking consensus as common ground is not the only solution to the problem, but it is a sound one. On the one hand, there might be other formal approaches. For example, (De Cooman & Troffaes, 2004) consider different (possibly incompatible) sources of information about independent variables and propose an aggregation method considering product algebras and probabilistic (lower previsions) extensions to them. On the other hand, there might be other philosophical approaches, by giving another interpretation to the aggregation process. One might think, for example, that an agent that has a prior defined over a more refined event or sample space has some kind of epistemic priority over a coarser (less “sophisticated”) agent. Conversely, an expert’s algebra may be coarser because it removed irrelevant distinctions.
The Priestley and Lavoisier debate served as a motivating example of the kind of disagreements that can be found in science, or inquiry in general. I argued that some cases of conceptual incommensurability can be modeled as a disagreement about what are the relevant sample and event spaces, what are the best natural joints to carve. But even in the face of such discrepancy, some form of consensus can be defined. At the outset, disagreements about what variables are relevant for explanation should begin by giving a fair treatment to all the possibilities. During inquiry, some of those possibilities may be discarded. But a pooling function cannot be expected to give an armchair account of the outcome of inquiry. In order to resolve radical disagreement rationally agents need start the conversation by taking others’ world views as possible.
Notes
Or for that matter, doxastic attitudes.
A proposition A is basic or atomic in the algebra if it is non-empty and there is no stronger (non-empty) proposition \(A'\subset A\) in the algebra. This implies that if both P and DP are basic, their intersection is empty and therefore you can not have the both be true at the same time.
Cases of true Kuhnian revolution where there are no identities across the parties logical carving.
This is the algebra \({\mathscr {A}}_*\) such that (i) \({\mathscr {A}}_L\subseteq {\mathscr {A}}_*\) and \({\mathscr {A}}_P\subseteq {\mathscr {A}}_*\), and (ii) for any \({\mathscr {A}}^*\) with \({\mathscr {A}}_L\subseteq {\mathscr {A}}^*\) and \({\mathscr {A}}_P\subseteq {\mathscr {A}}^*\), \({\mathscr {A}}_*\subseteq {\mathscr {A}}^*\).
Say \(\Omega _1=\Omega _2=\{w_1,w_2,w_3,w_4\}\), while \({\mathscr {A}}_1=\sigma (\{\emptyset ,\{w_1\},\{w_2\},\{w_3,w_4\}\})\) and \({\mathscr {A}}_2=\sigma (\{\emptyset ,\{w_3\},\{w_4\},\{w_1,w_2\}\})\).
Notice that although the event \(\{w_2,w_3\}\) was not considered possible, some of the states (worlds) constituting the event were considered by the agents. In the language introduced here, this amounts to partial radical disagreement, which is different from full radical disagreement. The Priestley-Lavoisier debate illustrates the importance of the former.
\({\varvec{p}}_*\) need not be a probability function.
In general the marginalization operation \({\varvec{p}}_i^*\restriction _{{\mathscr {A}}_i}\) is defined only when \({\mathscr {A}}_i\) is a subalgebra of \({\mathscr {A}}^*\), but this needs not to be the case here and that is why the definition is necessary.
This means generalizing RB so that only the denominator is required to be non-null.
Yet, if only marginalization, RB, SRR, WRR and divergence measures are required, then imprecision will be required too.
If \({\varvec{p}}_i^*\in {\mathbb {P}}_i\), then for all \(H\in {\mathscr {A}}_i\), \({\varvec{p}}_i^*(H)={\varvec{p}}_i(H)\). Hence, \({\varvec{p}}_i^*(H|E)=\frac{{\varvec{p}}_i^*(H\cap E)}{{\varvec{p}}_i^*(E)}=\frac{{\varvec{p}}_i(H\cap E)}{{\varvec{p}}_i(E)}={\varvec{p}}_i(H|E)\).
Let \(\Omega _i=\{w_1,w_2\}\), \({\mathscr {A}}_i={\mathscr {P}}(\Omega _i)\), and \({\varvec{p}}_i(w_1)=\frac{1}{2}\). On the other hand, let \(\Omega ^*=\{w_1,w_2,w_3\}\), \({\mathscr {A}}^*={\mathscr {P}}(\Omega ^*)\), and \({\varvec{p}}_i^*(w_1)={\varvec{p}}_i^*(w_2)={\varvec{p}}_i^*(w_3)=\frac{1}{3}\). Then \({\varvec{p}}_i^*\) satisfies SRR but \({\varvec{p}}_i^*\notin {\mathbb {P}}_i\).
This is related yet different to coherence as sure loss avoidance.
Notice that nothing in the definition requires the elements of \({\mathbb {P}}\) to be probability functions, just that they assign values in [0,1] to the elements of \(\mathscr{A}.\)
An unweighted geometric pool of n numerical values is given by \(\root n \of {x_1\cdot \cdot \cdot x_n} = x_1^{\frac{1}{n}}\cdot \cdot \cdot x_n^{\frac{1}{n}}\).
The domain of geometric pooling operators is restricted to profiles of regular pmfs, i.e., those \({\varvec{p}}\) such that \({\varvec{p}}(\omega ) > 0\) for all \(\omega \in \Omega\). We denote the set of regular pmfs \(P'\) making the relevant domain \(P'^n\).
As with geometric pooling functions, the domain of multiplicative pooling functions will be restricted to \(P'^n\).
Here \(F^B({\varvec{p}}_1, ..., {\varvec{p}}_n)\) refers to updating the pool function \(F({\varvec{p}}_1, ..., {\varvec{p}}_n)\) with the event B.
The requirement is that updating the individual probabilities on a common likelihood function (as opposed to updating on an event) \(\uplambda\) and then pooling is the same as pooling and then updating the pool on that likelihood function. A likelihood function, \(\uplambda : \Omega \rightarrow [0, \infty )\), is intended to encode, given any \(\omega \in \Omega\), how expected some evidence is with the number \(\uplambda (\omega )\). In conditionalizing, \(\uplambda (\cdot )\) serves the same role as the conditional probability \({\varvec{p}}(E| \cdot )\) in Bayes’ theorem.
This particular principles does require considering probabilistic irrelevance rather than probabilistic independence.
H(A) here is the convex closure of A.
Here \([{\mathbb {P}}_i\restriction _{{\mathscr {A}}'^*}]=\{[{\varvec{p}}_i\restriction _{{\mathscr {A}}'^*}]: {\varvec{p}}_i\in {\mathbb {P}}_i\}\).
Here \({\mathbb {P}}_i^\uplambda =\{{\varvec{p}}_i^\uplambda :{\varvec{p}}_i\in {\mathbb {P}}_i\}\).
The proof of this proposition is straightforward and so is omitted here. Also, Proposal 2 satisfies a stronger version of irrelevance preservation, stochastic preservation: If \({\varvec{p}}(A \cap B) = {\varvec{p}}(A){\varvec{p}}(B)\), for all \({\varvec{p}}\in \bigcup _{i=1}^n{\mathbb {P}}_i\), then, for all \({\varvec{p}}\in {\mathcal {F}}({\mathbb {P}}_1, ..., {\mathbb {P}}_n),\ {\varvec{p}}(A \cap B) = {\varvec{p}}(A){\varvec{p}}(B).\)
References
Bacharach, M. (1972). Scientific disagreement. Unpublished Manuscript.
Bradley, R. (2017). Decision theory with a human face. Cambridge University Press.
Bradley, S. (2019). Aggregating belief models. In Proceedings of ISIPTA 2019, Proceedings of machine learning research.
Cresto, E. (2008). A model for structural changes of belief. Studia Logica, 88(3), 431–451.
De Cooman, G., & Troffaes, M. (2004). Coherent lower previsions in systems modelling: Products and aggregation rules. Reliability Engineering & System Safety, 85, 113–134.
Dekel, E., Lipman, B., & Rustichini, A. (1998). Standard state-space models preclude unawareness. Econometrica, 66(1), 159–174.
Diaconis, P., & Zabell, S. L. (1982). Updating subjective probability. Journal of the American Statistical Association, 77(380), 822–830.
Dietrich, F. (2010). Bayesian group belief. Social Choice and Welfare, 35(4), 595–626.
Dietrich, F., & List, C. (2014). Probabilistic opinion pooling. In A. Hájek & C. Hitchcock (Eds.), Oxford handbook of probability and philosophy. Oxford University Press.
Dubois, D., Liu, W., Ma, J., & Prade, H. (2016). The basic principles of uncertain information fusion. An organised review of merging rules in different representation frameworks. Information Fusion, 32, 12–39.
Elga, A. (2007). Reflection and disagreement. Noûs, 41(3), 478–502.
Elkin, L., & Wheeler, G. (2018). Resolving peer disagreements through imprecise probabilities. Noûs., 52, 260–278.
Fagin, R., & Halpern, J. Y. (1987). Belief, awareness, and limited reasoning. Artificial Intelligence, 34(1), 39–76.
Feyerabend, P. K. (1962). Explanation, reduction and empiricism. In H. Feigl & G. Maxwell (Eds.), Crítica: Revista Hispanoamericana de Filosofía (pp. 103–106). University of Minnesota Press.
French, S. (1985). Group consensus probability distributions: A critical survey. In M. H. DeGroot, D. V. Lindley, J. M. Bernardo, & A. F. M. Smith (Eds.), Bayesian statistics: Proceedings of the second Valencia international meeting, North-Hollan (Vol. 2, pp. 183–201).
Genest, C. (1984). A characterization theorem for externally Bayesian groups. The Annals of Statistics, 12, 1100–1105.
Genest, C., McConway, K. J., & Schervish, M. J. (1986). Characterization of externally Bayesian pooling operators. The Annals of Statistics, 12, 487–501.
Genest, C., & Zidek, J. V. (1986). Combining probability distributions: A critique and an annotated bibliography. Statistical Science, 1, 114–135.
Girón, F. J., & Ríos, S. (1980). Quasi-Bayesian behaviour: A more realistic approach to decision making? Trabajos de Estadística y de Investigación Operativa, 31(1), 17–38.
Halpern, J. Y. (2001). Alternative semantics for unawareness. Games and Economic Behavior, 37(2), 321–339.
Jeffrey, R. C. (1990). The Logic of Decision. McGraw-Hill series in probability and statistics. University of Chicago Press.
Karni, E., Valenzuela-Stookey, Q., & Viero, M.-L. (2018). Reverse bayesianism: A generalization. Unpublished Manuscript.
Karni, E., & Viero, M.-L. (2011). Reverse Bayesianism: A choice-based theory of growing awareness. American Economic Review, 103, 2790–2810.
Kitcher, P. (1978). Theories, theorists and theoretical change. The Philosophical Review, 87(4), 519–547.
Konieczny, S., & Pino Pérez, R. (2011). Logic based merging. Journal of Philosophical Logic, 40, 239–270.
Kuhn, T. S. (1970). The structure of scientific revolutions. University of Chicago Press.
Kuhn, T., & Wilson, K. (2001). The Road Since Structure: Philosophical Essays, 1970–1993, with an Autobiographical Interview. Physics Today. https://doi.org/10.1063/1.1366068.
Lehrer, K., & Wagner, C. (1981). Rational consensus in science and society: A philosophical and mathematical study (vol. 21). Springer.
Levi, I. (1978). In foundations and applications of decision theory (pp. 263–273). Springer.
Levi, I. (1985). Consensus as shared agreement and outcome of inquiry. Synthese, 62(1), 3–11.
Madansky, A. (1964) Externally Bayesian groups. RAND Corporation.
Mahtani, A. (2021). Awareness growth and dispositional attitudes. Synthese, 198, 8981–8997.
McConway, K. J. (1981). Marginalization and linear opinion pools. Journal of the American Statistical Association, 76(374), 410–414.
Modica, S., & Rustichini, A. (1999). Unawareness and partitional information structures. Games and Economic Behavior, 27(2), 265–298.
Moral, S., & Sagrado, J. (1998). Aggregation of imprecise probabilities (pp. 162–188). Physica-Verlag HD.
Pettigrew, R. (2017). Aggregating incoherent agents who disagree. Synthese, 196, 2737–2776.
Predd, J. B., Seiringer, R., Lieb, E. H., Osherson, D. N., Poor, H. V., & Kulkarni, S. R. (2009). Probabilistic coherence and proper scoring rules. IEEE Transactions on Information Theory, 55(10), 4786–4792.
Seidenfeld, T., Kadane, J. B., & Schervish, M. J. (1989). On the shared preferences of two Bayesian decision makers. The Journal of Philosophy, 86(5), 225–244.
Smith, A., & Haakonssen, K. (2002). Adam Smith: The theory of moral sentiments, Cambridge texts in the history of philosophy. Cambridge University Press.
Steele, K., & Stefánsson, H. O. (2021a). Belief revision for growing awareness. Mind, 130, 1207–1232.
Steele, K., & Stefansson, O. (2021b). Beyond uncertainty: Reasoning with unknown possibilities. Cambridge University Press.
Stewart, R. T., & Ojea Quintana, I. (2016). Probabilistic opinion pooling with imprecise probabilities. Journal of Philosophical Logic, 47, 17–45.
Stewart, R. T., & Ojea Quintana, I. (2018). Learning and pooling, pooling and learning. Erkenntnis, 83, 369–389.
Stone, M. (1961). The opinion pool. The Annals of Mathematical Statistics, 32(4), 1339–1342.
Troffaes, M. C. M., & De Cooman, G. (2014). Lower previsions Wiley series in probability and statistics. Wiley.
Wagner, C. (2009). Jeffrey conditioning and external bayesianity. Logic Journal of IGPL, 18(2), 336–345.
Walley P. (1982) The elicitation and aggregation of beliefs. Technical report.
Williams, P. M. (1980). Bayesian conditionalisation and the principle of minimum information. The British Journal for the Philosophy of Science, 31(2), 131–144.
Acknowledgements
I would like to thank Katie Steele, Michael Nielsen, Rush Stewart, and the anonymous reviewers for their insightful comments. This paper was supported by Australian Research Council Grant DP190101507 and funding from the Humanising Machine Intelligence Grand Challenge Project at the Australian National University.
Funding
Open Access funding enabled and organized by CAUL and its Member Institutions.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
A. Proofs
A. Proofs
Proof
Proposition 1
Suppose \({\varvec{p}}^1,{\varvec{p}}^2\in {\mathbb {P}}_i\). I want to show that for \(\alpha \in [0,1]\), \({\varvec{p}}^*=\alpha .{\varvec{p}}^1 + (1-\alpha ).{\varvec{p}}^2\in {\mathbb {P}}_i\).
It is enough to show that \({\varvec{p}}^*\restriction _{{\mathscr {A}}_i}={\varvec{p}}_i\). Given any \(E\in {\mathscr {A}}_i\), \({\varvec{p}}^*(E)=\alpha .{\varvec{p}}^1(E)+(1-\alpha ).{\varvec{p}}^2(E)=\alpha .{\varvec{p}}_i(E)+(1-\alpha ).{\varvec{p}}_i(E)={\varvec{p}}_i(E)\).
\(\square\)
Proof
Proposition 2
SRR entails WRR tivially, since \(\Omega _i\in {\mathscr {A}}_i\) and \({\varvec{p}}_i(\Omega _i)=1\). WRR and the definition of conditional probabilities secure that for all \(E,H\in {\mathscr {A}}_i\), \({\varvec{p}}_i(H|E)=\frac{{\varvec{p}}_i(H\cap E)}{{\varvec{p}}_i(E)}=\frac{{\varvec{p}}_i(H\cap E|\Omega _i)}{{\varvec{p}}_i(E|\Omega _i)}=\frac{{\varvec{p}}_i^*(H\cap E|\Omega _i)}{{\varvec{p}}_i^*(E|\Omega _i)}=\frac{{\varvec{p}}^*_i(H\cap E\cap \Omega _i)/{\varvec{p}}^*_i(\Omega _i)}{{\varvec{p}}^*_i(E\cap \Omega _i)/{\varvec{p}}^*_i(\Omega _i)} = \frac{{\varvec{p}}^*_i(H\cap E\cap \Omega _i)}{{\varvec{p}}^*_i(E\cap \Omega _i)}=\frac{{\varvec{p}}^*_i(H\cap E)}{{\varvec{p}}^*_i(E)}={\varvec{p}}_i^*(H|E)\). \(\square\)
Proof
Proposition 3
Since both A and B are non-null with respect to \({\varvec{p}}_i\) and \({\varvec{p}}_i^*\), \({\varvec{p}}_i(A|B), {\varvec{p}}_i(B|A), {\varvec{p}}_i^*(A|B)\) and \({\varvec{p}}_i^*(B|A)\) are all well defined. Furtherm Suppose that SRR is true so that \({\varvec{p}}_i(A|B)={\varvec{p}}_i^*(A|B)\) and \({\varvec{p}}_i(B|A)={\varvec{p}}_i^*(B|A)\).
SRR also ensures that \({\varvec{p}}(A\cap B)\ne 0\ne {\varvec{p}}^*(A\cap B)\) or \({\varvec{p}}(A\cap B)=0={\varvec{p}}^*(A\cap B)\).
Suppose \({\varvec{p}}(A\cap B)\ne 0\ne {\varvec{p}}^*(A\cap B)\), then \({\varvec{p}}_i(A|B), {\varvec{p}}_i(B|A), {\varvec{p}}_i^*(A|B)\) and \({\varvec{p}}_i^*(B|A)\) are all non-null. The argument is then: \({\varvec{p}}_i(B\cap A).{\varvec{p}}_i^*(A\cap B)={\varvec{p}}_i(A\cap B).{\varvec{p}}_i^*(B\cap A)\) iff (by definition of conditional probability) \(({\varvec{p}}_i(A).{\varvec{p}}_i(B|A)).({\varvec{p}}_i^*(B).{\varvec{p}}_i^*(A|B))=({\varvec{p}}_i(B).{\varvec{p}}_i(A|B)).({\varvec{p}}_i^*(A).{\varvec{p}}_i^*(B|A))\) iff (using the identities provided by SRR and non-nullity) \({\varvec{p}}_i(A).{\varvec{p}}_i^*(B)={\varvec{p}}_i(B).{\varvec{p}}_i^*(A)\) iff \(\frac{{\varvec{p}}_i(A)}{{\varvec{p}}_i(B)}=\frac{{\varvec{p}}_i^*(A)}{{\varvec{p}}_i^*(B)}\).
Now assume \({\varvec{p}}(A\cap B)=0={\varvec{p}}^*(A\cap B)\). Classically, \({\varvec{p}}(A\cup B)={\varvec{p}}(A)+{\varvec{p}}(B)-{\varvec{p}}(A\cap B)\). Using the assumption we get \({\varvec{p}}(A\cup B)={\varvec{p}}(A)+{\varvec{p}}(B)\) and similarly \({\varvec{p}}^*(A\cup B)={\varvec{p}}^*(A)+{\varvec{p}}^*(B)\). By SRR \({\varvec{p}}(A|A\cup B)={\varvec{p}}^*(A|A\cup B)\). So \(\frac{{\varvec{p}}(A)}{{\varvec{p}}(A)+{\varvec{p}}(B)}=\frac{{\varvec{p}}^*(A)}{{\varvec{p}}^*(A)+{\varvec{p}}^*(B)}\). Hence, after some basic algebra, \({\varvec{p}}_i(A).{\varvec{p}}_i^*(B)={\varvec{p}}_i^*(A).{\varvec{p}}_i(B)\), which is all we need. \(\square\)
Proof
Proposition 4
Assume RB holds for \(A, B\in {\mathscr {A}}_i\) non-null with respect to \({\varvec{p}}_i\) and \({\varvec{p}}_i^*\) [i.e. \({\varvec{p}}_i(A)\ne 0\ne {\varvec{p}}_i(B)\) and \({\varvec{p}}_i^*(A)\ne 0\ne {\varvec{p}}_i^*(B)\)], but that there is H with \(H \cap E\) null in \({\varvec{p}}_i\) but not in \({\varvec{p}}_i^*\) (or viceversa). Then \({\varvec{p}}_i^*(H|E)\ne {\varvec{p}}_i(H|E)\) and SRR fails. \(\square\)
Proof
Proposition 5
This follows easily by taking \(A = E\cap H\) and \(B = E\). Notice that \(A = E\cap H\) needs to be non-null on both credences for this argument to work. \(\square\)
Proof
Proposition 6
Suppose we generalize RB so that only the denominator is required to be non-null.
On the one hand, taking \(A = E\cap H\) and \(B = E\) would do the trick to show RB implies SRR.
On the other hand, assume SRR and suppose for contradiction that unconstrained RB does not hold for \(A,B\in {\mathscr {A}}\): \(\frac{{\varvec{p}}_i(A)}{{\varvec{p}}_i(B)}\ne \frac{{\varvec{p}}_i^*(A)}{{\varvec{p}}_i^*(B)}\). Clearly, it can’t be the case that \({\varvec{p}}(A)=0={\varvec{p}}^*(A)\). Alternatively, consider the case where \({\varvec{p}}(A)=0\) but \({\varvec{p}}^*(A)\ne 0\). Using WRR [equivalent to SRR] we have that \(0={\varvec{p}}(A)={\varvec{p}}(A|\Omega )={\varvec{p}}^*(A|\Omega )=\frac{{\varvec{p}}^*(A)}{{\varvec{p}}^*(\Omega )}\ne 0\). So we again get a contradiction, and the same would hold in the case where \({\varvec{p}}(A)\ne 0\) but \({\varvec{p}}^*(A)=0\). The fourth and final case in the one in which \({\varvec{p}}(A)\ne 0\ne {\varvec{p}}^*(A)\); but this is just constrained RB which was shown to be implied by SRR in Proposition 4. \(\square\)
Proof
Proposition 7
Note 12 showed that the \({\varvec{p}}_i^*\in {\mathbb {P}}_i\) satisfy SRR, and they trivially satisfy Structural Conservatism. Suppose \({\varvec{p}}_i^*\) satisfies SRR and Structural Conservatism. Let \(H\in {\mathscr {A}}_i\) (so \(H\subseteq \Omega _i\)) and consider \({\varvec{p}}_i^*(H)\). By Structural Conservatism \({\varvec{p}}_i^*(H)={\varvec{p}}_i^*(H|\Omega _i)\). By SRR and Observation 4, \({\varvec{p}}_i^*\) satisfies WRR and therefore \({\varvec{p}}_i^*(H|\Omega _i)={\varvec{p}}_i(H)\). \(\square\)
Proof
Proposition 8
The observation follows from the fact that ABD is a divergence measure as defined before. If \({\varvec{p}}_i^*\in {\mathbb {P}}_i\) then for all \(E\in {\mathscr {A}}_i\), \({\varvec{p}}_i^*(E)={\varvec{p}}_i(E)\), and hence each element of the summation will be null. On the other hand, if \({\varvec{p}}_i^*\notin {\mathbb {P}}_i\), then there is \(E\in {\mathscr {A}}_i\) such that \({\varvec{p}}_i^*(E)\ne {\varvec{p}}_i(E)\). I will rely on the well known fact that \(\phi\) is strictly convex if and only if \(\forall x\ne y\in [0,1], \phi (x)>\phi (y) + \phi '(y)(x-y)\). This implies that for any \(E\in {\mathscr {A}}_i\), if \({\varvec{p}}_i^*(E)\ne {\varvec{p}}_i(E)\), then \(\phi ({\varvec{p}}(E))-\phi ({\varvec{p}}^*(E))-\phi '({\varvec{p}}^*(E))({\varvec{p}}(E)-{\varvec{p}}^*(E))>0\). \(\square\)
Proof
Proposition 9
Suppose \({\varvec{p}}^1,{\varvec{p}}^2\in {\mathbb {P}}_i\). I want to show that for \(\alpha \in [0,1]\), \({\varvec{p}}^*=\alpha .{\varvec{p}}^1 + (1-\alpha ).{\varvec{p}}^2\in {\mathbb {P}}_i\).
By the supposition we get that there are \({\varvec{p}}_i^1,{\varvec{p}}_i^2\in P\) with \({\varvec{p}}_i^1(A)={\varvec{p}}^1(A)\) and \({\varvec{p}}_i^2(A)={\varvec{p}}^2(A)\) for all \(A\in {\mathscr {A}}_i\). Since P is convex, \({\varvec{p}}_i^*=\alpha .{\varvec{p}}_i^1 + (1-\alpha ).{\varvec{p}}_i^2\in P\).
But then for any \(A\in {\mathscr {A}}_i\), \({\varvec{p}}^*(A)=\alpha .{\varvec{p}}^1(A) + (1-\alpha ).{\varvec{p}}^2(A)=\alpha .{\varvec{p}}_i^1(A) + (1-\alpha ).{\varvec{p}}_i^2(A)={\varvec{p}}_i^*(A)\). So \({\varvec{p}}^*\restriction _{{\mathscr {A}}_i}={\varvec{p}}_i^*\) and \({\varvec{p}}^*\in {\mathbb {P}}_i\). \(\square\)
Proof
Proposition 10
This is an adaptation McConway’s (1981) proof.
WSFP \(\Rightarrow\) MP. Assume that \({\mathcal {F}}\) has the WSFP, i.e., there is a function \(G: {\mathscr {A}}^{*} \times {\mathscr {P}}([0,1])^n \rightarrow {\mathscr {P}}([0,1])\) such that \({\mathcal {F}}({\mathbb {P}}_1, ..., {\mathbb {P}}_n)(A) = G(A, {\mathbb {P}}_1(A), ..., {\mathbb {P}}_n(A))\). By WSFP, we have \({\mathcal {F}}([{\mathbb {P}}_1\restriction _{{\mathscr {A}}'^{*}}],...,\)
\([{\mathbb {P}}_n\restriction _{{\mathscr {A}}'^{*}}])(A)\) \(=\) \(G(A, [{\mathbb {P}}_1\restriction _{{\mathscr {A}}'^{*}}](A), ..., [{\mathbb {P}}_n\restriction _{{\mathscr {A}}'^{*}}](A))\). Since G is a function and \({\mathbb {P}}_i(A) = [{\mathbb {P}}_i \restriction _{{\mathscr {A}}'^{*}}](A)\) for any \(A \in {\mathscr {A}}'^{*}\) (all such \(A \in {\mathscr {A}}'^{*}\) are also in \({\mathscr {A}}^{*}\)), it follows that \(G(A, [{\mathbb {P}}_1\restriction _{{\mathscr {A}}'^{*}}](A), ..., [{\mathbb {P}}_n\restriction _{{\mathscr {A}}'^{*}}](A))=G(A, {\mathbb {P}}_1(A), ..., {\mathbb {P}}_n(A))= {\mathcal {F}}({\mathbb {P}}_1, ..., {\mathbb {P}}_n)(A)\). Hence, \({\mathcal {F}}({\mathbb {P}}_1, ..., {\mathbb {P}}_n)(A) = {\mathcal {F}}([{\mathbb {P}}_1\restriction _{{\mathscr {A}}'^{*}}], ..., [{\mathbb {P}}_n\restriction _{{\mathscr {A}}'^{*}}])(A)\).
MP \(\Rightarrow\) WSFP. Assume that \({\mathcal {F}}\) has the MP. Let \(A \in {\mathscr {A}}^*\). We want to show that \({\mathcal {F}}({\mathbb {P}}_1, ..., {\mathbb {P}}_n)(A)\) depends only on A and \({\mathbb {P}}_i(A), i = 1, ..., n\).
First, if \(A = \emptyset\) or \(A = \Omega\), then, since the range of \({\mathcal {F}}\) is \({\mathscr {P}}({\mathbb {P}})\), \({\mathcal {F}}({\mathbb {P}}_1, ..., {\mathbb {P}}_n)(A)\) depends only on A and \({\mathbb {P}}_i(A), i = 1, .., n\), for any profile because, setting \({\mathcal {F}}({\mathbb {P}}_1, ..., {\mathbb {P}}_n)(A) = {\mathcal {G}}(A, {\mathbb {P}}_1(A), ..., {\mathbb {P}}_n(A))\) and \({\mathcal {F}}({\mathbb {P}}_1', ..., {\mathbb {P}}_n')(A) = {\mathcal {G}}(A,{\mathbb {P}}_1'(A), ..., {\mathbb {P}}_n'(A))\), it follows that \({\mathcal {G}}(A,{\mathbb {P}}_1(A), ...,{\mathbb {P}}_n(A)) =\) \({\mathcal {G}}(A,{\mathbb {P}}_1'(A), ...,{\mathbb {P}}_n'(A))\). [i.e. \({\mathcal {G}}(A,{\mathbb {P}}_1(A), ...,{\mathbb {P}}_n(A)) =\) \({\mathcal {G}}(A,{\mathbb {P}}_1'(A), ...,{\mathbb {P}}_n'(A))\) is just \(\{0\}\) or \(\{1\}\).]
Next, suppose that \(\emptyset \ne A \ne \Omega\). Consider the \(\sigma\)-algebra \({\mathscr {A}}'^* = \{\emptyset, A, A^c, \Omega \}\). \({\mathscr {A}}^*\) contains A and has \({\mathscr {A}}'^*\) as a sub-algebra. By MP, then
\({\mathscr {A}}'^*\) is uniquely defined by A and any probability over \({\mathscr {A}}'\) is uniquely determined by the probability of A under that distribution. So the righthand side of the equation above is determined by A and \([{\mathbb {P}}_i\restriction _{{\mathscr {A}}'}](A) = {\mathbb {P}}_i(A)\). \(\square\)
Proof
Proposition 11
Recall \({\mathcal {F}}({\mathbb {P}}_1, ..., {\mathbb {P}}_n)(A) = \{{\varvec{p}}(A): {\varvec{p}}\in {\mathcal {F}}({\mathbb {P}}_1, ..., {\mathbb {P}}_n)\}\). We let G of the SSFP be \(G({\mathbb {P}}_1(A), ..., {\mathbb {P}}_n(A))=H(\bigcup _{i=1}^n{\mathbb {P}}_i(A))\), the convex hull operation applied over \(\bigcup _{i=1}^n{\mathbb {P}}_i(A)\). It is clear that G depends just on the probabilities \({\mathbb {P}}_i(A)\), \(i=1,...,n\). We need to show that
But \({\mathcal {F}}({\mathbb {P}}_1, ..., {\mathbb {P}}_n)=H(\bigcup _{i=1}^n({\mathbb {P}}_i))\) by assumption. So the identity is trivial.
But since SSFP clearly implies WSFP, WSFP is satisfied, too. By Proposition 10, it follows immediately that \({\mathcal {F}}\) has the MP.
Because \({\mathcal {F}}({\mathbb {P}}_1, ..., {\mathbb {P}}_n)\) is a set of probability functions, \({\mathcal {F}}({\mathbb {P}}_1, ..., {\mathbb {P}}_n)(\emptyset ) = \{0\}\). Let \({\mathbb {P}}_i(A) = 0,\ i = 1, ..., n.\) Since there is a function, \({\mathcal {G}}\), such that \({\mathcal {F}}({\mathbb {P}}_1, ..., {\mathbb {P}}_n)(A) =\) \({\mathcal {G}}({\mathbb {P}}_1(A), ..., {\mathbb {P}}_n(A))\), we have it that
So, ZPP follows from SSFP.
For any profile \(({\mathbb {P}}_1, ..., {\mathbb {P}}_n) \in {\mathbb {P}}^n\), if all \({\mathbb {P}}_i\) are identical, then the convex hull is just \(\{{\mathbb {P}}_i\}\). So \({\mathcal {F}}\) satisfies unanimity preservation. \(\square\)
Proof
Lemma 1
This generalizes a proof due originally to (Levi, 1978; Girón & Ríos, 1980).
We want to show that given any two members, \({\varvec{p}}^\uplambda, {\varvec{p}}'^\uplambda \in {\mathcal {F}}^\uplambda ({\mathbb {P}}_1, ..., {\mathbb {P}}_n)\) and \(\alpha \in [0, 1]\), \({\varvec{p}}^\star = \alpha {\varvec{p}}^\uplambda + (1-\alpha ) {\varvec{p}}'^\uplambda\) is in \({\mathcal {F}}^\uplambda ({\mathbb {P}}_1, ..., {\mathbb {P}}_n)\).
If there is a convex combination of \({\varvec{p}}\) and \({\varvec{p}}'\), \({\varvec{p}}_\star =\beta {\varvec{p}}+ (1-\beta ){\varvec{p}}\), such that \({\varvec{p}}_\star ^\uplambda = {\varvec{p}}^\star\), then the convexity of \({\mathcal {F}}^\uplambda ({\mathbb {P}}_1, ..., {\mathbb {P}}_n)\) is established as a consequence of the convexity of \({\mathcal {F}}({\mathbb {P}}_1, ..., {\mathbb {P}}_n)\).
Where \({\varvec{p}}_\star ^\uplambda (\cdot ) = \frac{{\varvec{p}}_\star (\cdot )\uplambda (\cdot )}{\sum _{\omega ' \in \Omega }{\varvec{p}}_\star (\omega ')\uplambda (\omega ')} = \frac{\beta {\varvec{p}}(\cdot )\uplambda (\cdot )+(1-\beta ) {\varvec{p}}'(\cdot )\uplambda (\cdot )}{\beta \sum _{\omega ' \in \Omega }{\varvec{p}}(\omega ')\uplambda (\omega ')+(1-\beta ) \sum _{\omega ' \in \Omega }{\varvec{p}}'(\omega ')\uplambda (\omega ')}\).
For any \(\alpha\) we want to find some \(\beta\) such that:
For \(\beta =\frac{\alpha \sum _{\omega ^* \in \Omega }{\varvec{p}}'(\omega ^*)\uplambda (\omega ^*)}{\alpha \sum _{\omega ^* \in \Omega } {\varvec{p}}'(\omega ^*)\uplambda (\omega ^*)+(1-\alpha ) \sum _{\omega ^* \in \Omega }{\varvec{p}}(\omega ^*)\uplambda (\omega ^*)}\), the equality is verifiable with some tedious algebra. \(\square\)
Proof
Proposition 12
We want \({\mathcal {F}}({\mathbb {P}}_1^\uplambda, ..., {\mathbb {P}}_n^\uplambda ) = {\mathcal {F}}^\uplambda ({\mathbb {P}}_1, ..., {\mathbb {P}}_n)\).
\({\mathcal {F}}({\mathbb {P}}_1^\uplambda, ..., {\mathbb {P}}_n^\uplambda ) \subseteq {\mathcal {F}}^\uplambda ({\mathbb {P}}_1, ..., {\mathbb {P}}_n)\). It is clear that for each \(i = 1, ..., n\), \({\mathbb {P}}_i^\uplambda \subseteq {\mathcal {F}}^\uplambda ({\mathbb {P}}_1, ..., {\mathbb {P}}_n)\), since \({\mathbb {P}}_i\subseteq {\mathcal {F}}({\mathbb {P}}_1, ..., {\mathbb {P}}_n)\). By Lemma 1, \({\mathcal {F}}^\uplambda ({\mathbb {P}}_1, ..., {\mathbb {P}}_n)\) is convex. It follows that \({\mathcal {F}}({\mathbb {P}}_1^\uplambda, ..., {\mathbb {P}}_n^\uplambda ) \subseteq {\mathcal {F}}^\uplambda ({\mathbb {P}}_1, ..., {\mathbb {P}}_n)\).
We now want \({\mathcal {F}}^\uplambda ({\mathbb {P}}_1, ..., {\mathbb {P}}_n) \subseteq {\mathcal {F}}({\mathbb {P}}_1^\uplambda, ..., {\mathbb {P}}_n^\uplambda )\).
\({\mathcal {F}}({\mathbb {P}}_1, ..., {\mathbb {P}}_n)=H(\bigcup _{i=1}^n{\mathbb {P}}_i)\). Hence every \({\varvec{p}}\in {\mathcal {F}}({\mathbb {P}}_1, ..., {\mathbb {P}}_n)\) is a convex combination of elements in \(\bigcup _{i=1}^n{\mathbb {P}}_i\). Let us denote \({\varvec{p}}=\sum _j\alpha _j{\varvec{p}}_j\), with \({\varvec{p}}_j\in \bigcup _{i=1}^n{\mathbb {P}}_i\).
On the other hand, \({\mathcal {F}}^\uplambda ({\mathbb {P}}_1, ..., {\mathbb {P}}_n)=\{{\varvec{p}}^\uplambda : {\varvec{p}}\in {\mathcal {F}}({\mathbb {P}}_1, ..., {\mathbb {P}}_n)\) and \({\varvec{p}}^\uplambda (\cdot )=\frac{{\varvec{p}}(\cdot )\uplambda (\cdot )}{\sum _{\omega ' \in \Omega } {\varvec{p}}(\omega ')\uplambda (\omega ')}\}\).
We show that any \({\varvec{p}}\in {\mathcal {F}}^\uplambda ({\mathbb {P}}_1, ..., {\mathbb {P}}_n)\) is identical to some member of \({\mathcal {F}}({\mathbb {P}}_1^\uplambda, ..., {\mathbb {P}}_n^\uplambda ).\)
where \(\beta _j =\) \(\dfrac{\alpha _j \cdot \sum _{\omega ' \in \Omega } {\varvec{p}}_j(\omega ') \uplambda (\omega ')}{\sum _{\omega ' \in \Omega } \sum _j\alpha _j{\varvec{p}}_j(\omega ') \uplambda (\omega ')}\) with \(\beta _j \ge 0\) for all \(j = 1, ..., n\) and \(\sum _j \beta _j = 1.\) \(\square\)
Proof
Proposition 13
Notice first that Irrelevance preservation is not Stochastic preservation. Stochastic preservation states that if \({\varvec{p}}(A \cap B) = {\varvec{p}}(A){\varvec{p}}(B)\), for all \({\varvec{p}}\in \bigcup _{i=1}^n{\mathbb {P}}_i\), then, for all \({\varvec{p}}\in {\mathcal {F}}({\mathbb {P}}_1, ..., {\mathbb {P}}_n),\ {\varvec{p}}(A \cap B) = {\varvec{p}}(A){\varvec{p}}(B).\)
Suppose that \({\varvec{p}}(A|B)={\varvec{p}}(A)\) for all \({\varvec{p}}\in \bigcup _{i=1}^n{\mathbb {P}}_i\). We want \({\mathcal {F}}({\mathbb {P}}_1, ..., {\mathbb {P}}_n)(A)\) \(=\) \({\mathcal {F}}^B({\mathbb {P}}_1, ..., {\mathbb {P}}_n)(A)\). Consider \({\varvec{p}}^\star (A) \in {\mathcal {F}}({\mathbb {P}}_1, ..., {\mathbb {P}}_n)(A)\) and \({\varvec{p}}_\star (A) \in {\mathcal {F}}^B({\mathbb {P}}_1, ..., {\mathbb {P}}_n)(A)\). By convexity we have that \({\varvec{p}}^\star (A) = \sum _j \alpha _j {\varvec{p}}_j(A)\) with all the \({\varvec{p}}_j\in \bigcup _{i=1}^n{\mathbb {P}}_i\), for appropriate \(\alpha _j\).
By Proposition 12 (external Bayesianity), \({\mathcal {F}}^B({\varvec{p}}_1, ..., {\varvec{p}}_n)(A) = {\mathcal {F}}({\varvec{p}}_1^B, ..., {\varvec{p}}_n^B)(A)\). So \({\varvec{p}}_\star (A)\in {\mathcal {F}}({\varvec{p}}_1^B, ..., {\varvec{p}}_n^B)(A)\). Again using convexity we have that \({\varvec{p}}_\star (A) = \sum _j \beta _j {\varvec{p}}_j^B(A)\), with \({\varvec{p}}_j^B\in \bigcup _{i=1}^n{\mathbb {P}}_i^B\) and for appropriate \(\beta _j\).
By hypothesis \({\varvec{p}}_i^B(A) = {\varvec{p}}_j(A)\) for all \({\varvec{p}}_j\in \bigcup _{i=1}^n{\mathbb {P}}_i\), \({\varvec{p}}_j^B\in \bigcup _{i=1}^n{\mathbb {P}}_i^B\). Hence, \({\varvec{p}}_\star (A) = \sum _j \beta _j {\varvec{p}}_j^B(A) = \sum _j \beta _j {\varvec{p}}_j(A)\). Letting \(\alpha _j = \beta _j\), it follows that \({\mathcal {F}}({\varvec{p}}_1, ..., {\varvec{p}}_n)(A) = {\mathcal {F}}^B({\varvec{p}}_1, ..., {\varvec{p}}_n)(A)\). \(\square\)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Quintana, I.O. Radical Pooling and Imprecise Probabilities. Erkenn 89, 153–180 (2024). https://doi.org/10.1007/s10670-022-00527-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10670-022-00527-9