Abstract
This paper aims to formalize Galileo’s argument (and its variations) against the Aristotelian view that the weight of free-falling bodies influences their speed. I obtain this via the application of concepts of parthood and of mereological sum, and via recognition of a principle which is not explicitly formulated by the Italian thinker but seems to be natural and helpful in understanding the logical mechanism behind Galileo’s train of thought. I also compare my reconstruction to one of those put forward by Atkinson and Peijnenburg (Stud Hist Philos Sci 35(1):115–136, 2004), and propose a formalization which is based on a principle introduced by them, which I shall call the speed is mediative principle.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 The Verification of Hypotheses and Galileo’s Reasoning
Confronting a scientific hypothesis which a scientist is convinced is false and lacking suitable empirical machinery to reject it, she may resort to the power of pure thought. If h is such a hypothesis and \(\mathscr {K}\) is the body of knowledge the scientist is working with, one of the possible pure-thought strategies is to assume h obtains, incorporate it into the body of knowledge and check what the consequences of \(\mathscr {K}+h\) are. If from \(\mathscr {K}+h\) the scientist manages to draw a false statement, then something among \(\mathscr {K}+h\) is false (because false sentences cannot be consequences of true ones). Since h is the main suspect, the reasonable strategy is to reject it and accept the negation of h instead as an element of one’s knowledge.
Since Aristotle, and before Galileo, people had been convinced that if two falling bodies differ in weight, then their speeds must be different as well: the heavier one falls faster than the lighter. This view was (and still is) supported by everyday experience. It called for a genius of Galileo’s to break through the surface of things and to discover that if it indeed was like that, the ontological principle of consistency would be violated.
Whether the great thinker of Pisa performed the famous experiment dropping cannonballs from the leaning tower of his hometown is still an object of debate among the historians and the philosophers of science. What is undeniable is his thought experiment in which he demonstrates the falsity of the widespread view on falling bodies. The thought experiment depicts the following situation:
-
(G1)
Consider two falling stones, B and b, assuming that the weight of the first one is larger than that of the second.
-
(G2)
Assume that the stones are united somehow.
-
(G3)
According to Galileo (1954): “[...] on uniting the two, the more rapid one will be partly retarded by the slower, and the slower will be somewhat hastened by the swifter.” (i.e. B is retarded by b, and b is hastened by B).
-
(G4)
“[...] if a large stone moves with a speed of, say, eight, while a smaller stone moves with a speed of four, then when they are united, the system will move with a speed less than eight; but the two stones when tied together make a stone larger than that which before moved with a speed of eight. Hence the heavier body moves with less speed than the lighter; an effect which is contrary to your supposition.”
-
(G5)
in other words, the united body \(\llbracket B,b\rrbracket \) is heavier than B but moves with less speed than B.
In the above, \(\mathscr {K}\) is elementary knowledge about the behaviour of spatial things, h is Aristotle’s viewpoint. The contradictory statement (G4) (i.e., that there is an object which at the same time does have and does not have some property) allows for the repudiation of h. The Aristotelian principle has led us to a contradiction, and we are justified in rejecting it—it is not true that heavier bodies fall with greater speed than lighter ones. Since it is tacitly rejected that lighter bodies fall with greater speed than heavier ones, one may conclude that weight itself does not influence the speed of falling bodies.
2 The Nature of Thought Experiments
The nature of mental operations known as thought experiments did stir a heated debated in the 80s and 90s of the previous century, with opposite views represented mainly by John D. Norton and James Robert Brown.Footnote 1 To set the stage for my interpretation of the Galilean thought experiment let me recapitulate the main points of the debate.
Norton (1991) defines a thought experiment as
an argument which posits a state of affairs being either hypothetical or counterfactual, and invokes particulars which do not harm the generality of the conclusion of the argument.
In consequence, by its very definition every thought experiment can be reconstructed as an argument, a stance which is embodied in the following Reconstruction Thesis:
-
(RT)
All thought experiments can be reconstructed as arguments based on tacit or explicit assumptions. Belief in the outcome-conclusion of the thought experiment is justified only insofar as the reconstructed argument can justify the conclusion.Footnote 2
From (Norton 1996) we can infer that in order to make a fully satisfactory analysis of the thought experiment we have to:
-
(RT1)
explicitly formulate all the premises incorporated in the experiment, including enthymematic ones upon which the experimenter may seem not to rely at first sight,
-
(RT2)
formulate a statement which embodies the posited hypothesis,
-
(RT3)
show that the premises are strong enough to justify the conclusion as a consequence of the premises, either in a deductive or inductive sense (in which case embrace the hypothesis as part of knowledge), or use the reductio ad absurdum method to show that the posited hypothesis is inconsistent with knowledge (and reject it),Footnote 3
-
(RT4)
last but not least, ensure that it is clear which elements of the thought experiment are essential to the point and which are mere colourful details or ’stage-setting’ to make it imaginable.
Therefore, as Norton (1996) points out, “the success of the thought experiment is determined by the validity of the argument”. With reference to the opening section of this paper, the analysis of a thought experiment would require checking whether all the premises (both explicit and enthymematic) constitute an item of knowledge, formulating a hypothesis the experimenter wants to reject and finally demonstrating that from the premises and the hypothesis we can deduce some falsehood or absurdity (i.e., applying the reductio ad absurdum method).
Following Norton let me observe that the thought-experiment-as-argument stance gives us precise criteria for judging the reliability for thought experiments:
-
(C1)
the argument must be based on true premises (with the possible exception of a hypothesis put to a test),
-
(C2)
the argument must be valid, i.e., the process of reasoning must not be fallacious (which in particular means that all intermediate steps in the argument must be justified by the premises and accepted rules of inference).Footnote 4
Only when (C1) and (C2) are satisfied has the thought-experiment managed to produce real knowledge.
A somewhat opposite view on the nature of the thought experiments is advocated by James Robert Brown, this being what is known in the literature as the Platonic view of thought experiments. Brown proposes a taxonomy of thought experiments in which there is a special branch of those which are destructive and constructive at the same time:
-
(P1)
A Platonic thought experiment is a single thought experiment which destroys an old or existing theory and simultaneously generates a new one; it is a priori in that it is not based on new empirical evidence nor is it merely logically derived from old data; and it is an advance in that the resulting theory is better than the predecessor theory.Footnote 5
-
(P2)
This a priori knowledge is gained by a kind of perception of the relevant laws of nature which are, it is argued, interpreted realistically. Just as the mathematical mind can grasp (some) abstract sets, so the scientific mind can grasp (some of) the abstract entities which are the laws of nature.Footnote 6
According to Brown, Galileo’s thought experiment is the most prominent example—it destroys the Aristotelian theory and generates a new one according to which all bodies fall alike. Why is it Platonic? It gives us an instant glimpse into the abstract realm of laws of nature, which are relations among non-spatiotemporal objects (universals). Why the knowledge provided by the experiment is a priori? There are three distinct reasons for this:
-
(AP1)
there have been no new empirical data,
-
(AP2)
the new theory is not logically deduced from old data, nor is it any kind of logical truth,
-
(AP3)
the transition from Aristotle’s to Galileo’s theory is not just a case of making the simplest overall adjustment to the old theory; that, is we not only have a new theory, we have a better one.Footnote 7
Among these, (AP2) is in stark contrast with the Nortonian thought-experiment-as-argument view, and it is a crucial factor for the Brownian approach, as no empiricist should have any qualms about (AP1) and (AP3). But (AP2) is a serious bone of contention between Platonists and empiricists.
From the opening section it should be clear that I sympathize with Norton’s treatment of thought experiments and this strongly motivates my reconstruction of Galileo’s one in what follows. It is not the purpose of this paper to present a critique of the Platonic view; therefore, I will only point out these controversial aspects which are relevant for the remaining part of this paper, and which will allow for the exposition of my personal view on Galileo’s thought experiment.
Every thought experiment is accompanied by reasoning, understood as a kind of mental process. As such it is not intersubjective, but we make it so by means of verbalization, and thanks to this we put forward a model of this reasoning in the form of an argument. A good thought experiment should be easy to communicate (though not necessarily easy to comprehend), and so the thoughts behind it must be clear and precise enough to be conveyed by sentences of a language, either natural or mathematical, or a concoction of the two. From a logician’s point of view, the most important consequence of the above is that (C1) and (C2) serve as perspicuous criteria for testing the quality of a thought experiment. Once the premises have been verbalized and the argument carried out, we can ask about the status of the former and the validity of the latter. By employing this strategy, in Sect. 5 I will show that (G3) is a flaw in the Galilean thought experiment. And thanks to it I am able to propose a reasonable premise that could be accepted by the Aristotelian and allows for rejection of the Stagirite’s theory. The same strategy allows for analysis of different forms of argument based on the thought experiment which are examined mainly in Sect. 7.
The consequence of such an approach is that knowledge obtained by dint of the experiment is not a priori, but is justified (in a deductive way) by the data already included in the premises. From the point of view of this paper, the thought experiment does not open any door to the realm of laws of nature but lets us discern what is hidden in the information we possess, yet what is hard to see, so to say. Thus, for example, (AP1) seems to be satisfied by my analysis since the premises I propose do not contain any new empirical data compared to those available to the Stagirite and his followers (including the novel one I introduce), but (AP2) is unsustainable since all steps towards a new theory are taken via deduction from the premises. I basically agree with (AP3), since the Galilean outcome is in a way revolutionary, but this cannot be treated as an advantage on the side of a priori knowledge advocates. Any ground-breaking theory, however obtained and justified, satisfies (AP3). The choice of the argument approach to thought experiments is of course at the same time a rejection of (P1) and (P2).
The fact that I have chosen the mereological approach has one more important consequence which supports (RT4). My analysis embraces two initial steps: firstly, I expound the premises; and, secondly, I translate them into the formal language of mereology. This leaves us with the flesh and bones of the argument, setting all the particulars aside.
3 Galileo’s Thought Experiment as an Argument
Upon analysis, we may distinguish in the Galileo’s thought experiment the following premises:
-
(I)
every spatial body has a weight and a speed,
-
(II)
there are at least two disjoint bodies which differ in weight,
-
(III)
(disjoint) bodies can be united into a single body,
-
(IV)
any given body is heavier than any of its proper parts.
The fragment of the reasoning which is not addressed in the four points above is (G3). In the literature, it was recognized as a weak and controversial point which undermines Galileo’s conclusion (see e.g. Schrenk 2004). Galileo himself seems to assume it or to suggest that it stems from the assumptions of Aristotelian physics and introduces it into the thought experiment which allows him to repudiate Aristotle’s view. In the literature, the counterpart of (G3) has the form:
-
(V)
[...] natural speed is a property such that if a body A has natural speed \(s_1\), and a body B has natural speed \(s_2\), the natural speed of the combined body \(A\mathord {-}B\) will fall between \(s_1\) and \(s_2\). (Gendler 1998)
It is known under the name of the speed is mediative postulate. As I mentioned before, the postulate is contentious. Therefore, I not only present a mereological formalization of the thought experiment assuming the aforementioned postulate, but I also put forward a version of the experiment which instead of the contentious postulate uses the following simple and intuitive principle:
-
(V’)
every part of a falling spatial body has the same speed as the body itself,
which, as I point out in Sect. 7, is related to a certain principle used by Atkinson and Peijnenburg (2004). I will show that in the theory presented further in this paper, the contradiction can be obtained by means of the counterpart of (V’) and other axioms motivated by (II)–(IV) plus the principle formalizing the weak Aristotelian viewpoint (see (\(\mathtt {SWAD}\)) on page 13), but omitting (V’) results in a consistent system. From a philosophical point of view, this could be obtained by accepting (RT) as a leading thesis.
As it was rightly raised by one of the referees, (V’) (a) strongly suggests that the weight of a falling body is irrelevant for its speed and (b) its acceptance in place of (G3) changes the dialectic of the original reasoning.
As for (a) it should be noted that Aristotelian physics was the naïve physics of everyday experience. Therefore the hard step for an Aristotelian, concerning the phenomenon of falling bodies, was to treat two falling bodies (plunging with different speed) as a single entityFootnote 8 and draw the conclusion that it cannot be their weight that influences their speeds. Therefore, while articulating (V’) (and the remaining assumptions) I use the term “body” with the intended meaning of a rigid body, i.e. such whose deformations are null or negligible. With this interpretation in mind, and in light of the naïve physics interpretation of the Aristotelian theory, I venture to maintain that (V’) is a reasonable assumption that could be accepted by an Aristotelian, along with one which says that any pair of (disjoint) rigid bodies can be combined into a single one. I explicitly make this assumption later while couching the postulates in the language of mereology and distinguishing in the domain of discourse the subset of rigid bodies.
As for (b), it is true that the replacement of (G3) with (V’) alters the dialectic of the original reasoning, but there are reasons to do so.
Firstly, such a change of dialectic is no novelty in the literature, as, for example, Atkinson and Peijnenburg (2004) consider modifications of Galileo’s reasoning by replacing (G3) with different principles. In Sect. 7 I compare my approach to one of those proposed by them, and I also propose a new formalization of the argument which is based on the speed is mediative principle of Atkinson and Peijnenburg.
Secondly, to locate this situation in the thought-experiment-as-argument setting, let me point out that due to controversies surrounding (G3), Galileo’s original argument seems to fail criterion (C1), if we agree that (G3) is one of the assumptions. If we were to treat it as a consequence of the set of assumptions, the situation is no better, since it can be easily shown that (G3) is not a consequence of the very basic assumptions of the thought experiment, and together with the Aristotelian viewpoint results in an inconsistent set of sentences; therefore, the argument fails the other criterion, (C2). Hence my decision to introduce (V’) for rigid bodies, which (in presence of other postulates) allows for the rejection of the Aristotelian viewpoint, a rejection which is based on fairly reasonable assumptions, and thus for a reconstruction of Galileo’s aim (to establish by the power of pure thought that weight does not influence speed). To what extent have I really managed to do this is to be judged by the reader.
Before I continue, let me emphasize after Norton (1996, pp. 342–343) that any argument based on Galileo’s thought experiment is conclusive only if we accept the tacit assumption that “The speed of fall of bodies depends only on their weights”. No one who is not ready to embrace it will ever be convinced.Footnote 9
4 An Extended System of Mereology
The underlying logic of the system presented is first-order classical logic with identity. The symbols ‘\(\lnot \)’, ‘\(\wedge \)’, ‘\(\vee \)’, ‘\(\longrightarrow \)’, \(\longleftrightarrow \), ‘\(\forall \)’, ‘\(\exists \)’ and ‘\(=\)’ are interpreted, respectively, as negation, conjunction, disjunction, material implication, material equivalence, big and small quantifier, and identity. If A and B are sets, then \(A\times B\) is their Cartesian product, i.e., the set of all ordered pairs \(\langle a,b\rangle \) such that \(a\in A\) and \(b\in B\). For a set A, \(\mathcal {P}(A)\) is its power set, i.e. the collection of all subsets of A.
For a fixed domain M, whose elements will be called (spatial) bodies, let \(\mathord {\sqsubset }\subseteq M\times M\) be the part of relation. By means of \(\sqsubset \) (and logical constants) I define auxiliary relations of ingrediens (also called improper parthood), overlap and disjointness:

Ingrediens and overlap are of course reflexive, disjointness is irreflexive.
In terms of the parthood and overlap relations, the key notion of mereology, a mereological sum of a given set of objects, is defined thus:

So \(\mathord {\mathrel {{\textsf {Sum}}}}\subseteq M\times \mathcal {P}(M)\). From philosophical point of view, a mereological sum may be treated as a faithful mathematical model of the assembly of an object from given entities. The notion of a mereological sum seems to be a good candidate to “spell out exactly what would constitute a proper unification of bodies”, the problem raised, among others, by Schrenk (2004).
In order to avoid controversy related to (V’)—addressed in Sect. 3—in the set M of all bodies I distinguish a set R whose elements will be called rigid bodies, and I accept the following axiom of sum existence:

which says that every pair of rigid objects has a rigid sum. In the special case when \(M=R\) (i.e. we only consider a universe of rigid bodies), (\(\exists \mathord {\mathrel {{\textsf {Sum}}}}_R\)) postulates the existence of mereological sums of arbitrary finite collections of things. In general, I do not assume that mereological sum is an operation, i.e., in most cases, it does not have to be the case that any collection of objects has exactly one rigid sum. But, assuming that \(r:M\times M\longrightarrow \mathcal {P}(R)\) is the function which attributes to any pair of objects all its rigid sums:
I define a binary operator \(\llbracket -\rrbracket :M\times M\longrightarrow M\) such that:

Thus \(\llbracket x,y\rrbracket \) is a randomly chosen rigid sum of x and y.
Of course, where we use the part of relation and mereology to model spatio-temporal dependencies, the sum uniqueness property is a more than reasonable assumption. The fact that I do not include it into the body of axioms has nothing to do with any ontological or philosophical stance whatsoever. I just want to show that uniqueness is not necessary to model Galileo’s thought experiment. Thus the reason to exclude uniqueness is purely logical.Footnote 10
I assume that each element of M has a weight and a speed (see (I)). These are normally expressed using real numbers, but for the sake of analysis of the reasoning, it is enough to assume that we have a non-empty set \(\mathbb {V}\) of values, which may or may not be ordered by some binary relation. Thus, there are two functions:
For any spatial body z, \(w(z)\) plays the role of the weight of z, and \(s(z)\) the role of its speed. The only place where I do assume that the set of values is the field of real numbers is Sect. 7 in which an Atkinson’s and Peijnenburg’s version of the argument is examined.
From the point of view of modern logic the paper deals with two-sorted structures \(\langle M,\mathbb {V},R,\mathord {\sqsubset },w,s\rangle \), which can additionally be extended with other relations and operations (as is done, for example, when we want an order on the set of values).
5 Natural Speeds are Mediative
This section is devoted to the formalization of Galilean thought experiment in which the speed is mediative postulate is used.Footnote 11 To properly express it within the system introduced in the previous section I must equip the set of values with a strict order relation < (i.e. irreflexive and transitive) which allows for the comparison of elements of \(\mathbb {V}\). I standardly assume that the order is total, i.e., any two distinct elements are comparable with respect to <.
In this setting the speed is mediative postulate can be formalized as the condition:

which says that in the case the speed of x is less than the speed of y, the speed of any sum of x and y falls in between the speeds of x and y.
We now need to interpret the Aristotelian postulate, according to which the weight of a body influences its speed. Atkinson and PeijnenburgFootnote 12 call the weak dogma this Aristotelian stance according to which “heavier bodies fall more quickly than lighter ones”. By the name of the strong dogma they call “the quantitative statement that the natural motion of a body is proportional to its weight”. I will stick to the weak dogma, which can be nicely expressed as:

The counterpart of (IV) takes the form of:

Finally, let me introduce the formal analogue of (II):

according to which there are at least two rigid bodies with distinct weights. This is a bit weaker than (II), since I skipped the disjointness requirement, but still strong enough to obtain the results I am aiming for. If the reader feels uncomfortable about the absence of disjointness, she can easily add this to (\(\exists \mathtt {2}\)) and convince herself that all the proofs can be repeated along similar lines as those to follow.
Conventions
From now on, in the case \({\mathscr {S}}\) is a set of axioms (postulates) and \(\varphi _1,\ldots ,\varphi _n\) are sentences, then by:
I denote the set \({\mathscr {S}}\cup \{\varphi _1,\ldots ,\varphi _n\}\). In a similar way, in the case where \(\varphi \) is a sentence:
is a set of postulates from which \(\varphi \) has been removed. \(\square \)
It is routine to verify that  is consistent. Let us take the three-element mereological structure (see Fig. 1Footnote 13) and put \(R:=M\) (all bodies are rigid). Let \(\mathbb {V}:=\{1,2,3\}\) and \(1<2<3\). Define:
is consistent. Let us take the three-element mereological structure (see Fig. 1Footnote 13) and put \(R:=M\) (all bodies are rigid). Let \(\mathbb {V}:=\{1,2,3\}\) and \(1<2<3\). Define:
It is easy to see that all the conditions are satisfied in the structure. So, the conclusion is that without additional assumptions it cannot be demonstrated that the weak Aristotelian dogma is false.
The following set  is also consistent. Again, take the structure from Fig. 1 in which the interpretation is as in the case of \(\mathscr {P}_1\) except for:
is also consistent. Again, take the structure from Fig. 1 in which the interpretation is as in the case of \(\mathscr {P}_1\) except for:
and for all \(a\in M\), \(s(a):=1\).
Let me also observe that the presence of the mereological sum axiom is relevant for the derivation of the contradiction in the theorem to follow; that is, the set  is consistent as well. To see this consider a structure composed of two isolated bodies (see Fig. 2) x and y and \(\mathbb {V}:=\{1,2\}\) where:
is consistent as well. To see this consider a structure composed of two isolated bodies (see Fig. 2) x and y and \(\mathbb {V}:=\{1,2\}\) where:
(\(\exists \mathtt {2}\)) is obviously true, (\(\mathtt {Wght}\)) is vacuously true since \(\mathord {\sqsubset }=\emptyset \), (\(\mathtt {WAD}\)) holds in obvious way and (\(\mathtt {SpdM}\)) holds since although \(s(x)<s(y)\), there is no sum of x and y, so the consequent of the dogma is vacuously true.
Observe now that:
Theorem 1
 is inconsistent.
Footnote 14
is inconsistent.
Footnote 14
Proof
Assume all the postulates. Take \(x,y\in R\) such that (a) \(w(x)<w(y)\). By (\(\mathtt {WAD}\)) we obtain that \(s(x)<s(y)\). Fix \(\llbracket x,y\rrbracket \). We have two possibilities: \(y=\llbracket x,y\rrbracket \) or \(y\mathrel {\sqsubset }\llbracket x,y\rrbracket \). In the first case (i) \(s(y)=s(\llbracket x,y\rrbracket )\). In the second one, firstly (\(\mathtt {Wght}\)) entails that \(w(y)<w(\llbracket x,y\rrbracket )\), and secondly, (\(\mathtt {WAD}\)) gives us that (ii) \(s(y)< s(\llbracket x,y\rrbracket )\). Yet by (\(\mathtt {SpdM}\)) we obtain that:
so \(s(\llbracket x,y\rrbracket )<s(\llbracket x,y\rrbracket )\) in both (i) and (ii), a contradiction. \(\square \)
The reasoning in the proof of Theorem 1 is within, so to say, Galileo’s dialectic. We take two bodies, consider their unification into a single body (in the form of their mereological sum), apply the remaining assumptions (of which (\(\mathtt {Wght}\)) is implicitly used in (G3)) and arrive at a contradictory conclusion that there is a body faster than itself. In the reasoning, the speed is mediative principle plays a crucial role in deriving a contradiction, and is one of the assumptions. The problem is that it is controversial, so the argument seems to fail to satisfy criterion (C1). Moreover, it is easy to see that  plus the negation of (\(\mathtt {SpdM}\)) is consistent by putting in the model from Fig. 1 (with the set of values \(\{1,2\}\)):
plus the negation of (\(\mathtt {SpdM}\)) is consistent by putting in the model from Fig. 1 (with the set of values \(\{1,2\}\)):
and
Therefore the speed is mediative postulate cannot be a consequence of the basic premises, and the argument fails the validity criterion. Adding both the postulate and the weak Aristotelian dogma the inconsistency is obtained, so a hardened Aristotelian could easily defend his view by attacking (\(\mathtt {SpdM}\)).
In the next section I venture to put forward a remedy for this situation.
6 Galileo’s Argument Cleared of the Flaw
From now on I will try to deploy a minimal amount of concepts and make my assumptions as weak as possible, yet strong enough to achieve Galileo’s objective. First of all, until Sect. 5 I will no longer require that values in the set \(\mathbb {V}\) are ordered—it is not necessary for the setting I propose. And so, the postulate (\(\mathtt {Wght}\)) is replaced by:

saying that any proper part of a given body must have different weight from the body itself. This is, of course, weaker than (\(\mathtt {Wght}\)) which entails the former. As I already pointed out, we are perfectly entitled to accept the stronger condition, but it is irrelevant for what follows.Footnote 15
The following axiom is a formal counterpart of (V’):

and says that every part of a given falling rigid body must have the same speed as the body itself. If the reader finds herself uncomfortable with the second quantifier ranging over the whole set of bodies, she may restrict it to the set R of rigid bodies—it does not influence the argument. Or she may accept a reasonable axiom according to which every part of a rigid body must itself be rigid.
Let me show how (\(\mathtt {Spd}\)) relates to the sentence:

which says that all rigid bodies fall alike. In the absence of (\(\exists \mathord {\mathrel {{\textsf {Sum}}}}_R\)) neither (\(\mathtt {Spd}\)) entails (\(\mathtt {Spd}^*\)), nor vice versa, even in the case when both (\(\exists \mathtt {2}\)) and (\(\mathtt {w\text {-}Wght}\)) hold. For the first, take the structure from Fig. 3 where \(R:=\{x,y\}\), \(\mathbb {V}:=\{\bullet ,\star \}\) and:
and:
For the second, consider the same structure but this time put:
and
Observe that in both cases the models satisfy (\(\mathtt {w\text {-}Wght}\)) and (\(\exists \mathtt {2}\)), yet fail to meet (\(\exists \mathord {\mathrel {{\textsf {Sum}}}}_R\)), since x and z are rigid bodies without a mereological sum. If we agree that the set (\(\mathtt {w\text {-}Wght}\))+(\(\exists \mathtt {2}\)) constitutes elementary knowledge about bodies with respect to weight, then we conclude that such knowledge is too weak to establish any dependency between (\(\mathtt {Spd}^*\)) and (\(\mathtt {Spd}\)).
However we have the following
Fact 2
(\(\mathtt {Spd}^*\)) is a consequence of (\(\exists \mathord {\mathrel {{\textsf {Sum}}}}_R\))+(\(\mathtt {Spd}\)).
Proof
Fix arbitrary rigid bodies x and y and take \(\llbracket x,y\rrbracket \). Since both x and y are parts of \(\llbracket x,y\rrbracket \), (\(\mathtt {Spd}\)) entails that \(s(x)=s(\llbracket x,y\rrbracket )=s(y)\). \(\square \)
Yet (\(\mathtt {Spd}\)) is not a consequence of (\(\exists \mathord {\mathrel {{\textsf {Sum}}}}_R\)) + (\(\mathtt {Spd}^*\)). To see this take the structure from Fig. 4 and put:
Under this interpretation all rigid bodies have the same speed, while z has a part with a different speed from z itself.
So, I have identified two postulates—(\(\exists \mathord {\mathrel {{\textsf {Sum}}}}_R\)) and (\(\mathtt {Spd}\))—which together entail that all rigid bodies fall alike. However, from a logical point of view, these are not enough to reject Aristotle’s stance. Let us remember that the Aristotelian viewpoint was that the lighter body would have a smaller speed than the heavier one. From point of view of the correctness of the argument, it is irrelevant in which way weight influences speed, it is enough to assume that it indeed has influence, so we will consider the following hypothesis, which partially reflects Aristotle’s stance:

(\(\mathtt {SWAD}\)) is the acronym for super-weak Aristotelian dogma. Since both the strong and the weak dogmas of Atkinson and Peijnenburg (2004) entail the super-weak one, the refutation of the latter is enough to falsify the former two. Observe now that there are models of (\(\exists \mathord {\mathrel {{\textsf {Sum}}}}_R\)) + (\(\mathtt {Spd}\)) + (\(\mathtt {SWAD}\)), e.g. any structure with \(R=\emptyset \) and only isolated bodies (atoms) in which every element has different weight and speed, or a degenerate one-element structure \(M:=\{x\}=:R\) (this is the model with which Parmenides would have been probably very content). Therefore we need more to derive a contradiction and reject the super-weak dogma.
In reference to the opening section let:

constitute the body of knowledge which we take into account, the common ground between an Aristotelian and Galileo. Let me show that \(\mathscr {K}\) satisfies the very minimal requirement for knowledge, i.e. it is consistent. To this end, take again the structure from Fig. 1, put \(R:=M\), \(\mathbb {V}:=\{1,2\}\) and:
As for the speed, I define it to be 1 for all bodies in the structure. We leave it to the reader to check that all the sentences from \(\mathscr {K}\) are indeed true in the model.
Now, Galileo’s reasoning can be encapsulated in the proof of the following theorem:
Theorem 3
 is inconsistent.
is inconsistent.
Proof
By (\(\exists \mathtt {2}\)) there are rigid bodies x and y with different weights: \(w(x)\ne w(y)\). Therefore by (\(\mathtt {SWAD}\)) they have different speeds: \(s(x)\ne s(y)\). On the other hand, by Fact 2 we have that \(s(x)=s(y)\): a contradiction. \(\square \)
Going back to the opening section of the paper, \(\mathscr {K}\) constitutes knowledge and (\(\mathtt {SWAD}\)) is the hypothesis which we aim to reject. This is achieved by accepting (\(\mathtt {SWAD}\)) and deriving a contradiction from  . To anyone who accepts classical logic, the argument satisfies Norton’s (C2) requirement. Does it also satisfy (C1)? Well, today we do not need this argument to convince ourselves that it is not the weight that influences the speed of falling bodies. So a better question is whether the premises could count as true for Galileo and Aristotelians. (\(\exists \mathtt {2}\)) should not raise questions for anyone, similarly (\(\mathtt {Spd}\)) is very appealing and intuitively plausible. As for the sum existence axiom, probably the most controversial among the three, in the next theorem I show that it is relevant for deriving a contradiction from \(\mathscr {K}\). In consequence, if we want Galileo’s argument to be valid, we should at least consider taking it as a true premise.Footnote 16
. To anyone who accepts classical logic, the argument satisfies Norton’s (C2) requirement. Does it also satisfy (C1)? Well, today we do not need this argument to convince ourselves that it is not the weight that influences the speed of falling bodies. So a better question is whether the premises could count as true for Galileo and Aristotelians. (\(\exists \mathtt {2}\)) should not raise questions for anyone, similarly (\(\mathtt {Spd}\)) is very appealing and intuitively plausible. As for the sum existence axiom, probably the most controversial among the three, in the next theorem I show that it is relevant for deriving a contradiction from \(\mathscr {K}\). In consequence, if we want Galileo’s argument to be valid, we should at least consider taking it as a true premise.Footnote 16
Theorem 4
 is consistent.
is consistent.
Proof
A structure \(\langle M,\mathbb {V},R,\mathord {\sqsubset },w,s\rangle \) which satisfies the postulates looks as follows (see Fig. 2): \(R:=M:=\{x,y\}\), where \(x\mathrel {\bot }y\), \(\mathbb {V}:=\{\bullet ,\star \}\), \(\mathord {\sqsubset }:=\emptyset \) and:
\(\square \)
I also show that (\(\mathtt {Spd}\)) is relevant for deriving the contradiction, which justifies its inclusion in the body of knowledge.
Theorem 5
 is consistent.
is consistent.
Proof
I use the structure from Fig. 1 yet another time. Define: \(M:=\{x,y,z\}=:R\), \(\mathbb {V}:=\{\bullet ,\star \}\) and:
Notice that (\(\mathtt {Spd}\)) fails, since \(x\sqsubset z\), yet \(s(x)\ne s(z)\), and all axioms from the set are satisfied by the structure. (\(\exists \mathord {\mathrel {{\textsf {Sum}}}}_R\)) holds since \(z\mathrel {{\textsf {Sum}}}\{x,y\}\) and it is routinely verified property of mereological sum that for every a, \(a\mathrel {{\textsf {Sum}}}\{a\}\). For (\(\mathtt {w\text {-}Wght}\)) it is enough to notice that only \(x\sqsubset z\) and \(y\sqsubset z\), and by the definition of \(w\) function we have: \(w(x)\ne w(z)\ne w(y)\). For (\(\mathtt {SWAD}\)) notice that \(s(x)\ne s(z)\ne s(y)\). \(\square \)
7 Natural Speeds are Intensive: Division Versus Summation
The speed is mediative postulate was replaced in Atkinson and Peijnenburg (2004) by the axiom according to which the natural speeds of falling bodies are intensive, by which they mean that:
if two bodies with the same natural speeds are bound together, the natural speed of the composite is the same as that of each of the two constituent bodies.
In our setting this can be nicely presented in mereological notation as followsFootnote 17:

I omit the prefix of universal quantifiers since for this section, until Theorem 8, I assume that \(R=M\), i.e. all bodies are rigid. I make this assumption to avoid unnecessary complications which could cloud the focus of this section.
The above postulate is closely related to (\(\mathtt {Spd}\)) in the sense that (\(\mathtt {Z1}\)) is its consequence, for (\(\mathtt {Spd}\)) entails that \(s(x)=s(\llbracket x, y\rrbracket )\). However, (\(\mathtt {Spd}\)) is not only strictly stronger than (\(\mathtt {Z1}\)), but the latter is also too weak to prove the counterpart of Theorem 3, even in the presence of the stronger version of the sum existence axiom, according to which every pair of rigid objects has exactly one sum:

Let \(\mathscr {K}'\) be \(\mathscr {K}\) in which (\(\exists \mathord {\mathrel {{\textsf {Sum}}}}_R\)) has been replaced by the stronger version of sum existence axiom (\(\exists !\mathord {\mathrel {{\textsf {Sum}}}}_R\)).
Theorem 6
 is consistent.
is consistent.
Proof
Take the mereological structure from Fig. 1. Put \(\mathbb {V}:=\{1,2,3\}\) and \(s(x):=1=:w(x)\), \(s(y):=2=:w(y)\) and \(s(z):=3=:w(z)\). (\(\mathtt {Z1}\)) is satisfied since there are no distinct objects with the same speed. The same is enough to see that (\(\mathtt {SWAD}\)) must be satisfied in the structure. Checking (\(\mathtt {w\text {-}Wght}\)) is straightforward. On the other hand, (\(\mathtt {Spd}\)) fails, because \(x\sqsubseteq z\) but the objects have different speeds. \(\square \)
Atkinson and Peijnenburg reproduce a version of the Italian thinker’s argument with the aid of (\(\mathtt {Z1}\)), which means that they use principles other than those used by me so far, and it is interesting to see how their argument can be recaptured in a mereological setting. The two other mentioned principles are: (Z2) weight is extensive, according to which any body composed of two bodies of the same weight is twice as heavy as either of the bodies:

and (Z3): the natural speed of a falling body is a continuous function of its weight. In order to interpret this postulate in my setting an additional function \(\Phi :\mathbb {V}\longrightarrow \mathbb {V}\) is needed, and the set of values must be such that it allows for speaking of continuity of \(\Phi \). I standardly assume that \(\mathbb {V}\) is the set of \(\mathbb {R}\) of all real numbers and that \(\mathfrak {R}\) is the field of real numbers (we need the standard operations on reals to properly express the reasoning). Thus, in Atkinson and Peijnenburg’s setting we are dealing with structures:
where \(R=M\).
The two additional axioms put upon \(\Phi \) (which together form (Z3)) are:
-
(Z3a) \(\Phi \) is continuous,
-
(Z3b) the speed of a body is a \(\Phi \)-function of its weight: \(s(x)=\Phi (w(x))\).
To carry out the reasoning we will need an axiom concerning divisibility of bodies (tacitly assumed by Atkinson and Peijnenburg):

Define:

The following theorem and its proof are based on the thought experiment carried out by Atkinson and Peijnenburg (2004, p. 121).
Theorem 7
Assuming the Axiom of Dependent Choices, it is a consequence of \(\mathscr {A\!\!P}\) that all bodies fall alike, and the set  is inconsistent.
is inconsistent.
Proof
Take a body x whose weight is \(r\in \mathbb {R}\). By (\(\mathtt {Div}\)) there are bodies \(x_1\) and \(x'_1\) which are proper parts of x and such that  . Further, divide \(x_1\) into bodies \(x_2\) and \(x'_2\) which satisfy (\(\mathtt {Div}\)), so we have that
. Further, divide \(x_1\) into bodies \(x_2\) and \(x'_2\) which satisfy (\(\mathtt {Div}\)), so we have that  . Choose \(x_2\) and fix
. Choose \(x_2\) and fix  . When the n-th stage is reached, chose \(x_n\) and fix
. When the n-th stage is reached, chose \(x_n\) and fix  .
.
Applying the Axiom of Dependent Choices we come up with countable sequences of bodies \((x_n)_{n\in \mathbb {N}}\) (with \(x_0=x\)) and their weights  . The limit of the latter sequence is 0. By (\({\mathtt {Z3b}}\)) we have that for every \(n\in \mathbb {N}\):
. The limit of the latter sequence is 0. By (\({\mathtt {Z3b}}\)) we have that for every \(n\in \mathbb {N}\):

and so by (Z3a) it must be the case that the limit of \((s(x_n))_{n\in \mathbb {N}}\) is \(\Phi (0)\). By construction and by (\(\mathtt {Div}\)), for every \(n\in \mathbb {N}\), \(x_n=\llbracket x_{n+1},x'_{n+1}\rrbracket \) and \(w(x_{n+1})=w(x'_{n+1})\). From this and (\(\mathtt {Z3b}\)) we obtain that \(s(x_{n+1})=s(x'_{n+1})\). By the speed is intensive postulate we obtain that:

so we have that:

and the continuity of \(\Phi \) entails that \(s(x)=\Phi (0)\) (for \(w(x)=r\) and \(s(x)=\Phi (w(x)))\). By the arbitrariness of x we obtain that for every body its natural speed is \(\Phi (0)\), and therefore all bodies fall alike, i.e. \(\forall _{x,y\in M}\,s(x)=s(y)\).
Since, by assumption, there is a body x whose weight \(w(x)\) different from 0, the divisibility axiom entails that it has a proper part y such that \(w(y)<w(x)\), and so by (\(\mathtt {SWAD}\)) it must be the case that \(s(x)\ne s(y)\): a contradiction. \(\square \)
To see that the assumption that there is a body with non-zero weight is relevant for the contradiction observe that the set  is consistent. As a model take the infinite binary tree \(\mathfrak {T}\) from Fig. 5 and define \(w(z):=0\), \(s(z):=1\) for every z on the tree. (\(\mathtt {Z1}\)) is true in \(\mathfrak {T}\), since all bodies have the same speed, and (\(\mathtt {Z2}\)) is true, since all bodies have 0 weight. For (Z3a) and (Z3b) put \(\Phi \) as the constant function \(\Phi (r)=1\). So \(\Phi \) is continuous, and for every body x we have \(s(x)=\Phi (w(x))\), as required. The divisibility axiom is true in \(\mathfrak {T}\) since for every \(x_i\) on the tree, \(x_i\mathrel {{\textsf {Sum}}}\{x_{i1},x_{i0}\} \). The super-weak Aristotelian dogma holds vacuously in the model, since there are no bodies with different weights.
is consistent. As a model take the infinite binary tree \(\mathfrak {T}\) from Fig. 5 and define \(w(z):=0\), \(s(z):=1\) for every z on the tree. (\(\mathtt {Z1}\)) is true in \(\mathfrak {T}\), since all bodies have the same speed, and (\(\mathtt {Z2}\)) is true, since all bodies have 0 weight. For (Z3a) and (Z3b) put \(\Phi \) as the constant function \(\Phi (r)=1\). So \(\Phi \) is continuous, and for every body x we have \(s(x)=\Phi (w(x))\), as required. The divisibility axiom is true in \(\mathfrak {T}\) since for every \(x_i\) on the tree, \(x_i\mathrel {{\textsf {Sum}}}\{x_{i1},x_{i0}\} \). The super-weak Aristotelian dogma holds vacuously in the model, since there are no bodies with different weights.
It is also interesting to observe that the mereological sum axiom fails at \(\mathfrak {T}\), since if we put \(R:=M\), objects, for example, \(x_{10}\) and \(x_{01}\) do not have any sum. The only candidate is x which is the upper bound of \(\{x_{10},x_{01}\}\), however, \(x_{11}\) is part of x and is disjoint from both these objects. Therefore, Aristotle’s aim can be obtained without the axiomFootnote 18, yet it comes at the expense of employing the axiom postulating the (potential) infinite divisibility of objects on the ontological side and one of the weak forms of the Axiom of Choice on the logical side of the argument.
Let me emphasize that from now on I drop the assumption that \(R=M\). Theorem 6 shows that (\(\mathtt {Spd}\)) is stronger than (\(\mathtt {Z1}\)). Its strength is manifest in the following:
Theorem 8
-
(i)
(\(\mathtt {Spd}\)) together with ‘\(R\ne \emptyset \)’ and the following weaker version of axiom of divisibility :
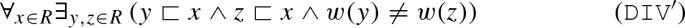
is inconsistent with the super-weak Aristotelian dogma.
-
(ii)
Similarly, the set (\(\mathtt {Spd}\)) +(\(\mathtt {w\text {-}Wght}\)) is inconsistent with the dogma, if only \(R\ne \emptyset \) and every rigid body has a rigid proper part : \(\forall _{x\in R}\exists _{y\in R}\,y\sqsubset x\).
Proof
(i) By assumption there is a rigid body x, and by (\(\mathtt {DIV'}\)) there are, rigid as well, \(y,z\sqsubset x\) such that \(w(y)\ne w(z)\). So (\(\mathtt {SWAD}\)) entails that \(s(y)\ne s(z)\). On the other hand by (\(\mathtt {Spd}\)) we have that \(s(y)=s(z)\).Footnote 19
(ii) Let \(x,y\in R\) be such that \(y\sqsubset x\). By (\(\mathtt {w\text {-}Wght}\)) it is the case that \(w(y)\ne w(x)\), so (\(\mathtt {SWAD}\)) entails that \(s(y)\ne s(x)\). But the speeds of y and x must be equal by (\(\mathtt {Spd}\)), a contradiction. \(\square \)
It remains to verify that the sets of premises without the super-weak Aristotelian dogma are consistent. For (\(\mathtt {Spd}\)), (\(\mathtt {DIV'}\)) and ‘\(R\ne \emptyset \)’ take the full binary tree \(\mathfrak {T}\) from Fig. 5 and put: \(R:=M\), \(\mathbb {V}:=\mathbb {R}\), \(w(x):=1\), and for every \(x_{i}\) on the tree whose weight is r, let  and
and  . Let the speed of all objects be equal to 1.
. Let the speed of all objects be equal to 1.
A slightly simpler model—the infinite descending chain from Fig. 6—is enough to demonstrate the consistency of the premises from the second point of the theorem. Put \(R:=M\), \(\mathbb {V}:=\mathbb {R}\), fix a positive real number r, let  , \(s(x_n):=1\) for every natural number n. It is routine to check that the postulates are true in the model.
, \(s(x_n):=1\) for every natural number n. It is routine to check that the postulates are true in the model.
The most serious objection we can raise against the above versions of the argument is that they significantly change the thinking behind Galileo’s original thought experiment, as the unification of objects is replaced by their division. So, can we reject the Aristotelian dogma by means of the speed is intensive postulate and some weaker logical apparatus than that applied in the proof of Theorem 7, remaining at the same time as close to Galileo’s original idea as possible? Of course, this just boils down to finding reasonable assumptions, and the question is can we find such assumptions? Yes, we can, and I am going to put forward yet another version of the argument in which (\(\mathtt {Spd}\)) is replaced with the weaker the speed is intensive postulate and the mereological sum is used in a relevant way.
Take the following existence postulate (which is a formal analogue of (II)):

and the following weight measurability axiom:

assuming at the same time that < is a strict linear order on the set of values. Define:

where (WS) is the following, self-explanatory, principle:

Observe that this is a consistent set of postulates. Indeed, as a model take the mereological structure from Fig. 1, put \(R:=M\) and \(\mathbb {V}:=\{1,2\}\) with \(1<2\). Let \(w(x):=1=:w(y)\), \(w(z):=2\) and for all \(a\in R\), \(s(a):=2\). I leave it to the Reader to check that \(\mathscr {R}\) is true in the model, and that the part of relation of the model is transitive.
However, we have:
Theorem 9
\(\mathscr {R}\) is inconsistent with the super-weak Aristotelian dogma (assuming that parthood is transitive).
Proof
Fix rigid disjoint bodies x and y. We have two possibilities.
(i) If \(w(x)=w(y)\), then by (WS) and the speed is intensive postulate we have that \(s(x)=s(\llbracket x,y\rrbracket )\). But the disjointness of the bodies and the reflexivity of \(\sqsubseteq \) entail that \(x\sqsubset \,\llbracket x,y\rrbracket \), so by (\(\mathtt {w\text {-}Wght}\)) it must be the case that \(w(x)\ne w(\llbracket x,y\rrbracket )\). In consequence, by the super-weak Aristotelian dogma: \(s(x)\ne s(\llbracket x,y\rrbracket )\), a contradiction.
(ii) In the second case the weights of x and y are different and without the loss of generality we may assume that \(w(x)<w(y)\). By (\(\mathtt {Msr}\)) there is a rigid body \(z\sqsubset y\) such that \(w(x)=w(z)\). By (WS) and the speed is intensive postulate we obtain that \(s(x)=s(\llbracket x,z\rrbracket )\). However, x and z are disjoint (since x and y are , and transitivity holds), and so again \(x\sqsubset \,\llbracket x,z\rrbracket \), which together with (\(\mathtt {w\text {-}Wght}\)) entails that \(w(x)\ne w(\llbracket x,z\rrbracket )\). Therefore \(s(x)\ne s(\llbracket x,z\rrbracket )\) by (\(\mathtt {SWAD}\)). \(\square \)
Let me verify that none of the sentences from \(\mathscr {R}\) can be left out (transitivity holds in all models below).
-
(a)
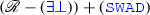 is consistent. Take the degenerate one-element structure. It is easy to verify that it satisfies all the postulates.
is consistent. Take the degenerate one-element structure. It is easy to verify that it satisfies all the postulates. -
(b)
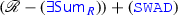 is consistent. Take the two-element structure from Fig. 2 and put \(R:=M\) and \(\mathbb {V}:=\{1\}\).
is consistent. Take the two-element structure from Fig. 2 and put \(R:=M\) and \(\mathbb {V}:=\{1\}\). -
(c)
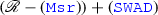 is consistent. Change the model of \(\mathscr {R}\) preceding the theorem above (the one based on the structure from Fig. 1) by setting \(\mathbb {V}:=\{1,2,3\}\) with the standard order, \(w(x):=1=:s(x)\), \(w(y):=2=:s(y)\) and \(w(z):=3=:s(z)\). Observe that (\(\mathtt {Msr}\)) fails, since \(w(x)<w(y)\), but y has no proper parts.
is consistent. Change the model of \(\mathscr {R}\) preceding the theorem above (the one based on the structure from Fig. 1) by setting \(\mathbb {V}:=\{1,2,3\}\) with the standard order, \(w(x):=1=:s(x)\), \(w(y):=2=:s(y)\) and \(w(z):=3=:s(z)\). Observe that (\(\mathtt {Msr}\)) fails, since \(w(x)<w(y)\), but y has no proper parts. -
(d)
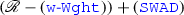 is consistent. For this, again take the model of \(\mathscr {R}\), but modify it by putting \(\mathbb {V}:=\{1\}\).
is consistent. For this, again take the model of \(\mathscr {R}\), but modify it by putting \(\mathbb {V}:=\{1\}\). -
(e)
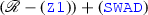 Let the model be again the same as for \(\mathscr {R}\), but this time: \(w(x):=1=:w(y)\), \(s(x):=1=:s(y)\) and \(w(z):=2=:s(z)\). x and y have the same speed, but \(s(x)\ne s(z)\) and \(z\mathrel {{\textsf {Sum}}}\{x,y\}\).
Let the model be again the same as for \(\mathscr {R}\), but this time: \(w(x):=1=:w(y)\), \(s(x):=1=:s(y)\) and \(w(z):=2=:s(z)\). x and y have the same speed, but \(s(x)\ne s(z)\) and \(z\mathrel {{\textsf {Sum}}}\{x,y\}\). -
(f)
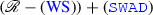 Take again the mereological structutre from Fig. 1 with all bodies rigid an define: \(w{x} := 1= : w(y), s(x) := 1, s(y) := 2 w(z) := 3 =: s(z)\). (\(\mathtt {WS}\)) fails in obvious way, and again I leave it to the Reader to check that all other postulates are satisfied
Take again the mereological structutre from Fig. 1 with all bodies rigid an define: \(w{x} := 1= : w(y), s(x) := 1, s(y) := 2 w(z) := 3 =: s(z)\). (\(\mathtt {WS}\)) fails in obvious way, and again I leave it to the Reader to check that all other postulates are satisfied
There are at least a couple of aspects that make the version of the Galilean argument from Theorem 9 interesting. Firstly, the rather strong postulate (\(\mathtt {Spd}\)), according to which every part of a rigid body has the same speed as the body itself, has been eliminated in favour of the weaker the speed is intensive postulate. Secondly, the remaining assumed postulates seem to be at least reasonable and could be accepted by Aristotle’s followers. Thirdly, none of the premises assumes the potential infinite divisibility of objects. Lastly, in the course of the proof, only the standard transformations based on the principles from the classical logic are made.
8 Conclusion
The observant reader might have noticed that the notion of mereological sum might be too strong to obtain the goal of the paper. If the reader is so kind to go through all the facts involving the notion and the sum existence axiom, she will see that the right-hand conjunct from (\(\mathtt {df}\,\mathord {\mathrel {{\textsf {Sum}}}}\)) is never used. That is, in none of the proofs it is important that the sum of two bodies x and y is not too large, so to speak. From a logical point of view, what matters is that the body \(\llbracket x,y\rrbracket \) is an upper bound of the two, i.e. contains x and y as its parts. However, such a choice, if logically correct, could somewhat mar the ontological flavour of the paper, especially in the analysis of the speed is mediative principle in Sect. 5. For these reasons, I have decided to stick to the mereological sum concept since it is the best formalization of the unification of bodies I am aware of.
The reader may also ask in what way the formalization put forward is superior to other reconstructions that have been given in the literature. As I would not like to advocate for superiority, I believe that certain points make this formalization at least interesting. Since the argument concerns falling bodies and their parts, mereology is a very natural setting for its logical reconstruction. As Galileo’s original thought experiment relies heavily on the unification of falling bodies, the question why not use a mereological sum principle as a mathematical model of the process? is very natural and investigation of its consequences is, in my opinion, interesting for mereologists, Galileo scholars and philosophers of science, as well as for philosophically-minded logicians. It is also an advantage of the mereological approach of this paper that all premises have been couched in a uniform precise language which allows for the scrutiny of the mutual dependencies between them and between various forms of the argument.
I have encountered an objection that since my reconstruction relies heavily on a contentious mereological sum principle, it is quite hard to find a justification for the whole process of formalization within the mereological setting. However, if the reader has similar thoughts I would like to ask her to change her perspective. Although I agree that unrestricted mereological sum principles might be contentious from an ontological point of view,Footnote 20 I ask the reader to notice that (\(\exists \mathord {\mathrel {{\textsf {Sum}}}}_R\)) is restricted to rigid bodies only, and turns into the unrestricted version only if we apply an extra axiom saying that all bodies are rigid. Of course, one may still object that the unrestricted sum principle for rigid bodies is no better from an ontological point of view, as it postulates the existence of beings well beyond the limits of necessity. But, on the other hand, in order to precisely reconstruct Galileo’s thought experiment we must address the issue of unification (which in the context seems to be more important than the notion of the division of bodies). The sum principle is a reasonable proposal since it is precise, relatively simple and, as I have proven, it is relevant for the whole process of the reasoning in the formalized form. Also, if we aim at the universality of principles we want to establish, we cannot say that we only accept the possibility of unification for particular bodies, since in such a case the conclusion could be only applied to the same particular bodies. What Galileo does is formulate the universal law of nature: the weight of falling bodies does not influence their speed. If unification is relevant for a derivation of the law, then it is more than reasonable to accept the unification in a strong form. So the change in perspective is that we do not perceive the mereological sum as just another postulate frowned upon due to its contentious consequences, but we treat it as a postulate which permits the explication of the establishment of one of the basic laws of nature. Therefore, there might be more to strong mereological sum principles than meets the eye, I venture to say.
Notes
Norton (1996).
See for example Norton’s reconstruction of the thought experiment on pages 341–342 of the paper.
See Norton (1996).
See Brown (1991).
See Brown (1991).
It is no longer for us, of course, with the advanced technology at hand. See: B. Cox, Galileo’s Famous Gravity Experiment, BBC Two, https://www.youtube.com/watch?v=E43-CfukEgs&t=194s.
See also Atkinson and Peijnenburg (2004, p. 123).
However, I refer to uniqueness in Sect. 7, where I analyze an interesting dependency between certain postulates, but only to show that even in presence of uniqueness one of those is too weak to achieve Galileo’s goal, i.e., reject Aristotle’s viewpoint.
Ibid.
The diagrams should be read from the bottom up, with lines heading upwards indicating that a lower object is a proper part of objects above it.
Obviously:
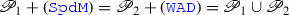 .
.Notice that (\(\mathtt {w\text {-}Wght}\)) entails that \(\sqsubset \) is irreflexive.
See also the final section of the paper for a short discussion of the mereological sum axiom and its role in the context of Galileo’s thought experiment.
I have kept the original tagging of postulates from Atkinson and Peijnenburg (2004).
But not without the notion of the sum of bodies.
I would like to thank to one of the referees for turning my attention to this mode of reasoning.
See Varzi (2016) for an extensive discussion.
References
Atkinson, D., & Peijnenburg, J. (2004). Galileo and prior philosophy. Studies in History and Philosophy of Science, 35(1), 115–136.
Brown, J. R. (1986). Thought experiments since the scientific revolution. International Studies in the Philosophy of Science, 1, 1–14.
Brown, J. R. (1991). The laboratory of the mind. London: Routledge.
Brown, J. R. (1993). Author’s response. Metascience, 3, 38–40.
Galileo, G. (1954). Dialogues concerning two new sciences (H. Crew & A. de Salvio, Trans.). New York: Dover Publications. (First published 1638)
Gendler, T. S. (1998). Galileo and the indispensability of scientific thought experiment. The British Journal for the Philosophy of Science, 49(3), 397–424.
Norton, J. D. (1991). Thought experiments in Einstein’s work. In T. Horowitz & G. J. Massey (Eds.), Thought experiments in science and philosophy (pp. 129–148). Savage, MD: Rowman and Littlefield.
Norton, J. D. (1993). Seeing the laws of nature. Metascience, 3, 33–38.
Norton, J. D. (1996). Are thought experiments just what you thought? Canadian Journal of Philosophy, 26(3), 333–366.
Schrenk, M. (2004). Galileo vs. aristotle on free falling bodies. In Logical Analysis and History of Philosophy. History of philosophy of nature (Vol. 7, pp. 1–11).
Varzi, A. (2016). Mereology. In E. N. Zalta (Ed.), The Stanford Encyclopedia of Philosophy (Spring 2016th ed.).
Funding
Funding was provided by Narodowe Centrum Nauki (Grant No. 2014/13/B/HS1/00766).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Gruszczyński, R. Parts of Falling Objects: Galileo’s Thought Experiment in Mereological Setting. Erkenn 87, 1583–1604 (2022). https://doi.org/10.1007/s10670-020-00263-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10670-020-00263-y










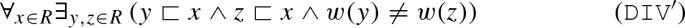

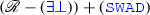 is consistent. Take the degenerate one-element structure. It is easy to verify that it satisfies all the postulates.
is consistent. Take the degenerate one-element structure. It is easy to verify that it satisfies all the postulates.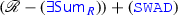 is consistent. Take the two-element structure from Fig.
is consistent. Take the two-element structure from Fig. 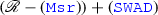 is consistent. Change the model of
is consistent. Change the model of 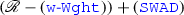 is consistent. For this, again take the model of
is consistent. For this, again take the model of 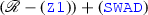 Let the model be again the same as for
Let the model be again the same as for 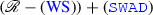 Take again the mereological structutre from Fig.
Take again the mereological structutre from Fig. 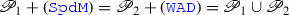 .
.