Abstract
Following Marr’s famous three-level distinction between explanations in cognitive science, it is often accepted that focus on modeling cognitive tasks should be on the computational level rather than the algorithmic level. When it comes to mathematical problem solving, this approach suggests that the complexity of the task of solving a problem can be characterized by the computational complexity of that problem. In this paper, I argue that human cognizers use heuristic and didactic tools and thus engage in cognitive processes that make their problem solving algorithms computationally suboptimal, in contrast with the optimal algorithms studied in the computational approach. Therefore, in order to accurately model the human cognitive tasks involved in mathematical problem solving, we need to expand our methodology to also include aspects relevant to the algorithmic level. This allows us to study algorithms that are cognitively optimal for human problem solvers. Since problem solving methods are not universal, I propose that they should be studied in the framework of enculturation, which can explain the expected cultural variance in the humanly optimal algorithms. While mathematical problem solving is used as the case study, the considerations in this paper concern modeling of cognitive tasks in general.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
This paper addresses a question of great theoretical interest in philosophy, psychology and cognitive science: how should we assess the complexity of cognitive tasks? Although the analysis carried out in this paper is applicable to cognitive tasks in general, here I am particularly interested in mathematical problem solving as a case study. In addition to the theoretical aspect, although not usually framed in these terms, this is also a practical question that mathematics educators face constantly. In designing exams, for example, the teacher has to use some kind of (perhaps implicit) measure for evaluating problems in terms of the complexity of the cognitive task of solving them. The required cognitive tasks cannot be too complex, but they should be complex enough in order to assess the knowledge and skills relevant to the mathematical concepts.
So how can the complexity of the cognitive task of problem solving be assessed? In mathematics education, this is often a question tested in practice. Low performance by students in a particular problem is easy to interpret as showing high cognitive complexity of the task of solving it. However, from a theoretical perspective, this practical approach is unsatisfactory, as it does not necessarily distinguish between the cognitive processes involved. From the perspective of cognitive science, we are primarily interested in identifying those processes, after which we can assess their complexity.
One common method for this is modeling the cognitive tasks computationally, i.e., identifying a mathematical function that models the particular cognitive task. To assess the complexity of the task, we then assess the computational resources it takes for an algorithm to compute the function. When it comes to mathematical problem solving, this approach gives rise to a clear research paradigm. In theoretical computer science, the complexity of mathematical problems is studied in terms of their complexity, which is characterized by the resources (time or space) required for running algorithms that solve the problems. It is thus understandable to characterize the complexity of the cognitive task of solving a mathematical problem in terms of the complexity of that problem. In this paper, however, I will show that this approach is flawed and we need distinct concepts of cognitive complexity and computational complexity.
In particular, I will study the question of cognitive complexity from two directions. In the first part of the paper, I will study what we can achieve with the computational complexity approach to cognitive complexity. I will show that this is an important research paradigm because we can establish explicit complexity measures in it, which we can then use to discuss the possible characteristics of cognitive processes. However, I will also argue that this approach alone is not sufficient for studying cognitive complexity. In the second part of the paper, I will show that the reason for this is that it fails to take into consideration the plurality of processes used by human cognizers when solving a mathematical problem. The method of assessing the computational complexity of mathematical problems is closely related to the idea of optimal algorithms, i.e., algorithms requiring a minimum of computational resources for solving the problem. Here I will argue, however, that human cognizers use problem solving algorithms that may in fact be computationally suboptimal.Footnote 1 I will show, among other examples, that diagrams and other heuristic and didactic tools play an important role in mathematical problem solving, yet they add to the complexity of the problem solving algorithm. On these grounds, I will argue that we should distinguish between computationally optimal and what I will call humanly optimal algorithms.Footnote 2
The first part of this paper (Sects. 2–5) studies the approach based on computational complexity. In the first section, I will present the modern computational-level paradigm for studying cognitive complexity, which will then be given a more detailed treatment in Sect. 3. In Sects. 4 and 5, I will present the possibilities and the limits of this paradigm in explaining cognitive phenomena. In the second part of the paper (Sects. 6, 7), I expand the methodology beyond the computational complexity approach. In Sect. 6, I aim to show how the human problem solving algorithms may be different from the optimal algorithms studied in the computational complexity approach. Finally, in Sect. 7, I discuss the notion of humanly optimal algorithm, concluding that rather than looking for a uniform notion of mathematical competence, we should expect both cross-cultural and intra-cultural variation in the problem solving methods.
While my focus is on mathematical problem solving, the approach applies also to other domains of cognitive modeling. This paper targets mathematical cognition partly because it works as a case study of modeling cognitive tasks. However, an important reason for the focus on mathematical problem solving is that there is a well-established paradigm in place for characterizing mathematical problems in terms of their computational complexity. Finally, given the importance of mathematics in our culture, I believe that there is a great need to treat mathematical problem solving explicitly when it comes to modeling cognitive capacities. This should include philosophical questions concerning that research.
2 What is Cognitive Complexity?
Cognitive complexity as a scientific term does not have a fixed cross-disciplinary meaning. If we take the dictionary definition of “cognitive” as referring to conscious or conscious mental processes such as remembering, reasoning and knowing (among others), cognitive complexity can be understood as the measure of simplicity of such activity. However, both the relevant activity and its simplicity can be understood in different ways.
Let us start by establishing a general sense in which one cognitive process can be more complex than another. Think of two people reasoning about the weather. The sky is red during sunrise and John remembers the saying “Red sky at morning, sailors take warning”, thus concluding that he should not go boating. Mary, on the other hand, reasons that since the sun is in the eastern horizon, the red color must mean that there is clear sky in the east which allows sunlight to color the clouds in the west. Since winds in that particular region (e.g., the Atlantic) tend to be from west to east, Mary concludes that more clouds and perhaps storms are coming and thus it is better to stay ashore. This way, both John and Mary make the same observation and end up with the same action, yet it is clear that Mary’s reasoning is more complex.
Even though there is quite some variation in how cognitive complexity is understood in psychology, the account of John and Mary can be seen as representative of the traditional psychological understanding of the term. Importantly, cognitive complexity is seen as a property of the process of the individual cognizing subject (Bieri 1955; van Hiel and Mervielde 2003). But of course this approach to cognitive complexity is not limited to determining individual differences in cognitive processing. We can also ask more general questions about cognitive tasks. Even with individual differences, it is clear that human beings have great inter-individual similarity in their cognitive processes, which makes it feasible to study the complexity of those tasks, rather than individual cognitive processes.
In the cognitive task of mathematical problem solving, we can see the usefulness of both approaches clearly. Let us think of a simple mathematical problem, such as finding a solution to the equation \(n^{2}=2\) when \(n\in {\mathbb {{N}}}\). Or equivalently, to frame it as a decision problem (i.e., yes/no-problem), \(\exists n(n^{2}=2)\) when \(n\in {\mathbb {{N}}}\). Let’s call this proposition p. Clearly p is false, but the way two people establish this falsehood may be quite different, even if both were valid. This way, the cognitive task of John concluding that p is false can be less complex than Mary’s cognitive task of establishing that p is false. But now it is natural to ask what would be the least complex process of establishing the truth-value of p. This approach is taken in theoretical computer science: complexity is understood to be a computational property of a problem, measuring the simplest possible way of correctly solving a decision problem.Footnote 3
With this brief account, we have arrived at three different aspects of cognitive complexity: the complexity of individual cognitive processes, the complexity of general cognitive tasks, and the complexity of problems. There is an intuitive way in which the three aspects are connected: the more complex the problem, the more complex the cognitive tasks required, and thus the more complex the individual cognitive processes. Equally intuitively, the converse chain of implications from the individual cognitive processes to the problem does not necessarily hold. It is possible for a problem to be simple and yet for the individual human processing of it to be highly complex. This way, to study the complexity of mathematical problem solving, it would seem that we need to work on all three aspects.
In cognitive science, however, that has not been seen as a satisfactory state of affairs. Since cognitive scientists are interested in the general features of human cognition, they have understandably largely disregarded the kind of different cognitive styles that make humans use needlessly complex cognitive processes. Chomsky (1965) presented a fundamental distinction in linguistics (in particular syntax) between competence and performance, which has later been widely transferred to the study of cognitive phenomena. In studying the nature of cognitive tasks, we are not primarily interested in the actual performance of the cognizers. Rather, we want to study an idealized version of his/her cognitive abilities, i.e., what we would expect from a fully competent user of that cognitive capacity.
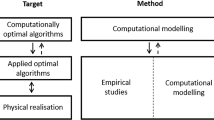
This approach leaves us with two aspects: the complexity of cognitive tasks in general and the complexity of problems. Intriguingly, as we will see, in the subject of mathematical problem solving these two levels can come to be equated when focusing on the computational level of explanation in cognitive science. The complexity of decision problems is a widely researched topic in theoretical computer science and in recent times, it has also become influential in the discussion on modeling cognitive tasks in cognitive science (see, e.g., Frixione 2001; van Rooij 2008). In what is called the computational level of explanation, cognitive tasks are understood as employing cognitive capacities to transfer input states (e.g., perceptions) into output states (e.g., decisions) (Cummins 2000). In the widely-used distinction by Marr (1977, 1982), three levels of explanation of cognitive tasks are identified: the computational level, the algorithmic level, and the implementation level (Table 1). In the context of mathematical problems, the three levels can be understood, respectively, as the computational characterization of the problem, the algorithm used to solve the problem, and the neuronal action involved in solving it. Marr’s distinction has become widely accepted as the basic framework for studying cognitive capacities (see, e.g., Newell 1982; Pylyshyn 1984; Horgan and Tienson 1996; Frixione 2001; van Rooij 2008).
Marr (1982) argued that for maximal progress in cognitive science, the focus should be on the computational level. His view (p. 27) was that by studying the computational level, we also get a better understanding of the algorithmic and implementational levels. According to the Principle of Rationality, as presented by Newell (1982), agents choose actions they know to lead to their goals. Following that, Anderson (1990) has argued that through the evolutionary process human competence in cognitive tasks has been optimized, thus explaining why studying the computational level will also provide explanations on the algorithmic and implementational levels. The evolutionary process and rationality are thought to ensure that human cognitive acts are generally optimized for the task and thus the focus can be on the computational level of explanation. As cognitive scientists have developed the computational modeling of cognitive tasks, the focus has indeed moved to the computational level more than to the algorithmic and implementation levels (see, e.g., Isaac et al. 2014; Szymanik 2016; for a recent example, see Piantadosi et al. 2016).Footnote 4
In this paper, I call the approach that combines computational-level explanations with results from computational complexity theory the computational complexity approach to cognitive complexity. In many ways, it is an understandable development. First, it is a practical fact that computational-level modeling is a field in which great progress has been made. We know much less about the actual algorithms used in cognitive tasks, let alone the neuronal activity that correlates with them. Second, the results from computational complexity are often easily applicable to the study of cognitive complexity. As we will see, there are classes of problems which have been shown to take prohibitive time to solve. When applied to cognitive complexity, such results immediately rule out many algorithms as explanations of cognitive tasks. Third, in focusing on the computational level, there is a natural line of development in terms of abstraction. When making the Chomskyan move from performance to competence, the purpose is to get rid of the inter-individual variations in order to establish the general nature of a cognitive ability. In applying the results from the mathematical study of computational complexity, we are taking one abstraction step further and talk about the computational properties of the mathematical functions we believe to model cognitive tasks. This way, if we model a cognitive task accurately, we can determine its complexity objectively. Perhaps the human performance on algorithmic and implementational levels is less than optimal, but the focus should be on modeling the cognitive task itself, not the full variety of its practical implementations.
We can thus see the computational level as representing competence whereas the algorithmic and implementational levels are associated with performance. This was also how Marr viewed the matter when presenting his three-level distinction:
Chomsky’s (1965) theory of transformational grammar is a true computational theory [...] It is concerned solely with specifying what the syntactic decomposition of an English sentence should be, and not at all with how that decomposition should be achieved. Chomsky himself was very clear about this - it is roughly his distinction between competence and performance (Marr 1982, p. 28)
When it comes to mathematical problem solving, the corresponding view means specifying what the solution to a problem should be, and not how that solution should be achieved. The advantages of this approach are immediately visible. Let us think of a simple mathematical decision problem, such as whether \(27+38=65\) is true. People may apply different algorithms for solving it, but it would be quite strange to claim that all the algorithms are equally representative of human competence. From all the possible algorithms for solving the problem, there must be one (or perhaps more) that is optimal in that it requires the least amount of cognitive processing. As will be seen in the next section, this closely mirrors the computational complexity approach. In studying computational complexity, we are interested in finding optimal algorithms for solving a problem. If we accept the idea that cognitive abilities are (evolutionarily or otherwise) optimized for their tasks, it is understandable to equate the human competence in mathematical problem solving with a computationally optimal problem solving algorithm.
Indeed, in the cognitive domain of mathematical problem solving, I agree that this is how Marr’s focus on the computational level should be interpreted. As explained by Frixione (2001), the computational-level approach allows us to focus on the characteristics of the functions that are proposed as models of particular cognitive tasks:
The relation existing between a computational theory and the algorithmic level can be regarded as the relation between a function (in a mathematical sense) that is computable and a specific algorithm for calculating its values. The aim of a computational theory is to single out a function that models the cognitive phenomenon to be studied. Within the framework of a computational approach, such a function must be effectively computable. However, at the level of the computational theory, no assumption is made about the nature of the algorithms and their implementation. (Frixione 2001, p. 381)
This way, once the function is identified, we can focus on the properties of that function and leave aside considerations on algorithms and their implementation. But when we consider mathematical problems, we are already working within the paradigm of such functions. If we dismiss the algorithmic and implementational levels, we are left with explaining the task of taking a mathematical decision problem as the input and providing the correct answer (yes or no; true or false) as the output. When studying the complexity of this cognitive task, it is understandable to characterize it in terms of the computational complexity of the problem in question. This way, the number of computational steps required to reach a solution is seen as characterizing the complexity of the cognitive task. In the cognitive science literature, this is called problem complexity and it is often considered to be the central variable in the research on mathematical cognition (Ashcraft 1992, 1995; LeFevre et al. 2005).
Generally speaking, this approach is fruitful and reliable. To give an idea why that is the case, let us think of a simple example. It is easy to agree that the task of solving whether \(27+38=65\) is true is cognitively less complex than \(645+472=1117\), even without conducting any experiments. Since the latter sum involves more computational steps—as seen, for example, when calculating the sums with the standard method learned in school—it must be more complex. From the point of view of computational complexity theory, however, the two problems here are in fact instances of the same computational problem; namely, the addition of integers. In complexity theory, as will be seen in the next section, we can study differences in complexity between general mathematical problems. So, for example, we can know that the general problem of finding the best strategy for the game reversi (Othello) is less complex than that of chess (Iwata and Kasai 1994; Fraenkel and Lichtenstein 1981).
Importantly, this result can be established without basing it on any experiments on reversi and chess players. Although there is obviously a great deal of details concerning the neuronal activity and the actual algorithms that are manifested in solving such problems, the computational-level explanations are informative without involving the other two levels. This way, focusing on the computational-level has a great practical advantage: whereas the algorithmic and implementational levels may be extremely difficult to study, research on computational complexity has an established and highly fruitful methodology when it comes to mathematical (as well as many other) problems.
However, this is not to suggest that the computational level is preferred merely due to pragmatic considerations. Marr (1982) and Anderson (1990) have stressed that there is greater explanatory power in understanding the computational characteristics of a particular cognitive task than in explaining the algorithmic and physical manifestations of the task. Indeed, Marr argued that the computational level of explanation is in fact crucial when we try to explain cognitive tasks on the algorithmic and implementational levels:
an algorithm is likely to be understood more readily by understanding the nature of the problem being solved than by examining the mechanism (and the hardware) in which it is embodied. (Marr 1982, p. 27)
Seen in our present mathematical context, the implications of this approach are clear. If we want to examine the way human beings solve mathematical problems, we should focus on understanding the computational nature of those problems. This way, the computational complexity approach to studying mathematical problems can be explicitly formulated as the primary route to explaining human mathematical problem solving competence.
In the first part of this paper, I will evaluate the computational complexity approach to the cognitive complexity of mathematical problem solving. In the next two sections, we will see how useful it can be in limiting the space of possible functions that can work as characterizations of human cognitive capacities. In addition, much of the information we can gather from the research on computational complexity of mathematical problems can be used to assess the complexity of the cognitive tasks involved in solving them. Overall, there is nothing necessarily wrong with the general guideline that the more complex a problem is computationally, the more complex it is for humans to solve it.
However, there is no compelling argument why this should always be the case. The evolutionary argument for the optimization of cognitive tasks, for example, while perhaps appealing in many cases, seems to be a bad fit for mathematical problem solving. On an evolutionary scale, the emergence of mathematics appears to be too recent an event to allow for the optimization of problem solving strategies (Fabry 2019). While an accurate timing of the emergence of the first finger counting and other body part systems is impossible, the earliest known written systems of numerals are from around 3000–2000 BC (Ifrah 1998). Of course mathematical cognition may apply cognitive patterns that have been evolutionarily developed for other purposes, but with this relatively recent history it seems quite plausible that our mathematical problem solving ability can include aspects that are suboptimal. Indeed, in Sect. 6 I will argue that such suboptimal algorithms play an important role in actual human problem solving processes.
3 Computational Complexity
Before we consider the limitations of the computational complexity approach to explaining cognitive complexity of human mathematical problem solving, we should first establish what explanations based on computational complexity can achieve. Let us think of a simple cognitive task, such as finding the largest number out of a small set of numbers. For a set of two numbers, the task consists of taking the numbers a, b as the input and then giving as output the correct answer f(x), where \(x\in \{a,b\}\). Thus we have three components: the input (the domain), the output (the image) and the function modeling the cognitive phenomenon of finding the largest number. On the computational level, it is then a straight-forward matter to analyze the complexity of the task of finding the largest of two distinct numbers. We can move the pursuit to the mathematical study of computability and determine how much resources the task requires.
As a naive initial description, we can calculate the steps it takes to get the correct answer. Given the input a, b, we go through the process characterized by the following algorithm:
-
(1)
Is \(a<b\)? If yes, move to (2). If no, move to (3)
-
(2)
Output a.
-
(3)
Output b.
Although actual human problem solvers may use a variety of algorithms for solving the problem, this three-line pseudo program appears to characterize the problem solving task. In standard mathematical notation, the computational model of the cognitive task is thus the function \(f(a,b)=max(a,b)\).
For a set of three distinct numbers a, b, c we get the following algorithm:
-
(1)
Is \(a<b\)? If yes, move to (3). If no, move to (2)
-
(2)
Is \(a<c\)? If yes, move to (6). If no, move to (4)
-
(3)
Is \(b<c\)? If yes, move to (6). If no, move to (5)
-
(4)
Output a.
-
(5)
Output b.
-
(6)
Output c.
From these simple examples, it is already easy to see the potential fruitfulness of the computational complexity approach. Clearly the case of three numbers appears to be a cognitively more complex problem, as seen from the fact that the pseudo program for solving it consists of six lines, compared to the three lines of the two-number problem. We have not given any consideration to the algorithmic level, i.e., how human reasoners actually compute the output of a given input. Yet the way we found that characterizing the complexities of the two problems seems to be apt from the cognitive perspective, as well. As an important upshot, we can now study the question of complexity of the two cognitive tasks by studying the complexity of the two functions modeling it computationally, i.e., \(f(a,b)=max(a,b)\) and \(f(a,b,c)=max(a,b,c)\). Since an algorithm computing the latter function takes up more resources than the former, we can state with confidence that the cognitive task of solving the latter problem is more complex than the former. It is of course possible that for some individual, the latter problem is easier to solve than the former. But with the focus on competence, such cases are seen as anomalies that do not need to be taken into consideration when we are studying the general cognitive task. In essence, we have eliminated possible inter-individual variation from the explanations, thus moving from studying performance to studying competence, as Marr and Chomsky intended.
But just what do we mean when we talk about the complexity of mathematical problems? In the above case, we characterized it in terms of the length of the algorithm that solves the problem. However, clearly there are many algorithms of different lengths that could solve a particular problem. What we are interested in is not just any algorithm that gives the correct solution, but the one that demands the least resources. The most popular paradigm for determining this is studying complexity in terms of Turing machines. Turing (1936) presented the machine as a way to study computation theoretically. In a nutshell, a Turing machine takes as its input symbols on a tape, one at a time. The Turing machine is always in some inner state and based on the input symbol and the state, the machine is given instructions to read and write symbols on the tape, move the tape, and change to a new inner state (or remain in the same state). The set of these instructions is called an algorithm, giving us an explicit definition of the concept. Since the Turing machine is a theoretical construct, no limits are made to the size of the tape. Most importantly, according to the generally accepted Church-Turing thesis, if there is a mechanical procedure for solving a problem, then there is a Turing machine that can solve it (Turing 1936; Church 1936).
The Turing machine has become the established paradigm for studying algorithmic, mechanical procedures. In the study of complexity in theoretical computer science, researchers are not interested in the computing capacities of particular computers. Instead, they want to study the inherent complexities of different tasks free from the limitations of physical computers. Under this approach, the complexity of a mathematical problem can be characterized by the complexity of the least complex Turing machine (i.e., the algorithm run by a Turing machine that takes a minimum of resources) that solves the problem. Such an algorithm is called optimal.Footnote 5
The Turing machine is closely connected to the computational-level approach in cognitive science. It can be seen as providing a theoretical framework that connects the study of computational complexity and computational-level explanations in cognitive science. Marr’s work on the computational level was influenced by Newell and Simon (1976, 1980, 1982), who argued that cognitive science should focus on functional explanations of what they called physical symbol systems, i.e., general classes of systems capable of manipulating symbols. Marr then developed this idea into the computational level of explanation. For Newell and Simon, the concept of physical symbol system is specified as an “instance of a universal [Turing] machine” (Newell and Simon 1976, p. 117). This way, the computational level of explanation has been from the very beginning in close relation to Turing machines and therefore also the study of computational complexity.
When it comes to Turing machines, there are two main ways of measuring the complexity of algorithms: the time and the space it takes to run an algorithm. Since the Turing machine is an abstract model, time and space are not measured in seconds or bits. Instead, they are measured as a function of the size of the input. This has proven to be a highly fruitful approach and as perhaps the most important result, we can divide computational problems into complexity classes.
Taking time as the measure, one of the most important complexity classes is called P and it is defined as the class of decision problems that can be solved by a deterministic Turing machine in polynomial time (Cobham 1964; Edmonds 1965). An algorithm (i.e., a Turing machine) is said to run for polynomial time if its running time has an upper bound of a polynomial function of the size of the input for the algorithm. This means that if the size of the input is n, the running time has an upper bound of some function \(n^{k}\) for some constant k.
Another important complexity class is called EXP (or EXPTIME) and it is the class of decision problems that are solvable by a deterministic Turing machine in exponential time. An algorithm runs for exponential time if its running time has a lower bound of some exponential function of the size of the input, i.e., for input size of n, the running time has a lower bound of some function \(2^{p(n)}\) where p(n) is some polynomial function of n.
P and EXP form an important pair of complexity classes for two reasons. First, according to the widely accepted Cobham’s (or Cobham-Edmonds) thesis, P is generally seen as the class of problems that can be feasibly solved by a computer. Second, it has been proven that the complexity class EXP is strictly greater than P. Algorithms for solving problems in P are called efficient, or tractable. Algorithms for solving problems in EXP (that are not in P), on the other hand, are inefficient or intractable. As we will see, this distinction is very important when we consider the computational complexity of functions that model cognitive tasks. For computer science, the distinction is crucial. A simple example of an efficient algorithm is multiplying integers, which takes roughly \(n^{2}\) steps of computation for two n-digit integers with the standard algorithm that computers use. The operation of factoring integers into primes, on the other hand, is a good example of an inefficient algorithm. An n-digit integer takes about \(2^{n^{1/3}}\)computational steps (Pomerance 1996).
On first glance, this may look like a terribly useless characterization of efficient and inefficient algorithms. We can have an algorithm that runs for \(n^{99999999999999999999}\) computational steps, which is sure to take longer than the \(2^{n^{1/3}}\)computational steps for prime factoring for any feasible input size n. Yet according to Cobham’s thesis, it is the former algorithm that counts as efficient. There are also rates of growth that are neither polynomial nor exponential, such as \(n^{\log n}\). So why do computer scientists use such a theoretically flawed distinction? The short answer is that in most cases it works. Based on empirical evidence of computation, polynomial time came to be a good characterization for what was considered efficient in practice and exponential time for what was considered in practice inefficient (Aaronson 2012).Footnote 6
However, the distinction between P and EXP is not the only interesting difference in complexity classes. For our purposes, a particularly interesting case is the complexity class NP, which is defined as the class of decision problems that can be solved by a non-deterministic Turing machine in polynomial time.Footnote 7 It is easy to see that P is a subclass of NP, but it has proven to be difficult to show whether it is a proper subclass of it, i.e., whether P = NP. Although this is perhaps the most famous unsolved problem in theoretical computer science, it is a generally accepted conjecture that the class NP is strictly greater than P. This conjecture plays an important role because it is related to the important concept of a computationally hard problem. Hard (or NP-hard) problems are understood to be those problems that are at least as hard to solve as the hardest problems in NP (i.e., those that are not in P). A problem is said to be NP-complete if it is both NP-hard and in NP.
All this is important for us for two reasons. First, since the conjecture \(\mathbf {P\ne NP}\) is generally accepted, the complexity class NP is de facto the lowest complexity class of problems which are thought to be computationally intractable. Second, the class of NP-complete problems includes many famous mathematical problems, such as graph coloring and the traveling salesman problem (in its decision version). It also includes many familiar games, such as Rubik’s cube (finding an optimal solution) and Sudoku (generalized). In short, many of the kind of problem solving tasks that human beings engage themselves in are NP-complete.
If it were the case that P = NP, we would know that all those problems would in fact be included in the complexity class P, and thus be solvable by efficient algorithms. There would still of course remain complexity classes strictly greater than P (for example, the above-mentioned EXP), but computational problems currently seen as computable only by inefficient algorithms would no longer be considered intractable. Here, however, we follow the consensus and accept the conjecture that P = NP is indeed false. Thus we get the following basic distinction: problems belonging to P are efficiently solvable, whereas problems that are NP-complete (or harder) are not. Although strictly speaking at many points in this paper we need to appeal to the conjecture that \(\mathbf {P\ne NP}\), this will not be explicitly mentioned. As we will see, this conjecture that the complexity class P can be identified with solvable problems has had great influence in computational modeling of cognitive tasks.Footnote 8
4 Tractable Cognition Thesis
In computer science, an algorithm refers generally to a finitely describable well-defined procedure which takes an input and after a finite number of steps produces some output and halts. From a modern perspective, the Turing machine gave a highly intuitive characterization of algorithms: essentially, they are the kind of procedures that can be run by digital computers. In this paper, we are interested in algorithms from two perspectives. First, in computational complexity theory, we are interested in optimal algorithms for solving a mathematical problem. Second, from the cognitive perspective, we are interested in algorithms that model human cognitive capacities. As was characterized in Sect. 2, in the computational complexity approach to modeling cognitive tasks those two approaches are merged.
In short, we want to study algorithms for computing functions that work as models of human cognitive capacities. We can define that A is an algorithm for computing a function \(f:I\rightarrow O\) if and only if A is an algorithm, and for any input \(i\in I\) it is the case that A produces output \(A(i)\in O\) such that \(A(i)=F(i)\). When we talk about mathematical problems in this paper, we are in fact interested in algorithms for solving problems. Thus, solving a problem P means to correctly determine the output of function \(f_{p}\) for all inputs in its domain. In this manner, problems and functions are treated here essentially as synonyms and considerations on the complexity of a problem should be understood as dealing with the computational complexity of a problem in terms of an optimal algorithm for solving it, i.e., computing the output of the function for all the inputs in the domain.
Now the question is: what kind of functions can feasibly model human cognitive capacities? In mathematical problem solving, the complexity classes give us a highly fruitful framework for studying this question. For example, to say that a problem P is NP-hard means that computing the solution for every input in the domain of P is not bounded by a polynomial function of the size of the input. This means that an algorithm A for computing the function \(f_{P}:I\rightarrow O\) for all \(i\in I\) takes nonpolynomial time. Because of this prohibitive amount of time that non-polynomial algorithms take to run, they are called computationally intractable. Consequently, \(f_{p}\) cannot feasibly model the problem solving capacity of solving P. This way, computationally intractable algorithms in general are not considered to be feasible Marr’s algorithmic-level explanations for cognitive processes (Frixione 2001).
It should be noted that there are some differing voices on this matter. NP-hard functions have been suggested as models at least for visual search (Tsotsos 1990) and analogical reasoning (Thagard 2000). In addition, some researchers have suggested that humans are able to solve the NP-hard Euclidean Traveling Salesperson Problem near-optimally in a short time (Graham et al. 2000; Dry et al. 2012). However, we should not confuse the actual use of NP-hard functions as models with them being accurate models by the strict criteria applied here. Neither should we believe that near-optimal performance in NP-hard tasks implies that the cognitive processing can only be modeled with NP-complete functions. It is conceivable that in many problems we can reach very good solutions with an approximate algorithm, but these should not be confused with proper exact solutions. In addition, the results presented in Ormerod and Chronicle (1999) suggest that human performance is often not even nearly optimal in the Euclidean Traveling Salesperson Problem.
This way, even though there may not be full consensus over the issue, it is generally accepted that computationally intractable algorithms cannot accurately model human cognitive tasks. This has become known as the tractable cognition thesis in the literature (van Rooij 2008; Isaac et al. 2014). According to the thesis, when we are looking for functions that model cognitive capacities, we should limit ourselves to those functions that can be computed by tractable algorithms. Standardly, based on Cobham’s thesis, this has been understood as the P-cognition thesis, stating that we should limit our considerations to functions that compute problems in the complexity class P (Arora and Barak 2007).Footnote 9
From this perspective, it may seem strange that many of the problems accepted to be NP-complete are actively studied and strategies for solutions are presented (Markman and Gentner 2000; Chater et al. 2006). How is this possible if the required algorithms are conjectured to be intractable? The answer can be found in heuristic procedures (Garey and Johnson 1979; Ausiello et al. 1999). The idea behind them is that while a heuristic procedure H is known to not compute a function f exactly, there is some close relation between the function f and the function \(f_{H}\), which is computed exactly by H. This relation cannot be equality, so it must be the case that for some \(i\in I\), \(f(i)\ne f_{H}(i)\). Normally, the purpose of heuristic algorithms is to render NP-hard problems solvable in polynomial time (i.e., make them P-hard) by using an approximative function the relative error of which we can determine to be under some threshold “not too far from the optimum” (Papadimitriou 1994). Such “quick-and-dirty” algorithms are commonly used in many practical applications, in particular optimization tasks.
Do such heuristic algorithms offer us tools to go beyond tractable cognition? Although this may be seen as a feasible way to handle intractable algorithms, as van Rooij et al. (2012) have argued, there are fundamental problems involved in such claims if we consider the matter from a philosophical rather than a practical perspective. First, the introduction of H makes the computational and algorithm-level explanations inconsistent. Since for some \(i\in I\) it must be the case that \(f(i)\ne f_{H}(i)\), we can confirm \(f_{H}\) as the algorithm-level solution to a problem only if f is disconfirmed as the computational level solution to the problem, and vice versa. Second, H must fail as a cognitive explanation of solving f, because the cognizer with the procedure H does not compute the function f, but rather \(f_{H}\), which is by definition another problem.
All this should of course not be confused with thinking that human cognizers do not use heuristic procedures, nor that they are irrelevant for the study of cognitive complexity. Instead, what van Rooij et al. (2012) argued was that if we appeal to heuristic procedures as ways out of intractable algorithms, we are subtly—or indeed often not so subtly—moving the goalposts. Van Rooij and her colleagues go through many proposed counter arguments (such as heuristic procedures providing partial explanations, optimism from many successful cases where \(f(i)=f_{H}(i)\), and perhaps most strongly, approximations), but their argument seems to be left unharmed. Heuristic procedures do not give us a way to make intractable algorithms tractable, regardless of their great usefulness in achieving just that in the kind of approximative manner sufficient for many practical purposes.
From the considerations above, it becomes clear that heuristic algorithms do not allow us to drop the P-cognition thesis. We may discuss the details, but it seems that we should adopt some form of the tractable cognition thesis. Based on the physiological limitations of our brains (as well as our computing tools), algorithms above some complexity level cannot be feasibly implemented by us. Consequently, there must be some level of complexity after which problems are no longer computable for us. This is an extremely important point and the way we can analyze it in terms of complexity classes shows the great fruitfulness of the computational complexity approach to modeling cognitive tasks. A vast class of functions can be feasibly dismissed as potential models of human cognitive tasks due to their prohibitive complexity. Equally importantly, considering the topic of this paper, a vast class of mathematical problems can be deemed to be unfeasible for humans to solve efficiently.
Throughout these considerations, we should keep in mind the pragmatic character of the complexity classes. For small inputs, NP or EXP-hard problems can be perfectly solvable for human beings, whereas P-hard problems are unsolvable for large enough inputs. The complexity classes, as well as the tractable cognition thesis based on them, should be seen more as guidelines for evaluating complexity than strict results. Thus the P-cognition thesis should not be understood to claim that NP-hard functions, for example, cannot be used to model cognitive capacities. Rather, the thesis implies that for each such model, ultimately—perhaps for larger input—there must be a P-hard function that models the capacity more accurately.
But this pragmatic nature of the complexity classes notwithstanding, the acceptance of the tractable cognition thesis has very strong implications for philosophy of mathematics and beyond. Indeed, if mathematical problems beyond a certain complexity are thought to be unsolvable, this is a strong conclusion generally for philosophy of mind and epistemology. It imposes explicit limits on what our cognitive capacities can achieve, as well on the class of problems whose truth-values we can know.
5 Complexity Within P and the Computational Paradigm
As fruitful as the computational approach to both cognitive modeling and mathematical problem solving has proven to be, it is clear that the limits it imposes are in practice rather weak. Even by accepting the P-cognition thesis we are left with an enormous class of functions that can potentially model human cognitive capacities, namely all functions computable in polynomial time. Finding the greatest common divisor (GCD) of two integers, for example, is known (in its decision form) to be in the complexity class P, yet a sequential solution for it can take a prohibitive amount of time. It could be the case that the GCD could be solved faster by parallel processing, yet there is no known way of parallelizing the computation effectively.Footnote 10 The algorithm for solving GCD may thus be seen as unfeasible as a model of human cognitive capacities.
Although the case of GCD is not clear, it reminds us of an important point: we should not treat all mathematical problems in the complexity class P as being the same in terms of complexity. Crucially, even if a problem were solvable in polynomial time, it could be in practice beyond the human capacity to solve it. All the P-cognition thesis gives us is an upper bound for human problem solving capacity. But within P there are problems with very different computational complexities. When studying the complexity of human mathematical problem solving ability, we should be interested in those differences. If it is possible to identify within P complexity measures that characterize mathematical problems in a more fine-grained manner, we would get important information also for identifying the cognitive tasks involved in the problem solving process.
There are many ways to expand our approach in order to be able to study complexity within P. We can, for example, stay within the prevalent paradigm of studying complexity in terms of the time or space needed to solve a problem. We simply need to look for complexity measures within P. In addition to the complexity class NC mentioned above, one interesting complexity class is L, the class of problems decidable in logarithmic memory. It is known that both NC and L are subsets of P, but it is not known whether NC = P or L = P. These problems may turn out to be as difficult as the problem P = NP, but it is conceivable that results from the study of complexity of classes provides us with more tools to distinguish between complexity classes within P.Footnote 11
However, it could also turn out that in order to have maximally useful computational characterizations of mathematical problems for the study of cognitive complexity, we need to introduce more fine-grained measures of complexity than provided by complexity classes like NC, L, P, NP and EXP. This can be done by studying the functions that are upper bounds for the running time of an algorithm that solves a problem. Or in a pragmatic approach, we can measure the actual running times of algorithms on physical computers. Finally, we could also introduce another notion of complexity, such as Kolmogorov complexity, to work as the relevant unit of measure.Footnote 12 Alternatively, complexity for particular cases can also be measured in terms of computational steps, as in the example in the beginning of Sect. 3 of this paper. All these approaches have their difficulties, but a wider research paradigm with a plurality of measures of complexity can give us tools to introduce more informative distinctions between the complexity of mathematical problems.
What all such approaches have in common, however, is that they do not focus on the human aspect of mathematical problem solving. As we have seen, we can do a great deal of important work purely theoretically in the computational approach to cognitive modeling. But obviously there are limits to this: at some point we need to study the actual human cognitive capacities in order to find out which functions can model them. To assess the computational complexity of different cognitive tasks, we obviously first need to model those cognitive tasks as mathematical functions. The interesting thing about mathematical problem solving, however, is that we often seem to be able assess the complexity in a purely a priori manner. By studying the two simple problems presented in Sect. 3, for example, it is quite understandable to deem the three-number case as cognitively more complex than the two-number case, without ever conducting empirical research on how human reasoners in practice solve the problems.
It should be noted that while it may seem that cognitive complexity of mathematical problem solving can be studied independently of all empirical data, the matter may not be that simple. It is certainly true that the complexity of the cognitive task of solving a problem is often assessed based on the computational complexity of the problem, which can give the impression that the assessment is purely a priori. However, it seems feasible that this methodology would not be used if it were in conflict with empirical data. There are at least two ways in which the seemingly a priori assessment of cognitive complexity can in fact be based on empirical results. First, all the data we have about cognitive capacities in general can be used to justify the assessment of the complexity of mathematical tasks. The limits of working memory, for example, impose limits on our problem solving capacity, as do physical limitations in using external tools. We do not need to empirically study each mathematical problem if we can establish that a certain class of problems puts more demands on working memory than another class. Second, the general method of using computational complexity to characterize the complexity of the problem solving tasks only works because in many cases we know the human competence to be modeled reasonably well by computationally optimal algorithms. Empirical data on the competence in the addition of (small) natural numbers, for example, implies that an optimal algorithm can be used to characterize the complexity of the human cognitive task (Fuson 1992).
This way, what may seem like a priori assessment of cognitive abilities may in fact be at least partly based on empirical considerations. Although the empirical data may not be explicitly acknowledged, using computational complexity to explain the complexity of cognitive tasks may be empirically justified. This empirical aspect notwithstanding, however, in practice the exclusive focus on the computational level of explanation can make the approach largely a priori. In a purely computational-level approach it is natural to assume that human competence can be modeled by optimal algorithms for solving mathematical problems, rather than studying empirically what kind of problem solving algorithms actual human reasoners use.
While this computational-level approach has clear advantages, I submit that there should be limits to how strong and wide the application of the a priori computational methodology should be. As fruitful as the computational complexity paradigm may be, we should not dismiss the possibility that human competence in mathematical problem solving may indeed differ in important and systematic ways from the optimal algorithms studied in the computational complexity approach. In the rest of this paper, I will argue that by including considerations on the algorithmic level, we can get a more informative framework for studying the actual human problem solving capacity. Furthermore, I will show that the algorithmic-level approach does not move the discussion from competence to performance. Instead, we get a theoretical framework that is better-equipped for explaining human competence by including considerations of the algorithms that are cognitively optimal for human reasoners.Footnote 13
6 Humanly Optimal Algorithms
When we study human mathematical problem solving abilities, it is quite obvious that we will encounter a great deal of suboptimal performance. Humans make errors and even when correct, they may use algorithms that are less than optimal. In the tradition of Chomsky and Marr, such use of suboptimal algorithms is deemed to be variation in performance and as such irrelevant for studying competence. Since that paradigm aims to explain general human competence when it comes to mathematical problem solving, in that respect it is not important that people do not always reach the full competence, nor that even competent problem-solvers are not always completely error-free and optimal.
However, when seen in the current setting of the computational complexity approach to modeling cognitive processes in mathematical problem solving, there is a potentially serious difficulty involved. In the study of computational complexity we are (in this regard) mostly interested in optimal algorithms. If we characterize the complexity of the cognitive task of solving a mathematical problem through the complexity of the problem, we are implicitly assuming that the competence of human reasoners can be characterized by a computationally optimal algorithm.
This approach seems to be unproblematic when it comes to some mathematical problems. Human competence in the addition of integers, for example, seems to use an optimal algorithm, and there is also evidence that this is the case in certain logical tasks (Szymanik 2016, Section 5). However, in what follows, I will argue that there is no reason to believe that this is generally the case. In fact, I will argue that there are several ways in which the human problem solving cognitive capacity differs essentially from the optimal algorithms for solving mathematical problems.Footnote 14
There have been some arguments (e.g., Penrose 1989) to the effect that human mathematical ability could actually rise above the power of any algorithms, by a special intuition or mathematical insight. I consider those arguments to be dubious and will not focus on them here. I believe that mathematical intuition and insight are important subjects and they no doubt play an important role in mathematical problem solving. However, based on the definition of optimal algorithms, I cannot see how they could lead to super-optimal solutions to mathematical problems. If they did, we would presumably be able to model this “insightful” solution, which would then turn out to be an optimal solution.Footnote 15 Under the computational complexity approach—when possible—the complexity of mathematical problems is characterized by optimal algorithms. Such algorithms do not need to be unique, but by definition, every other algorithm for solving the problem takes equally long or longer to run than an optimal algorithm (or performs at best a constant factor better).Footnote 16 With human insight, we may be able to provide feasible hypotheses, partial or approximate solutions, or structures and strategies for solutions—and this process may take less time than an optimal algorithm. But we cannot have full step-by-step solutions that are faster than an optimal solution.
However, this does not mean that special human cognitive characteristics (what we might call “insight”) do not play an important role in mathematical problem solving. Here I want to distinguish between optimal algorithms and humanly optimal algorithms. The key idea is that the solution that is most easily accessible to human cognizers may not always be a computationally optimal one.
Let us say that an algorithm A is optimal for reaching the solution S to the problem P and it takes time t to run it (Fig. 1). Now by studying human performance in solving P, we may find out that even if the solution S is correct, the actual algorithm A* may have been different from the optimal algorithm A (or an equivalent other optimal algorithm) and by definition the time taken t*> t (Fig. 2).
In the computational-level approach of Chomsky and Marr, such a result would be dismissed due to it concerning performance rather than competence. But what if we acquired extensive data and found out that humans generally use a suboptimal algorithm like A* to solve the problem? In that case there would clearly be a unique algorithm to describe the human competence, yet it would not correspond to an optimal algorithm. Such an example would show, contra Marr, that the explanation cannot focus mainly on the computational level. As we have seen, in the computational complexity approach optimal algorithms are used to model human cognitive competence. But if human performance generally follows a suboptimal algorithm, how can we retain this approach?
In the rest of this paper I will argue that indeed we cannot, and we must take into account also Marr’s Level 2, the algorithmic level of explanation.Footnote 17 We will start by looking at three cases in which the humanly optimal algorithms for mathematical problem solving are not the same as the algorithms with the lowest complexity, and assess the computational approach in each of them.
Before that, however, we need to ask how we should understand a “human” problem solver and what exactly is meant by “humanly optimal algorithm”. Clearly human mathematical problem solving is in most cases aided by some tools, ranging from fingers to pens and paper to computer programs. Indeed, anything we can achieve with the help of computers is human endeavor and thus it could be argued that all mathematical problem solving is ultimately human problem solving. Perhaps we could limit human problem solving to mental operations carried out in the working memory without any external aids, but that would seem to be needlessly limiting given the importance of external tools for mathematical practice in all its levels. In the face of this, it may seem that any characterization of “human” problem solving is largely arbitrary. Moreover, many problem solving processes include several human beings. Should we limit the approach to individual problem solvers? But then how should we assess the cultural input of other people on that individual?
Similar questions may be asked about “humanly optimal” algorithms. Should we consider the tools used in problem solving processes? If so, how should we account for the differences in tools that different cultures have? For example, there can be different cultural emphasis how pen-and-paper methods and tools like abacus are used for solving arithmetical problems. Indeed, problem solving strategies in mental arithmetic also differ culturally—partly due to the different tools used—and this can be seen as differences in the brain region activation associated with mental arithmetic (Tang et al. 2006). How is it possible, from this background, to characterize a problem solving algorithm as “humanly optimal”?
These are all relevant questions and a full treatment of them is unfortunately not possible. We treat these issues in detail in (Fabry and Pantsar 2019). However, it should be pointed out here that while I do not want to suggest a particular limitations, I believe that even in the face of such questions, there can be meaningful characterizations of “human” problem solving and they can be explanatorily useful. What such characterizations should do, at the minimum, is pick out problem solving processes which are used generally enough, and in which the cognitive process is essential to reaching the solution. Importantly for the purposes of this paper, under such a characterization, simply typing an input to a computer program and reading an output does not count as a human problem solving process.
Similarly, I want to introduce the term “humanly optimal algorithm” as a characterization that we can use as a tool in modeling the problem solving strategies that human cognizers use, rather than something that could be universally defined for particular mathematical problems. As will be discussed in Sect. 7, what is humanly optimal depends on how our problem solving processes are culturally determined. As such, the general use of the term “humanly optimal algorithm” should be understood as a tool that can be used to introduce a new approach to modeling human problem solving processes and characterizing their complexity. The important idea is that humanly optimal algorithms are not necessarily computationally optimal, but cognitively optimal for human cognitive agents with specific learning trajectories. I will argue that this approach allows for more accurate characterizations than the computational-level approach focusing on computational complexity. In the final section of this paper, we will see in more detail how the concept of humanly optimal algorithm can be used in pursuing more accurate models of human problem solving processes, and therefore also more accurate characterizations of their cognitive complexity. But first, let us take a look at some examples of the ways in which human problem solving processes can be computationally suboptimal.
-
Example 1: Fast computer algorithms
In many cases, it is understandable that computer algorithms for solving mathematical problems are modeled after the algorithms we have learned in school. In the case of addition, for example, the most common human algorithm would also appear to be an optimal one. Also for multiplication, there would seem to be nothing wrong with using the standard schoolbook algorithm. Multiplying integers with the standard method we have learned in school takes roughly \(n^{2}\) steps for two n-digit integers, thus making it a relatively low-complex problem in P. However, Schönhage and Strassen (1971) have shown that there are also more advanced algorithms for multiplying large integers, ones that have lower upper bounds for the running time. The so-called Fast Fourier transforms are another algorithmic method that greatly reduces the complexity of computing discrete Fourier transforms of sequences. Yet another example can be found in matrix multiplication, in which the Strassen algorithm is quicker for large matrices than the standard method we learn in school. Multiplying two matrices of the size \(2\times 2\) with the standard method learned requires 8 multiplications. The Strassen algorithm, however, manages to reduce this to 7 multiplications by adding new addition and subtraction operations. In this way, the algorithm is actually more complex in that it requires more steps, but since multiplications take more time than addition and subtraction, for large matrices the Strassen algorithm becomes faster than the standard algorithm. Even faster algorithms for matrix multiplication have been invented, thus making the standard method increasingly less optimal in terms of time-complexity (Skiena 2008).
Due to limits in space, it is not possible to present the details of these algorithms, but in all three cases, human problem solvers do not generally use the faster algorithm to solve the task. Thus all three examples appear to give us clear cases where algorithms with lower time-complexities are not used by human problem solvers. This would seem to go against the basic paradigm of the computational complexity approach to mathematical problem solving: for some mathematical problems, the lowest-complexity algorithms cannot feasibly characterize the cognitive processes of human problem solvers.
However, it could be that all three cases are relevant in a limited manner, since the advantage of the fast algorithms only starts to show with operations that involve very large numbers. The Karatsuba algorithm, for example—which used to be the fastest multiplication algorithm before the Schönhage-Strassen algorithm—only starts to outperform the standard algorithm when the integers are hundreds of bits long (Karatsuba and Ofman 1962). It is unfeasible that a human problem solver (as characterized above) would ever perform this kind of multiplication, and it could thus still be the case that for all the relevant multiplications—those that human beings could in principle engage in—the standard algorithm is also a computationally optimal one, and not merely humanly optimal. Thus we should perhaps look elsewhere for more widely relevant humanly optimal algorithms which are not computationally optimal.
-
Example 2: Diagrams
Based on the above considerations, it is unlikely that these kinds of simple mechanical operations are where we can find the kinds of humanly optimal algorithms we are after. For that, we should look at more complex mathematical tasks, in which the human cognitive task could differ importantly from an optimal computational solution. Unfortunately, however, the more complex a mathematical task is, the more problematic it becomes to study the cognitive processes that are involved in solving it. Still, mathematical practice gives us reason to believe that mathematical problem solving generally is not a case of applying an optimal algorithm. Instead of merely constructing step-by-step solutions, in mathematics a wide array of different cognitive resources are used. As analyzed by, e.g., Schoenfeld (1985), it is clear that problem solving is not a straight-forward process where different algorithms are tested until the correct one is iteratively hit upon. In Schoenfeld’s analysis, mathematical problem solving draws from four factors: resources, heuristics, control and belief systems. While control (i.e., resource management) and belief systems (i.e., mathematical world view) form interesting research questions, here I am more interested in the first two. How do human cognizers typically use their body of knowledge about mathematics to solve a particular problem? And crucially to the matter at hand, can analyzing human problem solving from this perspective provide insight into cognitive complexity that goes beyond the computational complexity approach?
One strategy that humans constantly use in mathematical problem solving are different types of heuristic, or didactic, processes. These should not be confused with the heuristic algorithms we discussed earlier. Whereas heuristic algorithms in computer science provide partial or approximate solutions, humans use heuristic processes also in processes that lead to exact solutions.Footnote 18 Among these heuristic and didactic processes, drawing diagrams is probably the most prevalent. Ever since Polya’s How to solve it (1945) and Hadamard’s The Psychology of Invention In The Mathematical Field (1954) were first published, the study of heuristics and didactic methods of mathematical problem solving has been an important topic in mathematics education. Starting from perhaps Polya’s most commonly applied rule “If you are having difficulty understanding a problem, try drawing a picture”, some didactic rules have become the standard way in which mathematics is taught. The great usefulness of pictures and diagrams has been confirmed in an enormous number of studies (see, e.g., Jamnik 2001; Uesaka et al. 2007; Diezmann and English 2001). Yet applying already that simple rule of Polya takes us away from the computational complexity approach to characterizing human problem solving. Generally speaking, computers do not benefit from visualizing problems and adding this sort of didactic process to a problem solving computer program makes it less optimal, thus (from the computational perspective) needlessly increasing the complexity of the solution.Footnote 19 For human problem solvers, however, the matter is quite different. The computationally superfluous pictures, analogues and such can be absolutely crucial for finding the solution.
Let us consider a simple theorem from analysis, Bolzano’s theorem, stating that if a continuous function gets both negative and positive values inside an interval, it must have a root in that interval. Most students of mathematics are familiar with some diagram explaining the idea of the theorem (Fig. 3). Furthermore, for most students, this kind of diagram helps grasp the content of the theorem (Zachariades et al. 2007). Yet it is clear that in the mathematical community, drawing this kind of a diagram would not be considered to be an acceptable solution to a problem. Instead, the diagram works as a didactic tool that helps us better understand the formal theorem.
But from the computational point of view, drawing the diagram only makes the algorithm human cognizers use more complex than an optimal algorithm (Fig. 4). Since A’ introduces a parallel process, it must be the case that the time used by it is more than the time used by an optimal algorithm, i.e., t’> t.
In fact, in many cases, the diagram does not advance the formal solution at all. In such cases, the function of the diagram is purely didactic (Fig. 5). What the diagram does in such cases is assist us in finding the formal solution. For a problem solving computer program, this would mean that the initial representation of a mathematical problem is changed into another mode of representation, but ultimately the solution must be presented in terms of the initial representation. The solution via this process is generally computationally more complex than an optimal algorithm for solving the problem. In the case of Bolzano’s theorem, for example, it seems clear that a theorem-proving computer program would not benefit from changing into a visual representation.
It is of course possible that diagrams and other didactic methods are not indispensable for all humans in solving any particular mathematical problem. Even if diagrams were generally useful, it is possible that all mathematical problems could be solved by some human reasoners without them. In that case we could in principle find for any problem a solution in which the human cognizer uses a computationally optimal algorithm. Indispensability, however, is too strong a condition for the current purpose. What we want to know is whether there are problems in which human reasoners generally benefit from diagrams or other didactic and heuristic tools. With many problems, it seems highly probable that this is the case. If we are looking to establish what the human competence in certain problem solving task is, as indeed is the purpose in the paradigm established by Chomsky and Marr, it seems clear that we should be interested in this general trait, rather than possible outliers.
If our aim is to model human cognitive tasks accurately, we must include considerations on didactic processes such as constructing and interpreting diagrams. The problem is that such matters can be hard to study. The cognitive processes involved in solving even a moderately difficult mathematical problem are not easy to identify with brain scanning methods, thus making explanations on the implementational level problematic. On the algorithmic level, we can measure problem solving time for simple problems, and thus compare the cognitive efficiency of different algorithms used to reach the solution. For more difficult problems of the type that mathematicians actually deal with, however, also this method can be tricky. As the problems become more complex, it becomes increasingly difficult to trace all the parts of the algorithm that the problem solver uses. Often we have to rely either on observing mathematical practice or the testimony of the mathematicians. Both of these methods have significant drawbacks. Observing mathematical practice is likely to include many stages of thought process which are difficult, if not impossible, to detect. Questionnaires and interviews of mathematicians are also potentially problematic. Not only are there the usual problems with unreliability of introspective inquiry, but the kind of didactic, heuristic and intuitive aspects of mathematical thinking that we would wish to identify are often likely to be unconscious and difficult to get reliable data on.
That practical difficulty notwithstanding, however, heuristic and didactic processes like diagrams seem to give us a clear case in which the humanly optimal algorithms may differ from the optimal algorithms, as studied in a purely computational approach to mathematical problems. Consequently, heuristic and didactic processes are also a clear case in point that we should not work exclusively on Marr’s computational level. In the computational complexity approach to mathematical problem solving on the computational level, such computationally suboptimal tools are by definition ignored. But given the great use that human problem solvers have for such cognitive tools, it becomes obvious that we should also be interested in the actual algorithms that human cognizers use. Indeed, to understand the human problem solving capacity as well as possible, it is the humanly optimal algorithms that we should be looking for—as suboptimal as they may be computationally.
It should be noted here that taking didactic processes into consideration does not in any way imply that the cognitive task of mathematical problem solving could not be computationally modeled. Rather, the argument here is that instead of focusing only on the input (the problem) and the output (the solution), we must be prepared to take into account all the relevant cognitive processes involved in mathematical problem solving. Some of these processes concern individual performance and should not be included in accounts of mathematical competence. But some processes, like those including diagrammatic reasoning, are likely to be generally applied by human problem solvers (at least those with a shared cultural background) and cannot be dismissed as dealing with performance. When it comes to modeling mathematical competence computationally, we need to identify these latter processes before we can know what we are modeling.
-
Example 3: The Distance effect
Above I have argued that diagrams and other heuristic and didactic methods contribute to humanly optimal algorithms. But there are also ways in which we use suboptimal algorithms which actually make solving problems unnecessarily hard for us. Diagrams concern a relatively sophisticated level of mathematical thinking, but we can see computationally suboptimal algorithms in use already on the very basic, unconscious level of treating mathematical concepts.
Consider the simple task of determining which of the following numbers is bigger:
Compare this now to the task of determining which of these numbers is bigger:
One would expect that the task is so simple that in both cases it takes equally long to get the answer. However, the data shows that even for adult subjects, the (4 5) pairing takes considerably longer than (4 9). This is called the distance effect: the greater the numerical distance between the two numbers, the quicker we are in solving the problem. The distance effect is usually explained in terms of our automatic tendency to process numerical symbols as quantities. When we process quantities we use the so-called approximate number system which is an estimation system that becomes less accurate as the distance between numbers becomes smaller (and the magnitude of numbers becomes larger) (Dehaene 1997/2011, pp. 62–64).Footnote 20
Interestingly, we cannot get rid of the distance effect even if we are trained to solve these types of problems. The effect is also a remarkably strong one, as seen from the following example. Let us have the same task with the these numbers:
And these numbers:
Now we would certainly expect the solution to take an equally long time. After all, we can clearly grasp an optimal algorithm for solving the problem, which would be to first compare whether there is a difference in the first digit and only consider the second digit if no such difference exists. Yet also in this case there is a clear difference, the pair (71 65) takes more time than the pair (79 65) (Hinrichs et al. 1981; Pinel et al. 2001).
In fact the distance effect can also be detected when asked whether two numbers are the same. When given numbers:
We are faster in determining that the numbers are not the same as with:
This is also the case when numerals were use instead of number symbols (TWO NINE takes shorter than TWO THREE) (Dehaene and Akhavein 1995). For some reason, we cannot treat number symbols or numerals without thinking of them as quantities and reverting to the approximate number system.
The distance effect has important consequences for the topic at hand. The kind of problems we have been dealing with in this example may not be particularly interesting as mathematical problems, but they show how we automatically assign meaning to number symbols and words.Footnote 21 Sometimes this may be beneficial. For example, we may be quick to establish that 23 + 56 = 15 is false because the approximate sum is so far away from the suggested answer. But we cannot help associating this approximate quantity with number symbols even in cases in which it only adds to the complexity of the problem.
It is not the fact that we have different connotations for different number symbols that is important here. When we think about a mathematical problem, many of the connections we make—and thus much of the neural activity in our brain—can in fact be irrelevant for solving the problem. When solving whether \(27+38=65\), I might for example make notice of the fact that I was born on the twenty-seventh, which does nothing to advance the solution. Another example are people who associate numbers with colors. This digit-color synesthesia makes it harder to identify numbers when they do not correspond to the synesthetic experience (Kadosh and Henik 2006). Of course it is just such incidental connections that we try to get rid of by moving from performance to competence. While our performance in the addition of integers may involve task-unrelated associations, our competence does not. From the point of view of the computational approach, we treat integers independent of their conceptual connections. If our actual algorithms for doing addition sometimes involves detours like birth-dates and colors, this does not need to be taken into consideration.
However, the empirical data strongly suggests that whenever human cognizers see number symbols, they automatically process them as magnitudes, and the effect is present in everyone familiar with number symbols. With this type of general cognitive tendency, we can longer dismiss the suboptimal algorithm as dealing with performance. Instead, our cognitive competence with integers includes the distance effect, and if we want to model the cognitive capacity accurately, also the distance effect must be included in the model.
Certainly there is nothing in the distance effect that suggests that it could not be computationally modeled, and such models have indeed been proposed (starting from Dehaene and Changeux 1993). But the modeling of it goes against much of what we would expect from an algorithm that takes numerical distance into account. For a computer algorithm to count the distance between two numbers, we should expect the reverse of the distance effect: the smaller the difference, the faster it is to compute. Thus the suboptimal problem solving algorithms due to the distance effect seem to be a genuinely human (and possibly animal)Footnote 22 phenomenon whose modeling requires moving beyond the computational-level approach and including the algorithmic level of explanation.
It could of course turn out to be the case that the distance effect does not play a role in human arithmetical calculations. It could merely be “noise” that disturbs arithmetical calculations by making us process numerical symbols as magnitudes. The arithmetical calculations themselves could follow algorithms that are computationally optimal. This is a possibility that should be empirically pursued. What we do know is that even for mathematically highly educated subjects, the total cognitive process of being presented with an arithmetical problem and solving it is not algorithmically optimal. When we study the human competence in solving arithmetical problems, this needs to be taken into account.
7 How to Study Humanly Optimal Algorithms
Above we have arrived at an important conclusion: the computational complexity of a mathematical problem cannot be equated with the complexity of a humanly optimal algorithm for solving it. As a direct consequence, the complexity of the cognitive task of solving a mathematical problem is not necessarily the same as the computational complexity of the problem. In Sect. 2, Marr’s computational level of explanation was characterized in terms of identifying a function that models a cognitive capacity in terms of its input and output. Due to the considerations above, we have established that such modeling does not always give the best characterization of the cognitive capacity in question. We should also consider the algorithms that human cognizers use to compute the values of the function.
Therefore, in the Marrian three-level distinction between explanations in cognitive science, at least some cognitive tasks are not best characterized purely in terms of the computational-level approach. Moreover, the entire distinction between the computational and algorithmic levels becomes problematic: without including the algorithmic level we cannot identify the phenomena we aim to model on the computational level. In principle, there is of course nothing to prevent determining the complexity of the algorithms that human beings use in their cognitive tasks purely computationally. However, with too much focus on the computational approach, how can we find out what the human algorithms are? If the algorithms that most accurately model the problem solving strategies of human cognizers are not necessarily computationally optimal ones, we should already include considerations on algorithms—and possibly also their implementations—in the initial research question.
In fact this approach can already be seen in the actual computational modeling of human cognitive capacities. Sun (2008), for example, has noted that the distinction between Marr’s three levels is relatively insignificant in modern computational modeling:
One cannot specify algorithms without at least some considerations of possible implementations, and what is to be considered “computation” (i.e., what can be computed) relies on algorithms, especially the notion of algorithmic complexity, and so on. Therefore, one often has to consider computation, algorithms, and implementation together somehow (especially in relation to cognition). (Sun 2008, p. 15)
This developing modern paradigm fits well with the theoretical considerations of this paper. As we have seen, the computational approach can be needlessly limiting and may preclude finding important data about the algorithms used by human cognizers. Without including the algorithmic level, we may not be able to identify the cognitive phenomena we want to model in the first place. This way, dismissing the algorithmic level leads to problems also on the computational level.Footnote 23
However, acknowledging the need for a wider methodological paradigm is only the first step. As important as expanding the study of cognitive complexity to include algorithmic aspects is, there are many understandable difficulties involved. Most importantly, the characteristics of advanced mathematical cognition can be very difficult to study. This is the case especially on the level of implementation, but also in terms of identifying the algorithms that humans use in problem solving (see, e.g., Tall 2002; Dowker 2016). Perhaps in their minds the test subjects make cognitive moves that do not show up as behavioral patterns, nor are the test subjects able to identify them introspectively (Peters and Bjalkebring 2015). The design of pertinent experiments is an enormous challenge and even with ideal circumstances for testing we cannot be entirely sure that we have accurately identified the algorithmic procedures. While that does not mean that we cannot gather reliable data at all, it does bring in the kind of inexactness that is a bad fit with the exact notions involved in the study of computational complexity (see, e.g., Carruthers and Stege 2013).
These practical difficulties of studying mathematical cognition should not be downplayed, yet at the same time they should not be thought of as an argument against engaging in the algorithmic level of explanation. From the perspective of computational complexity, it may be asked why we should be interested in modeling suboptimal algorithms in the first place, whether they concern diagrams and other didactic and heuristic tools, or unconscious processes like those underlying the distance effect. After all, the computational complexity approach has an established fruitful methodology, and including algorithmic considerations only makes the problems more complicated and difficult to study. However, the fruitfulness and established methodology of the computational complexity approach should not lead to a streetlight effect in which the ease of explanation becomes a determining factor in establishing the research paradigm.Footnote 24
However, aside from such practical worries, there is also a potentially important theoretical problem in algorithmic-level explanations. In the previous section, I proposed that we can consider an algorithm humanly optimal if it is generally beneficial for human problem solvers. But as was also mentioned in that section, there is no reason to believe that there are unique humanly optimal algorithms for mathematical problems. Indeed, since mathematical practices (including symbols, tools, etc.) vary in different cultures, it seems clear that we should be looking for optimal algorithms in culturally specific contexts. For example, let us consider the “Japanese” visual multiplication method (Fig. 6), in which orthogonal lines are drawn for ones, tens and hundreds, etc. and the result is reached by counting the intersections of the lines.Footnote 25
Whereas that method may be heuristically less complex for children acquainted with it—at least with numbers where the digits are small like in Fig. 6—for children not acquainted with such visual methods this is usually not the case. In addition to such cultural differences, there are also individual differences in how helpful we find different heuristic methods. More visually inclined students, for example, are likely to find diagrams and other visual methods more helpful, and students with diverse learning abilities generally benefit from different heuristic and didactic tools (van Garderen et al. 2013).Footnote 26
In this way, many mathematical practices are enculturated. Enculturation refers to the transformative process in which interactions with the surrounding culture influence the way cognitive practices develop (Menary 2015; Fabry 2018). Through the mechanism Menary (2014) calls “learning driven plasticity”, new cognitive capacities can be acquired due to the neural plasticity of the human brain, which allows for both structural and functional changes (Dehaene 2009; Ansari 2012; Anderson 2014). In learning mathematics, the methods and practices of the surrounding culture thus play an important role in how the cognitive mathematical capacities develop. This theoretical framework can help explain the different methods that human problem solvers use (Pantsar 2018, 2019).
The computational complexity approach to mathematical problem solving, and computational-level explanation based on it, is unable to account for the enculturated nature of problem solving processes. This is where the present approach has an advantage. By including the algorithmic level in the explanations, we can study which problem solving methods are cognitively beneficial for human problem solvers within a particular culture. We can also study how these methods vary inter-culturally. Perhaps for many mathematical problems there is relatively little cultural variation. With some problems, it may make sense to speak of universal, humanly optimal problem solving algorithms. In some cases, these may also coincide with computational optimal algorithms. However, we should not assume that this is generally the case. That is why humanly optimal algorithms must be considered conceptually separate from computationally optimal algorithms. For the same reason, cognitive complexity should be considered to be conceptually separate from computational complexity. Because of the expected cultural variation, humanly optimal algorithms—and hence cognitive complexity of mathematical problem solving—should be considered in cultural contexts. With these conceptual differences in place, our approach can account for the enculturated nature of mathematical practices.Footnote 27
At this point, one might ask whether this cultural and individual variation is not about performance while we are interested in competence? But based on all the considerations we have been through in this paper, it is impossible to retain this distinction in the sense that there is one human competence in mathematical problem solving. Mathematical problem solving is an ability with great cultural and individual variation and a single notion of mathematical competence seems thus misplaced. The distinction between performance and competence is important to make, but instead of having a uniform notion of an optimal algorithm (and one corresponding notion of competence) we should look for general patterns in performance in order to establish a wider, more fine-grained conception of enculturated competence. With the focus on enculturated competence, we can have a theoretical framework that is more sensitive to particular culturally determined mathematical practices, such as constructing and interpreting diagrams.
In studying enculturated mathematical competence, it is clear that we should use as much information about the computational complexity of mathematical problems as we can. While the cultural and individual differences are important, much of the complexity of the cognitive task of solving a mathematical problem can indeed be traced to the computational complexity of that problem. In this way, the approach here is not meant to question the value of the established fruitful methods of studying complexity. Instead, I want to suggest that the established methodology can be augmented by including considerations of the actual, sometimes suboptimal, enculturated algorithms that human problem solvers use.
It should also be noted that mathematical competence is a much wider phenomenon than simple problem solving. Throughout this paper the focus has been on problem solving, and even that only in a very limited paradigm set by Turing machines, i.e., step-by-step algorithmic solutions. Actual mathematical problem solving is of course a much more complicated phenomenon in which there are many important socially and culturally determined aspects, such as clarity of expressions and proof structures. In addition, there are numerous epistemic considerations involved in mathematical cognition, whereas in this paper we have only focused on problem solving. From verifying the solutions to communicating and explaining them, enculturated mathematical competence includes various dimensions which have not been analyzed here. This is not an oversight, as I believe that research of mathematical practice is crucial in determining what enculturated mathematical competences are on higher levels of mathematics. Rather than dismissing the importance of such considerations, my purpose in this paper has been to show that we need a notion of humanly optimal algorithms and enculturated competence already when we seek to explain mathematical cognition in the limited paradigm of problem solving algorithms. In order for us to be able to study mathematics as a human phenomenon in all its richness, we may need to expand the paradigm even more.
One important aspect of developing this notion of enculturated competence is that we should also consider the question of human-computer interaction in mathematical problem solving. To present just one example, as computer-assisted problem solving becomes more prevalent, it makes sense to move the focus to the cognitive and computational complexity involved in the computer-assisted process. It is easy to predict that if mathematics relies increasingly on problem solving (or solution-checking) computer programs, many of the human heuristic and didactic tools, such as diagrams, may no longer play the same kind of role as they currently do. However, in this scenario we get new interesting questions concerning cognitive complexity, including considerations on the understandability of computer programs. Increasing human-computer interaction will undoubtedly change the way mathematics is practiced and learned, but it seems unrealistic to assume that the heuristic and didactic elements important for human understanding will disappear. In this way, although the study of cognitive complexity may evolve into new directions, there is no reason to believe that the cognitive complexity of human mathematical problem solving will become completely reducible to the computational complexity of the problems. Instead, what will emerge is a new enculturated notion of mathematical competence, one involving algorithms with their own particular characteristics. In that scenario, it is important to have a research paradigm that does not focus only on computational complexity and the computational level of explanation.
Notes
These algorithms can be either conscious or unconscious, as will be seen in the examples presented in Sect. 6.
We will later get a definition of algorithm, but for now it is enough to think of algorithms as step-by-step procedures, such as computer programs.
In this paper, we will work in the paradigm of decision problems. In computer science, many other types of problems are also studied, such as counting, search, function and optimization problems (Goldreich 2008). The focus on decision problems is not meant to suggest that other types of problems are not relevant for computational complexity. Algorithms for solving optimization problems, for example, may well provide better models for some human cognitive tasks. There are two main reasons for focusing on decision problems. First, research on decision problems is the most developed field in complexity theory. Second, the discussion in cognitive science and its philosophy has focused mostly on decision problems when it comes to computational modeling. It should also be noted that these distinctions between problems are somewhat arbitrary, as many problems can be framed in different ways.
This is not to suggest that researchers working in cognitive modeling are ignorant of, or uninterested in, the algorithmic and implementational levels, only that computational-level explanations currently form the most important area in computational modeling of cognitive tasks.
Here it should be noted that for practical purposes, optimality may include considerations of various aspects, such as stability, verifiability, simplicity of coding, etc. The context of Turing machines here is a purely theoretical one in which such matters are ignored, important as they are in practice. It should also be noted that optimal algorithms are not unique. In theoretical computer science, an algorithm is called (asymptotically) optimal if it never performs more than a constant factor worse than the best possible algorithm. There can thus many (even an infinite number of) optimal algorithms. Finally, although the method of characterizing complexity of a problem in terms of an optimal algorithm for solving it is commonplace, we know from Blum’s speedup theorem (Blum 1967) that it is not possible in all cases to define the computational complexity of functions in terms of optimal algorithms for solving them (I thank an anonymous reviewer for bringing up this point).
A well-known example of this practice is the use of cryptography in computers, which is based on the widely-shared, but unproven, conjecture by computer scientists that multiplying integers is efficient while factoring them is inefficient.
Whereas a deterministic Turing machine is programmed to have at most one action for each situation, a non-deterministic Turing machine can choose the action from several options.
For the current state of the art in the rapidly advancing field of complexity classes, the reader is referred to Scott Aaronson’s excellent website “Complexity Zoo” (https://complexityzoo.uwaterloo.ca/Complexity_Zoo).
It should be noted that there has been criticism against the P-cognition thesis as the appropriate formulation of the tractable cognition thesis. van Rooij (2008) argues that with suitable parameters concerning the size of input (see Downey and Fellows 1999 for more), also super-polynomial time computation can be feasible in modeling cognitive tasks. van Rooij calls this the “FPT-cognition thesis”, for fixed-parameter tractable.
More technically, although it is known that there are parallel algorithms faster than the standard sequential Euclidean algorithm (Chor and Goldreich 1990), it is not known whether GCD is in the complexity class NC (“Nick’s Class”), which is the class of problems decidable in polylogarithmic time with a polynomial number of parallel processors. Furthermore, it is not known whether NC = P (Arora and Barak 2007).
There are complexity classes that are known to be strictly smaller than P, such as \(\mathbf {AC^{0}}\), a class of circuit complexity. But these classes are generally very weak and thus of little use in distinguishing between mathematical problems. \(\mathbf {AC^{0}}\), for example, does not even contain integer multiplication (Vollmer 1999).
Kolmogorov complexity refers to the length of the shortest computer program that has an informative object, such as a string of symbols, as its output. For example, the string of symbols “aaaaaaaaaaaaaaaaaaaa” has a lower Kolmogorov complexity than the string of symbols “keehfydo38dkrislero29s”. Both strings are 20 symbols long, but whereas the second string cannot be described with a shorter string, the former can. For instance, the English description “20 times a” is 10 symbols long. However, Kolmogorov complexity is not without problems. While it may seem like a straight-forward concept, it has turned out that determining the Kolmogorov complexity of even short strings of symbols is a highly difficult task (Soler-Toscano et al. 2014).
In this way, the approach here resembles that of Peacocke (1986), who proposed amending the Marr classification by adding a level “1.5” of cognitive explanation (1 being the computational level and 2 the algorithmic). He argued that the purely extensional computational approach corresponds neither to Chomsky’s competence nor even to the scientific practice that Marr intended. If we are concerned only with the output and the input, we are left with a multitude of characterizations of the functions involved. For example, if we think of functions simply as Cartesian sets of ordered pairs (i.e. purely extensionally), we learn nothing about the intensional intricacies of the function. But surely such purely syntactic pairing of inputs with outputs (with, e.g., a look-up table) is a inferior characterization (cognitively) than a description of a function that implies how it is cognitively computed. In this way, the characterization of the function may already point us toward the algorithms used in cognitive processing.
An upshot of this approach is that we can also better understand why human competence sometimes can be modeled by an optimal algorithm and sometimes not.
Of course this argument fails if we believe that human insight cannot be even in principle computationally modeled, as Penrose does.
Or it requires as much as or more space, or it has equal or higher Kolmogorov complexity, etc.
To be clear, I am not claiming that researchers in the cognitive sciences generally dismiss the importance of algorithmic-level explanations. Often considerations on the algorithmic and implementational levels of processing can also influence computational-level explanations, the Marrian focus on computational level of explanation notwithstanding.
Of course in addition to the many applications humans have for heuristic processes that do not lead to exact solutions.
Assuming that the computer is required to provide the solution to the problem in the initial mode of representation. Perhaps there could be an exception in highly complex computer programs, but it is enough for present purposes to note that changing the domain of representation is generally likely to add to the complexity of the algorithm.
This connection between the distance effect and the approximate number system is widely accepted, but not universally so. Tzelgov and Ganor-Stern (2005), for example, argue that the distance effect could be due to lexical factors of how we have acquired number words. My argumentation in this paper, however, does not rely on the particular explanation of the distance effect.
Provided of course that we are familiar with the meanings of those symbols and words.
The distance effect itself is a general characteristic of the approximate number system and it has been detected in various nonhuman animals, including rats, pigeons, dolphins and apes (Dehaene 19972011, p. 16). However, most nonhuman animals cannot grasp symbolic representations of quantities, so it is difficult to see the distance effect as causing suboptimal problem solving strategies. Recently there have been experiments on monkeys that suggest an ability to make addition of symbolically represented magnitudes (Livingstone et al. 2014). In such case, it would not be unfeasible to think that the distance effect can cause the monkey to use a suboptimal problem solving algorithm.
In this, the present approach is similar to that of Varma (2014) who argues that restricting focus to one of Marr’s levels of explanation can be detrimental for progress in cognitive science.
The name “streetlight effect” comes from the old joke in which a drunk looks for his keys in the better visibility of a streetlight, instead of the place where he lost them.
The origin of the name for this method, which has recently received a lot of attention on the Internet, is unknown, but most often it is referred to as the Japanese multiplication method. This use also seems to adopted in academic contexts. See, e.g., http://www.cemc.uwaterloo.ca/events/mathcircles/2013-14/Fall/Junior6_Multiplication_Nov5.pdf.
The usefulness of visual heuristic methods can also be present without actual visual input, as seen in the “mental abacus” used in many especially Asian cultures for calculations (Frank and Barner 2012).
See Fabry and Pantsar (2019) for a detailed treatment of this topic.
References
Aaronson, S. (2012). Why philosophers and cognitive scientists should care about computational complexity. In J. Copeland, et al. (Eds.), Computability: Gödel, Turing, Church, and beyond. Cambridge: MIT Press.
Anderson, J. R. (1990). The adaptive character of thought. Hillsdale, NJ: Lawrence Erlbaum Associates.
Anderson, M. (2014). After phrenology: Neural reuse and the interactive brain. Cambridge, MA: MIT Press.
Ansari, D. (2012). Culture and education: New frontiers in brain plasticity. Trends in Cognitive Sciences, 16(2), 93–95.
Arora, S., & Barak, B. (2007). Computational complexity. A modern approach. Cambridge: Cambridge University Press.
Ashcraft, M. H. (1992). Cognitive arithmetic: A review of data and theory. Cognition, 44(1–2), 75–106.
Ashcraft, M. H. (1995). Cognitive psychology and simple arithmetic: A review and summary of new directions. Mathematical Cognition, 1(1), 3–34.
Ausiello, G., Crescenzi, P., Gambosi, G., Kann, V., Marchetti-Spaccamela, A., & Protasi, M. (1999). Complexity and approximation: Combinatorial optimization problems and their approximability properties. Berlin: Springer.
Bieri, J. (1955). Cognitive complexity–simplicity and predictive behavior. Journal of Abnormal and Social Psychology, 51, 263–268.
Blum, M. (1967). A machine-independent theory of the complexity of recursive functions. Journal of the ACM (JACM), 14(2), 322–336.
Carruthers, S., & Stege, U. (2013). On evaluating human problem solving of computationally hard problems. Journal of Problem Solving, 5(2), 42–70.
Chater, N., Tenenbaum, J. B., & Yuille, A. (2006). Probabilistic models of cognition: Conceptual foundations. Trends in Cognitive Sciences, 10(7), 287–291.
Chomsky, N. (1965). Aspects of the theory of syntax. Cambridge, MA: MIT Press.
Chor, B., & Goldreich, O. (1990). An improved parallel algorithm for integer GCD. Algorithmica, 5(1–4), 1–10.
Church, A. (1936). An unsolvable problem of elementary number theory. American Journal of Mathematics, 58(58), 345–363.
Cobham, A. (1964). The intrinsic computational difficulty of functions. In Proceedings of the 1964 congress on logic, mathematics and the methodology of science (pp. 24–30).
Cummins, R. (2000). How to solve it. How does it work? vs. What are the laws? Two conceptions of psychological explanation. In F. Keil & R. Wilson (Eds.), Explanation and cognition (pp. 117–145). Cambridge, MA: MIT Press.
Dehaene, S. (1997/2011). The number sense: How the mind creates mathematics, 2nd edn. 2011. New York: Oxford University Press.
Dehaene, S. (2009). Reading in the brain: The new science of how we read. London: Penguin.
Dehaene, S., & Akhavein, R. (1995). Attention, automaticity, and levels of representation in number processing. Journal of Experimental Psychology: Learning, Memory, and Cognition, 21(2), 314.
Dehaene, S., & Changeux, J. P. (1993). Development of elementary numerical abilities: A neuronal model. Journal of Cognitive Neuroscience, 5(4), 390–407.
Diezmann, C. M., & English, L. D. (2001). Promoting the use of diagrams as tools for thinking. In 2001 National Council of Teachers of Mathematics Yearbook: The role of representation in school mathematics (pp. 77–89). National Council of Teachers of Mathematics.
Dowker, A. (2016). Factors that influence improvement in numeracy, reading, and comprehension in the context of a numeracy intervention. Frontiers in Psychology, 7, 1929.
Downey, R. G., & Fellows, M. R. (1999). Parameterized complexity. New York: Springer.
Dry, M., Preiss, K., & Wagemans, J. (2012). Clustering, randomness, and regularity: Spatial distributions and human performance on the traveling salesperson problem and minimum spanning tree problem. The Journal of Problem Solving, 4(1), 2.
Edmonds, J. (1965). Paths, trees, and flowers. Canadian Journal of Mathematics, 17(3), 449–467.
Fabry, R. E. (2018). Betwixt and between: The enculturated predictive processing approach to cognition. Synthese, 195, 1–36.
Fabry, R. E. (2019). The cerebral, extra-cerebral bodily, and socio-cultural dimensions of enculturated arithmetical cognition. Synthese. https://doi.org/10.1007/s11229-019-02238-1.
Fabry, R. E. & Pantsar, M. (2019). A fresh look at research strategies in computational cognitive science: The case of enculturated mathematical problem solving. Synthese. https://doi.org/10.1007/s11229-019-02276-9.
Fraenkel, A. S., & Lichtenstein, D. (1981). Computing a perfect strategy for $\text{ n }\times \text{ n }$ chess requires time exponential in n. Journal of Combinatorial Theory, Series A, 31(2), 199–214.
Frank, M., & Barner, D. (2012). Representing exact number visually using mental abacus. Journal of Experimental Psychology, 141(1), 134–149.
Frixione, M. (2001). Tractable competence. Minds and Machines, 11(3), 379–397.
Fuson, K. C. (1992). Research on learning and teaching addition and subtraction of whole numbers. In G. Leinhardt, R. T. Putnam, & R. A. Hattrup (Eds.), Analysis of arithmetic for mathematics teaching (pp. 53–187). Hillsdale, NJ, US: Lawrence Erlbaum Associates.
Garey, M. R., & Johnson, D. S. (1979). Computers and intractability: A guide to the theory of NP-completeness. San Francisco: W.H. Freeman.
Goldreich, O. (2008). Computational complexity: A conceptual perspective. ACM Sigact News, 39(3), 35–39.
Graham, S. M., Joshi, A., & Pizlo, Z. (2000). The traveling salesman problem: A hierarchical model. Memory & Cognition, 28(7), 1191–1204.
Hadamard, J. (1954). The psychology of invention in the mathematical field. Mineola, NY: Dover Publications.
Hinrichs, J. V., Yurko, D. S., & Hu, J. M. (1981). Two-digit number comparison: Use of place information. Journal of Experimental Psychology: Human Perception and Performance, 7(4), 890.
Horgan, T., & Tienson, J. (1996). Connectionism and the philosophy of psychology. Cambridge, MA: MIT Press.
Ifrah, G. (1998). The universal history of numbers: From prehistory to the invention of the computer, Translated by Bellos, D., Harding, E. F., Wood, S., & Monk, I. London: Harville Press.
Isaac, A. M., Szymanik, J., & Verbrugge, R. (2014). Logic and complexity in cognitive science. In S. Smets & A. Baltag (Eds.), Johan van Benthem on logic and information dynamics (pp. 787–824). Berlin: Springer.
Iwata, S., & Kasai, T. (1994). The Othello game on an $\text{ n }\times \text{ n }$ board is PSPACE-complete. Theoretical Computer Science, 123(2), 329–340.
Jamnik, M. (2001). Mathematical reasoning with diagrams. Chicago: University of Chicago Press.
Kadosh, R. C., & Henik, A. (2006). Color congruity effect: Where do colors and numbers interact in synesthesia? Cortex, 42(2), 259–263.
Karatsuba, A., & Ofman, Y. (1962). Multiplication of many-digital numbers by automatic computers. Physics-Doklady, 7(1963), 595–596.
LeFevre, J., DeStefano, D., Coleman, B., & Shanahan, T. (2005). Mathematical cognition and working memory. In J. Campbell (Ed.), Handbook of mathematical cognition (pp. 361–378). New York: Psychology Press.
Livingstone, M. S., Pettine, W. W., Srihasam, K., Moore, B., Morocz, I. A., & Lee, D. (2014). Symbol addition by monkeys provides evidence for normalized quantity coding. Proceedings of the National Academy of Sciences, 111(18), 6822–6827.
Markman, A. B., & Gentner, D. (2000). Structure mapping in the comparison process. The American Journal of Psychology, 113(4), 501.
Marr, D. (1977). Artificial intelligence—A personal view. Artificial Intelligence, 9(1), 37–48.
Marr, D. (1982). Vision: A computational investigation into the human representation and processing of visual information. San Francisco: W.H. Freeman and Company.
Menary, R. (2014). Neural plasticity, neuronal recycling and niche construction. Mind & Language, 29(3), 286–303.
Menary, R. (2015). Mathematical cognition: A case of enculturation. In T. Metzinger & J. M. Windt (Eds.), Open MIND (pp. 1–20). Frankfurt am Main: MIND Group. https://doi.org/10.15502/9783958570818.
Newell, A. (1980). Physical symbol systems. Cognitive Science, 4(2), 135–183.
Newell, A. (1982). The knowledge level. Artificial Intelligence, 18(1), 87–127.
Newell, A., & Simon, H. A. (1976). Computer science as empirical inquiry (The 1975 ACM Turing Award Lecture). Communications of the ACM, 19(3), 113–126.
Ormerod, T. C., & Chronicle, E. P. (1999). Global perceptual processing in problem solving: The case of the traveling salesperson. Perception & Psychophysics, 61(6), 1227–1238.
Pantsar, M. (2018). Early numerical cognition and mathematical processes. Theoria, 33(2), 285–304.
Pantsar, M. (2019). The Enculturated Dove From Proto-Arithmetic to Arithmetic. Frontiers in Psychology, 10, 1454. https://doi.org/10.3389/fpsyg.2019.01454.
Papadimitriou, C. (1994). Computational complexity. Reading: Addison-Wesley.
Peacocke, C. (1986). Explanation in computational psychology: Language, perception and level 1.5. Mind and Language, 1(2), 1010–1023.
Penrose, R. (1989). The Emperor’s new mind: Concerning computers, minds and the laws of physics. Oxford: University Press.
Peters, E., & Bjalkebring, P. (2015). Multiple numeric competencies: When a number is not just a number. Journal of Personality and Social Psychology, 108(5), 802.
Piantadosi, S. T., Tenenbaum, J. B., & Goodman, N. D. (2016). The logical primitives of thought: Empirical foundations for compositional cognitive models. Psychological Review, 123(4), 392.
Pinel, P., Dehaene, S., Riviere, D., & LeBihan, D. (2001). Modulation of parietal activation by semantic distance in a number comparison task. Neuroimage, 14(5), 1013–1026.
Polya, G. (1945). How to solve it. Princeton: Princeton University Press.
Pomerance, C. (1996). A tale of two sieves. Notices of the American Mathematical Society, 43(12), 1473–1485.
Pylyshyn, Z. W. (1984). Computation and cognition: Towards a foundation of cognitive science. Cambridge, MA: MIT Press.
Schoenfeld, A. H. (1985). Mathematical problem solving. London: Academic Press.
Schönhage, A., & Strassen, V. (1971). Schnelle Multiplikation großer Zahlen. Computing, 7, 281–292.
Skiena, S. (2008). The algorithm design manual. Berlin: Springer.
Soler-Toscano, F., Zenil, H., Delahaye, J. P., & Gauvrit, N. (2014). Calculating Kolmogorov complexity from the output frequency distributions of small turing machines. PLoS ONE, 9(5), e96223.
Sun, R. (Ed.). (2008). Introduction to computational cognitive modeling. In The Cambridge Handbook of Computational Psychology (pp. 3–19). Cambridge: University Press.
Szymanik, J. (2016). Quantifiers and cognition: Logical and computational perspectives, studies in linguistics and philosophy (Vol. 96). Berlin: Springer.
Tall, D. (Ed.). (2002). Advanced mathematical thinking. Mathematics education library (Vol. 11). Dordrecht: Springer.
Tang, Y., Zhang, W., Chen, K., Feng, S., Ji, Y., Shen, J., et al. (2006). Arithmetic processing in the brain shaped by cultures. Proceedings of the National Academy of Sciences, 103(28), 10775–10780.
Thagard, P. (2000). Coherence in thought and action. Cambridge, MA: Cambridge University Press.
Tsotsos, J. K. (1990). Analyzing vision at the complexity level. Behavioral and Brain Sciences, 13, 423–469.
Turing, A. M. (1936). On computable numbers, with an application to the Entscheidungsproblem. Proceedings of the London Mathematical Society, 42, 230–265.
Tzelgov, J., & Ganor-Stern, D. (2005). Automaticity in processing ordinal information. In J. Campbell (Ed.), Handbook of Mathematical Cognition (pp. 55–66). New York: Psychology Press.
Uesaka, Y., Manalo, E., & Ichikawa, S. I. (2007). What kinds of perceptions and daily learning behaviors promote students’ use of diagrams in mathematics problem solving? Learning and Instruction, 17(3), 322–335.
van Garderen, D., Scheuermann, A., & Jackson, C. (2013). Examining how students with diverse abilities use diagrams to solve mathematics word problems. Learning Disability Quarterly, 36(3), 145–160.
van Hiel, A., & Mervielde, I. (2003). The measurement of cognitive complexity and its relationship with political extremism. Political Psychology, 24(4), 781–801.
van Rooij, I. (2008). The tractable cognition thesis. Cognitive Science, 32, 939–984.
van Rooij, I., Wright, C. D., & Wareham, T. (2012). Intractability and the use of heuristics in psychological explanations. Synthese, 187(2), 471–487.
Varma, S. (2014). The subjective meaning of cognitive architecture: A marrian analysis. Frontiers in Psychology, 5, 440.
Vollmer, H. (1999). Introduction to circuit complexity. A uniform approach., Texts in theoretical computer science Berlin: Springer.
Zachariades, T., Jones, K., Giannakoulias, E., Biza, I., Diacoumopoulus, D., & Souyoul, A. (2007). Teaching calculus using dynamic geometric tools. Southampton: University of Southampton.
Acknowledgements
Open access funding provided by University of Helsinki including Helsinki University Central Hospital. Funding was provided by Academy of Finland. I would like to thank Regina Fabry, Cyrille Imbert and Stefan Buijsman for their very helpful comments on earlier versions of this manuscript. I would also like to thank Gabriel Sandu for making this work possible as part of his project “Dependence and Independence in Logic” at the University of Helsinki.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Pantsar, M. Cognitive and Computational Complexity: Considerations from Mathematical Problem Solving. Erkenn 86, 961–997 (2021). https://doi.org/10.1007/s10670-019-00140-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10670-019-00140-3