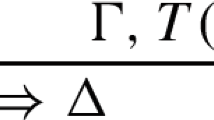Abstract
According to the implicit commitment thesis, once accepting a mathematical formal system S, one is implicitly committed to additional resources not immediately available in S. Traditionally, this thesis has been understood as entailing that, in accepting S, we are bound to accept reflection principles for S and therefore claims in the language of S that are not derivable in S itself. It has recently become clear, however, that such reading of the implicit commitment thesis cannot be compatible with well-established positions in the foundations of mathematics which consider a specific theory S as self-justifying and doubt the legitimacy of any principle that is not derivable in S: examples are Tait’s finitism and the role played in it by Primitive Recursive Arithmetic, Isaacson’s thesis and Peano Arithmetic, Nelson’s ultrafinitism and sub-exponential arithmetical systems. This casts doubts on the very adequacy of the implicit commitment thesis for arithmetical theories. In the paper we show that such foundational standpoints are nonetheless compatible with the implicit commitment thesis. We also show that they can even be compatible with genuine soundness extensions of S with suitable form of reflection. The analysis we propose is as follows: when accepting a system S, we are bound to accept a fixed set of principles extending S and expressing minimal soundness requirements for S, such as the fact that the non-logical axioms of S are true. We call this invariant component the semantic core of implicit commitment. But there is also a variable component of implicit commitment that crucially depends on the justification given for our acceptance of S in which, for instance, may or may not appear (proof-theoretic) reflection principles for S. We claim that the proposed framework regulates in a natural and uniform way our acceptance of different arithmetical theories .
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Preamble
The acceptance of a system formalizing some portion of mathematics is the outcome of a complex justificatory process that is constrained by philosophical and ontological attitudes, influenced by pragmatical considerations (fruitfulness, generality), and also hospitable to aesthetical ones (simplicity, elegance). The acceptance of a formal system S, therefore, encompasses the possibility that some of the components of this justificatory process are not expressible or even formalizable in the language of S and that some crucial constituents of this acceptance are only left implicit by the process itself. Examples abound: just to remain on the formal side, for instance, soundness assertions for S involving the notion of truth are not expressible in the language of S, while most of their truth-free surrogates are not provable in S.
We have come to the core idea underlying the notion of implicit commitment: when accepting a theory S, we are also bound to embrace a cluster of formal or semi-formal assertions that are not immediately available in S itself.Footnote 1 Historically, the notion of implicit commitment of formal systems of arithmetic, and for mathematical theories more in general, emerged in the work of logicians and philosophers already in the 50s and 60s of the last century. Their main concern is clearly expressed in a later work by Solomon Feferman:
To what extent can mathematical thought be analyzed in formal terms? Gödel’s theorems show the inadequacy of single formal systems for this purpose, except in relatively restricted parts of mathematics. However at the same time they point to the possibility of systematically generating larger and larger systems whose acceptability is implicit in acceptance of the starting theory. The engines for that purpose are what have come to be called reflection principles (Feferman 1991, p. 1).
The articulation of this version of implicit commitment was crucial for the analysis of predicativism and, in particular, for the identification of predicatively definable sets of natural numbers.Footnote 2 In one well-known Feferman’s formulation, the limit for the generation of such sets is articulated in terms of iterations of uniform reflection principles and predicative comprehension over Peano Arithmetic (see Feferman 1962, 1964; Kreisel 1970). This project was refined and reshaped several times by Feferman in the past decades, moving from iterations of ramified analysis (Feferman 1964) to more succinct formulations such as the reflective closure of the starting theory involving a primitive notion of truth (see Sects. 3, 4).
At any rate, no matter what formulation of Feferman’s hierarchy of systems one chooses, the resulting picture of implicit commitment will entail that in accepting a starting theory S one is committed to statements that are not provable in S itself. Nevertheless, as we shall see later in the paper, it has recently become clear that the inclusion of reflection principles for the starting theory among the claims we are implicitly committed to when accepting it, although integral part of Feferman’s foundational program, may clash with other philosophical standpoints. Therefore, we opt for a more neutral and more general formulation of the implicit commitment thesis:
(ICT) In accepting a formal systems S one is also committed to additional resources not available in the starting theory S but whose acceptance is implicit in the acceptance of S.Footnote 3
As it is formulated, (ICT) has the advantage of reflecting many instances of disagreement in the existing literature over what these “additional resources” should amount to. Several authors, following Feferman, allow for conceptual resources that are not immediately available in S due to familiar Gödelian phenomena, such as consistency statements and reflection principles. Some of these authors go even further and argue that, once soundness extensions of S are admitted, they should be formulated by explicitly resorting to a notion of truth and not merely by implicitly referring to it via schemata (Feferman 1991; Shapiro 1998; Ketland 1999; Cieśliński 2010). Other authors maintain instead that whatever we are committed to when endorsing the system S should already be expressible in the very language of S (Tennant 2002). And finally, proponents of a more drastic view, like Jean-Yves Girard, even deny that reflection on our acceptance of S may have any epistemological value because it relies on a pre-existing agreement on what axioms and rules should be believed to be true (Girard 1987).
It’s important to notice, nonetheless, that the positions just sketched are extracted from works that are not directly concerned with a clarification of the notion of implicit commitment, but mainly with the notion of truth in the context of truth-theoretic deflationism.Footnote 4 A direct analysis of the notion of implicit commitment, however, is much needed. As Horsten and Leigh put it:
philosophers of mathematics have hitherto largely failed to investigate the notion of implicit commitment, and have not spent much philosophical energy on analysing our warrant for reflection principles (Horsten and Leigh 2017, p. 32).
Recently Walter Dean has claimed that what is traditionally taken as part of the principles we are committed to when accepting a system S—such as reflection principles—may clash with the justification provided for the acceptance of S itself (Dean 2015). In particular, he focuses on the well-known theses by William Tait and Daniel Isaacson, according to which finitary mathematics coincides with what can be proved in Primitive Recursive Arithmetic (PRA) and first order Peano Arithmetic (PA) respectively. Dean observes that both theses can be understood as suggesting that PRA and PA are epistemically stable, “in the sense that there exists a coherent rationale for accepting [these systems] which does not entail or otherwise oblige a theorist to accept statements which cannot be derived from [their] axioms”(Dean 2015, p. 53). Although we are not primarily interested in analyzing the notion of epistemic stability introduced by Dean, we will be concerned with some of its effects: the predicativist à la Feferman and the first-orderist à la Isaacson—who takes PA to delimit the boundaries of finite mathematics, although both assigning a privileged status to Peano Arithmetic, will do so on different grounds and this will heavily affect their stance on (ICT). For Feferman there will be a recognizable set of statements that are not derivable in PA, while being part of our implicit commitment to it; for Isaacson, by contrast, the additional resources hinted at in (ICT) will likely be non-existent. This determines a form of relativity of implicit commitment with respect to the acceptance of one’s preferred arithmetical system that will be a recurring theme of this paper.
In what follows, we propose an alternative analysis of the notion of implicit commitment of arithmetical theories. On our account, implicit commitment exhibits a variable and invariant component. We maintain, with Dean, that the set of principles defining the implicit commitment with respect to the acceptance of a theory S is relative to the justification given for this very acceptance. However, we also argue—contra Dean—that the acceptance of a system does involve an explicit soundness extension in the form of a fixed set of semantic principles, which we call ‘semantic core’. The relative aspect of implicit commitment thus takes the form of different, possible extensions of this ubiquitous core. In other words, we will claim that there is a fundamental body of ‘reflection’ principles formulated through the notion of truth—such as the claim that all non-logical axioms of the accepted theory S are true—that are part of the implicit commitment relative to any reasonable justification offered for the acceptance of a theory S. What extends such a kernel is variable and constrained by the justification given by the idealized mathematician.
Here is a sketch of the structure of the paper. In the next section, we briefly discuss Dean’s critical analysis of (ICT) in relation to Tait’s and Isaacson’s theses and we extend his remarks to Nelson’s ultrafinitism. We claim that Dean’s analysis does not lead to a dismissal of (ICT) but rather to an alternative interpretation of it. In Sect. 3, in fact, we introduce the necessary toolbox to take up this possible interpretation of (ICT), whereby the “additional resources” we are committed to when accepting a system S do not entail statements that are unprovable in S. Our aim is to isolate the semantic core of an arithmetical theory, amounting to the fixed, invariable component of our commitment to it. In Sect. 4 we defend the thesis that the distinction between semantic core and variable components of implicit commitment resolves the tension between Tait’s and Isaacson’s theses and (ICT); in addition, we show that the resulting picture of implicit commitment is also compatible with the traditional reading of (ICT) associated with positions such as Feferman’s. Section 5 contains some concluding remarks.
2 Implicit Commitment and Foundational Theses
As we mentioned in the previous section, Dean (2015) examines the way in which Tait and Isaacson respectively justify the acceptance of PRA and PA from a “finitist” and a “first-orderist” perspective. In both cases he concludes that (ICT) is incompatible with the justification that they give for the acceptance of the theories. Let us now briefly recall Tait’s and Isaacson’s theses and how Dean employs them to criticize this strong reading of (ICT).
On the view articulated by Tait, the formal system of PRA captures precisely the finitist portion of mathematics.Footnote 5 Inasmuch as the “finitist portion of mathematics” is not itself a mathematical notion, Tait draws an analogy between his thesis and Church’s thesis, suggesting that “any plausible attempt to construct a finitist function that is not primitive recursive either fails to be finitist [...] or else turns out to be primitive recursive after all” (Tait 1981, p. 533, 537). In accordance with the spirit of Hilbert’s program, Tait then investigates what counts as finitistic proof of an open formula \(\varphi (\vec x)\) of the language of \({\mathsf{PRA}}\), and concludes that its proofs are precisely the formal proofs of \(\varphi (\vec {x})\) in PRA. Tait’s proof principles involve only a limited form of induction for finitistically acceptable types (cf. Tait 1981, p. 537), much closer to primitive recursion than to the first-order schema of induction.Footnote 6 In fact, already the schema of induction for \(\Sigma _2\)-formulas, let alone the full schema of induction, would enable one to define recursive but not primitive recursive operations such as the Ackermann function. Such instances of induction are therefore not available to the finitist.
To discuss the consequences of accepting (ICT) for the finitist à la Tait, we move from the quantifier-free language to a more comfortable base theory formulated in the first-order language of arithmetic. As Dean emphasizes, Kalmar Elementary Arithmetic (EA) (cf. Beklemishev 2005) is a good choice because (1) it enjoys a smooth arithmetization of the syntax and (2) it is a proper subtheory of the conservative extension of PRA in which we allow for full-predicate logic but still quantifier-free induction.Footnote 7 Let us then consider the so-called uniform reflection principle for an elementary theory S, namely the claim
for \(\phi (v)\) a formula of \({{\mathcal {L}}}_S\) with only v free, where \({\mathsf{Pr}}_S(\ulcorner \phi (\dot{x})\urcorner )\) canonically expresses that the result of formally substituting the variable v with the numeral for x in \(\phi (v)\) is provable in S. The following is well-known:
Proposition 1
(Kreisel and Lévy 1968) OverEA, full induction is equivalent toRFN(EA).
Therefore, if one understands (ICT) as including RFN(EA), then the finitist should also be committed to the very induction principle of PA, which clearly isn’t available in the finitist’s preferred theory PRA—nor obviously in its first-order variant QF-IA. Dean thus concludes that the finitist à la Tait cannot include RFN(EA) (and a fortiori RFN(PRA)) into the set of principles she is implicitly committed to when embracing PRA. If principles such as \(\mathsf{RFN(PRA)}\) are taken to be, as in Feferman’s own reading, necessary for (ICT), then (ICT) is simply an inadequate account of implicit commitment across reasonable arithmetical systems. This is basically Dean’s conclusion.
Such conclusion is based on the presuppositions that (ICT) can only be interpreted along the lines of Feferman’s own account of it and, as a consequence, the reference to “resources not available in S” in the formulation of (ICT) could only be read in terms of assertions that imply, or even that are equivalent, to sentences in the language of S that are not provable in it. As we shall see later on, however, our proposal will rest indeed on refuting such presupposition; there are in fact many senses in which a resource not available in S may fail to entail unprovable sentences in S. Indeed, the lesson that we draw from Dean’s point is not that (ICT) has to be rejected given the incompatibility of the finitist’s justification of PRA and RFN(PRA). On the contrary, Dean’s objection points at the possibility of embracing a plausible version of (ICT) that—relative to certain restrictive standpoints such as the finitist’s—does not invoke principles equivalent to or stronger than RFN(EA). Such a version of (ICT) will be articulated in the following sections.
Dean draws a similar conclusion in relation to Isaacson’s thesis, according to which PA captures “an intrinsic, conceptually well-defined region of arithmetical truth” (Isaacson 1996, p. 203). Indeed, Isaacson suggests that PA may be regarded as sound and complete with respect to a conception of arithmetical truths as “directly perceivable” by articulating “our grasp of the structure of the natural numbers” (Isaacson 1996, p. 217, 1991). Unprovable truths in PA such as Goodstein theorem and the Paris-Harrington sentence are ones that involve hidden higher-order (or infinitary) concepts.Footnote 8 If these claims have a clear mathematical meaning, however, it is also well-known that they are equivalent, over PA, to claims of apparent meta-mathematical meaning such as the Gödel sentence for PA or a canonical consistency statement Con(PA).
A similar correspondence between the mathematical and the meta-mathematical can be found at the level of the principles which are usually involved in strong readings of (ICT) such as Feferman’s. Let’s consider again RFN(PA). It is a classical result by Gentzen that \({\mathsf{PA}}\) proves transfinite induction up to any ordinal smaller than \(\varepsilon _0\) (henceforth \(\mathsf{TI}_{\omega _n}\))—i.e. up to the limit of all ordinals of the form
 for towers of order n (Gentzen 1969). Hence, by the properties of formal provability, \({\mathsf{PA}}\) proves the formalization of this fact for all n. By RFN(PA), therefore, one can conclude, within PA + RFN(PA), the claim that for all n, \(\mathsf{TI}_{\omega _n}\), that is the schema of transfinite induction up to \(\varepsilon _0\) (\(\mathsf{TI}_{\varepsilon _0}\)). Also the other direction—that is the claim that \({\mathsf{PA}}+\mathsf{RFN(PA)}\) proves \(\mathsf{TI}_{\varepsilon _0}\)—is well-known, although the proof, which can be found in Kreisel and Lévy (1968), is definitely more involved.
for towers of order n (Gentzen 1969). Hence, by the properties of formal provability, \({\mathsf{PA}}\) proves the formalization of this fact for all n. By RFN(PA), therefore, one can conclude, within PA + RFN(PA), the claim that for all n, \(\mathsf{TI}_{\omega _n}\), that is the schema of transfinite induction up to \(\varepsilon _0\) (\(\mathsf{TI}_{\varepsilon _0}\)). Also the other direction—that is the claim that \({\mathsf{PA}}+\mathsf{RFN(PA)}\) proves \(\mathsf{TI}_{\varepsilon _0}\)—is well-known, although the proof, which can be found in Kreisel and Lévy (1968), is definitely more involved.
As a consequence, a principle that is naturally justified by appealing to semantic or metamathematical considerations such as RFN(PA) on the one hand, and a principle concerning how many countable transfinite ordinals can be well-ordered on the other, are equivalent over \({\mathsf{PA}}\). Therefore, if Isaacson’s thesis on \({\mathsf{PA}}\) is to be understood in a radical way as to entail that anything that is unprovable in \({\mathsf{PA}}\) should not be part of the principles allowed by (ICT), both \(\mathsf{RFN(PA)}\) and \(\mathsf{TI}_{\varepsilon _0}\) should be ruled out. In a less categorical reading of Isaacson’s thesis, one may still think that principles that are not provable in PA may be allowed in the set specified by (ICT); however, as stressed by Dean himself, these truths should now assume the instrumental role of confirming the theorems of PA as clear boundaries for finite mathematics (see Isaacson 1996, sect. 3).Footnote 9 However, it is not clear to us in which sense this more liberal reading of (ICT) should differ from the radical one, since the inclusion of these additional arithmetical truths in the set specified by (ICT) only reaffirms and does not characterize PA as a self-standing portion of mathematical truth. The message that Dean extracts from Isaacson’s thesis looks, again, uncontroversial: if one endorses it, she is also committed to a reading of (ICT) that eschews claims that are unprovable in PA, casting serious doubts on the plausibility of (ICT) itself. And again, we will see in the next section that there are senses in which the “resources not available in \({\mathsf{PA}}\)” we might be implicitly committed to when accepting \({\mathsf{PA}}\) may fail to imply statements that are unprovable in \({\mathsf{PA}}\) itself.
In addition to the cases examined by Dean, similar questions arise in analogous foundational theses that rely on a restriction of the full induction schema of PA. For instance, one might look at the ultrafinitist thesis advocated by Nelson (1986), and echoed in several commentator’s works, according to which one should mistrust the assumption of the totality of exponentiation.Footnote 10 A theory that fully meets Nelson’s standards is the theory \(\mathsf{S^1_2}\) from Buss (1986, 1998). \(\mathsf{S^1_2}\) has several further advantages: besides being consistent with the negation of exponentiation, \(\mathsf{S^1_2}\) is also remarkable from a purely proof-theoretic point of view: it can be seen as improving on EA as a theory for formalizing in a natural way the syntax of first-order theories as it is commonly done for the incompleteness theorems and as it is required for formulating reflection principles and semantic extensions of our starting theories. These notions are in fact all p-time and the functions \(\Sigma _1\)-definable in \(\mathsf{S^1_2}\) coincide with the p-time computable functions. \(\mathsf{S^1_2}\) is formulated in \({{\mathcal {L}}}^*={{\mathcal {L}}} \cup \{0,{\mathsf{S}},+,\times ,|\cdot |,\#,\lfloor \tfrac{1}{2}\cdot \rfloor \}\), where \(|\cdot |\) is the length function that gives the number of symbols in the binary representation of the input, \(\#\) is such that \(x\#y=2^{|x|\times |y|}\) and \(\lfloor \tfrac{1}{2}\cdot \rfloor \) gives the lower integer part of \(\frac{x}{2}\). Its axioms are the defining equation of these symbols and the schema
for \(\varphi \) in the class \(\Sigma ^b_1\), which is similar to the usual class \(\Sigma _1\) formulas with the additional assumption that quantifiers in the formula have to be bounded by a term of the form |t|, except the outermost string of existential quantifiers that can be bounded by an arbitrary term. Crucially, \(\mathsf{S^1_2}\) is interpretable in Robinson arithmetic Q, witnessing its minimality, and is finitely axiomatizable (Hájek and Pudlák 1998, Chap. V).
Assuming therefore that \(\mathsf{S^1_2}\) is ultrafinitistically acceptable, let us consider a reflection principle of the form
where \({\mathsf{Pr}}_\varnothing (\ulcorner \varphi (\dot{x})\urcorner )\) expresses the fact that an arbitrary numeral instance of the formula \(\varphi \) is provable in first-order predicate logic. It’s important to notice that now, for the formalization of provability in \(\mathsf{S^1_2}\), instead of non standard numerals one has to consider but dyadic numerals whose formalization is polynomially bounded.Footnote 11 However, even under these minimal assumptions, we obtain a result similar to Proposition 1.
Proposition 2
PA is a subtheory of \({\mathsf{S}}_2^1+\) \({\mathsf{RFN}}(\varnothing )\)
Proof Sketch
It is clear that, for each \(m\in \omega \),
is provable in first-order logic by a series of modus ponens and universal instantiations starting from \(\varphi (\bar{0})\). This proof, however, may not be captured in general by \(\mathsf{S^1_2}\). Therefore we argue as follows: assuming that \(\varphi \) is provably progressive in \(\mathsf{S^1_2}\)—that is, \(\mathsf{S^1_2}\) proves that it holds for 0 and that, if it holds for x, it holds for \(x+1\) as well —, by employing Solovay’s shortening of cuts technique (cf. again Hájek and Pudlák 1998, Chap. V), we downwards close \(\varphi \) under \(\le \) so that the resulting formula defines an initial segment of the \(\mathsf{S^1_2}\)-numbers \({\mathcal {J}}\). We can safely assume \({\mathcal {J}}\) to be closed under multiplication and the function \(\#\).
Then we can prove that
by crucially considering dyadic numerals.
Now reasoning in \(\mathsf{S^1_2}\) and starting with the proof of \({\mathcal {J}}(0)\), we can reason as usual to obtain a proof of \({\mathcal {J}}(n)\). Therefore, in \(\mathsf{S^1_2}\), which can be expressed as a single sentence A, plus \({\mathsf{RFN}}(\varnothing )\),
□
Proposition 2 strengthens the conclusion that, if one reads (ICT) as referring to “resources not available in S” that entail claims that are not provable in S, then S cannot be taken to capture a self-standing, self-justifying portion of mathematical reality. The ultrafinitist embracing \(\mathsf{S^1_2}\), in fact, cannot even be committed to a reflection principle for logic, on the pain of the acceptance of the full induction schema of \(\mathsf{PA}\) that, obviously, also entails the claim that the exponentiation function is total.
To summarize, the discussion of the theses of Tait, Isaacson, and Nelson, coupled with a strong reading of (ICT) à la Feferman that seems to be taken for granted by Dean, leads to at least two options: either we reject (ICT) across the board, deeming it as inadequate, or we provide a different interpretation of (ICT) equipped with an alternative reading of what the “resources not available” in the chosen system could amount to. In the next section we set the basis for such an alternative interpretation: we will introduce in particular a wide array of semantical extensions of an arithmetical system S that, although crucially resorting to notions that are not immediately available in S—such as a truth predicate—do not entail sentences in the language of S that are not provable in S itself.
3 Soundness Extensions and the Semantic Core
As noticed by several authors,Footnote 12 resorting to schemata such as \({\mathsf{RFN}}(S)\) above may be plausibly seen as a surrogate for single sentences of the form
where \(\mathsf{T}\) is unary truth predicate. These surrogates only become necessary when a notion of truth is not part of the signature of the theory. Any soundness claim seems in fact to be intrinsically related to the notion of truth. If one wants to express in the object language that all non-logical axioms of S are true, for instance, one can of course resort to a schema of the form
where \(\mathsf{Ax}_S(\cdot )\) is the representation of all non-logical axioms of S. Yet, this option merely highlights the fact that we are relegating the notion of truth in the meta-theory.
Clearly someone might have independent motivations to stick with the expressive limitations of the arithmetical language in asserting the soundness of a theory. Tennant (2002), for example, has made use of the well-known fact that schematic versions of reflection, such as \({\mathsf{RFN}}(S)\), enable us to go beyond what’s provable in S to defend the possibility of a deflationary account of the notion of truth employed in these soundness claims. However, Tennant does not fully articulate a justification for these principles, although he hints at the schematic version of reflection as sufficient for fixing the norms for assertion of these soundness claims (Tennant 2002, p. 574). More generally, while it is uncontroversial that a soundness extension of S will contain forms of reflection such as \({\mathsf{RFN}}(S)\), it remains problematic whether the presence of \({\mathsf{RFN}}(S)\) is sufficient for defining a soundness extension, in the sense that its principles amount to a coherent articulation of the concepts needed to state soundness claims for S. A good illustration of how soundness claims can be derived within an adequate framework for provability and truth is provided by Feferman’s reflective closure of PA (\(\mathsf{Ref}(S)\)), nowadays commonly known as KF from “Kripke-Feferman”Footnote 13:
Which statements in the base language L of S [\(\dots \)] ought to be accepted if one has accepted the basic axioms and rules of S? The answer is given as an ordinary theory Ref(S) formulated in a language L(T, F) [\(\dots \)] where T and F are partial truth and falsity predicates which are self-applicable in the sense that they apply to (codes of) statements of L(T, F) [...] Thus, for example, we may reason in Ref(PA) by induction about the truth of statements which contain the notion of truth, and so arrive at statements of the form: \(\forall x[Prov_{PA}(x) \rightarrow T(x)]\), and by repeating this kind of argument derive iterated reflection principles for arithmetic (Feferman 1991, p. 2).
Note well that we are not suggesting the impossibility of convincing arguments supporting the absence of the notion of truth from soundness extensions of a given theory; we are simply holding that given the usual way of introducing and justifying soundness claims for a theory S, the notion of truth is hard to do without. Proposals such as Tennant’s, and the subsequent debate it generated (Ketland 2005; Cieśliński 2010; Piazza and Pulcini 2015), clearly show how hard it is to eradicate the intuition that reflection principles are conceptually dependent on the notion of truth. But the onus is on those who do not share this intuition to tell a principled story about soundness claims by resorting to surrogates that can play the role of semantic notions. It’s hard to say what this story could amount to. Thus, throughout the paper we will stick with the widespread view and hold that soundness claims are best formulated by employing a notion of truth governed by suitable axioms.
However, this does not immediately mean that these axioms added on top of Sneed to entail \(\mathsf{GRP}(S)\). Such a requirement, indeed, would be too strong for an arbitrary S (namely, when S also varies over, for instance, theories with restricted induction). The case made by Tait for PRA from the finitist point of view is indeed one example where one needs to be careful in calibrating the strength of the principles for the truth predicate. Similar considerations apply to Isaacson’s thesis on PA and ultrafinitist’s position viewed through the lens of \(\mathsf{S^1_2}\). Prima facie, there is not much room for the choice of the truth principles: for instance, the next proposition shows that already weak truth axioms seem to collapse the fine structure of the subsystems of \({\mathsf{PA}}\).
Proposition 3
The result of extending\(\mathsf{S^1_2}\)—whose language is expanded with a fresh predicate\(\mathsf{T}\)—with the schemaFootnote 14
for all\({\mathcal {L}}\)-formulas\(\varphi (v)\)derives the full induction schema of\({\mathcal {L}}\).
Proof
Since \(\mathsf{S^1_2}\) in \(\mathcal L_\mathsf{T}:={{\mathcal {L}}}\cup \{\mathsf{T}\}\) contains \(\mathsf{I}\Delta _0\) in \(\mathcal L_\mathsf{T}\), the following is derivable in the former
for a formula \(\varphi (v)\) of \({\mathcal {L}}\) of arbitrary complexity, because \(\mathsf{T}\ulcorner \varphi (\dot{x})\urcorner \) is a \(\Delta _0\)-formula of \(\mathcal L_\mathsf{T}\). By employing (utb), (3) yields the desired result.□
The argument employed in Proposition 3 applies equally well—with the obvious modifications—to other subsystems of PA obtained by restricting induction such as \(\mathsf{EA}\), \(\mathsf{PRA}\), of \(\mathsf{I}\Sigma _n\) for every n.Footnote 15 At any rate, Proposition 3 seems to slim our chances of finding a reasonable truth-theoretic extension of an arbitrary arithmetical theory S, that is fixing a set of reasonable truth axioms that are compatible with the principles we are implicitly committed to when we endorse S. Proposition 2 and Kreisel and Levy’s result already told us that a soundness extension involving the uniform reflection principle for S may clash with the foundational standpoints —such as the ones just discussed in the previous section—advocating a restriction of the full schema of induction of \({\mathsf{PA}}\). Proposition 3 extends these limitations to the truth-theoretic context: if even weak axioms such as (utb) are sufficient to lead us from, \(\mathsf{S^1_2}\), \(\mathsf{EA}\), or \(\mathsf{PRA}\) to full \({\mathsf{PA}}\), then there seems to be no hope to harmonize (ICT) and foundational positions that do not permit arithmetical consequences exceeding those of the systems associated with such positions.
Nevertheless, concluding this would simply be trading on a confusion on the meaning of “truth axiom”. The theory of truth employed in Proposition 3 is obtained by extending the mathematical induction schemata of the base theory to the truth predicate. If the axioms (utb) are unequivocally truth-theoretic in character, it is natural to think of the extended induction as a mathematical and not as a truth-theoretic axiom. There seems to be in fact a substantial difference between metalinguistic principles declaring the truth conditions for a sentence of \({{\mathcal {L}}}\), as (utb) seems to be (partially) doing, and the extension to the truth predicate of a schema whose justification is apparently non-metalinguistic. As observed by Hartry Field, such a justification essentially depends on a “fact about natural numbers, namely, that they are linearly ordered with each element having finitely many predecessors” (Field 1999, p. 538).
For example, the formula \(\mathsf{T}\ulcorner 0=0\urcorner \wedge 2^x>x\) can occur into instances of the induction schema of \(\mathsf{EA}\) formulated in \(\mathcal L_\mathsf{T}\)\((:={{\mathcal {L}}}\cup \{2^\cdot ,\mathsf{T}\})\); however, it would be rather implausible to consider the corresponding instance of induction as a genuinely truth-theoretic sentence. By contrast, the truth predicate in it is merely idling and the bulk of the induction is instead a basic mathematical property of the exponential function. On the contrary, the induction instance corresponding to the \(\mathcal L_\mathsf{T}\)-formula \(\mathsf{T}\ulcorner 2^{\dot{x}}>\dot{x}\urcorner \) is expressing a metalinguistic fact, namely that all substitutional instances of the formula \(2^x>x\) are true. The shift in meaning between the two properties is subtle but crucial: in one case we talk about properties of a mathematical function, in the second one about formulas of \({{\mathcal {L}}}\).
Let’s be clear about this point to avoid further confusion: from the internal point of view of the theory of truth, the two instances of induction corresponding to the formulas \(\mathsf{T}\ulcorner 0=0\urcorner \wedge 2^x>x\) and \(\mathsf{T}\ulcorner 2^{\dot{x}}>\dot{x}\urcorner \) are, strictly speaking, indistinguishable. However, from the external point of view of our informal metamathematical practice, they are clearly distinct. It is only because arithmetic plays a double role of theory of syntax and of object theory, that we can consider both instances as belonging to essentially the same class. This observation even led to the formulation of theories of truth that keep separate the domain of syntactic objects from the mathematical or, more generally, the object theoretic universe (see Halbach 2011; Heck 2015; Nicolai 2015). It’s not our intention here to consider the details of this alternative framework: we will keep implicit the distinction between metalinguistic and object-linguistic instances of the induction schema. However, in what follows we will not extend the induction schema of S to the truth predicate to avoid any conflation between the two levels.
This is not to say, however, that we will not be able to state the truth of the induction schemata of S: if in fact the extended induction schema in combination with natural truth axioms would lead us to very strong theories, the assumption of the truth of all its instances is fairly innocent. As we shall see shortly, indeed, the result of adding to a wide class of base theories S the claim “all instances of the induction schema of S are true” is still compatible with the alternative reading of (ICT) that we suggested in the previous section and that is aimed at harmonizing (ICT) with foundational standpoints such as Tait’s, Isaacson’s and Nelson’s.
3.1 The Semantic Core
We have seen that a strong reading of (ICT) may conflict with foundational standpoints based on a form of “arithmetical completeness” or “epistemic stability” of some arithmetical system S. In fact, if (ICT) entails reflection principles for S and therefore claims in the arithmetical language that are not provable in S alone, then in accepting S one is also bound to accept arithmetical consequences that go beyond S, thus contradicting its alleged completeness.
In concluding Sect. 2, we envisaged the possibility of an alternative reading of (ICT) that could be immune from this problem. But how could this alternative reading look like? A hasty thought may be to let (ICT) depend exclusively on one’s foundational standpoint. This is highly problematic. Let’s consider, for example, someone who embraces only what’s derivable or interpretable in PA: by a well-known result of Feferman, she will also accept \(\lnot \mathsf{Con(PA)}\).Footnote 16 By contrast, we have seen that there are several authors disposed to accept \(\mathsf{Con(PA)}\) after accepting PA. Under this relativistic view of (ICT), therefore, different readings of it would not only lead to alternative sets of principles, but rather to sets of principles inconsistent with each other. In the specific case of \(\lnot \mathsf{Con(PA)}\) just mentioned, moreover, there is a clear departure from what we previously defended as a necessary condition for any plausible reading of (ICT), namely the truth of the principles at play. The interpretation of (ICT) that we now introduce will keep a strong link with the notion of truth, while rejecting the sort of rigidity detected in Feferman’s reading of (ICT). Our approach substantiates a dynamic reading of (ICT) as displaying a fixed, semantic component—called the semantic core of implicit commitment—and a variable component that is relative to one’s foundational standpoint.
The semantic core amounts to a set of principles of meta-theoretic nature that enable us to reflect in a natural and uniform way on our acceptance of different arithmetical theories. To introduce it, we argue in three stages. In the first step, we need to expand the language of S with semantic resources, a truth predicate \(\mathsf{T}\) in particular, and characterize it with a minimal set of principles capturing its disquotational nature. More precisely, given a suitable S, the theory \(\mathsf{TB}[S]\) is obtained by expanding \({\mathcal {L}}_S\) with the predicate \(\mathsf{T}\) and extending its axioms with the schema
for all \(\mathcal {L}_S\)-sentences \(\varphi \). An immediate consequence of tb is the truth of each axiom of S; it is clear therefore that if S has finitely many non-logical axioms, tb suffices to conclude \(\forall x\,(\mathsf{Ax}_S(x) \rightarrow \mathsf{T}x)\), that is the single sentence expressing the truth of all (non-logical) axioms of S. Further claims of clear metalinguistic nature are also provable in tb. For instance, \(\mathsf{TB}[S]\) proves the claim that the global reflection principle for S entails the consistency of S. Formally:
This implication is simply obtained by instantiating (the code of) an S-falsity in GRP(S).
Already in this first step, it should be clear that we aim at semantic extensions of S in the sense of coherent articulations of a concept of truth over the base theory S. For instance, one could simply extend S with the sentences \(\forall x\,(\mathsf{Ax}_S(x) \rightarrow \mathsf{T}x)\) or GRP(S) as new axioms. The sentences above clearly do not suffice to count as axioms for the truth predicate \(\mathsf{T}\): in the first case the resulting theory is clearly interpretable in S by taking the truth predicate in question to be defined by \(\mathsf{Ax}_S(x)\) itself; in the second case, the full schema tb is not necessary to derive (4), as the “modal” axiom \(\mathsf{T}\ulcorner \phi \urcorner \rightarrow \phi \) suffices. This suggests that, in these extensions of S, concepts other than truth could be employed as natural readings for the predicate \(\mathsf{T}\).
From the perspective of the theorems of S, \(\mathsf{TB}[S]\) looks fairly innocent. First of all, it is conservative over S. Moreover, if S is reflexive [i.e. the consistency of any finite sub-theories of S is provable in S, (Mostowski 1952)], \(\mathsf{TB}[S]\) is also relatively interpretable in S. This is because in any given proof in S the truth predicate \(\mathsf{T}\) can be replaced by a S-definable truth predicate. This suffices to witness the conservativity and, by Orey’s compactness theorem (see Lindstrom 1997, §7), the interpretability of \(\mathsf{TB}[S]\) in S for reflexive S.
The disquotational principles tb, however, fall short of many further desiderata that we would like to ascribe to the semantic core of implicit commitment. For instance the schema tbcannot enable us to establish that instances of modus ponens preserve truth because every generalization crucially involving truth provable in \(\mathsf{TB}[S]\) can be reduced to a finite conjunction. This means, in particular, that \(\mathsf{TB}[{\mathsf{PA}}]\) can only prove the weaker
where \(\mathsf{Sent}^n_{{{\mathcal {L}}}}(x)\) expresses that x is a sentence of \({{\mathcal {L}}}\) of complexity \(\le n\) for any given n but not for arbitrary sentences of \({{\mathcal {L}}}\) and the expression \(\underset{\cdot }{\rightarrow }\) (and \(\underset{\cdot }{f}\) more generally) represents in S the syntactic operation of entailment (resp. f).Footnote 17
Therefore, pure disquotation is not sufficient for our purposes. As second step, one might think of extending \(\mathsf{TB}[S]\) with further truth-theoretic principles so as to derive the non-restricted versions of (5). Obvious candidates are the so-called compositional truth axioms such as “\(\lnot \varphi \) is true if and only if \(\varphi \) is not true”, which govern the interaction of the truth predicate and the logical constants. For instance, since we might safely assume that S is formulated in a calculus in which modus ponens is the only logical rule of inference [see, for instance, Enderton (2001)], we would only need to add to S the sentence
to derive the truth-preserving character of modus ponens.
If S is finitely axiomatized, therefore, \(\mathsf{TB}[S]\) + (6) enables us to prove that all non-logical axioms of S are true and that—if the logic is rightly chosen—that all rules of inferences of S preserve truth. However, there are at least two problems with this theory: in the first place, it does not articulate a coherent semantic notion as we usually demand that the truth of a compound sentence depends on the truth of its compounds, and this theory has no such feature. In short, the theory is not (fully) compositional. Secondly, if S is not finitely axiomatizable, it cannot prove that all non-logical axioms of S are true. In fact, as the next lemma shows, it cannot do so even if we add to S a fully compositional theory of truth:
Lemma 1
Let S be formulated in \(\mathcal L_\mathsf{T}\) and assume it satisfies full induction for \({{\mathcal {L}}}_S\) —that is the truth predicate is not allowed into instance of induction. This theory extended with the sentences
cannot prove that all axioms of S are true.
In (7), R ranges over the relation symbols of \({{\mathcal {L}}}_S\).
Proof
Assume that S \(+\) (7–10) proves
We can then show that the formula
is progressive in it. In (12), \(\mathsf{Prv}_{S}\) is a \(\Delta _1^b\) predicate expressing the notion of being a proof in S and \(\mathsf{end}(\cdot )\) is a \(\Sigma _1^b\)-function that outputs the last element of of a S-proof. Therefore, still by Solovay’s result on subcuts (see Proposition 2), we find an initial segment of the S-numbers satisfying the property expressed by \(\mathcal K(x)\) in which all logical axioms of S are true and then prove the consistency of S relative to this initial segment.Footnote 18 By a strengthening of Gödel’s second incompleteness theorem due to Pudlák (1985, Cor. 3.5), therefore, this is sufficient to show that S cannot interpret S \(+\) (7–10). However, S \(+\) (7–10) is known to be interpretable in S (see Enayat and Visser 2015, §16.5).□
The full compositional clauses (7–10) are without doubt desirable features for a notion of truth. Moreover, this notion of truth is a natural component of the acceptance of S via soundness claims, and soundness claims are, in turn, an integral part of many accounts of implicit commitment. As we have seen, however, there are also limitations to which soundness claims one can assume, depending on one’s foundational stance. We have considered already examples of such limitations: for example the ones related to the reflection principles \(\mathsf{RFN(EA)}\) or \(\mathsf{RFN(PA)}\)—and, a fortiori, their global versions—for positions such as finitism or first-orderism à la Isaacson. Nonetheless, as we shall soon point out, no such limitations occur for the compositional truth clauses. What is even more surprising is that we can allow explicit soundness claims relative to the non-logical axioms of an arbitrary theory S without trespassing into the realm of what’s unprovable in S. This can be established in full generality.
As the third, and final step of the construction of the semantic core we consider the theory \(\mathsf{CT}[S]\) obtained by expanding the language of the theory S with a truth predicate not allowed into instances of the non-logical axiom schemata, and of extending S with the principles (7–11).
Halbach (2011) attempts to prove the conservativity of \(\mathsf{CT}[S]\setminus \)(11) via a cut elimination argument. His argument relies on a reformulation of \(\mathsf{CT}[S]\) in a (finitary) two-sided sequent calculus with cut by rewriting (7–10) as rules of inference, e.g.

and then proceeds via an attempt to eliminate cuts on formulas of the form \(\mathsf{T}s\) from derivations in this theory. Leigh (2015) shows that this strategy can only remove cuts of a provably fixed complexity (cf. Leigh 2015, §3.7). He then shows how to fix Halbach’s strategy by finding suitable bounds to the complexity \(\mathsf{c}(\cdot )\) of truth-cut-formulas in \(\mathsf{CT}[S]\)-derivations—for S interpreting EA—so that \(\mathsf{CT}[S]\) can be embedded in the system resulting from replacing the full cut rule for formulas of the form \(\mathsf{T}s\) with a weaker set of rules

for each n and a suitably bounded version of (11). Crucially, this system enjoys a standard version of cut-elimination for cuts on truth ascriptions. Derivations of truth-free sequents of the form \(\Gamma \Rightarrow \Delta \) are then regimented via the notion of approximation of a sequent, first considered by Kotlarski et al. (1981), that enables one to control such proofs in \(\mathsf{CT}[S]\) and transform them into proofs of the same sequent where only applications of the modified rules are employed. Finally, one eliminates cuts on formulas of the form \(\mathsf{T}s\) in a standard manner. This strategy yields the following:
Proposition 4
(Leigh 2015, Thm. 2) For\(S\supseteq \mathsf{EA}\), \(\mathsf{CT}[S]\)is a conservative extension ofS.
Proposition 4 tells us that the semantic principles of the theory \(\mathsf{CT}[S]\) can safely be included into the semantic core of the implicit commitment of S. Our main thesis is now taking shape: in accepting an arithmetical theory S, we are always implicitly committed to the theory \(\mathsf{CT}[S]\), which amounts to the fixed, invariable component of our commitment. Crucially, whether or not \(\mathsf{CT}[S]\)exhausts our commitments depends on the particular foundational standpoint that led us to accept a given theory S in the first place.Footnote 19
This completes the presentation of the semantic core for implicit commitment: it amounts to an extension of S with compositional truth axioms and the claim that all the (non-logical) axioms of S are true. In our account, it is a necessary condition for implicit commitment but possibly not a sufficient one: this will depend on the foundational standpoint that one is adopting in justifying a specific formal system S.
Before giving concrete examples of how our reading of (ICT) in the light of the semantic core applies to the positions considered above, we anticipate two possible objections to the structure of the semantic core.Footnote 20 The semantic core may be accused of being too artificial given (1) the absence of natural soundness principles such as \(\mathsf{Con}(S)\), and (2) the absence of the closure under first-order reasoning. We consider the two objections separately.
To the first objection a natural reply is that it is not the task that we are assigning to the semantic core to decide which soundness extension of the base theory S is natural or not. The question we are addressing is in fact whether someone who considers a base theory S as epistemically stable in the sense of Sect. 1 can consistently accept (ICT): with the semantic core we aim at providing a framework to answer this question affirmatively. In other words, we do not claim that, say, \(\mathsf{Con}(S)\) is not a natural principle to endorse once that one has endorsed S, but we share with Dean the view that if the justification of \(\mathsf{Con}(S)\) is equivalent to principles that are incompatible with the alleged epistemic stability of S, as we have seen is the case in the case of finitism and first-orderism, then such a justification cannot be implicit in the mere acceptance of S but should stem from more general considerations. For instance, as we shall see in a moment, although Isaacson considers \(\mathsf{Con}(\mathsf{PA})\) a principle of infinitary nature, this does not mean that its acceptance should be denied: this principle simply follows from the acceptance of a suitable portion of infinitary mathematics although it is not implicit in the acceptance of PA that—according to first-orderism—delimits the boundaries of finite mathematics. This is all compatible with the framework provided by the semantic core.
To address the second objection a similar line of reasoning can be employed: closure of truth under logical reasoning is not a principle that we deem incorrect or undesirable. However, under the condition of the epistemic stability of a theory S, the reflection principle for logic entails principles that are incompatible with this epistemic status such as \(\mathsf{Con}(S)\). Still, we have shown that there are weaker forms of soundness—such as the truth of all axioms of S—that are on the one hand not available in S but on the other deductively innocent with respect to S: this makes, we will argue, these weaker soundness claims fit the demands of the implicit commitment thesis (ICT) without falling prey to Dean’s objections. Once again, the point is that someone may be implicitly committed to the semantic core even if she believes that in accepting S she is not implicitly committed to accept principles unprovable in S: in turn, this does not rule out that she might also have an independent justification for these unprovable claims such as \(\mathsf{Con}(S)\) or the reflection principle for logic.
4 Schematic Reasoning and the Structure of Implicit Commitment
Several foundational standpoints, including the ones considered above, can be compared and distinguished by taking into account the role of the schemata of induction of the arithmetical systems associated to them. In this section we employ these different understandings of schematic reasoning to assess the effectiveness of our dynamic analysis of implicit commitment based on the distinction between the constant semantic core and its variable components.
At one end of the spectrum, we find advocates of restrictions of the arithmetical induction schema. Tait’s finitism and Nelson’s ultrafinitism are paradigmatic examples of this sort: in both cases claims about the totality of natural numbers can only be reached for a class of “acceptable” predicates that are proper subclasses of the ones expressible by formulas of the language of arithmetic. The remaining instances of the induction schemata are, according to these standpoints, at least suspicious if not false. At the other end of the spectrum, we find authors defending the view that, once accepting a system S, not only we should impose no restriction to non-logical axiom schemata, but we should also allow for extensions of these schemata to possible expansions of the starting language.
This latter view can be understood of course in different senses. On a radical reading, similar to what Vann McGee suggested in (1997), the acceptance of, say, PA, should commit us to instances of induction corresponding to any subset of natural numbers. This possibility is supposed to be rooted in how mathematical language itself is learned and communicated.Footnote 21 This radical form of open-endedness of axiom schemata leads quickly to very strong theories, in fact, categorical ones. Critics of this position notice in fact that—despite McGee’s efforts—it is also committed to the rich ontology of second-order logic (see Pedersen and Rossberg 2010).
Feferman’s notions of reflective closure of a theory S (see Feferman 1991) represent a less radical alternative. It comes in two versions: the reflective closure of S and the schematic reflective closure of S. In both cases, the interaction of semantic resources and the power of the induction of PA enable one to reach strong subsystems of second-order arithmetic. In the case of the reflective closure of PA one reaches the strength of ramified analysis up to \(\varepsilon _0\) via the theory of self-applicable truth \(\mathsf{KF}\), whereas the schematic reflective closure of \(\mathsf{PA}\) takes the form of a type-free theory of truth as strong as ramified analysis up to the Feferman-Schütte ordinal \(\Gamma _0\) (i.e, roughly speaking, the theory resulting form iterating predicative comprehension \(\alpha \)-times for \(\alpha <\Gamma _0\)) (Feferman 1964; Schütte 1965).Footnote 22 Feferman’s approach therefore, although clearly committed to schematic reasoning, is clearly weaker than McGee’s, since it only delivers a proper subsystem of second-order arithmetic.
Among the authors that hold an intermediate position between the ones just considered we find Isaacson himself. He does not seem to impose any restriction to the class of formulas allowed to appear into instances of induction; however, he also clearly states that any further instance of induction involving extra-vocabulary would be intrinsically higher-order, inasmuch as the axioms of full PA suffice to characterize what he calls “finite mathematics” (Isaacson 1996, p. 204).
4.1 Restricted Schemata and (ICT)
In Sect. 2, we have defended the claim that the notion of truth is integral to any reasonable articulation of what we are implicitly committed to when accepting a given arithmetical theory. Of course this comes as no surprise and, as we have seen, our view is shared by many authors. Our intention, however, is not to reformulate a widespread position on the role of truth in foundations, but to suggest something further. What concern us, indeed, is to examine how the notion of truth, as a device to unravel our commitments, can coexist with narrow readings of the implicit commitment thesis (ICT), namely readings which do not allow for claims that are underivable in the accepted arithmetical theory, above all uniform reflection principles.
The case studies of narrow readings of (ICT) stem Dean’s analysis of Tait’s and Isaacsons’ theses. For instance, in the case of Tait’s finitism, the uniform reflection principle for the subtheory EA of PRA was sufficient to deliver the full schema of induction of PA (see Proposition 1). If the finitist’s reading of (ICT) involved principles such as RFN(PRA), she would also be committed to PA, which clearly outstrips primitive recursive reasoning. There is, therefore, a strong temptation for concluding that (ICT) is incompatible with finitism or, even more drastically, that it is false. This temptation, we argue, should be resisted. The semantic core for implicit commitment introduced in Sect. 3gives us a way to accommodate the strong intuition that, even for the finitist’s defense ofPRA, (ICT) is best spelled out in terms of truth; the semantic core also tells us, however, that these additional resources, being clearly of meta-theoretic and not of object-theoretic nature, do not interfere with the arithmetical content ofPRAthat the finitist wants to preserve.
Over PRA—or better its conservative extension in first-order logic QF-IA—which is known to be not finitely axiomatizable, the semantic core does not only involve compositional truth axioms of the form (7–10) on page 19, but also the single sentence stating the truth of all the infinitely many non-logical axioms of PRA. By Proposition 4, the resulting theory \(\mathsf{CT}[\mathsf{PRA}]\) does not yield new arithmetical consequences. Nonetheless, it is capable of deeming true the equations for all primitive recursive functions and all instances of the induction ofPRA, all instances of each individual propositional tautology of\({{\mathcal {L}}}_\mathsf{T}\), and establishing that the rules of inference of the chosen logical calculus are truth-preserving. The first and last fact follow respectively from the assumption (11) and the axiom (9). The truth of all instances of each propositional tautology follows from a suitable instance of a logical axiom schema of \(\mathsf{CT}[S]\) and the axioms (7–10): for instance, in the case of the law of excluded middle, one starts with \(\mathsf{T}x \vee \lnot \mathsf{T}x\) for \(\mathsf{Sent}_{{{\mathcal {L}}}_S}(x)\) and concludes, by (8) and (9), \(\forall x (\mathsf{Sent}_{{{\mathcal {L}}}_S}(x)\rightarrow \mathsf{T}(x\underset{\cdot }{\vee }\underset{\cdot }{\lnot }x))\).
The bearing of this fact should now be clear: we have already argued that truth provides a powerful and natural tool to express one’s commitment to a base theory, PRA in the case at hand. Dean cast doubts on the possibility of harmonizing a satisfactory notion of truth and the exclusive commitment to theorems of PRA that appears to be essential to Tait’s standpoint. The semantic core offers a minimal sense in which this balancing process can actually succeed; we do have a notion of truth satisfying some adequacy requirements, such as the partial metalinguistic reflection available in\(\mathsf{CT}[\mathsf{PRA}]\)just considered, and yet we cannot go beyond what’s provable inPRA.
Moving to what we called ultrafinitism, in order to draw conclusions along the lines of the ones just obtained for PRA, we would need an analogue of Proposition 4 for all theories containing \(\mathsf{S^1_2}\). This claim is, unfortunately, still only a likely conjecture. At any rate, this more general version of Proposition 4 would then establish that the semantic core for implicit commitment relative to a theory S gives us a theory that does not give us new theorems in \({{\mathcal {L}}}_S\), and in particular \(\Pi _1\)-sentences such as the consistency of Robinson arithmetic, \(\mathsf{Con(Q)}\), that are not available in ultrafinitistically acceptable theories.
4.2 Full Arithmetical Induction and Beyond
Isaacson considers PA as specifying a self-standing portion of mathematical reality. In his view, full-induction on \({{\mathcal {L}}}\) still belongs to or even delimits the realm of finite mathematics: principles that properly extend PA, such as RFN(PA), must therefore appeal to infinitary resources. Again, the semantic core offers us the possibility of identifying a metalinguistic component of the implicit commitment to PA and by distinguishing it from the object-linguistic, or mathematical content of PA. The conservativeness of \(\mathsf{CT}[\mathsf{PA}]\) over \({\mathsf{PA}}\) tells us that proofs of theorems in the language of \({{\mathcal {L}}}\) in \(\mathsf{CT}[{\mathsf{PA}}]\) are not affected by the metalinguistic component embodied in the truth principles of \(\mathsf{CT}[{\mathsf{PA}}]\).
Arguably, Isaacson would regard the semantic components of \(\mathsf{CT}[\mathsf{PA}]\) as intrinsically infinitary, but this is not a problem for our reading of (ICT). The implicit commitment to PA, if one regards it as “arithmetically complete”, would be delimited by the semantic core, and its non-arithmetical, infinitary components do not interfere in any way with its mathematical ones in \(\mathsf{CT}[\mathsf{PA}]\)-proofs. This is once more an example of how the semantic core can combine the idea of a privileged access to a definite portion of mathematical reality given by a specific theory with the natural act of reflection on the metalinguistic aspects of this theory via semantic notions.Footnote 23
Isaacson’s position clearly contrasts with views such as Feferman’s, who considers the extension of the induction schema of PA as essential to unravel the class of arithmetical assertions we are implicitly committed to when accepting PA in the first-place. In such positions, schemata are open-ended, and there is no need to stop the truth predicate to interact with the arithmetical content of PA. The semantic core \(\mathsf{CT}[\mathsf{PA}]\), in such view, counts only as a class of necessary conditions that our notion of truth has to satisfy. The theory of truth Feferman is putting forward to fully articulate our commitment to PA, namely KF, contains \(\mathsf{CT}[{\mathsf{PA}}]\) and is spectacularly stronger than it: it corresponds in fact to \(\varepsilon _0\)-many iterations of ACA. In terms of classical ordinal analysis, KF will prove the same arithmetical theorems as PA plus transfinite induction up to \(\phi _{\varepsilon _0}(0)\).Footnote 24 According to our proposed reading of (ICT), therefore, Feferman’s acceptance of PA is tied not only to the semantic core, but to a substantial amount of mathematical principles that can be measured by the big gap separating the transfinite induction schemata for \({{\mathcal {L}}}\) associated to the ordinals \(\epsilon _0\) and \(\phi _{\varepsilon _0}(0)\). In moving from Isaacson’s to Feferman’s position, the semantic core stayed the same, whereas the variable component, which was empty in the case of Isaacson, now includes a large amount of analysis.
There is, however, an unexpected bridge between Isaacson’s and Feferman’s positions. Once the truth predicate is not allowed into the induction schema of PA, KF becomes much closer to \(\mathsf{CT}[{\mathsf{PA}}]\). This theory, called \(\mathsf{KF}\!\upharpoonright \) in Halbach (2011), is in fact conservative over \({\mathsf{PA}}\). Any model \({\mathcal {M}}\) of PA can be expanded to a model \(({\mathcal {M}},S)\) of \(\mathsf{KF}\!\upharpoonright \) by tanking S to be a fixed point of a suitable positive inductive definition capturing the clauses of the construction of a Kripke truth set (see Kripke 1975).
Instead of being a mere curiosity, this point highlights how the difference between the view of implicit commitment associated with the first-orderist à la Isaacson and with the predicativist may be seen as not lying in their conception of truth, but in their understanding of schematic reasoning. If in fact our distinction between object-linguistic and metalinguistic component of a truth theory is granted, then the first-orderist can articulate a robust notion of truth and yet distinguishing between the arithmetical reality that PA is isolating and the mere metalinguistic consequences that become available once one moves to its extension \(\mathsf{CT}[{\mathsf{PA}}]\). She might even move to a type-free notion of truth, as articulated by \(\mathsf{KF}\upharpoonright \), for instance, without exceeding the arithmetical consequence of PA. Once the truth predicate is allowed to do mathematical work, however, the situation drastically changes.
This scenario reinforces the usefulness of our analysis of implicit commitment via the semantic core: the latter in fact gives us necessary conditions for soundness extensions of a mathematical theory we accept and it is compatible with both restrictive and relaxed readings of (ICT).
Of course once one has reached a satisfactory halting point, such as KF for Feferman’s analysis of implicit commitment, nothing prevents one from asking herself what we are implicitly committed to when we are accepting the theory of truth. If Feferman’s strategy is extended to the theory of truth, for instance, one can obtain extensions of KF via uniform reflection principles. Indeed, Horsten and Leigh (2017) have shown that extensions of KF can be obtained by starting with \(\mathsf{TB[PA]}\) via finitely many iterations of uniform reflection.Footnote 25 However, since we are not interested in the theory of truth itself, but only in the boundary between acceptable and non-acceptable characterizations of the implicit commitment of the base theory, we do not consider further this possible extension of our analysis.
5 Conclusion
The implicit commitment thesis (ICT) prescribes that, in accepting a system S formalizing some portion of mathematics—arithmetic in our case studies—one is committed to resources not immediately available in S. Traditionally, these additional resources have been understood in terms of sentences in the language of S that are not provable in S already, typically reflection principles for S expressing the soundness of S.
As recently shown by Dean, however, certain foundational standpoints consider a particular arithmetical theory S as delimiting a privileged region of mathematical reality. Reflection principles for the theory S therefore, being closely related to mathematically meaningful principles that lie beyond the space of mathematics occupied by S (see Sect. 2), should be considered as incompatible with those foundational standpoints. Examples of such positions are Tait’s justification of PRA, Isaacson’s thesis on PA, and to some extent Nelson’s strict finitism.
Starting with the observation that soundness claims of S can only be fully articulated by resorting to the notion of truth, we have proposed a dynamic and widely applicable reading of (ICT). The additional resources we are committed to when accepting S will contain principles for truth: these principles, what we called the semantic core for implicit commitment, are fixed and shared by any reasonable justification for the acceptance of a system S. They amount to compositional truth principles and include minimal soundness claims for S such as the truth of all its non-logical axioms, the truth of all instances of each propositional tautology and, in reasonably chosen cases, the truth-preserving character of its rules of inference. Further principles extending the semantic core of implicit commitment depend on the justification for S provided by the idealized mathematician.
This analysis that we have provided is adequate with respect to the case studies considered in the first part of the paper: the semantic core, when added to S, prevents one from proving new consequences in the language of S besides the ones already available in S itself. Moreover, all natural articulations of soundness assertions of S in the form of stronger truth principles will contain the semantic core; whatever variable components one is willing to add to the semantic core, therefore, they will not be incompatible with it.Footnote 26
Notes
In what follows, we will always deal with systems S formulated in a language \({\mathcal {L}}_S\) extending the language of arithmetic \({\mathcal {L}}=\{0,{\mathsf{S}},+,\times ,\le \}\).
For an overview of this debate, see Feferman (2005).
A similar formulation can be found in Dean (2015, p. 32).
Girard and Feferman are obvious exceptions, although they also do not directly deal with conceptual analysis of the notion of implicit commitment.
In the literature one can find many formal systems that fall under the label PRA. In the following we refer to PRA as the extension of propositional logic with the defining equations of all primitive recursive functions and the schema of quantifier-free induction—for a precise definition, see for instance Troelstra and Schwichtenberg (2000, Chap. 4, §5).
The finitistic justification process for PRA sketched by Tait is rooted in the fundamental operation of manipulating finite sequences of objects. All operations and notions obtained by bootstrapping this operation are finistically kosher. In particular, this process of justification is not itself legitimate for the finitist because it assumes the general notion of function, which is not finitistically definable (cf., e.g., Tait 1981, pp. 531–533).
This theory is called \(\mathsf{QF}{\text {-}}\mathsf{IA}\) in Sieg (1981).
Note that Isaacson characterization of arithmetical truth seems to entail that sentences like the Goldbach conjecture are un-arithmetical, being neither directly perceivable by grasping the structure of natural number, nor perceivable from some arithmetical truth (Arana 2008). Against the claim that a proof of any true PA sentence which is independent of PA needs ideas that go beyond those that are required in understanding PA, see Piazza and Pulcini (2016).
It should be noticed that we haven’t made any reference to the notions of “higher-order” or “infinitary” in this description, and this is not by accident: it is not completely clear to us, indeed, where the boundary between finitary and infinitary should lie in the case of PA. Isaacson seems to think that such a boundary coincides with the distinction between what can be proved or not in PA: but can there be a sense in which “higher-order” or “infinitary” notions are not at odds with PA? To cite one simple example, consider well-orderings of order type \(\alpha <\varepsilon _0\), that can be proved in PA by a well-known theorem of Gentzen; other examples that come to mind are versions of semantical reflection that, unlike RFN(PA), are conservative over PA and therefore do not lead us outside of the realm of what is acceptable by the “first-orderist”. The next section will present and discuss examples of semantical reflection of this sort.
In particular, Nelson sketches in (1986, Chap. 31) a foundational program under the assumption of the negation of the totality of exponentiation. Admittedly, much less clear are the reasons why Nelson advocates such position. Besides his clear nominalistic stance (cf. Nelson 1986, Chap. 18), Nelson’s position can be taken to hold that
...the basic informal argument says, roughly, that the number of steps needed to terminate a recursion defining exponentiation is of the order of magnitude of exponentiation itself—a perceived circularity (Ferreira and Ferreira 2013, p. 2).
Dyadic numerals are defined as
$$\overline{2\times n}=({\mathsf{S}}{\mathsf{S}}0)\times \overline{n} \quad \overline{2\times n+1}={\mathsf{S}}(({\mathsf{S}}{\mathsf{S}}0)\times \overline{n}) $$The codes of the numeral n, in this way, is of order \(n^c\) for a fixed c—therefore can be handled with \(\#\)—and not \(2^{cn}\) for fixed c, which would require exponentiation.
See footnote 22 for a precise definition of KF.
Recall the slight shift in meaning of the numerals (cf. footnote 11).
A similar argument would even hold in the case of set theories formulated by syntactically restricting schemata.
See Feferman (1960).
Here the complexity of a formula can simply be taken as the number of logical symbols in it.
For details concerning this strategy, see Nicolai (2016).
If one grants a claim repeatedly reported in print (for instance by Fischer 2009, Thm 3.4) one might think that the theory \(\mathsf{CT}[S]\)could not be extended with the assertion of the truth of non-logical axioms of S because \(\mathsf{CT}[S]\)+ “all logical axioms of S are true” proves the consistency of S. Unfortunately, the argument for that claim contains a gap as shown in detail in the Appendix to Wcisło and Łełyk (2017). We strongly conjecture that \(\mathsf{CT}[S]\)+“all logical axioms of S are true” is conservative over S, but no full proof has been found yet.
We thank the anonymous referees for allowing us to clarify this point.
As McGee writes:
Our understanding of the language of arithmetic is such that we anticipate that the Induction Axiom Schema, like the laws of logic, will persist through all such changes. There is no single set of first-order axioms that fully expresses what we learn about the meaning of arithmetical notation when we learn the Induction Axiom Schema, since we are always capable of generating new Induction Axioms by expanding the language (McGee 1997, p. 58).
More precisely, such a theory amounts to an extension of the type-free theory of truth KF in \({{\mathcal {L}}}_\mathsf{T}\cup \{P\}\) equipped with a schematic rule of substitution \(\psi (P)/ \psi (\chi )\), with \(\varphi (P)\) not containing truth, that replaces every subformula P of \(\psi (P)\) with \(\chi \). The axioms of KF are the axioms of PA formulated in \({{\mathcal {L}}}\cup \{\mathsf{T}\}\) and the sentences
$$\begin{aligned}&\mathsf{Cterm}_{{{\mathcal {L}}}_\mathsf{T}}(\vec x)\rightarrow \big ((\mathsf{T}\ulcorner R(\dot{\vec x})\urcorner \leftrightarrow R(\vec x)) \wedge (\mathsf{T}\ulcorner \lnot R(\dot{\vec x})\urcorner \leftrightarrow \lnot R(\vec x ))\big ) \end{aligned}$$(13)$$\begin{aligned}&(\mathsf{T}\ulcorner \mathsf{T}(\dot{x})\urcorner \leftrightarrow \mathsf{T}x)\wedge (\mathsf{T}\ulcorner \lnot \mathsf{T}(\dot{x})\urcorner \leftrightarrow \mathsf{T}\underset{\cdot }{\lnot }x) \end{aligned}$$(14)$$\begin{aligned}&\mathsf{Sent}_{{{\mathcal {L}}}_\mathsf{T}}(x)\rightarrow (\mathsf{T}\underset{\cdot }{\lnot }\underset{\cdot }{\lnot }x \leftrightarrow \mathsf{T}x) \end{aligned}$$(15)$$\begin{aligned}&\mathsf{Sent}_{{{\mathcal {L}}}_\mathsf{T}}(x\underset{\cdot }{\wedge }y)\rightarrow (\mathsf{T}(x\underset{\cdot }{\wedge }y)\leftrightarrow \mathsf{T}x\wedge \mathsf{T}y) \end{aligned}$$(16)$$\begin{aligned}&\mathsf{Sent}_{{{\mathcal {L}}}_\mathsf{T}}(x\underset{\cdot }{\wedge }y)\rightarrow (\mathsf{T}\underset{\cdot }{\lnot }(x\underset{\cdot }{\wedge }y)\leftrightarrow \mathsf{T}\underset{\cdot }{\lnot }x\vee \mathsf{T}\underset{\cdot }{\lnot }y) \end{aligned}$$(17)$$\begin{aligned}&\mathsf{Sent}_{{{\mathcal {L}}}_\mathsf{T}}(\underset{\cdot }{\forall }vx)\rightarrow (\mathsf{T}\underset{\cdot }{\forall }vx\leftrightarrow \forall y\,(\mathsf{Cterm}_{{{\mathcal {L}}}_\mathsf{T}}(y)\rightarrow \mathsf{T}x(y/v)) \end{aligned}$$(18)$$\begin{aligned}&\mathsf{Sent}_{{{\mathcal {L}}}_\mathsf{T}}( \underset{\cdot }{\forall }vx)\rightarrow (\mathsf{T}\underset{\cdot }{\lnot }\underset{\cdot }{\forall }vx\leftrightarrow \exists y\,(\mathsf{Cterm}_{{{\mathcal {L}}}_\mathsf{T}}(y)\rightarrow \mathsf{T}\underset{\cdot }{\lnot }x(y/v)) \end{aligned}$$(19)This separation between object-linguistic and meta-linguistic aspects of theories can be made even more drastic. We refer to Nicolai (2015) for an overview of such options.
For a definition of the Veblen functions, see Pohlers (2009).
A similar strategy for a nonclassical setting in which the starting point are type-free principles of the form \(\mathsf{T}\ulcorner \varphi \urcorner \Leftrightarrow \varphi \), with \(\Leftrightarrow \) a suitable non classical biconditional has been carried out by Fischer et al. (2017).
We notice that not only truth principles may be added, but also principles for intensional predicates such as necessity. If genuine extensions of, say, KF may be reached via the interplay of truth and modal predicates, this would represent a genuine improvement of predicativism given the natural numbers à la Feferman.
References
Arana, A. (2008). Logical and semantic purity. In G. Preyer & G. Peter (Eds.), Philosophy of mathematics. Set Theory, Measuring Theories, and Nominalism (pp. 40–52). Frankfurt: Ontos Verlag.
Beklemishev, L. D. (2005). Reflection principles and provability algebras in formal arithmetic. Uspekhi Matematicheskikh Nauk, 60(2):3–78 (in Russian). English translation. Russian Mathematical Surveys, 60(2), 197–268.
Buss, S. R. (1986). Bounded arithmetic. Napoli: Bibliopolis.
Buss, S. R. (1998). First-order proof theory of arithmetic. In S. Buss (Ed.), Handbook of proof theory (pp. 79–147). North-Holland: Elsevier.
Cieśliński, C. (2010). Truth, conservativeness, and provability. Mind, 119, 409–422.
Dean, W. (2015). Arithmetical reflection and the provability of soundness. Philosophia Mathematica, 23(1), 31–64.
Enayat, A., & Visser, A. (2015). New constructions of satisfaction classes. In T. Achourioti (Ed.), Unifying the philosophy of truth (pp. 321–335). Berlin: Springer.
Enderton, H. B. (2001). A mathematical introduction to logic (2nd ed.). Cambridge: Academic Press.
Feferman, S. (1960). Arithmetization of metamathematics in a general setting. Fundamenta Mathematicae, 49, 35–92.
Feferman, S. (1962). Transfinite recursive progressions of axiomatic theories. The Journal of Symbolic Logic, 27, 259–316.
Feferman, S. (1964). Systems of predicative analysis. Journal of Symbolic Logic, 29, 1–30.
Feferman, S. (1991). Reflections on incompleteness. Journal of Symbolic Logic, 56, 1–49.
Feferman, S. (2005). Predicativity. In S. Shapiro (Ed.), The Oxford handbook of philosophy of mathematics and logic (pp. 590–624). Oxford: Oxford University Press.
Ferreira, F., & Ferreira, G. (2013). Interpretability in Robinson’s \( Q\). Bulletin of Symbolic Logic, 19, 289–317.
Field, H. (1999). Deflating the conservativeness argument. Journal of Philosophy, 96(10), 533–540.
Fischer, M. (2009). Minimal truth and interpretability. The Review of Symbolic Logic, 2(4), 799–815.
Fischer, M., Horsten, L., & Nicolai, C. (2017). Iterated reflection over full disquotational truth. Journal of Logic and Computation, 27(8), 2631–2651.
Gentzen, G. (1969). Die Widerspruchsfreiheit der reinen Zahlentheorie. Mathematische Annalen, 112, 493–565, 1936 (Trans. The consistency of arithmetic. In M. E. Szabo (Ed.), Collected Papers of Gerhard Gentzen. Amsterdam: North-Holland).
Girard, J.-Y. (1987). Proof-theory and logical complexity. Napoli: Bibliopolis.
Hájek, P., & Pudlák, P. (1998). Metamathematics of first-order arithmetic. Berlin: Springer.
Halbach, V. (2011). Axiomatic theories of truth. Cambridge: Cambridge University Press.
Heck, R. (2015). Consistency and the theory of truth. The Review of Symbolic Logic, 8(3), 424–466.
Horsten, L., & Leigh, G. E. (2017). Truth is simple. Mind, 126(501), 195–232.
Isaacson, D. (1991). Some considerations on arithmetical truth and the omega-rule. In M. Detlefsen (Ed.), Proof, logic, and formalization (pp. 49–138). Routledge.
Isaacson, D. (1996) Arithmetical truth and hidden higher-order concepts. In The Paris Logic Group (Ed.), Logic Colloquium ’85. (pp. 147–169). Amsterdam: North-Holland, 1987. Reprinted in W. D. Hart (Ed.), The philosophy of mathematics (pp. 203–224). Oxford University Press.
Ketland, J. (1999). Deflationism and Tarski’s paradise. Mind, 108, 69–94.
Ketland, J. (2005). Deflationism and the Gödel phenomena: Reply to Tennant. Mind, 114, 75–88.
Kotlarski, H., Krajewski, S., & Lachlan, A. H. (1981). Construction of satisfaction classes for nonstandard models. Canadian Mathematical Bulletin, 24, 283–293.
Kreisel, G. (1970). Principles of proof and ordinals implicit in given concepts. In J. Myhill & R. E. Vesley (Eds.), Intuitionism and proof theory, studies in logic and the foundations of mathematics (Vol. 60, pp. 489–516). Amsterdam: North-Holland.
Kreisel, G., & Lévy, A. (1968). Reflection principles and their use for establishing the complexity of axiomatic systems. Zeitschrift für mathematische Logik und Grundlagen der Mathematik, 36, 441–454.
Kripke, S. (1975). Outline of a theory of truth. The Journal of Philosophy, 72(19), 690–716.
Leigh, G. (2015). Conservativity for theories of compositional truth via cut-elimination. The Journal of Symbolic Logic, 80(3), 845–865.
Lindstrom, P. (1997). Aspects of incompleteness. Berlin: Springer.
McGee, V. (1997). How we learn mathematical language. The Philosophical Review, 106(1), 35–68.
Mostowski, A. (1952). On models of axiomatic systems. Fundamenta Mathematicae, 39, 133–158.
Nelson, E. (1986). Predicative arithmetic. Princeton: Princeton University Press.
Nicolai, C. (2015). Deflationary truth and the ontology of expressions. Synthese, 192(12), 4031–4055.
Nicolai, C. (2016). A note on typed truth and consistency assertions. Journal of Philosophical Logic, 45(89), 89–119.
Pedersen, N. J. L. L., & Rossberg, M. (2010). Open-endedness. Schemas and Ontological Commitment. Noûs, 44(2), 329–39.
Piazza, M., & Pulcini, G. (2015). A deflationary account of the truth of the Gödel Sentence \(\cal{G}\). In G. Lolli et al. (Eds.), From logic to practice. Boston studies in the philosophy and history of science (pp. 71–90). Berlin: Springer.
Piazza, M., & Pulcini, G. (2016). What is so special about the Gödel sentence \(\mathcal {G} \)? In F. Boccuni & A. Sereni (Eds.), Objectivity, realism, and proof. FilMat Studies in the Philosophy of Mathematics, Boston Studies in the Philosophy and History of Science (pp. 245–263). Berlin: Springer.
Pohlers, W. (2009). Proof theory: The first step into impredicativity. Berlin: Springer.
Pudlák, P. (1985). Cuts, consistency statements, and interpretations. The Journal of Symbolic Logic, 50, 423–441.
Schütte, K. (1965). Einge Grenze für die Beweisbarkeit der Transfiniten Induktion in der verzweigten Typenlogik. Archiv für Mathematische Logik und Grundlagen-forschung, 7, 45–60.
Shapiro, S. (1998). Proof and truth: Through thick and thin. The Journal of Philosophy, 95, 493–521.
Sieg, W. (1981). Inductive definitions, constructive ordinals, and normal derivations. In Iterated inductive definitions and subsystems of analysis: Recent proof-theoretical studies. Lecture Notes in Mathematics (Vol. 897). Berlin: Springer.
Tait, W. (1981). Finitism. The Journal of Philosophy, 78, 524–546.
Tennant, N. (2002). Deflationism and the Gödel phenomena. Mind, 111, 551–582.
Troelstra, A. S., & Schwichtenberg, H. (2000). Basic proof theory. Cambridge: Cambridge University Press.
Wcisło, B., & Łełyk, M. (2017). Notes on bounded induction for compositional truth predicates. The Review of Symbolic Logic, 10(3), 455–480.
Acknowledgements
We would like to thank Martin Fischer, Leon Horsten, and Graham Leigh for their comments to a previous version of the manuscript. The first author was supported by the European Commission (Grant 658285 - FOREMOTIONS) and by the Netherlands Organisation for Scientific Research (NWO, Grant 275-20-057).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Nicolai, C., Piazza, M. The Implicit Commitment of Arithmetical Theories and Its Semantic Core. Erkenn 84, 913–937 (2019). https://doi.org/10.1007/s10670-018-9987-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10670-018-9987-6