1 Introduction

Surface soil moisture (SSM) describes the water content of the top few centimeters of soil and is a fundamental boundary condition that influences land surface-atmosphere heat and water exchanges, essential for drought monitoring (Long et al., 2019), heat waves prediction (Fischer et al., 2007) and soil loss by water erosion estimation (Todisco et al., 2015).

Climate change is modifying SSM variability and its feedbacks with precipitation and temperature; a significant decrease in soil moisture has been registered since the 1950s in the Mediterranean region, particularly in south-eastern and south-western Europe (EEA, 2017; Kurnik et al., 2015). By the end of this century, a decrease of 20% in land surface water availability is predicted (Mariotti et al., 2008), due to the fast-warming trend and changes in the distribution and intensity of precipitations (EEA, 2017). In agricultural lands, SSM exerts relevant effects on yields, providing the transpirable water for plants, controlling rainfall-runoff response, and the diversity in ecosystems (Robinson et al., 2008). In a climate-smart agriculture (FAO, 2022) perspective, monitoring SSM in agricultural fields at high temporal and spatial resolution is essential to safeguard soil and water resources, developing sustainable cropping systems, and thus positively determine the adaptability to new climate scenarios (Lewis, 2019). SSM estimate can find applicability in irrigation scheduling, to facilitate a rational use of water, reduce plant stress and improving crop yield (Pradhan et al., 2018). It could also encourage diversification of production orientations at the expense, in areas where it is environmentally sustainable, of low-income crops (Zucaro et al., 2009).

In situ measurements of SSM provide distributed point measurements which, due to the large dynamism of the soil moisture parameter, are not sufficient to characterize its spatial and temporal variability at larger scale (Panciera & Monerris, 2013). Instead, microwave remote sensing techniques provide an exceedingly powerful means for SSM retrieval, both with passive (Mohanty et al., 2017), and active sensor (Bauer-Marschallinger et al., 2019; Hornacek et al., 2012). These measurements exploit the correlation between liquid water and the dielectric properties of soil, which influence, along with several other physical characteristics and sensor parameters, the interaction between the electromagnetic power and the target material (Woodhouse, 2017).

However, many passive microwaves satellites, which are providing SSM estimation at low resolution from the decades (Fang et al., 2019), are not suitable for agricultural monitoring.

Instead, Synthetic Aperture Radar (SAR) can provide higher-resolution data measuring the backscattering coefficient,\({\sigma }^{0}\), defined as the ratio of the incident to received signal intensity, normalized to the actual scattering area (Meyer, 2019; Pulvirenti et al., 2018). Nevertheless, ground roughness and the presence of vegetation complicate the SSM retrieval (Bindlish & Barros, 2002).

The models which have been developed to address the soil moisture retrieval problem can be divided into two main approaches: snap-shot algorithms and multi-temporal algorithms. Snap-shot model are usually grouped into theoretical (Fung et al., 1992; Hajnsek et al., 2003), empirical (Oh et al., 1992; Zribi & Dechambre, 2003)—among which the use of Artificial Neural Network techniques (Ge et al., 2018) has recently been introduced—and semiempirical algorithms (Panciera & Monerris, 2013). For vegetated areas, the popular semiempirical algorithm Water Cloud Model (WCM) uses calibration parameters to isolate the soil contribution and, subsequently, employs the linear correlation between SAR backscatter measurement and volumetric soil moisture (Baghdadi et al., 2006) to retrieve SSM. On the other side, multi-temporal approaches are popular techniques to generate global high-resolution soil moisture products (Bauer-Marschallinger et al., 2019; Bhogapurapu et al., 2022), using more acquisition to minimize the effect of vegetation and roughness.

Radar SSM retrieval over the Italian peninsula has been an object of interest in the last years, especially for the southern part of Italy, more vulnerable to drought and desertification (Filion et al., 2016; Montaldo et al., 2021).

Sentinel-1 mission provides dense time-series of SAR data, making possible to relate short term changes in the backscattering coefficient to SSM variations (Balenzano et al., 2010; Pulvirenti et al., 2018). To take advantage of the great availability of Sentinel-1 high-resolution acquisition, the Tu Wien multi-temporal change detection method, originally developed for ASCAT data, has been modified according to Sentinel-1 SAR data characteristics by Bauer-Marschallinger et al. (2019).

Nowadays, besides these case studies, the Copernicus Global Land Service estimates are available for SSM with a low spatial resolution (\(1\mathrm{km}\)) and the MULESME software, which makes use of multi-temporal Sentinel-1 acquisition to obtain a systematic mapping of surface soil, is tested.

In this study, the Marche region has been considered. Located in central east of Italy and characterized by an agrarian landscape of sharecropping origin, it is evaluated as highly vulnerable to climate variations, especially regarding agricultural productivity (Shukla et al., 2019). In 2007, 9% of the Marche territory was considered sensitive or vulnerable to desertification, while only 5 years before, in 2002, the region had not been included in the National Atlas of the areas at desertification risk (Costantini et al., 2007). The main regional soil degradation systems, that can lead to functional sterility, include denudation by water erosion and drought (Costantini et al., 2007).

In order to estimate the SSM in agricultural areas, a workflow has been developed in the cloud computing platform Google Earth Engine (GEE). Firstly, agricultural areas are derived from a land use/land cover (LULC) Random Forest classification, using both optical (Sentinel-2) and radar (Sentinel-1) data, and the Entropy-Alpha dual pol decomposition parameters. Subsequently, SSM is estimated using the semiempirical model WCM and the change detection Tu Wien model.

This study has two objectives:

  • the first goal is to investigate the use of polarimetric decomposition’s bands \(H\text{/}\alpha\) to improve the accuracy of classification (Banque et al., 2015)

  • the second goal is to implement in GEE Tu Wien and Water Cloud Model (WCM) using calibration parameters derived from literature, to test if an acceptable accuracy is reached without any in situ observation.

2 Materials and method

2.1 Study area

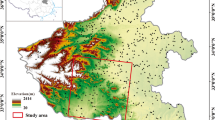
The study area is the Marche region, located in central-northern Italy and overlooking the Adriatic Sea (Fig. 1a). The Foglia River and the Tronto River indicatively delimit the northern and southern boundaries of the region, while the Apennines and the Adriatic Sea mark its western and eastern limits (Fig. 1b). The region covers a total area of \(\mathrm{9,694,51k}{\mathrm{m}}^{2}\).

Fig. 1
figure 1

Study area. (a) Marche region and its provinces. (b) Elevation and rivers (Reference system: WGS84/Pseudo-Mercator, EPSG: 3857)

Full size image

The regional territory is characterized by a hillside morphology that slopes towards the sea; the coast extends north to south for \(173\mathrm{km}\) and represents the only flat area of the region. Marche rivers cross the region from west to east, producing valley furrows that gradually expand near the mouth, forming a characteristic comb-like structure. Despite the rapid expansion of urbanized or infrastructure-occupied areas, especially in coastal area (Appiotti et al., 2014), Marche region remains largely rural (Istat, 2013), since the Total Farmland Area (TFA) and the Utilized Agricultural Area (UAA) cover 76.5% of the territory, and the agricultural lands are widely distributed throughout the region (Istat, 2013). Instead, forests and unused land, are found predominantly in the southwest, on the Appennino Umbro-Marchigiano mountains (Arzeni, 2003). The average surface area per farm has increased since 1980s, reaching 10.52 hectares in 2010, higher than the national average of 7.93 hectares (Istat, 2013).

Almost 80% of the UAA is planted with arable crops, just below \(375\) thousand hectares (Istat, 2013), and the most widely grown cereal is durum wheat. The presence of clay-rich soils and the rotation of durum wheat with spring–summer crops, among which sunflower, sugar beet and sorghum, implies the use of frequent tillage, which exposes the soil to erosion by surface runoff, organic matter mineralization and nitrate leaching for long periods (Zucaro et al., 2009).

Water erosion is particularly critical in the hilly terrain of the Marche region, where the relationships between cropping systems and the environment are strongly affected by crop water balance and water flows (Borrelli et al., 2016). Instead, the vulnerability to droughts is increased by the fact that the prevalence of durum wheat crops, a dry soil cultivation, has discouraged public investments on the creation of irrigation facilities. Consequently, it is more difficult for the farmers to diversify production in reaction to the decrease which interested the agricultural incomes of large-scale consumer products during the last decades.

2.2 Dataset

The dataset was created using Sentinel-1 (S1) and Sentinel-2 (S2) data (Table 1). All data were georeferenced in the default cartographic reference system of GEE WGS84/Pseudo-Mercator (EPSG: 3857). The Sentinel-1 mission comprises a constellation of two polar-orbiting satellites, both carrying a C-band SAR dual-polarized instrument with a frequency of \(5.405\mathrm{GHz}\) and a revisit period of 12 days (Torres et al., 2012). For this study, S1A and S1B data at interferometric wide swath (IW) mode and Level-1 of processing were used. IW acquires data with a \(250\mathrm{km}\) swath at \(5\mathrm{m}\) × \(20\mathrm{m}\) spatial resolution, and an incidence angle, \({\theta }_{i}\) which ranges between \(29.1^\circ\) and \(46.0^\circ ,\) i.e., the angle between the incoming EM wave and the normal to the reference surface.

Table 1 The list of acquisition dates for both radars, S1-SLC and S1-GRD, and optical datasets, S2
Full size table

Ground Range Detected (GRD, below called S1-GRD) images are already ingested in Google Earth Engine (GEE), while Single Look Complex (SLC, below called S1-SLC) were downloaded from the Alaska Satellite Facility (https://asf.alaska.edu/). S1-SLC images are used to calculate Entropy, Alpha and Anisotropy parameters through Dual-Polarimetric Entropy-Alpha dual polarimetric decomposition. Marche region is acquired by path 44 and 177 for ascending orbits, and 22 and 95 for descending orbits.

Sentinel-2 is a multi-spectral imaging mission with two polar-orbiting satellites carrying a Multispectral Instrument (MSI) which acquires passively in 13 spectral bands with a spatial resolution of \(60\mathrm{m}\) for the aerosol band, \(10\mathrm{m}\) for visible and \(20\mathrm{m}\) for infrared bands.

From 2015 to 2020, the land cover classification was carried out twice a year, for a total of 48 S1-GRD scenes, 48 S1-SLC scenes and 12 S2 intervals. The whole product names can be found in the Online Resource 1.

2.3 Procedure

Figure 2 shows the whole applied procedure (see GitHub repository). Each S1 and S2 scene has been preprocessed and used to extract the agricultural areas of the Marche region through a supervised Random Forest classification. Subsequently, Tu Wien and Water Cloud Model were implemented in the GEE cloud computing platform and validated using in situ measurements made by two International Soil Moisture Network (ISMN) stations in Umbria, in August 2015. Finally, the estimates were applied to an agricultural area of \(125\mathrm{ha}\), where the relationship between different agricultural land covers, soil moisture and precipitation was analyzed.

Fig. 2
figure 2

The workflow to retrieve surface soil moisture in agricultural fields in Marche region (Italy). The procedure was applied to each S1 and S2 data

Full size image

2.3.1 Preprocessing

Preprocessing of S2 and S1-GRD was realized in GEE, and the obtained data were then exported as Asset in the Code Editor. Instead, S1-SLC dataset was preprocessed in the Sentinel Application Platform (SNAP), because GEE does not support images with complex values, such as phase and amplitude, due to the inability to average them during pyramiding ingestion (“Google Earth Engine Guides”, n.d.).

Sentinel-2 data with level 1C processing provided by GEE were used. These data have been orthorectified and radiometrically corrected by GEE, providing top-of-atmosphere reflectance values; images bands have maintained their original spatial resolution. The masking of the cloud areas has been realized through the probability band in the dataset Sentinel-2 Cloud Probability, which was created with the sentinel2-cloud-detector library, and the Cloud Displacement Index (CDI), using the near-infrared parallax (AleksMat, 2022; Skakun et al., 2022). To obtain a cloud-free composite, images acquired in 30–45 days were temporally aggregated using the mean method.

Each S1-GRD scene provided by Google Earth Engine has been preprocessed using the SNAP Toolbox, applying the following steps: thermal noise removal, radiometric calibration and terrain correction using Shuttle Radar Topography Mission (SRTM) elevation digital model to \(30\mathrm{m}\) (Farr & Kobrick, 2000). The scenes for the land cover classification were filtered for the speckle. This is a physical phenomenon caused by the interference of coherent waves reflected from many elementary scatterers, corrigible through the Refined Lee Filter implemented in GEE by Guido Lemoine (Thorp & Drajat, 2021). Considering the hilly topography of the study area (Fig. 1b and Fig. 3a), an angular-based radiometric slope correction was applied to the images (Fig. 3b). The model, implemented by Vollrath et al. (2020), is based on the angular relationships between the SAR image and the terrain geometry, and it is optimized for surface scattering and, therefore, for soil characteristic analysis. In addition, a mask is applied for active layover and shadow (Fig. 4).

Fig. 3
figure 3

Comparison between an original image: (a), and a radiometric slope corrected image (b). Acquisition date: 10-09-2019. Descending orbit. RGB bands: VH, VV, VH

Full size image
Fig. 4
figure 4

Active layover (yellow) and shadow mask (red). Acquisition date: 12-09-2019. Ascending orbit. Local \({\theta }_{i}\) is the background image

Full size image

S1-SLC data were processed applying the following operators through SNAP: S-1 TOPS Split, Apply Orbit File, Calibrate, S-1 TOPS Deburst, S-1 TOPS Merge, C2 Polarimetric Matrix Generation, Polarimetric Decomposition, Multilooking. Both S1-GRD and S1-SLC images were finally mosaicked in GEE. Previous investigations into radiometric consistency reveal no significant radiometric biases between SLC and GRD products (Small, 2016). However, considering all applied preprocessings and that S1 assets in GEE have been processed at different times with several Toolbox versions and settings, GRD and SLC datasets were compared to ensure that their mean radiometric difference was below S1 radiometric accuracy (\(1\mathrm{dB}\)). The comparison was carried out on GEE using the preprocessed datasets (bold in Table 1), except for C2 Polarimetric Matrix Generation and Dual-Polarimetric Entropy-Alpha dual pol decomposition. The comparison shows mean difference values below \(1\mathrm{dB}\) in each scene, with maximum difference of \(0.40\mathrm{dB}\) (Std Dev \(1.54\)) for band VH and \(0.27\mathrm{dB}\) (Std Dev \(1.68\)) for band VV. Therefore, Entropy, Alpha and Anisotropy values derived from SLC can be considered representative of GRD images.

2.3.2 Polarimetric decomposition

Incoherent polarimetric decomposition was originally designed for full-polarimetric data to separate the 3 × 3 Hermitian average covariance \(\langle T\rangle\) and \(\langle C\rangle\) matrices as the combination of simpler or canonical objects, presenting an easier physical interpretation (Haldar et al., 2019; Harfenmeister et al., 2021). In this study, the Entropy-Alpha decomposition modified by Cloude and Pottier (1996) for dual-polarized data is used. Considering the scattering matrix \(\left[{S}_{VV-VH}\right]\)(Eq. 1):

$$\left[{S}_{VV-VH}\right]=\left[\begin{array}{cc}0& {S}_{HV}\\ {S}_{VH}& {S}_{VV}\end{array}\right]$$
(1)

Each of the elements \({S}_{pq}\) is a complex number, describing phase and amplitude of transmitted, \(p\), and received, \(q\), polarization (Woodhouse, 2017). Sentinel-1 is a linear dual-polarized instrument, and, in IW acquisition mode, it mainly transmits a vertical polarized signal, \(V\), and measures the echo in both vertical, \(V\), and horizontal, \(H\), polarization. \({S}_{VV}\) is the co-polarized signal, while \({S}_{VH}\) is the cross-polarized signal. The corresponding scattering vector based on the Pauli matrices, \(k\), is composed by the co-polarized term and twice the cross-polarized term (Eq. 2):

$$k={\left[{S}_{VV}2{S}_{HV}\right]}^{t}$$
(2)

\(k\) is needed as the scattering matrix \(\left[{S}_{VV-VH}\right]\) is only able to characterize the so-called coherent or pure scatterers; to describe distributed target scattering \(\langle {C}_{VV-VH}\rangle\) is calculated from (Eq. 3):

$$\langle {C}_{VV-VH}\rangle =k\cdot {k}^{t}$$
(3)

where \(\langle \rangle\) denotes ensemble averaging (Woodhouse, 2017). \(\langle {C}_{VV-VH}\rangle\) is decomposed (Eq. 4) as follows (Ji & Wu, 2015):

$$\langle {C}_{VV-VH}\rangle =\left[V\right]\cdot \left[\Lambda \right]\cdot\left[V\right]^{-1}$$
(4)

where \(\left[V\right]\) is the eigenvector matrix which contains the eigenvectors \(\overrightarrow{{v}_{i}}\) (Eq. 5):

$$\left[V\right]=\left[\overrightarrow{{v}_{1}}\overrightarrow{{v}_{2}}\overrightarrow{{v}_{3}}\right]$$
(5)

and \(\left[\Lambda \right]\) is the diagonal eigenvalues matrix, i.e., a diagonal representation of the covariance matrix in a Cartesian coordinate system, whose axes are the related eigenvectors.

Once \(\langle {\mathrm{C}}_{\mathrm{VV}-\mathrm{VH}}\rangle\) is decomposed, the three simpler canonical scattering mechanism matrices \(\left[{T}_{i}\right]\) are derived from the Eq. 6:

$$\langle {C}_{VV-VH}\rangle =\left[{T}_{1}\right]+\left[{T}_{2}\right]+\left[{T}_{3}\right]={\lambda }_{1}(\overrightarrow{{v}_{1}}\overrightarrow{{v}_{1}}*) + {\lambda }_{2}(\overrightarrow{{v}_{2}}\overrightarrow{{v}_{2}}*) + {\lambda }_{3}(\overrightarrow{{v}_{3}}\overrightarrow{{v}_{3}}*)$$
(6)

Each eigenvector \(\overrightarrow{{v}_{i}}\), multiplied by its complex conjugate \(\overrightarrow{{v}_{i}}\)*, corresponds to a scattering mechanism\(\left[{T}_{i}\right]\), while the related eigenvalue \({\lambda }_{i}\) expresses the importance of each mechanism on the total backscattered power, called SPAN. The analysis of the physical information provided by this eigen decomposition is usually carried out through three parameters, derived from the eigenvalues and the eigenvectors of\(\langle {C}_{VV-VH}\rangle\):

  • the Entropy \(H\) (Eq. 7), which expresses the degree of randomness of the scattering mechanism

    $$H = \sum\limits_{{i = 1}}^{3} {p_{i} } \cdot \log _{3} \left( {p_{i} } \right)$$
    (7)

    where \({p}_{i}\) (Eq. 8) expresses the relative importance of this eigenvalue \({\lambda }_{i}\) with respect to the SPAN:

    $${p}_{i}=\frac{{\lambda }_{i}}{{\sum }_{k=1}^{3}{\lambda }_{k}}$$
    (8)

  • the Anisotropy \(A\)(Eq. 9), which quantifies the relationship between the second and the third eigenvalue and is complementary to the Entropy:

    $$A=\frac{{\lambda }_{2}-{\lambda }_{3}}{{\lambda }_{2}+{\lambda }_{3}}$$
    (9)

  • the Alpha angle \(\alpha\) (Eq. 10), which describes the averaged scattering mechanisms:

    $$\alpha = \sum\limits_{{i = 1}}^{3} {p_{1} \cdot \alpha _{i} }$$
    (10)

    For fully polarized data \(\alpha \to 0\) indicates surface scattering;\(\alpha \to \pi /4\) indicates volume scattering and \(\alpha \to \pi /2\) indicates double bounce scattering.

Equations 7, 8, 9 and 10 are derived from Ouarzeddine et al. (2006). H, A and α has been calculated in each SLC scene. The results were uploaded in GEE in geoTIFF format, where they were filtered applying the Refined Lee Filter and radiometric slope corrected with Vollrath et al. (2020) model.

2.3.3 Agricultural areas extraction

Land use/land cover classifications were carried out through one the most frequently used supervised algorithm in GEE, the Random Forest (Kumar & Mutanga, 2019), with 500 trees testing several band datasets. Normalized Difference Vegetation Index (NDVI), Normalized Difference Built-up Index (NDBI), sum and ratio radar bands were considered also. Seven classes were selected: forest, bare soil, water, agricultural fields, urban areas, mixed vegetation, and snow. Training areas are manually added as polygons based on the official Land Cover Map created by Marche region (2007) and derived from visual interpretation of S2 natural color images (Fig. 5).

Fig. 5
figure 5

(a) Example of training and validations polygons (Background’s source: Google Earth), (b) forest example, (c) bare soil example, (d) agricultural fields and (e) vegetation example

Full size image

Training data are 6.48% of total pixels, while validation data, randomly extracted by the selected polygons, are 1.62%. Ascending and descending images are classified separately and, to speed the classification process, each province was classified individually. Table 2 shows the four datasets considered: optical dataset (OP, optical bands and their combinations), radar dataset (RD, radar bands), polarimetric dataset (PD, polarimetric parameter H and α, and radar band combinations) and total dataset (TD, optical dataset, radar dataset, and polarimetric dataset).

Table 2 Dataset for classifications: optical dataset (green); radar dataset (red) and polarimetric dataset (yellow)
Full size table

\({M}_{try}\) hyper-parameter, which controls the split-variable randomization feature of Random Forests, was set to \(3\). Consequently, each time a split is to be performed, the search for the split variable is limited to a subset of three bands. The sample size parameter, which determines how many observations are drawn for the training of each tree, is set to \(0.3\), to lower the correlation between trees and decrease the weight of outliers. The producer and user accuracy estimations were used to compare the classification accuracy between datasets; the producer accuracy quantifies how well reference pixels of the ground cover type are classified, and the user accuracy represents the probability that a pixel classified into a given category actually represents that category on the ground. The coefficient of agreement, kappa index, is also used to evaluate how well the classification performed, considering the effect of random agreement (Carrasco et al., 2019; Tang et al., 2015).

2.3.4 Surface soil moisture estimation

SSM estimations by Tu Wien and Water Cloud models were implemented and subsequently applied over agricultural areas extracted through the land cover classification.

The multi-temporal change detection Tu Wien Model was originally developed at Vienna University of Technology (TU Wien) to estimate soil moisture using ASCAT (Advanced SCATterometer) data, and subsequently adapted to S1. It relies on two assumptions: i) the relationship between the backscattering coefficient \({\sigma }^{0}\) and the surface soil moisture content is linear; ii) considering that soil roughness and vegetation exhibit a gradual change over time, any sudden change observed, within an appropriate time interval, is assumed to originate from a change in soil moisture (Panciera & Monerris, 2013).

To account for roughness and vegetation, a reference backscatter value \({\sigma }_{dry}^{0}\left({\theta }_{ref}\right)\), representing backscatter from the vegetated land surface under dry soil conditions, is subtracted from the actual backscatter measurement, normalized to a reference angle, \({\sigma }^{0}\left({\theta }_{ref}\right)\).

Therefore, relative soil moisture changes \({m}_{r,t}\) are calculated by dividing the result by the sensitivity, which is the difference between the maximum value, \({\sigma }_{wet}^{0}\left({\theta }_{ref}\right)\), and the minimum, \({\sigma }_{dry}^{0}\left({\theta }_{ref}\right)\) backscattering value measured in each pixel in the chosen time interval. Equation 11 is used:

$${m}_{r,t}=\frac{{\sigma }^{0}\left({\theta }_{ref,t}\right)-{\sigma }_{dry}^{0}\left({\theta }_{ref}\right)}{{\sigma }_{wet}^{0}\left({\theta }_{ref}\right)-{\sigma }_{dry}^{0}\left({\theta }_{ref}\right)}\left[\text{\%}\right]$$
(11)

To retrieve the volumetric soil moisture value in each scene, two parameters should be introduced:

  • the wilting point (WP), which is set to 9%, assuming that it corresponds to the minimum backscatter value registered in the time interval, \({\sigma }_{dry}^{0}\left({\theta }_{ref}\right)\);

  • the saturation point (SAT), assuming that it corresponds to the minimum backscatter value registered in the time interval, \({\sigma }_{wet}^{0}\left({\theta }_{ref}\right)\). SAT is set to 30%, as beyond 30–35% any further increase in SSM does not correspond to an increase in radar backscatter (Gao et al., 2017).

Then, the volumetric soil moisture is calculated by Eq. 12:

$${m}_{v,t}={m}_{r,t}\cdot \left(SAT-WP\right)+WP\left[{m}^{3}{m}^{3}\right]$$
(12)

Concerning the semiempirical Water Cloud Model, developed by Attema and Ulaby (1978), the total backscattering coefficient is defined in a linear scale by Eq. 13:

$${\sigma }^{0}={\tau }^{2}\cdot {\sigma }_{soil}^{0}\cdot {\sigma }_{veg}^{0}\left[dB\right]$$
(13)

where \({\sigma }_{veg}\) (Eq. 14) is the contribution from the vegetation to the total backscatter and \({\sigma }_{soil}\) (Eq. 15) is the contribution from bare soil attenuated by vegetation through \({\tau }^{2}\) (Eq. 16) (Baghdadi et al., 2017).

$${\sigma }_{veg}=A\cdot V\cdot cos\cdot \theta \cdot \left(1-{\tau }^{2}\right)\left[dB\right]$$
(14)
$${\sigma }_{soil}=C+D\cdot {m}_{v}\left[dB\right]$$
(15)
$${\tau }^{2}=exp\left(-2B\cdot V\cdot sec\theta \right)\left[dB\right]$$
(16)

where \(V\) is a vegetation’s descriptor, \(A\) and \(B\) are parameters of the model depending on the vegetation and radar’s configuration, parameter \(C\) is mainly related to surface roughness, while parameter \(D\) expresses the radar configuration sensitivity to soil moisture (Shamambo et al., 2019). In this study, the NDVI (Eq. 17) is used as vegetation descriptor.

$$V=NDVI=\frac{Nir-Red}{Nir+Red}$$
(17)

Others calibration parameters are derived from literature (Table 3).

Table 3 Water Cloud Model parameters
Full size table

Finally, for SSM validation, three parameters were used (Eqs. 18, 19, 20):

$$RMSD=\sqrt{{\sum }_{i=1}^{N}\frac{{\left({p}_{i}-{a}_{i}\right)}^{2}}{N}}$$
(18)

where \({p}_{i}\) is the predicted soil moisture value, \({\alpha }_{i}\) is the actual in situ moisture value and N is the number of agricultural fields pixel

$$Bias={\sum }_{i=1}^{N}\frac{{p}_{i}-{a}_{i}}{N}$$
(19)
$$ubRMSD=\sqrt{RMS{D}^{2}-Bia{s}^{2}}$$
(20)

3 Results

3.1 Classification accuracy

In order to evaluate the polarimetric characteristics contribution, a preliminary analysis for each land cover training class was carried out throughout mean and standard deviations statistics of Entropy, α and Anisotropy bands. For Entropy mean values a range of 0.35–0.73 was obtained, for Alpha mean values a range of 12.0–27.5 and for a range of 0.41–0.73 (Fig. 6).

Fig. 6
figure 6

On the right, mean Entropy and Alpha values for each training class. On the left, mean Entropy, and Anisotropy values. Vertical and horizontal lines represent, respectively \(\alpha\), Anisotropy and Entropy standard deviation

Full size image

Subsequently, the classification accuracy of each dataset scenario was assessed using kappa indices and confusion matrices (see Online Resource 2). Only optical data lead to a mean kappa index of 0.927, while only radar data lead to a mean kappa index of 0.783. Entropy and Alpha bands improve the kappa index to 0.948 for optical data and to 0.818 for radar data. Optical and radar bands result in a mean kappa index of 0.942, which is slightly improved by 0.007 by adding the polarimetric bands, obtaining a 0.949 kappa index for the entire dataset.

For every province, Fig. 7 shows the contribution of radar and decomposition’s bands to the optical classification, and the contribution of optical and decomposition’s bands to the radar classification using mean kappa indices.

Fig. 7
figure 7

Mean kappa indices for each province

Full size image

The Anisotropy band was not included in the dataset as it would not improve the classification, and it could even worsen it in some cases. The assessment of the variable’s importance was realized in GEE: each optical band contributes on average by 24.8%, NDVI and NDBI by 26.5%, VV and VH by 24.8%, and Entropy, Alpha, sum and ration contribute by 23.7% in the final classification.

Although decomposition’s bands contribute meanly less than any other dataset, Fig. 8 shows that these bands can greatly improve radar classification, especially in urban, snow and water classes. The accuracy was calculated by averaging the user and producer’s accuracy for each land cover class over all the classifications (Carrasco et al., 2019).

Fig. 8
figure 8

Accuracy obtained from the three datasets in each land cover class

Full size image

Figure 9 displays an example of comparison between the maps obtained from the different datasets.

Fig. 9
figure 9

Comparison between (a) Sentinel-2 image; (b) total dataset classification; (c) optical dataset classification; (d) radar dataset classification; (e) polarimetric dataset. Acquisition date: 21-12-2020. Descending orbit

Full size image

3.2 Surface soil moisture estimates

The surface soil moisture values were retrieved at a spatial resolution of 10 m. The validation of two models applied was carried out using RMSD, bias and ubRMSD (Eq. 18, Eq. 19, Eq. 20) between predicted SSM and in situ measurements acquired by the International Soil Moisture Network (ISMN) in Umbria region (Italy), in two stations, WEEF 1 and WEEF 2, in August 2015.

Both stations, belonging to the HYDROL-NET-PERUGIA network, were in agricultural dry-lands and measured soil moisture at three depth levels using a TDR- Soil Moisture Equipment Corp. TRASE-BE sensor. Considering that the band-C radar cannot penetrate the soil more in-depth, the data acquired at 5 cm were used.

Table 4 shows the validation results.

Table 4 Soil moisture validation results
Full size table

3.3 Application

Subsequently, the Tu Wien change detection method, which obtained lower RMDS, was applied to the agricultural area managed by the Università Politecnica delle Marche (UNIVPM, n.d.). The farm extends on a total surface of about \(125\mathrm{ha}\) in Agugliano and Gallignano (Ancona province), cultivated with trees and herbaceous crops to be part of research projects (UNIVPM, n.d.). The farm zone is part of the lower Esino river valley, whose lithologies belong to the Marche and Umbria succession, during which sedimentary rocks were deposited in the marine environment from the Upper Triassic (\(200\mathrm{ma}\)) until the Lower Pliocene (\(\mathrm{3,5ma}\)), on which rest the subsequent Quaternary Continental Deposits (Barchiesi, 2017). The farm’s area is located between two opposite slopes, which form at their feet a flat strip consisting of alluvial deposits. The study areas lie along this strip. The average slope of the area of interest is 4.131%. The ASSAM weather station, located beside the farm, provided precipitation data, used to investigate the relationship between soil moisture and precipitation in different crop types (Fig. 10). The mean soil moisture/precipitation correlation is 0.46 of Pearson correlation index.

Fig. 10
figure 10

Correlation between surface soil moisture and precipitation values for different crop classes

Full size image

Finally, minimum, maximum, and mean soil moisture values are retrieved from different land cover types in 2020 (Table 5) in order to evaluate them on the basis of the main crop phenological cycles.

Table 5 Percentage values of soil moisture in the various crop phenological stages
Full size table

4 Discussion

From the reported results, some observations arise. For fully polarimetric data, land cover classes may produce distinct clustering in the H/\(\alpha\) plane plot, in which Entropy and \(\alpha\) values are plotted on the x and y axis and the plane plot space is linearly separated to identify nine zones, each related to a different scattering mechanism. Thus, H/\(\alpha\) plane plot is often used for unsupervised classification.

Instead, as proven by Ji and Wu (2015), in Dual-Polarimetric H/\(\alpha\) dual pol decomposition the loss of information caused by the lack of co-polarized data, as in the case of S1, makes it impossible to distinguish the three canonical scattering mechanisms (surface, dihedral and volumetric) in the dual \(H\text{/}\alpha\) plane plot, where most zones are diffusing and transferring. Therefore, VV-VH polarization cannot distinguish isotropic surface, horizontal dipole, and isotropic dihedral scattering mechanism based on Alpha value, and it can only partially extract low, medium, and high Entropy scattering mechanisms (Ji & Wu, 2015).

Indeed, Fig. 6 shows that each mean \(\alpha\) value is below \(45^\circ\), even for urban areas, which should be characterized by dihedral scattering (\(\alpha \to \pi /4)\) and forested areas, characterized by volume scattering (\(\alpha \to \pi /8\)). High standard deviation values indicate low discriminability especially between vegetated surfaces (agricultural areas, forested areas, and vegetated areas).

Comparable results are obtained from Banque et al. (2015), who define the training sites for each land cover class with Sentinel-1 and get similar Entropy values; instead, in their study the \(\alpha\) band does not reach 20°, confirming that the use of a cross-polarized \(H\text{/}\alpha\) plane plot is not feasible for land cover classification.

Nevertheless, in this study the use of Entropy and Alpha values as supplementary bands in a radar data classification has improved the kappa index by 4.4% and the recognition of each land cover class (Table 4, Fig. 8). In fact, as expected (Carrasco et al., 2019; Steinhausen et al., 2018), radar data classifications obtained lower results than optical data, since some of the classes present similar backscattering power and they cannot be easily differentiated (Banque et al., 2015). It can be noticed that the radar bands obtained the worst classification results in Ascoli-Piceno and Fermo provinces, which are characterized by the predominant presence of Appennine mountains (Fig. 7); in fact, the radar signal is, despite the slope corrections, still strongly dependent on topography characteristics.

The main improvement of H, \(\alpha\), sum and ratio bands can be seen in urban, snow and water classes (Fig. 8). In the case of urban and water, VV, VH, H, \(\alpha\), sum and ratio bands exceed the accuracy of optical data, while for the soil class the accuracy is only 0.04 lower. This result, visible in Fig. 9, was expected for the urban class, where optical data obtained the worst accuracy, confusing artificial structures with bare soil (Fig. 9c); on the other side, for VV and VH bands these two classes are characterized by two different scattering mechanisms, dihedral and surface, thus are easily recognizable.

But only VV and VH bands still obtain low accuracy (Figs. 8, 9d), probably due to the high heterogeneity of these areas, which makes it not easy to distinguish them based on high backscattered power, especially in a hilly terrain, where high backscatter values can be found also in areas characterized by abrupt morphological changes. In fact, VV and VH detect urban areas even in isolated habitations, but often fail to distinguish them from the top of the hills or the vegetation found along drainage ditches between two agricultural fields. Thus, for urban classification, the combined use of optical, radar and decomposition dataset is crucial to achieve a good accuracy.

Concerning the water class, optical data may identify water in shaded bare soil areas while, for radar data, it was expected a good recognition with VV and especially VH band. However, as the sea area has been masked, only tiny mountain lakes and rivers are considered water bodies. Moreover, low VV and VH values can be seen also in other types of surfaces, especially bare soil, which may be confused with water. Entropy and Alpha bands have lower values in bare soil rather than in water, so they can improve their differentiation.

Forest and vegetation classes, instead, present the most limited improvement using H, \(\alpha\), sum and ratio bands, since they present similar Entropy and \(\alpha\) in the dual \(H/\alpha\) plane plot and maybe less discriminable.

Land cover classification is an important preliminary step for many other earth observation applications; regarding SSM retrieval, Sentinel-1 mission showed a strong potential at high/moderate spatial resolutions using multi-temporal acquisitions (Wagner et al., 2009), which are easily manageable in cloud computing platforms like Google Earth Engine (Gorelick et al., 2017; Volpini, 2021). Although the WCM proved to be effective on separation of soil and vegetation contributions using NDVI, it requires real calibration data in situ and sophisticated optimization methods to derive \(C\) and \(D\) parameters. Moreover, the WCM accuracy (RMSD = 12.3) is not adequate. Instead, Tu Wien accuracy (RMSD = 9.4) is still low, also compared to the Copernicus Global Land Service product. This retrieves SSM from Sentinel-1 using the same algorithm with an RMSD of 6% but with a spatial resolution of \(1km\). However, the result obtained is in accordance with that obtained by Bauer-Marschallinger et al. (2019), who investigated the Tu Wien algorithm performance using Sentinel-1 data over Italy. They obtained results that show an overall agreement between S1 SSM and in situ measurements in Umbria of RMSD = 8.8%; due to the interference of vegetation dynamics in summer the retrieval show a lower correlation (RSMD = 9%). Also, the MUSLEM software accuracy ranges between 3 and 12% (Pulvirenti et al., 2018).

Considering that Volpini, 2021 obtained a higher accuracy (6.5%) by applying the same algorithm and validating it using ISMN in Cabrières-d’Avignon (France), where the station is in a flat area, the topography factor may have influenced the results in this study.

While the agreement with ground data acquired at Umbria in situ stations is on average low, the moisture values show adequate correlation to precipitation, with a Pearson correlation index of 0.46 (Fig. 10). This finding can be considered another validation of Tu Wien model, as this value is coherent with the correlation found by Sehler et al., 2019 in Mediterranean region croplands.

The rainfall events always correspond to a peak in SSM values. It must be considered that, due to temporal intervals between the rainfall event and the soil moisture estimate (maximum of three days), the strength of the moisture peak may be reduced and, thus, the correlation between soil moisture and precipitation can be underestimated. SSM estimates in different land cover classes show a different \({R}^{2}\) index in different land cover types. A stronger correlation is visible in bare soil (R2 = 0.655) and cultivated lands (R2 = 0.58). The lower correlation is found in forested areas (R2 = 0.461), where the vegetation structure and dielectric constant may have a greater influence than surface backscattering.

Analyzing more specifically moisture values in different crops type (Tab. 5), corn requires considerable volumes of water during its development cycle: for the total growing season (from April to July) it is around \(580\mathrm{mm}\) (McKenzie & Wood, 2011). Therefore, it needs to be irrigated in the regions of central and southern Italy. During the maturation, it is preferable that the amount of water remains above half of the retention capacity of the soil (Pastrello, 2012). According to the classification made by the United States Department of Agriculture (USDA), the soil texture of the UNIVPM’s farm is clay loam (“Texture USDA class”, n.d.) and water retention capacity, in clay soils, corresponds to 50% of moisture content. The average moisture in which corn is found in the different growth stages, especially during the ripening period, is well below 50% of the water retention capacity. Although this threshold, of course, varies in every single soil, depending on its composition, the moisture of the corn field was in fact not sufficient to meet the water requirements in the final stages of maturation. However, an analysis of the vertical profile of moisture content would still be \(1\mathrm{m}\) depth (Pastrello, 2012).

Concerning the durum wheat, in the emergence and tillering phase water stress is quite rare, while it is higher during the stem elongation and ripening phase. The total growing season water use varies between \(400\) and \(480 \mathrm{mm}\) (McKenzie & Wood, 2011). During the lifting and ripening phases, it is also important that the temperature does not increase excessively, as it often happens in central and southern Italy. In addition to increasing evapotranspiration, the heat squeeze causes a rapid loss of moisture in the grain, causing a stunted harvest (Camerini, 2013). The year 2020 was characterized by high average monthly temperatures compared to the 1981–2010 average, especially in the month of February, where an anomaly of more than 3.7° was recorded (Tognetti & Leonesi, 2020). This aspect, together with the low rainfall winter season, explains the low value of average moisture in the germination-emergence phase. This situation is not unfavorable in wheat, which, on the contrary, fears winter frosts and water stagnation.

Finally, sorghum has been studied. This crop has a reduced water requirement, around 300–350 mm, and it is sufficient that it rains between 120 and 150 mm in the summer months. However, this condition was not guaranteed during the summer of 2020. Therefore, sorghum was irrigated twice a month during the reproductive phase between June and July. Usually, a couple of irrigations are sufficient to maintain adequate levels of moisture. Sorghum, in fact, has excellent adaptability to water stress, thanks to a very fit and deep developing root system, and to its leaves, covered by wax. Sorghum can remain in vegetative stasis for a period of drought, until the water becomes available again and the plant resumes its growth. In fact, sorghum shows ideal soil moisture levels for the period analyzed. For these reasons, and because of the possibility of being used as biomass, sorghum is of particular interest in the region (EU, 2017).

Finally, the main limitations of the methods applied are discussed below. It can be noticed that the major limitation of these classifications is the uncertainty of the training data selection, due to the unavailability of updated ground truth data. This uncertainty also affects the final kappa indices, which may be over-estimated, since the data used for validation are a random subset of the polygons drawn for training. The training data have been selected in the most representative areas of each class, anyway, avoiding edges or areas of uncertainty. Precisely within these areas, classification errors can occur that could be over-looked in the validation phase. In urban areas, it is essential to select only pure pixels (without vegetation), which have been classified correctly, as the confusion matrices reported (see Online Resource 2). Urban area mixed pixels (vegetation and urban) are often classified as natural vegetation. Mainly for this reason urban areas are underestimated, even with the radar data addition.

Regarding SSM retrieval, the main sources of error may be due to the fact that a high spatial resolution can generate greater uncertainty with respect to any objects on the surface, and the absence of pronounced wet conditions in the data record period, as at the end of summer mainly dry conditions can be expected. In this study, the short S1 data interval used can lead to underestimating or overestimating the severity of extreme events. Supposing the vegetation and roughness conditions are stable during the month, the other source of error may be the challenging topography and residuals error derived from the imperfect incidence angle normalization.

5 Conclusions

The integration of optical and radar images for land cover classification is of great value because of their complementary and the possibility to improve the temporal resolution of the classification. In this paper it has been shown that the combined use of radar and optical data can improve the classification results. The use of Entropy and Alpha band can be useful to improve radar classification, exceeding optical accuracy in urban and water areas, but still does not allow to reach the overall optical accuracy.

Land cover classification is also an essential precursor to many techniques for extracting geophysical and biophysical information from SAR data. In this study, the land cover results were used to create a mask and isolate the agricultural areas where soil moisture retrieval was carried out. While WCM accuracy was inadequate due to the lack of calibrations data, the extraction of surface soil moisture using Tu Wien change detection method in Google Earth Engine was found to be acceptable. As it showed a low RMDS of 9.4% with in situ measurement, but a correlation with precipitation (0.46) which is in line which the one obtained by Sehler (2019), a further in-depth study is required, to finally develop an easy-accessible and high temporal and spatial resolution method for soil moisture monitoring. In fact, SSM is a valuable information for developing context-specific climate-smart farm practices, such as drought monitoring, irrigation planning and assessment of soil erosion by water estimations, which is a critical Mediterranean region environmental issue. The use of SSM to replace the runoff term in the Modified Universal Soil Loss Equation model has been tested by Todisco et al. (2015) and could be further implemented using S-1 high resolution SSM estimate to calculate soil erosion at the field scale.