Abstract
Recycling of e-waste (waste electrical and electronic equipment) represents an important abatement of pressure on the environment, but recycling rates are still low. This study builds on common environmental economics approaches to identify the main driving forces of the e-waste recycling rate. The environmental Kuznets curve hypothesis was applied in the context of the STIRPAT (stochastic impacts by regression on population, affluence and technology) model to analyze data from 30 European countries over the period 2008–2018. Panel quantile regression was conducted to determine the relationship between e-waste recycling rate and economic growth, population, population density, energy intensity, energy efficiency, credit to private sector and e-waste collected. Strong evidence was found that the relationship between economic growth and e-waste recycling rate is an N-shaped curve, i.e., the e-waste recycling rate first increases with economic growth, then decreases in maturing economies and in mature economies starts increasing again as the economy continues to grow. In addition to the economic development stage of a country, e-waste collection was identified as an important determinant of the e-waste recycling rate, regardless of whether the already achieved recycling rate was low, medium or high. In all models, a rise of the collected e-waste quantity was linked to an increase in the recycling rate. Therefore, expanding e-waste collection represents a priority task for policy makers to achieve high e-waste recycling rates. Population, energy intensity and credit to private sector also had an impact and in tendency displayed a negative effect on the e-waste recycling rate; however, the impact of these variables was more relevant for countries with particularly low e-waste recycling rates.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Recycling, a central circular economy principle, denotes efforts toward purposely reducing pressure on the environment. The recycling rate commonly indicates which percentage of a generated waste stream goes to material recovery schemes (Eurostat, 2021; Forti et al., 2020); this captures progress toward environmental protection and sound resource management. Countries with higher recycling rates generate less waste (Antoni & Marzetti, 2019; Islam et al., 2019), emit fewer greenhouse gases (Magazzino et al., 2020; Turner et al., 2015) and achieve more economic prosperity and employment opportunities (Di Vita, 2001; George et al., 2015; Liu et al., 2020).
E-waste (waste electrical and electronic equipment) is the fastest growing solid waste stream in the world (Baldé et al., 2015; Forti et al., 2020), but its recycling rate amounted to only 17.4% (world average) in 2019 (Forti et al., 2020), which was even lower than the rate of 20% in 2016 (Baldé et al., 2017). Thus, e-waste is a material stream of high concern. The growing quantity of e-waste is a symptom of increasing economic prosperity because waste generation is closely linked to economic wealth (Awasthi et al., 2018; Huisman, 2010; Kusch & Hills, 2017), but the relationship between e-waste generation and economic growth is not necessarily a linear one (Boubellouta & Kusch-Brandt, 2021a).
To systematically understand a relationship between economic development and a parameter of concern, a common approach in environmental economics is the environmental Kuznets curve (EKC) hypothesis, which assumes an inverted-U-shaped relationship between economic growth and environmental degradation, i.e., environmental degradation increases with economic growth up to a certain level (called the turning point) and then declines as economic growth continues (Grossman & Krueger, 1991; Panayotou, 1993). Solid waste has been researched under the EKC hypothesis in more than 30 studies (Boubellouta & Kusch-Brandt, 2021b); i.e., in these works the proxy for environmental degradation was solid waste. Many of these studies focused on municipal solid waste generation, and the picture is still somewhat fragmented because not all confirmed the EKC hypothesis (Magazzino et al., 2021). When researching waste under the EKC hypothesis, nearly all studies analyzed waste generation, while two recent works used mismanaged waste as a proxy for environmental degradation (Barnes, 2019; Boubellouta & Kusch-Brandt, 2021b).
As a paradigmatic shift in how the EKC hypothesis is used, a fully novel perspective to the EKC framework has recently been introduced by Kasioumi and Stengos (2020) who applied waste recycling as main indicator, i.e., not pollution/environmental pressure was their focus under the EKC analysis, but efforts to mitigate pressure on the environment. Conceptually, recycling as a measure of environmental abatement is the opposite of environmental degradation or pollution (Kasioumi, 2021; Kasioumi & Stengos, 2020). This paradigmatic shift in applying the EKC hypothesis not to environmental pollution but to recycling represents a new and potentially powerful research approach to understand the economic elasticity of environmental abatement efforts. Using solid waste recycling data from 50 US states over the period 1988–2017 in a semi parametric partial linear two-way fixed effects panel data model, Kasioumi and Stengos (2020) found a J-shaped relationship (growth continues but at lower path) between recycling level and GDP (Gross Domestic Product) for poorer and the richest countries and an inverted-U-shaped curve (growth until a turning point followed by decline) for a set of middle-rich US countries.
Whether such economic phenomena also exist for the recycling of e-waste as one of the most dynamic solid waste streams has not previously been researched. To implement appropriate recycling policies, the factors affecting the recycling rate merit high attention. Therefore, this study aims to provide insights into the main determinants of the e-waste recycling rate. Europe is selected as the region under study due to good data availability, a relatively high number of countries and the diversity of the countries (income, e-waste recycling rates); this region includes best performers and low performers in terms of e-waste recycling. Overall, Europe is the region with the highest average e-waste recycling rate worldwide (Forti et al., 2020); for the European Union (EU28), Eurostat (2021), by compiling data from national statistics, reports an average e-waste recycling rate of 35.8% in 2015, 41.3% in 2016, 40.0% in 2017 and 42.1% in 2018. Panel data from 30 European countries over the period 2008–2018 are analyzed in this research.
This is the first work to systematically explore the relationship between economic growth and e-waste recycling rate; simultaneously, further independent variables are considered to comprehensively capture the drivers of the e-waste recycling rate. For this purpose, e-waste recycling is studied under an EKC framework in which the widely used STIRPAT approach is applied to capture the driving factors of the recycling rate. The EKC approach allows to examine for a potentially nonlinear relationship between economic growth and recycling rate. Quantile regression for panel data (QRPD) with non-additive fixed effects, proposed by Powell (2016), is used as econometric method. QRPD is more powerful than traditional approaches: (1) it provides robust results even if the data set contains outliers and (2) it provides appropriate results when the independent variables have different effects at various points of the conditional distribution of the dependent variable, while traditional approaches focus only on the mean effect.
2 Literature review and background information
2.1 IPAT and STIRPAT to capture the drivers of environmental pressure
The IPAT model proposed by Ehrlich and Holdren (1971) has been extensively used to explore the main determinants of environmental pressure. This model (Eq. 1) assumes that impact (I) on the environment (e.g., pollution) mainly comes from three factors: population size (P); affluence (A, commonly defined as GDP per capita); and technology (T).
This implies a proportional relationship between environmental pressure and its driving forces. To quantify the role of individual drivers, such a simple assumption of equally impactful determinants is rarely sufficient (Vélez-Henao et al., 2019). As a more comprehensive approach, Dietz and Rosa (1997) developed the STIRPAT (stochastic impacts by regression on population, affluence and technology) model, which is the stochastic form of IPAT. The standard STIRPAT model has the following form:
where suffixes i and t represent unit of observation (e.g., country) and time (year); I, P, A and T are the same as in Eq. (1); a is the constant term; b, c and d are the coefficients of P, A and T; and e is the error term. By adding logarithms to both sides of Eq. (2), the STIRPAT equation takes the following form:
STIRPAT, initially used in the natural sciences such as biology and physics, has been applied to a broad range of areas over the last 20 years, including environmental economics, sociology, engineering, finance and marketing (Kilbourne & Thyroff, 2020). Examining the SCOPUS database in 2019, Hashmi and Alam (2019) documented around 1300 articles working with STIRPAT, with half of these published during the last three years of analysis. Most STIRPAT studies used pollutant emissions as indicator of environmental degradation (Vélez-Henao et al., 2019), but some few successfully applied solid waste generation (Arbulu et al., 2016; Cheng et al., 2020; Fischer-Kowalski & Amann, 2001; Han et al., 2020); none used e-waste.
2.2 Environmental Kuznets curve hypothesis (EKC) to explore the relationship between environmental degradation and economic growth
IPAT and STIRPAT focus on the drivers of environmental pressure but do not model the economic pattern of environmental degradation (development of environmental degradation along economic growth). A common approach to express the relationship between economic growth and environmental degradation is the environmental Kuznets curve (EKC). A review of Asumadu and Vladimir (2019), using Web of Science as database, found 2341 EKC studies published between 1993 and 2018; this high number of studies indicates the productivity of this approach to capture the economic patterns of environmental pressure. The EKC is derived from the theory proposed by Kuznets (1955). Kuznets postulated an inverted-U-shaped curve between economic growth and inequality; he observed increasing income inequality in the first stages of economic development but a decrease when income per capita reached a certain level (turning point). Based on this pattern between economic growth and a parameter of concern, Grossman and Krueger (1991) transferred the Kuznets hypothesis to the environmental field and proposed the EKC: It assumes environmental degradation gets worse during early stages of economic development but then starts improving when income reaches a turning point and grows further (inverted-U-shaped curve between environmental degradation and economic growth).
Early applications of the EKC hypothesis mainly focused on direct pollutants such as sulfur dioxide or emission of particulate matter, while since the 2000s many studies addressed greenhouse gas emissions (CO2 emissions) and explicitly included related parameters such as energy consumption or renewable energy consumption (Pata, 2018a; Pata & Caglar, 2021; Thio et al., 2021). More complex parameters such as seawater quality (Wang et al., 2019), industrial wastewater discharge (Diao et al., 2009), ecological footprint (Al-Mulali et al., 2015; Pata, 2021) or water footprint (Sebri, 2015) have also been used as a proxy for environmental degradation in the last two decades. It is well acknowledged in the EKC literature that income is not the only factor affecting environmental degradation, and thus, it is common to include further relevant explanatory variables or control variables such as trade openness, industrialization, import, export, capital, labor, globalization, urbanization or technological development (Allard et al., 2018; Pata, 2018b).
Grossman and Krueger (1995) and Panayotou (1997) argued the relationship between economic development and environmental degradation might be N-shaped rather than inverted-U-shaped; in such case, environmental degradation would increase again at a high level of economic prosperity (called second turning point).
The basic EKC model is captured through the following equation:
where I represents the indicator of environmental pressure, GDP.cap is the gross domestic product per capita and X refers to control variables and ε is the error term. Based on the mathematical signs of the coefficients α of the GDP.cap terms (i.e., α1, α2, α3), the nature of the relationship between income per capita and environmental pressure can be identified:
-
If α1 = α2 = α3 = 0, there is no relationship.
-
If α1 > 0 and α2 = α3 = 0, there is a monotonically increasing linear relationship.
-
If α1 < 0 and α2 = α3 = 0, there is a monotonically decreasing linear relationship.
-
If α1 > 0 and α2 < 0 and α3 = 0, there is an inverted-U-shaped relationship.
-
If α1 < 0 and α2 > 0 and α3 = 0, there is a U-shaped relationship.
-
If α1 > 0 and α2 < 0 and α3 > 0, there is an N-shaped relationship.
-
If α1 < 0 and α2 > 0 and α3 < 0, there is an inverted N-shaped relationship.
An inverted-U-shaped curve has frequently been reported in the EKC literature; most of the more than 2000 previous studies used atmospheric pollution such as carbon dioxide, sulfur dioxide and greenhouse gas as proxy for environmental degradation (Asumadu & Vladimir, 2019). An N-shaped relationship has been reported in some works, based on analyzing air pollution parameters, e.g., sulfur dioxide, fine smoke and suspended particles (Grossman & Krueger, 1991, 1995) or water footprint (Sebri, 2015).
Solid waste (waste Kuznets curve), such as municipal solid waste, plastic waste and industrial waste, has been used in around 30 EKC studies (Boubellouta & Kusch-Brandt, 2021b), and results are inconclusive; most studies (3/4), but not all, identified an inverted-U-shaped relationship. A review of the literature related to the waste Kuznets curve is available elsewhere (Boubellouta & Kusch-Brandt, 2020, 2021a). An N-shaped EKC pattern had not been reported for solid waste over the last decades, but recently Wang et al. (2021) have found an inverted N-shaped EKC pattern for municipal solid waste generation in cities across the economically less developed region of western China.
Only four studies subjected e-waste to the EKC hypothesis: Three addressed e-waste generation and one focused on mismanaged e-waste quantities. Boubellouta and Kusch-Brandt (2020) were the first to explore e-waste generation under the EKC hypothesis; based on panel data over the period 2000–2016 for EU28 + 2 countries, they found strong EKC evidence (inverted-U-shaped relationship between GDP per capita and e-waste generation). Subsequently, Boubellouta and Kusch-Brandt (2021a), using e-waste generation for 174 countries for 2016, confirmed the EKC for a broader set of countries and regions worldwide. In addition, Boubellouta and Kusch-Brandt (2022) analyzed the generation of major e-waste categories for EU28 + 2 countries; for all categories under study (temperature exchange equipment, screens and monitors, lamps, large equipment, small equipment, and small IT and telecommunication equipment), the EKC hypothesis in the form of an inverted-U-shaped curve was confirmed. Unlike studies which focused on e-waste generation, Boubellouta and Kusch-Brandt (2021b) examined the relationship between GDP and mismanaged e-waste (uncollected and non-recycled/non-reused e-waste) for 27 European countries (2008–2016); the regression analysis found an inverted-U-shaped relationship between GDP and uncollected e-waste and also between GDP and non-recycled/non-reused e-waste.
2.3 Economic patterns of e-waste
The literature to understand economic patterns of e-waste is limited in quantity and scope. Previous studies mainly focused on e-waste generation, i.e., quantities of e-waste occurring in an economy. A linear relationship between economic development and e-waste generation was observed in some works, namely for European (Awasthi et al., 2018; Namlis & Komilis, 2019), pan-European (Kusch & Hills, 2017) or the most populous countries worldwide (Kumar et al., 2017), while Huisman (2010) identified a quadratic relationship for mature EU economies; this suggested that the assumption of a linear relationship might not be justified for all settings, and overall, a more complex relationship between economic growth and e-waste generation can be expected. Consequently, the EKC hypothesis was tested for e-waste, as described above, which disclosed existence of an inverted-U-shaped relationship between GDP per capita and e-waste generation for Europe (Boubellouta & Kusch-Brandt, 2020) and worldwide (Boubellouta & Kusch-Brandt, 2021a), and also for individual e-waste categories across Europe (Boubellouta & Kusch-Brandt, 2022). Thus, generation grows with the economy up to a certain point (turning point), while mature economies experience a decline of e-waste generation.
Waste generation, although a commonly used indicator in environmental economics (Huang et al., 2021; Jaligot & Chenal, 2018), is not fully comprehensive as indicator for environmental degradation when advanced waste management collection and treatment schemes exist. In such cases, environmental pressure will predominantly come from the mismanaged part of waste (Boubellouta & Kusch-Brandt, 2021b; Willis et al., 2021). Adopting an idea of Barnes (2019) who employed mismanaged plastic waste as indicator in an EKC framework, Boubellouta and Kusch-Brandt (2021b) researched mismanaged e-waste and confirmed the EKC hypothesis with panel data from 27 European countries (inverted-U-shaped curve between GDP and uncollected e-waste quantity, also between GDP and non-recycled/non-reused e-waste quantity). However, the quantity of mismanaged waste is the result of two overlapping factors, namely quantity of waste diverted to sound management such as recycling, and quantity of waste generated. For e-waste, both factors are highly dynamic: E-waste is rapidly growing, and many countries (with European countries taking the lead) are setting up advanced management schemes (Yla-Mella & Roman, 2019). Studying non-recycled waste quantities therefore does not conclusively reveal the economic pattern of recycled waste.
The recycling rate captures an element which is different from only looking at the quantity of non-recycled (or non-reused) waste: It is the recycling rate (share of recycled waste out of the total generated waste) which indicates the level at which an important environmental abatement opportunity is realized in a country. Thus, researching the recycling rate explores new aspects of the economic patterns of a material of environmental concern. Understanding the main driving forces of the e-waste recycling rate is essential to implement effective resource management policies.
2.4 Key driving forces of recycling
It is widely accepted that environmental attitudes (Bezzina & Dimech, 2011; Saphores & Nixon, 2014; Zen & Siwar, 2015) and education of citizens (Escario et al., 2020; Jenkins et al., 2003; Sidique et al., 2010; Song et al., 2019) positively influence solid waste valorization. However, the key driving forces of recycling at the macrolevel have not been well understood (Kirakozian, 2016; Önder, 2018; Razzaq et al., 2021). Clearly, population numbers or population density can impact efficiency of waste management systems, including recycling; in particular, sparsely populated regions are more challenging with view to establishing efficient systems (Richter et al., 2021). Household income and economic development stage of a region have been studied as determinants of waste recycling; however, results are inconsistent. A negative effect of household income on recycling behavior was demonstrated for 539 individuals in France (Kirakozian, 2016). On the other hand, Jenkins et al. (2003) found a positive effect of household income on recycling (especially of newspapers) among 1049 urban US households. Antoni and Marzetti (2019) looked at the economic development stage of regions in terms of GDP and found no significant impact of GDP per capita on the recycling rate when examining 116 provincial capitals in Italy over the period 2000–2012. However, Önder (2018) observed a negative impact of GDP per capita on the recycling rate of packaging waste, using panel data from 31 European countries over the period 2004–2014. Furthermore, for municipal solid waste, separate collection of recyclables (especially curbside collection) has been identified as one main factor to ensure elevated recycling rates (Antoni & Marzetti, 2019; Jenkins et al., 2003; Park & Berry, 2013; Shinkuma, 2003); volume-based waste fees for residual waste can support recyclables collection (Gellynck et al., 2011; Park & Lah, 2015; Sakai et al., 2008). In addition, interlinkages between economic development, renewable energy consumption and recycling rates have been reported for OECD countries (Cerqueira et al., 2021); the results suggest that high renewable energy consumption levels correspond to high solid waste recycling rates, which reflects technological progress in a country. For the USA, a correlation between municipal solid waste recycling and energy efficiency has been observed; high recycling rates were accompanied by high levels of energy efficiency (Razzaq et al., 2021). Another relevant factor is involvement of the private sector in waste management. The private sector has an essential role in establishing recycling schemes (Shah & Guha, 2021); however, it was also reported that for high-income countries higher levels of credit to private sector induced a higher share of mismanaged waste (Boubellouta & Kusch-Brandt, 2021b), and thus, the effective impact of this factor is not fully clear.
Based on the existing literature about solid waste recycling, it can be hypothesized that the following factors might impact the e-waste recycling rate at the macrolevel: population/population density, economic development stage, e-waste collection system, energy usage and its efficiency, and credit to private sector. Whether these factors indeed significantly influence the e-waste recycling rate is to be analyzed in the following.
3 Methodology and data
To capture the determinants of e-waste recycling, this work employs an extended STIRPAT model and conducts panel quantile regression with data from 30 European countries.
3.1 Extended STIRPAT model
The STIRPAT model is powerful in identifying the impact of population, affluence and technology on environmental pressure; however, it does not include other potentially impactful variables (Dietz & Rosa, 1994). Furthermore, based on the EKC hypothesis, economic growth can have a nonlinear relationship with environmental degradation, which is not captured by the standard STIRPAT model. To account for this, STIRPAT model and EKC hypothesis can be merged by including GDP per capita square and cube in the STIRPAT expression (Shahbaz et al., 2016; Xu et al., 2020). This uses GDP per capita cube as the highest GDP term of the model setting, which tests for the N-shaped EKC. To avoid omitted-variable bias, in this study further variables that could have an impact on the e-waste recycling rate are included as control variables: credit to private sector and collected e-waste. Thus, by incorporating GDP per capita square and cube, credit to private sector and collected e-waste into Eq. (3), the STIRPAT model becomes as follows:
where RECY denotes e-waste recycling rate, POP is population size, GDP.cap is gross domestic product per capita and EN.IN is energy intensity as a proxy of technology. Energy intensity, as the amount of energy used to produce a given level of GDP, reflects the environmental impacts of production activities in a country better than energy consumption, because the latter is affected by per capita income (Pata & Isik, 2021). CRED is credit to private sector, and COLL is collected e-waste. (For units of variables, see below in documentation of data used.) Since some previous studies used population density instead of population (Danish et al., 2021; Liddle, 2014) and energy efficiency as a proxy of technology (Xu et al., 2017; Yeh & Liao, 2017), both variables are employed in this research to check the robustness of results. Thus, a second STIRPAT model is used in this study as an alternative to Eq. (5), given by Eq. (6):
where DENS represents population density and EN.EF energy efficiency. (The other variables are the same as in Eq. 5.)
3.2 Panel quantile regression
Over the last years, environmental economics has revealed an increased interest in the quantile regression approach which was originally developed by Koenker and Bassett (1978). This method analyses single quantiles (i.e., percentiles) of the data set during regression. This gives more robust results compared to the traditional ordinary least squares (OLS) method and it yields more detailed insights. Traditional OLS is biased in the presence of outliers (one outlier can strongly affect OLS estimates), while quantile regression avoids such bias (Chen & Lei, 2018). Furthermore, quantile regression captures the conditional distribution of the dependent variable within the regression framework, while OLS focuses only on the conditional expectation (Zhu et al., 2016). In addition, if normal distribution of data is not fulfilled, OLS regression results will be inconsistent, while quantile regression provides consistent results with any distributional assumption (Xu & Lin, 2020).
The pooled quantile regression originally proposed by Koenker and Bassett (1978) does not factor in unobserved heterogeneity of a complex observation unit such as a country. In consequence, different researchers (Canay, 2011; Koenker, 2004; Ponomareva, 2010; Rosen, 2012) have developed a panel quantile regression with fixed effects (FEQR) to address unobserved individual heterogeneity (individual effects) of observation units. This approach is defined as follows:
where y denotes dependent variable, xi is the vector of independent variables, α represents individual fixed effects, τ is the τth quantile with τ ϵ (0, 1); and β(τk) is the τth quantile of coefficients to be estimated. A limitation of additive fixed effects quantile regression is the problem of the incidental parameter when the time dimension of panel data T is small, and furthermore, this method is not efficient to estimate a large number of fixed effects (i.e., many countries to analyze) (Albulescu et al., 2019).
To overcome such limitations, quantile regression for panel data with non-additive fixed effects (QRPD) was introduced by Powell (2014, 2016). While the FEQR estimator conceptually separates the disturbance term and assumes the parameters to be interpreted do not vary based on the fixed effect, QRPD assumes non-additive fixed effects with varying impact of the non-additive disturbance term on the parameters under study, while it also maintains a non-separable disturbance term in agreement with the basic quantile regression approach. Furthermore, QRPD determines the distribution of yit/Dit (where Dit is the set of explanatory variables), while FEQR estimates the distribution of (yit − αi)/Dit; Powell (2014, 2016) pointed out that applying FEQR may be an inappropriate choice, because observations located at the most elevated levels of the (yit − ai) term can belong to the lowest levels of the yit distribution, and thus, the outcome of the FEQR method can lack critical information. QRPD with non-additive fixed effects is expressed by Eq. (8).
where yit stands for the dependent variable, D′it represents the set of independent variables, β indicates the coefficient of the variables to be interpreted and U*it is the holistic error term. The error term is sensitive to moderation by various types of disturbances, of which some might be fixed while others can vary in time. In line with Powell, the QRPD model manifests linear in parameters, and the function D′itβ(τ) is strictly increasing with view to τ. For each quantile τ, the regression incorporates the conditional restriction of Eq. (9), with P being the probability (P ϵ (0, 1)). This conditional restriction encapsulates a probability of the dependent variable yit which is smaller or the same as the quantile function for all independent variables and which is equal to τ.
According to Powell (2014, 2016), the probability can be assumed to be subject to variations among the observed entities and even within-entity (over time), if the condition applies that such variation occurs orthogonal to the instruments of the model. Consequently, the QRPD model is specified to respect both a conditional and an unconditional restriction, in which Di = (Di1, …, Dit) is defined by Eqs. (10) and (11).
Using generalized method of moments (GMM) for the regressions, Powell’s QRPD estimator was built in an instrumental variable framework, with Zi = (Zi1, …, Zit) being the instruments adopted (Powell, 2014, 2016). Equation (12) provides the sample moments.
where \(\overline{Z}_{i} = \frac{1}{t}\mathop \sum \nolimits_{i = 1}^{T} Z_{it}\).
Building on Eq. (12), the set of parameters to be considered is defined with Eq. (13).
Then, Eq. (14) is applicable (\(\hat{A}\) is a weighting matrix).
Drawing from previous quantile regression studies, such as Xu et al. (2017), five quantiles are analyzed in this work: 10th, 25th, 50th, 75th and 90th percentile of the conditional e-waste recycling rate. The lower quantiles contain the countries with lower recycling rates and the upper quantiles the countries with higher recycling rates. In addition to QRPD, traditional ordinary least squares (OLS) regression is applied for comparison purposes.
To ensure that the used variables are stationary, unit root tests are conducted before running the regressions; test methods and results are presented in Sect. 3.4. Stata 15.1 was employed as the econometric software to implement the regressions. Markov Chain Monte Carlo (MCMC) optimization method was applied.
3.3 Data
This research is based on unbalanced data from 30 European countries (EU28 plus Norway and Iceland) covering the period 2008–2018 (11 years). Choice of countries and study period is based on data availability. The dependent variable is e-waste recycling rate (percentage of e-waste that goes to recycling/reuse in a country, out of total generated e-waste in the country); the data for each country and year are taken from Eurostat (2021), which creates a data set with 290 data points (for some countries, annual data are incomplete in Eurostat). Two sets of independent variables are used: (1) explanatory variables (GDP per capita, population size, population density, energy intensity, energy efficiency); and (2) control variables (credit to private sector, collected e-waste). The data for GDP per capita, energy intensity, energy efficiency and collected e-waste are taken from Eurostat (2021), while population size, population density and credit to private sector are extracted from the database of the World Bank (2021).
Table 1 provides the descriptive statistics and the results of the normality tests for all variables used. RECY is the e-waste recycling rate (in % of generated e-waste). GDP.cap is the gross domestic product per capita at constant 2010 EURO (GDP in chain linked volumes, reference year 2010). POP is the population number in a country, as one of the classical STIRPAT variables; DENS, as an alternative variable to capture the demographic element, is the population density, measured as people per square kilometer land area. EN.IN (capturing the technology factor of the STIRPAT model) is the energy intensity of the economy, expressed in kilograms of oil equivalent (kgoe) per thousand EURO (GDP in chain linked volumes 2010). EN.EF, as an alternative variable to capture the technology factor, represents the energy efficiency of a country; in line with the energy efficiency dashboard of the EU (Eurostat, 2021), this is total primary energy consumption of a country (in million tonnes of oil equivalent (Mtoe)). CRED is credit to private sector in % of a country’s GDP. COLL is e-waste collected in kilograms per inhabitant.
Before applying panel quantile regression, it is useful to know whether variables are normally distributed. For this purpose, two approaches are available: descriptive statistics and statistical tests. Regarding descriptive statistics, skewness and kurtosis are commonly applied. Skewness captures asymmetry of the data distribution. When the third moment (skewness) is equal to zero, the data are normally distributed. As shown in Table 1, the skewness coefficients for all variables are different from zero; therefore, the variables under study are not normally distributed. Kurtosis as a statistical measure identifies the dispersion of data. When the third moment (kurtosis) is equal to 3, the data are normally distributed. The results in Table 1 show the kurtosis coefficients of all variables of interest are different from 3, which confirms that all variables are not normally distributed. Regarding statistical tests, Shapiro–Wilk test (Royston, 1992) is applied, and the significant probability values for all variables confirm the variables are not normally distributed. These results indicate that conditional mean regression could provide biased results, while the panel quantile regression approach will provide robust results, and thus is the appropriate choice.
The correlation matrix for the variables is available from Table 2. Population has weak positive relationships with the rate of e-waste recycling. Moreover, GDP per capita, energy efficiency and e-waste collected have significant positive impacts on the e-waste recycling rate, while population density, energy intensity and credit to private sector negatively affect the rate of e-waste recycling at 1 and 5% level of statistical significance, respectively.
3.4 Unit root tests
Before running the panel quantile regression, all variables under study are tested for stationarity, i.e., if they contain unit root or not. If data contain unit root, they are non-stationary, with a risk of spurious regression, potentially delivering misleading regression results. This would negatively affect the interpretation of the relationship between e-waste recycling rate and its driving forces. The unit root test allows to identify whether the time series used is stationarity (has no unit root) or non-stationary (possesses a unit root) (Magazzino, 2016a, 2016b). Econometrics literature provides a variety of panel data unit root tests; methods can be divided into two types: (1) common unit root tests such as Lavin–Lin–Chu (LLC) test (Levin et al., 2002) and (2) individual unit root tests, including Im–Pesaran–Shin (IPS) (Im et al., 2003), augmented Dicky–Fuller (ADF) (Dickey & Fuller, 1979) and Phillips–Perron (PP) (Phillips & Perron, 1988). Four tests are used in this study to examine the unit root for all variables. For all tests, the null hypothesis assumes presence of a unit root, i.e., the time series is non-stationary, while the alternative hypothesis assumes nonexistence unit root, i.e., the time series is stationary. The Schwartz information criterion is adopted to determine the optimum lag.
The results of common and individual unit root tests are reported in Table 3. Energy efficiency is stationary in level. E-waste recycling rate, GDP per capita, population, population density, energy intensity, credit to private sector and e-waste collected are non-stationary in level; however, they are stationary in the first difference at 1% level of statistical significance. Therefore, stationarity of the variables is confirmed.
4 Results and discussion
4.1 Panel quantile regression results
This research uses panel quantile regression with non-additive fixed effects (QRPD) to examine the e-waste recycling rate determinants across 30 European countries. QRPD was selected as main method because it provides more robust results compared to traditional ordinary least squares (OLS) regression when the data set used contains outliers or when the time dimension of panel data is small. The dependent variable is the e-waste recycling rate. To determine its drivers, two different sets of explanatory variables are employed: (1) as specified with Eq. (5), the first set consists of GDP per capita (GDP.cap), population size (POP) and energy intensity (EN.IN); (2) as specified with Eq. (6), the second set of explanatory variables contains GDP.cap, population density (DENS) and energy efficiency (EN.EF). In both versions, credit to private sector (CRED) and collected e-waste (COLL) are added as control variables.
The panel quantile regression results obtained when using GDP.cap, POP and EN.IN as explanatory variables (and CRED and COLL as control variables) are reported in Table 4. For comparison purposes, pooled OLS regression is also conducted, and those results are included in the last column of the table.
The coefficients of GDP per capita, GDP per capita square and GDP per capita cube are positive, negative and positive, respectively, and statistically significant at 1% level across all quantiles. This result indicates that the relationship between e-waste recycling rate and GDP per capita is that of an N-shaped curve at the different quantiles. Similar results are obtained from pooled OLS regression. Thus, the recycling rate first increases with economic growth, then undergoes a stage of decrease and finally increases again along further economic growth. However, the picture differs across quantiles. GDP per capita square and of GDP per capita cube have a more pronounced impact in the upper quantiles (75th, 90th percentile, representing countries with high recycling rates); this suggests that in economies which have already established e-waste recycling schemes, the economic development has a more dominant impact over other influencing factors compared to countries where such recycling schemes are not yet widespread. This agrees with the note of Yla-Mella and Roman (2019) that in Europe high-income countries tend to have more elaborate e-waste management systems. Another interesting observation is the relatively soft impact of GDP per capita cube: The recycling rate turns from a negative development into growth at higher GDP levels, but effects of GDP per capita cube are relatively small compared to those of GDP per capita and GDP per capita square; thus, an increase in the e-waste recycling rate happens in very mature economies but at a slow rate only. These results are consistent with findings of Kasioumi and Stengos (2020) for solid waste recycling rates across US countries, both with view to differences observed between the wealthiest and poorer countries and with view to a slow increase in recycling in rich countries, although the authors interpreted the pattern for the wealthiest and the poorest countries as a J-shaped curve between income level and recycling, while they identified an inverted-U-shaped curve for middle-rich countries. Therefore, it can also be concluded that the approach of this study to test for the N-shaped EKC curve for e-waste recycling rate is advantageous compared to applying the more conventional inverted-U-shaped EKC testing; inclusion of the cube term to account for a potentially N-shaped curve provides a more comprehensive and robust picture. In this work, using GDP square as the highest term, thus testing for the inverted-U-shaped EKC, was also trialed, but results were less robust compared to including GDP per capita cube.
Population is a frequently used indicator to examine the effect of demographic pressure on the environment. For e-waste, previous studies found that population increases environmental pressure due to higher e-waste generation (Boubellouta & Kusch-Brandt, 2020, 2021b). The results of this study complement the existing knowledge. Table 4 shows that population size impacts the recycling rate: Population has a negative influence (statistically significant at 1% level) on the e-waste recycling rate across all quantiles, i.e., an increase in the population number means a lower recycling rate, while a decline in population number (which according to Eurostat data is the case for some European countries such as Bulgaria, Hungary, Italy and Romania) is accompanied by a higher recycling rate. An explanation might be a lag phase between a population change and the adaption of infrastructures and waste management schemes to account for such change. A lag phase between population changes and infrastructure adaptation has been reported or discussed in the literature for various infrastructural elements, including energy supply, transport and mobility systems, water supply and wastewater treatment schemes (Adshead et al., 2019; Churchill et al., 2021; Hummel & Lux, 2007). Most studies in this context focused on low- or middle-income countries, but a delay in infrastructure adaptation in response to population changes has also been documented for high-income countries such as Germany (Hummel & Lux, 2007). Regarding the impact of population on the e-waste recycling rate observed in this work, it can be identified from above data that this influence of the population number is slightly more pronounced in the lower middle quantiles (25th, 50th percentiles), and thus, a growing population number seems to reduce the rate of recycling rather in countries with a medium e-waste recycling rate, i.e., in countries which do not yet have in place highly effective recycling schemes. Thus, where recycling systems are not yet widely adopted, the overall recycling rate apparently is more susceptible to perturbations as a result of a change in population numbers.
Regarding the effect of energy intensity, Table 4 shows coefficients with mathematically negative sign (and significant at 1% level) across all quantiles; the same is obtained from pooled OLS. The negative sign of the coefficient indicates the e-waste recycling rate decreases when energy intensity increases. This can be explained because of more usage of electrical and electronic equipment occurring along a growing energy intensity (Morley et al., 2018) and consequently higher quantities of e-waste generated and left unrecycled in the context of the existing waste management systems of an economy. The implication of energy intensity is somewhat heterogeneous across quantiles; in upper quantiles, the effect is smaller than in low quantiles. Thus, energy intensity is a less relevant recycling rate determinant in countries with already elevated recycling rates, which traditionally include Sweden and Denmark and more recently Hungary and Bulgaria. This set of countries contains both high-income nations with an energy intensity below EU average (Sweden, Denmark) and lower-income nations with above average energy intensity (Hungary, Bulgaria). The role of energy intensity is therefore difficult to interpret for single quantiles. However, it is evident that for upper quantile countries (i.e., where high recycling rates have already been achieved), explanatory variables other than GDP, including energy intensity, and control variables are less relevant; therefore, in the upper quantile countries GDP has a more dominant role as a recycling rate driver compared to countries with lower recycling rates. Evidently, recycling rate drivers are more varied in their impact where the recycling rate is low; once the rate is elevated, the economic development stage of a country strengthens its role as most important recycling rate determinant. This is especially the case for the 75th percentile, which includes many of the most mature economies (Denmark, Norway, Sweden, Luxembourg).
Pooled OLS and quantile regression both show that the effect of control variables (credit to private sector, e-waste collection rate) is also significant. In agreement with observations presented above, the quantile regression results illustrate the variables’ impact is more pronounced in lower quantiles. Credit to private sector has a negative effect (and significant at 1% level) on the e-waste recycling rate across all quantiles except the highest quantile. This negative effect can be attributed to an increasing investment in response to the higher credit offered to the private sector, which is accompanied by more usage of electric and electronic devices and consequently more e-waste generation, without necessarily higher recycled e-waste volumes. This finding is consistent with earlier research: Boubellouta and Kusch-Brandt (2021b) found higher levels of credit to private sector were accompanied by more non-recycled/non-reused e-waste in 27 European countries.
Interestingly, the quantity of e-waste collected has a key role as e-waste recycling rate determinant. As shown in Table 4, pooled OLS and quantile regression both disclose a significant positive effect of e-waste collected, and this applies to all quantiles. This suggests that an increase in the amount of e-waste collected will lead to a higher e-waste recycling rate across European countries. This result supports conclusions of Boubellouta and Kusch-Brandt (2021b), who elaborated that the quantity of non-recycled e-waste in European countries is strongly determined by the quantity of e-waste that remains uncollected. Again, the impact of the control variable is in tendency lower toward upper quantiles, but e-waste collected is one of the most important drivers in all quantiles.
Finally, to check the significance of the estimated models presented in Table 4, the Wald test (Koenker & Bassett, 1982) is employed. The null hypothesis of the Wald test is that all the coefficients are equal to zero. As shown in the last line of Table 4, the null hypothesis in all estimated models is to be rejected; thus, the coefficients are different from zero and significance of the models is confirmed.
To provide a more comprehensive picture and check robustness of findings, a second regression round is conducted, using an alternative set of explanatory variables (as explained above). In this round, population density is used instead of population number as a proxy for the demographic characteristics and energy efficiency (in terms of total primary energy use of a country) is employed instead of energy intensity to account for the technology factor. Table 5 presents the results.
The response of e-waste recycling rate to GDP per capita, GDP per capita square and GDP per capita cube is positive, negative and positive, respectively, across all quantiles, at 1% of statistical significance, which indicates the relationship between recycling rate and GDP per capita is that of an N-shaped curve. This observation agrees with the earlier results obtained with population and energy intensity as explanatory variables (Table 4). In addition, similar results are also found from pooled OLS regression. This is strong evidence that the EKC hypothesis (N-shaped relationship) is fulfilled between economic growth and the e-waste recycling rate.
Further insights can be gained from analyzing the regression results in Table 5. Like in earlier observations with the first set of explanatory variables (Table 4), GDP per capita is the most relevant explanatory variable. Especially for the 75th and the 50th percentiles (i.e., where elevated or high e-waste recycling rates have already been achieved), the effects of GDP, GDP square and GDP cube are particularly pronounced. Mature European economies fall into those quantiles. This supports the earlier observation that for mature economies further economic development is clearly the most relevant, and in fact dominant, determinant of the e-waste recycling rate. For population density, pooled OLS suggests a negative effect on the e-waste recycling rate, but quantile regression finds this only where recycling rates are low. The explanatory power of population density as a variable is generally rather low across all quantiles. When looking at energy efficiency, pooled OLS indicates the result is statistically not significant, while quantile regression shows negative and statistically significant coefficients in all quantiles except the 10th percentile. However, compared to the earlier used variable energy intensity, the effect of energy efficiency is much lower. Therefore, the explanatory power of energy efficiency is small compared to energy intensity. Regarding control variables, the quantile regression results in Table 5 are consistent with those reported earlier from the first regression round (Table 4): Credit to private sector has a negative impact on the e-waste recycling rate across all quantiles, while e-waste collected has a significant positive influence across all quantiles (and pooled OLS agrees).
When applying the Wald test (Koenker & Bassett, 1982) to check the significance of the estimated models (last line in Table 5), the Wald test null hypothesis is to be rejected, confirming that all coefficients are different from zero; thus, significance of the elaborated models is confirmed.
So far, correlations among variables have been identified. To know whether a postulated causality is bidirectional or unidirectional, or to reveal whether there is no causal association between variables under study, the Granger causality approach is used. Table 6 displays the Granger causalities between independent variables and dependent variables for both equations used above and the respective directions thereof. The results show that there is a significant unidirectional Granger causality from GDP.cap, GDP.cap square, GDP.cap cube, population size, population density and collected e-waste to RECY (e-waste recycling rate). There is also a significant bidirectional Granger causality relationship between credit to private sector and e-waste recycling rate. Furthermore, there is no Granger causality from energy intensity or energy efficiency to e-waste recycling rate.
4.2 Conclusive findings across the different models used
In brief, when comparing results obtained from the different regressions (panel quantile regressions and pooled OLS), findings are consistent across different methods for all sets of variables used. Strong and new evidence was found that the relationship between economic growth and e-waste recycling rate is an N-shaped curve for European countries. In addition, e-waste collected has a significant positive effect on the rate of e-waste recycling. Furthermore, population size, energy intensity and credit to private sector have negative and statistically significant effects; interestingly, the effect of these variables is more pronounced where recycling rates currently are lower.
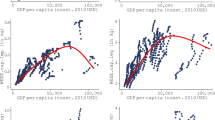
The N-shaped relationship between economic growth and e-waste recycling rate can also be illustrated graphically (Fig. 1). The recycling rate first increases rapidly at low GDP levels, then undergoes a period of decline and then increases again with the economy, albeit at a slow path. (This corresponds to the observation that the cube term of GDP in the regression analysis was small.) For economies with the highest maturity level, such slow increase in the recycling rate agrees with the J-shaped relationship (growth continues but at lower path) reported by Kasioumi and Stengos (2020) for solid waste recycling in the richest US states.
Figure 1 shows that the highest GDP levels in the set of European countries are in Luxembourg; here, the recycling rate is below the suggested EKC curve. Luxembourg has a strongly unconventional economic and infrastructural profile. It is a small country with an exceptional economic dominance of the financial sector and with many cross-border workers; unusually high GDP levels per capita persist (European Commission, 2016). In economic analyses, Luxembourg is often excluded because data from this country deviate from general patterns (Kusch & Hills, 2017). In this work, findings are robust regarding inclusion or exclusion of Luxembourg, and thus, the presented regressions are based on all 30 European countries for which e-waste recycling rates were available from Eurostat. By using QRPD, this work is based on a methodology that is robust against outliers.
Figure 1 shows that there is less variation of the recycling rate at higher GDP levels, while there is more variation at lower stages of the economic development. A similar observation was made by Kasioumi and Stengos (2020) for US states: They found more fluctuations for states with lower or medium income per capita compared to the wealthiest states. This suggests that mature economies are more stable regarding their efforts to mitigate environmental pollution. A possible explanation might be more financial resources of wealthy countries to invest in waste management infrastructures. Furthermore, high-income countries are more engaged in promoting cleaner technologies; this might respond to environmental concerns among the population or might reflect more awareness for negative economic effects of activities with high pollution/waste generation. At the same time, recycling rates achieved by wealthy European nations are not satisfactory; they typically range between 40 and 60% only.
4.3 Relevance of findings regarding policy implications
Based on these results, key policy implications can be highlighted. This contributes to better understanding current and future challenges of how to manage e-waste streams in a sound way.
First, since the relationship between e-waste recycling rate and economic growth in European countries displays an N-shaped pattern, the challenge of ensuring sound e-waste management becomes more acute while economies are maturing. Existing measures are insufficient to stabilize or continuously increase the e-waste recycling rate of growing economies. Maturing economies display below average recycling rates and therefore miss an important opportunity to abate environmental pressure. High recycling rates also stimulate economic growth (Di Vita, 2001; George et al., 2015) and therefore are not only to be favored under environmental criteria but also under economic aspects. Where e-waste recycling rates are low, an important opportunity is missed to harness economic value for a country or region. In this context, it is important to note that the first EKC turning point occurs at relatively low GDP levels, i.e., at early stages of economic maturity already. To alleviate a decline of the recycling rate in maturing economies, governments should increase their investment in waste management infrastructures (especially for the implementation and operation of recycling centers). Furthermore, governments should allocate more financial resources through programs which explicitly encourage the private sector to invest in e-waste treatment schemes. The regression analysis of this study revealed that the e-waste recycling rate is significantly impacted by credit to the private sector.
Second, the key effect of e-waste collection on the recycling rate should be noted. The regression analysis conducted in this study identified e-waste collection as an important determinant of the e-waste recycling rate regardless of whether the current recycling rate is at a low, medium or high level (a significant impact of e-waste collected on the recycling rate was found for all quantiles in the regression). Europe already has higher average e-waste collection rates than other regions, but the collection rates are still far from being satisfactory: The Global E-waste Monitor 2020 identified that 57.5% of the e-waste quantity generated across Europe remained uncollected in 2019 (Forti et al., 2020). The EU target collection rate of 85% of total e-waste generated has only been reached by Croatia (Baldé et al., 2020). Therefore, a key contribution to raising the rate of e-waste recycling across Europe can be made by increasing the number of e-waste collection points and by improving the effectivity of collection schemes. Thus, more attention is needed from European governments to foster e-waste collection in every country, i.e., regardless of whether the country has a lower or higher economic development stage and whether the country currently has a lower or higher e-waste recycling rate. Progress is required for all countries; however, in this context, especially wealthier nations should make more rapid progress in assuming their responsibility to manage e-waste in a sound way. The results of this research confirm that mature economies are more stable regarding their efforts to mitigate environmental pressure from e-waste, but the currently achieved recycling rates are not sufficient.
Third, increasing the e-waste recycling rate is an important priority topic for policy makers to address the challenge of sound e-waste management, but it should be noted that it is not the only priority topic in this complex context. This research focused explicitly on the recycling rate, and a solid knowledge base has been elaborated to better understand the determinants of the recycling rate. However, it is important to highlight that a focus on increasing the recycling rates should not deviate the attention of policy makers from the equally urgent challenge to reduce the actual generation of e-waste. Waste prevention stands on top of the waste management hierarchy and is thus a key element to advance toward more circular economies. In the e-waste context, extending the lifetime of electrical and electronic products, for example through more durable assemblies, or through repair, refurbishment or remanufacturing schemes, is a top priority regarding more sustainable usage of technical equipment and reduced e-waste occurrence. Resource efficient production processes and efficient usage of equipment are other relevant sustainability factors. Overall, recycling is an important, but not the only element to be considered when aiming for a society with reduced adverse environmental impacts.
4.4 Limitations of the study and further research needs
Although this study provides strong evidence for the determinants of the e-waste recycling rate in European countries, there are some limitations on the empirical side. The study period in this work spans more than a decade; however, this is still relatively short for an econometric analysis of this scope. The relative shortness of the study period is due to a still limited availability of reliable data over time. As more data become available over time, future research should analyze a longer period for European countries. Furthermore, this study does not allow conclusions on whether the observations made for Europe also apply to other regions. Therefore, further research should aim to expand the analysis to other regions. However, reliability of the data used including consistency of the data collection method used across different countries must be ensured, and this will be more challenging for regions other than Europe, where EU regulations have harmonized data collection and reporting procedures. Moreover, future research could utilize other recycling rates such as the rates for municipal waste, packaging waste or plastic waste to further test the EKC hypothesis on the solid waste recycling rate.
5 Conclusions
To examine the main driving forces of the e-waste recycling rate, unbalanced panel data over the period 2008–2018 from 30 European countries were analyzed in the framework of the EKC hypothesis and the STIRPAT model, employing panel quantile regression with non-additive fixed effects as main econometric approach and traditional pooled OLS regression for comparison purposes. This study provides new and robust results regarding the main e-waste recycling rate drivers. Thus, the work contributes to a field which so far has received little attention in the environmental economics literature and at the same time is highly relevant with view to reducing adverse impacts on the environment.
Independent variables of this study were GDP per capita, population, population density, energy intensity, energy efficiency, credit to private sector and e-waste collected; the impact of these variables on the dependent variable e-waste recycling rate was investigated through regression analysis. Clearly, GDP per capita was the most influential factor to determine the e-waste recycling rate. More specifically, the empirical findings provide strong support that the relationship between economic growth and e-waste recycling rate is an N-shaped curve for the European countries under study, i.e., as economy grows in a country, the e-waste recycling rate first increases rapidly, then decreases (turning point) and finally increases again (second turning point). This is the first study to have tested the EKC hypothesis on e-waste recycling, and very robust results regarding the existence of an N-shaped relationship were found. The first EKC turning point reflects increasing pressure on the environment (due to a decline in the recycling rate), while the second turning point signals that pressure on the environment will decrease again in very mature economies (because of an increasing recycling rate). It is a positive finding that e-waste recycling rates start increasing again when countries become economically mature; however, path of the e-waste recycling rate increase is slow after having crossed the second turning point, and current recycling rates in wealthy countries are too low to be satisfactory. This calls for more effective engagement of policy makers to proactively increase e-waste recycling rates.
In addition to GDP per capita, the regression results showed that the variables e-waste collected, population, energy intensity and credit to private sector all had a statistically significant effect (1% level of significance) on the e-waste recycling rate. Among these variables, the most relevant effect was found for e-waste collection (positive correlation with e-waste recycling rate), and this effect applied to all regression quantiles under study (all countries), i.e., regardless of whether the already achieved e-waste recycling rate in a country was low, medium or high. Population size, energy intensity and credit to private sector were negatively correlated with the e-waste recycling rate, i.e., an increase in these parameters meant a decline of the recycling rate. In addition, in contrast to GDP and e-waste collection rate, the impact of population size, energy intensity and credit to private sector was clearly heterogeneous across the quantiles; these variables were more relevant as determinants of the e-waste recycling rate for countries where the so far achieved recycling rate was lower.
Overall, the quantile regression showed that for above mean quantile countries (especially the 75th percentile), i.e., for countries where higher recycling rates have already been achieved, GDP per capita strengthens its dominant role as most important driver of the recycling rate. In low-quantile countries, GDP is the most important determinant as well, but the other explanatory and control variables (population size, energy intensity, e-waste collection, credit to private sector) come into play more effectively compared to the upper quantile countries. Mature economies among the set of 30 European countries under study typically have above average recycling rates, and thus, for those countries, the change in recycling rate will particularly strongly depend on GDP change. E-waste collection is an important driver in all quantiles. Thus, in all countries, governments should increase their efforts to effectively increase the collection of e-waste (e.g., more collection points, better performing collection schemes).
When testing population density as an alternative to population size as variable to account for demographic factors, the explanatory power of population density was low. Among the variables accounting for technology, the explanatory power of energy efficiency (in terms of total primary energy consumption) was rather low, while energy intensity (in terms of energy consumption per GDP) was a more meaningful choice. Therefore, in this research the alternative variables population density and energy efficiency were not found to be suitable choices when investing the main determinants of the e-waste recycling rate.
Further research must clarify whether the N-shaped relationship between GDP per capita and e-waste recycling rate and also applies to other regions. For Europe, it is concluded that maturing economies have a risk of experiencing a declining recycling rate while their economy grows, while a regrowth of the recycling rate can be expected for mature economies, albeit at a rather slow path. Policy makers should be aware of the N-shaped curve between recycling rate and economic growth and thus the increased efforts required to ensure high e-waste recycling rates also at growing and elevated GDP levels. Proactive engagement of policy makers is required in both maturing and mature economies. In this context, e-waste collection merits high attention as a promising area of effective governmental intervention; it represents a key determinant of the e-waste recycling rate, and it can be directly influenced through the implementation of adequate e-waste management schemes.
Availability of data and materials
The data used have been extracted from publicly accessible databases, as indicated in the manuscript.
References
Adshead, D., Thacker, S., Fuldauer, L. I., & Hall, J. W. (2019). Delivering on the sustainable development goals through long-term infrastructure planning. Global Environmental Change, 59, 101975.
Albulescu, C. T., Tiwari, A. K., Yoon, S.-M., & Kang, S. H. (2019). FDI, income, and environmental pollution in Latin America: Replication and extension using panel quantiles regression analysis. Energy Economics, 84, 104504.
Allard, A., Takman, J., Uddin, G. S., & Ahmed, A. (2018). The N-shaped environmental Kuznets curve: An empirical evaluation using a panel quantile regression approach. Environmental Science and Pollution Research, 25, 5848–5861.
Al-Mulali, U., Weng-Wai, C., Sheau-Ting, L., & Mohammed, A. H. (2015). Investigating the environmental Kuznets curve (EKC) hypothesis by utilizing the ecological footprint as an indicator of environmental degradation. Ecological Indicators, 48, 315–323.
Antoni, G. D., & Marzetti, G. V. (2019). Recycling and waste generation: An estimate of the source reduction effect of recycling programs. Ecological Economics, 161, 321–329.
Arbulu, I., Lozano, J., & Rey-Maquieira, J. (2016). Waste generation flows and tourism growth: A STIRPAT model for Mallorca. Journal of Industrial Ecology, 21(2), 1–10.
Asumadu, S. S., & Vladimir, S. (2019). A review on environmental Kuznets curve hypothesis using bibliometric and meta-analysis. Science of the Total Environment, 649, 128–145.
Awasthi, A. K., Cucchiella, F., D’Adamo, I., Li, J., Rosa, P., Terzi, S., Wei, G., & Zeng, X. (2018). Modelling the correlations of e-waste quantity with economic increase. Science of the Total Environment, 613–614, 46–53.
Baldé, C. P., Forti, V., Gray, V., Kuehr, R., & Stegmann, P. (2017). The global e-waste monitor 2017. United Nations University (UNU), International Telecommunication Union (ITU) & International Solid Waste Association (ISWA).
Baldé, C. P., Wagner, M., Iattoni, G., & Kuehr, R. (2020). In-depth review of the WEEE collection rates and targets in the EU-28, Norway, Switzerland, and Iceland. United Nations University (UNU)/United Nations Institute for Training and Research (UNITAR)—co-hosting the SCYCLE Programme.
Baldé, C. P., Wang, F., Kuehr, R., & Huisman, J. (2015). The global e-waste monitor 2014: Quantities, flows and resources. United Nations University, IAS—SCYCLE.
Barnes, S. (2019). Understanding plastics pollution: The role of economic development and technological research. Environmental Pollution, 249, 812–821.
Bezzina, F. H., & Dimech, S. (2011). Investigating the determinants of recycling behaviour in Malta. Management of Environmental Quality: An International Journal, 22(4), 463–485.
Boubellouta, B., & Kusch-Brandt, S. (2020). Testing the environmental Kuznets curve hypothesis for e-waste in the EU28+2 countries. Journal of Cleaner Production, 277, 123371.
Boubellouta, B., & Kusch-Brandt, S. (2021a). Cross-country evidence on environmental Kuznets curve in waste electrical and electronic equipment for 174 countries. Sustainable Production and Consumption, 25, 136–151.
Boubellouta, B., & Kusch-Brandt, S. (2021b). Relationship between economic growth and mismanaged e-waste: Panel data evidence from 27 EU countries analyzed under the Kuznets curve hypothesis. Waste Management, 120, 85–97.
Boubellouta, B., & Kusch-Brandt, S. (2022). Determinants of e-waste composition in the EU28 + 2 countries: A panel quantile regression evidence of the STIRPAT model. International Journal of Environmental Science and Technology. https://doi.org/10.1007/s13762-021-03892-0
Canay, I. A. (2011). A note on quantile regression for panel data models. The Econometrics Journal, 14, 368–386.
Cerqueira, P. A., Soukiazis, E., & Proença, S. (2021). Assessing the linkages between recycling, renewable energy and sustainable development: Evidence from the OECD countries. Environment, Development and Sustainability, 23, 9766–9791.
Chen, W., & Lei, Y. (2018). The impacts of renewable energy and technological innovation on environment-energy-growth nexus: New evidence from a panel quantile regression. Renewable Energy, 123, 1–14.
Cheng, J., Shi, F., Yi, J., & Fu, H. (2020). Analysis of the factors that affect the production of municipal solid waste in China. Journal of Cleaner Production, 259, 120808.
Churchill, S. A., Inekwe, J., Ivanovski, K., & Smyth, R. (2021). Transport infrastructure and CO2 emissions in the OECD over the long run. Transportation Research Part D: Transport and Environment, 95, 102857.
Danish, K., Ozcan, B., & Ulucak, R. (2021). An empirical investigation of nuclear energy consumption and carbon dioxide (CO2) emission in India: Bridging IPAT and EKC hypotheses. Nuclear Engineering and Technology, 53(6), 2056–2065.
Di Vita, G. (2001). Technological change, growth and waste recycling. Energy Economics, 23, 549–567.
Diao, X. D., Zeng, S. X., Tam, C. M., & Tam, V. (2009). EKC analysis for studying economic growth and environmental quality: A case study in China. Journal of Cleaner Production, 17, 541–548.
Dickey, D. A., & Fuller, W. A. (1979). Distribution of the estimators for autoregressive time series with a unit root. Journal of American Statistical Association, 74(366), 427–431.
Dietz, T., & Rosa, E. A. (1994). Rethinking the environmental impacts of population, affluence and technology. Human Ecology Review, 1, 277–300.
Dietz, T., & Rosa, E. A. (1997). Effects of population and affluence on CO2 emissions. Proceedings of the National Academy of Sciences, 94, 175–179.
Ehrlich, P. R., & Holdren, J. P. (1971). Impact of population growth. Science, 171(80), 1212–1217.
Escario, J., Rodriguez-Sanchez, C., & Casaló, L. V. (2020). The influence of environmental attitudes and perceived effectiveness on recycling, reducing, and reusing packaging materials in Spain. Waste Management, 113, 251–260.
European Commission. (2016). Country Report Luxembourg 2016. Commission Staff Working Document, European Commission, Brussels, Belgium. Available online. Retrieved July 22, 2021, from https://ec.europa.eu/info/sites/info/files/cr_luxembourg_2016_en.pdf
Eurostat. (2021). Data from the European Statistics Recovery Dashboard database, European Commission. Retrieved February 15, 2021, from https://ec.europa.eu/eurostat/data/database
Fischer-Kowalski, M., & Amann, C. (2001). Beyond IPAT and Kuznets curves: Globalization as a vital factor in analysing the environmental impact of socio-economic metabolism. Population and Environment, 23(1), 7–47.
Forti, V., Baldé, C. P., Kuehr, R., & Bel, G. (2020). The global e-waste monitor 2020: Quantities, flows and the circular economy potential. United Nations University (UNU)/United Nations Institute for Training and Research (UNITAR)—co-hosted SCYCLE Programme, International Telecommunication Union (ITU) & International Solid Waste Association (ISWA).
Gellynck, X., Jacobsen, R., & Verhelst, P. (2011). Identifying the key factors in increasing recycling and reducing residual household waste: A case study of the Flemish region of Belgium. Journal of Environmental Management, 92, 2683–2690.
George, D. A. R., Chi-ang Lin, B., & Chen, Y. (2015). A circular economy model of economic growth. Environmental Modelling and Software, 73, 60–63.
Grossman, G. M., & Krueger, A. B. (1991). Environmental impacts of a North American Free Trade Agreement. National Bureau of Economic Research, Working Paper 3194, Cambridge.
Grossman, G. M., & Krueger, A. B. (1995). Economic growth and the environment. The Quarterly Journal of Economics, 110(2), 353–377.
Han, X., Hu, C., & Lin, L. (2020). A study on the impact of China’s urbanization on the quantity of municipal solid waste produced. Waste Management and Research, 38(2), 184–192.
Hashmi, R., & Alam, K. (2019). Dynamic relationship among environmental regulation, innovation, CO2 emissions, population, and economic growth in OECD countries: A panel investigation. Journal of Cleaner Production, 231, 1100–1109.
Huang, J., Zhang, S., Zou, Y., Tai, J., Shi, Y., Fu, B., Zhao, J., & Qian, G. (2021). The heterogeneous time and income effects in Kuznets curves of municipal solid waste generation: Comparing developed and developing economies. Science of the Total Environment, 799, 149157.
Huisman, J. (2010). WEEE recast: From 4 kg to 65%: The compliance consequences. United Nations University.
Hummel, D., & Lux, A. (2007). Population decline and infrastructure: The case of the German water supply system. Vienna Yearbook of Population Research, 5, 167–191.
Im, K. S., Pesaran, M. H., & Shin, Y. (2003). Testing for unit roots in heterogeneous panels. Journal of Econometrics, 115, 53–74.
Islam, R., Nazifa, T. H., Yuniarto, A., Uddin, A. S. M. S., Salmiati, S., & Shahid, S. (2019). An empirical study of construction and demolition waste generation and implication of recycling. Waste Management, 95, 10–21.
Jaligot, R., & Chenal, J. (2018). Decoupling municipal solid waste generation and economic growth in the canton of Vaud, Switzerland. Resources, Conservation and Recycling, 130, 260–266.
Jenkins, R. R., Martinez, S. A., Palmer, K., & Podolsky, M. (2003). The determinants of household recycling: A material-specific analysis of recycling program features and unit pricing. Journal of Environmental Economics and Management, 45(2), 294–318.
Kasioumi, M. (2021). The environmental Kuznets curve: Recycling and the role of habit formation. Review of Economic Analysis, 13, 367–387.
Kasioumi, M., & Stengos, T. (2020). The environmental Kuznets curve with recycling: A partially linear semiparametric approach. Journal of Risk and Financial Management, 13, 274.
Kilbourne, W. E., & Thyroff, A. (2020). STIRPAT for marketing: An introduction, expansion, and suggestions for future use. Journal of Business Research, 108, 351–361.
Kirakozian, A. (2016). The determinants of household recycling: Social influence, public policies and environmental preferences. Applied Economics, 48, 1481–1503.
Koenker, R. (2004). Quantile regression for longitudinal data. Journal of Multivariate Analysis, 91(1), 74–89.
Koenker, R., & Bassett, G. (1978). Regression quantiles. Econometrica, 46(1), 33–50.
Koenker, R., & Bassett, G. (1982). Tests of linear hypotheses and l″1 estimation. Econometrica, 50(6), 1577–1583.
Kumar, A., Holuszko, M., & Espinosa, D. C. R. (2017). E-waste: An overview on generation, collection, legislation and recycling practices. Resources, Conservation and Recycling, 122, 32–42.
Kusch, S., & Hills, C. D. (2017). The link between e-waste and GDP—New insights from data from the Pan-European region. Resources, 6, 15.
Kuznets, S. (1955). Economic growth and income inequality. The American Economic Review, 45(1), 1–28.
Levin, A., Lin, C. F., & Chu, C. S. J. (2002). Unit root tests in panel data: Asymptotic and finite sample properties. Journal of Econometrics, 108(1), 1–24.
Liddle, B. (2014). Impact of population, age structure, and urbanization on carbon emissions/energy consumption: Evidence from macro-level, cross-country analyses. Population and Environment, 35(3), 286–304.
Liu, Y., Park, S., Yi, H., & Feiock, R. (2020). Evaluating the employment impact of recycling performance in Florida. Waste Management, 101, 283–290.
Magazzino, C. (2016a). Is per capita energy use stationary? Panel data evidence for the EMU countries. Energy Exploration & Exploitation, 34(3), 440–448.
Magazzino, C. (2016b). Is per capita energy use stationary? Time series evidence for the EMU countries. Energy Exploration & Exploitation, 35(1), 24–32.
Magazzino, C., Mele, M., & Schneider, N. (2020). The relationship between municipal solid waste and greenhouse gas emissions: Evidence from Switzerland. Waste Management, 113, 508–520.
Magazzino, C., Mele, M., Schneider, N., & Sarkodie, S. A. (2021). Waste generation, wealth and GHG emissions from the waste sector: Is Denmark on the path towards circular economy? Science of the Total Environment, 755(Part 1), 142510.
Morley, J., Widdicks, K., & Hazas, M. (2018). Digitalisation, energy and data demand: The impact of Internet traffic on overall and peak electricity consumption. Energy Research & Social Science, 38, 128–137.
Namlis, K., & Komilis, D. (2019). Influence of four socioeconomic indices and the impact of economic crisis on solid waste generation in Europe. Waste Management, 89, 190–200.
Önder, H. (2018). The socio-economic determiners of recycling: An analysis on European countries through a macro perspective. Amfiteatru Economic Journal, 20(48), 405–417.
Panayotou, T. (1993). Empirical test and policy analysis of environmental degradation at different stages of economic development. World Employment Research Programme, Working Paper WP238, International Labour Office, Geneva.
Panayotou, T. (1997). Demystifying the environmental Kuznets curve: Turning a black box into a policy tool. Environment and Development Economics, 2, 465–464.
Park, S., & Berry, F. S. (2013). Analyzing effective municipal solid waste recycling programs: The case of county-level MSW recycling performance in Florida, USA. Waste Management & Research: The Journal for a Sustainable Circular Economy, 31, 896–901.
Park, S., & Lah, T. J. (2015). Analyzing the success of the volume-based waste fee system in South Korea. Waste Management, 43, 533–538.
Pata, U. K. (2018a). Renewable energy consumption, urbanization, financial development, income and CO2 emissions in Turkey: Testing EKC hypothesis with structural breaks. Journal of Cleaner Production, 187, 770–779.
Pata, U. K. (2018b). The influence of coal and noncarbohydrate energy consumption on CO2 emissions: Revisiting the environmental Kuznets curve hypothesis for Turkey. Energy, 160, 1115–1123.
Pata, U. K. (2021). Renewable and non-renewable energy consumption, economic complexity, CO2 emissions, and ecological footprint in the USA: Testing the EKC hypothesis with a structural break. Environmental Science and Pollution Research, 28, 846–861.
Pata, U. K., & Caglar, A. E. (2021). Investigating the EKC hypothesis with renewable energy consumption, human capital, globalization and trade openness for China: Evidence from augmented ARDL approach with a structural break. Energy, 2016, 119220.
Pata, U. K., & Isik, C. (2021). Determinants of the load capacity factor in China: A novel dynamic ARDL approach for ecological footprint accounting. Resources Policy, 74, 102313.
Phillips, P. C. B., & Perron, P. (1988). Testing for a unit root in time series regression. Biometrika, 75(2), 335–346.
Ponomareva, M. (2010). Quantile regression for panel data models with fixed effects and small T: Identification and estimation. Working Paper, University of Western, Ontario.
Powell, D. (2014). Did the economic stimulus payments of 2008 reduce labor supply? Evidence from quantile panel data estimation. Working Paper WR-710-3, RAND Corporation.
Powell, D. (2016). Quantile regression with nonadditive fixed effects. RAND Corporation.
Razzaq, A., Sharif, A., Najmi, A., Tseng, M., & Lim, M. K. (2021). Dynamic and causality interrelationships from municipal solid waste recycling to economic growth, carbon emissions and energy efficiency using a novel bootstrapping autoregressive distributed lag. Resources, Conservation and Recycling, 166, 105372.
Richter, A., Tsun Wai Ng, K., Karimi, N., & Chang, W. (2021). Developing a novel proximity analysis approach for assessment of waste management cost efficiency in low population density regions. Sustainable Cities and Society, 65, 102583.
Rosen, A. M. (2012). Set identification via quantile restrictions in short panels. Journal of Econometrics, 166(1), 127–137.
Royston, P. (1992). Approximating the Shapiro-Wilk W-Test for non-normality. Statistics and Computing, 2(3), 117–119.
Sakai, S., Ikematsu, T., Hirai, Y., & Yoshida, H. (2008). Unit-charging programs for municipal solid waste in Japan. Waste Management, 28, 2815–2825.
Saphores, J. D. M., & Nixon, H. (2014). How effective are current household recycling policies? Results from a national survey of U.S. households. Resources, Conservation and Recycling, 92, 1–10.
Sebri, M. (2015). Testing the environmental Kuznets curve hypothesis for water footprint indicator: A cross-sectional study. Journal of Environmental Planning and Management, 59(11), 1933–1956.
Shah, R. V., & Guha, S. (2021). Private sector participation in solid waste management and regulatory strategy. Economic & Political Weekly, 56(32), 95–101.
Shahbaz, M., Loganathan, N., Muzaffar, A. T., Ahmed, K., & Jabran, M. A. (2016). How urbanization affects CO2 emissions in Malaysia? The application of STIRPAT model. Renewable and Sustainable Energy Reviews, 57, 83–93.
Shinkuma, T. (2003). On the second best policy of household’s waste recycling. Environmental and Resource Economics, 24, 77–95.
Sidique, S. F., Joshi, S. V., & Frank Lupi, F. (2010). Factors influencing the rate of recycling: An analysis of Minnesota counties. Resources, Conservation and Recycling, 54, 242–249.
Song, Q., Zhao, S., Lam, I., Zhu, L., Yuan, W., & Wang, C. (2019). Understanding residents and enterprises’ perceptions, behaviors, and their willing to pay for resources recycling in Macau. Waste Management, 95, 129–138.
Thio, E., Tan, M., Li, L., Salman, M., Long, X., Sun, H., & Zhu, B. (2021). The estimation of influencing factors for carbon emissions based on EKC hypothesis and STIRPAT model: Evidence from top 10 countries. Environment, Development and Sustainability. https://doi.org/10.1007/s10668-021-01905-z
Turner, D. A., Williams, I. D., & Kemp, S. (2015). Greenhouse gas emission factors for recycling of source-segregated waste materials. Resources, Conservation and Recycling, 105, 186–197.
Vélez-Henao, J. A., Vivanco, D. F., & Hernández-Riveros, J. A. (2019). Technological change and the rebound effect in the STIRPAT model: A critical view. Energy Policy, 129, 1372–1381.
Wang, K., Zhu, Y., & Zhang, J. (2021). Decoupling economic development from municipal solid waste generation in China’s cities: Assessment and prediction based on Tapio method and EKC models. Waste Management, 133, 37–48.
Wang, Z., Bu, C., Li, H., & Wei, W. (2019). Seawater environmental Kuznets curve: Evidence from seawater quality in China’s coastal waters. Journal of Cleaner Production, 219, 925–935.
Willis, K. A., Hardesty, B. D., & Wilcox, D. (2021). State and local pressures drive plastic pollution compliance strategies. Journal of Environmental Management, 287, 112281.
World Bank. (2021). Data from the database of the World Bank. Retrieved February 15, 2021, from https://data.worldbank.org
Xu, B., & Lin, B. (2020). Investigating drivers of CO2 emission in China’s heavy industry: A quantile regression analysis. Energy, 206, 118159.
Xu, F., Huang, Q., Yue, H., He, C., Wang, C., & Zhang, H. (2020). Reexamining the relationship between urbanization and pollutant emissions in China based on the STIRPAT model. Journal of Environmental Management, 273, 111134.
Xu, R., Xu, L., & Xu, B. (2017). Assessing CO2 emissions in China’s iron and steel industry: Evidence from quantile regression approach. Journal of Cleaner Production, 152, 259–270.
Yeh, J., & Liao, C. (2017). Impact of population and economic growth on carbon emissions in Taiwan using an analytic tool STIRPAT. Sustainable Environment Research, 27, 41–48.
Yla-Mella, J., & Roman, E. (2019). Waste electrical and electronic equipment management in Europe: Learning from best practices in Switzerland, Norway, Sweden and Denmark. In V. Goodship, A. Stevels, & J. Huisman (Eds.), Waste electrical and electronic equipment (WEEE) handbook, Woodhead Publishing series in electronic and optical materials, Duxford et al (2nd ed., pp. 483–519). Woodhead Publishing.
Zen, I. S., & Siwar, C. (2015). An analysis of household acceptance of curbside recycling scheme in Kuala Lumpur, Malaysia. Habitat International, 47, 248–255.
Zhu, H., Duan, L., Guo, Y., & Yu, K. (2016). The effects of FDI, economic growth and energy consumption on carbon emissions in ASEAN-5: Evidence from panel quantile regression. Economic Modelling, 58, 237–248.
Funding
Open Access funding enabled and organized by Projekt DEAL. This research received funding from the Directorate General for Scientific Research and Technological Development (DG-RSDT) Algeria (Direction générale de la recherche scientifique et du développement technologique (DG-RSDT) Algérie).
Author information
Authors and Affiliations
Contributions
BB and SK-B were responsible for conceptualization, formal analysis and investigation, preparing and writing the original draft, and writing, reviewing and editing; and BB was involved in methodology and funding acquisition.
Corresponding author
Ethics declarations
Conflict of interest
The authors have no relevant financial or non-financial interests to disclose.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Boubellouta, B., Kusch-Brandt, S. Driving factors of e-waste recycling rate in 30 European countries: new evidence using a panel quantile regression of the EKC hypothesis coupled with the STIRPAT model. Environ Dev Sustain 25, 7533–7560 (2023). https://doi.org/10.1007/s10668-022-02356-w
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10668-022-02356-w