Reconcilement of conflicting goals: a novel operations research-based methodology for environmental management

Abstract

The elements of the supply and environmental chain are identified and connected through an operations research process. A framework is developed to include these chains into a process that deals with operations research problems within two different, complex areas: economic (supply) and natural systems (environmental), and emphasizes the influence of the solution on both systems and their performance. The framework helps researchers to get a better insight into the issues considering both environmental and industry aspects. The study proposes a causal relationship between the supply chain and environmental chain and begins to make a bridge between these two chains using operations research methods and techniques. In this context, a multi-period scenario-based stochastic model is developed. To deal with the uncertainties and to investigate the trade-offs between the objective functions, an interactive fuzzy multi-objective method is performed. In the case study section, reconcilement of the conflicting objectives in a waste management case is questioned and the future recommendations are highlighted.

1 Introduction

An environment is a place rich with dynamic cultural, social, economic, political, historical contexts and perspectives that frame and construct the ecological processes within them (Cole, 2007). Population growth and industrial production consequently lead to pollution increase, land degradation, habitat fragmentation and unsustainable consumption and thus jeopardize the integrity of the global ecosystem of planet Earth.

The Club of Rome in its study The Limits to Growth (Meadows et al., 1972) drew attention by pointing out the finite resource supplies and predicted exhaustion of the several major resources within decades. Two decades later, the same authors published another book—Beyond the Limits (Meadows et al., 1992), and argued that the 1972 warnings were broadly correct, that some of the limits have already been exceeded, and that, if current trends continue, there is virtually certain to be global collapse within the lifetime of children alive today (Barrow, 2006). If a resource becomes scarcer, the price will tend to rise, promoting the search for discoveries and inducing reductions in demand (European Commission, 2012). But the threat of depletion remains. What drives these efforts to bring all stakeholders together to negotiate solutions to critical problems in natural resource management still needs further research (Hossu et al., 2018).

Environmental problems, which are the focus of our research, are characteristic for several reasons often, only the initial state of the problem is known and can be described more or less in detail. To proceed from the initial state to possible solutions, researchers must surmount multiple barriers. With environmental problems, target spaces (usually not well defined) rather than well-defined targets should be considered (Scholz et al., 1997). Problem formulation is of fundamental importance for the success of operations research applications (Krčevinac et al., 2013) in each research area, and in environmental research as well.

The interaction between any part of the industry and any part of the environment can initiate environmental problems. Thus, it is important to highlight and observe this interaction, as it indicates various environmental problems. The purpose of this study is to design a framework that will lead researchers and practitioners throughout the whole process of environmental operations research (OR) problem identification, problem analysis and problem-solving by operations research models and methods. The research question of this study refers to the statement: can the conflicting goals of the environmental issues in the operations research discipline be reconciled using OR methods for solving environmental problems. It is shown in the solid waste location case study presented in this paper that the compromise between conflicting goals of both economic and environmental concerns is achieved.

The rest of this paper is organized as follows: Sect. 2 examines a literature review regarding environmental concerns and specifics of natural resources, their functions and classification. Environmental operations research is described in Sect. 4. This section presents also the methodology, where a new conceptual framework for defining interaction between operations research and environmental management is given. A numerical example is given in this section. Section 5 provides concluding remarks and future research trends.

2 Literature review

Environmental management demands awareness that issues may be part of complex transnational, economic and social interactions (Barrow, 2006). Companies worldwide are continuously looking for a competitive edge and environmental issues are often put aside. In effect, environmental aspects are at risk of becoming a future burden if their effects cannot be identified and quantified in the same manner as time and costs (Aronsson & Brodin, 2006).

Today’s social concern has shifted towards the degradation of environmental resources. The world and its resources are finite, yet human demands continue to increase. The ultimate goal of environmental management is to address this issue and to seek sustainable development (Barrow, 2006).

Natural resources are the base of all activities and the survival of the human race itself. The field of natural resources includes a variety of areas related to agriculture, forestry, mining and water resources. According to Miranda (2007), the areas usually viewed within the natural resources field are agriculture, fisheries, forestry, mining and water resources.

The new awareness of the need to preserve natural habitats, protect endangered species, provide water and air quality, and promote biodiversity has come into the focus of researchers (Foley et al., 2005; Pimm et al., 2014; Salzman et al., 2001; Scherr & McNeely, 2008). This has often led to serious conflicts between production goals (with the need to derive efficient production processes) and environmental impacts, with increased public participation in decision processes. A wide variety of management science and operations research models have been used by policymakers and analysts throughout the public sector to gain insights into important problems that deal with the management of fish, forests, wildlife, and water (Golden & Wasil, 1994).

Resources provide the raw material used to produce goods and services, and this is one of two basic natural resources functions. It is often referred to as a source function. On the other hand, natural resources or the environment function can be a receiving medium for the waste originating from production and consumption and this function is often referred to as the sink function. Natural resource management applies scientific knowledge to identify, analyse and solve problems in this field regardless of the function or a type of resource, but considering the two effects that are of the most interest (European Commission, 2012)—depletion of resources and degradation of resources. Depletion of resources may be a result of over-exploitation of renewable resources, as use will reduce the total stock of non-renewable resources. The waste or side effects of consumption and production processes may degrade natural resources and a reduction in the level of physical and environmental services will result.

It is important to recognize that not all resources share the same characteristics. Some resources require a relatively minimal investment in extraction equipment, but other resources may require extensive investment in production technology (Lujala, 2003). For a better understanding of the natural resources industry and its aspects, two common classifications of natural resources are presented in Table 1.

Table 1 Classifications of natural resources

These two classifications are based on regeneration rate and besides this classification, there exists another classification based on the geographical concentration, and an interesting combination of these two classifications is given in Lujala (2003).

Regardless of the similarities and differences between the various types of natural resources, it is essential to ensure their efficient use, best protection and preservation. This can be achieved by conducting an efficient decision-making process in natural resources management, as shown in Fig. 1 (Tóth, 2015). Natural management and social science are overlapping in the whole decision-making process throughout three parts of the process with a different focus:

• Natural science focuses on data collection and processing using remote sensing, field surveys, permanent plots and questionnaires. Researchers and experts collect data regarding all the essential characteristics of the analysed problem and formulate adequate relations between them. In this way, the best input data are formed and used as input for the next part of the process.

• Management science focuses on decision tools and the generation of alternatives using management science methods and techniques such as optimization, simulation, finance tools, etc. To formulate a model (such as an optimization or simulation model) and obtain the optimal solution of the initial problem, the crucial step is to determine the essential characteristics of the phenomena being analysed and to extract the data in the required form. This is the area where natural and management science overlap and where researchers and scientists must cooperate and coordinate their research activities.

• Social science focuses on the demonstration and visualization of the alternatives, assess impacts of interventions and justifies the choice of interventions. Urban planning, public policy and some elements of environmental science are also the contribution of the social science in this area. The optimal solution or the alternatives generated in the process are now even further analysed using methods and techniques such as Delphi or Nominal group technique.

Fig. 1

The decision-making process in natural resources management (Tóth, 2015)

The output from the decision-making process is a decision based on knowledge from different fields of expertise. This efficient process leads to efficient usage and planning of resources (consumption rates and emissions) which prevent further deterioration of the environment in the future and removes or reduces existing damage where and when is possible. In this paper, we focus on the management science tool of mathematical programming to explore a wide range of modelling offers a full range of modelling techniques for modelling the interaction between man and the environment taking into account all activities related to natural resources and their use, to find alternative courses of action, and to obtain optimal solutions for various problems.

A great number of papers regarding the application of operations research in the field of natural resources are published: in the field of agriculture (Agrell et al., 2004; Andrić-Gušavac et al., 2014, 2019; Castrodeza et al., 2005; Epstein et al., 2007; Hameed et al., 2013; Hayashi, 2000; Marchamalo & Romero, 2007; Pacini et al., 2004; Peña et al., 2007; Romero, 2000; Romero & Rehman, 2003; Sørensen & Bochtis, 2010; Weintraub & Romero, 2006; Zekri & Boughanmi, 2007), forestry (Andalaft et al., 2003; Bjørndal et al., 2012; Church, 2007; Conrad et al., 2012; Gunn, 2007; Heinonen et al., 2009; Könnyű & Tóth, 2013; McDill et al., 2002; Tóth et al., 2011), water resources (Björndal et al., 2004; Herrero & Pascoe, 2003; Pascoe et al., 2001), and mining (Alford et al., 2007; Caccetta, 2007; Newman et al., 2010; Ramazan, 2007).

Authors in Bloemhof-Ruwaard et al. (1995) propose two ways of looking at the interaction between operations research and environment management:

• Impact on the supply chain. There is a need to adapt operations research tools to deal adequately with a new situation requiring green supply chain modelling.

• Impact on the environmental chain. The amount of waste and the level of emissions caused by the supply chain results in several serious environmental effects, such as global warming and acid rain. The interaction between operations research and environmental management can result in a clear formulation of these problems and new insights into the impacts of alternative policy measures.

The framework considering the supply chain and the environmental chain is presented in Fig. 2 and points out opportunities for operations research.

Fig. 2

The framework considers the supply chain and the environmental chain (Bloemhof-Ruwaard et al., 1995)

Literature regarding the supply chain includes the following phases: extraction of raw materials, manufacturing, distribution and the final use of goods. Waste, generated in each phase of the supply chain, is collected at the end of the chain. The supply chain causes emissions and waste which are transported and transformed and emitted into the water, air and soil pollution with damaging effects on the environment.

Literature regarding the environmental chain follows production activities that are focused on preventing or controlling of side effects of pollution. On the other hand, literature regarding the environmental chain follows human influence on the ecosystem. Any activity in the supply chain can harm the environment. And, at the same time, any disbalance of the ecosystem can have an impact on the production activities in the supply chain (Bloemhof-Ruwaard et al., 1995). Humans must find an alternative to their ingrained behaviour of burdening future generations resulting from our misplaced belief that there is a choice between the economy and the environment (Caccia, 1986). Daniel et al. (1997) suggest an extension of the framework presented in Fig. 2 by adding two phases (see Fig. 3):

• observation analysis and

• solution identification.

Fig. 3

Extension of the framework (Daniel et al., 1997)

No strict boundaries exist between the two stages presented in Fig. 2 since the information provided by the first one is essential to deal with the other, while operations research contributions are covering both stages (Daniel et al., 1997). Figure 3 shows this information flow through the supply and the environmental chain.

The phase observation analysis refers to the identification and the problem analysis in the supply chain or the environmental chain, and data collection. Phase solution identification refers to the formulation and mathematical model solving.

According to the previously presented frameworks, must be mentioned the two main domains of different factors for achieving environmental improvements: the micro and macro domain. Aronsson and Brodin (2006) point out these interesting types of action, where the macro domain is led by the actions of the government, and in the microdomain actions are taken by the companies. Non‐government institutions raise the environmental consciousness, so government should support the activities of these organizations and collaborate with them in preparing regulations and implementing them (Cetindamar, 2001). The proposed conceptual framework is seeking improvements in the microdomain but is focused on the specific problems which, sometimes, can be solved not only by one company but by consulting the environmental companies and respecting the legislative authority’s rules regarding environmental issues.

3 Conceptualization of research question

The research question is indicated in the topic of this paper: Can the supply and environmental chains be integrated? The answer can be (is) yes if the company is already an environmentally oriented company, environmentally conscious and some (or all) environmental initiatives are implemented through the company organization. On the other hand, when it comes to collaboration between the companies in the supply chain, especially the buyer and supplier relationship regarding environmental initiatives, Murfield and Tate (2017) present good research on this subject. The authors conduct data analysis (through literature review and interviews) and explain why environmental initiatives are successful and explain the way they are integrated within the firms across the supply chain. The core theme that emerges from the qualitative interview data is that relationships between the buying and supplying firms changed because of the implementation of the environmental initiatives within the supply chain (Murfield & Tate, 2017). Taking into account that environmental regulations are constantly changing (and are not consistent in different regions and countries of the world), the primary drivers of inter-organizational implementation of these regulations are financial impact, corporate culture and the external influence of customers and suppliers. Of course, the authors Murfield and Tate (2017) do not forget to emphasize that environmental initiatives and their implementation could be used as a competitive advantage. The above-mentioned research can be implemented through one supply chain—taking into consideration buyers and suppliers.

But the question in the research presented in this paper is not a question regarding one supply chain; it is a question regarding two chains and their cooperation and/or integration that must include environmental initiatives. The presented framework (see Fig. 4) applies to operational decisions (micro-level), where a company must include in the decision-making process some (selected or legally necessary) environmental initiatives. A good example can be a transport company (oriented towards profit) that must include some environmental initiatives regarding environmental safety requirements during transport, which can lead to profit reduction. Further explained, the application of the environmental initiative is not a must for all companies, for some of them it is imposed by a law of the origin country. In this paper, a presented framework aims to help in establishing such a research process which will be conducted by taking into consideration the economic focus of the company (higher profit, lower costs, etc.) with an environmental focus (lower energy use, reduction of air emissions, etc.), by determining the level of fulfilment of each goal.

Fig. 4

Operations research as a bridge between supply chain and environmental chain—a conceptual framework

4 Methodology

Two approaches (Bloemhof-Ruwaard et al., 1995; Daniel et al., 1997) described in Sect. 3, conduct a literature review of operations management methods for solving environmental problems and their classification, but they can help us notice the interaction between environmental problems and operational research. This interaction is crucial to efficiently solve many problems in the natural resources industry using operations research methods. The supply chain approach is mainly guided by the principles of technical sciences, and a proposed extension (see Fig. 3) brings together the focus of social sciences as well as technical sciences. Whereas the 'chain' approach focuses on the materials' flow through economic and natural systems and concerns principally engineering and natural sciences, the proposed extension examines the information flow through society and relies on human behaviour and decision sciences (Daniel et al., 1997).

4.1 Environmental operations research: a new conceptual framework

Following the entire process of building mathematical models is important for the successful application of operations research in the natural resources industry. The process of building mathematical models comprehends many activities or steps that should be crossed to reach an efficient solution. These activities are incorporated into the framework to gain a better insight into the considered problem. Nine phases of the mathematical models building process are given in (Krčevinac et al., 2013):

• Goal definition,

• Research planning,

• Problem formulation,

• Model formulation,

• Solution method selection,

• Programming and testing,

• Data collection,

• Model validation and solving and

• Solution implementation.

By incorporating the above-mentioned phases into the framework presented in Fig. 3, a new framework for environmental operations research methodology is developed with a focus on natural resources. This framework can help researchers in the process of solving the problems in the natural resources industry using operations research tools (see Fig. 4). The framework provides the basis for an analysis of the operations research problems related to environmental management, thus identifying the appropriate solutions and ensuring the sustainability of the proposed solutions. It stresses the correlation between the industry (supply chain) and the environment (environmental chain) and points out the possibilities for a detailed analysis of potential problems and appropriate solution methods and techniques. In such a way, the framework offers a management tool that can be applied in several different contexts: for conducting preliminary observations and for problem identification and analysis, for building mathematical models to solve the identified problem, and for the solution identification and implementation for the real case scenarios. The framework is specialized for the application of operations research tools in the identification and solving of problems that occur by changes and interaction between the industry and the environment.

The framework aims to:

• Provide a systematic approach to support problem identification and problem-solving within this specific area: the seven steps (adapted from Krčevinac et al., 2013) are broadened to 14 steps and sum-up the entire process of building mathematical models, and the supply and environmental chains provide a list of activities within these processes.

• Describe all connections between the phases of the supply and environmental chains and connections to and from the process of building mathematical models.

• Distinguish the effects of the solution on the environment and on the supply chain.

The core of the framework presents the environmental operations research (EOR) process of building mathematical models through 14 steps. These steps are grouped into six consecutive phases (see Fig. 4). In the following text, a detailed explication of all phases is given.

4.2 Phase I: Observation and problem analysis

The first phase involves steps of observation and problem analysis. It is started or initiated by the interaction between the supply chain (regarding any part of the industry) and the environmental chain (regarding any part of the environment) and the researcher is obligated to recognize that the problem is indeed an EOR problem.

4.3 Phase II: Problem identification

Identification of the problem is a rather difficult phase, where the researcher must clearly conceptualize a research problem; this is the moment where the researcher points out and explains the problem, including its scope and the results desired.

4.4 Phase III: Problem and model formulation

The third phase consists of six steps, and the output of this phase is formulated and tested a mathematical model for the identified problem. The first step of this phase is goal definition. Rajgopal (2004) describes general goals (increasing productivity or reducing quality problems) and defines more specific, well-defined objectives. An interesting definition of the three components of the goals are (Rajgopal, 2004): the statement of an unambiguous objective (to maximize profits from the sales of our products); specification of factors that will affect the objective (the planned production rates can be controlled but the actual market demand may be unpredictable); a specification of the constraints on the courses of action, i.e. of setting boundaries for the specific actions that the decision-maker may take (the availability of resources). Regarding the goal definition phase, the research studies in the field of natural resources can be roughly classified into two groups:

• Studies that are dealing with problems in the supply chain to better (economically) use natural resources,

• Studies that are dealing with problems in the environment to protect natural resources from an ecological point of view.

For example, Hervani et al. (2005) argued that the objective of a green supply chain is to eliminate or minimize negative environmental impacts (air, water, and land pollution) and waste of resources (energy, materials, products) from the extraction or acquisition of raw materials up to final use and disposal of products. Björklund et al. (2012) highlight that, although there are growing environmental demands and pressures from several different stakeholders, few attempts have been made to investigate how the outcomes from environmental measurement activities are externally communicated.

Based on the analysis conducted in Ahi and Searcy (2013), an original conceptual framework for structuring the development of metrics in green supply chain management (GSCM) and sustainable supply chain management (SSCM) is presented in Ahi and Searcy (2015). This paper presents one of the first in-depth investigations of the use of metrics in GSCM and SSCM.

A clear dividing line between these two groups does not exist, and every research within this field, according to the presented framework, must have a link to both—the supply chain and the environmental chain. This is the point where the constraints regarding environmental decisions become part of the top goal of the research problem. In this framework, it is proposed that the supply chain goals are being treated equally as environmental goals in such a way that they are united in the one goal of the research problem. Research planning is a common phrase for each study or research and is not specifically defined in the proposed framework. This phase includes time and resource planning and finalizing a plan needed for the successful fulfilment of the final goal.

To proceed from the initial state of the problem to possible solutions, researchers must surmount several barriers. The problem formulation phase, where criteria or criteria are defined, is of fundamental importance for the success of the next phase—model formulation (Krčevinac et al., 2013). The model formulation is the heart of every operations research problem and it is crucial for achieving an efficient solution to the initial problem. Relevant data is separated from the irrelevant and the model is formulated as a simplified representation of the reality (the initial problem). Model is solved using selected methods and programming and testing is performed for several test examples. The formulated mathematical model needs to be tested and verified using the test data and the selected computer program. Some standard modelling languages like Visual Basic, C, C++ or specialized like GMPL, AMPL, LINDO and GAMS can be used (Fourer et al., 2003; Makhorin, 2005; Schneider, 2013). The solution method is chosen regarding the type of the formulated model—linear versus nonlinear, stochastic or deterministic variables, etc. More on the solution methods in operations research can be found in Hillier (2012) and Winston and Goldberg (2004). The complexity of the formulated mathematical model together with the available resources (like time and costs) determines the selection of the solution method—should we use an exact method or adequate heuristics.

Stakeholders engage in collaborative activities when they perceive sufficient consequential incentives to do so (Hossuet al., 2018). Environmental concerns included in the operations research decisions often lead to higher costs for companies. But these decisions must be seen as value enabled activities in the value analysis of the problem-solving process. Activities that do not add value to the industry product are mandatory by the laws and legislative authorities. On the other hand, these environmental (concerns) activities add value to the environmental chain. The above mentioned is the cause of the disjunction of the goals and values for different chains. To reconcile these goals and assess each process step through the eyes of different customers (supply chain customer and environmental chain customer) and determine whether the step is a value adding activity (VA), a non-value adding activity (NVA) or a value enabled, the collaboration of activities in both chains are mandatory.

4.5 Phase IV: Data collection

Data are collected from the supply and the environmental chain. Although the data type and data format are predefined in the phases preceding the data collection phase, this phase can emerge many problems regarding the data availability, irrelevant or duplicate data, misinterpreted data, conflicting data, etc. Most practitioners use multiple approaches (West, 2015) for data collection, such as interviews (face-to-face), checklists, questionnaires, diagrammatic evaluation sheets, etc.

4.6 Phase V: Solution identification

Does the formulated mathematical model correspond to the real problem or is it a good abstraction of the real system? The answer to this question lies within the consistency, sensitivity and applicability of the model (Krčevinac et al., 2013) and corresponds to the solution identification phase, specifically the model validation step. In this step, it is necessary to determine how accurate a formulated mathematical model is as a representation of the defined problem. The formulated mathematical model has to be tested and verified using solvers, as for test examples (Phase III).

4.7 Phase VI: Solution implementation

Solution implementation is the final goal of the whole research. It reflects both the supply and the environmental chain and the cooperation between the participants is crucial for the success of the research. The solution efficiency is measured based on defined criteria. The proposed framework allows comprehending the knowledge of how some operations research decisions influence the environment, and vice versa.

The framework brings up two different ways of dealing with problems in the natural resource industry. Some researchers are solving natural resources problems driven by the supply chain and its effects, and some are driven by environmental effects. In order to achieve the best results, it's important to comprehend the effects of and on both chains, throughout the entire process of building mathematical models—from the problem identification to the solution implementation. The researchers should bridge the gap between the economic criteria of natural resources exploration and the unwanted negative impacts of exploration on the environmental chain. This conflict regarding different goals can and must be overcome by taking both of them into consideration right after the problem identification (see Fig. 4).

The framework can also be utilized as a means of ensuring that adequate, correct, and sufficient environmental information, (the need is emphasized in earlier studies (Armitage, 1995), are gathered and linked to appropriate and available implementation tools. The proposed model emphasizes economic factors influencing natural resources utilization and ecological sustainability, but the relative importance of the factors depends on the real problem goal and can be in some form of a consultative methodological approach.

Backlinks exist within the second phase, from step Programming and testing to step Model formulation and, another backlink from phase Solution identification (model validation and model solving) to the start of the third phase. The programming and testing phase ensures that the model “works” and that a solution for the test examples can be obtained. The backlink provides the possibility to remodel and correct the errors. If the model validation step shows that the model does not correspond to the real problem, the researcher must redo all the phases starting with the third phase. This integrated control ensures that the solution is valid and meets the requirements of the real problem.

According to Aronsson and Brodin (2006), there is still a missing piece in this puzzle, i.e. clear and direct association of different types of cost-saving measures that can reduce the environmental impact of the supply chain. The authors also underline the insufficient discussion on how to reach both goals: the goal of sustainable development through both reducing environmental impact and improved business profitability.

5 Empirical data and analysis

5.1 Phase I: Observation and problem analysis

In this study, a location-allocation problem for the solid waste supply chain (S.C.) management of Istanbul metropolitan city is investigated. A case study is an empirical method that investigates a contemporary phenomenon in depth and within its real-world context, especially when the boundaries between phenomenon and context may not be clearly evident (Yin, 2018). According to TSI (2018), the amount of generated solid waste per capita is 1.16 (kg/capita-day) in Turkey and is 1.28 (kg/capita-day) in Istanbul which is greater than the average amount of the country. Furthermore, Istanbul has the greatest proportion of the population in Turkey (TSI, 2020). Figure 5 presents the existing facilities in the S.C. network of the solid waste recycling system in Istanbul. These facilities are transfer centres, recycling centres, disposal centres and landfilling centres. In total, there are eight transfer centres, two recycling centres, two disposal centres and two landfilling centres are currently in operation in Istanbul (ISTAC, 2019; Municipality of Istanbul, 2020a, 2020b).

Fig. 5

The existing facilities in the S.C. network of the solid waste recycling system in Istanbul

S.C.'s management process of solid wastes has to be dealt with in economic and environmental contexts. The economic context consists of cost items such as operational costs, transformation costs, fixed costs etc. On the other hand, collection of the generated solid waste, dealing with pollution caused by the transformation of the waste, processing the waste, the distance of the facilities from the urban areas are some of the main environmental issues that have to be considered. As a result, both economical and environmental concerns have to be fulfilled for the sustainability and resilience of solid waste S.C.

5.2 Phase II: Problem identification

5.2.1 Goal definition

The amount of generated solid waste in Turkey is expected to reach 37.99 million tons in 2025 (REC Turkey, 2018). On the other hand, Istanbul has the fastest increasing population trend in Tukey (TSI, 2020). These statistical inputs indicate the necessity of a sustainable and environmentally friendly waste management system in Istanbul.

5.2.2 Research planning

In recent years, studies on the optimization of solid waste management (SWM) have attracted attention due to the increase in the cost of both collection and disposal of waste. A summary of the available studies for solid waste management is presented in Table 2. Abou Najm and El-Fadel (2004) presented an improved interface to formulate matrices associated with an integrated waste management optimization model. Badran and El-Haggar (2006) introduced a model for a municipal solid waste management system in Port Said, Egypt. They used mixed-integer programming to model the proposed system. Rathi (2007) proposed an optimization model for combined municipal SWM in Mumbai, India. Minciardi et al. (2008) studied an approach to sustainable municipal SWM to support the decision on optimum solid waste flow. They modelled the problem with a nonlinear, multi-objective formulation. In particular, they considered four goals that should be minimized, related to economic costs, unrecycled waste, disposal of landfills and environmental impact (incinerator emissions). Apaydin and Gonullu (2008) conducted a route optimization study to reduce emissions in the solid waste collection process. They stated that solid waste collection operations are carried out using diesel engine trucks. Anghinolfi et al. (2013) focused on recycling management and dynamic optimization of material collection. The dynamic decision model developed is expressed with state variables corresponding to the amount of waste in each bin per day, control variables that determine the amount of material collected in the area each day and vehicle collection ways. Levis et al. (2014) presented the first implementation of an optimizable dynamic life cycle assessment framework that can take account of changing policy requirements. Das and Bhattacharyya (2015) proposed an optimum municipal solid waste collection and transportation plan focusing on the problem of minimizing the length of each waste collection and transport route. Barreto et al. (2020) created a composition for Solidification and Stabilization (S/S) of electroplating solid waste, avoiding energy and environmental consumption. Optimization tests have been carried out to ensure that cement consumption and resources are greatly reduced, and these tests are supported by experimental design tools and statistical models. Babaee Tirkolaee et al. (2020) addressed a chance-constrained programming model based on fuzzy credibility theory for the multi-trip capacitated arc routing problem for urban solid waste management. Batur et al. (2020) formulated a novel mixed-integer linear programming model for the long-term planning of municipal solid waste management systems. Abdallah et al. (2020) presented a systematic optimization framework that defines the most useful waste-to-energy management strategies through nonlinear mathematical modelling. Table 2 presents the summary of available studies for solid waste management. Furthermore, it highlights the contribution of this study to the literature.

Table 2 Summary of the available real-life studies for solid waste management

In this section, the problem of locating the transfer and landfilling centres are investigated. Additionally, material flows between the facilities are analysed. In this context, the fuzzy multi-objective linear programming model developed by Karagoz et al. (2017) was revised and re-developed as a multi-period scenario-based stochastic-based fuzzy multi-objective model. Zimmermann (1975) used the fuzzy set theory of Zadeh (1965) for linear programming (LP) problems. The proposed model is considered as a MIP problem with fuzzy constraints and a fuzzy objective function.

Fuzzy sets are effective in solving complex, undefined problems characterized by the uncertainty of the environment and the vagueness of information. As preferences of decision-makers (DM) play an important role in a real-life problem, the fuzzy multi-objective linear programming (FMOLP) approach is an appropriate method in terms of satisfying DMs’ objectives. In this context, the interactive fuzzy multi-objective approach is a favourable method because of its simplicity and its success with representing the conflicting goals of the objective functions. Furthermore, scenario-based stochastic parameters are established because they represent various scenario probabilities rather than a fixed value.

5.3 Phase III: Problem and model formulation

In this section, the problem of locating the transfer and landfilling centres are investigated. Additionally, material flows between the facilities are analysed. In this context, the fuzzy multi-objective linear programming model developed by Karagoz et al. (2017) was revised and re-developed as a multi-period scenario-based stochastic-based fuzzy multi-objective model. The base model developed by Karagoz et al. (2017) presents a supply chain management plan for the solid waste recycling process in the European Side of Istanbul. Differently, both Anatolian and European Sides are investigated in this case study. Furthermore, the amount of generated solid waste in Istanbul is forecasted for 10 years period (2021–2030). The forecasting method is covered in Sect. 4.5. Indices, parameters and decision variables of the mathematical model are given in Table 3.

Table 3 Indices, parameters and decision variables

5.3.1 Model formulation

$$\min \beta o_{c} + \left( {1 - \beta } \right)o_{p}$$

(1)

Equation (1) presents a combination of objective functions for total cost and total pollution. The first component of the function represents the cost item, and the second component represents the pollution item of the objective function.

$$\begin{aligned} o_{c} & = \mathop \sum \limits_{j = 1}^{J} f_{j} y_{j} + \mathop \sum \limits_{l = 1}^{L} f_{l} z_{l} + \mathop \sum \limits_{i = 1}^{I} \mathop \sum \limits_{j = 1}^{J} \mathop \sum \limits_{t = 1}^{T} \mathop \sum \limits_{\omega = 1}^{\Omega } s_{\omega } \left[ {\left( {T_{1} d_{ij} + pr_{1} } \right)\left( {xct_{ijt}^{\omega } + wct_{ijt}^{\omega } + \theta ct_{ijt}^{\omega } } \right)} \right] \\ & \quad + \mathop \sum \limits_{j = 1}^{J} \mathop \sum \limits_{r = 1}^{R} \mathop \sum \limits_{t = 1}^{T} \mathop \sum \limits_{\omega = 1}^{\Omega } s_{\omega } \left[ {\left( {T_{2} d_{jr} + pr_{2} } \right)xtr_{jrt}^{\omega } } \right] + \mathop \sum \limits_{r = 1}^{R} \mathop \sum \limits_{s = 1}^{S} \mathop \sum \limits_{t = 1}^{T} \mathop \sum \limits_{\omega = 1}^{\Omega } s_{\omega } \left[ {\left( {T_{3} d_{rs} + pr_{3} } \right)xrs_{rst}^{\omega } } \right] \\ & \quad + \mathop \sum \limits_{r = 1}^{R} \mathop \sum \limits_{l = 1}^{L} \mathop \sum \limits_{t = 1}^{T} \mathop \sum \limits_{\omega = 1}^{\Omega } s_{\omega } \left[ {\left( {T_{4} d_{rl} + pr_{4} } \right)xrl_{rlt}^{\omega } } \right] + \mathop \sum \limits_{s = 1}^{S} \mathop \sum \limits_{l = 1}^{L} \mathop \sum \limits_{t = 1}^{T} \mathop \sum \limits_{\omega = 1}^{\Omega } s_{\omega } \left[ {\left( {T_{5} d_{sl} + pr_{4} } \right)xsl_{slt}^{\omega } } \right] \\ & \quad + \mathop \sum \limits_{j = 1}^{J} \mathop \sum \limits_{s = 1}^{S} \mathop \sum \limits_{t = 1}^{T} \mathop \sum \limits_{\omega = 1}^{\Omega } s_{\omega } \left[ {\left( {T_{6} d_{js} + pr_{3} } \right)wts_{jst}^{\omega } } \right] + \mathop \sum \limits_{s = 1}^{S} \mathop \sum \limits_{l = 1}^{L} \mathop \sum \limits_{t = 1}^{T} \mathop \sum \limits_{\omega = 1}^{\Omega } s_{\omega } \left[ {\left( {T_{4} d_{sl} + pr_{4} } \right)wsl_{slt}^{\omega } } \right] \\ & \quad + \mathop \sum \limits_{j = 1}^{J} \mathop \sum \limits_{l = 1}^{L} \mathop \sum \limits_{t = 1}^{T} \mathop \sum \limits_{\omega = 1}^{\Omega } s_{\omega } \left[ {\left( {T_{7} d_{jl} } \right)\theta tl_{jlt}^{\omega } } \right] - \mathop \sum \limits_{r = 1}^{R} \mathop \sum \limits_{t = 1}^{T} \mathop \sum \limits_{\omega = 1}^{\Omega } s_{\omega } RVxre_{rt}^{\omega } \\ \end{aligned}$$

(2)

Equation (2) stands for the cost item of the objective function which includes fixed costs, transportation costs, operational costs and revenue, respectively. The first item is the fixed cost that consists of setting up new facilities (transfer and landfilling centres). The rest of the function represents transportation/operation costs and revenue of the generated solid waste.

$$\begin{aligned} o_{p} & = \mathop \sum \limits_{i = 1}^{I} \mathop \sum \limits_{t = 1}^{T} p_{it} \left[ {\mathop \sum \limits_{j = 1}^{J} \mathop \sum \limits_{\omega = 1}^{\Omega } s_{\omega } \left( {\frac{{\pi_{j} \left( {\mathop \sum \nolimits_{i = 1}^{I} \left( {xct_{ijt}^{\omega } + wct_{ijt}^{\omega } + \theta ct_{ijt}^{\omega } } \right)} \right)}}{{e_{ij}^{2} }}} \right) + \mathop \sum \limits_{r = 1}^{R} \mathop \sum \limits_{\omega = 1}^{\Omega } s_{\omega } \left( {\frac{{\pi_{r} \left( {\mathop \sum \nolimits_{j = 1}^{J} xtr_{jrt}^{\omega } } \right)}}{{e_{ir}^{2} }}} \right)} \right. \\ & \quad + \mathop \sum \limits_{s = 1}^{S} \mathop \sum \limits_{\omega = 1}^{\Omega } s_{\omega } \left( {\frac{{\pi_{s} \left( {\mathop \sum \nolimits_{r = 1}^{R} xrs_{rst}^{\omega } + \mathop \sum \nolimits_{j = 1}^{J} wts_{jst}^{\omega } } \right)}}{{e_{is}^{2} }}} \right) \\ & \quad \left. { + \mathop \sum \limits_{l = 1}^{L} \mathop \sum \limits_{\omega = 1}^{\Omega } s_{\omega } \left( {\frac{{\pi_{l} \left( {\mathop \sum \nolimits_{r = 1}^{R} xrl_{rlt}^{\omega } + \mathop \sum \nolimits_{s = 1}^{S} \left( {xsl_{slt}^{\omega } + wsl_{slt}^{\omega } } \right) + \mathop \sum \nolimits_{j = 1}^{J} \theta tl_{jlt}^{\omega } } \right)}}{{e_{il}^{2} }}} \right)} \right] \\ \end{aligned}$$

(3)

Equation (3) calculates the released pollution for the waste types between the destinations. The pollution function is dependent on pollution factor coefficients of the facilities, Euclidean distances between the facilities and the city centres between the facilities and the city centres, amount of generated waste type and population in the city centres.

$$\begin{aligned} & \mathop \sum \limits_{j = 1}^{J} \left( {\frac{{\pi_{j} \left( {\mathop \sum \nolimits_{i = 1}^{I} \left( {xct_{ijt}^{\omega } + wct_{ijt}^{\omega } + \theta ct_{ijt}^{\omega } } \right)} \right)}}{{e_{ij}^{2} }}} \right) + \mathop \sum \limits_{r = 1}^{R} \left( {\frac{{\pi_{r} \left( {\mathop \sum \nolimits_{j = 1}^{J} xtr_{jrt}^{\omega } } \right)}}{{e_{ir}^{2} }}} \right) + \mathop \sum \limits_{s = 1}^{S} \frac{{\pi_{s} \left( {\mathop \sum \nolimits_{r = 1}^{R} xrs_{rst}^{\omega } + \mathop \sum \nolimits_{j = 1}^{J} wts_{jst}^{\omega } } \right)}}{{e_{is}^{2} }} \\ & \quad + \mathop \sum \limits_{l = 1}^{L} \left( {\frac{{\pi_{l} \left( {\mathop \sum \nolimits_{r = 1}^{R} xrl_{rlt}^{\omega } + \mathop \sum \nolimits_{s = 1}^{S} \left( {xsl_{slt}^{\omega } + wsl_{slt}^{\omega } } \right) + \mathop \sum \nolimits_{j = 1}^{J} \theta tl_{jlt}^{\omega } } \right)}}{{e_{il}^{2} }}} \right) \le \;PL, \;\;\forall i \in I,\;t \in T,\;\omega \in \Omega \\ \end{aligned}$$

(4)

Equation (4) enforces an upper bound of the pollution level for a populated area. This constraint aims to keep the pollution level within the tolerance limits. The tolerance limit can vary regarding the preferences of the DMs or the environmental experts.

$$\mathop \sum \limits_{i = 1}^{I} \mathop \sum \limits_{j = 1}^{J} \left( {xct_{ijt}^{\omega } + wct_{ijt}^{\omega } + \theta ct_{ijt}^{\omega } } \right) \le Tcap_{j} y_{j} , \;\;\forall j \in J,t \in T,\omega \in \Omega$$

(5)

$$\mathop \sum \limits_{j = 1}^{J} xtr_{jrt}^{\omega } \le Rcap_{r} , \;\forall r \in R,t \in T,\omega \in \Omega$$

(6)

$$\mathop \sum \limits_{r = 1}^{R} x_{rlt}^{\omega } + \mathop \sum \limits_{s = 1}^{S} \left( {xsl_{slt}^{\omega } + wsl_{slt}^{\omega } } \right) + \mathop \sum \limits_{j = 1}^{J} \theta tl_{jlt}^{\omega } \le Lcap_{l} z_{l} , \;\forall l \in L,t \in T,\omega \in \Omega$$

(7)

$$\mathop \sum \limits_{r = 1}^{R} xrs_{rst}^{\omega } + \mathop \sum \limits_{j = 1}^{J} wts_{jst}^{\omega } \le Scap_{s} , \;\forall s \in S,t \in T,\omega \in \Omega$$

(8)

Equations (5)–(8) are capacity constraints of transfer, recycling, landfilling and disposal centres. These constraints ensure that the capacities of the facilities are not less than the amount of solid waste that enters the facilities.

$$\mathop \sum \limits_{i = 1}^{I} xct_{ijt}^{\omega } - \mathop \sum \limits_{r = 1}^{R} xtr_{jrt}^{\omega } = 0, \;\forall t \in T,\omega \in \Omega$$

(9)

$$a_{1} \mathop \sum \limits_{j = 1}^{J} xtr_{jrt}^{\omega } - xre_{rt}^{\omega } = 0, \;\forall r \in r,t \in T,\omega \in \Omega$$

(10)

$$a_{2} \mathop \sum \limits_{j = 1}^{J} xtr_{jrt}^{\omega } - \mathop \sum \limits_{s = 1}^{S} xrs_{rst}^{\omega } = 0, \;\forall r \in r,t \in T,\omega \in \Omega$$

(11)

$$\left( {1 - a_{1} - a_{2} } \right)\mathop \sum \limits_{j = 1}^{J} xtr_{jrt}^{\omega } - \mathop \sum \limits_{l = 1}^{L} xrl_{rlt}^{\omega } = 0, \;\forall r \in R,t \in T,\omega \in \Omega$$

(12)

$$b\mathop \sum \limits_{r = 1}^{R} xrs_{rst}^{\omega } - \mathop \sum \limits_{l = 1}^{L} xsl_{slt}^{\omega } = 0, \;\forall s \in S,t \in T,\omega \in \Omega$$

(13)

Equations (9)–(13) formulates the material flow of type 1 waste for transfer, recycling and disposal centres. These constraints ensure the balance of the material flows in each facility for type 1 waste.

$$\mathop \sum \limits_{i = 1}^{I} wct_{ijt}^{\omega } - \mathop \sum \limits_{s = 1}^{S} wts_{jst}^{\omega } = 0, \;\forall j \in J,t \in T,\omega \in \Omega$$

(14)

$$b\mathop \sum \limits_{j = 1}^{J} wts_{jst}^{\omega } - \mathop \sum \limits_{l = 1}^{L} wsl_{slt}^{\omega } = 0, \;\forall s \in S,t \in T,\omega \in \Omega$$

(15)

Equations (14) and (15) calculate the material flow of type 2 waste for transfer and disposal centres. These constraints ensure the balance of the material flows in each facility for type 2 waste.

$$\mathop \sum \limits_{i = 1}^{I} \theta ct_{ijt}^{\omega } - \mathop \sum \limits_{l = 1}^{L} \theta tl_{jlt}^{\omega } = 0, \;\forall j \in J,t \in T,\omega \in \Omega$$

(16)

Equation (16) formulates the material flow of type 3 waste for transfer centres. These constraints ensure the balance of the material flows in each facility for type 3 waste.

$$\mathop \sum \limits_{j = 1}^{J} xct_{ijt}^{\omega } \ge wt1_{it}^{\omega } , \;\forall i \in I,t \in T,\omega \in \Omega$$

(17)

$$\mathop \sum \limits_{j = 1}^{J} wct_{ijt}^{\omega } \ge wt2_{it}^{\omega } , \;\forall i \in I,t \in T,\omega \in \Omega$$

(18)

$$\mathop \sum \limits_{j = 1}^{J} \theta ct_{ijt}^{\omega } \ge wt3_{it}^{\omega } , \;\forall i \in I,t \in T,\omega \in \Omega$$

(19)

Equations (17)–(19) represent that all generated type 1, 2 and 3 waste in the city centres is collected. These constraints enforce that amount of transferred solid waste from the city centres to the transfer centres are not less than the amount of generated waste types in the city centres.

$$o_{c} , o_{p} , s_{\omega } , xct_{ijt}^{\omega } , xtr_{jrt}^{\omega } , xrs_{rst}^{\omega } , xrl_{rlt}^{\omega } , xsl_{slt}^{\omega } , xre_{rt}^{\omega } , wct_{ijt}^{\omega } , wts_{jst}^{\omega } , wsl_{slt}^{\omega } , \theta ct_{ijt}^{\omega } , \theta tl_{jlt}^{\omega } \ge 0$$

(20)

$$y_{j} , z_{l} \in \left\{ {0,1} \right\} \;\forall j \in J, l \in L$$

(21)

$$\;\forall i \in I,j \in J,l \in L,r \in R,s \in S,t \in T,\omega \in \Omega$$

(22)

Equations (20)–(22) ensure the positivity of the decision variables, present binary variables and provide integrality constraints.

5.3.2 Solution method, programming and testing

As it is stated in Sect. 4.3, the developed scenario-based stochastic mathematical model is solved via fuzzy multi-objective modelling approach. The mathematical model is developed as a scenario-based stochastic mixed-integer model to consider the occurrence possibilities for various amounts of generated solid waste for the next 10 years. Furthermore, it’s solved to optimality via the fuzzy multi-objective modelling approach to deal with the uncertainties and vaguenesses such as conflicts in the preferences of decision-makers. The developed models are programmed via GAMS 23.5 software. The models are tested in terms of coding language, the validity of the mathematical model and the validity of the data.

5.4 Phase IV: Data collection

In the data collection process, the literature review of academic publications and technical reports published by governmental and industrial institutions is conducted. Furthermore, experts' opinions are utilized to obtain data from field studies. Table 4 represents sets and some of the parameters which are used in the mathematical model. The parameters in Table 4 are obtained from Eiselt and Marianov (2014), Karagoz et al. (2017), ISTAC (2019), Municipality of Istanbul (2020b) and experts’ opinions.

Table 4 Sets and parameters in the mathematical model

Table 5 represents the fixed cost and capacity parameters of the facilities in the mathematical model. The parameters in Table 5 are also obtained from Karagoz et al. (2017), ISTAC (2019), Municipality of Istanbul (2020b) and experimentally developments.

Table 5 Fixed cost and capacity parameters of the facilities

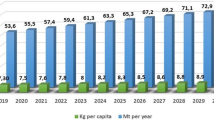
The total amount of waste generated between 2021 and 2030 is forecasted. The amount of generated solid waste in Istanbul between 2004 and 2019 is obtained from the dataset of the Municipality of Istanbul (2020a). Three forecasting approaches are applied and accuracy measurements are compared in Table 6. These approaches are Grey Forecasting, Moving Average, Single Exponential Smoothing and Double Exponential Smoothing. The Grey Forecasting approach is frequently used for waste management studies as it provides an efficient solution in uncertain environments. Moving Average is another forecasting approach that is preferred by many researchers for its simplicity and efficiency in decision-making processes. Exponential Smoothing approaches are generally preferred for short-term decision-making processes. The Single Exponential Smoothing uses weighted moving average and Double Exponential Smoothing applies exponential filter twice. To compare the effectiveness of the forecasting approaches, their mean absolute percentage error (MAPE), mean absolute deviation (MAD) and mean squared deviation (MSD) values are interpreted. MAPE expresses the percentage of the difference between the actual values and forecasted values. MAD and MSD also conceptualize the errors in a forecasting approach. Smaller values of MAPE, MAD and MSD indicate better fit. As Double Exponential Smoothing (α = 0.26, β = 0.1) provides the best accuracy score, this method is applied to forecast the amount of generated solid waste in Istanbul between 2021 and 2030. Figure 6 represents the forecasted amount of generated solid waste in Istanbul.

Table 6 Accuracy measurements of the forecasting approaches

Fig. 6

Forecasted amount of generated solid waste in Istanbul

The amount of generated solid waste in Istanbul is distributed to the city centres. The expected population of the city centres in Istanbul, 2021 are calculated as (population of the city centre i in 2020) × (1 + expected annual population growth of Istanbul) (Governorship of Istanbul, 2020). The expected annual population growth of Istanbul is assumed as constant (1.78%) for the years 2021–2030, and it is calculated as the average population increase rate between 2004 and 2019 (TSI, 2020).

In supplementary material, both driving and Euclidian distances (Table S1–Table S11) and the estimated population in the city centres between 2021 and 2030 (Table S12) are provided.

As preferences of decision-makers (DM) play an important role in this case study, the profile of DMs is presented in Table 7. In this study, there are two DMs. DM₁ stands for top-level DM whose environmental concerns are more dominant than his/her economical concerns. On the other hand, DM₂ stands for lower-level DM whose economical concerns are more dominant.

Table 7 Profiles of the DMs

Table 7 presents qualifications, fields, employment positions and experience of DMs in this case study. Both DMs are experienced in the decision-making process of waste management projects. According to Fig. 4, the proposed methodology provides a bridge that enables reconcilement of the conflicting goals which are environmental and industry (economic) goals. At this point, DM₁ represents the environmental goals and DM₂ represents the industry (economic) goals.

5.5 Phase V: Solution identification

To find the optimal values of the decision variables in a mathematical model, classical mathematical models are commonly used by decision-makers. However, parameters of the mathematical models, e.g. coefficients, are not always known by the decision-makers in real-life cases. Furthermore, only one objective function may not be sufficient to model a real-life case mathematically. As a consequence, fuzzy multi-objective linear programming (FMOLP) is employed by the decision-makers to cope with uncertainties in real-life cases (Karagoz et al., 2017). The mathematical model of FMOLP based on Paksoy et al. (2013) can be written as follows:

$$\max Z_{1} \left( x \right) = c_{1} x$$

(23)

$$\max Z_{2} \left( x \right) = c_{2} x$$

(24)

$$\vdots$$

$$\max Z_{k} \left( x \right) = c_{k} x$$

(25)

Subject to:

$$\tilde{A}x \le \tilde{b}$$

(26)

$$x \ge 0$$

(27)

where x is an n-dimensional vector of the decision variables, $Z_{k} \left( x \right)$ denotes the kth objective function, c_k denotes the kth n-dimensional vector of the cost factor, $m \times n$ denotes constraint matrix, $\tilde{b}$ denotes an m-dimensional constant fuzzy vector.

The membership functions of the fuzzy matrix $\tilde{A}$ and the vector $\tilde{B}$ are given as (Ali et al., 2021; Kushwaha et al., 2020):

$$\mu_{{\tilde{A}}} = \left\{ {\begin{array}{*{20}l} {1, x \le a_{ij} } \\ {\frac{{a_{ij} + d_{ij} - x}}{{d_{ij} }}, a_{ij} \le x \le a_{ij} + d_{ij} } \\ {0, x \ge a_{ij} + d_{ij} } \\ \end{array} } \right.$$

(28)

$$\mu_{{\tilde{B}}} = \left\{ {\begin{array}{*{20}l} { 1, x \le a_{ij} } \\ {\frac{{b_{i} + p_{i} - x}}{{p_{i} }}, b_{i} \le x \le b_{i} + p_{i} } \\ {0, x \ge b_{i} + p_{i} } \\ \end{array} } \right.$$

(29)

where x ∈ R and d_ij > 0, p_i > 0 (tolerance levels) for i = 1, 2, …, m and j = 1, 2, …, n.

In the literature, fuzzy multi-objective modelling approaches are classified as:

• The max–min approach by Zimmerman (1978),

• The interactive fuzzy multi-objective approach by Sakawa and Nishizaki (2002),

• The fuzzy multi-objective approach by Liang and Cheng (2009).

In this case study, the interactive fuzzy multi-objective approach is performed due to its simplicity and its success with representing the conflicting goals of the objective functions in the mathematical model.

5.5.1 The interactive fuzzy multi-objective approach

In contradistinction to Zimmermann (1978)’s Max–Min Approach, Sakawa and Nishizaki (2002)’s Interactive Fuzzy Approach assumes that there is a hierarchy between decision-makers (DM) in the decision-making process. The top-level DM (Z₀) has priority on the decision-making and Z₀ has supremacy compared to the lower-level DMs (Z₁, Z₂, …, Z_k) at minimizing their objectives. The multi-objective linear model is presented as:

$$\min Z_{0} \left( x \right) = \mathop \sum \limits_{i = 1}^{k} c_{i} x_{i} \quad ({\text{Top level DM's objective function}})$$

(30)

$$\min Z_{1} \left( x \right) = c_{1} x_{1} \quad ({\text{Lower level DM 1's objective function}})$$

(31)

$$\min Z_{2} \left( x \right) = c_{2} x_{2} \quad ({\text{Lower level DM 2's objective function}})$$

(32)

$$\vdots$$

$$\min Z_{k} \left( x \right) = c_{k} x_{k} \quad ({\text{Lower level DM }}k'{\text{s objective function}})$$

(33)

Subject to:

$$A_{i} x_{i} \le b_{i} , i = 1, 2, \ldots , k$$

(34)

$$x_{i} \ge 0, i = 1, 2, \ldots , k$$

(35)

According to Sakawa and Nishizaki (2002), objective functions in the mathematical model must be assumed as fuzzy due to uncertainties. As a first step, each objective function has to be solved to optimality independently to find the lower ($Z_{k}^{L}$) and upper-bounds ($Z_{k}^{U}$). Thereafter, the membership functions of the objective functions ($\mu_{0} \left( {Z_{0} \left( x \right)} \right)$, $\mu_{1} \left( {Z_{1} \left( x \right)} \right)$,…, $\mu_{k} \left( {Z_{k} \left( x \right)} \right)$) are determined on a maximization or minimization base.

$$\max \mu_{k} \left( {Z_{k} \left( x \right)} \right) \quad ({\text{Top level DM}})$$

(38)

$$\max \mu_{1} \left( {Z_{1} \left( x \right)} \right)\quad ({\text{Lower level DM 1}})$$

(39)

$$\max \mu_{2} \left( {Z_{2} \left( x \right)} \right)\quad ({\text{Lower level DM 2}})$$

(40)

$$\vdots$$

$$\max \mu_{k} \left( {Z_{k} \left( x \right)} \right) \quad ({\text{Lower level DM}}\;k)$$

(41)

Subject to:

$$A_{i} x_{i} \le b_{i} , i = 1, 2, \ldots , k$$

(42)

$$x_{i} \ge 0, i = 1, 2, \ldots , k$$

(43)

Since the main objective of the mathematical model is to maximize the minimum satisfaction levels of the DMs, the mathematical model can be revised as a single-objective model as:

$$\alpha = \min \left\{ {\mu_{0} \left( {Z_{0} \left( x \right)} \right),\;\min_{i = 1,2, \ldots ,k} \mu_{i} \left( {Z_{i} \left( x \right)} \right)} \right\}$$

(44)

$$\max \alpha$$

(45)

$$Z_{0} \left( x \right) + \left( {Z_{0}^{U} - Z_{0}^{L} } \right)\alpha \le Z_{0}^{U} \quad ({\text{Top level DM}})$$

(46)

$$Z_{1} \left( x \right) + \left( {Z_{1}^{U} - Z_{1}^{L} } \right)\alpha \le Z_{1}^{U} \quad ({\text{Lower level DM 1}})$$

(47)

$$Z_{2} \left( x \right) + \left( {Z_{2}^{U} - Z_{2}^{L} } \right)\alpha \le Z_{2}^{U} \quad ({\text{Lower level DM 2}})$$

(48)

$$\vdots$$

$$Z_{k} \left( x \right) + \left( {Z_{k}^{U} - Z_{k}^{L} } \right)\alpha \le Z_{k}^{U} \quad ({\text{Lower level DM }}k)$$

(49)

Subject to:

$$A_{i} x_{i} \le b_{i} , i = 1, 2, \ldots , k$$

(50)

$$x_{i} \ge 0, i = 1, 2, \ldots , k$$

(51)

$$0 \le \alpha \le 1$$

(52)

If α satisfies the top-level DM’s satisfaction level, the process completes. Otherwise, the minimum satisfaction level of top-level DM, $\tilde{\delta }$, is determined. The solution of the mathematical model above is expected to report a value that satisfies the top-level DM’s satisfaction level ($\tilde{\delta }$). The fact remains that satisfaction levels of the lower-level DMs (α) are also expected to be satisfied at the same time within the boundaries of top-level DM’s satisfaction level ($\tilde{\delta }$). To overcome this issue, the following steps should be performed:

$$\Delta = \frac{{\min_{i = 1,2, \ldots ,k} \mu_{i} \left( {Z_{i} \left( x \right)} \right)}}{{\mu_{0} \left( {Z_{0} \left( x \right)} \right)}}$$

(61)

The value Δ is expected to be between the lower bound ($\Delta_{L}$) and the upper bound ($\Delta_{U}$). If $\Delta > \Delta_{U}$, $\tilde{\delta }$ should be increased and Δ should be revised by the top-level DM. On the other hand, if $\Delta < \Delta_{L}$, $\tilde{\delta }$ should be increased and Δ should be revised. Under these circumstances, the following conditions are expected to be met:

• The satisfaction level of the top-level DM is greater than or equal to the revised satisfaction level, $\mu_{0} \left( {Z_{0} \left( x \right)} \right) \ge \tilde{\delta }$.

• The proportion of the minimum satisfaction level of a lower-level DM to the minimum satisfaction level of the top-level DM (Δ) is within the range of $\left[ {\Delta_{L} ,\Delta_{U} } \right]$.

  $$\Delta_{j} = \frac{{\mu_{j} \left( {Z_{j} \left( x \right)} \right)}}{{\mu_{0} \left( {Z_{0} \left( x \right)} \right)}},\;j = 1,2, \ldots ,k$$

  (62)

If $\Delta_{j} > \Delta_{U}$, the satisfaction level of the lower-level DM is revised as:

$$\overline{\delta } = \tilde{\delta } x \Delta_{U}$$

(63)

If $\overline{\delta }$ is within the range of $\left[ {\Delta_{L} ,\Delta_{U} } \right]$, the iteration completes. If not, $\overline{\delta }$ is revised until it attains a value within $\left[ {\Delta_{L} ,\Delta_{U} } \right]$. The computational details of the method are covered in the next section.

5.5.2 Model validation and model solving

In this section, validation of the proposed mathematical model is checked before running the model for the case study. The validation checking process is implemented in three stages. At the first stage, the accuracy of the proposed forecasting approach is questioned in Sect. 4.5 and it’s visualized in Fig. 6. At the second stage, the scenario-based stochastic model (Eqs. 1–22) is checked for attained values of weight factors of the objective functions (β), objective variables (o_p and o_c) and facility location selection variables (y_j and z_l). At the third stage, the fuzzy-based mathematical model is investigated in terms of attained values of membership functions ($\mu_{p} (o_{p} )$ and $\mu_{c} (o_{c} )$) and generated solid waste amounts ($R_{\omega }$). The results are interpreted and validation of the model is investigated.

At the second stage of the validation checks, values of 1, 0.8, 0.5 and 0 are assigned to β. β = 1 means, the scenario-based stochastic model is solved by only taking the cost item of the objective function into account and neglecting the pollution item (1 − β = 0). On the other hand, β = 0 means the model is solved by only considering the pollution item of the objective function and neglecting the cost item (1 − β = 1). Table 8 highlights that not surprisingly, o_c attains its minimum value and o_p attains its maximum value when β = 1 and all the facilities (y_j and z_l) are decided to be opened. As β attains 0.8 and 0.5, there is a significant decrease in the o_p and an increase in the o_c. Furthermore, only one landfilling centre (z₂) is opened as a result of the increase in the impact of pollution factor. When β attains the value of 0, o_c attains its worst value as the impact of the cost factor is completely ignored. These findings prove that developed scenario-based stochastic generates reasonable solutions in terms of changes in the impacts of cost and pollution factors.

Table 8 Experimental results of the stochastic model

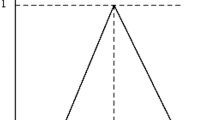
At the third stage of the validation checks, the fuzzy-based multi-objective model is investigated. As the objective variables obtained their minimum values when $\mu_{p} (o_{p} ) = 0.65$ and $\mu_{c} (o_{c} ) = 0.58$, a sensitivity analysis is performed to observe the corresponding results of the objective values regarding the changes in in the top-level ($\mu_{p} (o_{p} )$) and lower-level ($\mu_{c} (o_{c} )$) DM’s membership functions. Figure 7 depicts the results of the validation analysis regarding the changes in the values of the membership functions.

Fig. 7

Results of the validation analysis regarding the changes in the values of the membership functions

The membership functions of top and lower-level DMs are computed with Eqs. (72)–(73). The membership functions are dependent on the best and worst values of objective functions and they represent satisfaction levels of the DMs in the mathematical model. To find the best and the worst values of the objective variables, one of the objective functions are neglected and the other objective function is solved to optimality. The same steps are taken for the other objective function and β attains the values of 0 and 1, respectively. The impacts of the changes in the DM's preferences on the top and lower-level decision variables (environmental and industry goals) are visualized in Fig. 7.

In the validation analysis, six cases are generated. In Case 1, the value of top-level DM’s membership function ($\mu_{p} \left( {o_{p} } \right)$) obtains 0.35 and it is increased until it obtains the value of 0.95 in six cases. Figure 7 shows that in the first five cases, the value of lower-level DM’s membership function ($\mu_{c} \left( {o_{c} } \right)$) increased simultaneously with the top-level DM’s membership function ($\mu_{p} \left( {o_{p} } \right)$) and obtained its maximum value in Case 5 ($\mu_{c} \left( {o_{c} } \right) = 0.43)$. In Case 6, $\mu_{c} \left( {o_{c} } \right)$ obtained its minimum value (0.40) when $\mu_{p} \left( {o_{p} } \right)$ obtained its maximum value (0.95). The results of the validation analysis highlight that satisfaction levels of both DMs can be fulfilled simultaneously until top-level DM’s satisfaction level obtains the value of 0.95. It means both economical and environmental concerns of different level DMs can be fulfilled at this level.

Apart from the validation analysis of membership functions, a scenario analysis is performed to observe the corresponding results of the objective values and the values of the membership functions regarding the changes in the amount of generated solid waste in the optimistic and pessimistic scenario. $\omega_{1}$, $\omega_{2}$ and $\omega_{3}$ represent the optimistic scenarios, whereas R₁, R₂ and R₃ represent generated solid waste in these scenarios. Furthermore, $\omega_{5}$, $\omega_{6}$ and $\omega_{7}$ represent the pessimistic scenarios, whereas R₅, R₆ and R₇ represent the amount of generated solid waste in these scenarios. $\omega_{4}$ and R₄ represent the actual scenario and the generated amount of solid waste. The results of the scenario analysis are depicted in Table 9. The visualized results of the scenario analysis are represented in Fig. 8.

Table 9 Decision variables and membership function values for different amounts of generated solid waste

Fig. 8

Results of the scenario analysis regarding the changes in the generated amounts of solid waste in optimistic and pessimistic scenarios

Figure 8 depicts that changes in the amount of generated solid waste don’t have as much significant effect as on the top-level DMs membership value $(\mu_{p} \left( {o_{p} } \right)$) comparing to the lower-level DM’s value $(\mu_{c} \left( {o_{c} } \right)$). o_p obtains its worst value in Scenario 4 where the generated amount of solid waste in the most pessimistic scenario equals double the actual amount. On the other hand, o_c obtains its worst value Scenario 3. The results of the sensitivity and the scenario analysis underline that although o_p and o_c generally tend to conflict, reconcilement of the top-level and lower-level DMs’ objectives is possible under specific circumstances. DMs’ effective strategy with the determination of satisfaction levels and scenario coefficients play a crucial role within this scope.

5.5.3 Evaluation

Model validation and model solving processes reveal the stability of the proposed mathematical models. Furthermore, it is discovered that the preferences of different level decision-makers (economical and environmental preferences) can be fulfilled simultaneously. The values of weight factors of the objective functions (β), values of membership functions ($\mu_{p} \left( {o_{p} } \right)$ and $\mu_{c} \left( {o_{c} } \right)$) and generated solid waste amounts ($R_{\omega }$) have a significant impact on the decision variables.

5.6 Phase VI: Solution implementation

In this section, two objective functions; facility set up, operational and transportation costs (o_c) and total pollution (o_p) are minimized independently to find out the upper and lower bound of each objective function. In another saying, the results of the mathematical model are reported when $\beta = 1$ and $\beta = 0$, respectively. $o_{p}$ is considered as the top-level objective function. Subsequently, the membership functions are determined as follows:

$$\mu_{p} (o_{p} ) = \left\{ {\begin{array}{*{20}c} {1,} & { o_{p} \le 374,183*10^{7} } \\ {\frac{{117,266*10^{9} - o_{p} }}{{117,266*10^{9} - 374,183*10^{7} }},} & {374,183*10^{7} \le o_{p} \le 117,266*10^{9} } \\ {0,} & {o_{p} \ge 117,266*10^{9} } \\ \end{array} } \right.$$

(72)

$$\mu_{c} \left( {o_{c} } \right) = \left\{ {\begin{array}{*{20}c} {1,} & {o_{c} \le 29,713*10^{6} } \\ {\frac{{732,624*10^{5} - o_{c} }}{{732,624*10^{5} - 29,713*10^{6} }},} & {29,713*10^{6} \le o_{c} \le 732,624*10^{5} } \\ {0,} & {o_{c} \ge 732,624*10^{5} } \\ \end{array} } \right.$$

(73)

In the sequel, the satisfaction level (α) is added to the mathematical model and the mathematical model is converted to a single-objective model. The revised model is presented as:

$$\max \alpha$$

(74)

Subject to:

$$\alpha \le \mu_{p} \left( {o_{p} } \right) = \frac{{117,266*10^{9} - o_{p} }}{{117,266*10^{9} - 374,183*10^{7} }}$$

(75)

$$\alpha \le \mu_{c} \left( {o_{c} } \right) = \frac{{732,624*10^{5} - o_{c} }}{{732,624*10^{5} - 29,713*10^{6} }}$$

(76)

Equations (2)–(22)

$$0 \le \alpha \le 1$$

(77)

The mathematical model is solved to optimality with an Intel Core i7 processor within 49.733 CPU seconds. GAMS 23.5 software is used and CPLEX is selected as a solver. As a result, α obtained a value of 0.28. In another saying, both top-level ($\mu_{p} \left( {o_{p} } \right)$) and lower-level DMs’ satisfaction levels ($\mu_{c} \left( {o_{c} } \right)$) are calculated as 28%.

In this case, it is assumed that top-level DM is not happy with the results and determines that the satisfaction level of pollution should be at least 65%. The mathematical model is revised as:

$$\max \alpha$$

$$\overline{\delta } = 0.65 \le \mu_{p} \left( {o_{p} } \right) = \frac{{117,266*10^{9} - o_{p} }}{{117,266*10^{9} - 374,183*10^{7} }}$$

(78)

$$\alpha \le \mu_{c} \left( {o_{c} } \right) = \frac{{732,624*10^{5} - o_{c} }}{{732,624*10^{5} - 29,713*10^{6} }}$$

Equations (2)–(22)

$$0 \le \alpha \le 1$$

The revised mathematical model is solved to optimality. In this case, the lower-level objective variable attains a value that fails to satisfy lover-level DM’s expectations when $\alpha$ attains $0.43.$ According to the lower-level DM’s academic and practical experience, o_c shouldn’t exceed $480{,}000{*}10^{5}$ Ł for the sake of practicability and sustainability of the project. As a result, $\overline{\delta }$ is calculated (Eq. 63) and the revised mathematical model resolved. Table 10 presents the experimental results of the fuzzy multi-objective models. Table 10 presents that the objective variables of top-level (o_p) and lower-level (o_c) DMs obtained their best values when $\alpha = 0.58$ and $\overline{\delta } = 0.65$.

Table 10 Experimental results of the revised mathematical models

The experimental results presented in Table 10 highlight that the pollution objective variable (o_p) decreases more than 50% and the cost objective variable (o_c) decreases about 12% when the satisfaction levels of the top and lower-level DMs ($\tilde{\delta }$ and $\overline{\delta }$) are readjusted. Furthermore, all transfer centres (y_j) and landfilling centres (z_l) are kept open in the next 10 years.

6 Discussion

The review of existing literature and the development of a conceptual framework presented in this paper give an impulse for environmental operations researchers to explore this field. In this study, a Scenario-based Stochastic Interactive Fuzzy Multi-Objective Approach is performed to determine the amounts and the routes of the transferred materials and to determine the facility locations in a solid waste recycling system. To deal with the uncertainties and vagueness in the study, stochastic and fuzzy-based modelling approaches are performed and the results of the study are presented in Sects. 4.6 and 4.7. However, there are various limitations in this study that can have significant impacts on the results of the mathematical model. As generated amount of solid waste is considered as a stochastic-based parameter in this study, the scenario weights and the amounts of the generated waste in optimistic and pessimistic scenarios have to be determined by the experts. Furthermore, the fuzzy satisfaction levels of the DMs have to be predetermined. These factors cause subjectivity and expert dependency in the proposed model. Moreover, only environmental and economical objectives are considered in the case study. Other factors such as sustainability, resilience, social acceptance, land-use stress and climate change could have been included in the case study in various ways. Last but not the least, data collection is one of the biggest challenges in the mathematical modelling approaches as obtaining updated and valid data is a very demanding process.

In the case study section of this publication, supply chain management of the solid waste recycling system in Istanbul is highlighted. There are various reasons for selecting Istanbul as a pilot city. The authors’ practical and academic experience in the waste management projects in Istanbul and the authors’ ability to gather real-life data from the local authorities are the most significant reasons. Furthermore, Istanbul represents a sophisticated case in terms of its geographic location as Istanbul bridges Asia and Europe and it exemplifies both Eastern and Western socio-politic features. In this case study, the conflict of environmental (top-level) and economic (lower-level) objectives are reconciled with the Interactive Fuzzy Multi-Objective Approach. This method can be adapted and extended for different cases. For instance, the hierarchical structure and content of the objective functions can be revised. Furthermore, satisfaction levels of the DMs can be easily adapted regarding the practical expectations of the DMs. In this case study, solid waste is presented as an example, however, this study aims to enable future researchers to reconcile the conflicting goals in the supply chain process of various waste types (e.g. end-of-life vehicles, end-of-life buildings, waste of electrical and electronic equipments).

7 Conclusion and future research

The review of existing literature and the development of a conceptual framework presented in this paper give an impulse for environmental operations researchers to explore this field further. The research question posed in the title of this paper is: Can the different goals be reconciled? And the answer lies in the different research problems and implementation of the solution to these problems. The conceptual framework proposed in Sect. 5.1 and depicted in Fig. 4 has been formulated to improve the identification of problems regarding the green supply chain and to give a better insight into the whole process of building mathematical models for the environmental problems. This framework is based on strong theoretical grounds presented in Sects. 2, 3 and 4, and it presents an upgrade of the frameworks given in Bloemhof-Ruwaard et al. (1995) and Daniel et al. (1997). Application of the proposed framework should occur in a context where the need to promote sustainable resource use in a particular management unit has been of great importance, and the need to set research goals in order with the economic and environmental requests. The answer can be in prioritizing the problem goals, and the need for a compromise between the goals is necessary.

The correlation between economic and environmental variables defined in this framework qualitatively supports the methodology. Further research will be addressed to the quantification of the outcome specific to different environmental problems to develop new tools and parameters which can provide results easily comparable against benchmarks. In general, two major approaches to every research are quantitative, which is a positivist approach; and, qualitative, the more interpretive approach (Burger, 2008). Future research will, according to the previous stated, include analysis of the economic effects and environmental effects after the solution implementation. It is important to consider the natural resources problems concerning the entire environment. The potential for transferability of the framework to the resource management problems in the natural resource industry can be better assessed, using a broader range of management tools and techniques for solving and not only operations research methods.

Besides the industry participants, other stakeholders, like the community, nonprofit and non-governmental sectors are not included in this framework at this point. In our opinion, in order to include mentioned stakeholders’ requests regarding environmental issues, they have to be incorporated in the governmental policy and regulations. According to this, the role of these stakeholders are implicitly incorporated in the framework, but in future research, more attention will be paid to the role of community, nonprofit and non-governmental sector in causing, amplifying and responding to environmental problems. Special attention will be given to the conclusions in the paper Midgley et al. (2018), where authors conclude that the client’s perspective may be part of the problem. The framing of the environmental problem has to emerge from an engagement with relevant stakeholders, and these stakeholders also need to participate in developing plans for action and solution implementation. These authors emphasize that so many OR practitioners are satisfied with a practice that is only client-engaged, and not engaged in any wider sense. They assume that it is necessary for OR to be more engaged in the wider sense, but there are cultural and psychological barriers to overcome and notice the possibility that the majority of OR practitioners are actually right to resist stakeholder and community engagement.

The limitations of the research in this paper can be seen in the area of generalization of the framework and application, where we focused only on mathematical modelling and not on the entire area of decision modelling. Environmental problems that are suitable for the conceptual framework are quantitative. Other qualitative aspects are not incorporated in our research but could be of substantial importance for the solution implementation of the problem and future research of the environmental operations research can include a broader conception of other decision-making models and methods.