Skip to main content
SpringerLink
Log in

Spatial–temporal evolution and regional difference decomposition of urban environmental governance efficiency in China

  • Published:
Environment, Development and Sustainability Aims and scope Submit manuscript

Abstract

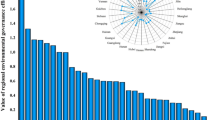
The three-stage DEA method and super-SBM are combined to measure the urban environmental governance efficiency of 30 provinces in China from 2004 to 2016. Then, ArcGIS software is used to illustrate the spatial–temporal evolution of urban environmental governance efficiency, and DagumGiniratio is calculated to show the regional difference. The results indicate that the provinces characterized by high or low environmental governance efficiency are shown to cluster in space over time, and the spatial dependence of the environmental governance behavior of government is the greatest source of the regional difference of urban environmental governance efficiency. Our findings imply that the environmental governance behavior of government is spatial dependent, which highlights that the policies for improve environmental governance efficiency should be made globally.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

Availability of data and material

Not applicable.

Notes

  1. DEA is an efficiency evaluation method that provides a comprehensive evaluation ofthe relative effectiveness of similar decision-making units (Charnes et al. 1978). It is a widely used linear programming technique for evaluate the performance of decision-making units on the basis of their inputs andoutputs.

  2. SBM (Tone 2001) is non-radial and deals with input/output slacks directly. The SBM returns an efficiency measure between 0 and 1, and gives unity if and only if the decision-making unit concerned is on the frontiers of the production possibility set with no input/output slacks.

  3. There are 34 provinces in China. For the reason of the lack of data, Tibet, Macau, Hong Kong and Taiwan are excluded from the sample. Therefore, the 30 provinces are Beijing, Tianjin, Hebei, Liaoning, Shanghai, Jiangsu, Zhejiang, Fujian, Shandong, Guangdong, Guangxi, Hainan, Shanxi, Inner Mongolia, Jilin, Heilongjiang, Anhui, Jiangxi, Henan, Hubei, Hunan, Chongqing, Sichuan, Guizhou, Yunnan, Shaanxi, Gansu, Qinghai, Ningxia and Xinjiang.

  4. The eastern region includes Beijing, Tianjin, Hebei, Liaoning, Shanghai, Jiangsu, Zhejiang, Fujian, Shandong, Guangdong, Guangxi and Hainan, the central region includes Shanxi, Inner Mongolia, Jilin, Heilongjiang, Anhui, Jiangxi, Henan, Hubei and Hunan, and thewestern region includes Chongqing, Sichuan, Guizhou, Yunnan, Shaanxi, Gansu, Qinghai, Ningxia and Xinjiang.

  5. The averages of Gini ratio of urban EGE within region are 0.181, 0.153 and 0.171 for eastern region, central region and western region, respectively.

  6. The standard deviations of Gini ratio of urban EGE within region are 0.003, 0.001 and 0.001 for eastern region, central region and western region, respectively.

  7. The averages of Gini ratio of urban EGE between regions are 0.201, 0.212 and 0.180 for eastern and central region, eastern and western region, and central and western region, respectively.

  8. The standard deviations of Gini ratio of urban EGE between regions are 0.001, 0.003 and 0.001 for eastern and central region, eastern and western region, and central and western region, respectively.

References

  • Adame, J. A., Hernández-Ceballos, M. A., & Bolívar, J. P. (2012). Assessment of an air pollution event in the south-western Iberian Peninsula. Atmospheric Environment, 55(8), 245–256.

    Article  CAS  Google Scholar 

  • Aigner, D., Lovell, C. A. K., & Schmidt, P. (1977). Formulation and estimation of stochastic frontier production function models. Journal of Econometrics, 6(1), 21–37.

    Article  Google Scholar 

  • Brandt, A. R., & Dale, M. A. (2011). General mathematical framework for calculating systems-scale efficiency of energy extraction and conversion: Energy return on investment (EROI) and other energy return ratios. Energies, 4(8), 1211–1245.

    Article  Google Scholar 

  • Charnes, A., Cooper, W. W., & Rhodes, E. (1978). Measuring the efficiency of decision making units. European Journal of Operational Research, 2(6), 429–444.

    Article  Google Scholar 

  • Cole, M. A., & Elliott, R. J. (2007). Do environmental regulations cost jobs? An industry-level analysis of the UK. The B.E. Journal of Economic Analysis & Policy, 7(1), 28–48.

    Article  Google Scholar 

  • Dagum, C. (1997). A new approach to the decomposition of the GiniIncome inequality ratio. Empirical Economic, 22(12), 515–531.

    Article  Google Scholar 

  • Dasgupta, S., Laplante, B., Mamingi, N., & Wang, H. (2001). Inspections, pollution prices, and environmental performance: Evidence from China. Ecological Economic, 36(3), 487–498.

    Article  Google Scholar 

  • Fried, H. O., Lovell, C. A. K., Schmidt, S. S., & Yaisawarng, S. (2002). Accounting for environmental effects and statistical noise in data envelopment analysis. Journal of Productivity Analysis, 17(1–2), 157–174.

    Article  Google Scholar 

  • Goto, M., Otsuka, A., & Sueyoshi, T. (2014). DEA (data envelopment analysis) Assessment of operational and environmental efficiencies on Japanese regional industries. Energy, 66(1), 535–549.

    Article  Google Scholar 

  • Guo, J., & Bai, J. H. (2019). The role of public participation in environmental governance: Empirical evidence from China. Sustainability, 11(17), 4696–4715.

    Article  Google Scholar 

  • Jin, H., Qian, Y., & Weingast, B. R. (2005). regional decentralization and fiscal incentives: Federalism, Chinese Style. Journal of Public Economics, 89(9–10), 1719–1742.

    Article  Google Scholar 

  • Jondrow, J., Lovell, C. A. K., & Materov, I. S. (1982). On the estimation of technical inefficiency in the stochastic frontier production function mode. Journal of Econometrics, 19(2–3), 233–238.

    Article  Google Scholar 

  • Liu, H., He, S., & Wang, Y. (2019). Research on rural environmental governance efficiency based on the three-stage DEA and super-SBM model. Ecological Economy, 35(8), 194–199. (in Chinese).

    Google Scholar 

  • Mandal, S. K., & Madheswaran, S. (2010). Environmental efficiency of the indian cement industry: An interstate analysis. Energy Policy, 38(2), 1108–1118.

    Article  CAS  Google Scholar 

  • Meeusen, W., & van den Broeck, J. (1977). efficiency estimation from Cobb-Douglas production functions with composed error. International Economic Review, 18(2), 435–444.

    Article  Google Scholar 

  • Morgenstern, R. D., Pizer, W. A., & Shih, J. S. (2002). Jobs versus the environment: an industry-level perspective. Journal of Environmental Economics & Management, 43(3), 412–436.

    Article  Google Scholar 

  • Ogawa, H., & Wildasin, D. E. (2009). Think locally, act locally: Spillovers, spillbacks and efficient decentralized policy making. The American Economic Review, 99(4), 1206–1217.

    Article  Google Scholar 

  • Song, M., Zhang, L., An, Q., Wang, Z., & Li, Z. (2013). Statistical analysis and combination forecasting of environmental efficiency and its influential factors since china entered the WTO: 2002–2010–2012. Journal of Cleaner Production, 42(3), 42–51.

    Article  Google Scholar 

  • Soytas, U., Sari, R., & Ewing, B. T. (2007). Energy consumption, income, and carbon emission in the United States. Ecological Economics, 62(3–4), 482–489.

    Article  Google Scholar 

  • Tan, Y., Tian, X., Zhang, C., & Zhao, H. (2014). Privatization and innovation: Evidence from a quasi-natural experiment in China. SSRN Electronic Journal.

  • Tone, K. (2001). A slacks-based measure of efficiency in data envelopment analysis. European Journal of Operational Research, 130(3), 498–509.

    Article  Google Scholar 

  • Tone, K. (2002). Slacks-based measure of super-efficiency in data envelopment analysis. European Journal of Operational Research, 143(1), 32–41.

    Article  Google Scholar 

  • Wang, B., & Luo, Y. J. (2015). An empirical study on China’s regional industrial production efficiency, environmental governance efficiency and comprehensive efficiency: An analysis based on the DEA model of RAM networks. World Economic Papers, 1, 99–119. (in Chinese).

    Google Scholar 

  • Westermann, G. (1999). Data envelopment analysis in the service sector. Wiesbaden: Deutscher Universitätsverlag.

    Book  Google Scholar 

  • Yi, H. T., Huang, C., Chen, T., Xu, X. L., & Liu, W. X. (2019). Multilevel environmental governance: Vertical and horizontal influences in local policy networks. Sustainability, 11(8), 2390–2403.

    Article  Google Scholar 

Download references

Funding

We would like to thank the funds from the National Natural Science Foundation of China (Grant No. 71863009), and the Natural Science Foundation of Hunan Province (Grant No. 2019JJ50482).

Author information

Authors and Affiliations

  1. Business School, Jiangsu University of Technology, Changzhou, 213001, China

    Geng Peng & Fang Liu

  2. Business School, Tianjin University of Finance and Economics, Tianjin, 300222, China

    Xiaodan Zhang

  3. Shiliang Law School, Changzhou University, Changzhou, 213164, China

    Lijuan Ruan & Kaiyou Tian

Authors
  1. Geng Peng
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Xiaodan Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Fang Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Lijuan Ruan
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Kaiyou Tian
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

Peng and Liu conceived and designed the study. Liu, Zhang, Ruan and Tian collected the data and done the empirical analysis. Peng, Zhang and Liu wrote, reviewed, revised and edited the manuscript. All authors read and approved the manuscript.

Corresponding author

Correspondence to Fang Liu.

Ethics declarations

Conflicts of interest

No conflict of interest exits in the submission of this manuscript, and manuscript is approved by all authors for publication.

Code availability

Not applicable.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Peng, G., Zhang, X., Liu, F. et al. Spatial–temporal evolution and regional difference decomposition of urban environmental governance efficiency in China. Environ Dev Sustain 23, 8974–8990 (2021). https://doi.org/10.1007/s10668-020-01007-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10668-020-01007-2

Keywords

Search

Navigation