Skip to main content
SpringerLink
Log in

How Carbon Tax Policy Affects the Carbon Emissions of Manufacturers with Green Technology Spillovers?

  • Research
  • Published:
Environmental Modeling & Assessment Aims and scope Submit manuscript

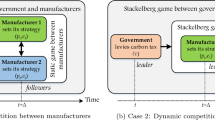
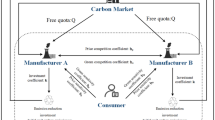
Abstract

This study examines the effects of carbon tax policies on carbon emissions in the context of green technology spillovers among manufacturers. We develop a differential game model that incorporates both horizontal and vertical green technology spillovers, analyzing scenarios with and without a carbon tax policy. Our equilibrium analysis demonstrates that a carbon tax policy effectively promotes carbon reduction in manufacturers experiencing green technology spillovers by increasing investment in green technology. The policy also mitigates the negative effect of free-riding among competing manufacturers (horizontal spillovers) while enhancing the positive effect of free-riding among non-competitors (vertical spillovers). Additionally, we find that raising carbon tax or fostering vertical spillovers can enhance the profitability of supply chain participants by expanding the market scale. Conversely, elevating consumer environment awareness yields greater benefits for those who innovate (the spiller) rather than those who adopt (the recipient). Our findings offer novel managerial insights for manufacturers navigating green technology spillovers in a landscape shaped by carbon tax policy.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

Data Availability

Data sharing is not applicable to this article as no datasets were generated or analyzed during the current study.

References

  1. Zhao, X., Ma, X., Chen, B., Shang, Y., & Song, M. (2022). Challenges toward carbon neutrality in China: Strategies and countermeasures. Resources, Conservation and Recycling, 176, 105959. https://doi.org/10.1016/j.resconrec.2021.105959

    Article  CAS  Google Scholar 

  2. Carroll, D. A., & Stevens, K. A. (2021). The short-term impact on emissions and federal tax revenue of a carbon tax in the U.S. electricity sector. Energy Policy, 158, 112526. https://doi.org/10.1016/j.enpol.2021.112526

    Article  Google Scholar 

  3. Jiao, J., Chen, C., & Bai, Y. (2020). Is green technology vertical spillovers more significant in mitigating carbon intensity? Evidence from Chinese industries. Journal of Cleaner Production, 257, 120354. https://doi.org/10.1016/j.jclepro.2020.120354

    Article  Google Scholar 

  4. Meng, X., & Yu, Y. (2023). Can renewable energy portfolio standards and carbon tax policies promote carbon emission reduction in China’s power industry? Energy Policy, 174, 113461. https://doi.org/10.1016/j.enpol.2023.113461

    Article  Google Scholar 

  5. Qian, Y., Yu, X., Shen, Z., & Song, M. (2023). Complexity analysis and control of game behavior of subjects in green building materials supply chain considering technology subsidies. Expert Systems with Applications, 214, 119052. https://doi.org/10.1016/j.eswa.2022.119052

    Article  Google Scholar 

  6. Wang, X., Yu, B., An, R., Sun, F., & Xu, S. (2022). An integrated analysis of China’s iron and steel industry towards carbon neutrality. Applied Energy, 322, 119453. https://doi.org/10.1016/j.apenergy.2022.119453

    Article  CAS  Google Scholar 

  7. Xin-gang, Z., Wenjie, L., Wei, W., & Shuran, H. (2023). The impact of carbon emission trading on green innovation of China’s power industry. Environmental Impact Assessment Review, 99, 107040. https://doi.org/10.1016/j.eiar.2023.107040

    Article  Google Scholar 

  8. Chen, J., Gao, M., Mangla, S. K., Song, M., & Wen, J. (2020). Effects of technological changes on China’s carbon emissions. Technological Forecasting and Social Change, 153, 119938. https://doi.org/10.1016/j.techfore.2020.119938

    Article  Google Scholar 

  9. Chien, F., Ananzeh, M., Mirza, F., Bakar, A., Vu, H. M., & Ngo, T. Q. (2021). The effects of green growth, environmental-related tax, and eco-innovation towards carbon neutrality target in the US economy. Journal of Environmental Management, 299, 113633. https://doi.org/10.1016/j.jenvman.2021.113633

    Article  CAS  Google Scholar 

  10. Fu, L., Yi, Y., Wu, T., Cheng, R., & Zhang, Z. (2023). Do carbon emission trading scheme policies induce green technology innovation? New evidence from provincial green patents in China. Environmental Science and Pollution Research, 30(5), 13342–13358. https://doi.org/10.1007/s11356-022-22877-1

    Article  Google Scholar 

  11. Khastar, M., Aslani, A., & Nejati, M. (2020). How does carbon tax affect social welfare and emission reduction in Finland? Energy Reports, 6, 736–744. https://doi.org/10.1016/j.egyr.2020.03.001

    Article  Google Scholar 

  12. Kumbhakar, S. C., Badunenko, O., & Willox, M. (2022). Do carbon taxes affect economic and environmental efficiency? The case of British Columbia’s manufacturing plants. Energy Economics, 115, 106359. https://doi.org/10.1016/j.eneco.2022.106359

    Article  Google Scholar 

  13. Raihan, A., Muhtasim, D. A., Farhana, S., Hasan, M. A. U., Pavel, M. I., Faruk, O., Rahman, M., & Mahmood, A. (2022). Nexus between economic growth, energy use, urbanization, agricultural productivity, and carbon dioxide emissions: New insights from Bangladesh. Energy Nexus, 8, 100144. https://doi.org/10.1016/j.nexus.2022.100144

    Article  CAS  Google Scholar 

  14. Wang, R., Wen, X., Wang, X., Fu, Y., & Zhang, Y. (2022). Low carbon optimal operation of integrated energy system based on carbon capture technology, LCA carbon emissions and ladder-type carbon trading. Applied Energy, 311, 118664. https://doi.org/10.1016/j.apenergy.2022.118664

    Article  CAS  Google Scholar 

  15. Hou, H., Su, L., Guo, D., & Xu, H. (2023). Resource utilization of solid waste for the collaborative reduction of pollution and carbon emissions: Case study of fly ash. Journal of Cleaner Production, 383, 135449. https://doi.org/10.1016/j.jclepro.2022.135449

    Article  CAS  Google Scholar 

  16. Xu, T., Kang, C., & Zhang, H. (2022). China’s efforts towards carbon neutrality: Does energy-saving and emission-reduction policy mitigate carbon emissions? Journal of Environmental Management, 316, 115286. https://doi.org/10.1016/j.jenvman.2022.115286

    Article  CAS  Google Scholar 

  17. Yang, Z., Zhang, M., Liu, L., & Zhou, D. (2022). Can renewable energy investment reduce carbon dioxide emissions? Evidence from scale and structure. Energy Economics, 112, 106181. https://doi.org/10.1016/j.eneco.2022.106181

    Article  Google Scholar 

  18. Brandão, L. G. L., & Ehrl, P. (2019). International R&D spillovers to the electric power industries. Energy, 182, 424–432. https://doi.org/10.1016/j.energy.2019.06.046

    Article  Google Scholar 

  19. Chen, X., Wang, X., & Zhou, M. (2019). Firms’ green R&D cooperation behaviour in a supply chain: Technological spillover, power and coordination. International Journal of Production Economics, 218, 118–134. https://doi.org/10.1016/j.ijpe.2019.04.033

    Article  Google Scholar 

  20. De Bondt, R. (1997). Spillovers and innovative activities. International Journal of Industrial Organization, 15(1), 1–28. https://doi.org/10.1016/S0167-7187(96)01023-5

    Article  Google Scholar 

  21. Quatraro, F., & Scandura, A. (2019). Academic inventors and the antecedents of green technologies. A regional analysis of Italian patent data. Ecological Economics, 156, 247–263. https://doi.org/10.1016/j.ecolecon.2018.10.007

    Article  Google Scholar 

  22. Chen, J., Long, X., & Lin, S. (2022). Special economic zone, carbon emissions and the mechanism role of green technology vertical spillover: Evidence from Chinese cities. International Journal of Environmental Research and Public Health, 19(18), 11535. https://doi.org/10.3390/ijerph191811535

    Article  Google Scholar 

  23. Lee, H., Kim, H., Choi, D. G., & Koo, Y. (2022). The impact of technology learning and spillovers between emission-intensive industries on climate policy performance based on an industrial energy system model. Energy Strategy Reviews, 43, 100898. https://doi.org/10.1016/j.esr.2022.100898

    Article  Google Scholar 

  24. Yang, X., Yang, Z., & Jia, Z. (2021). Effects of technology spillover on CO2 emissions in China: A threshold analysis. Energy Reports, 7, 2233–2244. https://doi.org/10.1016/j.egyr.2021.04.028

    Article  Google Scholar 

  25. Ma, Q., Murshed, M., & Khan, Z. (2021). The nexuses between energy investments, technological innovations, emission taxes, and carbon emissions in China. Energy Policy, 155, 112345. https://doi.org/10.1016/j.enpol.2021.112345

    Article  CAS  Google Scholar 

  26. Xie, P., Gong, N., Sun, F., Li, P., & Pan, X. (2023). What factors contribute to the extent of decoupling economic growth and energy carbon emissions in China? Energy Policy, 173, 113416. https://doi.org/10.1016/j.enpol.2023.113416

    Article  CAS  Google Scholar 

  27. Fan, X., Chen, K., & Chen, Y.-J. (2023). Is price commitment a better solution to control carbon emissions and promote technology investment? Management Science, 69(1), 325–341. https://doi.org/10.1287/mnsc.2022.4365

    Article  Google Scholar 

  28. Nie, P.-Y., Wang, C., & Wen, H.-X. (2022). Optimal tax selection under monopoly: Emission tax vs carbon tax. Environmental Science and Pollution Research, 29(8), 12157–12163. https://doi.org/10.1007/s11356-021-16519-1

    Article  Google Scholar 

  29. Zhao, A., Song, X., Li, J., Yuan, Q., Pei, Y., Li, R., & Hitch, M. (2023). Effects of carbon tax on urban carbon emission reduction: Evidence in China environmental governance. International Journal of Environmental Research and Public Health, 20(3), 2289. https://doi.org/10.3390/ijerph20032289

    Article  CAS  Google Scholar 

  30. Chen, X., & Lin, B. (2021). Towards carbon neutrality by implementing carbon emissions trading scheme: Policy evaluation in China. Energy Policy, 157, 112510. https://doi.org/10.1016/j.enpol.2021.112510

    Article  CAS  Google Scholar 

  31. Dong, Z., Xia, C., Fang, K., & Zhang, W. (2022). Effect of the carbon emissions trading policy on the co-benefits of carbon emissions reduction and air pollution control. Energy Policy, 165, 112998. https://doi.org/10.1016/j.enpol.2022.112998

    Article  CAS  Google Scholar 

  32. Jiao, J., Jiang, G., & Yang, R. (2018). Impact of R&D technology spillovers on carbon emissions between China’s regions. Structural Change and Economic Dynamics, 47, 35–45. https://doi.org/10.1016/j.strueco.2018.07.002

    Article  Google Scholar 

  33. Eichner, T., & Kollenbach, G. (2022). Environmental agreements, research and technological spillovers. European Journal of Operational Research, 300, 366–377.

    Article  Google Scholar 

  34. Feichtinger, G., Lambertini, L., Leitmann, G., & Wrzaczek, S. (2016). R&D for green technologies in a dynamic oligopoly: Schumpeter, arrow and inverted-U’s. European Journal of Operational Research, 249(3), 1131–1138. https://doi.org/10.1016/j.ejor.2015.09.025

    Article  Google Scholar 

  35. Guo, J.-X., & Fan, Y. (2017). Optimal abatement technology adoption based upon learning-by-doing with spillover effect. Journal of Cleaner Production, 143, 539–548. https://doi.org/10.1016/j.jclepro.2016.12.076

    Article  Google Scholar 

  36. Jamali, M.-B., & Rasti-Barzoki, M. (2022). A game-theoretic approach for examining government support strategies and licensing contracts in an electricity supply chain with technology spillover: A case study of Iran. Energy, 242, 122919. https://doi.org/10.1016/j.energy.2021.122919

    Article  Google Scholar 

  37. Yang, Y., & Nie, P. (2022). Subsidy for clean innovation considered technological spillover. Technological Forecasting and Social Change, 184, 121941. https://doi.org/10.1016/j.techfore.2022.121941

    Article  Google Scholar 

  38. Zhang, F., Zhang, Z., Xue, Y., Zhang, J., & Che, Y. (2020). Dynamic green innovation decision of the supply chain with innovating and free-riding manufacturers: Cooperation and spillover. Complexity, 2020, 1–17. https://doi.org/10.1155/2020/8937847

    Article  CAS  Google Scholar 

  39. Ruff, L. E. (1969). Research and technological progress in a Cournot economy. Journal of Economic Theory, 1(4), 397–415. https://doi.org/10.1016/0022-0531(69)90025-8

    Article  Google Scholar 

  40. d’Aspremont, C., & Jacquemin, A. (1988). Cooperative and noncooperative R&D in duopoly with spillovers. The American Economic Review, 78(5), 1133–1137.

    Google Scholar 

  41. De Bondt, R., Slaets, P., & Cassiman, B. (1992). The degree of spillovers and the number of rivals for maximum effective R & D. International Journal of Industrial Organization, 10(1), 35–54. https://doi.org/10.1016/0167-7187(92)90046-2

    Article  Google Scholar 

  42. De Bondt, R., & Veugelers, R. (1995). Strategic investment with spillovers. European Journal of Political Economy, 7(3), 345–366. https://doi.org/10.1016/0176-2680(91)90018-X

    Article  Google Scholar 

Download references

Acknowledgements

We would like to express our deepest gratitude to the scholars who provided invaluable feedback and insights during the review of this paper. Their expertise and thoughtful comments significantly contributed to the quality and rigor of our work.

Funding

This work is supported by the Major Project of Philosophy and Social Science Research in Colleges and Universities of Jiangsu Province (Grant Number, 2021SJZDA131).

Author information

Authors and Affiliations

  1. School of Management Science and Engineering, Nanjing University of Information Science and Technology, Nanjing, 210044, People’s Republic of China

    Qiyao Liu & Xiaodong Zhu

Authors
  1. Qiyao Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Xiaodong Zhu
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

Qiyao Liu: investigation, writing original draft, software, and visualization. Xiaodong Zhu: conceptualization, supervision, methodology, writing, review, and editing. All authors reviewed the manuscript.

Corresponding author

Correspondence to Xiaodong Zhu.

Ethics declarations

Ethics Approval

This article does not contain any studies with human participants or animals performed by any of the authors.

Consent to Participate

All authors participated in this article.

Consent for Publication

All authors have given consent to the publication of this article.

Competing Interests

The authors have no relevant financial or non-financial interests to disclose.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendix

Appendix

1.1 Proof of Theorem 1

According to formulas (6) to (7), the optimal profit value functions for the manufacturers and the supplier after time \(t\) are

$$\left\{\begin{array}{c}{{J}_{j}}^{N*}\left({e}_{j},{e}_{\overline{j} }\right)={e}^{-\rho t}\underset{{u}_{j}\left(t\right)\ge 0}{{\text{max}}}{\int }_{t}^{\infty }{e}^{-\rho \left(\xi -t\right)}\left[{\pi }_{j}{q}_{j}-\frac{{\mu }_{j}{{u}_{j}}^{2}\left(t\right)}{2}\right]dt,\\ {{J}_{S}}^{N*}\left({e}_{S}\right)={e}^{-\rho t}\underset{{u}_{S}\left(t\right)\ge 0}{{\text{max}}}{\int }_{t}^{\infty }{e}^{-\rho \left(\xi -t\right)}\left[{\pi }_{S}Q-\frac{{\mu }_{S}{{u}_{S}}^{2}\left(t\right)}{2}\right]dt,\end{array}\right.$$
(A.1)

where \(j\in \{L,F\}\).

Further, assume that

$$\left\{\begin{array}{c}{{V}_{j}}^{N}\left({e}_{j},{e}_{\overline{j} }\right)=\underset{{u}_{j}(t)\ge 0}{{\text{max}}}{\int }_{t}^{\infty }{e}^{-\rho (\xi -t)}[{\pi }_{j}{q}_{j}-\frac{{\mu }_{j}{{u}_{j}}^{2}(t)}{2}]d\xi ,\\ {{V}_{S}}^{N}\left({e}_{S}\right)=\underset{{u}_{S}\left(t\right)\ge 0}{{\text{max}}}{\int }_{t}^{\infty }{e}^{-\rho \left(\xi -t\right)}\left[{\pi }_{S}Q-\frac{{\mu }_{S}{{u}_{S}}^{2}\left(t\right)}{2}\right]d\xi ,\end{array}\right.$$
(A.2)

where \(j\in \{L,F\}\).

Then, the optimal profit value functions for the manufacturers and supplier after time \(t\) transforms into

$$\left\{\begin{array}{c}{{J}_{j}}^{N*}\left({e}_{j},{e}_{\overline{j} }\right)={e}^{-\rho t}{{V}_{j}}^{N}\left({e}_{j},{e}_{\overline{j} }\right),\\ {{J}_{S}}^{N*}\left({e}_{S}\right)={e}^{-\rho t}{{V}_{S}}^{N}\left({e}_{S}\right),\end{array}\right.$$
(A.3)

where \(j\in \{L,F\}\).

According to optimal control theory, the problem satisfies the following Hamiltonian-Jacobi-Bellman (HJB) equations:

$$\left\{\begin{array}{c}\rho {{V}_{j}}^{N}\left({e}_{j},{e}_{\overline{j} }\right)=\underset{{u}_{j}(t)>0}{{\text{max}}}[{\pi }_{j}{q}_{j}-\frac{{\mu }_{j}{{u}_{j}}^{2}(t)}{2}],\\ \rho {{V}_{S}}^{N}\left({e}_{S}\right)=\underset{{u}_{S}\left(t\right)>0}{{\text{max}}}\left[{\pi }_{S}Q-\frac{{\mu }_{S}{{u}_{S}}^{2}\left(t\right)}{2}\right],\end{array}\right.$$
(A.4)

where \(j\in \{L,F\}\).

It is easy to prove that formulas (A.4) are concave functions with respect to \({u}_{j}\left(t\right)\), \(j\in \{L,F,S\}\). The derivative of the solutions is equal to 0 to obtain

$$\left\{\begin{array}{c}{u}_{L}=\frac{{{V}_{LL}}^{N`}+{\alpha }_{1}{{V}_{LF}}^{N`}}{{\mu }_{L}},\\ {u}_{F}=\frac{{{V}_{FF}}^{N`}}{{\mu }_{F}},\\ {u}_{S}=\frac{{{V}_{SS}}^{N`}}{{\mu }_{S}},\end{array}\right.$$
(A.5)

where \({{V}_{ij}}^{N`}=\frac{\partial {V}_{i}}{\partial {e}_{j}},i,j\in \{L,F,S\}\).

Substitute formulas (A.5) into formulas (A.4) to obtain

$$\left\{\begin{array}{c}\rho {{V}_{L}}^{N}\left({e}_{L},{e}_{F}\right)={e}_{L}\left(s{\pi }_{L}-\delta {{V}_{LL}}^{N`}\right)-{e}_{F}\left(s{\pi }_{L}+\delta {{V}_{LF}}^{N`}\right)+\lambda Q{\pi }_{L}+\\ \frac{{({{V}_{LL}}^{N`}+{\alpha }_{1}{{V}_{LF}}^{N`})}^{2}}{2{\mu }_{L}}+\frac{{{V}_{FF}}^{N`}{{V}_{LF}}^{N`}}{{\mu }_{F}}+\frac{{{V}_{SS}}^{N`}({{V}_{LL}}^{N`}{\beta }_{1}+{{V}_{LF}}^{N`}{\beta }_{2})}{{\mu }_{S}},\\ \rho {{V}_{F}}^{N}\left({e}_{L},{e}_{F}\right)=[{e}_{F}\left(s{\pi }_{F}-\delta {{V}_{FF}}^{N`}\right)-{e}_{L}\left(s{\pi }_{F}+\delta {{V}_{FL}}^{N`}\right)+(1-\lambda )Q{\pi }_{F}+\\ \frac{({{V}_{FL}}^{N`}+{\alpha }_{1}{{V}_{FF}}^{N`})({V}_{LL}+{V}_{LF}{\alpha }_{1})}{{\mu }_{L}}+\frac{{{{V}_{FF}}^{N`}}^{2}}{2{\mu }_{F}}+\frac{{V}_{{\text{SS}}}({\beta }_{1}{{V}_{FL}}^{N`}+{\beta }_{2}{{V}_{FF}}^{N`})}{{\mu }_{S}},\\ \rho {{V}_{S}}^{N}\left({e}_{S}\right)=Q{\pi }_{S}+\frac{1}{2}{{V}_{SS}}^{N`}\left[\frac{2\left({{V}_{LL}}^{N`}+{\alpha }_{1}{{V}_{LF}}^{N`}\right){\alpha }_{2}}{{\mu }_{L}}+\frac{{{V}_{SS}}^{N`}}{{\mu }_{S}}-2\delta {e}_{S}\right].\end{array}\right.$$
(A.6)

Observe the structural features of formulas (A.6) and infer that the linear functions on \(e\) are the solutions to the HJB equations. Assume that

$$\left\{\begin{array}{c}{{V}_{L}}^{N}\left({e}_{L},{e}_{F}\right)={a}_{1}{e}_{L}+{a}_{2}{e}_{F}+{a}_{3},\\ {{V}_{F}}^{N}\left({e}_{L},{e}_{F}\right)={b}_{1}{e}_{L}+{b}_{2}{e}_{F}+{b}_{3},\\ {{V}_{S}}^{N}\left({e}_{S}\right)={c}_{1}{e}_{S}+{c}_{2}.\end{array}\right.$$
(A.7)

Substituting formula (A.7) and \({{V}_{ij}}^{`},i,j\in \{L,F,S\}\), into formula (A.6), we obtain

$$\left\{\begin{array}{c}{a}_{1}=\frac{s{\pi }_{L}}{\delta +\rho },{a}_{2}=-\frac{s{\pi }_{L}}{\delta +\rho },{a}_{3}=\frac{\lambda Q{\pi }_{L}}{\rho }+\frac{{s}^{2}{{\pi }_{L}}^{2}{\left(1-{\alpha }_{1}\right)}^{2}}{2\rho {\left(\delta +\rho \right)}^{2}{\mu }_{L}}-\frac{{s}^{2}{\pi }_{L}{\pi }_{F}}{\rho {\left(\delta +\rho \right)}^{2}{\mu }_{F}},\\ {b}_{1}=-\frac{s{\pi }_{F}}{\delta +\rho },{b}_{2}=\frac{s{\pi }_{F}}{\delta +\rho },{b}_{3}=\frac{Q\left(1-\lambda \right){\pi }_{F}}{\rho }+\frac{{s}^{2}{{\pi }_{F}}^{2}}{2\rho {\left(\delta +\rho \right)}^{2}{\mu }_{F}}-\frac{{s}^{2}{\pi }_{L}{\pi }_{F}{\left(1-{\alpha }_{1}\right)}^{2}}{\rho {\left(\delta +\rho \right)}^{2}{\mu }_{L}},\\ {c}_{1}=0,{c}_{2}=\frac{Q{\pi }_{S}}{\rho }.\end{array}\right.$$
(A.8)

Combine formulas (A.7) and (A.8) to obtain \({{V}_{ij}}^{`},i,j\in \{L,F,S\}\). Substitute this into formulas (A5) to obtain

$$\left\{\begin{array}{c}{{u}_{L}}^{N*}=\frac{s{\pi }_{L}(1-{\alpha }_{1})}{(\delta +\rho ){\mu }_{L}},\\ {{u}_{F}}^{N*}=\frac{s{\pi }_{F}}{(\delta +\rho ){\mu }_{F}},\\ {{u}_{S}}^{N*}=0.\end{array}\right.$$

Further manufacturers and supplier carbon reduction stabilization values can be obtained:

$$\left\{\begin{array}{c}{{e}_{L}}^{N*}=\frac{s{\pi }_{L}(1-{\alpha }_{1})}{\delta (\delta +\rho ){\mu }_{L}},\\ {{e}_{F}}^{N*}=\frac{s[{\pi }_{F}{\mu }_{L}+{\pi }_{L}{\alpha }_{1}{\mu }_{F}\left(1-{\alpha }_{1}\right)]}{\delta (\delta +\rho ){\mu }_{L}{\mu }_{F}},\\ {{e}_{S}}^{N*}=\frac{s{\pi }_{L}(1-{\alpha }_{1}){\alpha }_{2}}{\delta (\delta +\rho ){\mu }_{L}},\end{array}\right.$$

and carbon reduction trajectories as follows:

$$\left\{\begin{array}{c}{{e}_{L}}^{N*}\left(t\right)=\frac{s{\pi }_{L}(1-{\alpha }_{1})}{\delta (\delta +\rho ){\mu }_{L}}+{e}^{-\delta t}{e}_{0},\\ {{e}_{F}}^{N*}\left(t\right)=\frac{s[{\pi }_{F}{\mu }_{L}+{\pi }_{L}{\alpha }_{1}{\mu }_{F}\left(1-{\alpha }_{1}\right)]}{\delta (\delta +\rho ){\mu }_{L}{\mu }_{F}}+{e}^{-\delta t}{e}_{0},\\ {{e}_{S}}^{N*}\left(t\right)=\frac{s{\pi }_{L}(1-{\alpha }_{1}){\alpha }_{2}}{\delta (\delta +\rho ){\mu }_{L}}+{e}^{-\delta t}{e}_{0}.\end{array}\right.$$

The optimal profit trajectories are

$${{J}_{L}}^{N*}={e}^{-\rho t}\left({a}_{1}{{e}_{L}}^{N*}+{a}_{2}{{e}_{F}}^{N*}+{a}_{3}\right),$$
$${{J}_{F}}^{N*}={e}^{-\rho t}\left({b}_{1}{{e}_{L}}^{N*}+{b}_{2}{{e}_{F}}^{N*}+{b}_{3}\right),$$
$${{J}_{S}}^{N*}={e}^{-\rho t}\left({c}_{1}{{e}_{S}}^{N*}+{c}_{2}\right),$$

where \({a}_{1}=\frac{s{\pi }_{L}}{\delta +\rho },\;{a}_{2}=-\frac{s{\pi }_{L}}{\delta +\rho },\;{a}_{3}=\frac{\lambda Q{\pi }_{L}}{\rho }+\frac{{s}^{2}{{\pi }_{L}}^{2}{\left(1-{\alpha }_{1}\right)}^{2}}{2\rho {\left(\delta +\rho \right)}^{2}{\mu }_{L}}-\frac{{s}^{2}{\pi }_{L}{\pi }_{F}}{\rho {\left(\delta +\rho \right)}^{2}{\mu }_{F}}\), \({b}_{1}=-\frac{s{\pi }_{F}}{\delta +\rho },\;{b}_{2}=\frac{s{\pi }_{F}}{\delta +\rho },\;{b}_{3}=\frac{Q\left(1-\lambda \right){\pi }_{F}}{\rho }\), \(+\frac{{s}^{2}{{\pi }_{F}}^{2}}{2\rho {\left(\delta +\rho \right)}^{2}{\mu }_{F}}-\frac{{s}^{2}{\pi }_{L}{\pi }_{F}{\left(1-{\alpha }_{1}\right)}^{2}}{\rho {\left(\delta +\rho \right)}^{2}{\mu }_{L}}\), \({c}_{1}=0,{c}_{2}=\frac{Q{\pi }_{S}}{\rho }\).

1.2 Proof of Theorem 2

The solution process is similar to Theorem 1 and is omitted here. The parameters in the trajectories are as follows:

$$\begin{aligned}&{f}_{1}=\frac{\tau -s\tau +s{\pi }_{L}}{\delta +\rho },\\&{f}_{2}=\frac{s\left(\tau -{\pi }_{L}\right)}{\delta +\rho },\\&{f}_{3}=\frac{{[\tau -s\tau+s{\pi }_{L}+s\left(\tau -{\pi }_{L}\right){\alpha }_{1}]}^{2}}{2\rho {(\delta +\rho )}^{2}{\mu }_{L}}\\&\qquad\;+\,\frac{s\left(\tau -s\tau +s{\pi }_{F}\right)\left(\tau -{\pi }_{L}\right)}{\rho {(\delta +\rho )}^{2}{\mu }_{F}}\\& \qquad\;+\,\frac{\tau \left[\left(\tau -s\tau +s{\pi }_{L}\right){\beta }_{1}+s\left(\tau -{\pi }_{L}\right){\beta }_{2}\right]}{2\rho {(\delta +\rho )}^{2}{\mu }_{S}}\\& \qquad\;-\,\frac{\lambda Q(\tau -{\pi }_{L})}{\rho },\end{aligned}$$
$$\begin{aligned}&{g}_{1}=\frac{s\left(\tau -{\pi }_{F}\right)}{\delta +\rho },\\&{g}_{2}=\frac{\tau -s\tau +s{\pi }_{F}}{\delta +\rho },\\&{g}_{3}=\frac{\left[\tau -s(\tau -{\pi }_{L})(1-{\alpha }_{1})\right]\left[s(1-{\alpha }_{1})(\tau -{\pi }_{F})-\tau {\alpha }_{1}\right]}{\rho {(\delta +\rho )}^{2}{\mu }_{L}}\\&\qquad\;+\,\frac{{\left(\tau -s\tau +s{\pi }_{F}\right)}^{2}}{2\rho {(\delta +\rho )}^{2}{\mu }_{F}}\\&\qquad\;+\frac{\tau s({\beta }_{1}-{\beta }_{2})(\tau -{\pi }_{F})+{\tau }^{2}{\beta }_{2}}{\rho {(\delta +\rho )}^{2}{\mu }_{S}}\\&\qquad\;-\,\frac{\left(1-\lambda \right)Q\left(\tau -{\pi }_{F}\right)}{\rho },\\& {h}_{1}=\frac{s\tau }{\delta +\rho },\\&{h}_{2}=\frac{\tau {\alpha }_{2}\left[\tau -s\left(\tau -{\pi }_{L}\right)\left(1-{\alpha }_{1}\right)\right]}{\rho {\left(\delta +\rho \right)}^{2}{\mu }_{L}}\\&\qquad\;+\,\frac{{\tau }^{2}}{2\rho {\left(\delta +\rho \right)}^{2}{\mu }_{S}}-\frac{Q\left(\tau -{\pi }_{L}\right)}{\rho }.\end{aligned}$$

1.3 Proof of Proposition 1

  1. (a)

    \({{e}_{L}}^{T*}-{{e}_{L}}^{N*}=\frac{\tau \left[{\beta }_{1}{\mu }_{L}+\left(1-s+s{\alpha }_{1}\right){\mu }_{S}\right]}{\delta \left(\delta +\rho \right){\mu }_{L}{\mu }_{S}}>0,\) \({{e}_{F}}^{T*}-{{e}_{F}}^{N*}=\frac{\tau \left[{\beta }_{2}{\mu }_{L}{\mu }_{F}+\left(1-s\right){\mu }_{L}{\mu }_{S}+{\mu }_{F}{\mu }_{S}{\alpha }_{1}\left(1-s+s{\alpha }_{1}\right)\right]}{\delta \left(\delta +\rho \right){\mu }_{L}{\mu }_{F}{\mu }_{S}}>0,\) \({{e}_{S}}^{T*}-{{e}_{S}}^{N*}=\frac{\tau \left[{\mu }_{L}+\left(1-s+s{\alpha }_{1}\right){\alpha }_{2}{\mu }_{S}\right]}{\delta \left(\delta +\rho \right){\mu }_{L}{\mu }_{S}}>0\).

  2. (b)

    \({{u}_{L}}^{T*}-{{u}_{L}}^{N*}=\frac{\tau \left(1-s+s{\alpha }_{1}\right)}{\left(\delta +\rho \right){\mu }_{{\text{L}}}}>0,\) \({{u}_{F}}^{T*}-{{u}_{F}}^{N*}=\frac{\tau (1-s)}{\left(\delta +\rho \right){\mu }_{{\text{F}}}}>0,\) \({{u}_{S}}^{T*}-{{u}_{S}}^{N*}=\frac{\tau }{(\delta +\rho ){\mu }_{{\text{S}}}}\).

1.4 Proof of Proposition 2

  1. (a)

    \({{e}_{L}}^{N*}-{{e}_{F}}^{N*}=\frac{{(1-{\alpha }_{1})}^{2}{\mu }_{{\text{F}}}s{\pi }_{L}-{\mu }_{{\text{L}}}s{\pi }_{F}}{\delta (\delta +\rho ){\mu }_{{\text{L}}}{\mu }_{{\text{F}}}}\). As \(\delta \left(\delta +\rho \right){\mu }_{{\text{L}}}{\mu }_{{\text{F}}}>0,\) \({(1-{\alpha }_{1})}^{2}{\mu }_{{\text{F}}}s{\pi }_{L}-{\mu }_{{\text{L}}}s{\pi }_{F}>0\) can be transformed into \(\frac{{\pi }_{L}}{{\pi }_{F}}>\frac{{\mu }_{{\text{L}}}}{{(1-{\alpha }_{1})}^{2}{\mu }_{{\text{F}}}}\).

  2. (b)

    \({{e}_{L}}^{T*}-{{e}_{F}}^{T*}=\frac{\tau {\mu }_{{\text{L}}}{\mu }_{{\text{F}}}\left({\beta }_{1}-{\beta }_{2}\right)-{\mu }_{{\text{L}}}{\mu }_{{\text{S}}}\left(s{\pi }_{F}+\tau -s\tau \right)+{\mu }_{{\text{F}}}{\mu }_{{\text{S}}}(1-{\alpha }_{1})[\tau -s\tau +s{\pi }_{L}+s\left(\tau -{\pi }_{L}\right){\alpha }_{1}]}{\delta (\delta +\rho ){\mu }_{{\text{L}}}{\mu }_{{\text{F}}}{\mu }_{{\text{S}}}}\). As \(\delta \left(\delta +\rho \right){\mu }_{{\text{L}}}{\mu }_{{\text{F}}}{\mu }_{{\text{S}}}>0,\) \(\tau {\mu }_{{\text{L}}}{\mu }_{{\text{F}}}\left({\beta }_{1}-{\beta }_{2}\right)-{\mu }_{{\text{L}}}{\mu }_{{\text{S}}}\left(s{\pi }_{F}+\tau -s\tau \right)+{\mu }_{{\text{F}}}{\mu }_{{\text{S}}}\left(1-{\alpha }_{1}\right)\left[\tau -s\tau +s{\pi }_{L}+s\left(\tau -{\pi }_{L}\right){\alpha }_{1}\right]>0\) can be transformed into \({\beta }_{1}-{\beta }_{2}>{\Phi }_{2}(\tau )\), where \({\Phi }_{2}\left(\tau \right)=\frac{\left(\tau -s\tau +s{\pi }_{F}\right){\mu }_{{\text{L}}}{\mu }_{{\text{S}}}-\left[s{\pi }_{L}\left(1-{\alpha }_{1}\right)+\tau \left(1-s+s{\alpha }_{1}\right)\right]\left(1-{\alpha }_{1}\right){\mu }_{{\text{F}}}{\mu }_{{\text{S}}}}{\tau {\mu }_{{\text{L}}}{\mu }_{{\text{F}}}}\). If \({\beta }_{1}={\beta }_{2}=0,\) it can be transformed into \({\pi }_{L}>{\Phi }_{1}({\pi }_{F})\), where \({\Phi }_{1}\left({\pi }_{F}\right)=\frac{(\tau -s\tau +s{\pi }_{F}){\mu }_{1}+\tau (-1+{\alpha }_{1})(1-s+s{\alpha }_{1}){\mu }_{2}}{s{(1-{\alpha }_{1})}^{2}{\mu }_{2}}\).

1.5 Proof of Corollary 1

  1. (a)

    . \(\frac{\partial \Delta {e}^{N}}{\partial {\alpha }_{1}}=-\frac{2s{\pi }_{L}\left(1-{\alpha }_{1}\right)}{\delta \left(\delta +\rho \right){\mu }_{{\text{L}}}}<0.\)

  2. (b)

    \(\frac{\partial \Delta {e}^{T}}{\partial {\alpha }_{1}}=-\frac{\tau +2s(1-{\alpha }_{1})({\pi }_{L}-\tau )}{\delta (\delta +\rho ){\mu }_{{\text{L}}}},\) As \(\delta \left(\delta +\rho \right){\mu }_{{\text{L}}}>0,\) \(\tau +2s\left(1-{\alpha }_{1}\right)\left({\pi }_{L}-\tau \right)<0\) can be transformed into \(\tau +2s{\pi }_{L}-2s{\alpha }_{1}{\pi }_{L}-2s\tau \left(1-{\alpha }_{1}\right)<0\). If \(\tau >2{\pi }_{L},\) we have \(0<{\alpha }_{1}<\frac{\tau -2{\pi }_{L}}{2(\tau -{\pi }_{L})}\) and \(\frac{\tau }{2(\tau -{\pi }_{L})(1-{\alpha }_{1})}<s<1\).

  3. (c)

    \(\frac{\partial \Delta {e}^{T}}{\partial {\beta }_{1}}=\frac{\tau }{\delta (\delta +\rho ){\mu }_{{\text{S}}}}>0,\) \(\frac{\partial \Delta {e}^{T}}{\partial {\beta }_{2}}=-\frac{\tau }{\delta \left(\delta +\rho \right){\mu }_{{\text{S}}}}<0\).

1.6 Proof of Proposition 3

  1. (a)

    \({{e}_{L}}^{NH}={{e}_{L}}^{ND}=\frac{s{\pi }_{L}(1-{\alpha }_{1})}{\delta (\delta +\rho ){\mu }_{{\text{L}}}},\) \({{e}_{L}}^{NV}-{{e}_{L}}^{ND}=\frac{s{\pi }_{L}{\alpha }_{1}}{\delta \left(\delta +\rho \right){\mu }_{{\text{L}}}}>0.\)

  2. (b)

    \({{e}_{L}}^{TH}-{{e}_{L}}^{TD}=-\frac{\tau {\beta }_{1}}{\delta \left(\delta +\rho \right){\mu }_{{\text{S}}}}<0,\) \({{e}_{L}}^{TV}-{{e}_{L}}^{TD}=\frac{s{\alpha }_{1}\left({\pi }_{L}-\tau \right)}{\delta \left(\delta +\rho \right){\mu }_{{\text{L}}}}.\) As \(\delta \left(\delta +\rho \right){\mu }_{{\text{L}}}>0,\) \(s{\alpha }_{1}\left({\pi }_{L}-\tau \right)>0\) can be transformed into \({\pi }_{L}>\tau >0\).

1.7 Proof of Proposition 4

  1. (a)

    \({{e}_{L}}^{NH}-{{e}_{L}}^{NV}=-\frac{s{\pi }_{L}{\alpha }_{1}}{\delta \left(\delta +\rho \right){\mu }_{{\text{L}}}}<0\).

  2. (b)

    \({{e}_{L}}^{TH}-{{e}_{L}}^{TV}=\frac{s{\alpha }_{1}{\mu }_{{\text{S}}}(\tau -{\pi }_{L})-\tau {\beta }_{1}{\mu }_{{\text{L}}}}{\delta (\delta +\rho ){\mu }_{{\text{L}}}{\mu }_{{\text{S}}}}\). As \(\delta \left(\delta +\rho \right){\mu }_{{\text{L}}}{\mu }_{{\text{S}}}>0,\) \(s{\alpha }_{1}{\mu }_{{\text{S}}}\left(\tau -{\pi }_{L}\right)-\tau {\beta }_{1}{\mu }_{{\text{L}}}>0\) can be transformed into \(s{\alpha }_{1}{\mu }_{{\text{S}}}\left(\tau -{\pi }_{L}\right)>\tau {\beta }_{1}{\mu }_{{\text{L}}}\). If \(0<\tau <{\pi }_{L},\) we have \(s>\frac{\tau {\beta }_{1}{\mu }_{{\text{L}}}}{(\tau -{\pi }_{L}){\alpha }_{1}{\mu }_{{\text{S}}}}\); else if \(\tau >{\pi }_{L},\) we have \(s<\frac{\tau {\beta }_{1}{\mu }_{{\text{L}}}}{(\tau -{\pi }_{L}){\alpha }_{1}{\mu }_{{\text{S}}}}\).

1.8 Proof of Proposition 5

  1. (a)

    . \({{e}_{F}}^{NH}-{{e}_{F}}^{NV}=\frac{s{\pi }_{L}\left(1-{\alpha }_{1}\right){\alpha }_{1}}{\delta \left(\delta +\rho \right){\mu }_{{\text{L}}}}>0.\)

  2. (b)

    \({{e}_{F}}^{TH}-{{e}_{F}}^{TV}=\frac{\tau ({\alpha }_{1}{\mu }_{{\text{S}}}-{\beta }_{2}{\mu }_{{\text{L}}})-s(\tau -{\pi }_{L})(1-{\alpha }_{1}){\alpha }_{1}{\mu }_{{\text{S}}}}{\delta (\delta +\rho ){\mu }_{{\text{L}}}{\mu }_{{\text{S}}}}\). As \(\delta \left(\delta +\rho \right){\mu }_{{\text{L}}}{\mu }_{{\text{S}}}>0,\) if \(0<\tau <{\pi }_{L}\) and \({\alpha }_{1}{\mu }_{S}>{\beta }_{2}{\mu }_{L}\), we have \({{e}_{F}}^{TH}>{{e}_{F}}^{TV}\); else if \({\alpha }_{1}{\mu }_{S}<{\beta }_{2}{\mu }_{L}\), we have \(s>{\Phi }_{3}(\tau )\). If \(\tau >{\pi }_{L}\) and \({\alpha }_{1}{\mu }_{S}>{\beta }_{2}{\mu }_{L}\), we have \(s<{\Phi }_{3}(s)\), where \({\Phi }_{3}\left(\tau \right)=\frac{\tau ({\beta }_{2}{\mu }_{L}-{\alpha }_{1}{\mu }_{S})}{({\pi }_{L}-\tau )(1-{\alpha }_{1}){\alpha }_{1}{\mu }_{S}}\).

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Liu, Q., Zhu, X. How Carbon Tax Policy Affects the Carbon Emissions of Manufacturers with Green Technology Spillovers?. Environ Model Assess (2024). https://doi.org/10.1007/s10666-024-09965-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s10666-024-09965-x

Keywords

Search

Navigation