1 Introduction

Flooding is a major natural hazard in the UK [53], with more than 5 million people living or working in flood prone areas in England and Wales alone [54]. In fact, flooding had caused extensive damage to infrastructure. For example, there was £3.5 billion paid out by insurance industry due to flood damage between 1998 and 2005 according to [21]. Therefore, flooding is a serious risk of huge economic loss in the UK, particularly in winter (c.f. [1]). As one of the hydrological phenomena, flooding is a process that is complex and uneasy to understand. Our basic objective, in this study, is therefore to empirically investigate and assess the reliability of, and explore a potential to improve, the existing popular model for the UK index flood estimation.

Due to the emergence of modern data acquisition techniques together with powerful computational tools, voluminous hydrological data have been, and will continue to be, collected. There is an urgent need to explore the unknown and unexpected features in the flooding datasets and assess the reliability of the existing models in the literature. In particular, in hydrology, the issue of an ungauged basin is a challenging problem because drainage basins or waterways, in many parts of the world, are ungauged or poorly gauged, due to the fact that the river flow monitoring stations are mostly located at specific, strategic locations only (c.f. [40]).

It is a usual practice that hydrologists have to estimate the design flood using available information from nearby gauged sites and characteristics of locally regional flood catchments when a development project is located at an ungauged basin of a catchment area. This approach is known as a regionalization procedure. It was proposed by [47] for hydro-meteorological modelling with the basic principle of “substitute time for space.” There are several types of regionalization procedures available in the literature (see, for example, [16, 17]). Among them, a popular approach is the index flood procedure introduced by [18], which requires estimation of an index flood. The median value of annual maximum flow series has been chosen as the base for the index flood, that is denoted as QMED. The median means that half of all observed annual maximum flow data at the site of interest are greater than the QMED. In general, a return period, T, is the length of an average time interval between occurrences of two consecutive floods that exceed a threshold of particular magnitude. The probability of (re)occurrence or the so-called exceedance probability with the corresponding magnitude is therefore thought to be \(\frac {1}{T}\). This probability is equal to a half for the QMED with T = 2, which hence implies that the QMED stands for a flood with a return period of 2 years. The focus in this paper is on estimating this index flood at ungauged basins by using an indirect method, such as regression models, to forge a link between a hydrological parameter of index flood and a set of catchment descriptors, based on the assumption that the flood characteristics can be explained by the catchment descriptors (c.f. [42]).

Different regression models have been developed for estimating the index flood by using different catchment descriptors. A well-established model of this kind in the UK is the median annual maximum flood (QMED) model given in Flood Estimation Handbook (FEH) (c.f. [30, 36]). This model was first published in 1999 and later improved in 2008 by the Centre for Ecology and Hydrology (CEH), and has been widely applied in the UK, e.g., for flood defense planning, flood risk analysis, new development planning and rarity assessment of notable rainfalls or floods. Actually, the FEH has become the industry standard used to estimate local flood risk and develop resilient infrastructure. For details, the reader is referred to [30], [36] and [33]. In the wider literature of hydrological applications, a direct method of using arithmetic median or mean of annual maximum flow data is preferable, in determining the scale values (index flood), to the indirect statistical regression models when flow data of 2–5 years are available, which is however only possible at a gauged catchment area [28, 30]. The literature also shows that statistical indirect models through regression methods, such as the QMED model, are generally more accurate, for prediction of index flood in ungauged catchment, than conceptual indirect models (see, e.g., [9]), though the former may lack an ability to provide physical interpretation or insight into other inter-related factors in the flood process, causing possibly a large amount of uncertainty. In a broader context, a reliable and valid index flood estimation model is needed and the base for mitigating the hazards of an infrequent extreme event (say 1 in 1000 years event) through flood insurance (c.f. [25]). It can also be used to estimate the scale values that are crucial in determination of frequency and magnitude of the flood peak discharges at a particular ungauged catchment area when designing infrastructure and planning land use [55].

Assessing and improving estimation of index flood at ungauged basins still need a great deal of efforts to dedicate to owing to a large amount of uncertainties associated with index flood estimation procedures (c.f. [34, 50]). In this study, we are focusing to explore two fundamentals on the QMED type model of the FEH, or simply the FEH-QMED model hereafter, in estimating the UK index flood, on the basis of the flooding data of 586 gauged stations around the UK: (i) assessing the reliability of the non-linear functions of different catchment descriptors specified by the updated QMED type model and (ii) exploring the potential to improve the QMED type model. For these purposes, we will choose the FEH-QMED model as a benchmark due to its wide recognition and being taken as basis of most studies on the flood risk estimation and modelling in the UK. The updated flood information in conjunction with the gauged stations and the high quality data on flood peak are available through the National River Flow Archive. The Centre for Ecology and Hydrology (CEH) has as well published the FEH-CD ROM that provides a large number of catchment descriptors, and now the service is made by a website: https://fehweb.ceh.ac.uk/. These sources of data make it possible for us to explore our assessment and improvement analyses.

We are making our assessment and potential improvement by proposing appropriate spatial analysis tools to be applied to explore the flooding data set. In order to assess the reliability of the non-linear effects of the catchment descriptors identified by the FEH-QMED model, we will suggest a spatial additive regression analysis (c.f. [39]) to examine the non-linear effects of the catchment descriptor covariates in flood index estimation. This is a kind of semiparametric model [26], by which some unknown or unexpected complex nonlinear features, if existed, would be well identified from the data. Furthermore, in order to check any potential spatial neighboring dependence in the data, a diagnostic tool named Moran’s I test (c.f. [45, 48]) will be utilized to examine any significant dependence in the regression residuals. In the literature, although spatial correlation or neighboring impact has been noticed in the updated FEH procedure (c.f. [34, 35]), it appears to have only been partially considered for improvement by using the QMED model together with a transformation of the data from an appropriately selected (nearby) gauged site in estimating the index flood at an ungauged catchment (c.f. [33]). Differently from these references, in this study, by identification of spatial dependence, we will further suggest a spatial flooding model to explore any potential improvement over the FEH-QMED model by fitting the data with the surrounding neighboring impacts to be more fully considered in our model. Interestingly, we find that the additive analysis confirms the non-linear effects of the catchment descriptors specified by the FEH-QMED model, while the Moran test and a spatial error analysis show that the spatial autocorrelations significantly exist in our flood data. These facts lead us to propose spatial autoregressive index flood estimation models by more fully taking account of the spatial dependence, which we will demonstrate outperform the updated FEH-QMED model of [33] in improvement of prediction, which is robust in the sense of different error measures, say by a reduction of 13.8% of the mean squared error for prediction of the logarithmic QMED.

The structure of the remaining sections is organized as follows. Background information on the source of the UK flood data, the index flood procedure and the equation linking a certain hydrological parameters to a set of catchment descriptors will be briefly introduced in Section 2. Section 3 presents the methodology to be used for our spatial additive and error analyses of the UK flood data set. The detailed analyses and results of the empirical study by our suggested methods, including spatial additive analysis, diagnostic autocorrelation test, spatial index flood model analysis and evaluation, will be conducted and discussed in Section 4. Section 5 concludes with the findings of this study.

2 Data and Index Flood Estimation

We first introduce some background information on the UK flood data source used in this study and on the index flood procedure and the FEH-QMED model as a benchmark needed in the following sections.

2.1 Data Source

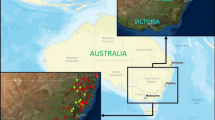
We are using the data from the National River Flow Archive (NRFA) to examine the FEH-QMED model for index flood estimation in the UK. Two types of data are used, including the observed flood peak data and the physical catchment descriptors data (see Section 2.3 below for more details). The observed flood peak data are from the HiFlows-UK project, which are available at http://nrfa.ceh.ac.uk/data/search, while the data on physical catchment descriptors are from the FEH CD-ROM 3.0, which now can also be accessed through the website at https://fehweb.ceh.ac.uk/. The observations for these two data sets are based on the 602 monitoring stations around the UK that were used in the scientific report of [36], published by the Environment Agency. However, some updates and changes have been made through the HiFlows-UK Notes. The important changes include the list of the stations that have been changed, either removed or added in the HiFlows-UK project for improvement of the dataset. Out of the 602 stations, 6 have been changed to other station numbers with the same station names due to incorrect information, 8 were removed and 2 closed due to data quality. As a result, only 586 rural stations will be considered in this study below. The locations for these 586 rural stations are showed in circle in Fig. 1. This figure has been plotted by using ArcGIS software with the background uploaded from Google Earth map, and then overlaid with the location data of the 586 river flow monitoring stations considered in this study.

Fig. 1
figure 1

Locations of the 586 gauging stations on rural catchments, with the background uploaded from Google Earth map

Full size image

2.2 The Flood Regionalization Procedure

If flood records are insufficient, regionalization technique is usually required. In fact, availability of the past flow data has always been problematic to hydrologists in estimating flood at the sites of interest such as where projects are to be designed or developed (see, e.g., [18, 28, 29]). Applying flood frequency analysis without use of regionalization at the sites with insufficient length of flow data records introduces significant uncertainties into the flood estimates. By regionalization technique, hydrologists can utilize the available data and information from nearby gauged stations to estimate the flood at the ungauged sites of interest. By [18], the T-year return flood (say the QMED for T = 2) at a given site can be expressed as the product of the index flood (i.e., QMED) and the dimensionless regional growth factor for the return period of T years. According to [28], the issue of estimation of the regional growth factor is well studied in the literature, while the main problem lies in estimation of the index flood. This research is therefore focused on improvement of the existing methodology on estimation of the index flood, denoted by μQ below. Note that the index flood μQ, or QMED, plays an important part of the FEH statistical method, as shown in [33, 34].

There are various issues in the regionalization procedure with the estimation of the index flood [28]. At the gauged sites, an estimate of μQ can be obtained directly by calculating the arithmetic median of the available annual maximum flood flow observations (i.e., QMED). However, at ungauged sites, indirect methods have to be used in estimating μQ (or QMED) and there is a large amount of uncertainty associated with the estimate [34]. The most widely used indirect methods are multiregression models, which link μQ to a set of appropriate morphological and climatic descriptors of the basins through a power form equation [9, 28]:

$$ \mu_{Q} = a x_{1}^{\beta_{1}} x_{2}^{\beta_{2}} {\ldots} x_{p}^{\beta_{p}}, $$
(1)

where xi is the ith catchment descriptor or some function of it, for i = 1,⋯ ,p, with p the number of the catchment descriptors taken as the explanatory variables for the model, and a and βi are the model parameters. Note that in the flood regionalization, it is a complex issue deciding an appropriate model structure to link the covariate variables of the chosen catchment descriptors to the dependent variable of river flow. Theoretically, it is impossible to know the “true” model structure (c.f. [55]). Therefore, in practice, hydrologists tend to use some familiar model structure such as the log linear model as indicted in Eq. (1), which is easy to deal with and apply mathematically. By this approach, many index flood estimation models have been developed (c.f. [2, 11, 27, 44, 46, 49]), including those with efforts for improved models [34, 50, 55] (see also [8] for the guidelines on choice of suitable methods and [55] on the potential difficulties for the index flood estimation and modelling). Among, the QMED model published by Flood Estimation Handbook (FEH) [30] is a well-established one for the flood data in the UK.

2.3 The FEH-QMED Model

To introduce the benchmark FEH-QMED model, we need provide some more information on two types of data used in this study.

Typically, there are many flood peaks associated with individual storm events, recorded as continuous time series of streamflow discharges throughout the year. The type of the flood peak data used in this study is the annual maximum (AM) series formed by the maximum discharge in each year, yielding the series \(\left \{w_{1} {\ldots } w_{n}\right \}\), with wi for the maximum discharge in the ith year of the n-years record. The AM series can be used to estimate the probability that the maximum flood discharge in a year exceeds a threshold of particular magnitude, say q. This probability is called the annual exceedance probability and can be estimated by \(\frac 1 n {\sum }_{j=1}^{n} I(w_{i} > q)\), where I(A) is an indicator function with value 1 if A is true and 0 otherwise. The AM series from the 585 stations, with a varying length from 7 to 127 years, will be used to determine the important hydrological parameter in the index flood estimation model, i.e., the median annual maximum flood (QMED) for the index flood.

The CEH (Central for Ecology and Hydrology, formerly known as the Institute of Hydrology, IH) in the UK has also published a CD ROM (c.f. [30]) containing a modified digital terrain model, called Institute of Hydrology Digital Terrain Model (IHDTM), that has been developed from digitally held rivers and contours taken from the Ordinance Survey 1:50 000 map. The calculation of catchment descriptors in the IHDTM is done through using gridded elevation data. The IHDTM can automatically derive catchment boundary by including the raster data set of drainage path direction based on the steepest route to the neighboring grid nodes in 50 m resolution. This boundary can be applied to compute a large number of catchment descriptors. Nevertheless, the variables that have previously been found to be useful in flood risk study will be included in this study (see Table 1 below for details). The selected characteristic variables are based on [36] who were responsible for improving the original FEH-QMED model, with the updated model, given in Equation (2), simpler but outperforming the original one. We will take this updated model as a benchmark in this study. The observations of all the variables in Table 1 are based on the same 586 stations around the UK.

Table 1 Summary of catchment descriptors
Full size table

The updated FEH-QMED model by [36] and [33, 35] uses the median annual maximum flow (QMED) as an index flood for the ungauged catchment flood estimation. The development of this model is based on Eq. (1) that has been linearized by taking logarithm on both sides of (1) for parameter estimation by using generalized least squares or maximum likelihood method for model (2) [19, 51, 52]. The variable selection is carried out by using an exhaustive search to find a relatively small set of variables, with criteria such as the coefficient of determination R2, the adjusted R2 or the predicted error sum of squares applied, providing a good statistical fit to the QMED. This index flood regression model links the QMED with a set of catchment descriptors, namely the catchment area (AREA), the standard average annual rainfall (SAAR), the index of flood attenuation attributable to reservoirs and lakes (FARL) and the based flow index (BFIHOST), explained in Table 1, where the observations for those variables are also based on the same 586 stations around the UK. Equation (2) below is a formula that is widely used in the UK by flood hydrologist to estimate the median flood at an ungauged catchment:

$$ \begin{array}{@{}rcl@{}} \ln(QMED)&=& 2.1170+0.8510\ln(AREA)\\ &&-1.8734\left( \frac{1000}{SAAR}\right)+3.4451\ln(FARL)\\ && -\> 3.080BFIHOST^{2}. \ \end{array} $$
(2)

In practice, the quality of flood data has to be ensured before it can be used in any hydrological application analysis. However, some unknown or unexpected features in the flood data cannot be controlled due to its nature. For example, the water level or river flow that represents the flood peak discharge at a particular point in a river has well-defined spatial effect due to the flow of the river and the lay of the land, while the direction in which the water will flow within a catchment is generally known. Therefore, the local factors influencing the index flood may not be adequately represented in the regression models, and it may be beneficial to adjust the estimates by using local data from the neighboring gauged catchments [33]. The Flood Estimation Handbook (FEH) [30] recommended the use of the data transferring procedure together with the QMED regression model when estimating the index flood at ungauged sites, where one or more suitable gauged sites can be found among the gauged catchments that are geographically close and hydrologically similar. There is no specific guidance as to the limit of the geographical area or necessary degree of hydrological similarity. Nevertheless, studies have shown that geographical proximity gives superior impact in estimating the index flood at ungauged sites in comparison with hydrological similarity [22, 34, 43]. Consecutive studies by [33,34,35] concluded that geographical proximity representing the spatial impact in the data transferring procedure is very important and useful to improve the regression results.

As [33] has showed, the new FEH-QMED model (2) has been developed by using observations of the spatial data from 602 guaged stations, instead of the 728 stations in the original model, together with the revised data-transfer method that performs better in estimating the index flood at an ungauged catchment. We will use it as a benchmark model as a comparison with our developed models in the following sections.

3 Methodology

It is interestingly noted that the FEH-QMED model (2) is a linear multiple regression model with non-linear effects of the catchment descriptors specified. We are first assessing the reliability of this model in estimating the UK index flood, and then aim to develop an improved model for a better index flood estimation. Here the median annual maximum flood (QMED) in logarithm is considered as the response variable, \(Y=\ln (QMED)\), which is a function of the four predictor variables, i.e., the catchment drainage area (AREA), the average annual rainfall (SAAR), the flood attenuation by reservoirs and lakes (FARL), and the base flow index by hydrology of soil type data (BFIHOST). Two assumptions underlying (2) are as follows: (i) the linearity between \(Y=\ln (QMED)\) and the explanatory covariates

$$ \begin{array}{@{}rcl@{}} (X_{1},X_{2},X_{3},X_{4})&=&(\ln(AREA),\frac{1000}{SAAR}, \ln(FARL),\\ && BFIHOST^{2}), \end{array} $$
(3)

and (ii) the independence in the residuals of the multiple regression model (2). These will be assessed by using spatial additive regression analysis to investigate the model structure of the explanatory variables and by spatial error analysis for diagnostic test on any dependence in the residuals, in order to achieve an improved model for index flood estimation. The background information on these methods is provided in Sections 3.1 and 3.2.

3.1 Spatial Additive Analysis

Suppose the response variable, Y, and the p = 4 explanatory variables, X1…Xp, given above, are observed with the spatial data, (Yi = Y (si),Xi1 = X1(si),…,Xip = Xp(si)), i = 1,2,⋯ ,n, from the n = 586 gauged stations around the UK (see Section 2.1), where si = (ui,vi) stands for the location in (latitude, longitude) of the i th gauged station. In general, the mean of Yi is a function of Xi1,…,Xip, say μi = E(Yi|Xi1,…,Xip) = f(Xi1,…,Xip). If the FEH model (2) is true, then it is a linear regression

$$ \mu_{i}= \beta_{0}+\sum\limits_{j=1}^{p}\beta_{j}X_{ij}, $$
(4)

where it is often assumed that \(e_{i}= Y_{i}-\mu _{i}\sim N(0, \sigma ^{2})\) for i = 1,2,⋯ ,n, with ei’s independent. Equation (4) indicates that the covariates are multiplied by the coefficients, β1,…,βp for prediction of Yi.

To explore if Eq. (2) or (4) holds for the given flood data, we are considering a more general model, an additive spatial regression model (c.f. [24, 26, 39]) that is more flexible than Eq. (4) by replacing the linear predictor with a sum of smoothing functions of the covariates in the form

$$ \mu_{i}= \beta_{0}+\sum\limits_{j=1}^{p}f_{j}(X_{ij}), $$
(5)

where the smooth functions, fj’s, are unknown non-linear functions of the p = 4 covariates (X1,X2,X3,X4) defined in Eq. (3) in this study, and for identifiability it is often supposed that Efj(Xijj) = 0 for j = 1,⋯ ,p. Here although we may assume ei = Yi − μi satisfies the conditions as specified under Eq. (4), but it is not necessary for estimation of Eq. (5) as showed in [39] and [26]. By the data (Yi,Xi1…Xip), i = 1,2,⋯ ,n, we can obtain the estimates of the unknown (nonparametric) functions, \(\hat {f}_{j}(X_{ij})\) for j = 1,⋯ ,p, and \(\hat {\beta }_{0}\), by using the so-called backfitting algorithm or other semiparametric smoothing methods; for details, the reader is referred to the related statistical references (c.f. [24, 26, 39]). We did the estimation by the statistical software R with the package “GAM” in the analysis of data in Section 4 below. Clearly, if the resultant estimate \(\hat {f}_{j}(X_{ij})\) is a linear function of Xij for all j = 1,2,⋯ ,p, then it just demonstrates that Eq. (2) or (4) is true, i.e., the non-linear effects of the catchment descriptors (AREA, SAAR, FARL, BFIHOST) identified in Eq. (3) (c.f. [36]) are well reliable in the FEH-QMED model (2).

3.2 Spatial Dependence and Autoregressive Analysis

After a regression model such as Eq. (4) or (5) is established, we need to check if the obtained model is appropriate by examining the residuals of the regression. In applications, we can define the residuals ei, i = 1,2,⋯ ,n, as above, with βj’s and fj’s based on their estimated values for calculating the residuals in Eqs. (4) and (5), respectively. Two statistical tests to detect the presence of spatial autocorrelation in the residuals are introduced in this study. Here a spatial weight matrix (c.f. [4]) need to be constructed based on the locations of the n = 586 monitoring stations. It is defined as a n × n matrix, W, for a set of n locations, with elements wij indicating whether the locations si and sj of the i th and the j th observations are spatially close, where i≠j, and wii = 0 as usual.

Two types of spatial weight matrices are popular, which are contiguity based and distance based, respectively, to be considered in this study. For a contiguity-based matrix, the (i,j)th element is define as

$$ w_{ij}= \begin{cases} 1,& \text{if \textit{i} is contiguous to \textit{j}}, \\ 0,& \text{otherwise}. \end{cases} $$
(6)

Here the weight wij equals one if stations i and j are neighbors in space, and zero otherwise, by the definition of neighbor based on sharing triangle edges using the Delaunay triangulation concept (c.f. [7, 12, 23, 41]). An advantage with this weight matrix lies in its representation of the proximal action that is an immediate action or neighboring correlation. For another type of spatial weight matrix based on distance, the element is defined as

$$ w_{ij}= \begin{cases} 1,& 0 < d_{ij} \leq D, \\ 0,& d_{ij} > D, \end{cases} $$
(7)

where dij is the distance between the locations i and j, with D a defined distance band. Equation (7) indicates that the stations within a defined distance band from each other are categorized as neighbors and have spatial weight equal to one, and zero otherwise. Typically, the upper bound D is taken as the greatest value of the Euclidean distance among the list of the first order nearest neighbors (c.f. [5, 6]). An advantage with this type of weight matrix is for its ability to represent a kind of short-distance action or quasi-proximal action. Both types need to be row-wise standardized so that the weights sum up to one on each row when applied.

We comment that the two types of spatial weight matrices above are much easier to apply than other more complex weight matrices. For example, these two weight matrices only select a relatively small number of the most relevant neighboring gauged sites to be taken into account in modelling, and are hence often more attractive from the application perspectives. For information on other types of more complex weight matrices like using a weight matrix that has values decreasing as distances increase, the reader is referred to the above-mentioned references, which would lead to more neighboring gauged sites to be taken into account in modelling. Whether we should use a more complex spatial weight matrix or not is an interesting model selection issue worth investigation. This is an issue that is beyond the scope of this paper and worth more study, so we will leave it for a future work.

Our first test for spatial dependence in the residuals of a regression model is by Moran’s I-statistic [45]. It is the most widely used method in detecting spatial autocorrelation of geo-referenced data (see, e.g., [20, 32, 37]). With a spatial weight matrix W as defined in Eq. (6) or Eq. (7), Moran’s I formula for a row-wise standardized weight matrix W reads as

$$ I = \frac{e^{\prime}We}{e^{\prime}e}, $$
(8)

where e = (e1,e2,⋯ ,en)′ is an n × 1 vector of the regression residuals. The statistic I asymptotically follows a standard normal distribution under the null hypothesis of no spatial dependence (c.f. [13,14,15]). In R, this test is implemented using function lm.morantest.

The Moran’s I test statistics has high power against a range of spatial alternatives, but does not provide much help in terms of which alternative spatial regression model would be most appropriate. An alternative test for spatial dependence is called Lagrange multiplier (LM) test, which allows a distinction between spatial error models and spatial lag models. Unlike the Moran test, the LM test relies on a structured hypothesis for test of spatial error dependence or spatial lag dependence.

The LM test for spatial error dependence, or the so-called LM error test, is based on the least-squares residuals of spatial error model (11) below involving a spatial weight matrix W, conditional on having a λ parameter not equal to zero in the model. The LM error test statistic takes the form [4]:

$$ LM_{err}=\frac{(e^{\prime}We/s^{2})^{2}}{T} \sim \chi^{2}(1), $$
(9)

with \(s^{2}=e^{\prime }e/n\), e denoting a vector of the least-squares residuals and \(T=tr[(W+W^{\prime })W]\). The LM test for spatial lag dependence, or the LM lag test, is based on the residuals from the spatial lag model (12). It can be used to examine whether inclusion of the spatial lag term eliminates spatial dependence in the residuals of the model. This test differs from the two tests outlined above because it allows for the presence of the spatial lag variable in the model. It is conditional on having a ρ parameter not equal to zero in the model, rather than relying on the least-squares residuals. The LM lag test takes the form [4]:

$$ LM_{lag}=\frac{(e^{\prime}Wy/s^{2})^{2}}{nJ} \sim \chi^{2}(1), $$
(10)

where nJ = T + (WXβ)′M(WXβ)/s2, \(T=tr[(w+w^{\prime })w],\)\(M=I-X(X^{\prime }X)^{-1}X^{\prime }\). Both LM tests and their robust forms are inplemented in the R function lm.LMtest.

As mentioned above, two cases of spatial dependence could arise in Eq. (4) or (5). A spatial error model is appropriate when the interest is in correcting spatial autocorrelation due to use of spatial data, irrespective of whether the model of interest is spatial or not. The spatial error model can be expressed as

$$ y = X\beta + e, $$
(11)
$$ e = \lambda We + \varepsilon, \ \ \varepsilon \sim N(0, \sigma^{2} I_{n}). $$

Here the n × 1 vector y contains the n observations of the dependent variable Y, and X represents the usual n × (1 + p) data matrix containing the explanatory variables from model (4), and W is a spatial weight matrix and the parameter λ is the coefficient on the spatially correlated errors. The (1 + p) × 1 vector of parameters, β, reflects the influence of the explanatory variables on variation in the dependent variable Y. We comment that, as often done in practice, assumption of normal distribution for the error vector \(\varepsilon \sim N(0, \sigma ^{2} I_{n})\), with In an n × n identity matrix, is applied in modelling here, which can at least be seen as an approximation, in particular at a stage of investigation with no further information on the distribution. Under such kind of Gaussian assumption (no matter if the true error is Gaussian or not), quasi-maximum likelihood estimation (QMLE) can be applied for estimation of Eq. (11) (see, e.g., [38] for detail of justification on the QMLE in theory). We have also provided a plot of kernel density estimate, together with a normal distribution of the estimated mean and variance, for the data of \(Y=\ln (QMED)\), which appears to be normally approximated in distribution as indicated in Fig. 2. Maximum likelihood estimation of the spatial error model [4] can be implemented by the R function errorsarlm.

Fig. 2
figure 2

A plot of kernel density estimate (kde), together with a normal distribution of the estimated mean and variance, for the data of \(Y=\ln (QMED)\)

Full size image

The alternative model is a spatial lag model, which is appropriate when the focus is on the spatial interactions of the dependent variable. Here the existence and strength of spatial interactions are the focus of interest to be assessed. The spatial lag model takes the form:

$$ y = \rho Wy + X\beta + \varepsilon, $$
(12)
$$ \varepsilon \sim N(0, \sigma^{2} I_{n}), $$

where y, X and W are similarly defined as in Eq. (11). The parameter ρ is the coefficient of the spatially lagged dependent variable, Wy, and the parameter β reflects the influence of the explanatory variables on variation in the dependent variable Y. Maximum likelihood method for estimating the parameters of this model [4] can be carried out with the R function lagsarlm.

4 Empirical Spatial Index Flood Estimation: Results

In this section, we are first conducting empirical spatial additive assessment of the non-linear effects of the covariates specified by the FEH-QMED model given in Eq. (2) and then attempting to develop an improved spatial autoregressive flooding model.

4.1 Empirical Spatial Additive Assessment of the FEH-QMED Model

The analysis starts with fitting the dataset by applying general linear model (4)), estimated by using an R function “lm,” with the identified covariates, given in Eq. (3), used in the FEH-QMED model (2). Then we are applying the spatial additive model (5) in Section 3.1, estimated by the “gam” function of the R package “mgcv” [56], to assess if the nonlinear parametric transformations of the catchment descriptors, in Eq. (3), as covariates are reliable in fitting the linear model (4), as given by the FEH-QMED model (2), for the data.

The results from fitting the general linear model (4) and the spatial additive model (5), with \(Y=\ln (QMED)\) and the four catchment descriptors in Eq. (3), for the UK flooding data at the 586 gauged stations are shown in Table 2, and the estimated functions of fj(⋅)’s in Eq. (5) are displayed in Fig. 3. Here the coefficients of the FEH-QMED model given in Eq. (2) (c.f. [36]) are also provided in Table 2 for an easy reference and comparison.

Table 2 Comparison between general linear and additive models
Full size table
Fig. 3
figure 3

Graphical display on effects of four catchment descriptors in additive model

Full size image

As noticed in Section 3.1, the FEH-QMED model (2) is represented actually in the form of linear regression model (4). The estimated values from the linear model (4) and the FEH-QMED model shown in Table 2 are essentially the same with slight difference owing to using slightly different data sets (c.f. Section 2.1 for detail about the reduced number of the gauged stations considered in this paper). Comparing the linear model with the additive model in Table 2 and Fig. 3, we can see that statistically, both models show the same conclusion with regard to the significance of the individual covariate effects. The equivalent degrees of freedom (edf, i.e., the number of free parameters for usual parametric models) for all the functions of the four variables are greater than or equal to 1, and the F-statistic values indicate them being significant with their p values less then the significance level of 5%, under the additive model, in Table 2. In terms of model comparison by adjusted R-squares, it is concluded that both the spatial additive and the linear models are very similar with the adjusted R-squared values being 0.938 and 0.935, respectively. Although the adjusted R-square for the additive model (5) is slightly larger, the linear model (4) has better interpretation. Furthermore, for the estimated smoothing functions of the additive model (5) with p = 4, plotted in Fig. 3, all the component functions with the four covariates given in Eq. (3) look to be rather linear. This confirms that the specified nonlinear effects of the catchment descriptors in the FEH-QMED model (2) look satisfactorily reliable for the UK flooding data.

4.2 Empirical Tests of Spatial Autocorrelation

We are further investigating whether there is any strong spatial autocorrelation in the residuals of the spatial additive or the linear FEH-QMED model. In fact, if the residuals were a white noise data set, then there should be none of significant autocorrelation when it is seen as a series, which is obviously violated by a simple autocorrelation plot of the residuals as a series for the linear model in Table 2, provided in Fig. 4. We therefore do the spatial tests more formally by using Moran’s I and Lagrange multiplier tests as sketched in Section 3.2. This study considers two types of spatial weight matrices that are widely used in estimating the relationship among the spatial observations, that is the contiguity-based and the distance-based matrices. The spatial neighborhoods under contiguity- and distance-based weights are displayed in panels (a) and (b) of Fig. 5, respectively (see Section 3.2 for detail on how to construct these spatial weight matrices with row-wise standardized elements).

Fig. 4
figure 4

A simple autocorrelation plot for the residuals seen as a series

Full size image
Fig. 5
figure 5

Illustration of spatial relationship in the UK flood peak data

Full size image

Six tests have been performed to assess the spatial dependence in the residuals. A summary of the six diagnostics tests is reported in Table 3. First, Moran’s I score of 0.213 is highly significant, indicating a strong spatial autocorrelation in the residuals, which are not white noise data. This conclusion is further confirmed by other five tests, including the simple Lagrange multiplier tests for spatial lag dependence (under the spatial lag model (12) and for spatial error dependence (under the spatial error model (11), and the robust Lagrange multiplier tests for spatial lag dependence in the presence of error dependence and for spatial error dependence in the presence of spatial lag dependent variable, and a portmanteau test. From Table 3, it clearly shows that both simple tests of the lag and the error are significant, indicating presence of spatial autocorrelation in the residuals for both types of weight matrices. The robust tests give a better understanding in terms of which alternative spatial dependence would be most appropriate for model fitting, showing that the spatial error model appears more acceptable than the lag model.

Table 3 Diagnostics for spatial dependence in the regression residuals
Full size table

4.3 An Improved Index Flood Estimation: Empirical Spatial Autoregressive Flooding Analysis

Based on the features identified in Sections 4.1 and 4.2, we are attempting to find an improved model for the UK index flood estimation. We consider fitting both the spatial error and the spatial lag models introduced in Section 3.2 to the UK flooding data by using both types of spatial weight matrices considered above. The results are summarized in Table 4, which gives the estimated values for each of the parameters in all models considered in this analysis, where the value in the round bracket represents the standard error of the estimate. All the estimated regressive coefficients are found to be significant for each model. In addition, the spatial coefficients λ and ρ are significant in both the spatial error and the spatial lag models, given in Eqs. (11) and (12), respectively, for both types of spatial weight matrices. These demonstrate that the spatial relationship in the UK flood peak data can be characterized by both contiguity-based and distance-based weight matrices.

Table 4 Comparison between general linear and spatial autoregressive models
Full size table

We compare both spatial error and spatial lag models associated with the two types of spatial weight matrices with the benchmark linear FEH-QMED model (Eq. 2). Model evaluation and selection among different fitted models are based on Akaike information criterion (AIC). The AIC is one of the most popular approaches in model selection that compares multiple models by taking into account both fitting accuracy and model parsimony [3, 10]. A preferred model can be selected via a minimal value of the AIC defined by

$$ AIC = 2K - 2\ln(L), $$
(13)

where K is the number of estimated unknown parameters in the model and L is the maximum value of the likelihood function for the model. In terms of the AIC value, it is clearly shown in Table 4 that taking account of the spatial dependence in modelling can improve the model performance over the FEH-QMED model. We also see that the spatial error model (11) outperforms the spatial lag model (12), with use of the contiguity weight matrix attaining the lowest AIC value of 519.34, which is significantly lower than the AIC values for other models.

Moran’s I test is also examined for the residuals in both the fitted spatial error and spatial lag models to assess whether these spatial flooding models are sufficiently acceptable. The results of the p values (denoted by Prob) given in Table 5 clearly show that spatial autocorrelation is still existent in the spatial lag models but not in the spatial error models. This indicates that allowing the FEH-QMED model error terms modelled by a spatial error model with a contiguity-based weight matrix is acceptable and can significantly improve the model fitting with the spatial effect well characterized. This further confirms that the contiguity-matrix-based spatial error model is more suitable for the UK flooding data than the spatial lag model and other models given in Table 4.

Table 5 Diagnostics for spatial dependence in residuals of spatial autoregressive models
Full size table

4.4 Cross-validation Assessment of Spatial Index Flood Estimation Models in Prediction

Model evaluation is important in assessing the quality and accuracy of the developed models for practical use in prediction. The key point in assessing the performance of a developed model is to accurately measure the ability of its prediction at an ungauged site by prediction error, \(\hat {\varepsilon }_{j}\), say, at site j. Note that the predicted value from a spatial model is not as easy to compute as that from a linear regression model because it involves spatial neighboring effects in the regression.

This study will suggest the evaluation of a method of computing the predicted values by using leave-one-out cross validation (LOOCV) technique. In this method, for each left-out gauged site j of the n = 586 observations of the data set, (n − 1) of them are used for model training and the j th left-out observation is for testing of the prediction at the j th site. By using the training data of (n − 1) observations (except the j th site), we can estimate the model parameters, denoted by \(\hat {\beta }\) and \(\hat {\lambda }\) or \(\hat {\rho }\) in model (11) or (12), which are used to get the predicted value \(\hat {y}_{j}\) that is shown in Table 6, where wik, k≠j, is the (i,k)-th element of standardized spatial weight matrix, W, i.e., \({\sum }_{k \ne j} w_{ik}=1\), for each j. This process is repeated for j from 1 until n.

Table 6 Computation of the predicted values
Full size table

Hence, the prediction error for each model can be computed as follows

$$ \hat{\varepsilon}_{j} = y_{j} - \hat{y}_{j}, \ \ j=1, 2,\cdots, n, $$
(14)

which we will call leave-one-out (LOO) prediction errors, or simply LOO errors. The squared or absolute values of the LOO errors (simply called the squared or absolute errors) are widely applied in evaluating model performance in particular for prediction. Their respective simple arithmetic averages are just the popular LOO cross-validation (LOOCV) mean squared error (MSE) and mean absolute error (MAE) in machine learning (c.f. [31]). In [33], an error measure equivalent to MSE, called root mean squared error (RMSE), is applied, which is a square root of MSE. These error measures are defined, for example, for prediction of \(Y=\ln (QMED)\), by

$$ MSE= \frac{1}{n}\sum\limits_{j=1}^{n}\hat{\varepsilon}_{j}^{2}=\frac{1}{n}\sum\limits_{j=1}^{n}(y_{j} - \hat{y}_{j})^{2}, $$
(15)
$$ RMSE=\sqrt{ \frac{1}{n}\sum\limits_{j=1}^{n}\hat{\varepsilon}_{j}^{2}}=\sqrt{\frac{1}{n}\sum\limits_{j=1}^{n}(y_{j} - \hat{y}_{j})^{2}}, $$
(16)
$$ MAE= \frac{1}{n}\sum\limits_{j=1}^{n}\vert\hat{\varepsilon}_{j}\vert=\frac{1}{n}\sum\limits_{j=1}^{n}\vert y_{j} - \hat{y}_{j}\vert. $$
(17)

Clearly, the smaller the MSE, RMSE or MAE, the better the model performs in prediction. but their values are scale dependent. An alternative measure that is based on absolute percentage error, \(|(y_{j} - \hat {y}_{j})/y_{j}|\), is the mean absolute percentage error (MAPE),

$$ MAPE= \frac{1}{n}\sum\limits_{j=1}^{n}\frac{\vert\hat{\varepsilon}_{j}\vert}{|y_{j}|}=\frac{1}{n}\sum\limits_{j=1}^{n}\frac{\vert y_{j} - \hat{y}_{j}\vert}{|y_{j}|}, $$
(18)

which is scale free. However, a shortcoming associated with this measure of MAPE is that it is very sensitive to a small number of outlying prediction errors, in particular potentially with small values of |yj|’s. We have also reported this measure of MAPE in model assessment below. We however should take care when explaining this measure for flood prediction, where we are concerned with extreme (large) values of QMED, rather than its small values, which we shall address below.

We are first comparing our proposed spatial flooding models (11) and (12), in terms of the MSE, RMSE and MAE, with the updated FEH-QMED model that is based on a revised data-transfer method of [33] with spatial autocorrelation partially taken account of in prediction. For detail on the updated FEH-QMED model in prediction, the reader is referred to [33] (page 5), where it is recommended that the estimates obtained at ungauged sites by using a regression model should be adjusted by transferring data from one nearby gauged site (if available) as there is a relatively dense gauging network in the UK. Differently from [33], the spatial dependence in our spatial flooding models (11) and (12) is taken into account by the spatial autoregressive models through considering two types of spatial neighboring relationship (i.e., contiguity-based and distance-based spatial weight matrices).

The results for prediction of \(Y=\ln (QMED)\) in terms of the MSE, the RMSE and the MAE for different models are summarized in Table 7. Note that the RMSE measure for prediction of \(Y=\ln (QMED)\) was considered by [33]. It is seen from Table 7 that our 4 proposed spatial flooding models, including the spatial error model with contiguity-based weight matrix (sperrcon), the spatial lag model with contiguity-based weight matrix (splagcon), the spatial error model with distance-based weight matrix (sperrdis) and the spatial lag model with distance-based weight matrix (splagdis), all look to outperform the updated FEH-QMED benchmark model of [33] from the prediction perspective in terms of both the MSE, the RMSE and the MAE. Here for ease of comparisons, the smallest value for each error measure among the 5 models is highlighted in italics in the table. Clearly, the spatial error model with contiguity-based matrix (sperrcon) performs the best in terms of the MSE, the RMSE and the MAE. The percentage of the improvement of this sperrcon flooding model over the updated FEH-QMED model of [33] in reduction of the MSE, the RMSE and the MAE is equal to (0.1586 − 0.1367)/0.1586 = 13.81%, 7.15% and 9.48%, respectively. Therefore, the sperrcon model significantly beats the [33] benchmark model, in terms of the MSE, RMSE and MAE, for the UK index flood estimation, which is consistent with the model selected by the AIC score in Table 4. As mentioned above, we have also reported, in the 6th column of Table 7, the performance of our 4 proposed spatial flooding models against the model of [33] in terms of the MAPE, defined in Eq. (18). Although in terms of this measure of MAPE it seems to show in Table 7 that the spatial lag models perform better than the spatial error models, but the difference in the MAPE between them is small, and note our sperrcon model still beats the model of [33] in prediction of \(Y=\ln (QMED)\) with a reduction of the MAPE by (0.3274 − 0.2924)/0.3274 = 10.69%. Here we should realize that this MAPE measure may be sensitive to a small number of outlying APE values particularly at the extreme quantile level, say, from 0.998 to 1 (c.f. the quantile curves for the spatial lag models are under those for other models as indicated in the right-hand sub-panel of panel (a) of Fig. 7).

Table 7 Comparison of model performance for \(Y=\ln (QMED)\) by LOOCV method
Full size table

Moreover, notice that it is the QMED that is of a direct interest, rather than \(Y=\ln (QMED)\) as an intermediate step, in the practice of index flood estimation. We have therefore also considered the four error measures of MSE, RMSE, MAE and MAPE for the prediction of the QMED directly, based on \(QMED=\exp (Y)\) with Y predicted as shown above, which are reported in Table 8. Here the MSE, RMSE, MAE and MAPE for prediction of the QMED are defined similarly to those for \(Y=\ln (QMED)\), with yj and \(\hat {y}_{j}\) in Eqs. (15)–(18) replaced by \(QMED_{j}=\exp (y_{j})\) and \(\widehat {QMED}_{j}=\exp (\hat {y}_{j})\). We have also displayed the scatter plots of the LOOCV based predicted value \(\widehat {QMED}\) against the observed value QMED for different models in Fig. 6, where the dashed lines stand for the predicted value equal to the observed value. From this figure, the [33] model appears not work well with most of the scattered points under the dashed line, but which model is preferred to in prediction cannot be clearly seen from the scatter plots. Nevertheless, in Table 8, we can clearly see that the spatial lag models perform worse than the other models inclduing the model of [33] in prediction of the QMED in terms of the MAPE. However, in terms of all the four error measures of the MSE, RMSE, MAE and MAPE, the spatial error flooding models, in particular the contiguity weight matrix based model, all beat the model of [33] significantly in prediction of QMED itself as indicated in Table 8. These results again well demonstrate that our spatial error flooding models (particularly the sperrcon model) outperform the model of [33], which are robust in the sense of different error measures, in estimation of the UK index flood.

Fig. 6
figure 6

The scatter plots of the LOOCV based predicted values (y-axis), versus the actual values (x-axis), of the QMED by the 4 models of sperrcon (spatial error model with contiguity weight matrix), splagcon (spatial lag model with contiguity weight matrix), sperrdis (spatial error model with distance weight matrix) and splagdis (spatial lag model with distance weight matrix), and the [33] model. Here the dashed lines stand for the predicted and the observed values being equal in the sub-panels

Full size image
Table 8 Comparison of model performance for \(QMED=\exp (Y)\) by LOOCV method
Full size table

We finally provide a comment on the results, particularly on the difference between predictions of \(Y=\ln (QMED)\) and QMED in terms of the MAPE. We hence further examine the distributions, in terms of quantiles, of the absolute percentage errors (APEs) for \(Y=\ln (QMED)\) and QMED with the different models considered above. Here the quantile value of the APE at the quantile level α, denoted by Qα, satisfies P(APE < Qα) = α. The plots of the quantile value Qα of the APE against the quantile level α for different models are displayed in panels (a) and (b) of Fig. 7 for \(Y=\ln (QMED)\) and QMED, respectively, where for clarity, the quantile levels from 0 to 0.90, from 0.90 to 0.99 and from 0.99 to 1 are partitioned and plotted on the left, the middle and the right panels, respectively. It can be seen in panel (a) of Fig. 7 that the curves of quantile values for both the spatial error and the spatial lag models are basically under that for the model of [33], in particular over the quantile level from 0.99 to 1 (the right-hand panel) with outlying (extremely large) APE values. This explains the performance of the spatial lag models and the spatial error models over the model of [33] in terms of MAPE in Table 7. However, in panel (b) of Fig. 7, the curves of quantile values for the spatial lag models are mostly slightly above that for the model of [33], in particular significantly above for the part of the quantile level from 0.90 and 0.99 (the middle panel). This may also explain why the spatial lag models are slightly worse than the model of [33] in terms of MAPE in Table 8. We can also see in panel (b) that the quantile curves for the spatial error models (sperrcon and sperrdis) are basically under that for the model of [33], so that the spatial error models outperform the [33] model in terms of the MAPE as shown in Table 8. For the performance of the models in terms of other error measures, the results from Tables 7 and 8 can be explained similarly with the spatial error models preferred to the [33] model for the UK index flood estimation by examining the distributions of other error measures, which are omitted to save space.

Fig. 7
figure 7

Plots of quantile value (y-axis) of the absolute percentage error (APE) for the LOOCV based prediction of: a \(Y=\ln (QMED)\), and b QMED, against the quantile level (x-axis) for the model of [33] and the 4 models of sperrcon , splagcon , sperrdis and splagdis . For clarity, the plots are made for the quantile level (x-axis) from 0 to 0.90 (left), from 0.90 to 0.99 (middle) and from 0.99 to 1 (right) in panels a and b, respectively

Full size image

5 Conclusion

Flood estimation for ungauged catchments is a challenging task. Urgent needs for efficient statistical method to identify and extract the unknown and unexpected complex features from the data sets are obvious, in order to have reliable index flood estimation models. For this purpose, the index flood regression model known as the QMED model in the Flood Estimation Handbook (FEH), which is the basis of most studies on flood risk estimation and modelling, has been assessed by spatial additive analysis. It is found that the FEH-QMED model (2) appears reliable in identifying the nonlinear effects of the catchment descriptors. Based on this, we have attempted to explore the unexpected features in the UK flood peak data set that went overlooked. We have found that the existing index flood estimation models can be significantly improved by spatial flooding models.

Our empirical findings through the work in the above are summarized as follows:

  1. 1.

    The nonlinear impacts of the explanatory catchment descriptors identified by the FEH-QMED model (2) appear reliable for the UK flooding data through spatial additive assessment.

  2. 2.

    To further improve the FEH-QMED model, we have suggested taking into account the spatial neighboring effects through spatial autoregressive analysis, since the spatial autocorrelation in the residuals of the FEH-QMED type model, as indicated in [35], is significantly strong through Moran’s I and Lagrange multiplier tests.

  3. 3.

    The UK flooding data appear to be more suitably modelled by the spatial error type model (11) than by the spatial lag type model (12). Our diagnostic assessment of spatial autoregressive analysis shows that the residuals of the spatial error type models are significantly uncorrelated with p values for contiguity- and distance-based spatial weights being as large as 68.89% and 95.59%, respectively, while the residuals of the spatial lag type models are detected to be significantly correlated yet.

  4. 4.

    We have empirically found that the spatial error type model (11) with contiguity-based spatial weight matrix is a significantly improved new model for the UK index flood estimation in terms of model selection by the AIC value. Moreover, our leave-one-out cross validation assessment shows that our new model outperforms the updated FEH-QMED model based on a revised data-transfer method of [33] in prediction. This conclusion is robust in terms of different error measures, for example, with a reduction of the mean squared prediction error by a percentage of 13.8%.

The improved index flood estimation model for the UK flooding data can be expressed, from Table 4, as

$$ \begin{array}{@{}rcl@{}} \ln(QMED_{i})&=& 2.1494 + 0.8497\ln(AREA_{i})\\ &&-3.2655(BFIHOST_{i})^{2} \\ &&+ 2.9526 \ln (FARL_{i}) \\ &&-1.8181 (1000SAAR_{i}^{-1}) + e_{i},\\ e & = & 0.4351 W e+\varepsilon , \end{array} $$
(19)

where e = (e1,e2,⋯ ,en)′ and ε = (ε1,ε2,⋯ ,εn)′ with εi being i.i.d. of normal distribution, and W is a n × n standardized contiguity-based spatial weight matrix based on (6).

It is well known that the FEH-QMED model has become the industry standard used to estimate local flood risk and develop resilient infrastructure. Similarly, it is interesting to investigate the applications of our improved index flood estimation model (19), e.g., for flood defense planning, flood risk analysis, new development planning and rarity assessment of notable rainfalls or floods in the UK, which are left for future research. In addition, potential improvement based on this work may be further considered as discussed in Section 3.2. For example, we may consider model selection with other spatial weight matrices that represent more neighboring sites than the contiguity- or distance-based matrix representation of a short-distance or quasi proximal action in this paper. We may also consider non-Gaussian distribution in model building as shown in Fig. 2. These are beyond the scope of this paper and worth more efforts of investigation for future work.