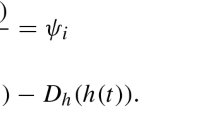Cover Crops and Water Quality

Abstract

This work deals with the regulation of water pollution caused by the use of nitrogen in agriculture. We investigate the policy instruments that should be implemented to induce socially optimal water quality. To do so, we propose a dynamic theoretical framework. We focus on the potential of cover crops to preserve water quality by considering the impact of soil quality on water quality to be endogenous: we consider two interrelated dynamic equations, one for soil quality and one for water pollution, that interact through soil quality. The land area devoted to cover crops increases the soil quality stock which, in turn, decreases the water pollution stock. We show that the socially optimal fiscal scheme consists in two parts: one that acts at the intensive margin (proportional to nitrogen use) and one at the extensive margin (proportional to land cultivated with cover crops).

Appendices

Appendix 1: Proof of Lemma 1

Three cases are to be distinguished.

• Case 1: l = 0 and 1 − l > 0.We deduce from KTC that, in this case, ϕ = 0 and $\frac {\partial \pi _{1}}{\partial l}-\frac {\partial \pi _{0}}{\partial \left (1-l\right ) }\leq 0$.The optimal solution then satisfies: x₀ = a₀ + bq_s and x₁ = 0.

• Case 2: l > 0 and 1 − l = 0.We deduce from KTC that, in this case, $\frac {\partial \pi _{1}}{\partial l}- \frac {\partial \pi _{0}}{\partial \left (1-l\right ) }-\phi = 0$ and ϕ ≥ 0, which means that $\frac {\partial \pi _{1}}{\partial l}-\frac {\partial \pi _{0}}{\partial \left (1-l\right ) }\geq 0$.The optimal solution then satisfies: x₁ = a₁ + bq_s and x₀ = 0.

• Case 3: l > 0 and 1 − l > 0.We deduce from KTC that, in this case, ϕ = 0 and $\frac {\partial \pi _{1}}{\partial l}-\frac {\partial \pi _{0}}{\partial \left (1-l\right ) }= 0$.If we put this into Eq. 5, we obtain ${\Phi }_{3}=-\frac { {x_{0}^{2}}}{2}+a_{0}x_{0}+bx_{0}q_{s}-f_{0}$ which leads to the same solution as case 1 where l = 0. Therefore, case 3 never occurs which indicates that discontinuities may arise.

Appendix 2: Proof of Proposition 1

We are looking for the solution of the following dynamic system:

$$ \left( \begin{array}{c} \dot{q}_{s,m0} \\ \dot{s}_{w,m0} \end{array}\right) =\underset{A_{m0}}{\underbrace{ \left( \begin{array}{cc} -\alpha & 0 \\ b-\beta & -\gamma \end{array}\right) }} \left( \begin{array}{c} q_{s,m0} \\ s_{w,m0} \end{array}\right) + \left( \begin{array}{c} 0 \\ a_{0} \end{array}\right) $$

The steady state (denoted ∞) of this system is given by:

$$ \left( \!\begin{array}{c} 0 \\ 0 \end{array}\!\right) = \left( \!\begin{array}{cc} -\alpha & 0 \\ b-\beta & -\gamma \end{array}\!\right)\! \left( \!\begin{array}{c} q_{s,m0\infty } \\ s_{w,m0\infty } \end{array}\!\right) + \left( \!\begin{array}{c} 0 \\ a_{0} \end{array}\!\right) \!\Leftrightarrow\! \left( \!\begin{array}{c} q_{s,m0\infty } \\ s_{w,m0\infty } \end{array}\!\right) = \left( \!\begin{array}{c} 0 \\ \frac{a_{0}}{\gamma } \end{array}\!\right) $$

We know from $\det (A_{m0})= \left |\begin {array}{cc}-\alpha & 0 \\ b-\beta & -\gamma \end {array}\right | =\alpha \gamma >0$ and tr(A_m0) = −α − γ < 0 that this equilibrium is stable.

Furthermore, A_m0 admits two eigenvalues, respectively eigenvectors, − α and − γ, respectively $\left (\begin {array}{c} \frac {\gamma -\alpha }{b-\beta } \\ 1 \end {array}\right )$ and $\left (\begin {array}{c} 0 \\ 1 \end {array}\right )$, that give the following general solution of the dynamic system under study:

$$ \left( \!\begin{array}{c} q_{s,m0}(t) \\ s_{w,m0}(t) \end{array}\!\right) \!=k_{1,m0} \!\left( \!\begin{array}{c} 0 \\ 1 \end{array}\!\right) e^{-\gamma t}+k_{2,m0} \!\left( \!\begin{array}{c} \frac{\gamma -\alpha }{b-\beta } \\ 1 \end{array}\right) e^{-\alpha t}+ \left( \begin{array}{c} 0 \\ \frac{a_{0}}{\gamma } \end{array}\right) $$

The constants k_{1, m0} and k_{2, m0} are computed based on initial conditions q_s(0) and s_w(0):

$$ \begin{array}{@{}rcl@{}} \left\{\!\!\begin{array}{c} {q_{s}(0)}\\ {s_{w}(0)} \end{array}\right. \! = \left\{\!\!\begin{array}{c} {k_{2,m0}\frac{\gamma -\alpha }{b-\beta }}\\ {k_{1,m0} + k_{2,m0} + \frac{a_{0}}{\gamma }} \end{array}\right.\\ &&{\kern-7.5pc}\Leftrightarrow\! \left\{\!\begin{array}{c} {k_{2,m0}}\\{k_{1,m0}} \end{array}\right. = \left\{\!\begin{array}{c} {\frac{(b-\beta )q_{s}(0)}{ \gamma -\alpha }}\\ {s_{w}(0) - \frac{(b-\beta )q_{s}(0)}{\gamma -\alpha } - \frac{ a_{0}}{\gamma}} \end{array}\right. \end{array} $$

We finally obtain the following solution:

$$ \begin{array}{@{}rcl@{}} \left( \begin{array}{c} q_{s,m0}(t) \\ s_{w,m0}(t) \end{array}\right) &=&\left( s_{w}(0)-\frac{(b-\beta )q_{s}(0)}{\gamma -\alpha }-\frac{a_{0}}{ \gamma }\right)\\ &&\times\left( \begin{array}{c} 0 \\ 1 \end{array}\right) e^{-\gamma t}\!+\frac{(b - \beta )q_{s}(0)}{\gamma -\alpha } \left( \!\begin{array}{c} \frac{\gamma -\alpha }{b-\beta } \\ 1 \end{array}\!\right) e^{-\alpha t}\\&&+ \left( \begin{array}{c} 0 \\ \frac{a_{0}}{\gamma } \end{array}\right) \end{array} $$

The path of nitrogen use is then directly deduced:

$$ x_{0,m0}(t)=a_{0}+bq_{s,m0}(t)=a_{0}+bq_{s}(0)e^{-\alpha t} $$

Appendix 3: Proof of Proposition 2

We are looking for the solution of the following dynamic system:

$$ \left( \begin{array}{c} \dot{q}_{s,m1} \\ \dot{s}_{w,m1} \end{array}\right) =\underset{A_{m1}}{\underbrace{ \left( \begin{array}{cc} -\alpha & 0 \\ b-\beta & -\gamma \end{array}\right) }} \left( \begin{array}{c} q_{s,m1} \\ s_{w,m1} \end{array}\right) + \left( \begin{array}{c} 1 \\ a_{1} \end{array}\right) $$

The steady state (denoted ∞) of this system is given by:

$$ \begin{array}{@{}rcl@{}} \left( \begin{array}{c} 0 \\ 0 \end{array}\right) &=& \left( \begin{array}{cc} -\alpha & 0 \\ b-\beta & -\gamma \end{array}\right) \left( \begin{array}{c} q_{s,m1\infty } \\ s_{w,m1\infty } \end{array}\right)+ \left( \begin{array}{c} 1 \\ a_{1} \end{array}\right)\\ &&\Leftrightarrow \left( \begin{array}{c} q_{s,m1\infty } \\ s_{w,m1\infty } \end{array}\right) = \left( \begin{array}{c} \frac{1}{\alpha } \\ \frac{a_{1}\alpha +b-\beta }{\gamma \alpha } \end{array}\right) \end{array} $$

Since A_m1 = A_m0, this equilibrium is stable. As before, the general solution of the dynamic system under study is given by:

$$ \left( \!\begin{array}{c} q_{s,m1}(t) \\ s_{w,m1}(t) \end{array}\!\right) = k_{1,m1} \left( \!\begin{array}{c} 0 \\ 1 \end{array}\!\right) e^{-\gamma t}+k_{2,m1} \left( \!\begin{array}{c} \frac{\gamma -\alpha }{b-\beta } \\ 1 \end{array}\!\right) e^{-\alpha t}+ \left( \!\begin{array}{c} \frac{1}{\alpha } \\ \frac{a_{1}\alpha +b-\beta }{\gamma \alpha } \end{array}\!\right) $$

The constants k_{1, m1} and k_{2, m1} are computed based on initial conditions q_s(0) and s_w(0):

$$ \begin{array}{@{}rcl@{}} \left\{\begin{array}{c} \!{q_{s}(0)}\\ \!{s_{w}(0)} \end{array}\right. \!&=&\! \left\{\begin{array}{c} {k_{2,m1}\frac{\gamma -\alpha }{b-\beta }}\\ {k_{1,m1}+k_{2,m1}+\frac{a_{1}}{\gamma }} \end{array}\right.\\ &&\!\Leftrightarrow \left\{\begin{array}{c} {k_{2,m1}}\\ {k_{1,m1}} \end{array}\right. \! =\! \left\{\begin{array}{c} {\frac{(b-\beta )\left( q_{s}(0)-\frac{1}{\alpha }\right) }{\gamma -\alpha }}\\ {s_{w}(0) - \frac{ (b-\beta )q_{s}(0)}{\gamma -\alpha }\! - \!\frac{a_{1}}{\gamma }\! + \! \frac{b-\beta }{ \gamma \left( \gamma -\alpha \right) }} \end{array}\right. \end{array} $$

We finally obtain the following solution:

$$ \begin{array}{@{}rcl@{}} &&{}\left( \begin{array}{c} q_{s,m1}(t) \\ s_{w,m1}(t) \end{array}\right)\\ {\kern10pt} & = & \!\left( s_{w}(0) - \frac{(b\! -\!\ \beta )q_{s}(0)}{\gamma -\alpha }\! -\!\ \frac{a_{1}}{ \gamma }\! +\! \frac{b-\beta }{\gamma \left( \gamma\! -\!\alpha \right) }\right)\! \left( \begin{array}{c} 0 \\ 1 \end{array}\right) e^{-\gamma t}\\ &&+\frac{(b\! -\! \beta )\left( q_{s}(0)-\frac{1}{\alpha }\right) }{ \gamma -\alpha } \left( \!\begin{array}{c} \frac{\gamma -\alpha }{b-\beta } \\ 1 \end{array}\!\right) e^{-\alpha t}+ \left( \begin{array}{c} \frac{1}{\alpha } \\ \frac{a_{1}\alpha +b-\beta }{\gamma \alpha } \end{array}\right) \end{array} $$

The path of nitrogen use is then directly deduced:

$$ x_{1,m1}(t)=a_{1}+bq_{s,m1}(t)=a_{1}+b\left( q_{s}(0)-\frac{1}{\alpha }\right) e^{-\alpha t}+\frac{b}{\alpha } $$

Appendix 4: Proof of Lemma 2

Three cases are to be distinguished.

• Case 1: l = 0 and 1 − l > 0.We deduce from KTC in Eq. 15 that, in this case, ψ = 0 and $\frac {\partial \pi _{1}}{\partial l}+\mu x_{1}+\lambda -\frac {\partial \pi _{0}}{ \partial \left (1-l\right ) }-\mu x_{0}\leq 0$.The solution of problem (10) then satisfies: x₀ = a₀ + bq_s + μ and x₁ = 0.

• Case 2: l > 0 and 1 − l = 0.We deduce from KTC in Eq. 15 that, in this case, $\frac {\partial \pi _{1}}{\partial l}+\mu x_{1}+\lambda -\frac {\partial \pi _{0}}{\partial \left (1-l\right ) }-\mu x_{0}-\psi = 0$ and ψ ≥ 0, which means that $\frac {\partial \pi _{1}}{\partial l}+\mu x_{1}+\lambda -\frac {\partial \pi _{0}}{\partial \left (1-l\right ) }-\mu x_{0}\geq 0$.The solution of problem (10) then satisfies: x₁ = a₁ + bq_s + μ and x₀ = 0.

• Case 3: l > 0 and 1 − l > 0.We deduce from KTC in Eq. 15 that, in this case, ψ = 0 and $\frac {\partial \pi _{1}}{\partial l}+\mu x_{1}+\lambda -\frac {\partial \pi _{0}}{ \partial \left (1-l\right ) }-\mu x_{0}= 0$.If we put this into Eq. 11, we obtain $L_{3}=-\frac {{x_{0}^{2}} }{2}+a_{0}x_{0}+bx_{0}q_{s}-f_{0}-cs_{w}-\lambda \alpha q_{s}+\mu \left (x_{0}-\beta q_{s}-\gamma s_{w}\right )$ which is equivalent to case 1. Therefore, case 3 never occurs which indicates that discontinuities may arise.

Appendix 5: Proof of Proposition 3

We are looking for the solution of the following system:

$$ \left( \!\begin{array}{c} \dot{q}_{s,so0} \\ \dot{s}_{w,so0} \\ \dot{\lambda}_{so0} \\ \dot{\mu}_{so0} \end{array}\!\right) = \underset{A_{so0}}{\underbrace{ \left( \!\begin{array}{cccc} -\alpha & 0 & 0 & 0 \\ b-\beta & -\gamma & 0 & 1 \\ -b^{2} & 0 & \delta +\alpha & \beta -b \\ 0 & 0 & 0 & \delta +\gamma \end{array}\!\right) }} \left( \!\begin{array}{c} q_{s,so0} \\ s_{w,so0} \\ \lambda_{so0} \\ \mu_{so0} \end{array}\!\right) + \left( \!\begin{array}{c} 0 \\ a_{0} \\ -ba_{0} \\ c \end{array}\!\right) $$

Before studying the steady state, we need to check the local stability of this system. To do so, we depart from Legras [16] whose proof follows Dockner [6]. Two conditions are necessary and sufficient to ensure the saddle point property: B < 0 and $0<\det A_{so0}<\left (\frac {B}{2}\right )^{2}$ where

$$ \begin{array}{@{}rcl@{}} B = \left|\begin{array}{cc} \frac{\partial \dot{q}_{s,so0}}{\partial q_{s,so0}} & \frac{\partial \dot{q} _{s,so0}}{\partial \lambda_{so0}} \\ \frac{\partial \dot{\lambda}_{so0}}{\partial q_{s,so0}} & \frac{\partial \dot{\lambda}_{so0}}{\partial \lambda_{so0}} \end{array}\right| + \left|\begin{array}{cc} \frac{\partial \dot{s}_{w,so0}}{\partial s_{w,so0}} & \frac{\partial \dot{s} _{w,so0}}{\partial \mu_{so0}} \\ \frac{\partial \dot{\mu}_{so0}}{\partial s_{w,so0}} & \frac{\partial \dot{\mu }_{so0}}{\partial \mu_{so0}} \end{array}\right| + 2 \left|\begin{array}{cc} \frac{\partial \dot{q}_{s,so0}}{\partial s_{w,so0}} & \frac{\partial \dot{q} _{s,so0}}{\partial \mu_{so0}} \\ \frac{\partial \dot{\lambda}_{so0}}{\partial s_{w,so0}} & \frac{\partial \dot{\lambda}_{so0}}{\partial \mu_{so0}} \end{array}\right| \end{array} $$

Basic computations lead to:

$$ \begin{array}{@{}rcl@{}} B&=& \left|\begin{array}{cc} -\alpha & 0 \\ -b^{2} & \delta +\alpha \end{array}\right| + \left|\begin{array}{cc} -\gamma & 1 \\ 0 & \delta +\gamma \end{array}\right| + 2 \left|\begin{array}{cc} 0 & 0 \\ 0 & \beta -b \end{array}\right| \\&=&-\alpha \left( \delta +\gamma \right) -\gamma \left( \delta +\gamma \right)<0 \end{array} $$

and

$$ \det A_{so0}=\alpha \gamma \left( \delta +\alpha \right) \left( \delta +\gamma \right) >0 $$

Furthermore,

$$ \left( \frac{B}{2}\right)^{2}-\det A_{so0}=\left[ \alpha \left( \delta +\alpha \right) -\gamma \left( \delta +\gamma \right) \right]^{2}>0 $$

The steady state (denoted ∞) of the previous system is given by:

$$ \begin{array}{@{}rcl@{}} \left( \!\begin{array}{c} 0 \\ 0 \\ 0 \\ 0 \end{array}\!\right) \! &=&\! \left( \!\begin{array}{cccc} -\alpha & 0 & 0 & 0 \\ b-\beta & -\gamma & 0 & 1 \\ -b^{2} & 0 & \delta +\alpha & \beta -b \\ 0 & 0 & 0 & \delta +\gamma \end{array}\!\right)\! \left( \begin{array}{c} q_{s,so0\infty } \\ s_{w,so0\infty } \\ \lambda_{so0\infty } \\ \mu_{so0\infty } \end{array}\right) \! +\! \left( \!\begin{array}{c} 0 \\ a_{0} \\ -ba_{0} \\ c \end{array}\!\right)\\ &&\Leftrightarrow\! \left( \!\begin{array}{c} q_{s,so0\infty } \\ s_{w,so0\infty } \\ \lambda_{so0\infty } \\ \mu_{so0\infty } \end{array}\!\right) = \left( \!\begin{array}{c} 0 \\ \frac{a_{0}\left( \delta +\gamma \right) -c}{\gamma \left( \delta +\gamma \right) } \\ \frac{ba_{0}}{\delta +\alpha }-\frac{c(b-\beta )}{\left( \delta +\alpha \right) \left( \delta +\gamma \right) } \\ -\frac{c}{\delta +\gamma } \end{array}\!\right) \end{array} $$

The general solution of this system is as follows:

$$ \begin{array}{@{}rcl@{}} \left( \! \begin{array}{c} q_{s,so0}(t) \\ s_{w,so0}(t) \\ \lambda_{so0}(t) \\ \mu_{so0}(t) \end{array}\!\right)\! &=&\!k_{1,so0}e^{-\gamma t} \left( \begin{array}{c} 0 \\ 1 \\ 0 \\ 0 \end{array}\right)\\ &&\!+k_{2,so0}e^{-\alpha t} \left( \begin{array}{c} \frac{2\alpha +\delta }{b^{2}} \\ -\frac{\left( 2\alpha +\delta \right) (b-\beta )}{(\alpha -\gamma )b^{2}} \\ 1 \\ 0 \end{array}\right) \\ &&\! +k_{3,so0}e^{(\delta +\gamma )t} \left( \begin{array}{c} 0 \\ 1 \\ \frac{2b\gamma +\delta b-2\beta \gamma -\delta \beta }{\alpha -\gamma } \\ 2\gamma +\delta \end{array}\right) \\ &&\! +k_{4,so0}e^{(\delta +\alpha )t} \!\left( \!\begin{array}{c} 0 \\ 0 \\ 1 \\ 0 \end{array}\!\right) \! +\! \left( \!\begin{array}{c} 0 \\ \frac{a_{0}\left( \delta +\gamma \right) -c}{\gamma \left( \delta +\gamma \right) } \\ \frac{ba_{0}}{\delta +\alpha }\! -\! \frac{c(b-\beta )}{\left( \delta +\alpha \right) \left( \delta +\gamma \right) } \\ -\frac{c}{\delta +\gamma } \end{array}\!\right) \end{array} $$

where k_{1, so0}, k_{2, so0}, k_{3, so0} and k_{4, so0} denotes the constants of integration.

The steady state given by this system of equations is globally unstable because of positive eigenvalues, δ + γ, and, δ + α, that prevent the transversality conditions from being satisfied. The stability set is such that k_{3, so0} = 0 and k_{4, so0} = 0. We then deduce from the initial conditions q_s(0) and s_w(0):

$$ \begin{array}{@{}rcl@{}} \left\{\begin{array}{c} {q_{s,so0}(0)}\\ {s_{w,so0}(0)} \end{array}\right. \! &=&\! \left\{\begin{array}{c} {k_{2,so0}\frac{\delta }{b^{2}}}\\ k_{1,so0}-k_{2,so0}\frac{\left( 2\alpha +\delta \right) (b-\beta ) }{(\alpha -\gamma)b^{2}}+\frac{a_{0}\left( \delta +\gamma \right) -c} {\gamma \left( \delta +\gamma \right) } \end{array}\right.\\ &&\!\Leftrightarrow \left\{\begin{array}{c} {k_{2,so0}=\frac{b^{2}q_{s}(0)}{2\alpha +\delta}}\\ \!{k_{1,so0}\! =\! s_{w}(0)+\frac{ q_{s}(0)(b-\beta )}{\alpha -\gamma }\! -\!\frac{a_{0}\left( \delta +\gamma \right) -c}{\gamma \left( \delta +\gamma \right) }} \end{array}\right. \end{array} $$

We finally obtain the following solution:

$$ \begin{array}{@{}rcl@{}} \left( \! \begin{array}{c} q_{s,so0}(t) \\ s_{w,so0}(t) \\ \lambda_{so0}(t) \\ \mu_{so0}(t) \end{array}\!\right) \! &=&\! \left( \begin{array}{c} q_{s}(0) \\ \frac{(b-\beta )q_{s}(0)}{\gamma -\alpha } \\ \frac{b^{2}q_{s}(0)}{2\alpha +\delta } \\ 0 \end{array}\right) e^{-\alpha t}\\ &&\! +\! \left( \! \begin{array}{c} 0 \\ s_{w}(0)\! +\! \frac{q_{s}(0)(b-\beta )}{\alpha -\gamma }\! -\! \frac{a_{0}}{\gamma }+ \frac{c}{\gamma (\delta +\gamma )} \\ 0 \\ 0 \end{array}\!\right) e^{-\gamma t}\\ &&\! +\! \left( \begin{array}{c} 0 \\ \frac{a_{0}\left( \delta +\gamma \right) -c}{\gamma \left( \delta +\gamma \right) } \\ \frac{ba_{0}}{\delta +\alpha }-\frac{c(b-\beta )}{\left( \delta +\alpha \right) \left( \delta +\gamma \right) } \\ -\frac{c}{\delta +\gamma } \end{array}\right) \end{array} $$

The path of nitrogen use is then directly deduced:

$$ \begin{array}{@{}rcl@{}} x_{0,so0}(t)&=&a_{0}+bq_{s,so0}(t)+\mu_{so0}\\ &&\Leftrightarrow x_{0,so0}(t)=a_{0}\\ &&+bq_{s}(0)e^{-\alpha t}-\frac{c}{\delta +\gamma } \end{array} $$

Appendix 6: Proof of Proposition 4

We are looking for the solution of the following system:

$$ \left( \!\begin{array}{c} \dot{q}_{s,so1} \\ \dot{s}_{w,so1} \\ \dot{\lambda}_{so1} \\ \dot{\mu}_{so1} \end{array}\!\right) = \left( \!\begin{array}{cccc} -\alpha & 0 & 0 & 0 \\ b-\beta & -\gamma & 0 & 1 \\ -b^{2} & 0 & \delta +\alpha & \beta -b \\ 0 & 0 & 0 & \delta +\gamma \end{array}\!\right)\! \left( \!\begin{array}{c} q_{s,so1} \\ s_{w,so1} \\ \lambda_{so1} \\ \mu_{so1} \end{array}\!\right) + \left( \!\begin{array}{c} 1 \\ a_{1} \\ -ba_{1} \\ c \end{array}\!\right) $$

This system is very similar to the previous one, except for the constant term of soil quality motion over time that will induce more complex expressions. As a consequence, the preceding proof of the local stability of the system remains valid.

The steady state (denoted ∞) of this system is given by:

$$ \begin{array}{@{}rcl@{}} \left( \!\begin{array}{c} 0 \\ 0 \\ 0 \\ 0 \end{array}\!\right) \!\!&=&\!\! \left( \!\begin{array}{cccc} -\alpha & 0 & 0 & 0 \\ b-\beta & -\gamma & 0 & 1 \\ -b^{2} & 0 & \delta +\alpha & \beta -b \\ 0 & 0 & 0 & \delta +\gamma \end{array}\!\right)\! \left( \!\begin{array}{c} q_{s,so1\infty } \\ s_{w,so1\infty } \\ \lambda_{so1\infty } \\ \mu_{so1\infty } \end{array}\!\right) \! + \left( \!\!\begin{array}{c} 1 \\ a_{1} \\ -ba_{1} \\ c \end{array}\!\!\right)\\ &\Leftrightarrow& \left( \begin{array}{c} q_{s,so1\infty } \\ s_{w,so1\infty } \\ \lambda_{so1\infty } \\ \mu_{so1\infty } \end{array}\right) = \left( \begin{array}{c} \frac{1}{\alpha } \\ \frac{a_{1}}{\gamma }+\frac{b-\beta }{\alpha \gamma }-\frac{c}{\gamma (\delta +\gamma )} \\ \frac{ba_{1}\alpha +b^{2}}{\alpha (\delta +\alpha )}+\frac{c(\beta -b)}{ (\delta +\gamma )(\delta +\alpha )} \\ -\frac{c}{\delta +\gamma } \end{array}\right) \end{array} $$

The general solution of this system is as follows:

$$ \begin{array}{@{}rcl@{}} \left( \begin{array}{c} q_{s,so1}(t) \\ s_{w,so1}(t) \\ \lambda_{so1}(t) \\ \mu_{so1}(t) \end{array}\right) &=&k_{1,so1}e^{-\gamma t} \left( \begin{array}{c} 0 \\ 1 \\ 0 \\ 0 \end{array}\right) \\ &&+k_{2,so1}e^{-\alpha t} \left( \begin{array}{c} \frac{2\alpha +\delta }{b^{2}} \\ -\frac{\left( 2\alpha +\delta \right) (b-\beta )}{(\alpha -\gamma )b^{2}} \\ 1 \\ 0 \end{array}\right)\\ && +k_{3,so1}e^{(\delta +\gamma )t} \left( \begin{array}{c} 0 \\ 1 \\ \frac{2b\gamma +\delta b-2\beta \gamma -\delta \beta }{\alpha -\gamma } \\ 2\gamma +\delta \end{array}\right)\\ &&+k_{4,so1}e^{(\delta +\alpha )t} \left( \begin{array}{c} 0 \\ 0 \\ 1 \\ 0 \end{array}\right)\\ &&+ \left( \begin{array}{c} \frac{1}{\alpha } \\ \frac{a_{1}}{\gamma }+\frac{b-\beta }{\alpha \gamma }-\frac{c}{\gamma (\delta +\gamma )} \\ \frac{ba_{1}\alpha +b^{2}}{\alpha (\delta +\alpha )}+\frac{c(\beta -b)}{(\delta +\gamma )(\delta +\alpha )} \\ -\frac{c}{\delta +\gamma } \end{array}\right) \end{array} $$

where k_{1, so1}, k_{2, so1}, k_{3, so1} and k_{4, so1} denotes the constants of integration.

The steady state given by this system of equations is globally unstable because of positive eigenvalues, δ + γ, and, δ + α, that prevent the transversality conditions from being satisfied. The stability set is such that k_{3, so1} = 0 and k_{4, so1} = 0. We then deduce from the initial conditions q_s(0) and s_w(0):

$$ \begin{array}{@{}rcl@{}} \left\{\!\begin{array}{c} {q_{s,so1}(0)}\\ {s_{w,so1}(0)} \end{array}\right. \!\! & = &\! \! \left\{\begin{array}{c} {k_{2,so1}\frac{\delta}{b^{2}}+\frac{1}{\alpha }}\\ {k_{1,so1}\! -\! k_{2,so1}\frac{\delta (b-\beta )}{(\alpha -\gamma )b^{2}}+\frac{a_{1}}{\gamma }\! +\!\frac{b-\beta }{\alpha \gamma } \! -\! \frac{c}{\gamma (\delta +\gamma )}} \end{array}\right.\\ &&\!\!\Leftrightarrow\! \left\{\begin{array}{c} {k_{2,so1}= \frac{b^{2}(\alpha q_{s}(0)-1)}{\alpha \left( 2\alpha +\delta \right) }}\\ \!\!{k_{1,so1}\!\! =\!\! s_{w}({\kern-.5pt}0{\kern-.5pt}) + \frac{\left( \gamma q_{s}(0){\kern-.5pt}-{\kern-.5pt}1\right) (b{\kern-.5pt}-{\kern-.5pt}\beta )}{\gamma \left( \alpha -\gamma \right) } - \frac{a_{1}(\delta +\gamma )-c}{ \gamma (\delta +\gamma )}} \end{array}\right. \end{array} $$

We finally obtain the following solution:

$$ \begin{array}{@{}rcl@{}} \!\left( \!\!\begin{array}{c} q_{s,so1}(t) \\ s_{w,so1}(t) \\ \lambda_{so1}(t) \\ \mu_{so1}(t) \end{array}\!\!\right) \!\! &=&\!\! \left( \!\!\begin{array}{c} q_{s}(0)-\frac{1}{\alpha } \\ \frac{(\alpha q_{s}(0)-1)(b-\beta )}{\alpha \left( \gamma -\alpha \right)}\\ \frac{b^{2}(\alpha q_{s}(0)-1)}{\alpha \left( 2\alpha +\delta \right)}\\ 0 \end{array}\!\!\right) e^{-\alpha t}\\ &&\! + \left( \!\!\begin{array}{c} 0 \\ s_{w}(0) + \frac{\left( {\kern-.5pt} \gamma{\kern-.5pt} q_{s}(0)-{\kern-.5pt}1{\kern-.5pt}\right) (b-{\kern-.5pt}\beta )}{\gamma \left( \alpha -\gamma \right) }\! -\! \frac{a_{1}}{\gamma }\! +\!\frac{c}{\gamma{\kern-.5pt} (\delta +\gamma{\kern-.5pt} )} \\ 0 \\ 0 \end{array}\!\!\right) \!e^{-\gamma t}\\ &&+ \left( \begin{array}{c} \frac{1}{\alpha } \\ \frac{a_{1}}{\gamma }+\frac{b-\beta }{\alpha \gamma }-\frac{c}{\gamma (\delta +\gamma )} \\ \frac{ba_{1}\alpha +b^{2}}{\alpha (\delta +\alpha )}+\frac{c(\beta -b)}{(\delta +\gamma )(\delta +\alpha )} \\ -\frac{c}{\delta +\gamma } \end{array}\right) \end{array} $$

The path of nitrogen use is then directly deduced:

$$ \begin{array}{@{}rcl@{}} x_{1,so1}(t)&=&a_{1}+bq_{s,so1}(t)+\mu_{so1}\\ &&\Leftrightarrow x_{1,so1}(t)=a_{1} +b\left( q_{s}(0)-\frac{1}{\alpha }\right)e^{-\alpha t}\\&&+\frac{b}{ \alpha }-\frac{c}{\delta +\gamma } \end{array} $$

Appendix 7: Proof of Remark 1

First, we assume that the set of parameters is such that x_{1, go} and x_{0, go} (the subscript go denotes the solution of such a problem which is similar to that of Goetz et al. [9]) are always positive. From problem (5.3) in which a fiscal scheme on fertilizer denoted T is introduced, we define a new optimization function:

$$ \begin{array}{@{}rcl@{}} L &:=&\left( -\frac{{x_{1}^{2}}}{2}+a_{1}x_{1}+bx_{1}q_{s}+Tx_{1}-f_{1}\right) l\\ && +\left( -\frac{{x_{0}^{2}}}{2}+a_{0}x_{0}+bx_{0}q_{s}+Tx_{0}-f_{0}\right) \left( 1-l\right)\\ &&+\lambda \left( l-\alpha q_{s}\right) +\psi (1-l) \end{array} $$

(20)

According to the maximum principle with inequality constraint, the optimal solution of problem (5.3) is defined by:

$$ \begin{array}{@{}rcl@{}} &&{}\underset{x_{1},x_{0},l}{\max }\left( \!-\frac{{x_{1}^{2}}}{2} +a_{1}x_{1}+bx_{1}q_{s}Tx_{1}-f_{1}\right) l\\ &&~~+\!\left( \!-\frac{{x_{0}^{2}}}{2} + a_{0}x_{0} + bx_{0}q_{s} + Tx_{0} - f_{0}\!\right) \!\left( 1 - l\right)\\ &&\text{ \ \ \ \ \ \ \ \ \ \ \!}+\lambda \left( l-\alpha q_{s}\right) \\ &&~~~\text{s.t.}\text{: } \text{ }0\leq l\leq 1 \end{array} $$

(21)

and

$$ \left\{\begin{array}{c} {\dot{\lambda}=\delta \lambda -bx_{1}l-bx_{0}\left( 1-l\right) +\alpha \lambda }\\ {\dot{q}_{s}=l-\alpha q_{s}} \end{array}\right. $$

(22)

along with the transversality conditions: $\underset {t\rightarrow \infty }{\lim }\lambda _{so}(t)\geq 0$ and $\underset {t\rightarrow \infty }{\lim } \lambda _{so}(t)q_{s,so}(t)= 0$.

In terms of the Lagrangian, problem (21) means:

$$ \left\{\begin{array}{c} {x_{1}=a_{1}+bq_{s}+T}\\ {x_{0}=a_{0}+bq_{s}+T} \end{array}\right. $$

(23)

and

$$ \left\{\begin{array}{c} \frac{\partial \pi_{1}}{\partial l}+Tx_{1}+\lambda -\frac{\partial \pi_{0}}{\partial \left( 1-l\right) }-Tx_{0}-\psi \leq 0,\text{ } l\geq 0,\\\text{ }l\left( \frac{\partial \pi_{1}}{\partial l}+Tx_{1}+\lambda - \frac{\partial \pi_{0}}{\partial \left( 1-l\right) }-Tx_{0}-\psi \right) = 0\\ {1-l\geq 0,\text{ }\psi \geq 0,\text{ }\psi \left( 1-l\right) = 0} \end{array}\right. $$

(24)

Comparing Eqs. 23 and 24 with Eqs. 14 and 15, we see that the optimum of function (20) coincides with the socially optimal optimum when $T:=-\frac {c}{\delta +\gamma }(=\mu )$.

Appendix 8: Proof of Proposition 6

For the sake of clarity, we assume that the set of parameters is such that x_{1, mμ} and x_{0, mμ} are always positive (the subscript mμ denotes the myopic case in which a tax on nitrogen is introduced). From problem (18), we form a new optimization function, similar to a Lagrangian:

$$ \begin{array}{@{}rcl@{}} {\Phi} &:=&\left( -\frac{{x_{1}^{2}}}{2}+a_{1}x_{1}+bx_{1}q_{s}-f_{1}+\mu x_{1}\right) l\\&&+\left( -\frac{{x_{0}^{2}}}{2}+a_{0}x_{0}+bx_{0}q_{s}-f_{0}+\mu x_{0}+\phi \right) \left( 1-l\right)\\ \end{array} $$

(25)

The first-order conditions (FOC):

$$ \left\{\begin{array}{c} {x_{1}=a_{1}+bq_{s}+\mu }\\ {x_{0}=a_{0}+bq_{s}+\mu } \end{array}\right. $$

(26)

along with the Khun-Tucker conditions (KTC):

$$ \left\{\begin{array}{c} \frac{\partial \pi_{1}}{\partial l}+\mu x_{1}-\frac{\partial \pi_{0}}{\partial \left( 1-l\right) }-\mu x_{0}-\phi \leq 0,\text{ }l\geq 0,\\ l\left( \frac{\partial \pi_{1}}{\partial l}+\mu x_{1}-\frac{ \partial \pi_{0}}{\partial \left( 1-l\right) }-\mu x_{0}-\phi \right) = 0\\ {1-l\geq 0,\text{ }\phi \geq 0,\text{ }\phi \left( 1-l\right) = 0} \end{array}\right. $$

(27)

define the optimal solution of problem (18).

Three cases are to be distinguished.

• Case 1: l = 0 and 1 − l > 0.We deduce from KTC in Eq. 27 that, in this case, ϕ = 0 and $\frac {\partial \pi _{1}}{\partial l}+\mu x_{1}-\frac {\partial \pi _{0}}{\partial \left (1-l\right ) }-\mu x_{0}\leq 0$.The solution of problem (18) then satisfies: x₀ = a₀ + bq_s + μ and x₁ = 0.

• Case 2: l > 0 and 1 − l = 0.We deduce from KTC in Eq. 27 that, in this case, $\frac {\partial \pi _{1}}{\partial l}+\mu x_{1}-\frac {\partial \pi _{0}}{\partial \left (1-l\right ) }-\mu x_{0}-\phi = 0$ and ϕ ≥ 0, which means that $\frac {\partial \pi _{1}}{\partial l}+\mu x_{1}-\frac {\partial \pi _{0}}{\partial \left (1-l\right ) }-\mu x_{0}\geq 0$.The solution of problem (18) then satisfies: x₁ = a₁ + bq_s + μ and x₀ = 0.

• Case 3: l > 0 and 1 − l > 0.We deduce from KTC in Eq. 27 that, in this case, ϕ = 0 and $\frac {\partial \pi _{1}}{\partial l}+\mu x_{1}-\frac {\partial \pi _{0}}{\partial \left (1-l\right ) }-\mu x_{0}= 0$.If we put this into Eq. 25, we obtain $L_{3}=-\frac { {x_{0}^{2}}}{2}+a_{0}x_{0}+bx_{0}q_{s}-f_{0}+\mu \left (x_{0}-\beta q_{s}-\gamma s_{w}\right )$ which is equivalent to case 1. Therefore, case 3 never occurs which indicates that discontinuities may arise.

Consequently, we focus on each of the solutions for l and furthermore assume that the set of parameters is such that the solution is the same along the entire time path.

For a set of parameters such that l = 0 ∀t ≥ 0, i.e. $\frac {\partial \pi _{1}}{\partial l}+\mu x_{1}<\frac {\partial \pi _{0}}{\partial \left (1-l\right ) }+\mu x_{0}$ ∀t ≥ 0, the farmer never cultivates cover crops and x_{1, mμ0} = 0. Furthermore, we know from the FOC that x_{0, mμ0} = a₀ + bq_{s, mμ0} + μ. Incorporating these values into both dynamics of soil quality in Eq. 2 and water pollution in Eq. 3 we obtain the following dynamic system:

$$ \left( \begin{array}{c} \dot{q}_{s,m0} \\ \dot{s}_{w,m0} \end{array}\right) = \left( \begin{array}{cc} -\alpha & 0 \\ b-\beta & -\gamma \end{array}\right) \left( \begin{array}{c} q_{s,m0} \\ s_{w,m0} \end{array}\right) + \left( \begin{array}{c} 0 \\ a_{0}+\mu \end{array}\right) $$

(28)

Following the same resolution process as in Proposition 1, we obtain the following paths:

$$ \begin{array}{@{}rcl@{}} q_{s,m\mu 0}(t)\! & = &\! q_{s}(0)e^{-\alpha t}=q_{s,so0}(t)<q_{s,so1}(t)\\ x_{0,m\mu 0}(t)\! & = &\! a_{0}+bq_{s}(0)e^{-\alpha t}+\mu =x_{0,so0}(t)<x_{1,so1}(t)\\ s_{w,m\mu 0}(t)\! & = &\! \left( s_{w}(0)-\frac{(b-\beta )q_{s}(0)}{\gamma -\alpha }- \frac{a_{0}+\mu }{\gamma }\right) e^{-\gamma t}\\ &&+\frac{(b-\beta )q_{s}(0)}{ \gamma -\alpha }e^{-\alpha t}+\frac{a_{0}+\mu }{\gamma }=s_{w,so0}(t)\\ &&\underset{t\rightarrow \infty }{\lim }\left( s_{w,so1}(t)-s_{w,m\mu 0}(t)\right)\\ & = &\! \underset{t\rightarrow \infty }{\lim }\left\{ s_{w,m0}(t)\mid_{a_{0}=a_{1}}+\frac{b-\beta}{\alpha \gamma (\gamma -\alpha )}\right.\\ &&{\kern17pt}\left.\vphantom{\frac{b-\beta}{\alpha \gamma (\gamma -\alpha )}}\times\!\left[\! \alpha\! \left( {\kern-.5pt} e^{-\gamma t}\! -\! 1{\kern-.5pt}\right) \! +\! \gamma\! \left( {\kern-.5pt}1\! -\! e^{-\alpha t}\right)\! \right] \! -\! s_{w,m0}(t)\right\} \\ & = &\!\frac{a_{1}}{\gamma }+\frac{b-\beta }{\alpha \gamma }-\frac{a_{0}}{\gamma }<0\Leftrightarrow a_{1}-a_{0}<\frac{ \beta -b}{\alpha} \end{array} $$

For a set of parameters such that l = 1 ∀t ≥ 0, i.e. $\frac {\partial \pi _{1}}{\partial l}+\mu x_{1}>\frac {\partial \pi _{0}}{\partial \left (1-l\right ) }+\mu x_{0}$ ∀t ≥ 0, the farmer cultivates cover crops on all his land and, consequently, x_{0, mμ1} = 0. We obtain the following dynamic system:

$$ \left( \begin{array}{c} \dot{q}_{s,m1} \\ \dot{s}_{w,m1} \end{array}\right) = \left( \begin{array}{cc} -\alpha & 0 \\ b-\beta & -\gamma \end{array}\right) \left( \begin{array}{c} q_{s,m1} \\ s_{w,m1} \end{array}\right) + \left( \begin{array}{c} 1 \\ a_{1}+\mu \end{array}\right) $$

(29)

Following the same resolution process as in Proposition 2, we obtain the following paths:

$$ \begin{array}{@{}rcl@{}} q_{s,m\mu 1}(t)&=&q_{s}(0)e^{-\alpha t}+\frac{1}{\alpha }\left( 1-e^{-\alpha t}\right) =q_{s,so1}(t)\\ x_{1,m\mu 1}(t)&=&a_{1}+bq_{s}(0)e^{-\alpha t}+\frac{b}{\alpha }\left( 1-e^{-\alpha t}\right) +\mu =x_{1,so1}(t) \end{array} $$

$$ \begin{array}{@{}rcl@{}} s_{w,m\mu 1}(t)&=&\left( s_{w}(0)-\frac{(b-\beta )q_{s}(0)}{\gamma -\alpha }- \frac{a_{1}+\mu }{\gamma }\right) e^{-\gamma t}\\ &&+\frac{(b-\beta )q_{s}(0)}{\gamma -\alpha }e^{-\alpha t}+\frac{a_{1}+\mu }{\gamma }\\&&+\frac{b-\beta }{\alpha \gamma \!(\gamma - \alpha )}\!\left[ \alpha \!\left( e^{-\gamma t} - 1\right) + \gamma \!\left( 1 - e^{-\alpha t}\right) \right] \!=s_{w,so1}(t) \end{array} $$

Comparison between this taxation case and the socially optimal solution in the stylized example are direct from comparisons already made in the text.

The set of parameters such that cultivating cover crops is preferred by the myopic farmer incurring a nitrogen tax is given by the so-called bang-bang condition, $\frac {\partial \pi _{1}}{\partial l}-\frac {\partial \pi _{0}}{ \partial \left (1-l\right ) }+\mu \left (x_{1}-x_{0}\right ) >0$.

For instance, at the initial time t = 0,

$$ \begin{array}{@{}rcl@{}} \frac{\partial \pi_{1}(0)}{\partial l}\! &-&\! \frac{\partial \pi_{0}(0)}{\partial \left( 1-l\right) }+\mu \left( x_{1}(0)-x_{0}(0)\right)\\ &=&\! -\frac{ {x_{1}^{2}}(0)}{2}{\kern-.5pt}+{\kern-.5pt}a_{1}x_{1}(0){\kern-.5pt}+{\kern-.5pt}bx_{1}(0)q_{s}(0){\kern-.5pt}-{\kern-.5pt}f_{1}+\frac{{x_{0}^{2}}(0)}{2}\\ &&-a_{0}x_{0}(0)-bx_{0}(0)q_{s}(0)\\&&+f_{0}+\mu \left( x_{1}(0)-x_{0}(0)\right) \\ &=&\! -\frac{\left( a_{1}+bq_{s}(0)\right)^{2}}{2}+{a_{1}^{2}}-\frac{\left( a_{0}+bq_{s}(0)\right)^{2}}{2}-{a_{0}^{2}}\\ &&+\left( a_{1}-a_{0}\right) \left( 2bq_{s}(0)+\mu \right) +f_{0}-f_{1}\\ &=&\!\frac{1}{2} (a_{1}\! -\! a_{0})\!\left( \! a_{1}\! + \!a_{0}\! +\! 2bq_{s}(0)\! -\! \frac{2c}{\delta +\gamma }\!\right) \! +\! f_{0}\! -\! f_{1}. \end{array} $$

After standard computations, the bang-bang necessary condition can be rewritten: $F_{m\mu }:=\frac {{\Xi }_{1}^{2}}{2}-f_{1}-\frac {{\Xi }_{0}^{2}}{2} +f_{0}>0$.

Appendix 9: Proof of Proposition 7

For the sake of clarity, we assume that the set of parameters is such that x_{1, mλ} and x_{0, mλ} are always positive (the subscript mλ denotes the myopic case in which a subsidy on cover crops is introduced). From problem (19), we form a new optimization function, similar to a Lagrangian:

$$ \begin{array}{@{}rcl@{}} {\Phi} &:=&\left( -\frac{{x_{1}^{2}}}{2}+a_{1}x_{1}+bx_{1}q_{s}-f_{1}\right) l\\&&+\left( -\frac{{x_{0}^{2}}}{2}+a_{0}x_{0}+bx_{0}q_{s}-f_{0}+\phi \right) \left( 1-l\right) +\lambda l\\ \end{array} $$

(30)

The FOC:

$$ \left\{\begin{array}{c} {x_{1}=a_{1}+bq_{s}}\\ {x_{0}=a_{0}+bq_{s}} \end{array}\right. $$

(31)

along with the KTC:

$$ \left\{\begin{array}{c} {\frac{\partial \pi_{1}}{\partial l}-\frac{\partial \pi_{0}}{\partial \left( 1-l\right) } - \phi +\lambda \!\leq\! 0,\text{ }l\!\geq\! 0, l\left( \frac{\partial \pi_{1}}{\partial l} - \frac{\partial \pi_{0}}{\partial \left( 1-l\right) } - \phi +\lambda \right) = 0}\\ {1-l\geq 0,\text{ } \phi \geq 0,\text{ }\phi \left( 1-l\right) = 0} \end{array}\right. $$

(32)

define the optimal solution of problem (19).

Three cases are to be distinguished.

• Case 1: l = 0 and 1 − l > 0.We deduce from KTC in Eq. 32 that, in this case, ϕ = 0 and $\frac {\partial \pi _{1}}{\partial l}-\frac {\partial \pi _{0}}{\partial \left (1-l\right ) }+\lambda \leq 0$.The solution of problem (19) then satisfies: x₀ = a₀ + bq_s and x₁ = 0.

• Case 2: l > 0 and 1 − l = 0.We deduce from KTC in Eq. 32 that, in this case, $\frac {\partial \pi _{1}}{\partial l}-\frac {\partial \pi _{0}}{\partial \left (1-l\right ) }-\phi +\lambda = 0$ and ϕ ≥ 0, which means that $\frac {\partial \pi _{1}}{\partial l}-\frac {\partial \pi _{0}}{\partial \left (1-l\right ) }+\lambda \geq 0$.The solution of problem (19) then satisfies: x₁ = a₁ + bq_s and x₀ = 0.

• Case 3: l > 0 and 1 − l > 0.We deduce from KTC in Eq. 32 that, in this case, ϕ = 0 and $\frac {\partial \pi _{1}}{\partial l}-\frac {\partial \pi _{0}}{\partial \left (1-l\right ) }+\lambda = 0$.If we put this into Eq. 30, we obtain $L_{3}=-\frac { {x_{0}^{2}}}{2}+a_{0}x_{0}+bx_{0}q_{s}-f_{0}+\lambda l$ which is equivalent to case 1. Therefore, case 3 never occurs which indicates that discontinuities may arise.

Consequently, we focus on each of the solutions for l and furthermore assume that the set of parameters is such that the solution is the same along the entire time path.

For a set of parameters such that l = 0 ∀t ≥ 0, i.e. $\frac {\partial \pi _{1}}{\partial l}+\lambda <\frac {\partial \pi _{0}}{\partial \left (1-l\right ) }$ ∀t ≥ 0, the farmer never cultivates cover crops and x_{1, mλ0} = 0. The optimal paths are given by Proposition 1 and:

$$ \begin{array}{@{}rcl@{}} q_{s,so1}(t) & - & q_{s,m\lambda 0}(t) = \frac{1}{\alpha }\left( 1-e^{-\alpha t}\right) >0\\ x_{1,so1}(t)& - & x_{0,m\lambda 0}(t)\\ &=&a_{1}+\frac{b}{\alpha }\left( 1-e^{-\alpha t}\right) -\frac{c}{\delta +\gamma }-a_{0}>0\\ &&\Leftrightarrow a_{1}-a_{0}> \frac{c}{\delta +\gamma}-\frac{b}{\alpha }\left( 1-e^{-\alpha t}\right)\\ s_{w,so1}(t) & - & s_{w,m\lambda 0}(t)\\ & = & \left( s_{w}(0)+\frac{\left( \gamma q_{s}(0)-1\right) (b-\beta )}{\gamma \left( \alpha -\gamma \right) }\right.\\ &&{\kern5pt}\left. -\frac{ a_{1}}{\gamma }+\frac{c}{\gamma (\delta +\gamma )}\right) e^{-\gamma t}\\ &&- \frac{(\alpha q_{s}(0)-1)(b-\beta )}{\alpha (\alpha -\gamma )}e^{-\alpha t}+ \frac{a_{1}}{\gamma }\\&&+\frac{b-\beta }{\alpha \gamma}-\frac{c}{\gamma (\delta +\gamma )}\\ && -\left( s_{w}(0)-\frac{(b-\beta )q_{s}(0)}{\gamma -\alpha } -\frac{a_{0}}{\gamma }\right) e^{-\gamma t}\\ &&-\frac{(b-\beta )q_{s}(0)}{\gamma -\alpha}e^{-\alpha t}-\frac{a_{0}}{\gamma }\\ \end{array} $$

$$ \begin{array}{@{}rcl@{}} & = & \left( \frac{\left( \gamma q_{s}(0)-1\right) (b-\beta )}{\gamma \left( \alpha -\gamma \right) }+\frac{ (b-\beta )q_{s}(0)}{\gamma -\alpha}\right.\\ &&~~\left.+\frac{a_{0}}{\gamma }-\frac{a_{1}}{ \gamma }+\frac{c}{\gamma (\delta +\gamma )}\right) e^{-\gamma t}\\ && +\left( \! -\! \frac{(b\! -\! \beta )q_{s}(0)}{\gamma -\alpha }\! -\! \frac{(\alpha q_{s}(0)\! -\! 1)(b\! -\! \beta )}{\alpha (\alpha -\gamma )}\right) e^{-\alpha t}\\ &&+\frac{a_{1}}{\gamma }- \frac{a_{0}}{\gamma }+\frac{b-\beta }{\alpha \gamma }-\frac{c}{\gamma (\delta +\gamma )}\\ & = &\ \left( \frac{\beta -b}{\gamma \left( \alpha -\gamma \right) }+\frac{a_{0}-a_{1}}{\gamma }+\frac{c}{\gamma (\delta +\gamma )}\right) e^{-\gamma t}\\ &&+\frac{(b-\beta )}{\alpha (\alpha\! -\! \gamma )} e^{-\alpha t}\! +\! \frac{a_{1}\! -\! a_{0}}{\gamma }\! +\! \frac{b\! -\! \beta }{\alpha \gamma }\! -\! \frac{c}{\gamma (\delta +\gamma )} \end{array} $$

At the steady state, this last difference is given by:

$$ \begin{array}{@{}rcl@{}} &&\underset{ t\rightarrow \infty }{\lim }(s_{w,so1}(t)-s_{w,m\lambda 0}(t))\\ &&=\frac{ a_{1}-a_{0}}{\gamma }+\frac{b-\beta }{\alpha \gamma }-\frac{c}{\gamma (\delta +\gamma )}<0\\ &&\Leftrightarrow a_{1}-a_{0}<\frac{c}{\delta +\gamma }+ \frac{\beta -b}{\alpha}. \end{array} $$

Note that it is impossible to both have $\underset {t\rightarrow \infty }{ \lim }\left (x_{1,so1}(t)-x_{0,m\lambda 0}(t)\right ) <0$ and $\underset { t\rightarrow \infty }{\lim }(s_{w,so1}(t)-s_{w,m\lambda 0}(t))>0$ since this translates into $\frac {c}{\delta +\gamma }+\frac {\beta -b}{\alpha } <a_{1}-a_{0}<\frac {c}{\delta +\gamma }-\frac {b}{\alpha }$ which is satisfied only for β < 0. Furthermore, $a_{1}-a_{0}<\frac {c}{\delta +\gamma }- \frac {b}{\alpha }\Rightarrow a_{1}-a_{0}<\frac {c}{\delta +\gamma }-\frac {b}{ \alpha }\left (1-e^{-\alpha t}\right )$ and $a_{1}-a_{0}<\frac {c}{\delta +\gamma }+\frac {\beta -b}{\alpha }$.

Note also that $a_{1}-a_{0}>\frac {c}{\delta +\gamma }+\frac {\beta }{\alpha } \Rightarrow a_{1}-a_{0}>\frac {c}{\delta +\gamma }-\frac {b}{\alpha }\left (1-e^{-\alpha t}\right )$ and $a_{1}-a_{0}>\frac {c}{\delta +\gamma }+\frac { \beta }{\alpha }-\frac {b}{\alpha }$. And that $\frac {c}{\delta +\gamma }+ \frac {\beta -b}{\alpha }>a_{1}-a_{0}>\frac {c}{\delta +\gamma }\Rightarrow a_{1}-a_{0}>\frac {c}{\delta +\gamma }-\frac {b}{\alpha }\left (1-e^{-\alpha t}\right )$.

For a set of parameters such that l = 1 ∀t ≥ 0, i.e. $\frac {\partial \pi _{1}}{\partial l}+\lambda >\frac {\partial \pi _{0}}{\partial \left (1-l\right ) }$ ∀t ≥ 0, the farmer cultivates cover crops on all his land and, consequently, x_{0, mλ1} = 0. The optimal paths are given by Proposition 2. In this case, the comparison of the paths obtained with the paths in the socially optimal case is the same as in the standard case.

The set of parameters such that cultivating cover crops is preferred by the myopic farmer subsidized for cultivating cover crops is given by the so-called bang-bang condition, $\frac {\partial \pi _{1}}{\partial l}-\frac {\partial \pi _{0}}{\partial \left (1-l\right ) }+\lambda >0$.

For instance, at the initial time t = 0,

$$ \begin{array}{@{}rcl@{}} \frac{\partial \pi_{1}(0)}{\partial l}\! -\! \frac{\partial \pi_{0}(0)}{\partial \left( 1-l\right) }+\lambda\! & = &\! -\frac{{x_{1}^{2}}(0)}{2} \! +\! a_{1}x_{1}(0)\! +\! bx_{1}(0)q_{s}(0)\\ &&-f_{1}+\frac{{x_{0}^{2}}(0)}{2}-a_{0}x_{0}(0)\\ &&-bx_{0}(0)q_{s}(0)+f_{0}+\lambda\\ &=&\! \frac{{a_{1}^{2}}}{2}\! +\! a_{1}bq_{s}(0)-\frac{{a_{0}^{2}}}{2}-a_{0}bq_{s}(0)\\ &&+f_{0}-f_{1}+\lambda\\ &=&\!\frac{1}{2}\left( a_{1}-a_{0}\right) \left( a_{1}+a_{0}+ 2bq_{s}(0)\right)\\ &&+f_{0}-f_{1}+\lambda. \end{array} $$

After standard computations, the bang-bang necessary condition can be rewritten: $F_{m\lambda }:=\frac {\chi _{1}^{2}}{2}-f_{1}-\frac {\chi _{0}^{2} }{2}+f_{0}$ + λ > 0.