Assessing the Sustainability of Optimal Pollution Paths in a World with Inertia

Abstract

Most formal optimal pollution control models in environmental economics assume a constant natural assimilative capacity, despite the biophysical evidence on feedback effects that can degrade this environmental function, as is the case with the reduction of ocean carbon sinks in the context of climate change. The few models that do consider this degradation establish a bijective relation between the pollution stock and the assimilative capacity, thus ignoring the inertia mechanism at stake. Indeed the level of assimilative capacity is not solely determined by the current pollution stock but also by the history of this stock and by the length of time the ecosystem remains above the degradation threshold. We propose an inertia assessment tool that tests the sustainability of any benchmark optimal pollution path when the inertia of the assimilative capacity degradation process is taken into account. Our simulations show a strong sensitivity to both the inertia degradation speed and the discount rate, thus stressing the need for increased monitoring of natural assimilative capacity in environmental policies.

Appendix

1.1 A.1 The Benchmark Model

Let us solve the benchmark optimal pollution control problem with constant assimilative capacity:

$$\begin{array}{@{}rcl@{}} && \max_{y(t)}{{\int}_{0}^{\infty}\left[ f(y(t))-D(Z(t))\right] e^{-\rho t}dt}, \\ && \:\:\text{s.t.} \\ && \:\:\dot{Z}(t)=y(t)-\alpha_{0} Z(t), \quad Z(0)=Z_{0}>0,\\ \end{array} $$

with the standard properties: f, the concave benefit function from pollution; D, the environmental damage function (increasing and convex); ρ, the discount rate; Z₀, the initial pollution stock; and α₀ the constant assimilative capacity (0 < α₀)

We thus get the following Hamiltonian with λ the co-state variable associated to Z

$$ \mathcal{H}_{c}(t)=f(y(t))-D(Z(t))+\lambda (t)(y(t)-\alpha_{0} Z(t)), $$

(14)

which yields the standard first-order conditions

$$\begin{array}{@{}rcl@{}} && f^{\prime }(y(t))=-\lambda (t), \end{array} $$

(15)

$$\begin{array}{@{}rcl@{}} && \dot{\lambda}(t)=(\rho +\alpha_{0})\lambda (t)+D^{\prime }(Z(t)). \end{array} $$

(16)

1.1.1 A.1.1 Benchmark Steady State

Given the dynamics of Z and λ and the properties of f and D, a unique Z_ss exists such that

$$\begin{array}{@{}rcl@{}} && f^{\prime}(\alpha_{0} Z_{ss}) >0, \\ && f^{\prime}(\alpha_{0} Z_{ss})(\rho+\alpha_{0})- D^{\prime}(Z_{ss})= 0. \end{array} $$

(17)

Let us introduce the standard functional forms commonly found in the literature that we will use for further calculations and that respect the basic properties required:

$$f(y){}={}cy-\frac{b}{2}y^{2}, \:\: with\;c,b{}>{}0,\:\: \quad D{}(Z){}={}\frac{d}{2}Z^{2}{}, \:\: with\;d{}>{}0. $$

With these functional forms, Eq. 17 is tantamount to

$$ Z_{ss}=\frac{(\rho+\alpha_{0})c}{(\rho+\alpha_{0})b\alpha_{0}+d}. $$

(18)

1.1.2 A.1.2 Characterization of the Optimal Path

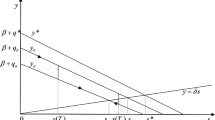
We can determine analytically the expression of Z^∗(t), λ^∗(t) and y^∗(t) along the optimal pollution path by solving the first-order conditions (15), (16) for the quadratic linear functional forms.

$$\begin{array}{@{}rcl@{}} &&Z^{*}(t) = e^{- \bar{\rho} t} (Z(0) - Z_{ss}) + Z_{ss}, \end{array} $$

(19)

$$\begin{array}{@{}rcl@{}} &&y^{*}(t)=\frac{c+\lambda}{b}, \end{array} $$

(20)

$$\begin{array}{@{}rcl@{}} &&\lambda^{*}(t) = b (- \rho + \alpha_{0}) e^{- \bar{\rho} t} (Z(0) \,-\, Z_{ss}) \,-\, \frac{d}{\rho + \alpha_{0}} Z_{ss}, \end{array} $$

(21)

where $\bar {\rho } = \sqrt {(\rho /2 + \alpha _{0})^{2} + d/b} - \rho /2 >0$. $\bar {\rho }$ is the speed of convergence of the dynamic.

Equations 19 and 20 will enable us to analyze the comparative statics we are interested in but they will also be used in Section 4 to simulate numerically benchmark optimal pollution paths and to test their behavior in the presence of inertia.

1.1.3 A.1.3 Proof of Proposition 1

Proof The proof is straightforward. According to Eq. 1 we have

$$\frac{\partial Z_{ss}}{\partial{\alpha_{0}}} = \left( c \frac{d - b (\alpha_{0} + \rho)^{2}}{(d + \rho \alpha_{0} b + {\alpha_{0}^{2}} b)^{2}}\right). $$

Hence, defining $\bar {\alpha }= \sqrt {d/b} - \rho$

$$\frac{\partial Z_{ss}}{\partial{\alpha_{0}}} \gtreqqless 0 \iff \alpha_{0} \lesseqqgtr \bar{\alpha}. $$

• if $\rho > \sqrt {d/b}$, $\bar {\alpha }<0$ and thus ∀α₀ > 0 we have $\alpha _{0} >\bar {\alpha }$ and $\frac {\partial Z_{ss}}{\partial {\alpha }} < 0$.

• if $\rho < \sqrt {d/b}$ then $\frac {\partial Z_{ss}}{\partial {\alpha _{0}}} > 0$ for $0 < \alpha _{0} < \bar {\alpha }$ and $\frac {\partial Z_{ss}}{\partial {\alpha _{0}}} < 0$ for $\bar {\alpha } < \alpha _{0}$.

1.1.4 A.1.4 Assimilative Capacity and Social Welfare at the Steady State

We check that the intuitive positive effect of α on the social welfare at the steady state is actually true. The social welfare can be written as:

$$W(\alpha)=f(\alpha Z_{ss}(\alpha)) - D(Z_{ss}(\alpha)). $$

Hence, taking into account (17)

$$\begin{array}{@{}rcl@{}} \frac{\partial{W}}{\partial{\alpha}}&=&\left( \alpha \frac{\partial{Z_{ss}}}{\partial{\alpha}} + Z_{ss}(\alpha) \right) f^{\prime}(\alpha Z_{ss}(\alpha))\\ &&-\frac{\partial{Z_{ss}}}{\partial{\alpha}}D^{\prime}(Z_{ss}(\alpha))\\ &=& \left( - \rho \frac{\partial{Z_{ss}}}{\partial{\alpha}}+ Z_{ss}(\alpha) \right) f^{\prime}(\alpha Z_{ss}(\alpha)). \end{array} $$

As by first-order condition f^′(αZ_ss(α)) > 0, when $\frac {\partial {Z_{ss}}}{\partial {\alpha }} <0$ we have $\frac {\partial {W}}{\partial {\alpha }} >0$. Nevertheless, with our specific forms we can prove that it is always positive, in fact:

$$W(\alpha) = \frac{1}{2}\frac{ c^{2} (\alpha + \rho) (d \alpha + \rho \alpha^{2} b + b \alpha^{3} - d \rho)}{(d + \rho \alpha b + b \alpha^{2})^{2}}, $$

and thus

$$\frac{d W(\alpha)}{d \alpha} = \frac{c^{2} d (b (\rho+ \alpha)^{3} + d\alpha)}{(d + \rho \alpha b + b \alpha^{2})^{3}} > 0. $$

1.2 A.2 Injection of a Benchmark Optimal Path

1.2.1 A.2.1 Proof of Proposition 2

Proof

• 1. is straightforward.

• 2. if a steady state with α > 0 exists, we have

  $$\alpha_{ss} Z_{ss} =\lim\limits_{t\to \infty} y^{*}(t). $$

  Hence, according to Eq. 8:

  $$Z_{ss} =\frac{\alpha_{0}}{ \alpha_{ss}} Z_{ss}^{*}. $$

  A steady state exists if Eq. 10 is verified, given that α > 0, i.e. if

  $$ Z_{ss} \leq\bar{Z} \quad \iff \frac{\alpha_{0}}{ \alpha_{ss}} Z_{ss}^{*}\leq\bar{Z} \quad \iff Z_{ss}^{*}\leq \frac{\alpha_{ss}}{\alpha_{0}} \bar{Z}. $$

  (22)

1.2.2 A.2.2 Proof of Condition (12)

Let us state the following corollary to Proposition 2:

Corollary 3

If $Z^{*}_{ss}>\bar {Z}$ , the BP is not sustainable.

Proof

• If α_ss = 0, then according to Proposition 2 no sustainable steady state can be reached.

• If α_ss > 0, since by definition α_ss ≤ α₀, then $Z^{*}_{ss}>\bar {Z} \Rightarrow \frac {Z_{ss}^{*}}{ \alpha _{ss}}>\frac {\bar {Z}}{\alpha _{0}}$

  Condition (22) is not verified and no sustainable steady state can be reached.

Corollary 3 can be translated with our functional forms into the following condition. Let us define ρ_u such that

$$\rho_{u}=\frac{d\bar{Z}-\alpha_{0}c+b{\alpha_{0}^{2}}\bar{Z}}{c-b\alpha_{0}\bar{Z}}. $$

We have

$$ \rho> \rho_{u} \Rightarrow Z_{ss}^{*} >\bar{Z}. $$

(23)