1 Introduction

Mercury contamination is severely threatening for human health and all aspects of the environment. The UNEP’s report on mercury [38] indicates that the combustion of fossil fuels is one of the key (main) sources [24] of mercury emission into the air. In Poland, 90% of energy used in 2012 (ca. 55% of mercury released into the air) came from combustion in the public electricity and heat production sector [8].

The Polish national emission inventory [31] also emphasizes that combustion of fossil fuels is significant source of energy and also the mercury air emission.

A number of studies [15, 23, 47] provide estimated values of mercury air emissions, however the statistical uncertainty assessment has not been prepared so far due to a strong variability of mercury content in fuel [2, 3, 25, 27, 28, 43, 44].

Moreover, a significant lack of data and an insufficient recognition of the applied air pollution control technologies hindered such an assessment from being carried out. The first general assessment of the uncertainty of mercury air emission using the methodology based on official guidelines [10, 22] and selected technical studies [13, 24, 40] is provided in the Polish official emission report [31]. This paper presents an approach based on detailed statistical and technological analysis.

Apart from the uncertainty assessment, the presented paper includes the monthly distribution of the mercury air emission using the Denton-Cholette approach [6].

2 Materials and Methods

A generalized scheme of the analysis is presented in Fig. 1 based on the data derived from the literature, from which we determined the average Hg content in hard coal and lignite.

Fig. 1
figure 1

Scheme of analysis

Full size image

After analyzing the outliers, we assessed mercury air emissions from the public power and energy sector. The analysis of the applied APC technologies (years 1990–2012) made it possible to estimate the possibility of Hg removal in emission abatement installations.

The Monte Carlo simulation is used to determine the confidence intervals (CIs) for estimated emissions. The monthly distributions of mercury air emissions are carried out using the time series analysis approach in comparison with previously published results [21].

2.1 Plant Location and Emission Estimation

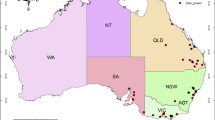
Plant location and emissions estimation locations of Polish public utility plants are presented in Fig. 2. Size of applied symbols is proportional to energy input [TJ] in solid fuels (hard coal and lignite).

Fig. 2
figure 2

Public utility plants locations in Poland

Full size image

Mercury emissions from energy and heat production are frequently estimated using bottom-up equations [46, 47], however the emission inventory for Poland uses a top-down approach (Eq. 3) based on the activity of the emission source which is the total energy supplied by the combusted fuel.

$$ ME=FC \times C \times (1-\eta) $$
(1)

where ME, mercury emission [kg]; FC, fuel consumption [ 106kg]; C, mercury content (concentration) in fuel [kg Hg ⋅ 10−6kg]; η, mercury removal efficiency in APC installations [%/100].

The same scheme of inventory (Eq. 2) is applied separately for both: hard coal and lignite plants.

$$\begin{array}{@{}rcl@{}} \sum\limits_{i} C_{i} \times (1-\eta_{i}) \times FC_{i} \text{\hspace{2em}bottom-up} \end{array} $$
(2)
$$\begin{array}{@{}rcl@{}} \hat{C} \times (1-\hat{\eta}) \times FC \text{\hspace{3.7em}top-down} \end{array} $$
(3)

where C i , mercury content of fuels from various sources and plants; \(\hat {C}\), average mercury content in fuel; η i , mercury removal efficiencies in various APCs; \(\hat {\eta }\), average mercury removal efficiency in all installations.

2.2 Fuel Consumption

The emission data submitted for the purposes of international obligations [31, 39] uses the activity data in bottom-up (2010–2012) [30] and top-down (1995–2009) [11] approaches. According to the official guidelines on quality assurance and quality control in emission inventories [10], the comparison between coal/lignite consumption provided by these data sources did not exceed 2%, as in Eq. 4 for the public power and energy sector.

$$ 0.98 \cdot FC_{td} \leq \sum\limits_{i} FC_{i} \leq 1.02 \cdot FC_{td} $$
(4)

where F C t d , top-down data on fuel consumption; F C i , fuel consumption in individual combustion installation (bottom-up approach).

This analysis is carried out to harmonize the air mercury emission trend (1990–2012). The influence of APC devices installed in particular plants since 1990 is also considered. That means the emission trend 1990–2012 is based mainly on top-down fuel consumption (1990–2009, as above); however, the analysis of the efficiency of APC installations uses only the bottom-up approach.

Fuel consumption for the years 1990 to 2010 (with a 5-year interval) and 2012 is presented in Table 1.

Table 1 Fuel consumption by Eurostat [11] [kt = 106kg] (years: 1990, 1995, 2000, 2005, 2010, and 2012)
Full size table

2.3 Mercury Content in Fuel used in the Polish Power and Energy Sector

The mercury concentration in Polish coals and lignites is characterized by a strong variability [23]. To determine the average mercury content in Polish hard coals and lignites, we used data derived from various studies carried out in 1991–2013 (hard coals), 1994–2013 (lignites). The result of our investigation into studies on mercury content in Polish hard coals (Fig. 3) and lignites (Fig. 4) is presented below.

Fig. 3
figure 3

Average Hg content in hard coals

Full size image
Fig. 4
figure 4

Average Hg content in lignites

Full size image

Based on data derived from studies enumerated in Figs. 3 and 4 [2, 3, 15, 16, 25, 27,28,29, 36, 43,44,45], the mercury content in hard coals and lignites is determined using spectrometric techniques. That fact permits a comparison between specific results. We determined the mean Hg content in Polish hard coals and lignites using a combination of average values taken from these studies.

Statistical analysis of the mercury content consists of a test for sample normality, and an investigation of outliers using the Grubbs’ T test [18, 19].

2.4 Combustion Process

Mercury during the combustion process occurs in two main species: total gaseous mercury (TGM) and total particulate mercury (TPM). TGM consists of the vapours of elemental mercury (Hg 0) and volatile oxidized mercury (Hg +2). Only the volatile oxidized mercury and TPM may be controlled by application of wet flue gas desulphurization and dedusting [42].

2.4.1 Mercury Speciation

The split between TGM and TPM is assumed based on [33], 4.6 to 14.4% of the total mercury bound to the particulate matter, however this value is slightly different from the data taken from other studies [37, 41].

2.4.2 Chlorine Content in Fuel

The efficiency of mercury removal strongly depends on the chlorine content in fuel. Increasing the concentration of chlorine in the combustion process facilitates the creation of Hg +2 [4, 42]. The amounts of chlorine in Polish hard coals and lignites are derived from studies: [1] and [9].

It varies from 0 .02 to 0 .6% (the most frequent interval: 0 .08–0 .3%) and 0%, respectively. Finally, due to a rather low level of chlorine content in Polish fuels, we did not take into account the influence of chlorine.

2.4.3 Structure of Applied Air Pollution Control Devices

The structure of APCs installed in the Polish public power and energy sector for 2012 is determined using data collected for purposes of the Polish emissions management system [30] and split into classes, for hard coal and lignite. The type and quality of APCs for previous years were fixed based on a study about flue gas desulphurisation in the Polish power and energy sector [14].

Mercury removal efficiencies of APCs installed in Polish power plants, including the combined heat and power (CHP), are derived from available publications and assigned according to the similarity of installations and the fuel used. The uncertainties of estimation are assumed by analysing the difference between the maximal and minimal efficiency corresponding to each analysed case. Due to a lack of detailed information, the most complete analysis we carried out was for 2012.

2.5 Stochastic Simulation

To determine the uncertainty of the mercury emission, we carried out a stochastic simulation using the Monte Carlo technique [26]. The simulation is carried out separately for parameters taken into account during emission estimation (Eq. 1): FC, C, and η [5, 13, 37, 46].

The simulation uses datasets prepared before a time series of fuel consumption (1990-2012), data on mercury concentration in fuel, and the analysis of efficiencies of the APC technologies applied in the Polish power and energy sector. The simulation uses randomly generated parameters (FC, C, η) from normal distributions, as folows:

  • \(FC \sim \mathcal {N}(\hat {FC}, \sigma _{FC})\),

  • \(C \sim \mathcal {N}(\hat {C}, \sigma _{C})\),

  • \(\eta \sim \mathcal {N}(\hat {\eta }, \sigma _{\eta })\),

where: \(\hat {\{\cdot \}}\), mean value of FC, C, and η, respectively; σ {⋅}, standard deviations of the parameters.

The normal distribution for the fuel consumption (FC) is a result of homogenous data (analysis concerning one sector). Over the period 1990–2012 the energy mix was stable, and the coal fuels (hard coal, lignite) remain the main fuel types used in the Polish public power and energy sector.

The normal distribution of mercury content (C) is assumed after tests for normality (see Section 2.3). Due to no detailed information about the quality of fuels used in particular plants (only the split between hard coal and lignite), or the data about measured efficiencies of mercury removal, we assumed normal distribution for η, on the contrary to assumptions given in [13, 37, 46]. The simulation carried out in the article is similar to [5].

The total (“combined”) uncertainty for Hg air emissions is determined according to Rule B (Eq. 5) taken from international guidelines [10].

$$ U_{total} = \sqrt{U_{FC}^{2}+{U_{C}^{2}}+U_{\eta}} $$
(5)

where U t o t a l , total combined uncertainty; U {⋅}, uncertainties for: fuel consumption (FC), mercury content in fuel (C), and efficiency of APC installations (η), respectively.

Rule B is commonly applied in emission inventories to associate the uncertainties of each components of emission estimation. Considering mercury air emissions as a combination of three components (FC, C, and η, Eq. 1) applying Eq. 5 makes it possible to determine the total uncertainty of the estimation.

We performed the stochastic simulation for the years given in Table 1 (1990, 1995, 2000, 2005, 2010, 2012) using selected emission scenarios built applying a sensitivity analysis and by checking the compliance between the determined scenarios and original time series (national emission inventory) [31]. The empirical probability density functions (PDFs) for the enumerated years are determined using a basic kernel density estimator from statistical programming language R (Eq. 6).

$$ \hat{f}_{kde}(x) = \frac{1}{n} \sum\limits^{n}_{i=1} K \left( \frac{x - x_{i}}{h} \right) $$
(6)

where K, kernel function; h, bandwith.

The kernel function K is symmetric (even), usually positive, and integrates to one. The bandwidth is the smoothing parameter [7]. The bandwidth is selected by minimising the mean integrated square error (MISE) known also as L 2 risk function (Eq. 7).

$$ MISE(\hat{f}) = E \left[ \int\left( \hat{f}(x) - f(x) \right)^{2} dx \right] $$
(7)

2.6 Monthly Distribution of Mercury Emissions

Temporal variability coefficients for mercury emissions are elaborated in the Institute for Ecology of Industrial Areas (Poland) [21] (Fig. 5).

Fig. 5
figure 5

Temporal variability of mercury air emission

Full size image

To determine the temporal disaggregation of mercury emissions, we used the dependency between mercury emissions and the data on monthly coal production [12]. The emission value is disaggregated using the Denton-Cholette approach included in the statistical programming language R [34, 35].

The approach, given in [6], uses the principle of movement preservation. The movement in the original (time) series s t is reproduced by the benchmarked series 𝜃 t (Eq. 8).

$$\begin{array}{@{}rcl@{}} s_{t} = \theta_{t} + e_{t} \end{array} $$
(8)

where s t , observed sub-annual series (monthly fuel consumption); 𝜃 t , benchmarked series (disaggregated); e t , error.

The error function: e t = s t − 𝜃 t is further described as an objective function (f) which is minimized. Expressing f using matrix algebra is given in Eq. 9.

$$\begin{array}{@{}rcl@{}} f(\theta, \gamma) &=& (\theta - s)'D^{\prime}D(\theta \!- s) - 2\gamma^{\prime}(a - J\theta)\\ &=& \theta^{\prime}D^{\prime}D\theta - 2\theta^{\prime}D^{\prime}Ds \,+\, s^{\prime}D^{\prime}Ds - 2\gamma^{\prime}a + 2\gamma^{\prime}J\theta \end{array} $$
(9)

where a, benchmarks; s, 𝜃, time series: observed and benchmarked, respectively; γ, matrix of the Lagrange multipliers associated with the linear constraints a − J 𝜃 = 0; J is the temporal sum operator equaled to Kronecker product: J = I M ⊗1; 1, unit row vector containing zeroes in the first eleven columns for monthly series; D is non-seasonal difference operator (dimensions: (T − 1) × T = 11 × 12 for monthly disaggregation):

$$D = \left[\begin{array}{llllll} -1 & 1 & 0 & 0 & {\dots} \\ 0 & -1 & 1 & 0 & {\dots} \\ 0 & 0 & -1 & 1 & {\dots} \\ {\vdots} & {\vdots} & {\vdots} & {\vdots} & \ddots \end{array}\right]. $$

Optimization of the objective function means that the derivative of the objective function (Eq. 9) is equal to zero with respect to the parameters (Eq. 10).

$$\begin{array}{@{}rcl@{}} \frac{\partial f(\theta, \gamma)}{\partial \theta} &=& 2D^{\prime}D\theta - 2D^{\prime}Ds + 2J^{\prime}\gamma = 0\\ \frac{\partial f(\theta, \gamma)}{\partial \gamma} &=& 2J\theta - 2a = 0 \end{array} $$
(10)

The sufficient condition for a minimum of the objective function (Eq. 9) is met. The matrix A containing the second order derivatives is positive definite due to its form (Eq. 11).

$$\begin{array}{@{}rcl@{}} A = \frac{\partial^{2} f(\theta, \gamma)}{\partial \theta^{2}} = D^{\prime}D \end{array} $$
(11)

The solution is given in the following formula (Eq. 12).

$$ \left[\begin{array}{ll} \hat{\theta}\\ \hat{\gamma} \end{array}\right] = \left[\begin{array}{ll} D^{\prime}D & J^{\prime} \\ J & 0 \end{array}\right]^{-1} \left[\begin{array}{ll} D^{\prime}D & 0_{T \times M} \\ J & I_{M} \end{array}\right] \left[\begin{array}{ll} s \\ (a-Js) \end{array}\right] $$
(12)

Methodology is given in [6, 34, 35].

3 Results and Discussion

3.1 Mercury Content in Fuel

Based on the data obtained from the literature (Figs. 3 and 4), two independent vectors of average mercury content typical for each mine [ppm] are constructed: for hard coals and lignites. Vectors are analysed for the occurence of outliers using Grubbs’ T test, and then the sample’s normality (Shapiro-Wilk normality test).

3.1.1 Hard Coal

Results of Grubbs’ T test for outlier values, and the Shapiro-Wilk normality test (for both α = 0.05 applied) are presented in Table 2.

Table 2 Hard coal—statistical analysis
Full size table

The value 0.720 ppm (Fig. 3) [25] is classified as “non representative” and was rejected from the sample after personal consultation with experts from the Central Mining Institute (Katowice, Poland). However, the initial approach [25] considered the mercury content in hard coal, the sample contained coal muds (mercury coming from the stone associated with mud) or was affected by strong pyrite sulphur intrusion (mercury associated with the pyrite sulphur). Summary statistics for hard coals are shown in Table 3.

Table 3 Summary statistics after outliers correction—hard coal [ppm]
Full size table

Compared with the literature, the mean mercury content in Polish hard coals is nearly 40% lower than assumed in [15, 47] (derived from [3]). The data given in [44] indicated that the mean mercury content in hard coals is slightly higher, however it varies for particular particle size distributions. The determined mean value is close to the mean values given in [2, 45], 0.085 and 0.120 [ppm], respectively.

3.1.2 Lignite

Results of Grubbs’ T test for outliers, and Shapiro-Wilk normality test (for both α = 0.05 applied) are presented in Table 4.

Table 4 Lignite—statistical analysis
Full size table

After applying the Lilliefors test for normality, the p value was slightly higher than 0.05. A normal distribution of sample is assumed. The 95% CIs calculated for hard coal and lignite are presented with values calculated based on [28] (Table 5).

Table 5 95% CIs for mercury content in fuel [ppm]—comparison
Full size table

Compared with the literature, the mean value for Polish lignites (0.2743 ppm) is comparable to the data assumed by [47] (derived from [2]), taking into account all the main Polish lignite mines. Summary statistics for Polish hard coals and lignites is presented in Table 6.

Table 6 Mercury content in fuel [ppm]—summary statistics
Full size table

Comparing 95% CIs for Polish hard coals and lignites given in this paper and [28], the values for hard coals are similar to lignites [28], and conversely. Mean Hg contents in Polish coal and lignites given in [28] are 0.2ppm (hard coal) and 0.1ppm (lignite) (Table 5).

3.2 Type of APCs Applied

The structures of applied APC devices [30] are presented in Tables 7 and 8. Information about fuel consumption per year (Fuel cons., [kt]) and the percentage of total power capacity equipped with particular types of APC installation (Str2012, [%]) are included.

Table 7 Current type (2012) of APC devices in Polish public power and energy sector—hard coal
Full size table
Table 8 Current type (2012) of APC devices in Polish public power and energy sector—lignite
Full size table

The reduction of air emission of particulate matter and sulphur oxides in the Polish energy sector due to the increasing efficiency of installed APCs by [20] is presented in Table 9.

Table 9 Reduction of emission (1990-2011) basing on [20]
Full size table

The factors of emission decrease since 1990 to 2011 are a decrease of ash content in fuel (− 19%), and also an increase of dedusting efficiency (also dust capture efficiency) of up to 97% in 2011 [20].

Characteristics of APC installations in previous years (1990-2010) is given in Table 10.

Table 10 Type of desulphuristaion applied in previous years, basing on [14]
Full size table

3.3 Combining the Uncertainties

The total uncertainty of the mercury air emission from the Polish power and energy sector is determined according to methodology described in [10]. Rule B (Eq. 5), associates uncertainties connected with: fuel consumption (FC), mercury content in fuel (C), and efficiencies of the APC technologies applied in the combustion process (η).

3.3.1 Amount of Fuel Combusted

Based on international guidelines on uncertainty analysis of emission inventories [10, 22] the proposed uncertainty level is 2%. Taking into account possible discrepancies, inconsistencies, heterogeneity or another factors of uncertainty, the data on fuel combusted (Table 1) [11] is finally associated with a 5% uncertainty range.

The 5% uncertainty range, given in [10], is the lowest uncertainty range for statistics taken from the International Energy Agency, and United Nations’ data bases.

3.3.2 Mercury Content in Fuel and Speciation during the Combustion Process

For the purposes of this paper, the uncertainty range of mercury content in fuels is derived from Table 5.

Data for 1990 and 1995 are associated with the uncertainty resulting from the study [28]. The rest of the years 2000, 2005, 2010, and 2012 are associated with the uncertainty level determined in this paper.

Mercury speciation was assumed based on [33], as: 90% of Hg 0 and 10% of TPM.

3.3.3 Assumed APCs’ Efficiencies

The efficiencies of the APC installations applied during the combustion process are derived from [37] (Tables 11 and 12) and our investigation, given briefly below.

  • 1994/5: first WFGD installation (’Bełchatów’ Powerplant) covered approximately 60% of combusted lignite;

  • 2000: wider application of WFGD devices in hard-coal firing installations;

  • 2010: no SCR installations;

  • 2011/12: first SCR installation (“Opole” Powerplant), new WFGD installation (“Bełchatów” Powerplant).

Table 11 Assumed mercury removal efficiencies 1990–2010
Full size table
Table 12 Assumed mercury removal efficiencies—2012
Full size table

Currently, the applied methodology published in the official Polish national report uses emission factors for hard coal and lignite derived from a country study carried out since 2011 to 2013 by the Polish Energy Group PGE [31]. Considering the types and technologies of APC devices installed since 1990 to 2010, the currently applied emission factors (whole trend 1995–2012) are not suitable for the years before 2010. The technological structure of APC devices applied before 2010 [47] based on data derived from the ENVIRO database is comparable with data included in this paper.

Based on available elaborations [4, 17, 32, 37], also papers and guidelines on uncertainty assessment [10, 13, 40, 46], the mercury removal efficiencies are assigned with a 30% uncertainty range. Results are presented in Table 13.

Table 13 Uncertainty of mercury air emission estimation
Full size table

3.4 Sensitivity Analysis

The sensitivity analysis was carried out for the total emission estimated from the Polish power sector based on guidelines on emission inventory and reporting [10]. We assumed three main scenarios (denoted: A, average; B, low; and C, high) based on data on Hg content in Polish coals/lignites taken from [28], assumptions on the mercury content in fuels and development of APC technologies collected in this paper, and official Polish emission inventory. The scenario denoted “3” is an officially submitted emission trend [31].

The idea of the sensitivity analysis was to investigate the possible range of estimation and matching the “most probable” scenario for emission projections (forecasting) [10, 24].

Comparing the data given in Table 14, the most similar trends those to originally submitted (3) are 1.B and 2.B. The mercury emission for 2000 from scenarios 1.A (8.6 Mg), and 1.C (11.5 Mg) are close to those given in [15] (nearly 10 Mg). The Hg air emission for 2005 from the scenario 2.C (17.2 Mg) is close to the data given for 2005 in [47] (18.4 Mg). Results of the sensitivity analysis are shown in Table 14. To compromise the emission data presented in studies [15, 47] with the national Polish emission inventory [31], we chose scenario 2.B. The emissions given in the the 2.B scenario are between the scenarios: 1.A and 1.B.

Table 14 Sensitivity analysis for estimation of mercury air emission [kg] (Polish public power and energy sector)
Full size table

3.5 Monte Carlo Simulation

The Monte Carlo simulation is based on the scenario 2.B presented in Table 14 and carried out according to international guidelines on emission inventory and reporting [10]. The standard deviations determined for the Monte Carlo simulation are shown in Table 15. They are derived from an analysis of the CIs and assumed uncertainty levels of the amount of fuel used in the Polish power and energy sector, mercury content in fuels (hard coal and lignite), and efficiencies of the applied APC technologies. In each case, the standard deviation is taken from an uncertainty level [%] of: FC, C, and η. The split between hard coals and lignites is weighted using the annual consumption of a particular fuel. The standard deviation of the Hg concentration in fuels is assessed using the normal (Gaussian) distribution.

Table 15 Monte Carlo simulation parameters
Full size table

Results of the Monte Carlo simulation (scenario ‘2.B’) with additional data on 95% confidence intervals are given in Table 16.

Table 16 Monte Carlo simulation results, estimated Hg emission [kg]
Full size table

The presented emissions are estimated using the official statistics on fuel used in the Polish power and energy sector, compliant with the original datasets submitted for international purposes [31]. The main difference between estimations is taking into account the technological development of the energy sector in the field of air pollution control. In contrast to officially submitted data, the emission factor of mercury is decreasing mildly due to the constant development of air pollution control technologies applied in Polish power plants.

A histogram of a simulated values (scenario “2.B,” 10,000 iterations) with empirical density functions is presented in Fig. 6.

Fig. 6
figure 6

Monte Carlo simulation results, Colours of lines indicate year: 1990, red (dashed); 1995, green (dashed); 2000 blue (dashed); 2005, orange (dashed); 2010, purple (dashed); 2012, black (solid)

Full size image

3.6 Monthly Distribution

The average values of a simulated scenario “2.B” are disaggregated to monthly values using two separate ways: the Denton-Cholette algorithm [6, 34, 35], also experimentally determined constant factors by Hławiczka [21]. The Hławiczka’s approach is based on the heat comfort of inhabitants and the timing of power-usage for personal heating in Poland. The results of disaggregation are presented in Figs. 7 and 8, respectively.

Fig. 7
figure 7

Denton-Cholette disaggregation

Full size image
Fig. 8
figure 8

Hławiczka’s disaggregation

Full size image

Comparing bar plots representing two ways of disaggregation, values derived from the Denton-Cholette algorithm (Fig. 7) generating overestimation during the summer (July, all years). This is caused by the production of fuels for the public power and energy sector. Combustion of lignite is always on-site; however, hard coal can be stored for a particular time before usage.

4 Conclusions

In this paper, we presented a detailed uncertainty analysis of mercury air emission from the Polish public power and energy sector, by analyzing available data on mercury content in Polish coals and lignites, the current and historical structure of the technology of combustion, the fuel used and abatement technologies applied.

Our approach based on international guidelines [10], including an investigation of identification and qualitative analysis of the Polish coal-fired power and energy sector, the amount of hard coal and lignite combusted, the mercury content in fuel and mercury removal efficiencies of APC devices. Based on the available data derived from various studies two main scenarios of mercury air emission were elaborated.

Our result has shown that the estimation of the emission of mercury from that sector included in the Polish IIR report [31] is charged with significant uncertainty, ca. 32% and 42% in case of hard coals and lignites, respectively. A comparison with the empirical study’s results [28] shows the uncertainties for hard coal are comparable, however we found that the uncertainty of Hg concentration in lignites is almost 20% higher. That fact is connected with a stronger variability of mercury content in the analysed samples of Polish lignites.

The analysis of the mercury emission scenarios given in [15, 47] made it possible to reconcile these datasets with the data taken from the national emission inventory [31] using the scenario 2.B based on assumptions on the amount of fuel combusted, Hg content in fuels, and efficiencies of the applied APC technologies, given in this paper.

A historical estimation (1990–2005) indicated that current data submitted for the purposes of international inventory and global scale mercury air emission modelling [31] does not reflect real changes and the technological development of the Polish public power and energy sector; however, we found the compliance between our assumptions (this paper) and historical technological data (year 2005) collected in the ENVIRO database [47].

The emission trend submitted for international purposes [31] should be corrected (years 1995–2009) to be compliant with the actual emission of mercury from the Polish power sector.

The Monte Carlo simulation carried out for the 2.B scenario shows a mild Hg emissions decrease from 1990 to 2012 caused mainly by the developments in the power and energy sector.

To obtain disaggregated emission, we used the Denton-Cholette algorithm [6], performed by [34, 35]. However, to the disadvantage of the approach based on the time series analysis which is an overestimation during warmer parts of year in comparison to the currently used Hławiczka’s approach [21], it can be successfully applied using modified factor of disaggregation.