1 Introduction

Disinfection contact tanks (CTs) are designed to prevent waterborne pathogen transmission and are integral components of water treatment works. In CTs the wastewater is exposed to disinfectant concentrations for a given time, either prior to distribution via water supply networks or before the return into natural water bodies at the final stages of wastewater treatment. While the design of CTs somewhat depends on the disinfection method adopted, they are frequently divided into compartments using internal baffles, thus facilitating a meandering flow structure. Ideally, the hydrodynamics in serpentine CTs resembles plug flow conditions [27, 39]. For plug flow and a uniform cross-sectional distribution of the disinfectant (e.g. chlorine or ozone), the optimal contact time for the desired quality standards would be consistently achieved. However, viscous (e.g. near-wall) effects and turbulence induce flow dispersion, resulting in a deviation from plug flow. The hydrodynamics in CTs deviates further from plug flow if the flow recirculates due to the tank geometry. Preceding tracer studies highlighted that CT design can be evaluated using residence time distribution (RTD) curves (e.g. [24, 26, 28, 32]). RTD curves are able to detect short-circuiting, leading to insufficient exposure of pathogens to disinfectants, or internal recirculation, resulting in overexposure and the formation of by-products, which are of concern in the light of their association with health implications [27].

From an operational point of view, and in consideration of the necessity to address the uncertainty of insufficient treatment, the C ⋅ t concept was introduced in the United States through the US Environmental Protection Agency (EPA) as part of the Surface Water Treatment Rule [1]. Following earlier studies in the United States, and complementary studies in Europe, various parameters have been adopted worldwide for the assessment of disinfection systems. In the US EPA C ⋅ t concept, the level of inactivation is estimated by the product of residual disinfectant at the CT outlet (C) multiplied by the residence time at 10 % of the cumulative RTD curve (t 10) [19]. Computed C ⋅ t 10 values are compared with reference values for given pathogens to assess whether the required level of inactivation has been accomplished. Using the hydraulic efficiency indicator (HEI) t 10 accounts for the effects of short-circuiting through the reactor. In addition, the CT outflow is typically monitored for by-product concentrations, to ensure that they are below the maximum contaminant levels (MCLs) [29].

The principles of CT design stem from previous tracer studies (e.g. [24, 34]), where a correlation was identified between the tank flow length-to-width ratio (β) and the dispersion index (σ 2). It was postulated that a high value of β (≥40) is associated with a very low dispersion index σ 2 (≤0.02), which should ensure an optimal hydraulic performance [24]. In general, it has been assumed that CTs can be treated as shallow basins where the flow is two-dimensional (2-D). Rapid developments in the field of computational modelling have led to 2-D numerical model studies (e.g. [15]; [36]; [38]; [12]; [35]), which allowed the assessment of CT facilities before their construction based on numerically predicted HEIs [33]. However, several experimental studies, which have focused on the hydrodynamics of CTs [26, 28], have illustrated a complex three-dimensional (3-D) nature to the internal flow structure due to the inlet and outlet configurations. Consequently, accurate reproduction of the flow and transport in such CTs requires 3-D models ([30]; [20]; [13, 31]; [23]; [4, 21]).

Recently, disinfection specific processes, such as disinfectant decay and pathogen inactivation, have been modelled numerically by several authors [5, 37–39], which has been achieved through the incorporation of mathematical formulations representing kinetic processes and interactions. For detailed reviews of recent CT research advances, the interested reader is directed to the work of Zhang et al. [39] and Rauen et al. [27].

In this paper simulation results of disinfection processes in a small-scale contact tank model are presented. The goal of this study is to demonstrate and quantify the effects of contact tank design modifications, which are based on the tank’s existing deficient hydrodynamics (instead of simply and conventionally maximising its length-to-width ratio). These are considered to enhance the tank disinfection performance and reduce the risk of by-product formation.

2 Research Methodology

2.1 Numerical Modelling Approach

In this study the Reynolds-averaged Navier-Stokes (RANS) equations were solved numerically using a finite-volume method on a structured orthogonal grid to simulate the hydrodynamic structure in CTs. This is a well-known standard procedure to solve the hydrodynamics in contact tanks and, for the sake of brevity, is not repeated here. More details can be found in associated studies [3, 21, 22]. Once the hydrodynamic simulation converged to a steady state, the unsteady transport of scalar quantities was simulated through the transient solution of the three-dimensional advection-diffusion equation:

$$ \frac{\partial \varphi }{\partial t}+{U}_j\frac{\partial \varphi }{\partial {x}_j}=\left(D+{D}_{\mathrm{t}}\right)\frac{\partial^2\varphi }{\partial {x}_j^2}+{S}_{\varphi } $$
(1)

where φ is the scalar quantity (e.g. tracer and chlorine). D is the molecular diffusivity, which is negligibly small against the eddy diffusivity D t, calculated as ν t/S c. The turbulent Schmidt number (S c) was given the value of 0.7, as in Kim et al. [23]. The treatment of the volumetric source term S φ is specific to the characteristics of scalar quantities transported through the system. Table 1 summarises the mathematical models used to compute: chlorine decay, pathogen (Giardia lamblia) inactivation and by-product (total trihalomethanes – TTHM) formation during the disinfection process. The general form of the source terms for both the disinfectant decay and by-product formation is detailed in Brown et al., [10, 11], with further information available in associated studies (e.g. [9, 38]) guiding the selection of appropriate model inputs (Table 1). For pathogen inactivation, the Hom [18] model was adopted, since it has been proven for its robustness when representing the particular reactive process as expanded in Haas et al. [17] and Greene [13]. Appropriate input parameters for pathogen inactivation were derived from their findings, as indicated in Table 1.

Table 1 Source terms imposed for scalar quantities transported through the CT models
Full size table

For the source terms of Table 1, even for steady-state hydrodynamic conditions, t can vary as dictated by the RTD at each particular point. Therefore, the contact time was firstly calculated through tracer transport simulations for all computational cells. In turn, disinfection was assessed under contact time fields established for t 10, the peak concentration time (t p), the average residence time (t g) and 90 % of the cumulative RTD tracer curve time (t 90) respectively.

2.2 Numerical Model Validation and Research Background

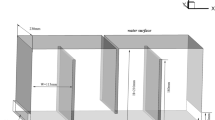
Experimental data were acquired within a scaled disinfection tank, located in the Hydraulics Laboratory at Cardiff University (CT-1). The eight-compartment serpentine disinfection tank physical model (CT-1) of Fig. 1a was designed to provide evidence of the interconnection between the contact tank geometry and its process efficiency. Acoustic Doppler velocity (ADV) data were collected for a constant flow rate (=4.72 l/s) with the goal being to quantify the hydrodynamics in the tank for steady-state conditions. In addition, pulse tracer experiments were carried out using rhodamine WT injections at the inlet. Submerged sensors monitored fluorescence levels at designated locations, from which normalised RTD curves were obtained. More details of this experimental study can be found in the paper of Angeloudis et al. [6].

Fig. 1
figure 1

Sketches of the a original CT Design (CT-1), b, c geometric modifications examined computationally and d baffling configurations examined previously in the physical model. Dimensions are in millimetres

Full size image

The suitability of the numerical model to reproduce scalar transport in CT geometries was assessed through comparisons of simulated and measured hydrodynamic and tracer concentration data. Figures 2 and 3 serve as a testament of the numerical model performance for the hydrodynamics and scalar transport. Figure 2 presents measured and simulated velocity and turbulent kinetic energy (TKE) profiles along the centreline (i.e. x/W t = 0.50) at elevations z/H t = 0.05, 0.50 and 0.95 respectively. The velocity predictions generally agree well with the available measurements, and so do the predicted turbulent kinetic energy profiles, especially from compartment 3 onwards. The discrepancies between the predicted and measured TKE profiles in the first and second compartments are due to the significant unsteadiness in the flow downstream of the inlet, which cannot be reproduced accurately using a steady-state RANS approach. Only more sophisticated (and much more computationally expensive) methods, such as large eddy simulations (LESs) [21], are able to resolve such unsteadiness.

Fig. 2
figure 2

Horizontal profiles of computed and measured a streamwise velocity and b turbulence kinetic energy at three different vertical planes (i.e. z/H t = 0.05, 0.50 and 0.95) where x/W t = 0.50 for the CT-1 configuration

Full size image
Fig. 3
figure 3

Residence time distribution curves obtained for the CT-1 configuration. The figure includes both experimental and computational results for comparison and validation of the numerical methodology

Full size image

Nonetheless, the observed TKE profile deviations do not affect significantly the predicted scalar transport, as shown for the simulated and measured RTD curves presented in Fig. 3. The numerical model is able to predict successfully the overall shape of the RTDs, particularly in compartments 4–8. A hydraulic efficiency analysis of the CT-1 tank was also conducted [6], which showed close agreement between the predicted and experimentally obtained HEI quantities, such as t 10 and the mixing indices σ 2 and Μο, which are defined as: σ 2  = σ t 2/t g 2 and Mo = t 90/t 10.

Figure 4 collates available data relating the β factor to the dispersion index σ 2 from several sources, namely (1) the empirical relationship due to Markse and Boyle [24], (2) experiments by Teixeira [32], (3) the alternative baffling configurations (Fig. 1d) of Rauen [26], and (iv) the study by Angeloudis et al. [6]. The data indicate that greater values of β lead to reduced σ 2 as described by Markse and Boyle [24]. However, the experimental results are all generally above Marske and Boyle’s trend line.

Fig. 4
figure 4

Length-to-width ratio (β) as a function of the dispersion index (σ 2) deduced from experimental and computational data from relevant studies

Full size image

This can be attributed to the design of the inlet of CTs, which is typically a pipe or channel [26, 32] and which promotes flow three-dimensionality and mixing early in the tank as shown by Angeloudis et al. [4], Barnett and Venayagamoorthy [8]) and Greene et al. [14]. In the case of CT-1, the very shallow inlet channel created an inflow jet, which led to a large vertical recirculation zone that occupied the entire first compartment of the tank and caused further complex hydrodynamic structures downstream [4]. Modifications to the inlet design, e.g. an idealised full tank depth inlet (marked FDI in Fig. 4) instead of a shallow inlet channel, resulted in closer agreement with Marske and Boyle’s curve. This shows that both the length-to-width-ratio β and flow three-dimensionality have a significant influence on the dispersion index σ 2. Therefore, β should only be used when the flow is considered to be purely two-dimensional.

In the following section contact tank design modifications are proposed with the goal being to assess their combined effect on the contact tank hydrodynamic and disinfection processes.

2.3 Contact Tank Design Modifications

Serpentine contact tanks are designed based on the principle of two-dimensional meandering flow. Regardless of inlet conditions, horizontal recirculation due to flow separation at baffle corners occurs, resulting in a pronounced advective flow path where the average velocity is faster than the cross-sectional mean velocity U b [34]. Hence, pathogens transported in this flow path short-circuits through the system. Additionally, high velocities in a portion of the tank lead to an increase in shear turbulence, so that solutes (e.g. disinfectants) are transported by means of turbulent diffusion into recirculation or dead zones and where they remain in the system for longer than the mean retention time T [6]. In order to optimise the chemical processes in CTs, short-circuiting and excessive residence times need to be understood and minimised, or ideally eradicated.

For instance, the disinfection tank in the study of Gualtieri [16] included rounded-off compartment corners with the goal of mitigating the formation of internal recirculation zones. However, such modifications reduce the tank volume and it is unclear how this impacts on the treatment processes. The effect of rounded tank corners on the treatment processes has therefore been studied herein. Figure 1b ii depicts the associated modified geometry and this tank design is henceforth referred to as CT-2. Similarly, areas behind baffle corners are prone to recirculation, which can be more substantial than in corners [4, 21, 39]. Set-up CT-3, as depicted in Fig. 1b iii, was considered to prohibit recirculation in such regions. Design configurations CT-4, CT-6 and CT-7 combined certain geometric aspects of CT-2 and CT-3 (Fig. 1). An alternative approach to minimising internal circulation was investigated through set-ups CT-5 and CT-8, where guiding walls were included to aspire to achieve plug flow around baffle edges (Fig. 1b iv).

The presence of large, low-velocity recirculation zones can lead to the production of by-products, because the disinfectant could be detained within these regions for longer periods and thereby react with organic material (TOC). Therefore, set-up CT-6 considered an inclined channel inflow as a means of militating against the large vertical recirculation zone that forms at the inlet due to the shallow inflow jet. In set-ups CT-7 and CT-8, the inlet was rotated by 90°, as depicted in Fig. 1b v, in an attempt to reduce the size of the vertical recirculation zone, i.e. extending the zone over the width of the compartment instead of over the length. The geometric modifications for all of the modified designs are summarised in Table 2 for clarity.

Table 2 Geometric modifications featured in the contact tank designs
Full size table

3 Results and Discussion

3.1 Tracer Transport Analysis

RTD curves were obtained for the modified CT configurations (Fig. 5), illustrating the influence of the modifications on the shape of the curves for compartments 1, 2, 6 and 8. With the exception of CT-7 and CT-8, all of the modified designs exhibited an RTD peak occurring earlier compared with the original set-up at the outlet monitor point (Fig. 5d). This was attributed to the reduced retention time in the models as a consequence of the volume displaced by geometric alterations. Generally, while RTD tailing appeared to be as pronounced as for CT-1, it was noticeably less for CT-6, CT-7 and CT-8, i.e. the only designs attempting to avoid the large vertical recirculation zone encountered in compartments 1 and 2.

Fig. 5
figure 5

Simulation residence time distribution curves obtained for the different contact tank set-ups at the sampling points of compartments a 1, b 2, c 6 and d 8

Full size image

Operational and hydraulic efficiency parameters for each design are summarised in Table 3, highlighting how the theoretical retention time (T m) was altered according to the internal volume occupied by the geometry modifications. The t 10 values at the outlet are also reported, as they are typically used for the assessment of disinfection efficiency through the C ⋅ t concept. According to the non-normalised results and using the residual chlorine concentration predicted at the outlet, the C × t 10 product (CT value, Table 3) and the Morril index (Mo) of the original design (CT-1) suggests a superior hydraulic performance against the modified designs, apart from the tank configurations CT-6, CT-7 and CT-8. For normalised values of t 10 on the other hand, improvements in the CT performance were found for all CT designs except for CT-5. The contradictory HEI interpretation presents an ambiguity with regard to the significance of the results for pathogen inactivation through the conventional methodology that treats the CT interior as a ‘black box’, limited to the analysis of a single short-circuiting indicator.

Table 3 Contact tank operational parameters, hydraulic efficiency indicators and C ⋅ t values for specified flow rate and the disinfectant residual predicted at the outlet
Full size table

3.2 Contact Tank Internal Flow Patterns

Figure 6 presents streamlines of the flow at the water surface for all eight CT designs. In the original design (Fig. 6a), recirculation regions, i.e. departure from plug flow, can be observed. The CT-2 design mitigated the formation of corner dead zones, while the modifications of CT-3, CT-4, CT-6 and CT-7 neutralised the recirculation zones behind the baffle lee edges from compartment 3 onwards. Nevertheless, due to the jet-like inflow of these configurations, the large recirculation in compartment 2 was not removed and was more pronounced than previously (i.e. in CT-1). A consequence of these recirculations was the occurrence of extensive reverse flow in compartment 2, indicated by the streamlines in Fig. 6a–d, f. Internal guide walls in the design CT-5 remedied the horizontal internal recirculation, even though this tank appeared to be the most inefficient in terms of t 10 (Table 3). The guiding walls in CT-5 seemed to promote short-circuiting for the upper part of the flow, thus explaining the predicted HEIs and specifically t 10. However, by changing the orientation of the inlet (CT-8), the design became substantially more hydraulically efficient. Similarly, changing the inlet orientation of CT-4 led to an improved t 10 value (CT-7).

Fig. 6
figure 6

Contact tank design flow patterns at z/H t = 1.00 demonstrating the impact of the modifications on the hydrodynamics. a CT-1. b CT-2. c CT-3. d CT-4. e CT-5. f CT-6. g CT-7. h CT-8

Full size image

A greater insight into local flow features and the effect of geometric alterations are given in Figs. 7 and 8. Figure 7 depicts vector plots at z/H t = 0.50 for the fifth and sixth compartments of CT-1, CT-4 and CT-8. In these compartments the flow was quasi-two-dimensional on the x-y plane, since it had recovered from the complex flow structures near the inlet (compartments 1 and 2) and was not influenced by the outlet conditions (compartment 8). Cross-sectional velocity profiles in the original design (Fig. 7a) illustrate areas prone to reverse flow, with vectors indicating recirculation zones and the near-stagnant flow adjacent to compartment corners. Figure 7b, c demonstrate how the geometric modifications, here exemplified for CT-4 and CT-8, correspond to a more desirable pattern with minimal eddies.

Fig. 7
figure 7

Vector plots in compartments 5 and 6 for a CT-1, b CT-4 and c CT-8. The red velocity profiles are the ones considered for comparison against experimental results for CT-1 in Fig. 2, while the blue profiles show the impact of the baffle design on the local cross-sectional velocity profiles. Streamlines, coloured according to the velocity magnitude, highlight the deviation from the bulk velocity across the compartment cross-section

Full size image
Fig. 8
figure 8

Computed velocity vectors on longitudinal planes in compartment 1 for a CT-1, b CT-6 and c CT-7. Experimental vectors are included in a for comparison

Full size image

The aforementioned vertical recirculation zone developed in CT-1 due to an inlet water jet (also seen in the experiments) is illustrated through computed velocity vectors (black) on a longitudinal plane (Fig. 8a). Also plotted are experimentally obtained velocity vectors (red) for CT-1 and the fairly good match between modelled and measured data proves the model’s predictive capabilities. The inclined tank bottom of CT-6 leads to a similar recirculation zone (Fig. 8b). However, the velocity magnitudes are higher, which promotes higher turbulence and thus increased mixing and removal of the dead zone in the bottom corner. The RTD curve of CT-6 features less tailing in comparison with other designs. In CT-7 (and CT-8) the change of orientation of the inflow confined the longitudinal recirculation zone to the compartment width and led to an earlier transition to a profile in the absence of substantial reverse flow, as indicated by the vectors once x/W t > 0.7 (Fig. 8c).

3.3 Effect of Geometry Modifications on Disinfection Efficiency

In the previous section it was highlighted how geometric modifications had an impact on the CTs’ hydrodynamics. Table 4 provides the exposure times by which the status of pathogen inactivation and by-product formation were assessed through the refined computational fluid dynamics (CFD) modelling methodology.

Table 4 Predicted t 10, t p, t g and t 90 contact time exposures at the cross-sectional middle of the outlet of each configuration
Full size table

Tables 5 and 6 present the range of pathogen survival ratio (G. lamblia survival ratio – N/N 0) and by-product concentration (TTHM) values predicted at the outlet respectively. These results are accompanied by the isosurface plots of Fig. 9 for pathogen inactivation under a short-circuiting regime (t 10) and by-product accumulation potential for longer disinfectant exposure times (t 90 values). Despite the fact that the hydrodynamics was improved from the original CT (i.e. CT-1) for all of the modified configurations, this was not consistently reflected in the reactive simulation results of Tables 5 and 6, with these tables quantitatively summarising the impact of the modifications on the reactive processes.

Table 5 Pathogen survival ratio (G. lamblia N/N 0) range predictions for t 10, t p, t g and t 90 at the outlet surface
Full size table
Table 6 Outlet surface disinfection by-product (total trihalomethanes – TTHM) accumulation predictions for t 10, t p, t g and t 90
Full size table
Fig. 9
figure 9

Isosurfaces of pathogen inactivation (for t 10) and by-product formation (for t 90) in a CT-1, b CT-4, c CT-6 and d CT-8

Full size image

For CT-2, the design featuring corner modifications, pathogen inactivation was compromised by 8 % in comparison to the original design CT-1 (Table 5). The improved hydraulic efficiency (t 10/T m = 0.724 compared to 0.720 previously, Table 3) at the expense of a smaller tank volume did not improve the CT’s disinfection performance. The impact of CT-2 on TTHM accumulation was similarly negligible (Table 6), and, therefore, the corner modifications alone did not seem to benefit the disinfection processes of the particular contact tank.

CT-3 and CT-4 designs performed similarly, and both behaved worse than the original CT-1 in terms of their disinfection performance. The pathogen inactivation potential was reduced by 17 and 24 % respectively (Table 5), while the by-product accumulation was increased by 4 % (Table 6). These results can be explained by Fig. 9a, b. In comparison with CT-1 (Fig. 9a), a higher pathogen inactivation and by-product concentration was observed in the recirculation zones of compartments 1 and 2 for both CT-3 and CT-4 (Fig. 9b). This implies that a greater fraction of the inflow disinfectant was trapped for longer in these regions. The poor performance of these two configurations was a result of the baffle modification introduced in compartment 2. A typical issue when designing such CTs is again the assumption that the flow developed is two-dimensional. Under such a scenario, a flow separation region would develop around the baffle edge, such as in latter compartments of CT-1 (e.g. compartments 4–8, Figs. 5a and 6a). However, in this compartment the flow pattern was more complex and the baffle modification acted detrimentally by increasing the size, and therefore the severity, of the recirculation zone (Fig. 6c, d).

CT-5 was the worst-performing CT design, an unexpected outcome considering the flow pattern predicted (Fig. 6e). Disinfection simulations suggested a drastic reduction in the inactivation efficiency of 147 %, (Table 5) and an increased by-product accumulation at the outlet of 25 % (Table 6) compared with CT-1. In the previous configurations (CT-1, CT-2, CT-3 and CT-4), the strong recirculation zone in compartment 1 (e.g. Fig. 8), caused by the momentum of the jet, mixed the disinfectant vertically. In CT-5, the guiding walls direct the near-surface jet straight into the upper layer of the second compartment and only a small percentage of the flow is deflected to the bottom layers of compartments 1 and 2. Clearly, the guiding walls in CT-5 prevented an even distribution of scalar quantities and the velocities remained high in the upper part of the tank and low near the bottom until the exit. Consequently, scalars transported near the bottom of CT-5 were prone to higher than usual residence times, thereby facilitating the formation of by-product concentrations. In contrast, scalars flowing closer to the water surface short-circuited. All of these effects contributed to the CT-5 outlet RTD shape (Fig. 5d), i.e. an early peak appearance and a long and flat tail of the curve.

The CT-6 design featuring an inclined bottom in compartment 1 (Figs. 1c and 8b) had a comparable pathogen inactivation level to the original configuration CT-1 (the difference is −3 %, Table 5). On the other hand, it resulted in a distinct reduction in the maximum TTHM concentrations, which was predicted to be 15 % less than for CT-1. This remarkable improvement can be attributed to the hydrodynamics downstream of the inlet, with the inclined bottom leading to stronger recirculation, increased turbulence and fewer dead zones (e.g. vector plots for CT-1 vs. CT-6 in Fig. 8a, b). Due to the dead zone formation and disinfectant entrapment, the TTHM threshold of 10 μg/l was exceeded in compartment 1 of CT-1 (indicated in Fig. 9a, b), whilst the TTHM threshold of 10 μg/l was not surpassed in the CT-6 design (Fig. 9c).

The CT-7 design confined the vertical recirculation to the compartment width and also featured strong mixing as a result of the alternative inlet configuration. Consequently, TTHM accumulation (or absence thereof) was similar to that for the CT-6 design, i.e. 14 % reduction from the CT-1 by-product concentration (Table 6). However, improved flow conditions and a minimal reduction in the tank volume in this case led to an approximately 38 % improved inactivation from the original design (Table 5).

CT-8 combined guiding walls with the alternative inlet orientation. This design had a 32 % superior pathogen inactivation level (Table 5) and a 14 % by-product reduction against CT-1 predictions. As a result, this configuration was substantially more efficient than CT-5. The simulations suggested that the three-dimensionality near the inlet were beneficial for the disinfection process, as the disinfectant was mixed more evenly across the compartment cross-section before the flow transformed to quasi-plug-flow conditions with the aid of the guiding walls. These results show that for this particular tank the modifications took advantage of the initial three-dimensionality to promote uniform mixing of scalars across the compartment cross-section, rather than trying to mitigate against them completely (e.g. CT-5).

Within CT-8 it was interesting to note how significantly the N/N 0 ratio and TTHM concentration ranges were increased at the outlet compared to the set-ups without guiding walls (Fig. 9d, Tables 5 and 6). Considering the streamlines for CT-8 in the centre of the flow path (Fig. 7c), scalars transported along these consistently maintained a greater velocity (U > U b) than for streamlines closer to the baffle or sidewalls. This was because the centre of the cross-section was more independent of near-wall friction effects. By taking the above into account, it should be expected for scalars in the centre of the cross-section to short-circuit; as also suggested by the higher G. lamblia survival ratio and the lower TTHM concentrations in the centre of the outlet surface in Fig. 9d. In contrast, for the cases without the guiding walls, the range at the outlet was lower, due to the more pronounced transverse mixing in the latter compartments. Indicatively, if the corresponding streamlines in the compartment centre for other configurations (e.g. CT-1 or CT-4 in Fig. 7a, b) are considered, the streamwise velocity was approximately equal to the bulk velocity (U ≈ U b), whereas near the baffles it alternated from U > U b in one compartment to U < U b in the next, resulting in a more even contact time at the outlet surface.

The simulation results demonstrated that minor modifications could lead to a greater pathogen inactivation, as well as a reduction in the by-product accumulation of the effluent (e.g. CT-7 and CT-8; Tables 5 and 6). This could have substantial implications for the success of the treatment operation. Specifically, it has been reported [11] that 40–60 % of TTHM by-products are currently formed within water treatment facilities and predominantly during disinfection. Therefore, this methodology offers the potential to provide an indication of whether MCLs from treatment works can be contained within acceptable levels, subject to the provided water quality specifications acknowledged by the modelling methodology.

4 Conclusions

A RANS-based computational fluid dynamics model was used to provide insights into the mixing and disinfection characteristics of a standard eight-compartment disinfection contact tank. The validity of the numerical model data was assessed through comparisons of (a) predicted time-averaged velocities and (b) transient tracer transport breakthrough curves against available experimental data. The effects of internal geometric modifications on the flow patterns and tracer transport processes were outlined and discussed with reference to their significance on the disinfection efficiency, through direct modelling of pathogen inactivation and by-product formation.

Using this methodology, we intended to demonstrate how design optimisation of water treatment tanks can influence the reactive processes, without undergoing particularly invasive changes in the internal baffle configuration. Recirculation zones that have been typically associated with poor hydraulic performance, under a rapid mixing regime and depending on the location where they develop, could be useful to distribute evenly the disinfectant across the flow path cross-section. This was applicable for the first compartment of the design considered herein and the altered CTs explored throughout this investigation. Certain modifications invariably enhanced the uniformity of the reactive processes downstream and subsequently resulted in a more controlled operation. Moreover, the potential to reduce the disinfectant concentration through further optimisation analyses has been highlighted, in consideration of the superior pathogen inactivation predicted on better-performing designs.

Even though this study focused on a standard baffle disinfection tank design, the hydrodynamic conditions discussed could be encountered in any CT geometries to a certain extent. The capacity of state-of-the-art CFD simulations to predict how the hydrodynamics is altered due to geometric modifications can be invaluable in terms of optimising the hydraulic efficiency of disinfection tanks and other related treatment facilities. The further integration of kinetic models highlights the link between the hydrodynamics and bio-chemical processes. In this context, process and hydraulic engineers can make the best use of the available space and existing facilities at water treatment works, which will eventually reduce operational costs and carbon footprints of the water industry.