Buckling phenomenon of vertical beam/column of variable density carrying a top mass

Abstract

This study focuses on modeling ideal nonuniform standing beams and towers supporting a constant top mass. We also analyze their dynamical stability, as determining the design parameters influencing their shape and stability holds significant value for structural engineering. Initially, we employ a statical mechanics approach to balance the mechanical and gravitational forces. By solving an initial-value problem, we derive the cross-sectional areas of the columns. Our findings reveal that these areas, rather than the shapes, are the primary contributors to the engineering performance of the columns. Additionally, the top mass acts as a multiplying factor for the cross-sectional areas, and the density distribution along the column determines whether the top should be heavier or lighter. Furthermore, we demonstrate that exponential, parabolic, or linear cross-sections with significantly wider base profiles are crucial for accommodating heavier top loads. Moving on to the dynamical analysis, we consider two ideal tower configurations: FC and SC. Numerical and analytical results reveal that higher modes exhibit shorter amplitudes. FC modes necessitate higher design parameters to resist buckling phenomena, whereas SC modes show lower resistance to vibrational deflections. In terms of stability, a heavier top mass enhances the vertical beam’s stability, while towers with parabolic bases are more susceptible to instabilities.

1 Introduction

Determining the design parameters that influence the shape and stability of columns, beams, and towers is crucial in structural engineering. This knowledge allows for optimal design of both uniform and nonuniform beam structures [1,2,3,4,5,6]. This study focuses on exploring the shapes of nonuniform vertical columns supporting a constant top mass, with a subsequent analysis of how sudden changes in the shape affect their vibrational dynamics.

Many scholars have been working on the subject of Euler beam/column and its stability features under various physical mechanisms. Only the recent literature review associated with diverse engineering applications will be given here omitting the older valuable efforts on the topic. To cite, conservative loading effects of buckling considering follower axial force on the structural frames were studied numerically in [7]. In [8], light weight structures of tower carrying wind power were optimized by means of tapered tubular structure. Mechanical actuation and energy harvesting applications of bistable and multistable structures under axial load were analyzed through buckling phenomenon in [9]. Impact loading effects of precast concrete segmental columns were simulated in [10]. Stability of steel cold formed silo column was given in [11], based on axisymmetric and non-axisymmetric loads. [12] explored mono-symmetric channels from the perspective of lateral buckling using finite element method. Statics and dynamics of beams were compared in [13] with Sheremetev-Pelekh-Reddy-Levinson micro-beam model. The performance of tall mass-timber buildings against wind-induced vibrations was explored in-depth in [14]. A general formulation for the steel columns, beams, and beam-columns of variable geometry, loads, and supports was reported in [15]. Dynamic stability of curvilinear size-dependent beam with large deflections was analyzed in [16]. Thin-walled metallic and composite beam structures were examined in [17]. Primary and secondary external resonance situations in vibration of cantilever structures were studied in [18]. The research in [19] reported on the buckling estimates of thin shells of high-strength materials with huge thickness of the elements. Masonry walls subjected to blasts were reviewed from experimental and numerical approaches in Godi et all 2021. A simple computation method for length factors on framed stepped columns was proposed in [21]. One-three dimensional formulations of Euler-Bernoulli and Timoshenko nonlinear beams were presented in [22]. Kirchhoff plate equations were modified in [23] with insertion of couple stress model in determining the buckling and elastic properties of the graphene sheet. Further recent applications can be found in [24, 25], and [26]. Experimental and theoretical studies were also conducted for elaborating seismic response of powered columns in terms of the bearing capacity, corrosion endurance, ductility, cyclic loading, single-cycle energy dissipation, combined loadings, ultimate torsion, and stiffness in [27], in [28, 29], in [30], and in [31]. Various buckling phenomena were furthermore explored recently, for estimating core and nanocomposite skin characteristics of anisogrid lattice-core sandwich plates in [32], for testing centric pull-out of helically ribbed bars with nine different diameters on the bond strength in [33], and for assessing impacts of inertial load for huge slenderness piles in [34].

A vast body of research in the literature explores the shapes and dynamic properties of various beams. This study builds upon that foundation by focusing on two key aspects: (i) Identifying the cross-sectional shapes of vertical towers: We consider towers supporting a constant top mass and composed of material with a variable density. Base density-to-stress ratio, top mass-to-stress ratio, and density distribution parameters play crucial roles in determining the shape of the column. Our analysis reveals that exponential, parabolic, or linear ideal cross-sections are most effective in accommodating the top load, (ii) Analyzing the stability of these columns: Our goal is to understand the vibrational conditions leading to buckling phenomena under the combined influence of the top mass and the column’s rigidity. We focus on two configurations: freely moving top with a clamped bottom and clamped bottom with a sliding top. Both numerical and analytical methods are employed to examine the deflection modes and stability of these columns. Our results demonstrate that lighter tops are more susceptible to instabilities compared to heavier ones. Towers with more pronounced exponential bases exhibit enhanced stability against buckling. This study contributes to the field of structural engineering by providing insights into the optimal design of towers with variable-density materials, considering both shape and stability under dynamic loading.

2 The Column Beam Model

Fig. 1

A vertical nonuniform beam column configuration of height L holding a mass $m_T$ on the top

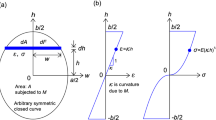
A tall L tower column holding a mass load $m_T$ on top it, as depicted in Fig. 1, is considered. The practical viability and scientific application in structural engineering could be Taiwan’s tallest building, Taipei 101, carrying a 660 tone pendulum on the top. Therefore, we are interested in determining the potential cross-sectional area A(x) subject to the subsequent constraints, in a manner to identify the shape of a load carrying column. An Euler beam is assumed without inertial rotation and shear defect. We further assume a variable density $\rho (x)$ of the material as a function of vertical location x in the power form

$$\begin{aligned} \rho (x)= & {} \mu (1+ax)^m. \end{aligned}$$

(1)

Today’s world also witnesses structures like this with graduating materials and a tip mass for multi purposes. For instance, construction of skyscrapers with helipads at the top, or high buildings/hotels with infinity pools at the top.

With such scientific and industrial background in mind, at any position x, a finite thickness slice ${\text {d}}x$ of cylindrical shell having infinitesimal mass

$$\begin{aligned} {\text {d}}M= & {} \rho A {\text {d}}x \end{aligned}$$

(2)

is exerted a gravitational force due to the gravitational acceleration g in the form

$$\begin{aligned} {\text {d}}F_1= & {} {\text {d}}M g. \end{aligned}$$

(3)

It is clear that at the top of the building when $x=L$, the force $F_1$ is only due to load $m_T$ given by

$$\begin{aligned} F_1(x=L)= & {} m_T g. \end{aligned}$$

(4)

On the other hand, the cross-sectional area A(x) exposed to a uniform tension $\tau$ can stand the mechanical pressure force

$$\begin{aligned} F_2(x)= & {} \tau A(x), \end{aligned}$$

(5)

whose differential is

$$\begin{aligned} {\text {d}}F_2= & {} \tau {\text {d}}A. \end{aligned}$$

(6)

At the equilibrium state, since no upward force is present, the net force by summing the forces in (3) and (6) must balance the zero force owing to the Newton’s law, resulting in the following initial-value problem regarding the function A(x) on account of (4)

$$\begin{aligned} {1\over A}{ {\text {d}}A\over {\text {d}}x}= & {} -{g\rho \over \tau } (1+ax)^m,\quad 0\le x <L \nonumber \\ A(1)= & {} {m_T g\over \tau }. \end{aligned}$$

(7)

Upon making the quantities dimensionless, the area by $L^2$ and the x coordinate by L, it is further possible to convert the system (7) into its dimensionless form

$$\begin{aligned} {1\over A}{ {\text {d}}A\over {\text {d}}x}= & {} -\alpha (1+bx)^m,\quad 0\le x <1 \nonumber \\ A(1)= & {} \beta , \end{aligned}$$

(8)

where

$$\begin{aligned} \alpha ={\mu g L\over \tau },\quad \beta ={m_T g\over \tau L^2},\quad b=aL \end{aligned}$$

are the dimensionless physical parameters governing the statics of the tower. We see that $\alpha$ measures the ratio of base mass to stress, while $\beta$ measures the ratio of top load mass to stress, when g and L are maintained.

Having solved the initial-value problem in (8) yields the analytical solution

$$\begin{aligned} A(x)= & {} e^{\frac{\left( (1+b)^{1+m}-(1+b x)^{1+m}\right) \alpha }{b(1+m)}} \beta , \end{aligned}$$

(9)

whose form when $m=-1$ can be achieved by taking the limit of (9)

$$\begin{aligned} A(x)= & {} \left( \frac{1+b}{1+b x}\right) ^{\frac{\alpha }{b}} \beta . \end{aligned}$$

(10)

3 Dynamic behavior of the column beam

The structural stability of towers laid in formula (9) can be studied from vibrational analysis making use of the dynamic beam equation [35,36,37,38])

$$\begin{aligned} (E I u_{xx})_{xx}+(F_2u_x)_x+\rho A u_{tt}= & {} 0, \end{aligned}$$

(11)

Assuming an oscillation of frequency $\omega$ represented by the wave modes

$$\begin{aligned} u(x,t)= & {} Y(x)e^{i\omega t}+c.c., \end{aligned}$$

(12)

the dimensionless form of the dynamic equation (11) can be rewritten as

$$\begin{aligned} \nu (A^2Y'')''+(AY')'-\alpha \Omega ^2A (1+b x)^m Y= & {} 0, \end{aligned}$$

(13)

where the normalized frequency is $\Omega =\omega (L/g)^{1/2}$ and the normalized Young’s modulus is $\nu =cE/\tau$.

In order to examine the vibration dynamics, various beam boundary conditions can be taken into account as usual in the beam stability analysis. We prefer here a free top with a clamped base and a sliding top with a clamped base. The relevant boundary conditions are then

$$\begin{aligned} Y(0)= & {} 0,\quad Y'(0)\;=\;0,\quad Y''(1)\;=\;0\qquad (FC),\nonumber \\ Y(0)= & {} 0,\quad Y'(0)\;=\;0,\quad Y'(1)\;=\;0\qquad (SC). \end{aligned}$$

(14)

Alongside with (14), a fourth boundary condition associated with both cases can be accomplished via balancing load momentum with the transverse shear stress at the top, yielding

$$\begin{aligned} \nu (A^2Y'')'+AY'= & {} -\beta \Omega ^2Y, \quad (x=1). \end{aligned}$$

(15)

A final normalization A by the factor $\beta$ and $\Gamma ^2=\nu \beta$ reveals that the complete dynamics can be simulated from the perturbation boundary-value problem

$$\begin{aligned} \Gamma ^2(A^2Y'')''+(AY')'-\alpha \Omega ^2A (1+b x)^m Y= & {} 0,\nonumber \\ \Gamma ^2(A^2Y'')'+AY'+\Omega ^2Y= & {} 0,\quad (x=1) \nonumber \\ Y(0)\;=\;0,\quad Y'(0)\;=\;0,\quad Y''(1)= & {} 0\qquad (FC),\nonumber \\ Y(0)\;=\;0,\quad Y'(0)\;=\;0,\quad Y'(1)= & {} 0\qquad (SC). \end{aligned}$$

(16)

From (16), the vibrational dynamics is governed by the ratio of base mass to stress parameter $\alpha$, the frequency $\Omega$, the scaled rigidity $\Gamma$, and the cross-section area function A. An exact solution of the vibrating beam modes for the general cross-sectional areas A(x) from (16) cannot be unfortunately gained. However, for certain special parameters, exact solutions can be determined, as can be literally outlined in the Appendix. Accordingly, for instance, the threshold SC buckling modes (with $\Omega =0$) when $m=-1$, $\alpha =-2b=1$ possess the reduced scaled Young’s moduli

$$\begin{aligned} \Gamma= & {} \frac{2}{\sqrt{9+\frac{4\pi ^2 k^2}{\ln ^2 2}}},\quad k=1,2,3,\cdots , \end{aligned}$$

(17)

while in the case of constant cross-sectional area when the base density is negligible (with $\alpha =0$), the stationary critical modes are found from

$$\begin{aligned} \Gamma= & {} \frac{1}{(2k-1)\pi },\qquad k=1,2,3,\cdots \quad (SC),\nonumber \\ \Gamma= & {} \frac{2}{(2k-1)\pi },\qquad k=1,2,3,\cdots \quad (FC). \end{aligned}$$

(18)

4 Numerical/analytical simulation results and discussions

The analytical formula (9) and its numerical/analytical stability treatment will be presented in this section.

4.1 Equilibrium column beams

The main result in (9) clearly indicates that the shape of the tower is insignificant, because the cross-sectional area takes the crucial structural role of the tower. For example, if solids of revolution are taken into account, the shape of tower can be determined by revolving the below function about the $x-$axis

$$\begin{aligned} Y_s(x)= & {} \sqrt{A(x)\over \pi }, \end{aligned}$$

(19)

given A(x) in (9). It is worthy to note that the base cross-sectional area arising from (9) is formulated through

$$\begin{aligned} A(0)= & {} e^{\frac{\left( -1+(1+b)^{1+m}\right) \alpha }{b(1+m)}}\beta . \end{aligned}$$

(20)

This is significant to understand the base supportive area of the tower influenced by the design parameters $\alpha ,\beta ;b,m$. Actually, the total weight of the loaded tower is met precisely by the base area A(0) in (20), since the dimensionless

$$\begin{aligned} total\; mass=\alpha \beta \int _0^1 (1+bx)^mA(x) {\text {d}}x+1=\beta A(0). \end{aligned}$$

Moreover, the column’s cross-sectional area is represented via natural exponential function

$$\begin{aligned} A(x)= & {} e^{\alpha -x \alpha } \beta , \end{aligned}$$

(21)

when m or b is zero. This special case exactly matches with the constant density analysis in [39], hence validating our present findings. Indeed, the corresponding buckling modes to $\alpha =0$ as derived above through formulas (18) completely collide with those given in [39].

It is also intriguing to see from (10) that purely tapered conical towers are obtained, for instance,

$$\begin{aligned} A(x)= & {} \frac{(1+b x) \beta }{1+b},\quad (\alpha =-b),\nonumber \\ A(x)= & {} \frac{(1+b x)^2 \beta }{(1+b)^2},\quad (\alpha =-2b). \end{aligned}$$

(22)

Fig. 2

Density distributions across the vertical beam. a $m=2$, b $m=1$, c $m=-1$ and d $m=-2$

The density variations across the tower are depicted in Fig. 2a–d for a variety of parameters m and b. Although not shown, $m=0$ corresponds to constant density distribution, as also the case when $b=0$, see Fig. 2a–d. It is observed that for a fixed positive power m, density increases from the bottom and the top of the tower will be heaviest if $b>0$, the lightest otherwise. The scenario of course reverses when instead a fixed negative power m is considered.

The resultant cross-sectional areas of the load supporting column normalized by $\beta$ are demonstrated next through Fig. 3a–f for various parameters m, b, and $\alpha$. It is inferred from the figures that exponential (refer to Fig. 3a–c for $m\ge 0$), parabolic (refer to Fig. 3d, f for $m=-1,-2$), and linear (refer to Fig. 3e for $m=-1$) cross-sectional structures are possible. Arbitrary mixture of parameters are selected from the domain to seize diverse column characters. We anticipate that the common feature of the towers is to possess narrowing cross-sections starting from the base, except the limiting cases of $\alpha ,b,m$ tending to zero. In the case of a positive power index m, as b reverts its sign from negative to positive, the vertical column beam should be supported with a much widening exponential base in order to compensate for the heavier upper narrowing portions. Otherwise, more straight bases are adequate to carry the top load through the equilibrium tower profiles. For negative power index m, the same support aforementioned toward the heavier top due to sign switch of b from positive to negative should be provided by means of parabolic or linear structural shapes. Notice the purely exponential cross-section in Fig. 3c from Eq. (21) and the tapered conical sections in Fig. 3e from equation (22). It is remarked that capturing the correct cross-sectional profile influenced by a variable density as illustrated through Fig. 3a–f is important in structural design engineering.

Fig. 3

Tower cross-sectional areas across vertical locations for a variety of b. a $m=2$, $\alpha =1$, b $m=1$, $\alpha =1$, c $m=0$, d $m=-1$, $\alpha =3/4$, e $m=-1$, $\alpha =-b$, and f $m=-2$, $\alpha =3/4$

4.2 Vibrating column beams

It is recalled that buckling phenomenon of beams occurs when $\Omega <0$, thus the conditions at the critical vibration frequency $\Omega =0$ is crucial. Table 1 lists the critical buckling modes ($\Omega =0$) for some selected parameters associated with five FC modes, and also SC modes in Table 2. They are numerically computed from (16), which are also in full agreement with the analytical formulas (17), (18), and (27) (refer to Fig. 10). Overall, columns with SC modes require smaller design parameters.

Table 1 First five critical buckling modes at several picked values of $\alpha$, m, and $b=-1/2$ for FC column

Table 2 First five critical buckling modes at several picked values of $\alpha$, m, and $b=-1/2$ for SC column

Beam deflection buckling modes corresponding to constant cross-sectional area in the case of negligible density with $\alpha =0$ are illustrated in Fig. 4a, b. Only three modes with $\Gamma$ from (18) are given through the graphs. Apparently, bending vibration is higher for FC modes owing to the freely moving top. Higher modes have also shorter amplitudes than the first fundamental (first) mode, indicating that they will oscillate much widely than the fundamental mode.

Fig. 4

Beam deflection modes for constant cross-section areas. a FC and b SC

Fig. 5

Buckling domain and modes for freely vibrating top at $b=-1/2$. a, b First critical buckling mode, c, d second critical buckling mode, and e, f third critical buckling mode for the selected physical parameters

Fig. 6

Buckling domain and modes for freely vibrating top at $b=1/2$. a, b First critical buckling mode, c, d second critical buckling mode, and e, f third critical buckling mode for the selected physical parameters

Figures 5a–f and 6a–f illustrate the evolution of the physical parameter range and buckling modes for the first three FC column modes across a vast parameter interval, for $b=-1/2$ and $b=1/2$, respectively. Bending vibrations are analyzed at $\alpha =2$. Notably, similar trends are observed for both b values because the slight changes in design parameters lead to minor deviations in wave amplitudes. Interestingly, the figures reveal that for these modes, exponentially supported columns require higher design parameters but experience less bending compared to parabolically supported ones. This suggests that towers with a parabolic base might be more susceptible to instabilities. As shown in Figs. 5(f) and 6(f), higher modes exhibit more pronounced and potentially uncontrollable oscillatory twisting behavior.

Fig. 7

Buckling domain and modes for sliding top at $b=-1/2$. a, b First critical buckling mode, c, d second critical buckling mode, and e, f third critical buckling mode for the selected physical parameters

Fig. 8

Buckling domain and modes for sliding top at $b=1/2$. a, b First critical buckling mode, c, d second critical buckling mode, and e, f third critical buckling mode for the selected physical parameters

Figures 7a–f and 8a–f depict the physical parameter range and buckling modes for SC modes across a wide parameter interval, for cases where $b=-1/2$ and $b=1/2$, respectively. Consistent with the observations from Figs. 4(a,b), SC modes exhibit smaller bending vibrations due to the sliding top. In other aspects, they share similar characteristics with the modes presented in Figs. 5 and 6, with the key difference being that higher-order SC modes vibrate at higher frequencies. This suggests that SC modes may have lower resistance to vibrations, potentially leading to greater instability.

Based on the cross-sectional area formula in equation (9), we can conclude that the mass on top of the tower (represented by parameter $\beta$) has minimal influence (as a multiplying factor) during the determination of the column beam’s size. However, the mass parameter $\Gamma$ plays a significant role in identifying the vibrating modes. A heavier top mass leads to a more stable vertical column because $\beta$ is larger for the fundamental modes investigated. The effectiveness of a tuned mass damper was demonstrably illustrated during the April 2024 earthquake in Taiwan. The steel ball at the top of the Taipei 101 skyscraper acted as a damper, allowing the structure to gently sway and dissipate energy, thereby contributing to its stability. It is important to clarify that the top mass refers to a hanging mass, not a heavy impact load. Impact loads can cause irreversible damage to the structure’s natural vibration characteristics through external shock waves, unless properly absorbed.

The analysis revealed the key strengths of the employed analytical algorithm. It offers a simple and direct method for predicting the behavior of axially graded high-rise structures and towers with top masses. This includes evaluating their buckling modes and displacements, which can be invaluable for designers in constructing stable vertical columns. However, the current limitations lie in its inability to incorporate seismic sensitivity, necessitating further research. Additionally, the model neglects inertial rotation and shear deformation to some extent. Therefore, employing Timoshenko nonlinear beam theory would be a more accurate approach. Furthermore, the growing trend of constructing new shaped high-rises and modern skyscrapers with piecewise continuous density distributions and cross-sections necessitates further development. Future studies could focus on extending the current algorithm’s advantages to analyze these novel structures and explore its applicability in broader civil and mechanical engineering domains.

5 Conclusions

This research focuses on designing ideal shapes and analyzing the transverse vibration dynamics of column beams/towers with variable cross-sections and variable density, supporting a top load. In structural engineering, determining the design parameters that influence the shape and stability of vertical columns is crucial. This study employs both statical and dynamical approaches: (i) Statical approach: This enables us to formulate the cross-sectional areas of the columns, taking into account their variable density and top load, (ii) Dynamical approach: This allows us to scrutinize the characteristics of the vibrational modes of the derived ideal columns. To sum up the key findings; the cross-sectional area of nonuniform columns is more important than the shapes they receive. The top mass contributes as a multiplying factor of cross-sections. Whether the top of the tower will be heavier or lighter depends on the density distribution across the column. Vertical columns should be narrowing from the bottom to the top, supported with exponential, parabolic, or linear cross-sectional structures. Much widening base profiles are essential to accommodate the heavier top loads. FC towers demand higher design parameters for buckling phenomena rather than SC towers. Bending vibration is higher for FC modes owing to the freely moving top. Higher modes response with shorter amplitudes than the first fundamental mode. Towers with parabolic base are more prone to the instabilities, while exponentially supported columns are more durable. The SC modes are less resistive to the vibrational deflections, and hence are more likely to be unstable. The heavier top mass makes the vertical beam more stable.

Appendix

Some analytical results of stability system (16) are presented in this Appendix.

The special case $m=-1$and $\alpha =-2b=1$:

Replacing the second condition in (16) by the re-normalization of eigenfunctions with the constraint

$$\begin{aligned} Y''(0)= & {} 1 \end{aligned}$$

(23)

results in the mode shapes for FC

$$\begin{aligned} Y(x){} & {} = -\Bigg (\Big (16 e^{-2 i c \pi } (-2+x)^{\frac{1}{2} (-3-c)} \Big (i 2^{1+\frac{c}{2}} \left( -3+2^{\frac{5+c}{2}}+c\right) e^{\frac{5 i c \pi }{2}} (-2+x) \Gamma ^2 \left( -1+2 \Gamma ^2\right) \nonumber \\ {}{} & {} \qquad +2 i e^{\frac{3 i c \pi }{2}} (-2+x)^{1+c} \Gamma ^2 \left( 2^{c/2} \left( 5+c-4 (3+c) \Gamma ^2\right) +2 \sqrt{2} \left( -2+(5+c) \Gamma ^2\right) \right) \nonumber \\ {}{} & {} \qquad +e^{2 i c \pi } (-2+x)^{\frac{1+c}{2}} \Big (-2^{2+\frac{c}{2}} (-2+x) \Gamma ^2 \left( -4+(9+c) \Gamma ^2\right) -2 \sqrt{2} \left( -1+2 \Gamma ^2\right) \nonumber \\ {}{} & {} \quad \times \left( x+(-3+c) (-1+x) \Gamma ^2\right) +2^{\frac{1}{2}+c} \left( 2 x-(5+c) (-2+3 x) \Gamma ^2+8 (3+c) (-1+x) \Gamma ^4\right) \Big ) \Big )\Big )\nonumber \\ {}{} & {} \quad \Big /\left( (-1+c) (1+c)^2 \Gamma ^2 \left( -2^{2+ \frac{c}{2}} c \Gamma ^2+\sqrt{2} \left( 1+(-3+c) \Gamma ^2\right) + 2^{\frac{1}{2}+c} \left( -1+(3+c) \Gamma ^2\right) \right) \right) \Bigg ), \end{aligned}$$

(24)

with $c=\sqrt{-4+9 \Gamma ^2}/\Gamma$. Enforcing the second of (16) then generates the eigenrelation

$$\begin{aligned} \Delta= & {} -\frac{32 \sqrt{2} \left( 1-2 \Gamma ^2\right) ^2 \left( -2 \left( 1+2^c\right) +\left( 3-c+2^{1+c} (3+c)\right) \Gamma ^2\right) }{(-1+c) (1+c)^2 \Gamma ^2 \left( -2^{2+\frac{c}{2}} c \Gamma ^2+\sqrt{2} \left( 1+(-3+c) \Gamma ^2\right) +2^{\frac{1}{2}+c} \left( -1+(3+c) \Gamma ^2\right) \right) }.\qquad \end{aligned}$$

(25)

Eventually, equating (25) to zero, the roots $\Gamma$ are as shown in Fig. 9.

Fig. 9

Eigenvalues $\Gamma$ (zero crossing points) from (25)

An analogous analysis yields fortunately exact eigenvalues for the SC modes computed from

$$\begin{aligned} \Gamma= & {} \frac{2}{\sqrt{9+\frac{4\pi ^2 k^2}{\ln ^2 2}}},\quad k=1,2,3,\cdots . \end{aligned}$$

(26)

The special case $m=-1$and $\alpha =-b=1/2$:

Similar to the above analysis, the stationary modes are expressible in terms of lengthy Bessel functions this time, whose eigenrelations from second of (16) read

$$\begin{aligned} \Delta= & {} \frac{2 \sqrt{2} \pi \Gamma \left( -J_2\left( \frac{2}{\Gamma }\right) Y_1\left( \frac{2 \sqrt{2}}{\Gamma }\right) +J_1\left( \frac{2 \sqrt{2}}{\Gamma }\right) Y_2\left( \frac{2}{\Gamma }\right) \right) }{\Gamma ^2-\pi J_2\left( \frac{2}{\Gamma }\right) Y_0\left( \frac{2 \sqrt{2}}{\Gamma }\right) +\pi Y_2\left( \frac{2}{\Gamma }\right) \underset{0}{\overset{1}{F}}\left( 1,-\frac{2}{\Gamma ^2}\right) }, \quad (FC),\nonumber \\ \Delta= & {} \frac{-2 \sqrt{2} \pi \Gamma J_1\left( \frac{2}{\Gamma }\right) Y_1\left( \frac{2 \sqrt{2}}{\Gamma }\right) +4 \pi Y_1\left( \frac{2}{\Gamma } \right) \underset{0}{\overset{1}{F}}\left( 2,-\frac{2}{\Gamma ^2}\right) }{\Gamma -\pi J_1\left( \frac{2}{\Gamma }\right) Y_0\left( \frac{2 \sqrt{2}}{\Gamma }\right) +\pi Y_1\left( \frac{2}{\Gamma }\right) \underset{0}{\overset{1}{F}}\left( 1,-\frac{2}{\Gamma ^2}\right) },\quad (SC), \end{aligned}$$

(27)

Fig. 10

Eigenvalues $\Gamma$ (zero crossing points) from (27). a FC and b SC

where, $J_i and Y_i$’s are the Bessel functions and $\underset{0}{\overset{1}{F}}$ is the regularized hypergeometric function. The mutual eigenvalues $\Gamma$ are demonstrated in Fig. 10a, b.

The special case $\alpha =0$:

In this case, the whole vibrating modes can be found analytically, since the main equation in (16) reduces to simple ordinary differential equation

$$\begin{aligned} Y''+\Gamma ^2Y^{(4)}= & {} 0. \end{aligned}$$

(28)

Together with the normalization condition in (23), as well as the third and fourth conditions in (16) give rise to the mode shapes

$$\begin{aligned} Y(x)= & {} \Gamma \left( \Gamma -x \cot \left( \frac{1}{\Gamma }\right) - \Gamma \csc \left( \frac{1}{\Gamma }\right) \sin \left( \frac{1-x}{\Gamma }\right) \right) ,\quad (FC),\nonumber \\ Y(x)= & {} \Gamma \left( \Gamma -x \cot \left( \frac{1}{2 \Gamma }\right) - \Gamma \csc \left( \frac{1}{2 \Gamma }\right) \sin \left( \frac{1-2x}{2 \Gamma }\right) \right) ,\quad (SC). \end{aligned}$$

(29)

The second of equation (16) turns out to be

$$\begin{aligned} \Omega ^2 Y(1)+Y'(1)+\Gamma ^2Y^{(3)}(1)= & {} 0, \end{aligned}$$

(30)

generating the vibrating mode parameters

$$\begin{aligned} \Omega= & {} \frac{1}{\sqrt{\Gamma \tan \left( \frac{1}{\Gamma }\right) -1}}, \quad (FC),\nonumber \\ \Omega= & {} \frac{1}{\sqrt{-1+2\Gamma \tan \left( \frac{1}{2\Gamma }\right) }}, \quad (SC). \end{aligned}$$

(31)

The critical buckling conditions corresponding to $\Omega =0$ in (31) lead to the thresholds for the studied columns

$$\begin{aligned} \Gamma= & {} \frac{1}{(2k-1)\pi },\qquad k=1,2,3,\cdots \quad (SC),\nonumber \\ \Gamma= & {} \frac{2}{(2k-1)\pi },\qquad k=1,2,3,\cdots \quad (FC). \end{aligned}$$

(32)