1 Introduction

Research into fluid sloshing motions in vessels forced to move in prescribed manners is a vast area of research in both science and technology (see [1] and [2] and references therein). The motion of the fluid is typically complex, and as the fluid interacts with the walls of the vessel, it generates forces and moments on these walls which can have unintended consequences, such as causing faults in fuel tanks which have been excited by phenomena such as earthquakes [3]. Other possible scenarios where fluid sloshing may occur might include maritime and terrestrial fuel transport [4]. If the vessel is free to move (either fully, or in some constrained way) then those fluid forces and moments can generate movement of the vessel, which in turn feedback into the motion of the fluid. This coupled motion is very complex and can lead to devastating destabilization consequences, such as capsizing King crab boats [5, 6] and the spilling of coffee from a mug while walking [7]. In order to mitigate against destabilization, it is important to recognize when destabilization is occurring and put measures in place to control the system. For example, a ‘carry cradle’ has been shown to be very successful in reducing fluid sloshing in carried coffee mugs [8]. The novel feature of this paper is we consider a time-dependent porous baffle as a mechanism to control the system.

Baffles that are non-porous have been utilized in sloshing systems to reduce the negative consequences of the sloshing fluid, essentially by blocking the flow [1, 9]. This blocking of the flow leads to a change in the natural frequency of the system which can alter the forces generated inside the vessel, making them less severe. Such a scenario was considered by [10] who considered a rectangular vessel with N surface-piercing baffles and found the natural frequency of the system increased as N was increased. Porous baffles can also modify the system’s natural frequency [11], but they play a more significant role by extracting energy from the system and damping the motion [12, 13]. There have been significant experimental and numerical studies on the effect of porous baffles on forced systems (not dynamically coupled), in particular focusing on their position, size and material construction [14,15,16,17,18,19,20,21,22,23]. The key features of the baffles turn out to be their size and construction. The baffle construction, i.e it a randomly drilled porous block or perforated plate, is particularly significant to its overall damping properties. In numerical simulations of the baffle systems in the literature, the flow though the baffle is not explicitly calculated, and instead fluid transmission through the baffle is modelled via a model equation. Such an equation can include using Darcy’s law in linear and weakly nonlinear scenarios [24,25,26,27], using a nonlinear pressure drop condition for highly nonlinear scenarios [28, 29] or using a Darcy–Forchheimer condition [30] for intermediate conditions. The Darcy–Forchheimer condition has proved particularly successful in modelling the sloshing motion of a fluid in a tuned liquid damper filled with a porous media [31, 32]. Turner [11] examined the linear normal modes for the coupled sloshing problem and investigated how the frequency of these modes varied with the system parameters.

In the current paper we perform, to the best of our knowledge, the first numerical simulations of a dynamically coupled system, to include porous baffles. To model the system, we approximate the fluid as a shallow-water layer, and use the Lagrangian Particle Path (LPP) approach, developed for dynamic sloshing systems by [33]. This approach has been widely implemented in similar dynamic sloshing problems [34,35,36] due to the fact that the scheme has a symplectic structure and, hence, can be integrated by a geometric integration scheme such as the implicit-midpoint rule [34, 37, 38]. Such a scheme preserves the partition of energy between the vessel and the fluid, and bounds any numerical leakage of energy from the fluid to the vessel. This is particularly important when we allow the porosity of the baffle to vary with time.

The current paper is laid out as follows. In §2, we formulate the governing equations for the nonlinear system and then take the shallow-water approximation of these equations. In Sect. 3, we consider the linear solution to these equations for scheme validation, while Sect. 4 formulates the numerical scheme in both the nonlinear and linear regimes. Results of the scheme are presented in Sect. 5. Linear validation results and weakly nonlinear simulations are found in Sect. 5.1, while a mode switching phenomena in the limit as the fluid layer depth goes to zero is presented in Sect. 5.2. Section 5.3 investigates the control properties on the system when a baffle with time-dependent porosity is considered. Concluding remarks can be found in Sect. 6.

2 Formulation of governing equations

2.1 Finite depth fluid equations

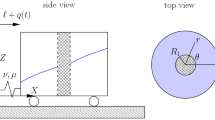
The problem we consider is that of a two-dimensional vessel with rectangular cross-section. The vessel is of length L and contains a surface-piercing porous baffle at \(x=L_1\), while the impermeable rigid side walls of the baffle lie at \(x=0\) and \(x=L=L_1+L_2\). The vessel is partially filled with an inviscid, incompressible, irrotational fluid of constant density \(\rho \), which has a mean depth of H, meaning that the vessel is filled with a fluid of mass \(m_f=\rho H L\). Figure 1 depicts a schematic of the problem of interest, where variables are indexed by subscripts 1 and 2 in the left and right compartments, respectively.

Fig. 1
figure 1

Schematic diagram of the problem under investigation. The rectangular vessel undergoes rectilinear motion in the X-direction and is partially filled with an inviscid, incompressible fluid which is allowed to pass through the porous baffle at \(x=L_1\). The vessel restoring force is given by the linear spring connecting the vessel to \(X=0\)

Full size image

In the spatial frame,the coordinates are \(\textbf{X}=(X,Y)\), while in the body frame fixed to the vessel, the rectangular coordinates are \(\textbf{x}=(x,y)\) as shown in Fig. 1. The vessel undergoes unidirectional motion parallel to the x-direction, of amplitude q(t) and hence the two reference frames are related via

$$\begin{aligned} X = X_0+x+q(t)\quad \text{ and }\quad Y = Y_0+y\,, \end{aligned}$$

where \((X_0,Y_0)\) is a constant displacement. The vessel is attached to a wall at \(X=0\) by a linear spring, which acts as a restoring force on the vessel, hence the function q(t) is determined as part of the solution. In each compartment, the fluid occupies the region

$$\begin{aligned} 0\le y \le {h}_{j}(x,t), \quad \text{ with }\quad x_{j-1}\le x \le x_j\,, \end{aligned}$$

for \(j=1,2\), where \(x_0=0\) and \(x_2=L\). We represent the fluid velocity field via the two-dimensional vector \((u_j(x,y,t),v_j(x,y,t))\) and the pressure field via the scalar quantity \(p_j(x,y,t)\). Thus, the Eulerian representation of the fluid momentum equations and the conservation of mass equation in each compartment, relative to the body coordinates, are given by the Euler equations

$$\begin{aligned} \frac{Du_j}{Dt} + \frac{1}{\rho }\frac{\partial p_j}{\partial x} = -\ddot{q} \,,~~~~~~\displaystyle \frac{Dv_j}{Dt} + \frac{1}{\rho }\frac{\partial p_j}{\partial y} = -g \,, ~~~~~~\displaystyle \frac{\partial u_j}{\partial x}+\frac{\partial v_j}{\partial y} = 0 \,, \end{aligned}$$
(2.1)

for \(j=1,2\). Here, g is the gravitational constant, \(\displaystyle \frac{D}{Dt} := \frac{\partial }{\partial t} + u_j\frac{\partial }{\partial x} + v_j \frac{\partial }{\partial y}\) is the two-dimensional material derivative and the overdots denote derivatives with respect to t.

On the free surface of the fluid in each compartment, the pressure and velocity fields satisfy the dynamic and kinematic boundary conditions, namely

$$\begin{aligned} p_j = 0, \quad \text{ and }\quad \frac{\partial h_j}{\partial t} + u_j\frac{\partial h_j}{\partial x} = v_j \,,\quad \text{ at }\quad y = h_j\left( x,t\right) \,, \quad \text{ for }\quad j=1,2 .\nonumber \\ \end{aligned}$$
(2.2)

The boundary conditions on the rigid side walls and vessel bottom are

$$\begin{aligned} \begin{array}{rcl} u_1\left( 0,y,t\right) &{}=&{} u_2\left( L,y,t\right) = 0,\\ v_j\left( x,0,t\right) &{}=&{} 0, \quad \text{ for }\quad j=1,2 \end{array} \end{aligned}$$
(2.3)

while the baffle at \(x=x_1=L_1\) is porous and thus fluid can be exchanged between the two compartments. We do not explicitly calculate the flow through the baffle, and instead, we model the transmission of the fluid through the baffle with a model equation. We assume that at the baffle the fluid velocities and the fluid pressure satisfy a Darcy–Forchheimer model [30] and hence these quantities are related via

$$\begin{aligned}{} & {} \gamma u_j(L_1,y,t)+\beta |u_j\left( L_{1},y,t\right) |u_j\left( L_{1},y,t\right) \nonumber \\{} & {} \quad = -\frac{\beta \gamma }{\rho }\Big [p_2(L_1,y,t)-p_1(L_1,y,t)\Big ] \, \quad \text{ for }\quad j=1,2. \end{aligned}$$
(2.4)

The coefficient \(\beta \in \mathbb {R}\) is a measure of the porosity of the baffle and \(\gamma \in \mathbb {R}\) is known as the internal permeability. If \(\beta \) or \(\gamma \) is zero, with the other non-zero, then we have an impermeable baffle [34], while if \(\beta \) and \(\gamma \) is infinite, then the baffle is no longer present, and we now have a single compartment vessel [33].

Using (2.2) and the second equation of (2.1), we can modify the right-hand side of the transmission boundary condition (2.4) at the baffle such that it is written in terms of the surface elevations \(h_j\) rather than the pressures \(p_j\). To do this,we integrate the second equation of (2.1) with respect to y to give

$$\begin{aligned} p_j(x,y,t)=\rho g(h_j-y)+\int _y^{h_j} \frac{D v_j}{Dt} \,\text {d}s,~~~~\textrm{for}~~~~j=1,2, \end{aligned}$$
(2.5)

using the dynamic boundary condition. Thus

$$\begin{aligned} p_2(x_1,y,t)-p_1(x_1,y,t)= & {} \rho g\left( h_2(x_1,t)-h_1(x_1,t)\right) \nonumber \\{} & {} +\int _y^{h_2} \frac{D v_2}{Dt} \,\text {d}s-\int _y^{h_1} \frac{D v_1}{Dt} \,\text {d}s. \end{aligned}$$
(2.6)

This is an exact equation for the pressure difference between the two compartments, which will simplify further once we make assumptions about the depth of the fluid layer in Sect. 2.2.

Rather than using the velocity field throughout the whole fluid, we instead choose to express the momentum equations (2.1) in terms of the surface velocity field, defined by

$$\begin{aligned} U_j(x,t) := u_j(x,h_j(x,t),t) \quad \text{ and }\quad V_j(x,t) := v_j(x,h_j(x,t),t)\,. \end{aligned}$$
(2.7)

This transformation is laid out in detail in [33] for the single compartment vessel, and so here we just quote the result, which is that the surface velocity components in each compartment satisfy the two exact equations

$$\begin{aligned} \begin{array}{rcl} \displaystyle \frac{\partial U_j}{\partial t} + U_j\frac{\partial U_j}{\partial x} + g\frac{\partial h_j}{\partial x} +\ddot{q} &{}=&{} \displaystyle -\frac{Dv_j}{Dt}\frac{\partial h_j}{\partial x} \,, \\ \displaystyle \frac{\partial h_j}{\partial t} + \frac{\partial (h_jU_j)}{\partial x} &{}=&{} \displaystyle V_j + h_j\frac{\partial U_j}{\partial x}\, , \end{array} \end{aligned}$$
(2.8)

at \(y=h_j(x,t)\) for \(j=1,2\), where (2.5) has been used to eliminate the pressure.

The motion of the vessel is determined by a forced pendulum equation and is derived using a variational principle. This derivation was laid out clearly for the impermeable baffle problem in [34], and hence we just state the equation as

$$\begin{aligned} \begin{array}{rcl} &{}&{}\displaystyle \frac{\text {d}}{\text {d}t}\left( \sum _{j=1}^2\int _{x_{j-1}}^{x_j} \rho h_j U_j \text {d}x + \left( m_v+m_{f}\right) \dot{q}\right) +\nu q \\ &{}&{}\quad = \displaystyle \frac{\text {d}}{\text {d}t}\sum _{j=1}^2\int _{x_{j-1}}^{x_j}\int _{0}^{h_j}\rho y\frac{\partial u_j}{\partial y} \text {d}y\text {d}x \,, \end{array} \end{aligned}$$
(2.9)

where \(m_f\) is the fluid mass. Note, in this work,we only consider a linear spring equation, but a nonlinear spring can easily be incorporated by including a \(-\nu _2q^3\) term on the LHS of (2.9) [34].

2.2 Shallow-water approximation to governing equations

The exact set of equations for the motion of the system (2.8) and (2.9) are not closed because the terms on the right-hand sides contain terms involving \(v_j(x,y,t)\), \(u_j(x,y,t)\) and \(V_j(x,t)\). In order to close this set of equations, we need to neglect the right-hand sides of (2.8) and (2.9), which can be achieved by making the shallow-water assumption for our problem. The principle assumptions in this limit are then

$$\begin{aligned} \left. \begin{array}{rcl} \displaystyle \bigg |\frac{Dv_j}{Dt}\bigg |^{y=h_j} \bigg | &{}\ll &{} g \,, \\ \displaystyle \bigg |V_j+h_j\frac{\partial U_j}{\partial x}\bigg | &{}\ll &{} U_0 \,, \\ \displaystyle \bigg |\frac{\text {d}\ }{\text {d}t} \sum _{j=1}^n\int _{x_{j-1}}^{x_j}\int _{0}^{h_j}\rho y\frac{\partial u_j}{\partial y}\, \text {d}y\text {d}x\bigg | &{}\ll &{} |\nu q|\,, \end{array} \right\} \end{aligned}$$
(2.10)

for \(j=1,2\), where \(U_0\) is an order-one reference velocity. These assumptions are the usual shallow-water fluid theory assumptions. Namely, that the vertical Lagrangian acceleration at the free-surface is smaller than the gravitational restoring force, and that the horizontal velocity is independent of the vertical coordinate y. The first condition in (2.10) is a special case of the more common shallow-water assumption that the Lagrangian acceleration in the vertical direction is small everywhere [39], while if we assume \(\partial u_j/\partial y=0\) in each compartment, then integrating the continuity equation leads to \(v_j+y\partial u_j/\partial x=0\) which leads to the second condition when evaluated on the free surface. The third condition is then a consequence of this assumption.

Applying these assumptions to our governing equations from Sect. 2.1 gives the shallow-water equations for the fluid motion as

$$\begin{aligned} \left. \begin{array}{rcl} \displaystyle \frac{\partial U_j}{\partial t} + U_j\frac{\partial U_j}{\partial x} + g\frac{\partial h_j}{\partial x} &{}=&{} -\ddot{q} \,, \\ \displaystyle \frac{\partial h_j}{\partial t} + h_j\frac{\partial U_j}{\partial x}+U_j\frac{\partial h_j}{\partial x} &{}=&{} 0 \,, \end{array} \right\} \quad \text{ for }\quad x_{j-1}\le x\le x_j \,, \end{aligned}$$
(2.11)

for \(j=1,2\), and these are coupled to the vessel motion via the forced pendulum equation which is written as

$$\begin{aligned} \frac{\text {d}}{\text {d}t}\left( \sum _{j=1}^2\int _{x_{j-1}}^{x_j} \rho h_j U_j\, \text {d}x + \left( m_v+m_{f}\right) \dot{q}\right) +\nu q = 0 \,. \end{aligned}$$
(2.12)

In the shallow-water regime, the rigid side-wall boundary conditions and the porous baffle transmission condition become

$$\begin{aligned}&U_1(0,t)=U_2(L,t)=0,&\end{aligned}$$
(2.13)
$$\begin{aligned}&\gamma U_j(L_1,t)+\beta |U_j(L_1,t)|U_j(L_1,t)=-\beta \gamma g\left[ h_2(L_1,t)-h_1(L_1,t)\right] \quad \text{ for }\quad j=1,2.&\nonumber \\ \end{aligned}$$
(2.14)

The governing shallow-water equations above can be determined by the Euler-Lagrange equations of the Lagrangian functional

$$\begin{aligned} \mathscr {L}=\int _{t_1}^{t_2} \mathcal {L}\,\text {d}t, \end{aligned}$$

and

$$\begin{aligned} \mathcal {L}(x,h,q)= & {} \sum _{j=1}^2\int _{x_{j-1}}^{x_j}\left[ \frac{1}{2}h_j(U_j+\dot{q})^2-\frac{1}{2}gh_j^2+\lambda _j(h_{jt}+(h_jU_j)_x)\right] \rho \,\text {d}x+\frac{1}{2}m_v\dot{q}^2-\frac{1}{2}\nu q^2, \nonumber \\{} & {} +\lambda _3\left[ \gamma U_1(x_1,\tau )+\beta |U_1(x_1,\tau )|U_1(x_1,\tau )+\beta \gamma g(h_2(x_1,\tau )-h_1(x_1,\tau ))\right] \nonumber \\{} & {} +\lambda _4\left[ \gamma U_2(x_1,\tau )+\beta |U_2(x_1,\tau )|U_2(x_1,\tau )+\beta \gamma g(h_2(x_1,\tau )-h_1(x_1,\tau ))\right] , \nonumber \\ \end{aligned}$$
(2.15)

where \(\lambda _i\) are Lagrange multipliers. This Lagrangian is of the form

$$\begin{aligned} \mathcal {L}=KE-PE+\textrm{constraints} \end{aligned}$$

where the kinetic (KE) and potential (PE) energies are

$$\begin{aligned} KE= & {} \sum _{j=1}^2\int _{x_{j-1}}^{x_j}\frac{1}{2}h_j(U_j+\dot{q})^2 \rho \,\text {d}x+\frac{1}{2}m_v\dot{q}^2, \\ PE= & {} \sum _{j=1}^2\int _{x_{j-1}}^{x_j} \frac{1}{2}gh_j^2\rho \,\text {d}x+\frac{1}{2}\nu q^2, \end{aligned}$$

with the constraints imposed. It is also possible to show that the total energy of the system

$$\begin{aligned} E(t)=\sum _{j=1}^2\int _{x_{j-1}}^{x_j}\left[ \frac{1}{2}h_j(U_j+\dot{q})^2+\frac{1}{2}gh_j^2\right] \rho \,\text {d}x+\frac{1}{2}m_v\dot{q}^2+\frac{1}{2}\nu q^2, \end{aligned}$$
(2.16)

decays with time, see Appendix 7.

In the next section, we consider the solution of the shallow-water equations in the linear regime of small amplitude motions.

3 Linear coupled problem

The solution of the shallow-water problem in the linear regime of small amplitude motions allows us to determine the natural frequencies of the system, i.e. those frequencies at which the system wants to naturally oscillate. To consider the small amplitude motions of the system, we seek small velocity perturbations about a quiescent free-surface at \(y=H\) and hence the governing shallow-water equations in each compartment reduce to

$$\begin{aligned} \displaystyle \frac{\partial h_j}{\partial t} + H \frac{\partial U_j}{\partial x} = 0,~~~~~~\displaystyle \frac{\partial U_j}{\partial t} + g \frac{\partial h_j}{\partial x} = -\ddot{q}\,, \end{aligned}$$
(3.17)

for \(j=1,2\), with the boundary conditions given by (2.13) and (2.14). The linearized form of (2.14) for small velocities about a quiescent system is

$$\begin{aligned} U_1(L_1,t)=U_2(L_1,t)=-\beta g\left[ h_2(L_1,t)-h_1(L_1,t)\right] , \end{aligned}$$
(3.18)

while the coupled linear vessel equation, linearized about \(q=0\) reduces to

$$\begin{aligned} \frac{\text {d}}{\text {d}t} \left( \sum _{j=1}^2\int _{x_{j-1}}^{x_j} \rho H U_j\,\text {d}x + (m_v+m_f) \dot{q} \right) + \nu q = 0 \,. \end{aligned}$$
(3.19)

To identify the characteristic equation for this system of equations, we consider a normal mode decomposition of the perturbation quantities, hence we let

$$\begin{aligned} h_j(x,t)=\widehat{h}_j(x)e^{\text {i}\omega t}+\mathrm{c.c},~~~U_j(x,t)=\widehat{U}_j(x)e^{\text {i}\omega t}+\mathrm{c.c},~~~q(t)=\widehat{q}e^{\text {i}\omega t}+\mathrm{c.c}, \end{aligned}$$

where c.c denotes the complex conjugate. This leads to the linearized set of equations

$$\begin{aligned} \text {i}\omega \widehat{h}_j+H \widehat{U}_{jx}=0,~~~~~\text {i}\omega \widehat{U}_j+g\widehat{h}_{jx}=\omega ^2\widehat{q}, \end{aligned}$$

for \(j=1,2\), where here the subscripts denote partial derivatives. Eliminating \(\widehat{h}_j\) from each pair of equations leads to a governing equation for each \(\widehat{U}_j\) as

$$\begin{aligned} \widehat{U}_{jxx}+\alpha ^2\widehat{U}_j=-\text {i}\omega \alpha ^2\widehat{q}, \end{aligned}$$

where \(\alpha ^2=\dfrac{\omega ^2}{gH}\).

Solving this expression for \(j=1,2\) gives

$$\begin{aligned} \widehat{U}_1= & {} A_1\cos \alpha x+B_1\sin \alpha x-\text {i}\omega \widehat{q},\\ \widehat{U}_2= & {} A_2\cos \alpha (x-L)+B_2\sin \alpha (x-L)-\text {i}\omega \widehat{q}, \end{aligned}$$

for unknown constants \(A_j\), \(B_j\). The two side-wall conditions from (2.13) imply that

$$\begin{aligned} A_1=A_2=\text {i}\omega \widehat{q}, \end{aligned}$$

giving

$$\begin{aligned} \begin{array}{l} \widehat{U}_1=\text {i}\omega \widehat{q}\left( \cos \alpha x-1\right) +B_1\sin \alpha x,\\ \widehat{U}_2=\text {i}\omega \widehat{q}\left( \cos \alpha (x-L)-1\right) +B_2\sin \alpha (x-L), \end{array} \end{aligned}$$
(3.20)

while the second two equations lead to the pair of equations

$$\begin{aligned} B_1\sin \alpha L_1+B_2\sin \alpha L_2= & {} \text {i}\omega (\cos \alpha L_2-\cos \alpha L_1)\widehat{q},\\ \left( \sin \alpha L_1-\frac{\text {i}\beta \omega }{\alpha }\cos \alpha L_2\right) B_1+\frac{\text {i}\beta \omega }{\alpha }B_2= & {} -\text {i}\omega (\cos \alpha L_1-1)\widehat{q}\\{} & {} +\frac{\beta \omega ^2}{\alpha }(\sin \alpha L_1+\sin \alpha L_2)\widehat{q}, \end{aligned}$$

where \(L_2=L-L_1\) is the length of the second compartment.

The case when \(\sin \alpha L_1=\sin \alpha L_2=0\) was examined in [11] and this case leads to symmetric sloshing modes in a stationary vessel, i.e. modes which do not link to the vessel motion. For the case when these quantities are non-zero,the above pair of equations are solvable, giving

$$\begin{aligned} B_1= & {} \frac{1}{\alpha |\Delta _0|^2}\left[ \beta \omega ^2\frac{\tan \frac{1}{2}\alpha L_1+\tan \frac{1}{2}\alpha L_2}{\sin \alpha L_1}\right. \\{} & {} \left. +\text {i}\left( \omega \alpha \tan \frac{1}{2}\alpha L_1+\frac{\beta ^2\omega ^3}{\alpha }\tan \frac{1}{2}\alpha (L_1+L_2)\left( \cot \alpha L_1+\cot \alpha L_2\right) ^2\right) \right] \widehat{q},\\ B_2= & {} -\frac{1}{\alpha |\Delta _0|^2}\left[ \beta \omega ^2\frac{\tan \frac{1}{2}\alpha L_1+\tan \frac{1}{2}\alpha L_2}{\sin \alpha L_2}\right. \\{} & {} \left. +\text {i}\left( \omega \alpha \tan \frac{1}{2}\alpha L_2+\frac{\beta ^2\omega ^3}{\alpha }\tan \frac{1}{2}\alpha (L_1+L_2)\left( \cot \alpha L_1+\cot \alpha L_2\right) ^2\right) \right] \widehat{q}, \end{aligned}$$

where

$$\begin{aligned} \Delta _0=1-\frac{\text {i}\omega \beta }{\alpha }\left( \cot \alpha L_1+\cot \alpha L_2\right) . \end{aligned}$$

The linearized vessel equation gives a third equation linking \(B_1,B_2\) and \(\widehat{q}\). To evaluate this equation, we use the fact that

$$\begin{aligned} \int _0^{L_1}\widehat{U}_1\,\text {d}x= & {} \frac{\text {i}\omega }{\alpha }\widehat{q}\sin \alpha L_1-\text {i}\omega L_1\widehat{q}+\frac{B_1}{\alpha }(1-\cos \alpha L_1),\\ \int _{L_1}^{L_1+L_2}\widehat{U}_2\,\text {d}x= & {} \frac{\text {i}\omega }{\alpha }\widehat{q}\sin \alpha L_2-\text {i}\omega L_2\widehat{q}-\frac{B_2}{\alpha }(1-\cos \alpha L_2), \end{aligned}$$

giving the third equation as

$$\begin{aligned}{} & {} \frac{\text {i}\omega \rho H}{\alpha }(1-\cos \alpha L_1)B_1-\frac{\text {i}\omega \rho H}{\alpha }(1-\cos \alpha L_2)B_2\nonumber \\{} & {} \quad -\frac{\omega ^2\rho H}{\alpha }(\sin \alpha L_1+\sin \alpha L_2)\widehat{q}+\nu \widehat{q}=0.\nonumber \\ \end{aligned}$$
(3.21)
Fig. 2
figure 2

Plots of a, c normal mode frequencies \(\omega _r(\beta )\) and (b,d) normal mode decay rates \(\omega _i(\beta )\) from (3.22) for a, b \(L_1=L_2=0.5\,\textrm{m}\) and c, d \(L_1=0.25\,\textrm{m}\), \(L_2=0.75\,\textrm{m}\). The other parameters are fixed and given in (5.50). The circles at \(\beta =0\) signify modes which are symmetric modes in a stationary vessel in this limit. Here \(\beta \) has units sm\(^{-1}\) and \(\omega _r,\omega _i\) have units rad s\(^{-1}\)

Full size image

Writing these three equations as a matrix system and solving for non-trivial solutions lead to a characteristic equation of the form

$$\begin{aligned}{} & {} -(\nu -\omega ^2 m_v)\alpha ^2\left( \sin \alpha L_1\sin \alpha L_2-\frac{\text {i}\beta \omega }{\alpha }\sin \alpha (L_1+L_2)\right) \nonumber \\{} & {} +2\alpha \rho H\omega ^2(\tan \frac{1}{2}\alpha L_1+\tan \frac{1}{2}\alpha L_2)\sin \alpha L_1\sin \alpha L_2\nonumber \\ {}{} & {} -2\text {i}\omega ^3\rho H\beta \left( 1-\cos \alpha (L_1+L_2)\right) =0. \end{aligned}$$
(3.22)

The above formulation gives the natural frequencies of the system. These natural frequencies give the eigenbasis for the nonlinear formulation of the problem, i.e. nonlinear solutions are superpositions of these linear eigenmodes. These linear solutions are also vital for providing initial conditions allowing us to validate the numerical scheme against known results. We discuss the solutions to (3.22) in Sect. 5.1 to which there are an infinite number of modes, the lowest frequency ones of which are plotted in Fig. 2.

4 Numerical scheme for nonlinear simulations

The numerical scheme used to solve the governing shallow-water equations is based on a Lagrangian Particle Path (LPP) formulation [33] and is very similar to that laid out for the impermeable baffle problem in [34]. The reader is referred to [34] for more details of the formulation.

The LPP formulation comes from converting from Eulerian to Lagrangian coordinates via the non-degenerate mapping

$$\begin{aligned} (\tau ,a) \mapsto (t(\tau ),x(a,\tau )) \,,\quad \text{ with }\quad 0\le a \le L \,,\quad \tau \ge 0 \,, \end{aligned}$$
(4.23)

which when substituted into (2.11) and (2.12) gives

$$\begin{aligned} \displaystyle \frac{\partial ^2 x}{\partial \tau ^2}+\frac{g\dfrac{\partial \chi ^{(j)}}{\partial a}}{\left( \dfrac{\partial x}{\partial a}\right) ^2}-\frac{g\chi ^{(j)}}{\left( \dfrac{\partial x}{\partial a}\right) ^3}\frac{\partial ^2 x}{\partial a^2} = -\frac{\partial ^2 q}{\partial \tau ^2} \,, \end{aligned}$$
(4.24)

for \(0<a<a_B\) for \(j=1\) and \(a_B<a<L\) for \(j=2\). Here \(a_B\) is the unknown Lagrangian coordinate which fixes the position of the baffle in the Eulerian framework and needs to be determined as part of the solution. The vessel equation becomes

$$\begin{aligned} \displaystyle \frac{\text {d}^2}{\text {d}\tau ^2}\left( \sum _{j=1}^2 \int _{a_{j-1}}^{a_j} \rho \chi ^{(j)}x \text {d}a + (m_v+m_{f})q \right) +\nu q = 0 \,, \end{aligned}$$
(4.25)

where

$$\begin{aligned} \chi ^{(j)}(a)=h_j\frac{\partial x}{\partial a}\bigg |_{\tau =0}, \end{aligned}$$
(4.26)

comes from the mass conservation equation and \(a_0=0\), \(a_1=a_B\) and \(a_2=L\). Here \(\chi ^{(j)}(a)\) is independent of \(\tau \) and hence is fixed at \(\tau =0\). From this equation, we are able to determine the free-surface elevation via \(h_j=\chi ^{(j)}/x_a\). In this LPP formulation, the unknowns are \(x(a,\tau )\) and \(q(\tau )\).

The above equations (4.24) and (4.25) in Lagrangian coordinates can be determined from a variational principle from the Lagrangian (2.15) where we use (4.23) to convert the Lagrangian to these Lagrangian coordinates. Converting the Lagrangian and performing a Legendre transformation leads to a non-autonomous Hamiltonian functional

$$\begin{aligned}{} & {} \mathscr {H}(x,q,w,p,\tau ) = \sum _{j=1}^2\int _{a_{j-1}}^{a_j} \left( \frac{1}{2}w^2 +g\frac{\chi ^{(j)}}{2\left( \frac{\partial x}{\partial a}\right) }\right) \rho \chi ^{(j)} \text {d}a \nonumber \\{} & {} \quad +\frac{1}{2m_v} \left( p-\sum _{j=1}^2\int _{a_{j-1}}^{a_j}w\rho \chi ^{(j)}\text {d}a\right) ^2+\frac{1}{2}\nu q^2, \end{aligned}$$
(4.27)

where the constraints hold and \(\left( x,w,q,p\right) \) are the canonical variables with momentum variables

$$\begin{aligned} w(a,\tau ) = \dfrac{\partial x}{\partial \tau }(a,\tau ) + \dfrac{\partial q}{\partial \tau }(\tau ), ~~~~ p(\tau ) = \displaystyle \sum _{j=1}^2\int _{a_{j-1}}^{a_j} w(a,\tau )\rho \chi ^{(j)} \text {d}a + m_{v}\frac{\partial q}{\partial \tau } \,.\nonumber \\ \end{aligned}$$
(4.28)

The governing equations can be written in Hamiltonian form as

$$\begin{aligned} \left. \begin{array}{rcl} \dfrac{\partial w}{\partial \tau } &{}=&{}-\dfrac{\delta \mathscr {H}}{\delta x} = \dfrac{-g\chi _{a}^{(j)}}{\left( \dfrac{\partial x}{\partial a}\right) ^{2}} +\dfrac{g\chi ^{(j)}}{\left( \dfrac{\partial x}{\partial a}\right) ^{3}}\dfrac{\partial ^2 x}{\partial a^2} \,, \quad { \begin{array}{ll} 0<a<a_B &{} \textrm{for}~~j=1 \\ a_B<a<L &{} \textrm{for}~~j=2, \end{array}}\\ \dfrac{\partial x}{\partial \tau }&{}=&{} \dfrac{\delta \mathscr {H}}{\delta w} = w-\dfrac{1}{m_v}p +\dfrac{1}{m_v}\displaystyle \sum _{j=1}^2\displaystyle \int _{a_{j-1}}^{a_j} w\rho \chi ^{(j)} \text {d}a \,,\quad { \begin{array}{ll} 0<a<a_B &{} \textrm{for}~~j=1 \\ a_B<a<L &{} \textrm{for}~~j=2, \end{array}}\\ \dfrac{\partial p}{\partial \tau } &{}=&{}-\dfrac{\delta \mathscr {H}}{\delta q} = -\nu q \,, \\ \dfrac{\partial q}{\partial \tau } &{}=&{} \dfrac{\delta \mathscr {H}}{\delta p} = \dfrac{1}{m_v}p-\dfrac{1}{m_v}\displaystyle \sum _{j=1}^2\displaystyle \int _{a_{j-1}}^{a_j} w\rho \chi ^{(j)} \text {d}a \,. \end{array} \right\} \nonumber \\ \end{aligned}$$
(4.29)

The impermeable side-wall boundary conditions to be solved together with (4.29) are

$$\begin{aligned} x(0,\tau ) = 0,~~~~\textrm{and}~~~~x(L,\tau )=L, \quad \forall ~\tau , \end{aligned}$$
(4.30)

and

$$\begin{aligned} w(0,\tau )=w(L,\tau )=\displaystyle \frac{1}{m_v}p - \frac{1}{m_v}\sum _{j=1}^2\int _{a_{j-1}}^{a_j} w(a,\tau )\rho \chi ^{(j)}\text {d}a \, \quad \forall ~\tau \, . \end{aligned}$$
(4.31)

For the conditions at the porous baffle, the transmission conditions are

$$\begin{aligned} x(a_B,\tau )=L_1, \quad \forall ~\tau \end{aligned}$$
(4.32)

and from (2.4)

$$\begin{aligned}{} & {} \gamma \left[ w(a_B,\tau )-\displaystyle \frac{1}{m_v}p + \frac{1}{m_v}\sum _{j=1}^2\int _{a_{j-1}}^{a_j} w\rho \chi ^{(j)}\text {d}a\right] \nonumber \\{} & {} +\beta \left| w(a_B,\tau )-\displaystyle \frac{1}{m_v}p + \frac{1}{m_v}\sum _{j=1}^2\int _{a_{j-1}}^{a_j} w\rho \chi ^{(j)}\text {d}a\right| \nonumber \\{} & {} \left[ w(a_B,\tau )-\displaystyle \frac{1}{m_v}p + \frac{1}{m_v}\sum _{j=1}^2\int _{a_{j-1}}^{a_j} w\rho \chi ^{(j)}\text {d}a\right] +\beta \gamma g\left( \frac{\chi ^{(2)}}{\dfrac{\partial x}{\partial a}}-\frac{\chi ^{(1)}}{\dfrac{\partial x}{\partial a}} \right) =0,\nonumber \\ \end{aligned}$$
(4.33)

which implicitly gives an equation for the unknown variable w at \(a=a_B\). Equation (4.32) essentially defines the position of the baffle \(a_B\) in the Lagrangian framework. However, we find the form (4.32) troublesome to work with, as \(a_B\) needs to be found via interpolation which introduces unnecessary errors. This can be overcome by forming an ODE for the value of \(a_B(\tau )\) by differentiating (4.32) with respect to \(\tau \) to give

$$\begin{aligned} \frac{\partial x}{\partial \tau }(a_B,\tau )+\frac{\partial a_B}{\partial \tau }\frac{\partial x}{\partial a}(a_B,\tau )=0. \end{aligned}$$

Using (4.29), we can then write this equation as

$$\begin{aligned} \frac{\partial a_B}{\partial \tau }=\left( \frac{\partial x}{\partial a}\right) ^{-1}\left( -w+\frac{1}{m_v}p - \frac{1}{m_v}\sum _{j=1}^2\int _{a_{j-1}}^{a_j} w \rho \chi ^{(j)}\text {d}a\right) ~~~~\textrm{at}~~~~a=a_B.\nonumber \\ \end{aligned}$$
(4.34)

Note that the introduction of the condition (4.33) means that this system, unlike the impermeable baffle problem in [34], is no longer conservative and thus energy is not conserved. However, it has been shown that symplectic integration schemes work very well for symplectic equations with dissipative perturbations, even capturing the actual dissipation better than non-symplectic schemes [38]. They have also been shown to be very efficient at preserving the energy budget between the fluid and the vessel [33], hence we choose to use a symplectic scheme here.

4.1 The semi-discretization of (4.29)

The challenging numerical aspect of solving the system (4.29)-(4.34) is that the Lagrangian coordinate \(a_B\) is a function of \(\tau \), and so the domains on which the governing equations are solved are not fixed. To overcome this, we make the following change of variables to a fixed domain in each region, namely

$$\begin{aligned} \tau:= & {} \tau , \end{aligned}$$
(4.35)
$$\begin{aligned} a:= & {} \left\{ \begin{array}{rl} \xi _1(\tau )A^{(1)} &{} \textrm{for}~~~0\le A^{(1)}\le 1,\\ a_B(\tau )+\xi _2(\tau )A^{(2)} &{} \textrm{for}~~~0\le A^{(2)}\le 1\end{array}\right. , \end{aligned}$$
(4.36)

where \(\xi _1(\tau )=a_B(\tau )\) and \(\xi _2(\tau )=L-a_B(\tau )\).

The domains \(A^{(1)}\) and \(A^{(2)}\) can then be regularly discretized by setting

$$\begin{aligned} A_i^{(1)}= & {} \frac{(i-1)}{N},~~~~\textrm{for}~~~i=1,...,N+1,\\ A_i^{(2)}= & {} \frac{(i-1)}{M},~~~~\textrm{for}~~~i=1,...,M+1,\\ \end{aligned}$$

where N and M are integers and we define \(\Delta A^{(1)}=1/N\) and \(\Delta A^{(2)}=1/M\). Notationally, we write \(x_i^{(j)}(\tau ):= x(A^{(j)}_i,\tau )\) and \(w_i^{(j)}(\tau ):= w(A_i^{(j)},\tau )\) where \(j=1,2\) denotes the region of the vessel.

The change of variables and discretization of the equations (4.29)-(4.34) is relatively straightforward, except for the \(w_\tau \) equation, which requires a variational discretization, where the Hamiltonian function (4.27) is first discretized and then variations of this are then taken. In this case, following [33], these equations become

$$\begin{aligned}{} & {} \frac{\partial w^{(1)}_i}{\partial \tau }-\frac{\xi _{1\tau }A^{(1)}}{\xi _1}\left( \frac{w^{(1)}_{i+1}-w^{(1)}_{i-1}}{2\Delta A^{(1)}}\right) \nonumber \\{} & {} \quad = \frac{\xi _1g\Delta A^{(1)}}{2\chi _i^{(1)}} \left( \frac{(\chi _{i-1}^{(1)})^2}{(x^{(1)}_i-x^{(1)}_{i-1})^2}- \frac{(\chi _i^{(1)})^2}{(x^{(1)}_{i+1}-x^{(1)}_i)^2}\right) , \end{aligned}$$
(4.37)
$$\begin{aligned}{} & {} \frac{\partial w^{(2)}_i}{\partial \tau }-\frac{(a_{B\tau }+\xi _{2\tau }A^{(2)})}{\xi _2}\left( \frac{w^{(2)}_{i+1}-w^{(2)}_{i-1}}{2\Delta A^{(2)}}\right) \nonumber \\{} & {} \quad = \frac{\xi _2g\Delta A^{(2)}}{2\chi _i^{(2)}} \left( \frac{(\chi _{i-1}^{(2)})^2}{(x^{(2)}_i-x^{(2)}_{i-1})^2}- \frac{(\chi _i^{(2)})^2}{(x^{(2)}_{i+1}-x^{(2)}_i)^2}\right) ,\nonumber \\ \end{aligned}$$
(4.38)

Thus the full semi-discretization of the transformed equations are then given by (4.37) and (4.38) together with

$$\begin{aligned} \left. \begin{array}{rcl} \dfrac{\partial x^{(1)}_i}{\partial \tau }-\dfrac{\xi _{1\tau }A^{(1)}}{\xi _1}\left( \dfrac{x^{(1)}_{i+1}-x^{(1)}_{i-1}}{2\Delta A^{(1)}}\right) &{}=&{} \displaystyle w^{(1)}_{i}-\frac{1}{m_v}p+\frac{1}{m_v}\sigma _{N}^{(1)} +\frac{1}{m_v}\sigma _{M}^{(2)} \,, \\ \dfrac{\partial x^{(2)}_i}{\partial \tau }-\dfrac{(a_{B\tau }+\xi _{2\tau }A^{(2)})}{\xi _2}\left( \dfrac{x^{(2)}_{i+1}-x^{(2)}_{i-1}}{2\Delta A^{(2)}}\right) &{}=&{} \displaystyle w^{(2)}_{i}-\frac{1}{m_v}p+\frac{1}{m_v}\sigma _{N}^{(1)} +\frac{1}{m_v}\sigma _{M}^{(2)} \,, \\ \dfrac{\partial p}{\partial \tau } &{}=&{} -\nu q\,, \\ \dfrac{\partial q}{\partial \tau } &{}=&{} \displaystyle \frac{1}{m_v}p-\frac{1}{m_v}\sigma _{N}^{(1)} -\frac{1}{m_v}\sigma _{M}^{(2)} \,, \\ \end{array} \right\} \nonumber \\ \end{aligned}$$
(4.39)

where \(i=2,\ldots , N\) for \(j=1\) and \(i=2,\ldots , M\) for \(j=2\), and where

$$\begin{aligned} \begin{array}{rcl} \sigma _N^{(1)}(\tau ) &{}:=&{} \displaystyle \xi _1\sum _{i=2}^{N} w^{(1)}_i\,\rho \chi _i^{(1)}\Delta A^{(1)}+ \frac{1}{2}\rho \xi _1\left( \chi _1^{(1)}w^{(1)}_1 + \chi _{N+1}^{(1)}w^{(1)}_{N+1}\right) \Delta A^{(1)}\,, \\ \sigma _M^{(2)}(\tau ) &{}:=&{} \displaystyle \xi _2\sum _{i=2}^{M} w^{(2)}_i\,\rho \chi _i^{(2)}\Delta A^{(2)}+ \frac{1}{2}\rho \xi _2\left( \chi _{1}^{(2)}w^{(2)}_{1} + \chi _{M+1}^{(2)}w^{(2)}_{M+1}\right) \Delta A^{(2)}, \end{array}\nonumber \\ \end{aligned}$$
(4.40)

are the integral terms in (4.29) which have been discretized using the trapezoidal rule.

The semi-discretization of the side-wall boundary conditions is

$$\begin{aligned} x^{(1)}_1(\tau ) = 0 \,, \quad \text{ and }\quad x^{(2)}_{M+1}(\tau ) = L \,, \end{aligned}$$

and

$$\begin{aligned} \begin{array}{rcl} w^{(1)}_1(\tau ) = w^{(2)}_{M+1}(\tau ) = \displaystyle \frac{1}{m_v}\left( p-\sigma _{N}^{(1)}-\sigma _{M}^{(2)}\right) \,, \end{array} \end{aligned}$$

while at the porous baffle,the conditions (4.32)-(4.34) are

$$\begin{aligned}{} & {} x^{(1)}_{N+1}(\tau )=x^{(2)}_1(\tau )=L_1,\end{aligned}$$
(4.41)
$$\begin{aligned}{} & {} w^{(1)}_{N+1}(\tau )=w^{(2)}_1(\tau )=w_B,\end{aligned}$$
(4.42)
$$\begin{aligned}{} & {} \frac{\partial a_B}{\partial \tau }=\Gamma ^{-1}\left[ -w_B+\frac{1}{m_v}\left( p-\sigma _{N}^{(1)}-\sigma _{M}^{(2)}\right) \right] , \end{aligned}$$
(4.43)

where \(w_B\) is a solution of

$$\begin{aligned}{} & {} \gamma (\tau )\left[ w_B-\frac{1}{m_v}\left( p-\sigma _{N}^{(1)}-\sigma _{M}^{(2)}\right) \right] \nonumber \\ {}{} & {} +\beta (\tau )\left| w_B-\frac{1}{m_v}\left( p-\sigma _{N}^{(1)}-\sigma _{M}^{(2)}\right) \right| \left[ w_B-\frac{1}{m_v}\left( p-\sigma _{N}^{(1)}-\sigma _{M}^{(2)}\right) \right] \nonumber \\{} & {} +\beta (\tau )\gamma (\tau ) g\left( \frac{\xi _2\chi ^{(2)}_1\Delta A^{(2)}}{x^{(2)}_{2}-x^{(2)}_1}-\frac{\xi _1\chi ^{(1)}_{N+1}\Delta A^{(1)}}{x^{(1)}_{N+1}-x^{(1)}_{N}} \right) =0, \end{aligned}$$
(4.44)

and

$$\begin{aligned} \Gamma =\frac{1}{2}\left[ \frac{x^{(1)}_{N+1}-x^{(1)}_{N}}{\xi _1\Delta A^{(1)}}+\frac{x^{(2)}_{2}-x^{(2)}_1}{\xi _2\Delta A^{(2)}}\right] , \end{aligned}$$

is the average of the \(\dfrac{\partial x}{\partial a}\) values at \(A^{(1)}=1\) and \(A^{(2)}=0\).

Under the change of variables (4.35) and (4.36), equation (4.26) no longer states that \(\chi \) is independent of \(\tau \), and in fact, the conservation of mass equation now states that we must additionally solve

$$\begin{aligned} \dfrac{\partial \chi _i^{(1)}}{\partial \tau }-\frac{\xi _{1\tau }A^{(1)}}{\xi _1}\left( \frac{\chi ^{(1)}_{i+1}-\chi ^{(1)}_{i-1}}{2\Delta A^{(1)}}\right)= & {} 0,~~~i=2,...,N\end{aligned}$$
(4.45)
$$\begin{aligned} \dfrac{\partial \chi _i^{(2)}}{\partial \tau }-\frac{(a_{B\tau }+\xi _{2\tau }A^{(2)})}{\xi _2}\left( \frac{\chi ^{(2)}_{i+1}-\chi ^{(2)}_{i-1}}{2\Delta A^{(2)}}\right)= & {} 0,~~~i=2,...,M, \end{aligned}$$
(4.46)

with the corresponding forward and backward forms of \(\dfrac{\partial x}{\partial a}\) to evaluate the four end points \(i=1,N+1\) for \(j=1\) and \(i=1,M+1\) for \(j=2\). Now the free-surface elevation is given by

$$\begin{aligned} h_j(A^{(j)})=\frac{\chi ^{(j)}}{\xi _jx_A^{(j)}}, \end{aligned}$$

for \(j=1,2\).

4.2 Time discretization using the Implicit Midpoint Rule

The semi-discretization of the governing equations above has the form

$$\begin{aligned} \dfrac{\partial \textbf{p}}{\partial \tau } = \textrm{g}\left( \textbf{q},\textbf{p}\right) ,~~~~~~~~ \dfrac{\partial \textbf{q}}{\partial \tau } = \textrm{f}\left( \textbf{q},\textbf{p}\right) \,, \end{aligned}$$
(4.47)

where

$$\begin{aligned} \textbf{p}= & {} (p,w^{(1)}_1,\ldots ,w^{(1)}_{N+1}, w^{(2)}_{1}\ldots ,w^{(2)}_{M+1}),\\ \textbf{q}= & {} (q,a_B,x^{(1)}_1,\ldots ,x^{(1)}_{N+1},x^{(2)}_{1},\ldots ,x^{(2)}_{M+1},\chi _1^{(1)},\ldots \chi _{N+1}^{(1)},\chi _1^{(2)},\ldots \chi _{M+1}^{(2)})\,. \end{aligned}$$

We discretize \(\tau \) such that \(\tau _n=n\Delta \tau \) where \(\Delta \tau \) is a fixed time step and introduce the notation \(\textbf{q}(\tau _n)=\textbf{q}^{n}\). Then, equations of this form can be integrated by applying the implicit-midpoint rule [38], which is second-order accurate in time and discretizes the equations as

$$\begin{aligned} \begin{array}{rcl} \textbf{q}^{n+1} &{}=&{} \displaystyle \textbf{q}^{n}+\Delta \tau \textrm{f}\left( \frac{\textbf{q}^{n}+\textbf{q}^{n+1}}{2},\frac{\textbf{p}^{n}+\textbf{p}^{n+1}}{2}\right) \,, \\ \textbf{p}^{n+1} &{}=&{} \displaystyle \textbf{p}^{n}+\Delta \tau \textrm{g}\left( \frac{\textbf{q}^{n}+\textbf{q}^{n+1}}{2} ,\frac{\textbf{p}^{n}+\textbf{p}^{n+1}}{2}\right) \,. \end{array} \end{aligned}$$
(4.48)

The implicit nature of this algorithm means that larger time steps, \(\Delta \tau \), can be taken compared to an explicit scheme, which helps in keeping the scheme computationally fast when weakly nonlinear simulations are considered which require a higher spatial resolution.

The system of nonlinear equations and boundary conditions (4.40)-(4.44) is a system of \(3(N+M)+9\) equations with \(3(N+M)+9\) unknowns. We define the vector of unknown variables at time \(\tau _{n}\) as

$$\begin{aligned} \textbf{X}^{n}= & {} \left[ (x^{(1)}_1)^{n},\ldots ,(x^{(1)}_{N+1})^{n},(x^{(2)}_{1})^{n},\ldots ,(x^{(2)}_{M+1})^{n},\right. \\{} & {} (w^{(1)}_1)^{n},\ldots ,(w^{(1)}_{N+1})^{n},(w^{(2)}_{1})^{n},\ldots ,(w^{(2)}_{M+1})^{n},\\{} & {} \left. (\chi ^{(1)}_1)^{n},\ldots ,(\chi ^{(1)}_{N+1})^{n},(\chi ^{(2)}_{1})^{n},\ldots ,(\chi ^{(2)}_{M+1})^{n},a_B^n,q^{n},p^{n}\right] ^T \,. \end{aligned}$$

The system of nonlinear algebraic equations is solved using Newton’s method, where iterations are continued until \(||\textbf{X}^{n+1}-\textbf{X}^n||_2/||\textbf{X}^{n+1}||_2<10^{-8}\).

5 Numerical results

In this section, we present numerical results to the nonlinear equations (4.39)–(4.44). One of the limitations of the shallow-water model used in this paper is: for sloshing problems, the equations are only able to sustain a weak amount of nonlinearity before wave breaking occurs. Thus we are limited to parameter regimes where wave overturning does not occur and the nonlinearities observed are weak. In cases where the scheme approaches breaking, the code breaks down due to the free-surface becoming multiply defined. Therefore, we find that at most, our results are weakly nonlinear. Hence,we choose to fix \(\gamma (\tau )=1\) in the nonlinear transmission condition throughout this section and find no quantitative difference to the results presented if this value is significantly varied.

In all the results presented in this manuscript,the parameters N,  M and \(\Delta \tau \), which govern the resolution of the numerical scheme, were varied to ensure the presented results have converged.

5.1 Scheme validation and weakly nonlinear example

In this section, we validate our numerical scheme by making direct comparisons with the linear results presented in Sect. 3. Before we compare the numerical simulation results, we first consider what frequencies of solution, \(\omega =\omega _r+\text {i}\omega _i\), we expect to observe by solving the characteristic equation (3.22). Note that the value of \(\omega _i\) denotes the exponential decay rate of the mode as we only find solutions with \(\omega _i\ge 0\). In Fig. 2, we consider plots of \(\omega _r(\beta )\) and \(\omega _i(\beta )\) for (a,b) \(L_1=L_2=0.5\,\)m and (c,d) \(L_1=0.25\,\)m, \(L_2=0.75\,\)m with the other parameters given by

$$\begin{aligned}{} & {} \rho =1000\,\textrm{kg}\,\textrm{m}^{-3},~~~H=0.05\,\textrm{m},~~~m_v=10\,\textrm{kg},~~~\nonumber \\{} & {} \nu _1=70\,\textrm{kg}\,\textrm{s}^{-2},~~~\widehat{q}=5\times 10^{-5}\,\textrm{m}, \end{aligned}$$
(5.50)

with \(N=M=100\) and \(\Delta \tau =10^{-3}\,\textrm{s}\). The results show that those modes for which \(\omega _r\) varies considerably as \(\beta \rightarrow 0\) also have the largest decay rates. The lowest frequency modes (labelled 1) are likely to be the modes observed in a physical system, as these modes typically decay the slowest. More discussion on the modal results and how the various system parameters affect these results can be found in [11], while more information on this type of eigenvalue spectrum for similar coupled fluid/vessel systems without baffles can be found in [40,41,42,43].

Fig. 3
figure 3

Plots of the vessel displacement q(t) and Lagrangian coordinate value at the baffle \(a_B(t)-L_1\) for the parameters in (5.50) with a, b \(L_1=L_2=0.5\,\textrm{m}\) and c) \(L_1=0.25\,\textrm{m}\), \(L_2=0.75\,\textrm{m}\). In a \(\beta =0.508\,\textrm{sm}^{-1}\) and \(\omega =1.027+0.032\text {i}\,\textrm{rad}\,\textrm{s}^{-1}\), in b \(\beta =0.995\,\textrm{sm}^{-1}\) and \(\omega =10.225+2.529\text {i}\,\textrm{rad}\,\textrm{s}^{-1}\) and in c \(\beta =0.380\,\textrm{sm}^{-1}\) and \(\omega =1.019+0.023\text {i}\,\textrm{rad}\,\textrm{s}^{-1}\). Here t has units of s while q and \(a_B-L_1\) have units of m

Full size image

For the validation of our numerical scheme,we consider three cases from Fig. 2, namely for \(L_1=L_2=0.5\,\)m,we consider mode 1 when \(\beta =0.508\,\textrm{sm}^{-1}\), mode 6 when \(\beta =0.995\,\textrm{sm}^{-1}\) and for \(L_1=0.25\,\)m \(L_2=0.75\,\)m, we consider mode 1 when \(\beta =0.380\,\textrm{sm}^{-1}\). For each of these cases,we consider the exact linear initial condition, namely

$$\begin{aligned} q(0)= & {} \widehat{q}+\mathrm{c.c}, \end{aligned}$$
(5.51)
$$\begin{aligned} x^{(1)}(A^{(1)},0)= & {} \xi _1A^{(1)}-\left( \frac{\text {i}}{\omega }\widehat{U}_1(\xi _1A^{(1)})+\mathrm{c.c.}\right) ,\end{aligned}$$
(5.52)
$$\begin{aligned} x^{(2)}(A^{(2)},0)= & {} a_B+\xi _2A^{(2)}-\left( \frac{\text {i}}{\omega }\widehat{U}_2(a_B+\xi _2A^{(2)})+\mathrm{c.c.}\right) ,\end{aligned}$$
(5.53)
$$\begin{aligned} w^{(1)}(A^{(1)},0)= & {} \widehat{U}_1(\xi _1A^{(1)})+\text {i}\omega \widehat{q}+\mathrm{c.c},\end{aligned}$$
(5.54)
$$\begin{aligned} w^{(2)}(A^{(2)},0)= & {} \widehat{U}_2(a_B+\xi _2A^{(2)})+\text {i}\omega \widehat{q}+\mathrm{c.c},\end{aligned}$$
(5.55)
$$\begin{aligned} p(0)= & {} \left( \text {i}m_v\omega \widehat{q}+\mathrm{c.c}\right) +\sum _{j=1}^2\int _{0}^{1}\xi _jw(A^{(j)},0)\rho H\,\text {d}A^{(j)},\end{aligned}$$
(5.56)
$$\begin{aligned} a_B(0)= & {} L_1-x^{(1)}(1,0), \end{aligned}$$
(5.57)

where \(\widehat{U}_j\) are given in (3.20) for \(j=1\) and \(j=2\). The \(\mathrm{c.c.}\) denotes the complex conjugate.

Fig. 4
figure 4

Free-surface profiles h(x, t) for the case 1 in Fig. 3a, b at \(t=7.5, 15, 22.5, 30, 37.5, 45, 52.5\) and \(60\,\textrm{s}\), respectively. Here h and x have units of m

Full size image

In Figs. 3–6, we compare the numerical (solid black lines) and the exact analytical results (dashed red lines) for the three cases noted above. In all cases, the exact and analytical results for the vessel displacement q(t) and the free-surface elevations h(x, t) are in excellent agreement. Note that we plot our results in terms of the Eulerian variables (x, t) as these are more intuitive than \((A^{(j)},\tau )\). In this linear case,\(t=\tau \) and \(x=[\xi _1A^{(1)},(a_B+\xi _2A^{(2)})]\). The mode 6 result has \(\omega =10.225+2.529\text {i}\,\textrm{rad}\,\textrm{s}^{-1}\) and so decays very quickly compared to the other two cases where \(\omega =1.027+0.032\text {i}\,\textrm{rad}\,\textrm{s}^{-1}\) and \(\omega =1.019+0.023\text {i}\,\textrm{rad}\,\textrm{s}^{-1}\), respectively. However, even in this case, the agreement for q(t) and \(a_B(t)-L_1\) in Fig. 3b is excellent.

Fig. 5
figure 5

Free-surface profiles h(x, t) for the case 6 in Fig. 3a, b at \(t=0.6, 1.3, 1.9, 2.5, 3.1, 3.8, 4.4\) and \(5\,\textrm{s}\), respectively. Here h and x have units of m

Full size image

For the free-surface profiles, h(x, t), in Fig. 5, we see some numerical round off errors in the black numerical results, but the overall agreement is still excellent.

Fig. 6
figure 6

Free-surface profiles h(x, t) for the case 1 in Fig. 3c, d at \(t=7.5, 15, 22.5, 30, 37.5, 45, 52.5\) and \(60\,\textrm{s}\), respectively. Here h and x have units of m

Full size image

As \(\widehat{q}\) is increased, the problem becomes more nonlinear; however, the parameter window to observe the nonlinearity is limited, because if we increase \(\widehat{q}\) too much, then we get wave breaking and the numerical scheme breaks down. Hence we can only realistically model weakly nonlinear situations with this scheme, which we consider in Figs. 7 and 8 with \(\widehat{q}=0.05\,\textrm{m}\). In these figures, the spatial resolution has been increased to \(N=M=400\) to give converged results.

Fig. 7
figure 7

Plots of the nonlinear vessel displacement from the linear result \(q(t)-q^\textrm{linear}(t)\) and the nonlinear Lagrangian coordinate value at the baffle difference \(a_B(t)-a_B^\textrm{linear}(t)\) for the parameters in (5.50) with \(L_1=L_2=0.5\,\textrm{m}\), \(\beta =0.2,\textrm{sm}^{-1}\) and \(\widehat{q}=0.05\,\textrm{m}\) and with the resolution \(N=M=400\). Here t has units of s while q and \(a_B\) have units of m

Full size image

In Fig. 7, we consider the evolutions of q(t) and \(a_B(t)\) where we have subtracted off the equivalent linear solution functions. The results show small \(O(\widehat{q}^2)\) corrections to these values, with higher frequency oscillations appearing for the duration of the simulation. We saw in Fig. 2 that these higher frequency modes typically have faster decay rates than the lowest frequency mode and so these modes decay away as time evolves. The nonlinear terms grow in magnitude over \(t\in [0,50]\,\textrm{s}\) before decaying as the porous baffle removes the energy from the system.

Fig. 8
figure 8

Free-surface profiles h(x, t) for the case in Fig. 7 at \(t=12.5, 25.0, 37.5, 50.0, 62.5, 75.0, 87.5\) and \(100\,\textrm{s}\), respectively and with the resolution \(N=M=400\). Here h and x have units of m

Full size image

The weakly nonlinear free-surface profiles in Fig. 8 also show the presence of nonlinear oscillations, and these appear to persist throughout the whole simulation.

Now that the numerical scheme is validated, and we go on to highlight an interesting mode switching phenomena in the next section, before investigating the effects on the system of incorporating a baffle with time-dependent porosity.

5.2 Mode switching phenomena as \(H\rightarrow 0\)

In the zero-baffle problem considered by [44], they found a curious feature of the system where the dominant behaviour in the system switches to ever higher frequency modes, as the fluid depth \(H\rightarrow 0\), in order that the correct dry vessel oscillation frequency is achieved in the \(H=0\) limit. In the porous baffle case,we would expect the same behaviour to occur, but it is less clear as to how the decay rate of the system would behave as this limit is approached. This is investigated in this section.

Fig. 9
figure 9

Schematic diagram of the bifilar pendulum problem considered by [44], with the addition of a porous baffle at \(x=L_1\), which demonstrates the model switching phenomena examined in Sect. 5.2. In the linear regime, this problem is equivalent to that in Fig. 1 with \(\nu =\dfrac{g}{l}(m_v+m_f)\)

Full size image

The problem [44] considered is slightly different to that in Fig. 1 and actually comprises of a vessel hung as a bifilar pendulum with string lengths l, see Fig. 9, where here q(t) denotes the angle of the string to the vertical. However, in the linear regime, where this mode switching phenomena is observable, both problems are identical if the linear spring coefficient is allowed to vary with \(m_f(H)\) via

$$\begin{aligned} \nu =\frac{g}{l}(m_v+m_f). \end{aligned}$$
(5.58)

We use (5.58) together with the system parameters

$$\begin{aligned}{} & {} \rho =1000\,\textrm{kg}\,\textrm{m}^{-3},~~~m_v=16\,\textrm{kg},~~~L_1=0.25\,\textrm{m},~~~L_2=0.25\,\textrm{m},~~~\nonumber \\{} & {} \widehat{q}=5\times 10^{-5}\,\textrm{m},~~~\beta =1.0\,\textrm{sm}^{-1}, \nonumber \\ \end{aligned}$$
(5.59)

with \(N=M=100\) and \(\Delta \tau =10^{-3}\,\textrm{s}\), which match those parameters used by [44] in their calculation. In this section, we consider an initial condition such that

$$\begin{aligned} q(0)= & {} \widehat{q}+\mathrm{c.c.},\\ x^{(1)}(A^{(1)},0)= & {} \xi _1A^{(1)},\\ x^{(2)}(A^{(2)},0)= & {} a_B+\xi _2A^{(2)},\\ w^{(j)}(A^{(j)},0)= & {} 0,~~\textrm{for}~~j=1,2\\ p(0)= & {} 0,\\ a_B(0)= & {} L_1. \end{aligned}$$

This initial condition is one which is more readily observed in an experimental setup and comprises of a condition where the vessel is displaced from its equilibrium position, extending the spring or placing the hanging string at a non-zero angle, and then being released from rest. The solution in this case comprises of a superposition of all the modes of the system, with differing amplitudes.

We conduct a series of numerical simulations and from each of these, we consider the values of \(\omega _r\) and \(\omega _i\) as a function of \(m_f/m_v\) (which is equivalent to varying H for fixed \(m_v,~\rho ,~L_1+L_2\)) in Fig. 10.

In this figure, the five black lines signify the values of the five lowest frequency modes found by solving the characteristic equation (3.22), while the circles are estimates taken from the numerical simulations. The dashed line is the dry vessel frequency \(\sqrt{g/l}\) and hence is the system frequency at \(m_f=0\).

To calculate the values of the circles, we compute the vessel motion q(t) from \(t=0\) to \(t=10\,\)s. We then use the |MATLAB| subroutine |findpeaks| to identify the local maxima of this function and then use each pair of successive maxima to estimate a value for \(\omega _r\) and \(\omega _i\). We denote the numerical estimates by \(\omega _r^\textrm{num}\) and \(\omega _i^\textrm{num}\), respectively. Finally, we average these values over all maxima in \([0,10]\,\)s to get the estimate value we plot in Fig. 10.

Fig. 10
figure 10

Plot of a the normal mode frequencies \(\omega _r(m_f/m_v)\) and b the normal mode decay rates \(\omega _i(m_f/m_v)\) for the system parameters given (5.59). The black lines give the exact values from solving the characteristic equation (3.22) while the circles are the results of the numerical simulations. Here \(m_v\) and \(m_f\) have units kg and \(\omega _r,\omega _i\) have units rad s\(^{-1}\)

Full size image

These numerical results show the frequency of the simulations switching from the mode labelled 1 to the mode labelled 2 around \(m_f/m_v\approx 0.6\). The peculiar feature of the result here is that this transition does not occur exactly at the point where the two \(\omega _i\) values intersect. The numerical results follow mode 1 beyond this point \((m_f/m_v\approx 0.7\)) and then switch. What this switching actually amounts to is the time-dependent amplitude of the modes switching dominance, such that mode 2 has the largest amplitude for \(m_f/m_v\lesssim 0.5\), as the numerical solution is a superposition of all these modes. As \(m_f/m_v\) is reduced below 0.5, eventually the numerical results agree with the dry vessel result given by the dashed line. The decay rate of the solution reduces as \(m_v/m_f\rightarrow 0\), but very close to zero \((m_f/m_v\approx 0.04)\); there is a small increase in \(\omega _i\) before going to zero in the dry vessel limit.

Fig. 11
figure 11

Plot of the vessel displacement q(t) for the system parameters in (5.59) for a \(m_f/m_v=1\), b 0.5 and c 0.25. The black lines are the result of the numerical simulations, while the red dashed lines are the exact linear result for the mode labelled 1 in Fig. 10a, b and for the mode labelled 2 Fig. 10c. Here t has units s and q has units m

Full size image

This mode switching in the function q(t) can be seen in Fig. 11. In Fig. 11a, the value of \(m_f/m_v=1.0\) and it is clear that the frequency and decay rate agree very well with the exact linear result of mode 1, given by the red dashed line. For \(m_f/m_v=0.5\) in Fig. 11b, we are in the transition region between the two modes and clearly there are oscillations of a shorter wavelength (larger \(\omega _r\)) emerging, but there is a modulation similar to the frequency of the mode 1 result. Then at \(m_f/m_v=0.25\) in Fig. 11c, it is clear that both \(\omega _r\) is larger and \(\omega _i\) is smaller and in this figure, the red dashed line gives the exact result for mode 2, showing excellent agreement.

Such a switching phenomena could be significant in oscillating systems where the fluid is slowly being drained out. In such cases, being able to change the porosity of the baffle remotely might then be desirable, in order to control the system. In the next section, we consider baffles with time-dependent porosity to try to understand how such systems behave, and whether they allow for the system to be controlled.

5.3 Time-dependent baffle porosity

In this section, we again consider the system from Fig. 1, but we investigate the effect of prescribing the porosity of the baffle to vary with time. Such a baffle could consist of a regular holed slat screen [29], where the holes are mechanically opened and closed in some prescribed manner. The interest in this problem is to try and understand how the system behaves, with the main interest in whether the decay rate of the system can be increased from the maximum decay rate for the lowest frequency mode, by periodically oscillating the baffle’s porosity.

For the results in this section, we again consider the system parameters (5.50) with \(L_1=L_2=0.5\,\textrm{m}\) and \(\widehat{q}=5\times 10^{-4}\,\textrm{m}\). We consider five periodic forms for

$$\begin{aligned} \beta (\tau )=\left\{ \begin{array}{ll} 0 &{} \tau < T_\textrm{on}\\ \beta _{1-5}(\tau ) &{} \tau \ge T_\textrm{on} \end{array} \right. \end{aligned}$$
(5.60)

where

$$\begin{aligned} \beta _1(\tau )=\tanh ^{-1}\left[ \frac{1}{2}\left( 1-\cos \left( \Omega \left( \tau -T_\textrm{on}\right) \right) \right) \right] ,\end{aligned}$$
(5.61)
$$\begin{aligned} \beta _{2-5}(\tau )=\frac{A}{2}\left( 1-\cos \left( \Omega \left( \tau -T_\textrm{on}\right) \right) \right) , \end{aligned}$$
(5.62)

with the constant amplitudes \(A=A_2=2\,\mathrm{s\,m}^{-1}\), \(A_3=1\,\mathrm{s\,m}^{-1}\), \(A_4=4\,\mathrm{s\,m}^{-1}\) and \(A_5=0.5\,\mathrm{s\,m}^{-1}\).

Fig. 12
figure 12

Plot of different porosity functions \(\beta _{1-5}(\tau )\) which are labelled from 1 to 5, respectively. Here \(\tau \) has units s, and \(\beta \) has units sm\(^{-1}\)

Full size image

The forms of these functions are plotted in Fig. 12. The function \(\beta _1(\tau )\) is chosen as it uses the whole range of value of \(\beta \in [0,\infty )\), while for \(\beta _{2-5}(\tau )\), the time variations are a simpler periodic function with constant amplitude and hence are more likely to be manufacturable and implementable.

Fig. 13
figure 13

Contour plot of the numerical decay rate \(\omega _i^\textrm{num}\) in the \((\Omega ,T_\textrm{on})\)-plane for the system parameters (5.50) with \(L_1=L_2=0.5\,\textrm{m}\) and \(\widehat{q}=5\times 10^{-4}\,\textrm{m}\) and porosity function \(\beta _1(\tau )\). The black contours give the value \(\omega _i=\omega _i^\textrm{max}\) which is the maximum linear decay rate for the system if the baffle has \(\beta =\beta ^\textrm{max}\). Here \(\Omega \) has units s\(^{-1}\), \(T_\textrm{on}\) has units s and \(\omega _i\) has units rad s\(^{-1}\)

Full size image

In Fig. 13, we consider the numerical decay rate \(\omega _i^\textrm{num}\) for simulations with \(\beta =\beta _1(\tau )\), in the \((\Omega ,T_\textrm{on})\)-plane. The values of \(\omega ^\textrm{num}\) are calculated as in Sect. 5.2 except here we average over the time period \(\tau \in [0,100]\,\textrm{s}\). The black contour corresponds to the maximum linear decay, \(\omega _i^\textrm{max}=0.03218\,\mathrm{rad\,s}^{-1}\), rate for a fixed baffle with \(\beta =\beta ^\textrm{max}=0.508\,\mathrm{s\,m}^{-1}\). The lighter regions (green-yellow) signify parameter regions where the system decay rate is above \(\omega _i^\textrm{max}\), i.e. the system decays faster than would be seen in a system with a fixed baffle with \(\beta =\beta ^\textrm{max}\). What this figure shows is at low frequencies \(\Omega \lesssim 8\,\textrm{s}^{-1}\), there is some dependence on the \(T_\textrm{on}\) value when the baffle porosity switches on, but above this frequency, the results are independent of this value. The system results fall into stripes of regions with \(\omega _i^\textrm{num}>\omega _i^\textrm{max}\) and \(\omega _i^\textrm{num}<\omega _i^\textrm{max}\). There is no pattern for the sizes of these regions, but it appears that the peak values of \(\omega _i^\textrm{num}>\omega _i^\textrm{max}\) increase with \(\Omega \). The largest peaks we find have \(\omega _i^\textrm{num}\approx 0.057\,\mathrm{rad\,s}^{-1}\) around \(\Omega =25\,\textrm{s}^{-1}\), which is approximately to \(80\%\) larger than \(\omega _i^\textrm{max}\).

What we believe is happening here is a resonance between \(\beta (\tau )\) and the frequency \(\omega _r(\tau )\) of the dominant mode in the system. If the two values of these are such that the velocity of the fluid is relatively low at the baffle when the baffle is closed or partially open, then very little energy is removed from the system (hence a low \(\omega _i^\textrm{num}\)), whereas if the velocity at the baffle is high at these times, then the energy removed is larger (hence higher \(\omega _i^\textrm{num}\)).

Fig. 14
figure 14

Plot of the numerical decay rate \(\omega _i^\textrm{num}\) as a function of the time-dependent porosity function frequency \(\Omega \) from simulations with system parameters (5.50), \(L_1=L_2=0.5\,\textrm{m}\), \(T_\textrm{on}=2\,\textrm{s}\) and porosity functions a \(\beta _1(\tau )\), b \(\beta _2(\tau )\), c \(\beta _3(\tau )\), d \(\beta _4(\tau )\) and e \(\beta _5(\tau )\). The black dashed line gives the value \(\omega _i=\omega _i^\textrm{max}\) which is the maximum linear decay rate for the system if the baffle has \(\beta =\beta ^\textrm{max}\). Here \(\Omega \) has units s\(^{-1}\), and \(\omega _i\) has units rad s\(^{-1}\)

Full size image

In Fig. 14, we consider plots of \(\omega _i^\textrm{num}(\Omega )\) for fixed \(T_\textrm{on}=2\,\textrm{s}\) for \(\beta _1(\tau )\) to \(\beta _5(\tau )\). For the \(\beta _1(\tau )\) case in Fig. 14a, this corresponds to a horizontal slice though Fig. 13. This figure shows clearly those values of \(\Omega \) where \(\omega _i^\textrm{num}>\omega _i^\textrm{max}\) and it is clear that the magnitude of the peak decay rate increases with \(\Omega \). When we consider \(\beta _2(\tau )\) in Fig. 14b, we find that overall, the decay rate is lower, with no significant frequencies with \(\omega _i^\mathrm{}>\omega _i^\textrm{max}\) until \(\Omega >10\,\textrm{s}^{-1}\), and even then, these regions are small. It is again true that the magnitude of the peak decay rate increases with \(\Omega \). For \(\beta _3\) and \(\beta _4\) in panels (c) and (d), the amplitude of the porosity function is, on the whole, smaller and larger, respectively, than \(\beta _2\). What is curious is that the smaller amplitude case in (c) has significant values of \(\Omega \) where \(\omega _i^\textrm{num}>\omega _i^\textrm{max}\), whereas the larger amplitude function in (d) has predominantly \(\omega _i^\textrm{num}<\omega _i^\textrm{max}\). The reason for this could be down to the fact that \(\beta _1(\tau )\) and \(\beta _3(\tau )\) have a similar asymptotic behaviour close to \(\tau -T_\textrm{on}=2n\pi /\Omega \), \(n\in \mathbb {Z}\), as can be seen in Fig. 12. Overall, the peak values of \(\omega _i^\textrm{num}\) are smaller in Fig. 14c than Fig. 14a, and so opening up the baffle completely (\(\beta \rightarrow \infty \)) is important, but the most significant aspect is the rate at which the baffle is opened from the closed (\(\beta =0\)) position. In Fig. 14e where \(A=A_5=0.5\,\mathrm{s\,m}^{-1}\), we see that the decay rate drops again and \(\omega _i^\textrm{num}<\omega _i^\textrm{max}\) for all values of \(\Omega \) here.

Fig. 15
figure 15

Plot of the numerical decay rate \(\omega _i^\textrm{num}\) as a function of the time-dependent porosity function amplitude A for the system parameter (5.50), \(L_1=L_2=0.5\,\textrm{m}\) and the porosity function \(\beta _{2-5}(\tau )\) in (5.62) with a \(\Omega =5\,\textrm{s}^{-1}\) and b \(\Omega =25\,\textrm{s}^{-1}\). The black dashed line gives the value \(\omega _i=\omega _i^\textrm{max}\) which is the maximum linear decay rate for the system if the baffle has \(\beta =\beta ^\textrm{max}\). Panels c and d give plots of the corresponding \(q(\tau )\) figures for cases \((\Omega ,A)=(0,0.508)\) - red dashed line, (5, 1.2) - blue dot-dashed line and (25, 2) - black line. Here A has units sm\(^{-1}\), \(\omega _i\) has units rad s\(^{-1}\), \(\tau \) has units of s and q has units of m

Full size image

While the porosity function \(\beta _1\) appears to perform the best at controlling the decay rate of the coupled system, it is unlikely that such a baffle could be manufactured which has \(\beta \in [0,\infty )\), and it is more likely that a mechanical system with a more sinusoidal porosity would be possible. To this end, we examine the porosity function (5.62), but we allow A to vary in Fig. 15 for \(T_\textrm{on}=2\,\textrm{s}\) and (a) \(\Omega =5\,\textrm{s}^{-1}\) and (b) \(\Omega =25\,\textrm{s}^{-1}\). The results from Fig. 14 suggested that there is an amplitude value for which \(\omega _i^\textrm{num}\) is maximized for each \(\Omega \), and this appears to be the case in Fig. 15. In panel (a), we find \(\omega _i^\textrm{num}>\omega _i^\textrm{max}\) for \(A\in [0.7,1.76]\,\textrm{sm}^{-1}\) with maximum decay rate \(\omega _i^\textrm{num}=0.0358\,\mathrm{rad\,s}^{-1}\) at \(A=1.2\,\mathrm{s\,m}^{-1}\). For the more rapidly varying baffle in Fig. 15b, the range of amplitudes where \(\omega _i^\textrm{num}>\omega _i^\textrm{max}\) increases to \(A\in [0.64,6.40]\,\mathrm{s\,m}^{-1}\) and the maximum value \(\omega _i^\textrm{num}=0.059\,\mathrm{rad\,s}^{-1}\) occurs at \(A=2\,\mathrm{s\,m}^{-1}\). In this case, the maximum decay rate is \(86\%\) larger than the dashed line result. In Fig. 15c, we consider the evolution of \(q(\tau )\) for the case when \(\beta =\beta ^\textrm{max}\) and the two amplitudes giving the maximum values of \(\omega _i^\textrm{num}\) in panels (a) and (b). The results demonstrate the faster decay rate of the time-dependent baffle, in particular highlighting the significant decay of the system for \(\Omega =25\,\textrm{s}^{-1}\) (black line). Panel (d) gives a zoomed in plot of the final 50 seconds of the simulation where the changes in vessel amplitude are more clearly observed.

Fig. 16
figure 16

Contour plot of the numerical decay rate \(\omega _i^\textrm{num}\) as a function of the time-dependent porosity function parameters \((\Omega ,A)\) for the system parameters (5.50), \(L_1=L_2=0.5\,\textrm{m}\) and \(T_\textrm{on}=2\textrm{s}\). The black contours give the value \(\omega _i=\omega _i^\textrm{max}\) which is the maximum linear decay rate for the system if the baffle has \(\beta =\beta ^\textrm{max}\). Here \(\Omega \) has units s\(^{-1}\), A has units sm\(^{-1}\) and \(\omega _i\) has units rad s\(^{-1}\)

Full size image

When we consider a larger range of \((\Omega ,A)\) values in Fig. 16, we see that the largest decay rates are concentrated in small regions of \(\Omega \) around \(\Omega =15\,\textrm{s}^{-1}\) and \(\Omega =25\,\textrm{s}^{-1}\) with the peak amplitudes close to \(A=2\,\mathrm{s\,m}^{-1}\), akin to the Fig. 15b result. In addition to the small regions of large decay rates, there are also larger regions, which are periodic in \(\Omega \), for amplitudes \(A\in [1,2]\,\mathrm{m\,s}^{-1}\). These regions are more akin to the result in Fig. 15a where the maximum decay rate is only about 20–\(25\%\) larger than the dashed line. What these results show is that it is entirely possible to control the decay rate of the coupled sloshing system in Fig. 1 using a time-dependent baffle, at least at the lower fluid velocities considered here, where (2.14) is valid. Clearly, changing the porosity value of the baffle from one constant value to another constant value is one way to control the system, but if you wish to damp out the system oscillations faster than would occur with a fixed baffle, then periodically oscillating the porosity of the baffle is the best approach, although the amount of variation and the frequency of the variation depends carefully upon the parameters of the system.

6 Conclusions

In this work, we considered the coupled vessel-fluid dynamic system. In the system, a rectangular vessel partially filled with an inviscid incompressible fluid was allowed to move in a rectilinear motion connected to a linear spring, and the fluid was allowed to slosh back and forth in the vessel. The fluid and the vessel exhibit forces on one another, giving complex coupled motions. The main focus of this paper was to model these complex motions when a vertical, surface-piercing, porous baffle is inserted into the vessel, which was found to extract energy from the system causing the motion to decay in time. The fluid transmission condition at the baffle was modelled using a nonlinear Darcy–Forchheimer model to more accurately deal with the nonlinearity of the porous baffle in weakly nonlinear scenarios.

The complex motion was determined numerically via a fast and efficient numerical scheme which approximated the fluid layer as a shallow-water fluid and used a Lagrangian Particle Path approach. This approach was used together with a symplectic time integration scheme based on the implicit-mid-point rule as this approach preserved the energy partition between the vessel and the fluid and effectively captured the dissipation. The implicit nature of the scheme also allowed for larger time steps than an explicit scheme, such as Störmer–Verlet. Using an implicit scheme is beneficial because a larger time step can be used (typically 10–100 times larger than for an explicit scheme) which, despite the added iterations of the implicit scheme, generally make it faster than an explicit scheme.

Results were presented for a single baffle system, which splits the vessel into two compartments, in both the linear and weakly nonlinear regimes and excellent agreement was found with the exact linear solution for various test cases. Simulations were presented for a scenario where the baffle was assumed to mechanically open and close, such that its porosity properties varied in a time-periodic manner. It was shown that under such circumstances, the average decay rate of the system over a fixed period of time can be larger than the maximum decay rate for the lowest frequency solution for a fixed porosity baffle. This showed that time-dependent baffles are an effective mechanism to control the decay rate of the coupled system.