Response of SH waves in inhomogeneous functionally graded orthotropic layered structure with interfacial imperfections

Abstract

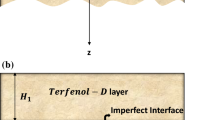
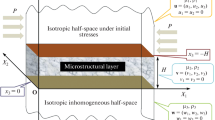
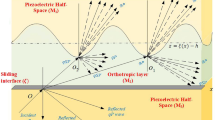
The current work examines shear wave propagation in inhomogeneous functionally graded orthotropic media (FGOM) with imperfect contacts. The intermediate stratum is assumed to be viscous FGOM, while the upper and lower FGOMs have been endowed with initial stress. Closed-form displacement fields have been derived for both the layers and half space. The derivation process involves employing the interfacial stress-displacement continuity condition, which accounts for sliding and loosely bonded parameters, in conjunction with the requirement of a stress-free upper interface and a bounded lower half space. Special cases of previously published results in the literature were used to validate the analytical form of the dispersion relation. The study also includes a mathematical analysis of the dispersion equation as well as numerical computations for the presented geophysical model to characterize the impact of initially stressed parameters, inhomogeneity parameters, dissipation factor, and the effect of interface imperfectness on shear wave velocity. Notably, the study emphasizes the effect of sliding interface on the propagation of SH waves at the lower contact. The current finding adds to our understanding of shear wave propagation dynamics in elastic inhomogeneous functionally graded materials, which can help with earthquake engineering design and execution.

Appendix: Details of the mathematical expressions used in the dispersion equation

${r}_{1}={k}_{1}^{2}{\rho }_{2}{c}^{2}-{k}_{1}^{2}{\delta }^{2}{\rho }_{2}{c}^{2}-{k}_{1}^{2}{\xi }_{66}+{k}_{1}^{2}{\delta }^{2}{\xi }_{66}+2{k}_{1}^{2}{\zeta }_{66}\omega \delta,$

${r}_{2}=2{k}_{1}^{2}\delta {\rho }_{2}{c}^{2}-2{k}_{1}^{2}\delta {\xi }_{66}-{\zeta }_{66}\omega {k}_{1}^{2}+{k}_{1}^{2}{\delta }^{2}{\zeta }_{66}\omega,$

${r}_{3}={\xi }_{44}$, ${r}_{4}={\xi }_{44}{Q}_{1}$, ${r}_{5}=4{r}_{2}+{\beta }^{2}{r}_{3}$, ${r}_{6}=4{r}_{2}+{\beta }^{2}{r}_{4}$, ${r}_{7}=4{r}_{3}$, ${r}_{8}=4{r}_{4},$

${r}_{9}=\frac{{r}_{5}{r}_{7}+{r}_{6}{r}_{8}}{{r}_{7}^{2}+{r}_{8}^{2}}$, ${r}_{10}=\frac{-{r}_{5}{r}_{8}+{r}_{6}{r}_{7}}{{r}_{7}^{2}+{r}_{8}^{2}},$ ${m}_{2}^{\prime}=\pm \sqrt{\frac{\sqrt{\left({r}_{9}^{2}+{r}_{10}^{2}\right)}+{r}_{9}}{2}},$

$${\chi }_{11}={a}_{1}\left[1+\sin({\alpha }_{1}{H}_{2})\right]\left\{\frac{{m}_{1}{e}^{{-m}_{1}{H}_{2}}}{\sqrt{1+\sin({\alpha }_{1}{H}_{2})}}+\frac{{\alpha }_{1}\cos({\alpha }_{1}{H}_{2}){e}^{{-m}_{1}{H}_{2}}}{{2\left[1+\sin({\alpha }_{1}{H}_{2})\right]}^{\frac{3}{2}}}\right\},$$

$${\chi }_{12}={a}_{1}\left[1+\sin({\alpha }_{1}{H}_{2})\right]\left\{\frac{{-m}_{1}{e}^{{m}_{1}{H}_{2}}}{\sqrt{1+\sin({\alpha }_{1}{H}_{2})}}+\frac{{\alpha }_{1}\cos({\alpha }_{1}{H}_{2}){e}^{{m}_{1}{H}_{2}}}{{2\left[1+\sin({\alpha }_{1}{H}_{2})\right]}^{\frac{3}{2}}}\right\},$$

$${\chi }_{21}={a}_{1}\left[1+\sin({\alpha }_{1}{H}_{1})\right]\left\{\frac{{m}_{1}{e}^{{-m}_{1}{H}_{1}}}{\sqrt{1+\sin({\alpha }_{1}{H}_{1})}}+\frac{{\alpha }_{1}\cos({\alpha }_{1}{H}_{1}){e}^{{-m}_{1}{H}_{1}}}{{2\left[1+\sin({\alpha }_{1}{H}_{1})\right]}^{\frac{3}{2}}}\right\},$$

$${\chi }_{22}={a}_{1}\left[1+\sin({\alpha }_{1}{H}_{1})\right]\left\{\frac{{-m}_{1}{e}^{{m}_{1}{H}_{1}}}{\sqrt{1+\sin({\alpha }_{1}{H}_{1})}}+\frac{{\alpha }_{1}\cos({\alpha }_{1}{H}_{1}){e}^{{m}_{1}{H}_{1}}}{{2\left[1+\sin({\alpha }_{1}{H}_{1})\right]}^{\frac{3}{2}}}\right\},$$

$${\chi }_{23}=-\left({\xi }_{44}+i\omega {\zeta }_{44}\right)\left[1+\mathrm{sin}\left({\alpha }_{1}{H}_{2}\right)\right]\left\{\frac{{-m}_{2}\mathrm{sin}\left({m}_{2}{H}_{1}\right)}{\sqrt{1-\mathrm{sin}\left(\beta {H}_{1}\right)}}-\frac{\beta \mathrm{cos}\left(\beta {H}_{1}\right)\mathrm{cos}\left({m}_{2}{H}_{1}\right)}{{2\left[1-\mathrm{sin}\left(\beta {H}_{1}\right)\right]}^{\frac{3}{2}}}\right\},$$

$${\chi }_{24}=-\left({\xi }_{44}+i\omega {\zeta }_{44}\right)\left[1+\mathrm{sin}\left({\alpha }_{1}{H}_{2}\right)\right]\left\{\frac{{m}_{2}\mathrm{cos}\left({m}_{2}{H}_{1}\right)}{\sqrt{1-\mathrm{sin}\left(\beta {H}_{1}\right)}}+\frac{\beta \mathrm{cos}\left(\beta {H}_{1}\right)\mathrm{sin}\left({m}_{2}{H}_{1}\right)}{{2\left[1-\mathrm{sin}\left(\beta {H}_{1}\right)\right]}^{\frac{3}{2}}}\right\},$$

$$ \begin{aligned} \chi _{{31}} & = a_{1} \left( {1 - \Omega } \right)\left[ {1 + {\text{sin}}\left( {\alpha _{1} H_{1} } \right)} \right]\left\{ {\frac{{m_{1} e^{{ - m_{1} H_{1} }} }}{{\sqrt {1 + {\text{sin}}\left( {\alpha _{1} H_{1} } \right)} }} + \frac{{\alpha _{1} {\text{cos}}\left( {\alpha _{1} H_{1} } \right)e^{{ - m_{1} H_{1} }} }}{{2\left[ {1 + {\text{sin}}\left( {\alpha _{1} H_{1} } \right)} \right]^{{\frac{3}{2}}} }}} \right\} \\ & \quad - \frac{{ikc}}{{c_{2} }}\Omega \left( {\xi _{{44}} + i\omega \zeta _{{44}} } \right)\left( {1 - {\text{sin}}\left( {\beta H_{1} } \right)} \right)\left( {\frac{{e^{{ - m_{1} H_{1} }} }}{{\sqrt {1 + {\text{sin}}\left( {\alpha _{1} H_{1} } \right)} }}} \right), \\ \end{aligned} $$

$$ \begin{aligned} \chi _{{32}} & = a_{1} \left( {1 - \Omega } \right)\left[ {1 + {\text{sin}}\left( {\alpha _{1} H_{1} } \right)} \right]\left\{ {\frac{{ - m_{1} e^{{ - m_{1} H_{1} }} }}{{\sqrt {1 + {\text{sin}}\left( {\alpha _{1} H_{1} } \right)} }} + \frac{{\alpha _{1} {\text{cos}}\left( {\alpha _{1} H_{1} } \right)e^{{m_{1} H_{1} }} }}{{2\left[ {1 + {\text{sin}}\left( {\alpha _{1} H_{1} } \right)} \right]^{{\frac{3}{2}}} }}} \right\} \\ & \quad - \frac{{ikc}}{{c_{2} }}\Omega \left( {\xi _{{44}} + i\omega \zeta _{{44}} } \right)\left( {1 - {\text{sin}}\left( {\beta H_{1} } \right)} \right)\left( {\frac{{e^{{m_{1} H_{1} }} }}{{\sqrt {1 + {\text{sin}}\left( {\alpha _{1} H_{1} } \right)} }}} \right), \\ \end{aligned} $$

$${\chi }_{33}=-\frac{ikc}{{c}_{2}}\Omega \left({\xi }_{44}+i\omega {\zeta }_{44}\right)\left(1-\mathrm{sin}\left(\beta {H}_{1}\right)\right)\left(\frac{\mathrm{cos}({m}_{2}{H}_{1)}}{\sqrt{1-\mathrm{sin}\left(\beta {H}_{1}\right)}}\right),$$

$${\chi }_{34}=-\frac{ikc}{{c}_{2}}\Omega \left({\xi }_{44}+i\omega {\zeta }_{44}\right)\left(1-\mathrm{sin}\left(\beta {H}_{1}\right)\right)\left(\frac{\mathrm{sin}({m}_{2}{H}_{1)}}{\sqrt{1-\mathrm{sin}\left(\beta {H}_{1}\right)}}\right),$$

${\chi }_{43}=-({\xi }_{44}+i\omega {\zeta }_{44})\frac{\beta }{2},$ ${\chi }_{44}=({\xi }_{44}+i\omega {\zeta }_{44}){m}_{2},$ ${\chi }_{45}=-{b}_{1}(1-\eta )\left(\frac{{\alpha }_{2}-2{m}_{1}}{2}\right)$

${\chi }_{53}=-\eta ({\xi }_{44}+i\omega {\zeta }_{44}){m}_{2}+(1-\eta )kF,$ ${\chi }_{54}=\eta ({\xi }_{44}+i\omega {\zeta }_{44}){m}_{2},$ ${\chi }_{55}=\left(1-\eta \right){k}_{1}F$

$${\chi^{\prime}}_{23}=-\left[1+\mathrm{sin}\left({\alpha }_{1}{H}_{2}\right)\right]{\xi }_{44}\left\{\frac{-{m}_{2}^{\prime}\mathrm{sin}\left({{m}^{\prime}}_{2}{H}_{1}\right)}{\sqrt{1-\mathrm{sin}\left(\beta {H}_{1}\right)}}-\frac{\beta \mathrm{cos}\left(\beta {H}_{1}\right)\mathrm{cos}\left({m}_{2}^{\prime}{H}_{1}\right)}{{2\left[1-\mathrm{sin}\left(\beta {H}_{1}\right)\right]}^{\frac{3}{2}}}\right\},$$

$${\chi^{\prime}}_{24}=-\left[1+\mathrm{sin}\left({\alpha }_{1}{H}_{2}\right)\right]{\xi }_{44}\left\{\frac{{{m}^{\prime}}_{2}\mathrm{cos}\left({m}_{2}^{\prime}{H}_{1}\right)}{\sqrt{1-\mathrm{sin}\left(\beta {H}_{1}\right)}}+\frac{\beta \mathrm{cos}\left(\beta {H}_{1}\right)\mathrm{sin}\left({m}_{2}^{\prime}{H}_{1}\right)}{{2\left[1-\mathrm{sin}\left(\beta {H}_{1}\right)\right]}^{\frac{3}{2}}}\right\},$$

$$ \begin{aligned} \chi ^{\prime } _{{31}} & = a_{1} \left( {1 - \Omega } \right)\left[ {1 + {\text{sin}}\left( {\alpha _{1} H_{1} } \right)} \right]\left\{ {\frac{{m_{1} e^{{ - m_{1} H_{1} }} }}{{\sqrt {1 + {\text{sin}}\left( {\alpha _{1} H_{1} } \right)} }} + \frac{{\alpha _{1} {\text{cos}}\left( {\alpha _{1} H_{1} } \right)e^{{ - m_{1} H_{1} }} }}{{2\left[ {1 + {\text{sin}}\left( {\alpha _{1} H_{1} } \right)} \right]^{{\frac{3}{2}}} }}} \right\} \\ & \quad - \frac{c}{{c_{2} }}\Omega \left( {k_{1} \delta \xi _{{44}} - \omega k_{1} \zeta _{{44}} } \right)\left( {1 - {\text{sin}}\left( {\beta H_{1} } \right)} \right)\left( {\frac{{e^{{ - m_{1} H_{1} }} }}{{\sqrt {1 + {\text{sin}}\left( {\alpha _{1} H_{1} } \right)} }}} \right), \\ \end{aligned} $$

$$ \begin{aligned} \chi ^{\prime } _{{32}} & = a_{1} \left( {1 - \Omega } \right)\left[ {1 + {\text{sin}}\left( {\alpha _{1} H_{1} } \right)} \right]\left\{ {\frac{{ - m_{1} e^{{ - m_{1} H_{1} }} }}{{\sqrt {1 + {\text{sin}}\left( {\alpha _{1} H_{1} } \right)} }} + \frac{{\alpha _{1} {\text{cos}}\left( {\alpha _{1} H_{1} } \right)e^{{m_{1} H_{1} }} }}{{2\left[ {1 + {\text{sin}}\left( {\alpha _{1} H_{1} } \right)} \right]^{{\frac{3}{2}}} }}} \right\} \\ & \quad - \frac{c}{{c_{2} }}\Omega \left( {k_{1} \delta \xi _{{44}} - \omega k_{1} \zeta _{{44}} } \right)\left( {1 - {\text{sin}}\left( {\beta H_{1} } \right)} \right)\left( {\frac{{e^{{m_{1} H_{1} }} }}{{\sqrt {1 + {\text{sin}}\left( {\alpha _{1} H_{1} } \right)} }}} \right), \\ \end{aligned} $$

$${\chi^{\prime}}_{33}=-\frac{c}{{c}_{2}}\Omega \left({k}_{1}\delta {\xi }_{44}-\omega {k}_{1}{\zeta }_{44}\right)\left(1-\mathrm{sin}\left(\beta {H}_{1}\right)\right)\left(\frac{\mathrm{cos}({m}_{2}^{\prime}{H}_{1)}}{\sqrt{1-\mathrm{sin}\left(\beta {H}_{1}\right)}}\right),$$

$${\chi^{\prime}}_{34}=-\frac{c}{{c}_{2}}\Omega \left({k}_{1}\delta {\xi }_{44}-\omega {k}_{1}{\zeta }_{44}\right)\left(1-\mathrm{sin}\left(\beta {H}_{1}\right)\right)\left(\frac{\mathrm{sin}({m}_{2}^{\prime}{H}_{1)}}{\sqrt{1-\mathrm{sin}\left(\beta {H}_{1}\right)}}\right),$$

${\chi^{\prime}}_{43}=-{\xi }_{44}\frac{\beta }{2}$ , ${\chi^{\prime}}_{44}={\xi }_{44}{m}_{2}$ , ${\chi^{\prime}}_{53}=-\eta {\xi }_{44}{{m}^{\prime}}_{2}+\left(1-\eta \right){k}_{1}F$ , ${\chi^{\prime}}_{54}=\eta {\xi }_{44}{m^{\prime}}_{2}.$