Skip to main content
SpringerLink
Log in

Numerical identification of the fractal orders in the generalized nonlocal elastic model

  • Published:
Journal of Engineering Mathematics Aims and scope Submit manuscript

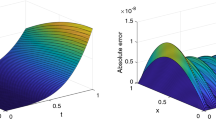
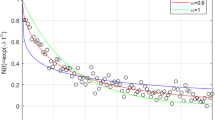
Abstract

This article deals with numerical solution and identification of the fractal orders for the generalized nonlocal elastic model. Based on the collocation-finite difference scheme for the forward operator, a regularized method is proposed for solving of the forward problem with the aid of Tikhonov regularization. This method is non-iterative and independent of preconditioning of the coefficient matrix, which gives a simple and direct approach to numerical solution of the nonlocal elastic model. The identification problem of determining the fractal orders is solved by using the optimal perturbation algorithm with additional observations at some measurable points. The inversion solutions with noisy data give good approximations to the exact orders demonstrating the validity of the numerical algorithms.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3

Similar content being viewed by others

References

  1. Eringen AC (2002) Nonlocal continuum field theories. Springer, New York

    MATH  Google Scholar 

  2. Eringen AC (2006) Nonlocal continuum mechanics based on distributions. Int J Eng Sci 44(3–4):141147

    MathSciNet  Google Scholar 

  3. Li C, Deng WH, Shen XQ (2014) Exact solutions and their asymptotic behaviors for the averaged generalized fractional elastic models. Commun Theor Phys 62:443–450

    Article  MathSciNet  MATH  Google Scholar 

  4. Majumdar SN, Bray AJ (2001) Spatial persistence of fluctuating interfaces. Phys Rev Lett 86:3700

    Article  Google Scholar 

  5. Benson DA (1998) The fractional advection-dispersion equation: development and application. Dissertation of Doctorial Degree, University of Nevada, Reno

  6. Carreras BA, Lynch VE, Zaslavsky GM (2001) Anomalous diffusion and exit time distribution of particle tracers in plasma turbulence models. Phys Plasmas 8:5096–5103

    Article  Google Scholar 

  7. Zaslavsky GM, Stevens D, Weitzner H (1993) Self-similar transport in incomplete chaos. Phys Rev E 48:1683–1694

    Article  MathSciNet  Google Scholar 

  8. Silling SA (2000) Reformulation of elasticity theory for discontinuities and long-range force. J Mech Phys Solids 48:175–209

    Article  MathSciNet  MATH  Google Scholar 

  9. Silling SA, Lehoucq RB (2010) Peridynamic theory of solid mechanics. Adv Appl Mech 44:73–168

    Article  Google Scholar 

  10. Askari E, Bobaru F, Lehoucq RB, Parks ML, Silling SA, Weckner O (2008) Peridynamics for multiscale materials modeling. J Phys Conf Ser 125:012078

    Article  Google Scholar 

  11. Gunzburger M, Lehoucq RB (2010) A nonlocal vector calculus with application to nonlocal boundary value problems. Multiscale Model Simul 8:1581–1598

    Article  MathSciNet  MATH  Google Scholar 

  12. Saravani M (2018) Continuum modes of nonlocal field theories. Class Quantum Gravity 35:074001

    Article  MathSciNet  MATH  Google Scholar 

  13. Silling SA, Lehoucq RB (2008) Convergence of peridynamics to classical elasticity theory. J Elast 93:13–37

    Article  MathSciNet  MATH  Google Scholar 

  14. Taloni A, Chechkin A, Klafter J (2010) Generalized elastic model yields a fractional Langevin equation description. Phys Rev Lett 104:160602

    Article  Google Scholar 

  15. Taloni A, Chechkin A, Klafter J (2013) Generalized elastic model: fractional Langevin description, fluctuation relation and linear response. Math Modell Nat Phenom 8:127–143

    Article  MathSciNet  MATH  Google Scholar 

  16. Taloni A (2016) Kubo fluctuation relations in the generalized elastic model. Adv Math Phys 8:7502472

    MathSciNet  MATH  Google Scholar 

  17. Taloni A (2017) From the underdamped generalized elastic model to the single particle Langevin description. Mathmatics 5(3):5010003

    MATH  Google Scholar 

  18. Li Y, Peng MQ, He TH, Tian XG, Liao K (2022) A fractional dual-phase-lag generalized thermoelastic model of ultrashort pulse laser ablation with variable thermal material properties, vaporization and plasma shielding. Int J Thermal Sci 177:107556

    Article  Google Scholar 

  19. Rodriguez RF, Salinas-Rodriguez E, Fujioka J (2018) Fractoinal time fluctuations in viscoelasticity: a comparative study of correlations and elastic moduli. Entropy 20:28

    Article  Google Scholar 

  20. Roudbari MA, Jorshari TD, Lu CF, Ansari R, Kouzani A, Amabili M (2022) A review of size-dependent continuum mechanics models for micro- and nano-structures. Thin-Walled Struct 170:108562

    Article  Google Scholar 

  21. Du Q, Gunzburger M, Lehoucq K, Zhou K (2012) Analysis and approximation of nonlocal diffusion problems with volume constraints. SIAM Rev 54:667–696

    Article  MathSciNet  MATH  Google Scholar 

  22. Ervin VJ, Roop JP (2005) Variational formulation for the stationary fractional advection dispersion equation. Numer Methods Partial Differ Equ 22:667–696

    MathSciNet  Google Scholar 

  23. Wang H, Du N (2013) A superfast-preconditioned iterative method for steady-state space-fractional diffusion equation. J Comput Phys 240:49–57

    Article  MathSciNet  MATH  Google Scholar 

  24. Du N, Wang H, Wang C (2015) A fast method for a generalized nonlocal elastic model. J Comput Phys 297:72–83

    Article  MathSciNet  MATH  Google Scholar 

  25. Jia LL, Chen HZ, Wang H (2017) Mixed-type Galerkin variational principle and numerical simulation for a generalized nonlocal elastic model. J Sci Comput 71:660–681

    Article  MathSciNet  MATH  Google Scholar 

  26. Meerschaert MM, Tadjeran C (2004) Finite difference approximations for fractional advection-dispersion flow equations. J Comput Appl Math 172:65–77

    Article  MathSciNet  MATH  Google Scholar 

  27. Cheng J, Nakagawa J, Yamamoto M, Yamazaki T (2009) Uniqueness in an inverse problem for a one-dimensional fractional diffusion equation. Inverse Probl 25:115002

    Article  MathSciNet  MATH  Google Scholar 

  28. Ghazizadeh HR, Azimi A, Maerefat M (2012) An inverse problem to estimate relaxation parameter and order of fractionality in fractional single-phase-lag heat equation. Intl J Heat Mass Transf 55:2095–2101

    Article  Google Scholar 

  29. Li GS, Zhang DL, Jia XZ, Yamamoto M (2013) Simultaneous inversion for the space-dependent diffusion coefficient and the fractional order in the time-factional diffusion equation. Inverse Probl 29:065014

    Article  MATH  Google Scholar 

  30. Li ZY, Yamamoto M (2015) Uniqueness for inverse problems of determining orders of multi-term time-fractional derivatives of diffusion equation. Appl Anal 94:570–579

    Article  MathSciNet  MATH  Google Scholar 

  31. Janno J, Kinash N (2018) Reconstruction of an order of derivative and a source term in a fractional diffusion equation from final measurements. Inverse Probl 34:025007

    Article  MathSciNet  MATH  Google Scholar 

  32. Li ZY, Fujishiro K, Li GS (2020) Uniqueness in the inversion of distributed orders in ultraslow diffusion equations. J Comput Appl Math 369:112564

    Article  MathSciNet  MATH  Google Scholar 

  33. Alimov S, Ashurov R (2020) Inverse problem of determining an order of the Caputo time fractional derivative for a subdiffusion equation. J Inverse Ill-Posed Probl 28:651–658

    Article  MathSciNet  MATH  Google Scholar 

  34. Ashurov R, Umarov S (2022) An inverse problem of determining orders of systems of fractional pseudo-differential equations. Fract Calc Appl Anal 25:109–127

    Article  MathSciNet  MATH  Google Scholar 

  35. Yamamoto M (2021) Uniqueness in determining fractional orders of derivatives and initial values. Inverse Probl 37:095006

    Article  MathSciNet  MATH  Google Scholar 

  36. Chi GS, Li GS, Jia XZ (2011) Numerical inversions of a source term in the FADE with Dirichlet boundary condition using final ovservations. Comput Math Appl 62:1619–1626

    MathSciNet  MATH  Google Scholar 

  37. Chi GS, Li GS (2018) Numerical inversions for diffusion coefficients in two dimensional space fractional diffusion equation. Inverse Probl Sci Eng 26:996–1018

  38. Podlubny I (1999) Fractional differential equations. Academic, San Diego

    MATH  Google Scholar 

  39. Kirsch A (1996) An introduction to mathematical theory of inverse problems. Springer, New York

    Book  MATH  Google Scholar 

Download references

Acknowledgements

This work is supported by the National Natural Science Foundation, China (No.11871313), the Natural Science Foundation of Shandong Province (No.ZR2019MA021), and the 2018 doctoral research innovation foundation of Inner Mongolia Autonomous Region, China.

Author information

Authors and Affiliations

  1. College of Science, Inner Mongolia University of Technology, Hohhot, 010100, Inner Mongolia, China

    Guangsheng Chi

  2. School of Mathematics and Statistics, Shandong University of Technology, Zibo, 255000, Shandong, China

    Gongsheng Li

Authors
  1. Guangsheng Chi
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Gongsheng Li
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

GC carried out all the numerical computations and the numerical inversions, and provided the figures and tables in the manuscript. GL put forward the identification problem and wrote the main manuscript text. Both of the authors reviewed the manuscript.

Corresponding author

Correspondence to Gongsheng Li.

Ethics declarations

Conflict of interest

The authors do not have any relevant financial or non-financial competing interests in this paper.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Chi, G., Li, G. Numerical identification of the fractal orders in the generalized nonlocal elastic model. J Eng Math 142, 4 (2023). https://doi.org/10.1007/s10665-023-10285-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s10665-023-10285-4

Keywords

Search

Navigation