Skip to main content
SpringerLink
Log in

Effect of internal heat source on stability analysis of a highly permeable vertical porous channel filled with nanofluid

  • Published:
Journal of Engineering Mathematics Aims and scope Submit manuscript

Abstract

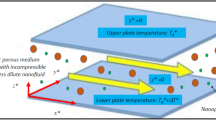
A comprehensive numerical study of convective instability of nanofluid flow in a vertical channel filled with a highly permeable porous material is investigated due to internal heat source effect. The Brinkman–Darcy model has been taken which incorporates the influences of thermophoresis and Brownian motion. A normal mode technique has been employed on the disturbances equations to get the generalized eigenvalue problem and which is solved by Chebyshev spectral collocation method via QZ algorithm in MATLAB. Finally, the critical modified Grashof number (\(Gr'_\text {c}\)) and corresponding wavenumber (\(\alpha _\text {c}\)) have been calculated and portrayed for the flow-governed parameters. It is found that instability boundaries can be reduced or increased by the governing parameters due to the heat source effect. Further, it is discovered that the shape of the isotherms and isonanoconcentrations changes from a bi-cellular structure to a tetra-cellular structure as strength of the internal heat increases, but the streamlines remain at bi-cellular structure.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13

Similar content being viewed by others

References

  1. Horton CW, Rogers FT Jr (1945) Convection currents in a porous medium. J Appl Phys 16(6):367–370

    Article  MathSciNet  MATH  Google Scholar 

  2. Lapwood ER (1948) Convection of a fluid in a porous medium. Math Proc Camb Philos Soc 44(4):508–521

    Article  MathSciNet  MATH  Google Scholar 

  3. Nield DA, Bejan A (2013) Convection in porous media. Springer, New York

    Book  MATH  Google Scholar 

  4. Vafai K (2015) Handbook of porous media. CRC Press, Boca Raton

    Book  MATH  Google Scholar 

  5. Darbhasayanam S, Barman D (2021) The variable gravity field and viscous dissipation effects on the double diffusive and Soret driven convective instability in a porous layer with throughflow. Int Commun Heat Mass Transf 120:105050

    Article  Google Scholar 

  6. Barman D, Srinivasacharya D (2021) The variable gravity field and viscous dissipation effects on the convective instability in a porous layer with throughflow: Brinkman model. J Porous Media 24(6):1–13

    Article  Google Scholar 

  7. Tveitereid M (1977) Thermal convection in a horizontal porous layer with internal heat sources. Int J Heat Mass Transf 20(10):1045–1050

    Article  MATH  Google Scholar 

  8. Capone F, Gentile M, Hill AA (2011) Double-diffusive penetrative convection simulated via internal heating in an anisotropic porous layer with throughflow. Int J Heat Mass Transf 54(7–8):1622–1626

    Article  MATH  Google Scholar 

  9. Bhadauria BS (2012) Double-diffusive convection in a saturated anisotropic porous layer with internal heat source. Transp Porous Media 92(2):299–320

    Article  MathSciNet  Google Scholar 

  10. Gaikwad SN, Kouser S (2014) Double diffusive convection in a couple stress fluid saturated porous layer with internal heat source. Int J Heat Mass Transf 78:1254–1264

    Article  Google Scholar 

  11. Deepika N, Narayana PAL, Hill AA (2017) Onset of Darcy-Brinkman convection with a uniform internal heat source and vertical throughflow. Int J Therm Sci 117:136–144

    Article  Google Scholar 

  12. Ali SA, Rudziva M, Sibanda P, Noreldin OAI, Goqo SP, Mthethwa HS (2022) A numerical study of double-diffusive convection in the anisotropic porous layer under rotational modulation with internal heat generation. Int Commun Heat Mass Transf 137:106266

    Article  Google Scholar 

  13. Kumar S, Sharma K (2023) Entropy optimization analysis of Marangoni convective flow over a rotating disk moving vertically with an inclined magnetic field and nonuniform heat source. Heat Transf 52(2):1778–1805

    Article  Google Scholar 

  14. Masuda H, Ebata A, Teramae K (1993) Alteration of thermal conductivity and viscosity of liquid by dispersing ultra-fine particles. Dispersion of \(\text{ Al}_2\)\(\text{ O}_3\), \(\text{ SiO}_2\) and \(\text{ TiO}_2\) ultra-fine particles. Netsu Bussei 7(4):227–233

    Article  Google Scholar 

  15. Choi SUS, Eastman JA (1995) Enhancing thermal conductivity of fluids with nanoparticles. Argonne National Lab, Lemont

    Google Scholar 

  16. Buongiorno J (2006) Convective transport in nanofluids. ASME J Heat Transf 128(3):240–250

    Article  Google Scholar 

  17. Tzou DY (2008) Instability of nanofluids in natural convection. ASME J Heat Transf 130(7):072401

    Article  Google Scholar 

  18. Tzou DY (2008) Thermal instability of nanofluids in natural convection. Int J Heat Mass Transf 51(11–12):2967–2979

    Article  MATH  Google Scholar 

  19. Nield DA, Kuznetsov AV (2009) Thermal instability in a porous medium layer saturated by a nanofluid. Int J Heat Mass Transf 52(25–26):5796–5801

    Article  MATH  Google Scholar 

  20. Kuznetsov AV, Nield DA (2010) Thermal instability in a porous medium layer saturated by a nanofluid: Brinkman model. Transp Porous Media 81(3):409–422

    Article  MathSciNet  Google Scholar 

  21. Yadav D, Agrawal GS, Bhargava R (2011) Thermal instability of rotating nanofluid layer. Int J Eng Sci 49(11):1171–1184

    Article  MathSciNet  MATH  Google Scholar 

  22. Yadav D, Bhargava R, Agrawal GS (2013) Thermal instability in a nanofluid layer with a vertical magnetic field. J Eng Math 80(1):147–164

    Article  MathSciNet  MATH  Google Scholar 

  23. Nield DA, Kuznetsov AV (2013) Onset of convection with internal heating in a porous medium saturated by a nanofluid. Transp Porous Media 99(1):73–83

    Article  MathSciNet  Google Scholar 

  24. Yadav D, Bhargava R, Agrawal GS (2012) Boundary and internal heat source effects on the onset of Darcy-Brinkman convection in a porous layer saturated by nanofluid. Int J Therm Sci 60:244–254

    Article  Google Scholar 

  25. Khalid IK, Mokhtar NFM, Hashim I, Ibrahim ZB, Gani SSA (2017) Effect of internal heat source on the onset of double-diffusive convection in a rotating nanofluid layer with feedback control strategy. Advn Math Phys 2017:2789024

    MathSciNet  MATH  Google Scholar 

  26. Chen YC, Chung JN (1996) The linear stability of mixed convection in a vertical channel flow. J Fluid Mech 325:29–51

    Article  MATH  Google Scholar 

  27. Hudoba A, Molokov S (2016) Linear stability of buoyant convective flow in a vertical channel with internal heat sources and a transverse magnetic field. Phys Fluids 28(11):114103

    Article  Google Scholar 

  28. Sharma A, Bera P (2018) Linear stability of mixed convection in a differentially heated vertical channel filled with high permeable porous-medium. Int J Therm Sci 134:622–638

    Article  Google Scholar 

  29. Srinivasacharya D, Barman D (2021) Linear stability of convection in a vertical channel filled with nanofluid saturated porous medium. Heat Transf 50(4):3220–3239

    Article  Google Scholar 

  30. Srinivasacharya D, Barman D (2022) Effect of local thermal nonequilibrium on the stability of the flow in a vertical channel filled with nanofluid saturated porous medium. ASME J Heat Transf 144(1):014501

    Article  Google Scholar 

  31. Srinivasacharya D, Barman D (2022) Influence of magnetic field on the stability of double diffusive nanofluid convection in a vertical porous channel. J Porous Media 25(9):1–16

    Article  Google Scholar 

  32. Brinkman HC (1949) A calculation of the viscous force exerted by a flowing fluid on a dense swarm of particles. Appl Sci Res A1:27–34

    Article  MATH  Google Scholar 

  33. Drazin PG, Reid WH (2004) Hydrodynamic stability. Cambridge University Press, Cambridge

    Book  MATH  Google Scholar 

  34. Caruto C, Hussaini MY, Quarteroni A, Zang TA (1988) Spectral method in fluid dynamics. Springer, Berlin

    Google Scholar 

  35. Orszag SA (1971) Accurate solution of the Orr-Sommerfeld stability equation. J Fluid Mech 50(4):689–703

    Article  MATH  Google Scholar 

  36. Chen YC, Chung JN (1998) Stability of mixed convection in a differentially heated vertical channel. ASME J Heat Transf 120(1):127–132

    Article  Google Scholar 

  37. Yao LS, Rogers BB (1989) Mixed convection in an annulus of large aspect ratio. ASME J Heat Transf 111(3):683–689

    Article  Google Scholar 

  38. Squire HB (1933) On the stability for three-dimensional disturbances of viscous fluid flow between parallel walls. Proc R Soc Lond Ser A 142(847):621–628

    Article  MATH  Google Scholar 

  39. Yao LS, Rogers BB (1989) The linear stability of mixed convection in a vertical annulus. J Fluid Mech 201:279–298

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, National Institute of Technology Warangal, Hanamkonda, Warangal, 506004, TS, India

    Dipak Barman

Authors
  1. Dipak Barman
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

Dipak Barman conceived the presented idea and developed the theory, performed the computations, and then verified the code by the number of collocation points. Then, Dipak Barman presents the instability boundaries due to the effect of various parameters graphically. Finally, Dipak Barman reviewed the results and contributed to the final manuscript.

Corresponding author

Correspondence to Dipak Barman.

Ethics declarations

Conflict of interest

The authors declare no competing interests.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Barman, D. Effect of internal heat source on stability analysis of a highly permeable vertical porous channel filled with nanofluid. J Eng Math 140, 11 (2023). https://doi.org/10.1007/s10665-023-10275-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s10665-023-10275-6

Keywords

Search

Navigation