Some aspects of the pressure field preceding the onset of critical jets in a breaking wave

Abstract

We consider in this article two-dimensional nonlinear free surface motions in potential theory. There are situations where the onset of critical jet along a free surface can be predicted by analyzing the temporal and spatial variation of the pressure itself and its successive derivatives. In particular, when a local maximum of pressure appears close enough to a free surface where the pressure vanishes, it is expected a great pressure gradient at the free surface and consequently a large Lagrangian acceleration. The present analysis examines this phenomenon. This analysis is facilitated after identifying a line along which the pressure gradient is parallel to one of the eigenvectors of the Hessian matrix of the pressure. In a standard overturning crest, this line connects the tip of the crest to the bottom of the tank in which the flow is simulated. The analysis of its time evolution gives much information into the onset of critical jets. Other types of critical jet can also appear when a region of positive Gaussian curvature of the pressure suddenly grows in the vicinity of the free surface.

Appendices

Appendix A: FSID

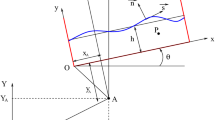
The software FSID solves the nonlinear free surface equations in potential theory. The configuration is two dimensional. A sketch of the flow configuration is shown in Fig. 11. The boundaries of the fluid domain are the walls of a tank and the free surface. For the present applications, the tank is rectangular and the fluid is hence contained in a half infinite strip. The velocity potential is decomposed as a finite sum of Rankine sources. These singularities are located outside the fluid domain so that the solution is said desingularized. By using a conformal mapping the fluid domain is described in the upper half space where the images of the walls are the horizontal real axis. By using mirror images of the singularities, the Rankine Green function easily accounts for the impermeability of the walls. Lagrangian markers are located along the free surface, they are transported over time with their local velocity. This velocity is obtained by updating the velocity potential at the free surface. The resulting time differential system is solved by using a fourth order Runge–Kutta algorithm. The distance of desingularization, the number of markers and the time step are chosen so that the relative errors on mass and energy conservation are ensured with a maximum relative errors of $10^{-4.5}$ and $10^{-3}$ respectively. In the present computations, the time step is decreased when the free surface deformation becomes faster and faster. Some numerical improvements could be achieved by choosing a more precise time marching scheme.

Fig. 11

Configuration of the flow in the rectangular tank. The fluid motion is described in a coordinate system attached to the tank. The length of the tank is L. The water depth at rest is h. The arclength $\sigma$ is measured positively from the left wall to the right wall

The conformal function is denoted $w=g(z)$ and z is a complex coordinate of a point in the physical plane. The fluid motion is described in a coordinate system attached to the tank. It is represented by a complex velocity potential and it is calculated at time t as

$$\begin{aligned} F(z,t)= \sum _{j=1}^{N} q_j(t) G(w,W_j(t)) \end{aligned}$$

(12)

at both complex coordinates z and w, provided that $w=g(z)$. The intensity of the source # j is $q_j$ and $W_j=g(Z_j)$ is the complex coordinate of the source # j in the transformed plane w. G is the complex potential of this source plus its mirror image with respect to the axis $\mathfrak {I}(w)=0$,

$$\begin{aligned} G(w,W_j) = G_j = \log ( w - W_j ) + \log ( w - \overline{W_j} ). \end{aligned}$$

(13)

The overline denotes the conjugate of the complex variable. The following formulæ give the first derivative in time and space of F.

$$\begin{aligned}{} & {} F_{z}= \frac{1}{J} F_{w}, \quad J= \frac{\textrm{d}z}{\textrm{d}w}, \end{aligned}$$

(14)

$$\begin{aligned}{} & {} F_{t} = \sum _{j=1}^{N} \dot{q}_j G_j + q_j G_{j,t}, \quad G_{j,t} = - \left( \frac{\dot{Z}_j}{J_j[w - W_j]} + \frac{\dot{\overline{Z}}_j }{\overline{J}_j[w - \overline{W}_j]} \right) , \quad J_j= \frac{\textrm{d}z}{\textrm{d}w}(W_j). \nonumber \\ \end{aligned}$$

(15)

The dot denotes the time derivative. The successive derivatives in (1), (4), (5) and (6) are calculated according to the same principle.

Fig. 12

Oscillation cycle of the horizontal motion of the tank. Temporal variation of the displacement (a), velocity (b) and acceleration (c). The reference signal is in black $X=1$. Only the signals obtained with the amplification factors $X=1.09$ and 1.19 are plotted

Appendix B: Description of the jets appear computations of [18]

As for the configuration studied in Sect. (3), the flow is generated in a rectangular tank whose motion consists of an oscillating horizontal motion. A parametric analysis is carried out in terms of an amplification factor (denoted X) that affects the amplitude of the motion, and consequently the amplitudes of the velocity and acceleration. Figure 12 illustrate the time variations of the kinematic of the tank. The reference motion (factor $X=1$) is generated with a given amplitude and period of the cycle. In Fig. 12, the time signals for two factors ($X=1.09$ and $X=1.19$) are superimposed. For the parametric analysis, the factor X varies in the range $X\in [1.0$ to 1.19] by steps of 0.01.

A common feature of all the numerical tests can be summarized as three successive stages: (1) beginning of the overturning of a crest, (2) this is stopped with the formation of a jet in the middle of the nascent barrel (called here pre-bazooka jet), and (3) the development of this jet is finally interrupted by the onset of a flip-through jet which runs up along the vertical wall. Figure 13 shows the free surface profiles for a given amplification factor $X=1.16$. One instant ($t=1.7024\,\textrm{s}$) just before the onset of the pre-bazooka jet is plotted: it corresponds to an almost vertical-free surface profile in the barrel below the wave crest. At later instants, ranged in the interval $t\in [1.728\,\textrm{s}:1.732\,\textrm{s}]$, the excrescence reaches a significant size. For all the other amplification factors X, the profiles have more or less the same features. It should be noted that the parabolic shape of the free surface at the wall announces that a flip through is likely to occur (see [21]).

Fig. 13

Successive profiles of the free surface for the amplification factor $X=1.16$. The instants of plots are ranged in the interval $t\in [1.728\,\textrm{s}:1.732\,\textrm{s}]$ and at one instant before the onset of the bazooka jet $t=1.7024\,\textrm{s}$ (thick line). For the last profiles, the time interval between each profile is $2\,\textrm{ms}$. Units along the horizontal and vertical axis: x/L and y/L with $L=1\,\textrm{m}$ the length of the rectangular tank and $h=0.25\,\textrm{m}$ the water depth at rest

In [18], comparisons are made with a Navier–Stokes solver CADYF developed in Polytechnique Montréal (see [22, 23]). The corresponding computations yield identical time variations of both the free surface profiles and energy distribution. Significant differences appear during the very last stages of the flow when flip through occurs. That is understandable since a Navier–Stokes solver may have numerical difficulties to capture extremely great acceleration along impermeable walls.

The parametric analysis achieved in [18] concludes that a power law (see Eq. 11) can be fitted to the time variation of the acceleration of the flip-through jet. The exponent is close to 1.