Flow induced by a line sink near a vertical wall in a fluid with a free surface Part I: infinite depth

Abstract

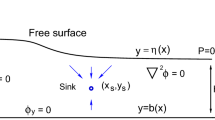
The two-dimensional, steady flow of an inviscid fluid induced by a line sink located near a vertical wall in a region of infinite depth is computed. The effects of surface tension are investigated. The solution in the limit of small Froude number is obtained analytically, and numerically for the nonlinear problem. The asymptotic solution is found to have a property that if the horizontal location of the sink, $x_\mathrm{{s}} < 1$, there is only one stagnation point on the surface, at the wall. However, if the horizontal location $x_{\mathrm{s}} > 1$, a second stagnation point forms on the free surface. Numerical solution for the nonlinear problem confirms these properties. The effect of moving the sink horizontally has also been considered. The maximum Froude numbers at which steady solutions exist are computed and compared with the previous work.

1 Introduction

Problems in mechanics that involve free surface flow have been the subject of intensive research over a long period of time, and have a wide range of important applications [1,2,3,4]. In general, if the fluid with which we are dealing is ideal, incompressible and inviscid, the general mathematical formulation leads to the definition of a velocity potential function $\phi (x,y)$ that has to satisfy Laplace’s equation, along with boundary conditions that state there is no flow through the boundary and dynamic and kinematic conditions on the surface. However, by virtue of the fact that the location of the free surface is unknown the problem becomes highly nonlinear as the shape of the free surface has to be found as a part of the solution. This paper is concerned with questions of when steady solutions exist and if they do, what are the characteristics of the surface of the fluid when a flow is generated by a submerged line sink? The sink is located at an arbitrary location in a fluid of infinite depth (see Fig. 1). This is the first of two papers in which we consider this problem. In the second, we consider a layer of fluid of finite depth [5]. Although similar in nature the two problems are fundamentally different in that the flow in a fluid of finite depth admits the possibility of waves in the far-field, as discussed by Lustri et al. [6] for the related case of a flow from a source. Their work showed the existence of waves of exponential order on the free surface. Such waves would not appear in the methods used in this work, and would not exist in the far-field as the flow becomes stagnant. The problem in finite depth has a nonzero flow velocity in the far-field, while the velocity must slow to zero for the case of infinite depth. Thus the details of the solution are quite different between the two cases.

In the case of two-dimensional flow into a line sink in a fluid of infinite depth, Tuck and Vanden-Broeck [7] re-examined the Peregrine [8] solution that assumed that the solution would exist for some range of Froude number, a measure of the flow strength, and that there was a limiting steady solution that he attempted to find using a Taylor-series expansion method. Tuck and Vanden-Broeck [7] showed that there are always two types of solution to this problem. The first solution is one in which the surface is drawn down towards the sink in a cusp shape, and the second is one in which a stagnation point forms above the sink or source. Since the free surface condition depends only on the square of the velocity term and the difference between the sink and source problems is the direction of the flow, the steady sink or source disturbance will be the same. Hocking and Forbes [9] and Forbes and Hocking [10] have studied this problem widely and found that whether the fluid has one or two layers the surface or interface will be drawn down into the sink if the withdrawal rate is large enough.

A spectral method in a conformally mapped plane was used by Tuck and Vanden-Broeck [7] to find a solution for the submerged line sink or source in a fluid of infinite depth. In cases with a free surface stagnation point, solutions were limited to values beneath a critical Froude number. They discovered that if the Froude number was left as an unknown parameter and found as a part of the solution, they could obtain the solution for the other type of flow for which the surface was drawn down towards the sink in a cusp shape. This cusp solution occurred at a unique value of Froude number $F\approx 3.553$ [7]. No attempt has been made to compute solutions with a cusped surface in this work, since it would require significant modifications to the numerical method, and the calculations in that case can be quite delicate due to the fact that they only exist at a unique value of flow rate.

Mekias and Vanden-Broeck [11] and Hocking and Forbes [12] sought solutions for free surface flows with a stagnation point on the free surface by using similar methods. Hocking and Forbes [12] used the method of Tuck and Vanden-Broeck [7] and confirmed that there was a solution for the free surface stagnation point flows provided the Froude number was limited to $F<1.4$.

Steady or unsteady withdrawal from a fluid of finite or infinite depth through a line sink or point sink including surface-tension effects has been the subject of considerable study. Hocking et al. [12,13,14], and Forbes and Hocking [10] found that the inclusion of even a small amount of surface tension has a big influence on the final values of the maximum flow rate. They were also able to show nonuniqueness in the solution domain. The unsteady case was studied by Stokes et al. [15, 16] and they showed that the zero surface tension case was problematic in terms of determining whether the surface draws down or reaches a steady state, and that the drawdown of the free surface depended in many cases upon the flow history.

All of the abovementioned studies were done for cases where the sink or source is located on the wall, on the base or completely isolated with no boundaries nearby. In the present study, we investigate the flow induced by a line sink in a fluid of infinite depth when the sink is located away from a vertical wall, including the effects of surface tension. The case of a fluid of finite depth will be considered elsewhere (Mansoor et al. [5]). In the case of infinite depth, it is not possible to have waves in the far-field as the flow slows to zero.

Fig. 1

Diagram of the nondimensionalized problem. The free surface is given by $y=\eta (x)$ and the sink is located at arbitrary location $(x_\mathrm{{s}},-1)$

2 The governing equations

Consider the two-dimensional, steady, irrotational flow due to a line sink of an inviscid, incompressible fluid of infinite depth. The sink is situated a distance H beneath the undisturbed free surface and has strength m, which is the volume rate at which it withdraws fluid, and sits a distance $X_\mathrm{{s}}$ from a vertical wall at $x=0$ (see Fig. 1). The sink is thus located at point $(X_\mathrm{{s}}, - H)$. We assume that some steady flow pattern is established, and the shape of the fluid surface will be determined as a part of the solution. Also, the free surface is assumed to have surface tension, T, and the effects of it will be included.

It is convenient to nondimensionalize the problem, using the depth H of the sink as the characteristic length scale and mH as the scaling for the velocity potential. From now on, all quantities will be assumed to be dimensionless according to this scaling. Therefore, there are only three nondimensional parameters:

$$\begin{aligned} F= & {} \left( \frac{m^2}{g H^3}\right) ^{1/2}, \end{aligned}$$

$$\begin{aligned} x_\mathrm{{s}}= & {} X_\mathrm{{s}}/H \end{aligned}$$

and

$$\begin{aligned} \beta =\frac{T}{g H^{2}}. \end{aligned}$$

The first parameter is the Froude number, F, and this is a measure of the withdrawal rate at the sink and $\beta$ is a dimensionless measure of the importance of surface tension. The quantity $x_\mathrm{{s}}$ is the distance of the sink from the vertical wall. Under these assumptions the velocity vector can be given as the gradient of the velocity potential $\phi$, according to the formula $\mathbf{u }=\bigtriangledown \phi$, where $\mathbf{u}=(u,v)$ is the velocity vector. The incompressibility of the fluid indicates that the velocity potential therefore satisfies Laplace’s equation

$$\begin{aligned} \nabla ^2 \phi (x,y)=0, \quad (x,y) \ne (x_\mathrm{{s}},-1), \end{aligned}$$

(1)

throughout the fluid domain ($x\ge 0$, $y<\eta (x)$), except at the point $(x,y)=(x_\mathrm{{s}},-1)$, the location of the line sink. As the line sink is approached, the velocity potential satisfies

$$\begin{aligned} \phi \rightarrow - {\frac{1}{2\pi }}\log ((x-x_\mathrm{{s}})^{2} + (y+1)^{2})^\frac{1}{2} \quad \text{ as }\ (x,y) \rightarrow (x_\mathrm{{s}},-1). \end{aligned}$$

(2)

Now, it is necessary to state the conditions that apply to the free surface $y=\eta (x)$, the shape of which is as yet unknown, and to the vertical boundary at $x=0$. There are kinematic conditions

$$\begin{aligned}&\phi _x=0 \quad { \text{ on } } x=0 \end{aligned}$$

(3)

$$\begin{aligned}&\phi _y-\phi _x\eta '(x) =0 \quad { \text{ on } }\; y=\eta (x), \quad x>0, \end{aligned}$$

(4)

which state that the fluid cannot cross through a boundary or its own surface $y=\eta (x)$. There is also a dynamic condition, which comes from Bernoulli’s equation, and expresses the balance between pressure within the fluid and the kinetic energy of fluid particles. Evaluated along the unknown fluid free surface, this condition takes the form

$$\begin{aligned} \eta +{\frac{1}{2}} F^2 \mathopen |\mathbf{u}\mathclose |^2-\frac{\beta \eta ^{''}}{(1+\eta ^{'2})^{\frac{3}{2}}}=0 \quad {\text{ on }}\; y=\eta (x), \end{aligned}$$

(5)

since the pressure on the free surface is constant at the value of the atmospheric pressure. The solution of this problem therefore consists of finding a velocity potential $\phi (x,y)$ and a surface elevation $y=\eta (x)$ that satisfy Eqs. (1)–(5).

3 Solution for small Froude number with zero surface tension

An approximate solution, valid as $F \rightarrow 0$ can be obtained for the case of zero surface tension. It turns out that the linear solution is very accurate in shape for even quite large flow rates, and this serves as a valuable check on the accuracy of the numerical solution described in the next section. The velocity potential $\phi$ and the free surface elevation $\eta$ are expressed as perturbation series of the form

$$\begin{aligned} \begin{aligned} \phi (x,y)=\phi _0(x,y)+F^{2} \phi _1(x,y)+0(F^{4}),\quad \eta (x)=F^{2} \eta _{1}(x)+0(F^{4}). \end{aligned} \end{aligned}$$

(6)

The expansions (6) are substituted into the system of equations (1)–(5), and linearized equations for the perturbation functions $\phi _{0}$ and $\eta _{1}$ are obtained. At the first order, it is found that the potential $\phi$ satisfies the Laplace equation (1), the sink condition (2) and the normal-derivative condition ${\partial \phi _{0}}/{\partial y}=0$ on $y=0$. The method of images, subject to the condition (2), at once yields the solution for $\phi _{0}$ in the form

$$\begin{aligned} \begin{aligned} \phi _{0}(x,y)&= - {\frac{1}{2\pi }}\log ((x-x_\mathrm{{s}})^{2} + (y+1)^{2})^\frac{1}{2} - {\frac{1}{2\pi }}\log ((x+x_\mathrm{{s}})^{2} + (y+1)^{2})^\frac{1}{2} \\&\,\,\,\qquad -{\frac{1}{2\pi }}\log ((x-x_\mathrm{{s}})^{2} + (y-1)^{2})^\frac{1}{2} - {\frac{1}{2\pi }}\log ((x+x_\mathrm{{s}})^{2} + (y-1)^{2})^\frac{1}{2} \end{aligned} \end{aligned}$$

(7)

and from the dynamic condition (5) it is found that the first-order free surface elevation function $\eta _{1}(x)$ takes the form

$$\begin{aligned} \eta _{1}(x)=-\frac{1}{2}(\phi _{0x}^{2}+\phi _{0y}^{2}), \end{aligned}$$

(8)

evaluated on $y=0$. Substituting (7) into (8) gives the asymptotic form of the free surface elevation, $y=\eta (x)$, to be

$$\begin{aligned} \begin{aligned} \eta (x)=-\frac{F^{2}}{2 \pi ^{2}} \bigg [ \frac{ (x-x_\mathrm{{s}})}{(x-x_\mathrm{{s}})^{2}+1}+\frac{ (x+x_\mathrm{{s}})}{(x+x_\mathrm{{s}})^{2}+1}\bigg ]^{2}. \end{aligned} \end{aligned}$$

(9)

Fig. 2

Contours of magnitude of velocity with $x_\mathrm{{s}}=0.75$ and $x_\mathrm{{s}}=4$, respectively, for the leading order solution. The slow flow near the wall for $x_\mathrm{{s}}=4$ is clear as is the second surface stagnation point on the surface above the sink

From this solution (9), we can note the following property of the free surface.

Theorem

The asymptotic solution has a single stagnation point on the free surface at $x=0$. It has a second stagnation point on the free surface at $x=\sqrt{x_\mathrm{{s}}^{2}-1}$, if and only if $x_\mathrm{{s}}$ > 1.

Proof

There are free surface stagnation points if the velocity potential satisfies the condition $\phi _{0x}(x,0)=\eta (x)=0$. Therefore, from (9)

$$\begin{aligned} \frac{(x-x_\mathrm{{s}})}{(x-x_\mathrm{{s}})^{2}+1}+\frac{(x+x_\mathrm{{s}})}{(x+x_\mathrm{{s}})^{2}+1}=0, \end{aligned}$$

(10)

and simplifying, there is a stagnation point on the free surface provided

$$\begin{aligned} \begin{aligned} x(x^{2}-x_\mathrm{{s}}^{2}+1)=0, \end{aligned} \end{aligned}$$

(11)

which means that $x=0$ or $x=\sqrt{x_\mathrm{{s}}^{2}-1}$. If $x_\mathrm{{s}}<1$, then only $x=0$ is a real solution, but if $x_\mathrm{{s}}>1$ then there are stagnation points at $x=0, \pm {\sqrt{(x_\mathrm{{s}}^{2}-1)}}$.

This interesting result highlights a fundamental change in behaviour if the separation of the line sink from the wall becomes greater than the depth of the sink. When $x_\mathrm{{s}}$ > 1 there is a relatively stagnant region between the sink and wall. Figure 2 shows contours of the magnitude of the velocity of the fluid for a case with $x_\mathrm{{s}}<1$, i.e. $x_\mathrm{{s}}=0.75$, and another with $x_\mathrm{{s}}>1$, i.e. $x_\mathrm{{s}}=4$. The secondary stagnation point can be clearly seen in the latter case, as can a broad region of very slow flow near the vertical wall. $\square$

4 Numerical method

In order to compare with the linear results and to gain a full picture of what is happening in the infinite depth case, we present a series of numerical simulations for the full nonlinear problem. An attempt was made to use a traditional boundary element method, but the nature of the singularity on the free surface in cases with a separated stagnation point proved to be difficult to represent accurately. As a consequence, we decided to use the fundamental singularity method used initially by Scullen and Tuck [17] and in an unsteady context by Stokes et. al. [15, 16]. The method is simple to implement and has no difficulty with the computation of the secondary stagnation point when it exists. The main idea of the method is to compute the value of the velocity potential using N source/sink points above the free surface and located symmetrically to satisfy the boundary conditions. The steady solution is generated by using a Newton iteration scheme based on the distributed sink technique.

A function $\phi$ that satisfies conditions (1), (2) and (3) has the form

$$\begin{aligned} \phi (x,y)=\phi _{0}(x,y)+\sum \limits _{k=1}^{\infty } \gamma _{k} \log ( R_{1k} R_{2k}), \end{aligned}$$

(12)

where $\phi _{0}(x,y)$ is the velocity given by (7), $\gamma _{k}$, $k=1,2,3,\dots$ is the strength of a sink situated just above the free surface at $(X_k,Y_k)$, $k=1,2,3,\dots$, and

$$\begin{aligned} R_{1k}(x,y)=\sqrt{(x-X_k)^{2}+(y-Y_{k})^{2}} \end{aligned}$$

and

$$\begin{aligned} R_{2k}(x,y)=\sqrt{(x+X_k)^{2}+(y-Y_{k})^{2}} \end{aligned}$$

are the distances between the kth source or sink point and the point (x, y), which lies in the fluid. Following the work of Stokes et al [16], the locations of the source/sink points $(X_{k},Y_{k})$ are chosen perpendicular to the surface point $(x_{k},\eta _{k})$ and at a distance equal to $\frac{1}{3}$ of the point separation. Different values of separation were tried, but this value was found to be close to optimal. The sink strengths $\gamma _{k}$ and surface heights $\eta _{k}$ are unknown and will be determined once the value of $\phi$ is known at N distinct surface points, $(x_{k},\eta _{k})$, $k= 1, 2,\ldots , N,$ after truncating the series to N terms.

By using N points to represent the surface shape $\eta (x)$, and N coefficients $\gamma _{k}$ we may use Eqs. (4) and (5) to determine the unknown terms with both needing to be satisfied at each of N points. Laplace’s equation is satisfied by the choice of basis functions. Thus we have 2N nonlinear equations for the 2N unknowns and can solve using a Newtonian iteration scheme. Results were found to converge to graphical accuracy with a space step, $\mathrm{{d}}x=0.02$ and truncation of the fluid domain at $x_{L}=20$ for most cases. In each case, it was found there was a limiting, maximum Froude number, $F_{\max }$, beyond which steady solutions could not be found as the numerical method failed to converge. The limiting behaviour manifested in the numerical method as small grid-scale oscillations in the solution (see Fig. 3). These oscillations are typical of results in other work [11, 12] for cases without surface tension. When even a small amount of surface tension is included, the maximum becomes much clearer and the numerical scheme simply fails to converge beyond the maximum value of F.

5 Presentation of results

We found that there is a three-parameter family of solutions to this problem; the Froude number, F, surface tension, $\beta$ and the horizontal sink location, $x_\mathrm{{s}}$. For all cases, the maximum Froude number $F_{\max }$ was identified from the numerical method, and its dependence on the other parameters was ascertained.

Fig. 3

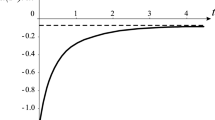
Asymptotic solution compared with the full nonlinear solution for different values of Froude number. The blue (dashed) line is the approximate solution in each case and the red (solid) line is the nonlinear solution. The effect of nonlinearity is clear in each, pulling the surface down more. The sink is located at $x_\mathrm{{s}}=0.1$, and d$x=0.02$. The limiting solution in this case is $F_{\max }\approx 0.72$, as can be seen by the small, numerically generated oscillations at the base of the trough. (Color figure online)

Figure 3 shows a comparison between the numerical solution (red solid line) and the asymptotic solution (blue dashed line), for several different Froude numbers with $\beta =0$ when the sink is located at $x_\mathrm{{s}}=0.1$. For smaller values of Froude number the linear solutions are graphically identical to the nonlinear solutions. The limiting numerical solution in this case is $F\approx 0.7$. The small, numerically generated oscillations are clear in this figure as the limiting value $F_{\max }$ is approached. For larger values of Froude number the two results are in a good agreement close to the stagnation zone, and the only distinction that we can observe occurs near the surface troughs, where nonlinear effects pull the surface down further. The results suggest that only one stagnation point has formed, in this case at the wall, as anticipated from the theorem and the asymptotic solution. After the dip above the sink the height returns to the stagnation level as $x \rightarrow \infty$ since the velocity will fall to zero.

Fig. 4

Comparison of the linear (blue dashed line) with the nonlinear (red solid line) for different Froude numbers and the sink is located at $x_\mathrm{{s}}=1.5$ and $\beta =0$, with $N=1000$. A second stagnation point appears on the surface for this case. (Color figure online)

Another comparison is shown in Fig. 4, which shows the linear solution (blue dashed line) and the nonlinear (red solid line) for different values of Froude number, $\beta =0$ and $x_\mathrm{{s}}=1.5$. At small values of Froude number the linear solution and numerical results match very well. However, even at larger Froude number the only minor difference is in the region close to the deepest trough on the surface, where the numerical solution has a slightly deeper dip than the asymptotic solution. There are two stagnation points in this case, the first stagnation point is clearly formed at the wall and located at $(x,y)=(0,0)$, and the second stagnation point occurs when the surface rises again to the stagnation height level at $y=0$ and is located very close to $(x,y)\approx (1.5,0)$, almost directly above the sink.

Figure 5 shows a third case in which $x_\mathrm{{s}}=6$, a relatively large value, and in this case we only show a single value of $F=0.9$ ($\beta =0$). The surface features are more clearly evident in this case. As the sink moves away from the wall the region around the central stagnation point tends to become symmetric. Again both solutions agree very well. However, they disagree slightly in the area near the base of the troughs, where the effects of nonlinearity again become evident. The stagnation region between the wall and the sink location increases in size and the dip on the wall side gradually deepens. Figures 3, 4 and 5 show that the predictions of the theorem are followed closely by the nonlinear numerical solution. All of these results show that the numerical method is working correctly by comparison with the asymptotic solutions.

Figures 7 and 8 address the effect of the presence of the wall on the withdrawal rate $F_{\max }$. It was found that when the sink is close to the wall and surface tension is $\beta =0$, $F_{\max }\approx {0.7}$ which is similar to Hocking and Forbes [12] who found $F_{\max }\approx {1.4}$ when the sink is in the wall and consequently has half of the influx (thus doubling the apparent F value). As the sink is moved further from the wall, $F_{\max }$ begins to increase as the effect of the wall decreases. At $x_\mathrm{{s}}=1.5$, $F_{\max }$ has risen to $F_{\max } \approx 0.95$, and if the sink moves further from the wall to say $x_\mathrm{{s}}=10$ that will result in a larger flow rate $F_{\max } \approx 1.37$, thus tending to the isolated value in [12] ($F_{\max }\approx {1.4}$). However, $x_\mathrm{{s}}$ needs to be quite large before symmetry in the surface shape is obtained because all of the flow must originate from only the upstream side. Our results for $F_{\max }$ are much more accurate than those in [12] because here the simulation was done with $N=2000$, while they used much smaller values of $N=100-200$, due to the computational limitations of the time. However, the results are consistent between the two works as the sink approaches the vertical wall and as $x_\mathrm{{s}} \rightarrow \infty$, with the values of $F_{\max }$ in Figure 7 levelling off at around $x_\mathrm{{s}}\approx 10$ at values very close to those obtained in Forbes and Hocking [10].

Fig. 5

Comparison between the linear solution (blue dashed line) and numerical solution (red solid line) for the case $x_\mathrm{{s}}=6$, $N=1100$, $F=0.9$ and $\beta =0$. The limiting steady solution for this case is $F_{\max }\approx 1.32$. (Color figure online)

The free surface profile has been studied for different values of the Froude number F when surface tension $\beta$ is included. In the surface shapes there are one or two dips that depend on the sink location. We have seen this in both the approximate solutions and the full nonlinear solutions when there is no surface tension. This pattern is repeated in results when moderate surface tension is included.

Fig. 6

Free surface shapes for different surface tension values, $\beta$, for the case of the sink located at $x_\mathrm{{s}}=8$ with $F=0.4$, $N=1200$

Figure 6 shows the effect of increasing surface tension $\beta$ on the shape of the free surface at the same value of F; the peaks and troughs are reduced in size. If $\beta$ is increased to completely unrealistic values $\beta =3, 6$, the peaks and troughs are almost eliminated. The result is that even for very small values of surface tension the limiting Froude number, $F_{\max }$, for steady flows increases dramatically. This is illustrated very clearly in Fig. 7 which shows the maximum value of F as $x_\mathrm{{s}}$ increases for different values of surface tension, $\beta$. As $x_\mathrm{{s}}$ increases, the maximum increases as the restriction of the flow by the wall is diminished, creating a smaller disturbance to the surface for an equivalent flow rate. In general as $x_\mathrm{{s}} \rightarrow \infty$ the maximum F value is approximately double the value as $x_\mathrm{{s}} \rightarrow 0$ a fact that can be explained by considering the method of images that would see a second “image” sink at $x=-x_\mathrm{{s}}$. As $x_\mathrm{{s}} \rightarrow \infty$ the influence of this image disappears. Even a small amount of surface tension seems to stabilize the flow so that the maximum value of F increases quite dramatically. However, once $\beta$ reaches values $\beta >0.1$ this effect is reduced and the variation in maximum F is smaller (see Fig. 7).

Fig. 7

The maximum rate of withdrawal, $F_{\max }$ for different values of surface tension $\beta$ at different sink locations

Fig. 8

Maximum depth of the outer dip of the free surface for a variety of sink locations, $x_\mathrm{{s}}$, near the maximum value of F, for different values of surface tension $\beta$

A possible indicator of the breakdown of solutions as F increases at larger surface tension can be seen in Fig. 8. The maximum depth of the deepest trough at the limiting (maximum) Froude number, $F_{\max }$, is shown for different sink locations $x_\mathrm{{s}}$ and surface tension $\beta$. The important feature of Fig. 8 is that the deepest point on the surface is quite deep and does not vary much for a given value of $\beta$ once $\beta$ gets bigger than about $\beta =0.1$. Indeed, with $\beta >0.1$ the maximum depth at maximum Froude number, $F_{\max }$, is very similar at around 70–80$\%$ of the sink depth once the horizontal sink location exceeds $x_\mathrm{{s}} \approx 5$. The exception to this is when there is very small value of surface tension ($\beta =0.01$) since then, as we have seen, the maximum $F_{\max }$ is much lower. If we think of this as being a measure of disturbance then in each case this appears to trigger the failure of the numerical method, i.e. once the dip in the surface reaches a depth approaching $70-80\%$ of the sink depth, for moderate values of surface tension, a steady solution no longer exists. The close proximity of the bottom of this dip to the sink location may suggest that a direct drawdown of the surface into the sink is likely if F were to increase further. It is also noticeable that once the sink moves away from the wall, the variation in maximum depth is very small, especially for the case with very low surface tension, $\beta =0.01$.

In the case of sink flows, there is an upper limit on the possible steady flows that is due to the drawdown of the free surface directly into the outlet. This has been identified in computations of two-layer flows and also in unsteady flows [15]. The fact that there is a gap in flow rate between the maximal steady flow and the drawdown is most likely due to instabilities on the free surface as the flow rate approaches the critical value.

6 Comments

An accurate numerical method has been used to compute the flow into a line sink placed at an arbitrary location in a fluid of infinite depth constrained by a vertical wall. The method is verified by comparison to an approximate solution for small values of withdrawal rate F. This asymptotic solution gives very good agreement with the numerical solutions, and the impact of the nonlinearity turns out to be significant only at large Froude number F, and even then, these impacts are shown to be confined to the area next to the free surface trough. However, it was found that, consistent with other works, the steady, nonlinear solutions have a limiting form when F reaches some maximum.

A qualitative change in the surface profile in which a second dip and a second stagnation point form on the free surface occurs if $x_\mathrm{{s}}>1$, and this is verified by the numerical solutions. Also as $x_\mathrm{{s}}$ increases the region near the wall becomes almost stagnant as most of inflowing fluid comes from upstream. As $x_\mathrm{{s}}$ increases it was found that the free surface shape approached that of a single, isolated sink, as shown in Hocking and Forbes [12], but this occurred quite slowly, with significant asymmetry still evident with $x_\mathrm{{s}}=10$. However, in spite of the difference in the surface shape, the critical value of $F_{\max }$ quite quickly approached that of Forbes and Hocking [10].

Similar results were also found by Forbes and Hocking [10], for a line sink in a quiescent fluid of infinite depth including surface tension. They reported a maximum Froude number with $\beta =0$ of $F \approx 1.4$ consistent with the current work. These authors stated that, at higher Froude number, steady state solutions would no longer happen, but some sort of unsteady configuration would result instead, possibly involving a breaking wave at the surface. Evidence to support this conjecture was provided in the unsteady simulations of Stokes et al. [15, 16]. They also showed that near to the limiting values multiple solutions may exist at the same values of F and $\beta$. We did not seek such solutions in this work.

The maximum value of Froude number F, at which limiting steady state solutions are formed is dependent on the horizontal sink location $x_\mathrm{{s}}$ and the surface tension $\beta$, as is evident by Fig. 7. It is to be expected that, as $x_\mathrm{{s}} \rightarrow \infty$, the effect of the wall is diminished and the maximum Froude number should reach the highest value. However, as $x_\mathrm{{s}} \rightarrow 0$, the effect of the wall becomes more pronounced, reducing the maximum by amplifying the disturbance.

No attempt has been made to obtain solutions with a cusp since the calculations involved would require a different approach to that used herein. Our results for the stagnation point solutions, however, suggest that there may be solutions with a cusp on the wall if the sink is sufficiently close to the wall, but that this may “move” to above the sink when the sink is away from the wall. This will be an interesting subject for further study.