Singularity analysis for the V-notch in functionally graded piezoelectric/piezomagnetic material

Abstract

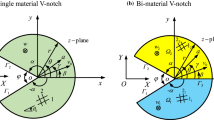
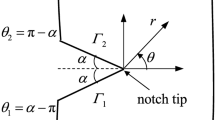
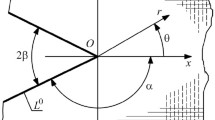
The singularity of the V-notch in the functionally graded piezoelectric/piezomagnetic (FGPE/PM) material, whose property is varying as a power function along the radial direction, is investigated in this paper. Basing on the assumption that the physical fields around the notch vertex are expressed as the series asymptotic expansions, the singularity characteristic equations for the FGPE/PM V-notch are derived from the equilibrium equation of elasticity and Maxwell equation of electric displacement and magnetic induction. Meanwhile, the mechanical, electrical, and magnetic boundary conditions on the radial face of the V-notch are converted into the combination of the singularity index, characteristic angular function, and its derivative. The interpolation matrix method is introduced to solve the singularity characteristic equations under the given boundary condition. The singularity index, characteristic angular function together with their first- and second-order derivatives can be yielded with the same order accuracy, which can be applied to construct the singular element in the numerical method to evaluate the complete singular physical field around the vertex of the FGPE/PM V-notch. From the numerical testing, it can be found that the first singularity index of the FGPE/PM V-notch decreases with an increase in the inhomogeneous exponent. The opening angle of the V-notch which shows the singularity becomes bigger when the inhomogeneous exponent is increasing. The first singularity index for the anti-plane FGPE/PM V-notch under the free-free boundary condition is greater than the one under the free-clamped boundary condition.

Appendices

Appendix A

The characteristic ordinary differential equation, such as Eqs. (8) and (17), can be written in a general form as follows:

$$\begin{aligned} \sum \limits _{j=0}^m {g_{j} (\theta )\cdot \tilde{{w}}_{k}^{(j)} (\theta )} -\lambda _{k} \sum \limits _{j=0}^m {q_{j} (\theta )\cdot \tilde{{w}}_{k}^{(j)} (\theta )} =0, \quad \theta \in [-\theta _{1} ,\theta _{1} ], \end{aligned}$$

(23)

where the superscript j denotes the $j\;\text {th}$ order derivative with respect to $\theta$, $g_{j} (\theta )$ and $q_{j} (\theta )$ are the coefficients which depend on $\theta$, and m is the highest order derivative of $\tilde{{w}}_{k} (\theta )$.

The boundary condition, such as Eqs. (10) and (21), can also be written in a general form as follows:

$$\begin{aligned} \sum \limits _{j=0}^{m-1} {\alpha _{j} \cdot \tilde{{w}}_{k}^{(j)} (\theta )} -\lambda _{k} \sum \limits _{j=0}^{m-1} {\beta _{j} \cdot \tilde{{w}}_{k}^{(j)} (\theta )} =0\,, \quad \theta \in [-\theta _{1} ,\theta _{1} ], \end{aligned}$$

(24)

where $\alpha _{j}$ and $\beta _{j}$ are the corresponding coefficients.

The interval $\theta \in [-\theta _{1} ,\theta _{1} ]$ is uniformly divided into n subintervals at divisions $\theta _{(0)} ,\theta _{({1})} ,\ldots ,\theta _{(n)}$, where $\theta _{(0)} =-\theta _{1}$ and $\theta _{(n)} =\theta _{1}$. The application of Eq. (23) at each division yields

$$\begin{aligned} \sum \limits _{j=0}^m {{\varvec{G}}}_{j} {{\varvec{W}}}_{k}^{(j)} (\theta )-\lambda _{k} \sum \limits _{j=0}^m {{\varvec{Q}}}_{j} {{\varvec{W}}}_{k}^{(j)} (\theta )=0, \end{aligned}$$

(25)

where ${{\varvec{W}}}_{k}^{(j)} (\theta )=(\tilde{{w}}_{k}^{(j)} (\theta _{(0)} ),\tilde{{w}}_{k}^{(j)} (\theta _{({1})} ),\ldots ,\tilde{{w}}_{k}^{(j)} (\theta _{(n)} ))^\mathrm{{T}}$. The $\tilde{{w}}_{k}^{(j-1)} (\theta )$ can be integrated by $\tilde{{w}}_{k}^{(j)} (\theta )$ as

$$\begin{aligned} \tilde{{w}}_{k}^{(j-1)} (\theta _{(m)} )-\tilde{{w}}_{k}^{(j-1)} (\theta _{(0)} )=\int _{\,\theta _{(0)} }^{\,\theta _{(m)} } \tilde{{w}}_{k}^{(j)} (\theta )\text {d}\theta , \quad m=\text {1,}\ldots {,}n, \end{aligned}$$

(26)

and $\tilde{{w}}_{k}^{(j)} (\theta )$ can be approximated using the Lagrangian polynomial function $L_{m} (\theta )$ as

$$\begin{aligned} \tilde{{w}}_{k}^{(j)} (\theta )=\sum \limits _{m=0}^n \tilde{{w}}_{k}^{(j)} (\theta _{(m)} )L_{m} (\theta ), \quad \theta \in [-\theta _{1} ,\theta _{1} ]. \end{aligned}$$

(27)

Thus, the recurrence relation of Eq. (26) for an arbitrary jis in the form as follows:

$$\begin{aligned} {{\varvec{W}}}_{k}^{(j)} ={{\varvec{P}}}_{kj} {{\varvec{W}}}_{k0} +{{\varvec{D}}}^{m-j}{{\varvec{W}}}_{k}^{(m)} , \quad j=1,\ldots ,m-1, \end{aligned}$$

(28)

where ${{\varvec{W}}}_{k0} =(\tilde{{w}}_{k} (\theta _{0} ),{\tilde{{w}}}'_{k} (\theta _{0} ),\ldots ,\tilde{{w}}_{k}^{(m-1)} (\theta _{0} ))^{{T}}$ and ${{\varvec{D}}}$ is the interpolating integral matrix.

By substituting Eqs. (28) into (25), the following algebraic equation can be obtained:

$$\begin{aligned} {{\varvec{A}}}_{k} {{\varvec{W}}}_{k0} +{{\varvec{B}}}_{k} {{\varvec{W}}}_{k}^{(m)} -\lambda _{k} ({{\varvec{A}}}_{\lambda k} {{\varvec{W}}}_{k0} +{{\varvec{B}}}_{\lambda k} {{\varvec{W}}}_{k}^{(m)} )=\text {0}. \end{aligned}$$

(29)

The boundary condition (24) can be discretized and written as the algebraic equation in a similar manner as follows

$$\begin{aligned} ({{\varvec{V}}}_{\alpha k} {{\varvec{W}}}_{k0} +{{\varvec{X}}}_{\alpha k} {{\varvec{W}}}_{k}^{(m)} )-\lambda _{k} ({{\varvec{V}}}_{\beta k} {{\varvec{W}}}_{k0} +{{\varvec{X}}}_{\beta k} {{\varvec{W}}}_{k}^{(m)} )=\text {0}, \end{aligned}$$

(30)

Once the system of equations (29) and (30) is solved by the numerical method such as QR method, one can get a finite term of the singularity index $\lambda _{k}$ and corresponding characteristic angular functions $({{\varvec{W}}}_{k0} ,{{\varvec{W}}}_{k}^{(m)} )^\mathrm{{T}}$.

Appendix B

See Tables 2 and 3.

Table 2 Material properties of PZT-4 [27]

Table 3 Material properties of $\text {BaTiO}_{{3}}$ and $\text {CoFe}_{{2}}\text {O}_{4}$ [24]