A model of an inflatable elastic aerofoil

Abstract

A novel method is presented to calculate the deformation of a simple elastic aerofoil with a view to determining its aerodynamic viability. The aerofoil is modelled as a thin two-dimensional elastic sheet whose ends are joined together to form a corner of prescribed angle, with a simple support included to constrain the shape to resemble that of a classical aerofoil. The weight of the aerofoil is counterbalanced exactly by the lift force due to a circulation set according to the Kutta condition. An iterative process based on a boundary integral method is used to compute the deformation of the aerofoil in response to an inviscid fluid flow, and a range of flow speeds is determined for which the aerofoil maintains an aerodynamic shape. As the flow speed is increased the aerofoil deforms significantly around its trailing edge, resulting in a negative camber and a loss of lift. The loss of lift is ameliorated by increasing the inflation pressure but at the expense of an increase in drag as the aerofoil bulges into a less aerodynamic shape. Boundary layer calculations and nonlinear unsteady viscous simulations are used to analyse the aerodynamic characteristics of the deformed aerofoil in a viscous flow. By tailoring the internal support the viscous boundary layer separation can be delayed and the lift-to-drag ratio of the aerofoil can be substantially increased.

1 Introduction

Inflatable aerofoils are of increasing interest in the aerospace industry. They have several advantages over traditional rigid aerofoils. They can be packed into a small volume for ease of transportation, and for this reason they have been suggested for use in extraterrestrial exploration [1, 2]. Their design typically involves some internal support structure which can be tailored in-flight to attain optimal performance in multiple roles with different flight requirements [3, 4].

Brown et al. [5] provide an overview of various inflatable aerofoil designs, including notably the Goodyear Inflatoplane [6]. Of particular relevance to this study is the design in the patent of Bain et al. [7], which is constructed using flexible pressurised panels with an internal support. More recently the experimental study of Simpson [4] considered other relevant designs which are formed by inflating a flexible chamber with internal support cables.

Here we present a novel method to calculate the deformation of a simple elastic aerofoil, and perform a preliminary study of its aerodynamic viability. We model the aerofoil as a smooth two-dimensional elastic aerofoil with a corner of fixed angle at the trailing edge, with a straight inextensible support joining two chosen points on the aerofoil boundary to constrain the deformation. The aerofoil is assumed to maintain a constant altitude, with its weight balanced by the lift force due to a circulation which is fixed according to the Kutta condition. We first evaluate the aerofoil deformation in response to an inviscid fluid flow using an iterative method based on a boundary integral approach. This allows an efficient exploration of parameter space to determine conditions under which a good aerodynamic shape can be maintained. We then compute the viscous flow past these aerofoil shapes using a combination of boundary layer calculations and full DNS using the software package Gerris [8, 9]. This allows us to assess the relevance of the inviscid calculations to a real flow and to determine the aerodynamic viability of the aerofoil by computing the lift-to-drag ratio. For simplicity, the deformed aerofoil is treated as a rigid body in the viscous flow calculations.

The layout of the paper is as follows. In Sect. 2 we formulate the inviscid problem, discuss the numerical method and present the inviscid results. In Sect. 3 we present the viscous results. Finally, in Sect. 4 we summarise our findings.

Fig. 1

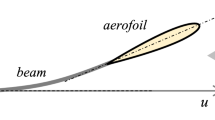
A sketch of the aerofoil with corner angle $\beta$ in a uniform stream of speed $u_\infty$. The straight internal support of length $\ell L$, where L is the perimeter of the aerofoil and $\ell$ is a dimensionless parameter, is shown with a thick line. The chord of the aerofoil is depicted as a dashed line from the trailing edge to the leading edge, where the leading edge is defined as the point on the aerofoil furthest from the trailing edge. The angle of attack $\alpha$ is defined as the angle in degrees between the chord and the horizontal

2 Inviscid flow calculations

We consider an inflatable aerofoil in a uniform fluid flow, as depicted in Fig. 1. The aerofoil is treated as a thin two-dimensional elastic sheet which is everywhere smooth except at the trailing edge, at which point it forms a rigid corner of fixed angle $\beta$. The aerofoil shape is assumed to be invariant in the spanwise direction. We allow for an inextensible internal support which restricts the deformation of the aerofoil. By adjusting the length and position of the support the extent of the elastic deformation can be controlled, allowing the aerofoil to attain a more aerodynamic shape. The elastic material is assumed to pass smoothly over the support points, as in the design of Bain et al. [7], which helps maintain a smooth aerofoil shape. In contrast, Simpson [4] considers an aerofoil consisting of multiple elastic components which can pivot freely at the support point, resulting in a bumpy aerofoil shape; this case is not considered here.

The fluid flow is taken to be a uniform stream of speed $u_\infty$ in the far-field, with circulation $\gamma$ chosen to satisfy the Kutta condition at the trailing edge. The flow is assumed to be incompressible, irrotational and inviscid, and invariant in the spanwise direction. These assumptions allow us to formulate the fluid flow in terms of a boundary integral equation, which facilitates an iterative method to determine the deformation of the aerofoil in response to the flow. The effects of viscosity, which are important in determining the aerodynamic characteristics of the deformed aerofoils, will be considered in Sect. 3.

2.1 Formulation

We parametrise the boundary of the aerofoil in vector form as $\varvec{\eta }(s)=x(s)\varvec{i}+y(s)\varvec{j}$, where $0\le s \le L$ is the arc-length distance from the trailing edge in the anticlockwise direction and L is the perimeter of the aerofoil. We define the leading edge of the aerofoil as the point on the curve $\varvec{\eta }(s)$ which maximises the distance $|\varvec{\eta }(s)-\varvec{\eta }(0)|$ from the trailing edge. The chord of the aerofoil is then defined as the straight line between the leading and trailing edges, with the angle of attack $\alpha$ defined as the angle in degrees the chord makes to the horizontal, as depicted in Fig. 1. Since the aerofoil is closed at the trailing edge we require $\varvec{\eta }(0) =\varvec{\eta }(L)={0}$, where the trailing edge is assumed to be located at the origin. The internal support is attached to the aerofoil at two points $0<S_1<S_2<L$, and exerts a point force of magnitude f in the direction $\hat{\varvec{r}}$ at $s=S_1$ and $-\hat{\varvec{r}}$ at $s=S_2$, where $\hat{\varvec{r}}$ is the unit vector defined as

$$\begin{aligned} \hat{\varvec{r}} = \frac{\varvec{\eta }(S_2)-\varvec{\eta }(S_1)}{\left| \varvec{\eta }(S_2)-\varvec{\eta }(S_1) \right| }. \end{aligned}$$

(1)

The value of f will be determined implicitly by fixing the length of the internal support relative to the perimeter L as

$$\begin{aligned} \left| \varvec{\eta }(S_2)-\varvec{\eta }(S_1) \right| = \ell L \end{aligned}$$

(2)

for a chosen value of the dimensionless parameter $\ell$.

We denote by T(s) and N(s) the tangential and normal components respectively of the internal tension per unit span $\varvec{R}(s) =T\hat{\varvec{\tau }} + N\hat{\varvec{n}}$, where $\hat{\varvec{\tau }}$ is the unit tangent vector in the anticlockwise direction and $\hat{\varvec{n}}$ is the unit outwards normal vector. A balance of moments about an infinitesimal section of the aerofoil gives $N=M_s$, where $M_s$ is the arc-length derivative of the elastic bending moment per unit span M(S). Since the internal support can pivot freely at the points $S_1$ and $S_2$, it exerts no moment on the aerofoil, and we thus require M(s) to be continuous at $s=S_1$ and $s=S_2$. We assume the bending moment at any point is proportional to the difference between the curvature at that point and its resting curvature. Such an assumption is justified by Pozrikidis [10] for a locally inextensible elastic material. This gives the constitutive equation for the bending moment

$$\begin{aligned} M = -E_\mathrm{{B}} (\kappa -\kappa _\mathrm{{R}}), \end{aligned}$$

(3)

where $\kappa = x_\mathrm{{ss}}y_\mathrm{{s}} - x_\mathrm{{s}}y_\mathrm{{ss}}$ is the signed curvature of the aerofoil boundary. $\kappa _\mathrm{{R}}$ is the resting curvature which is assumed to be constant, and $E_\mathrm{{B}}$ is the bending rigidity. According to thin-shell theory, the bending rigidity is given by $E_\mathrm{{B}} = \frac{Eh^3}{12(1-\nu ^2)}$, where E is the Young’s modulus, $\nu$ is the Poisson’s ratio, and h is the thickness of the elastic material.

For equilibria to occur we require a balance between the internal and external forces acting upon the aerofoil. We thus require

$$\begin{aligned} \varvec{R}_s - \varDelta p(s)\hat{\varvec{n}} - \varrho gh\varvec{j} +f\hat{\varvec{r}}\left[ \delta (s-S_1)-\delta (s-S_2)\right] = 0, \end{aligned}$$

(4)

where $\varDelta p(s)$ is the pressure difference between the exterior and interior of the aerofoil, $\varrho$ and h are the density and thickness of the cell material, g is the acceleration due to gravity, and $\delta (s)$ is the Dirac delta function. For $s\ne S_1,S_2$, we split (4) into tangential and normal components to obtain

$$\begin{aligned} T_s-\kappa N = \varrho hg y_s, \quad N_s+\kappa T =\varDelta p(s)-\varrho hg x_s. \end{aligned}$$

(5)

Recalling that the normal component of the tension is given by $N=M_s = -E_\mathrm{{B}}\kappa _s$, (5) is reduced to

$$\begin{aligned} T_s+ E_\mathrm{{B}}\kappa \kappa _s=\varrho hgy_s, \quad -E_\mathrm{{B}}\kappa _{ss}+\kappa T = \varDelta p(s) -\varrho hgx_s. \end{aligned}$$

(6)

Integrating, we obtain

$$\begin{aligned} T = E_\mathrm{{B}}\left( \frac{\sigma }{L^2}-\tfrac{1}{2}\kappa ^2\right) + \varrho hgy, \end{aligned}$$

(7)

and

$$\begin{aligned} \varDelta p(s) = -E_\mathrm{{B}} \left( \kappa _{ss}+\tfrac{1}{2} \kappa ^3 - \frac{\sigma \kappa }{L^2}\right) +\varrho hg(x_s+\kappa y), \end{aligned}$$

(8)

where $\sigma$ is a dimensionless piecewise-constant of integration whose value jumps across the points $s=S_1$ and $s=S_2$. The internal stress is thus given by

$$\begin{aligned} \varvec{R}(s) = \left( E_\mathrm{{B}}\left( \frac{\sigma }{L^2} -\tfrac{1}{2}\kappa ^2\right) + \varrho hgy\right) \hat{\varvec{\tau }} - E_\mathrm{{B}}\kappa _s \hat{\varvec{n}}. \end{aligned}$$

(9)

To remove the singularities in (4) we integrate over the points $S_1$ and $S_2$, giving

$$\begin{aligned} \varvec{R}(S_i+)-\varvec{R}(S_i-) = (-1)^if\hat{\varvec{r}}, \quad i = 1,2. \end{aligned}$$

(10)

Since the bending moment M and thus the curvature $\kappa$ are both continuous at $s=S_1$ and $s = S_2$, (9) gives

$$\begin{aligned} \varvec{R}(S_i+)-\varvec{R}(S_i-) = \frac{E_\mathrm{{B}}}{L^2} \big [\sigma (S_i+)-\sigma (S_i-) \big ]\hat{\varvec{\tau }} -E_\mathrm{{B}}\big [\kappa _s(S_i+)-\kappa _s(S_i-)\big ]\hat{\varvec{n}}. \end{aligned}$$

(11)

We thus obtain the two jump conditions

$$\begin{aligned} \sigma (S_i+)-\sigma (S_i-)&= (-1)^i\frac{fL^2}{E_\mathrm{{B}}}\hat{\varvec{r}} \cdot \hat{\varvec{\tau }}(S_i),\quad i = 1,2, \end{aligned}$$

(12)

$$\begin{aligned} \kappa _s(S_i+)-\kappa _s(S_i-)&= (-1)^{i+1}\frac{f}{E_\mathrm{{B}}} \hat{\varvec{r}}\cdot \hat{\varvec{n}}(S_i),\quad i = 1,2. \end{aligned}$$

(13)

Comparing Bernoulli’s equation for the fluid in the exterior of the aerofoil between the surface of the aerofoil and the far-field gives

$$\begin{aligned} \tfrac{1}{2}\rho q(s)^2 + \rho gy(s)+ p(s) = \tfrac{1}{2} \rho u_\infty ^2 + p_\mathrm{{a}} - \rho gH, \end{aligned}$$

(14)

where $\rho$ is the density of the fluid, q(s) is the flow speed evaluated at the aerofoil boundary, y(s) is the height of a point on the aerofoil relative to the trailing edge, p(s) is the exterior fluid pressure evaluated at the aerofoil boundary, $u_\infty$ is the far-field flow speed, and $p_\mathrm{{a}}$ is the atmospheric pressure evaluated at some reference height $-H$ which is assumed to be ground level. The interior of the aerofoil, which is taken to be a static fluid with density $\rho$ equal to that of the exterior fluid, has pressure

$$\begin{aligned} p_i(y) = p_0 - \rho gy, \end{aligned}$$

(15)

for some constant $p_0$. While this formulation can allow different values of $p_0$ either side of the internal support, we will henceforth assume that $p_0$ is uniform throughout the interior. The transmural pressure difference is thus given by

$$\begin{aligned} \varDelta p(s) = p(s)-p_i(y(s)) = p_\mathrm{{a}}-\rho g H-p_0+\tfrac{1}{2} \rho (u_\infty ^2-q^2). \end{aligned}$$

(16)

Substituting this expression for $\varDelta p(s)$ into (8) we obtain the dynamic condition on the surface of the aerofoil

$$\begin{aligned} \tfrac{1}{2}\rho \left( q^2-u_\infty ^2\right) + p_0-p_\mathrm{{a}} + \rho g H -E_\mathrm{{B}} \left( \kappa _{ss}+\tfrac{1}{2}\kappa ^3 -\frac{\sigma \kappa }{L^2}\right) +\varrho hg(x_s+\kappa y) =0. \end{aligned}$$

(17)

For equilibria to occur, the parameters must be chosen to ensure that the lift generated by the fluid flow is equal and opposite to the weight of the aerofoil. Making use of the Kutta–Joukowski theorem, we thus require

$$\begin{aligned} \rho \gamma u_\infty = -\varrho ghL, \end{aligned}$$

(18)

where the circulation $\gamma$ is taken to be negative to generate a positive lift. Note that an evenly distributed load force can be modelled by an appropriate choice of the value of $\varrho$.

We then non-dimensionalise the problem, taking the length scale to be the aerofoil perimeter L and the velocity scale to be $\sqrt{E_\mathrm{{B}}/(L^3\rho )}$. Enforcing (18) the dynamic condition (17) then becomes

$$\begin{aligned} \tfrac{1}{2} \left( q^2-U_\infty ^2\right) -\left( \kappa _{ss}+\tfrac{1}{2}\kappa ^3 - \sigma \kappa \right) +\varGamma U_\infty (x_s+\kappa y) +P=0, \end{aligned}$$

(19)

where all variables are now dimensionless and

$$\begin{aligned} U_\infty = u_\infty \sqrt{\frac{L^3\rho }{E_\mathrm{{B}}}}, \quad \varGamma = -\gamma \sqrt{\frac{L\rho }{E_\mathrm{{B}}}}, \quad P = \frac{(p_0-p_\mathrm{{a}}+\rho g H)L^3}{E_\mathrm{{B}}} \end{aligned}$$

(20)

are dimensionless quantities relating to the far-field flow speed, the negative circulation around the aerofoil, and interior pressure of the aerofoil relative to atmospheric pressure respectively. Note that $U_\infty ^2$ can also be considered the ratio between the dynamic pressure due to the uniform stream and the internal stress due the elasticity of the aerofoil.

The dimensionless flow field $\varvec{u}(\varvec{x})$, where $\varvec{x}$ is a point in the exterior of the aerofoil $\varvec{\eta }(s)$, must satisfy the following five conditions:

$$\begin{aligned}&\nabla \cdot \varvec{u} = 0 \quad \text {(incompressibility)}, \end{aligned}$$

(21)

$$\begin{aligned}&\nabla \times \varvec{u} = \varvec{0} \quad \text {(irrotationality)}, \end{aligned}$$

(22)

$$\begin{aligned}&\varvec{u}(\varvec{\eta }(s))\cdot \varvec{\hat{n}}(s) = 0 \quad \text {(kinematic condition)}, \end{aligned}$$

(23)

$$\begin{aligned}&\varvec{u}(\varvec{\eta }(0))=\varvec{0} \quad \text {(Kutta condition)}, \end{aligned}$$

(24)

$$\begin{aligned}&\varvec{u}(\varvec{x}) = U_\infty \varvec{i} + \frac{\varGamma }{2\pi } \frac{\varvec{x}\times \varvec{k}}{|\varvec{x}|^2} + {\mathcal {O}} \big (|\varvec{x}|^{-2}\big ) \quad \text {as} \quad |\varvec{x}|\rightarrow \infty \quad \text {(far-field condition).} \end{aligned}$$

(25)

The kinematic condition ensures the fluid velocity has no component normal to the aerofoil, the Kutta condition ensures the flow leaves the aerofoil smoothly at the trailing edge, and the far-field condition ensures the flow tends to a uniform stream with circulation $-\varGamma$ in the far-field.

We define the lift and drag coefficients and the lift-to-drag ratio as

$$\begin{aligned} C_\mathrm{{L}} = \frac{2\varvec{F}\cdot \varvec{j}}{\rho u_\infty ^2 L/2}, \quad C_\mathrm{{D}} = \frac{2\varvec{F}\cdot \varvec{i}}{\rho u_\infty ^2 L/2},\quad C_\mathrm{{L}}/C_\mathrm{{D}} = \frac{\varvec{F}\cdot \varvec{j}}{\varvec{F}\cdot \varvec{i}}, \end{aligned}$$

(26)

respectively, where $\varvec{F}$ is the net fluid force acting upon the aerofoil, $\varvec{i}$ and $\varvec{j}$ are unit vectors in the positive horizontal and vertical directions respectively, and the reference length is taken to be half the dimensional aerofoil perimeter to ensure the values are comparable between deformed aerofoil shapes. The lift-to-drag coefficient however is independent of the choice of reference length. For an inviscid flow we have $\varvec{F} = -\rho u_\infty \gamma \varvec{j}$, and so $C_\mathrm{{L}} = 4\varGamma /U_\infty$ and $C_\mathrm{{D}}=0$, while the viscous flow, which will be considered in Sect. 3, will generally have a non-zero value of $C_\mathrm{{D}}$.

2.2 Numerical method

The aim of the numerical method is to obtain an aerofoil shape $\varvec{\eta }(s)$ along with a flow field $\varvec{u}(\varvec{x})$ which satisfy the dynamic condition (19) along with the flow conditions (21)–(25). We obtain solutions numerically using an iterative method, first computing the cell shape $\varvec{\eta }(s)$ which satisfies (19) for a chosen flow speed q(s), and then finding the flow $\varvec{u}(\varvec{x})$ which satisfies (21)–(25) for the computed value of $\varvec{\eta }(s)$. We then use Newton’s method to obtain the value of q(s) which satisfies $q(s) = |\varvec{u}(\varvec{\eta }(s))|$.

To obtain the aerofoil shape $\varvec{\eta }(s) = x(s)\varvec{i} + y(s) \varvec{j}$, we note that

$$\begin{aligned} x_s = -\cos \theta , \quad y_s = \sin \theta , \quad \kappa = \theta _s, \end{aligned}$$

(27)

where $\theta$ is the angle between the tangent vector $\hat{\varvec{\tau }}$ and $-\varvec{i}$. We can then write the dynamic condition (19) as

$$\begin{aligned} \kappa _{ss} = \tfrac{1}{2}\left( q^2-U_\infty ^2\right) -\tfrac{1}{2}\kappa ^3 + \sigma \kappa +\varGamma U_\infty \left( \kappa y-\cos \theta \right) +P. \end{aligned}$$

(28)

Equations (27) and (28) form a system of explicit ODEs which must be solved on each of the three sections of the aerofoil, with jump and continuity conditions at $s=S_1$ and $s=S_2$ and boundary conditions at $s=0$ and $s=1$. At $S_1$ and $S_2$ we require x, y, $\theta$ and $\kappa$ to be continuous, while $\kappa _s$ and $\sigma$ must satisfy the jump conditions (12) and (13). At the trailing edge we require

$$\begin{aligned} x(0) = x(1) = y(0) = y(1) = 0, \quad \theta (1)-\theta (0) = \pi -\beta , \end{aligned}$$

(29)

and we are free to choose the value of $\theta (0)$ which implicitly determines the angle of attack $\alpha$. We also have the constraint

$$\begin{aligned} \left| \varvec{\eta }(S_2)-\varvec{\eta }(S_1) \right| = \ell . \end{aligned}$$

(30)

The system given by (27) and (28) can be integrated numerically for a known flow speed q(s) using a Runge–Kutta method to obtain the equilibrium aerofoil shape $\varvec{\eta }(s) = x(s)\varvec{i} + y(s)\varvec{j}$.

We approximate the flow speed q(s) as a piecewise Chebyshev series

$$\begin{aligned} q(s)\approx q_\mathrm{{c}}(s) \equiv \left\{ \begin{array}{ll} \sum \limits _{n=0}^N a_n T_n\big (2\frac{s}{S_1}-1\big ) &{} \text{ for } 0\le s< S_1, \\ \sum \limits _{n=0}^N b_n T_n\big (2\frac{s-S_1}{S_2-S_1}-1\big ) &{} \text{ for } S_1\le s \le S_2,\\ \sum \limits _{n=0}^N c_n T_n\big (2\frac{s-S_2}{1-S_2}-1\big ) &{} \text{ for } S_2< s \le 1. \end{array}\right. \end{aligned}$$

(31)

where $T_n(s) = \cos \big (n\cos ^{-1}(s)\big )$ is the degree n Chebyshev polynomial, N is some truncation value, and the $3N+3$ coefficients $a_n$, $b_n$ and $c_n$ are to be found. To ensure $q_\mathrm{{c}}(s)$ is continuous at $S_1$ and $S_2$, we take

$$\begin{aligned} a_0 = b_0 + \sum _{n=1}^{N} \left( b_n \cos \left( \frac{n\pi }{2}\right) -a_n\right) , \quad c_0 = b_0 + \sum _{n=1}^N \left( b_n-c_n\cos \left( \frac{n\pi }{2}\right) \right) . \end{aligned}$$

(32)

The $3N+1$ remaining coefficients will be found by enforcing the interpolation condition $q_\mathrm{{c}}(s_i)=q(s_i)$ at the $3N+1$ sample points

$$\begin{aligned} s_i = \frac{1+C_i}{2}S_1,\quad s_{i+N} = \frac{1-C_i}{2}S_1 +\frac{1+C_i}{2}S_2 , \quad s_{i+2N} =\frac{1-C_i}{2}S_2 +\frac{1+C_i}{2} \end{aligned}$$

(33)

for $i = 1,\dots ,N+1$, where $C_i$ are the Chebyshev nodes

$$\begin{aligned} C_i = -\cos \left( \frac{(i-1)\pi }{N}\right) , \quad i = 1,\ldots ,N+1, \end{aligned}$$

(34)

which correspond to the extrema of the Nth Chebyshev polynomial $T_N(s)$. By choosing coefficients $a_n$, $b_n$ and $c_n$ such that $q_\mathrm{{c}}(s_i)=q(s_i)$ at the rescaled Chebyshev nodes $s_i$, the Chebyshev series $q_\mathrm{{c}}(s)$ provides a near-best interpolation of the function q(s) [11].

Given an aerofoil shape $\varvec{\eta }(s)$, we can obtain the unique flow speed $q_b(s)$ which satisfies the flow equations (21)–(25) using a boundary integral method. Following Pozrikidis [12], we split the fluid velocity $\varvec{u}(\varvec{x})$ into a far-field component

$$\begin{aligned} \varvec{u}^\infty = U_\infty \varvec{i} + \frac{\varGamma }{2\pi }\frac{\varvec{x} \times \varvec{k}}{|\varvec{x}|^2} \end{aligned}$$

(35)

and a disturbance flow $\varvec{u}^\mathrm{{D}}$ which vanishes in the far-field. Since the flow is incompressible and irrotational, we can write the disturbance flow in terms of a velocity potential $\phi ^\mathrm{{D}}(\varvec{x})$ which must be harmonic and bounded in the far-field. The disturbance potential satisfies the boundary integral equation

$$\begin{aligned} \tfrac{1}{2}\phi ^\mathrm{{D}}(\varvec{x}_0) = -\int _{\varvec{\eta }(s)} G(\varvec{x},\varvec{x}_0) \nabla \phi ^\mathrm{{D}}(\varvec{x}) \cdot \hat{\varvec{n}}(s) \mathrm {d}s(\varvec{x}) +\int _{\varvec{\eta }(s)}^{PV} \phi ^\mathrm{{D}}(\varvec{x}) \nabla G(\varvec{x},\varvec{x}_0)\cdot \hat{\varvec{n}}(s)\mathrm {d}s(\varvec{x}), \end{aligned}$$

(36)

where both integrals are evaluated along the curve $\varvec{x} =\varvec{\eta }(s)$, $\varvec{x}_0$ is a point on the aerofoil boundary, $G(\varvec{x},\varvec{x}_0)$ is the free-space Green’s function

$$\begin{aligned} G(\varvec{x},\varvec{x}_0) = -\frac{1}{2\pi }\log |\varvec{x}-\varvec{x}_0|, \end{aligned}$$

(37)

and the principal value (PV) is taken for the second integral across the singularity at $\varvec{x} = \varvec{x}_0$.

To solve the boundary integral equation numerically, we discretise the aerofoil boundary as the 3N straight lines

$$\begin{aligned} \varvec{E}_i = \varvec{\eta }_i + \left( \varvec{\eta }_{i+1} -\varvec{\eta }_i\right) t \quad \text {for} \quad 0 \le t\le 1, \quad i = 1,\dots ,3N, \end{aligned}$$

(38)

between the $3N+1$ sample points $\varvec{\eta }_i = \varvec{\eta }(s_i)$. The tangent and normal vectors to the boundary element $\varvec{E}_i$, written as $\hat{\varvec{\tau }}_i$ and $\hat{\varvec{n}}_i$ respectively, are constant on each boundary element and are given by

$$\begin{aligned} \hat{\varvec{\tau }}_i = \frac{\varvec{\eta }_{i+1}-\varvec{\eta }_i}{|\varvec{\eta }_{i+1} -\varvec{\eta }_i|}, \quad \hat{\varvec{n}}_i = \frac{(y_{i+1}-y_i)\varvec{i} - (x_{i+1}-x_i)\varvec{j}}{|\varvec{\eta }_{i+1}-\varvec{\eta }_i|}. \end{aligned}$$

(39)

We approximate $\phi ^\mathrm{{D}}$ and $\nabla \phi ^\mathrm{{D}}$ as constants $\phi ^\mathrm{{D}}_i$ and $(\nabla \phi ^\mathrm{{D}})_i$ on each boundary element, which are assumed to be equal to the values of $\phi ^\mathrm{{D}}$ and $\nabla \phi ^\mathrm{{D}}$ at the midpoints $\varvec{\eta }_i^\mathrm{{M}} = \tfrac{1}{2}(\varvec{\eta }_{i+1}+\varvec{\eta }_i)$. Evaluating the kinematic condition (23) on the ith boundary element, we obtain

$$\begin{aligned} \hat{\varvec{n}}_i \cdot \big ( \nabla \phi ^\mathrm{{D}}\big )_i = -\hat{\varvec{n}}_i \cdot \varvec{u}^\infty \big (\varvec{\eta }_i^\mathrm{{M}}\big ) = -U_\infty \hat{\varvec{n}}_i\cdot \varvec{i} - \frac{\varGamma }{2\pi } \frac{\varvec{\eta }_i^\mathrm{{M}}\cdot \hat{\varvec{\tau }_i}}{\big |\varvec{\eta }^\mathrm{{M}}_i\big |^2}. \end{aligned}$$

(40)

The boundary integral equation (36) can then be discretised as

$$\begin{aligned} \tfrac{1}{2}\;\phi ^\mathrm{{D}}(\varvec{x}_0)&= U_\infty \sum _{i=1}^{3N} \hat{\varvec{n}}_i\cdot \varvec{i}\int _{\varvec{E}_i} G(\varvec{x},\varvec{x}_0) \mathrm {d}s(\varvec{x}) +\frac{\varGamma }{2\pi }\sum _{i=1}^{3N} \frac{\varvec{\eta }_i^\mathrm{{M}}\cdot \hat{\varvec{\tau }_i}}{\big |\varvec{\eta }^\mathrm{{M}}_i\big |^2} \int _{\varvec{E}_i} G(\varvec{x},\varvec{x}_0)\mathrm {d}s(\varvec{x})\nonumber \\&\quad +\sum _{i=1}^{3N} \phi _i^\mathrm{{D}} \int _{\varvec{E}_i}^{PV} \hat{\varvec{n}}_i\cdot \nabla G(\varvec{x},\varvec{x}_0)\mathrm {d}s(\varvec{x}), \end{aligned}$$

(41)

where the integrals are taken along the boundary elements. Taking $\varvec{x}_0$ to be the midpoint of the jth boundary element for $j=1,\dots ,3N$, we obtain

$$\begin{aligned}&\tfrac{1}{2}\phi ^\mathrm{{D}}_j-\sum _{i=1}^{3N} \phi _i^\mathrm{{D}} \int _{\varvec{E}_i}^{PV} \left[ \hat{\varvec{n}}_i\cdot \nabla G\left( \varvec{x},\varvec{\eta }_j^\mathrm{{M}}\right) \right] \mathrm {d}s(\varvec{x}) - \frac{\varGamma }{2\pi }\sum _{i=1}^{3N} \frac{\varvec{\eta }_i^\mathrm{{M}}\cdot \hat{\varvec{\tau }_i}}{\big |\varvec{\eta }^\mathrm{{M}}_i\big |^2} \int _{\varvec{E}_i} G\left( \varvec{x},\varvec{\eta }_j^\mathrm{{M}}\right) \mathrm {d}s(\varvec{x})\nonumber \\&\quad = U_\infty \sum _{i=1}^{3N} \hat{\varvec{n}}_i\cdot \varvec{i} \int _{\varvec{E}_i} G\left( \varvec{x},\varvec{\eta }_j^\mathrm{{M}}\right) \mathrm {d}s(\varvec{x}). \end{aligned}$$

(42)

Using the complex notation $z(s) = x(s) + y(s) \mathrm {i}$ for brevity, the integrals in (42) can be evaluated explicitly as

$$\begin{aligned}&\int _{\varvec{E}_i} G\left( \varvec{x},\varvec{\eta }_j^\mathrm{{M}}\right) \mathrm {d}s(\varvec{x})\nonumber \\&\quad =-\frac{|z_{i+1}-z_i|}{2\pi }\,\mathfrak {R}\left( \frac{\left( z_{i+1} -z_j^\mathrm{{M}}\right) \log \left( z_{i+1}-z_j^\mathrm{{M}}\right) -\left( z_{i}-z_j^\mathrm{{M}}\right) \log \left( z_{i}-z_j^\mathrm{{M}}\right) }{z_{i+1}-z_i}-1\right) \end{aligned}$$

(43)

and

$$\begin{aligned} \int _{\varvec{E}_i}^{PV}\hat{\varvec{n}}_i\cdot \nabla G(\varvec{x},\varvec{\eta }_j^\mathrm{{M}})\mathrm {d}s(\varvec{x})={\left\{ \begin{array}{ll} -\frac{1}{2\pi }\mathfrak {I}\left( \log \left( \dfrac{z_{i+1}-z_j^\mathrm{{M}}}{z_i-z_j^\mathrm{{M}}}\right) \right) &{} \text {for } i\ne j, \\ 0 &{} \text {for } i=j. \end{array}\right. } \end{aligned}$$

(44)

Equation (42) is linear in the unknowns $\phi _i^\mathrm{{D}}$ and $\varGamma$, giving 3N linear equations for $j = 1,\dots ,3N$ to be satisfied by the $3N+1$ unknowns $\phi _i^\mathrm{{D}}$ and $\varGamma$. To complete the system, we satisfy the Kutta condition (24) at the trailing edge, which can be written in terms of the velocity potential $\phi = \phi ^\mathrm{{D}} + \phi ^\infty$ as

$$\begin{aligned} \left. \frac{\mathrm {d}}{\mathrm {d}s}\phi \big (\varvec{\eta }(s)\big )\right| _{s=0}=0. \end{aligned}$$

(45)

This condition is satisfied approximately using the finite difference equation

$$\begin{aligned} \phi ^\mathrm{{D}}_1+\phi ^\infty _1 - \phi ^\mathrm{{D}}_{3N}-\phi ^\infty _{3N}=0. \end{aligned}$$

(46)

The flow speed along the aerofoil is then given as the central difference

$$\begin{aligned} q_b(s_i) = \frac{|\phi _{i}-\phi _{i-1}|}{|\varvec{\eta }_i -\varvec{\eta }_{i-1}|}, \quad i = 2,\dots ,3N, \end{aligned}$$

(47)

with $q_b(0)=q_b(1) = 0$.

We then use Newton’s method to obtain values of the Chebyshev coefficients $a_n$, $b_n$ and $c_n$ such that $q_b(s_i) = q_\mathrm{{c}}(s_i)$ for $i = 1,\dots ,3N+1$, which corresponds to an aerofoil shape $\varvec{\eta }(s)$ and flow speed q(s) which satisfy the dynamic condition (19) and the flow conditions (21)–(25). All results presented here were obtained using both $N=50$ and $N=100$ and it was confirmed that the variation of the aerofoil shape $\big |\varvec{\eta }_{(N=100)}(s)-\varvec{\eta }_{(N=50)}(s)\big |$ remained below $10^{-6}$ for all $0\le s \le 1$.

The numerical method we have presented allows us to determine solutions for chosen values of the parameters $U_{\infty }$, P, $\beta$, $\theta (0)$, $S_1$, $S_2$ and $\ell$. In fixing these the circulation parameter $\varGamma$ is determined implicitly by the Kutta condition. The angle of attack $\alpha$ comes as part of the solution. In practice we choose the value $\theta (0)$ in an iterative manner to obtain a value for $\alpha$ that is in line with what is common for rigid aerofoils (and typically we choose $\alpha =12^{\circ }$).

Fig. 2

Supported and unsupported equilibrium shapes in the absence of a flow with $P=0$ for varying trailing-edge corner angles $\beta$. The supported aerofoil has a support of length $\ell =0.12$ attached at $S_1=1/3$ and $S_2=2/3$, depicted as a broken line

2.3 Inviscid results

Figure 2 shows a comparison between the shape of an elastic aerofoil without an internal support to that of an aerofoil with an internal support of length $\ell =0.12$ in a static fluid. First considering the unsupported case, we note that the case of $\beta =\pi$ corresponds to a smooth cell, which was studied extensively by Yorkston et al. [13]. As the corner angle $\beta$ is decreased, a more aerofoil-like shape is obtained, although the aerofoil retains a relatively large maximum thickness. We then consider the case where the aerofoil has an internal support. For $\beta =3\pi /4$ and $\beta = \pi /2$ we see that while the internal support reduces the maximum thickness, the aerofoil bulges outwards either side of the support, retaining a fairly blunt shape. For $\beta = \pi /4$ and $\beta =0$ however a thin aerofoil is attained.

Fig. 3

Aerofoil shapes and streamlines for angle of attack $\alpha =12^\circ$, a corner angle of $\beta =\pi /6$ and a pressure difference of $P=0$. The internal support, depicted as a broken line, has length $\ell =0.12$ and is attached at the points $S_1=1/3$ and $S_2=2/3$. The streamlines are evenly spaced in the far-field, corresponding to evenly spaced values of the stream function in each panel, although the spacing of the stream function varies between panels as the far-field flow speed $U_\infty$ is varied. a Shows the limit as $U_\infty \rightarrow 0$, which corresponds to the flow past a rigid aerofoil

Figure 3 shows the aerofoil shapes as the flow speed parameter $U_\infty$ is increased, along with the streamlines of the flow. The corner angle and the length and position of the internal support were chosen to obtain a slender aerofoil profile. The angle of attack $\alpha = 12^\circ$ is towards the upper limit of a typical aerofoil and was chosen to exhibit the most severe deformation; for lower angles of attack we found the aerofoil exhibits a similar but less severe deformation. Note that $U_\infty =0$ can correspond to either the flow past a rigid aerofoil or the limit as the flow speed tends to zero. As the flow speed $U_\infty$ is increased, the cell starts to deform in response to the fluid flow. The upper section of the aerofoil boundary becomes concave and the aerofoil attains a negative camber, meaning that the camber line lies below the chord (the camber line is defined to be the locus of points halfway between the upper and lower surfaces of the aerofoil as measured perpendicular to the camber line itself [14]). This reduces the flow speed along the upper section of the aerofoil, resulting in a decrease in the lift coefficient $C_\mathrm{{L}}$.

Fig. 4

Lift coefficient against the angle of attack $\alpha$ in degrees for various dimensionless flow speeds $U_\infty$, with parameters $\beta =\pi /6$, $P=0$, $\ell =0.12$, $S_1=1/3$, $S_2=2/3$. The case $U_{\infty }=0$ corresponds to the limit $E_\mathrm{{B}}\rightarrow \infty$ (see Eq. 20) and a rigid aerofoil. The aerofoil shapes corresponding to $\alpha = 12^\circ$ are shown in Fig. 3

Figure 4 shows the inviscid lift coefficient against the angle of attack $\alpha$ of the supported aerofoil for various flow speeds. For low flow speed $U_\infty$, the elastic forces dominate over the fluid forces. The aerofoil thus acts rigidly as the angle of attack is increased, with the lift coefficient depending linearly on the angle of the trailing edge. As the flow speed $U_\infty$ is increased the aerofoil starts to deform in response to the fluid flow, as shown in Fig. 3, which results in a loss of lift. This loss in lift remains relatively small for low flow speeds $U_\infty$, while for $U_\infty >10$ a more severe loss of lift occurs, with the aerofoil achieving less than half of the lift of the corresponding rigid aerofoil. The inflatable aerofoils used for small unmanned aircraft typically have a chord length of approximately 40 cm [1, 4]. For the supported aerofoils considered here, this corresponds to a perimeter of approximately $L = 0.87\,\hbox {m}$. Taking the cruise speed of the aerofoil to be $u_\infty = 16\,\hbox {m}\,\hbox {s}^{-1}$ [4], we find that a value of $U_\infty =10$ corresponds to a bending rigidity of $E_\mathrm{{B}}=2\,\hbox {kg} \,\hbox {m}^{2}\,\hbox {s}^{-2}$. While this value is relatively high for a simple elastic material, the stiffness is increased for aerofoils constructed with composite materials [3] or inflatable panels [7].

Fig. 5

Aerofoil shapes and streamlines for angle of attack $\alpha =12^\circ$, a corner angle of $\beta =\pi /6$ and a far-field flow speed $U_\infty =15$. The internal support, depicted as a broken line, has length $\ell =0.12$ and is attached at the points $S_1=1/3$ and $S_2=2/3$. The streamlines are evenly spaced in the far-field, corresponding to evenly spaced values of the stream function

Figure 5 shows the aerofoil shapes and streamlines as the interior pressure P is increased, with the other parameters equal to those in Fig. 3d. As the interior pressure is increased, the aerofoil thickness increases towards the trailing edge, and the upper section of the aerofoil becomes less concave, resulting in a higher average flow speed along the upper section. This higher flow speed results in a lower pressure above the aerofoil, and thus a higher lift coefficient $C_\mathrm{{L}}$. However, by $P\approx 300$ the aerofoil thickness is significantly increased, particularly towards the trailing edge, which we expect to result in a larger viscous drag force. This thickness could be reduced by introducing more internal supports, which would allow for a higher internal pressure and thus a higher lift coefficient while limiting the corresponding viscous drag. For an aerofoil with perimeter $L = 0.87\,\hbox {m}$ and bending rigidity of $E_\mathrm{{B}}=2\,\hbox {kg}\,\hbox {m}^{2}\,\hbox {s}^{-2}$, as considered above, a value of $P=300$ corresponds to an inflation pressure $p_0-p_\mathrm{{a}}+\rho gH$ of approximately $0.9\,\hbox {kPa}$. This suggests that our aerofoil attains an aerodynamic shape at relatively low internal pressures, which is desirable due to the reduced risk of leaks [15].

3 Viscous flow calculations

To obtain the equilibria in Sect. 2 we have assumed that the fluid flow past the aerofoil is both inviscid and steady. While this assumption significantly simplifies the formulation of the problem, in a physical flow we would expect both a viscous boundary layer, and a turbulent wake downstream of the aerofoil. To compute the viscous flow we treat the aerofoil shapes obtained in Sect. 2 as rigid bodies, neglecting any deformation due to viscous effects. Such an approach is assumed to be valid as a first approximation for streamlined aerofoils in high Reynolds number flows, where the boundary layer separation occurs close to the trailing edge of the aerofoil and the inviscid flow provides a good approximation to the viscous flow. We will confirm the validity of this assumption further on.

We compute the viscous flow past the aerofoil using the software package Gerris [8, 9], which solves the unsteady incompressible Navier–Stokes equations numerically using an adaptive mesh refinement method with a minimum cell size of $2^{-10}L$. The flow is computed in a channel bounded by solid walls with a slip boundary condition, with the channel width taken to be large enough that the flow near the aerofoil is unaffected by the walls. The flow is initialised at time $t=0$ with a uniform horizontal flow of dimensionless speed $U_\infty$. While this simulation provides an accurate simulation of the unsteady viscous flow away from the aerofoil, the locally spatially isotropic mesh refinement used by Gerris is unsuitable for precisely resolving the boundary layer at the aerofoil boundary [8]; the viscous drag acting on the aerofoil must therefore be computed separately using boundary layer calculations as will be done below assuming that the boundary layer remains attached to the aerofoil and does not separate. The latter assumption is adopted as our focus is on obtaining aerofoil shapes, and flow conditions, where separation is minimal. Since the fluid pressure does not change across the boundary layer, an accurate value of the pressure drag acting on the aerofoil can still be obtained using the Gerris simulation.

The flow in the viscous boundary layer can be obtained using the method of Keller [16] by solving the rescaled boundary layer equation

$$\begin{aligned} f_{\zeta \zeta \zeta }+ \frac{1}{2}\left( (s-s^*)\frac{q_s}{q}+1\right) ff_{\zeta \zeta } + (s-s^*)\frac{q_s}{q}\left( 1-f_{\zeta }^2\right) =(s-s^*)\big (f_\zeta f_{\zeta s}- f_{\zeta \zeta }f_s\big ) \end{aligned}$$

(48)

with boundary conditions

$$\begin{aligned} f(s,0) = 0, \quad f_\zeta (s,0) = 0, \quad f_\zeta (s,\infty ) = 1, \end{aligned}$$

(49)

where s is the arc-length in the anticlockwise direction from the trailing edge, q(s) is the inviscid flow speed along the aerofoil boundary, $s^*$ is the location of the leading edge stagnation point where $q(s^*)=0$, $\zeta$ is a rescaled normal distance from the aerofoil, and $f(s,\zeta )$ is a rescaled stream function in the boundary layer.

Fig. 6

Simulations of the viscous flow past an unsupported aerofoil with parameters $U_\infty =5$, $\beta = \pi /6$, $P=0$, and $\alpha =6^\circ$. a and b Show a snapshot of the vorticity field at $t=10$, with black indicating negative vorticity, white indicating positive vorticity, and grey indicating zero vorticity. c Shows the lift-to-drag ratio of the aerofoil

Fig. 7

Simulations of the viscous flow past a supported aerofoil with parameters $U_\infty =5$, $\alpha = 6^\circ$, $\beta =\pi /6$, $P=0$, $\ell =0.12$, $S_1 = 1/3$ and $S_2 = 2/3$. a and b Show a snapshot of the vorticity field at $t=10$, with black indicating negative vorticity, white indicating positive vorticity, and grey indicating zero vorticity. c Shows the lift-to-drag ratio of the aerofoil

The net dimensional force per unit span acting on the aerofoil can then be approximated as

$$\begin{aligned} \int _0^1 -p(s)\hat{\varvec{n}}(s) L\,\mathrm {d}s + \rho L u_\infty ^2 \sqrt{\frac{1}{2\,{\text {Re}}}} \int _{s^-}^{s^+} \frac{\mathrm{sgn}(s-s^*)}{\sqrt{|s-s^*|}} \bigg (\frac{q(s)}{U_\infty }\bigg )^{3/2} f_{\zeta \zeta }(s,0)\, \hat{\varvec{\tau }}(s)\,\mathrm {d}s. \end{aligned}$$

(50)

Here p(s) is the dimensional pressure at the aerofoil boundary computed by the Gerris simulation, $\mathrm{{Re}} = u_\infty L/2\nu$ is the Reynolds number with the length scale taken to be half the perimeter of the aerofoil, $\nu$ is the kinematic viscosity of the fluid, $\hat{\varvec{\tau }}(s)$ is the unit tangent vector along the aerofoil in the direction of increasing s, $\hat{\varvec{n}}(s)$ is the unit outwards normal vector, and $s^-$ and $s^+$ are the points at which the boundary layer separates on the top and bottom of the aerofoil respectively. The first term in (50) is the net force due to the pressure acting on the aerofoil, and the second term is the viscous drag in the boundary layer. Note that this expression does not account for any viscous drag occurring beyond the point of boundary layer separation. However, for an aerodynamic aerofoil the separation will occur close to the trailing edge, so we expect any viscous drag past the separation point to be much smaller than the boundary layer drag and pressure forces.

Figure 6 shows the viscous flow past an unsupported aerofoil with angle of attack $6^\circ$, which is comparable to that of a typical rigid aerofoil. The viscous flow is computed for both $\mathrm{{Re}} = 1.25\times 10^5$ and $\mathrm{{Re}} = 2.5\times 10^5$; for the airflow past an aerofoil with perimeter $L=0.87\,\hbox {m}$ as considered in Sect. 2c, these values correspond to far-field flow velocities of $u_\infty =4\,\hbox {m}\,\hbox {s}^{-1}$ and $u_\infty =8\,\hbox {m}\,\hbox {s}^{-1}$ respectively. For $\mathrm{{Re}}=1.25\times 10^5$, which corresponds to $u_\infty =4\,\hbox {m}\,\hbox {s}^{-1}$, the viscous boundary layer on the upper edge of the aerofoil separates relatively early due to the thickness of the aerofoil, causing a large viscous wake. Figure 6c shows the lift-to-drag ratio for this simulation, with the lift and drag forces computed using (50). Note for a separated flow, as here, the lift-to-drag ratio is dominated by the pressure drag so that even though the presently used boundary-layer calculation assumes no separation, the results should nevertheless be indicative. The lift-to-drag ratio is volatile just after the flow is initiated, but by $t=10$ the lift-to-drag ratio tends to a value of 0.65, although small regular oscillations remain due to the vortex shedding seen in panel (a). For $\mathrm{{Re}}=2.5\times 10^5$, which corresponds to $u_\infty =8\,\hbox {m}\,\hbox {s}^{-1}$, the viscous boundary layer remains attached up to the trailing edge of the aerofoil, where it forms a thin, stable wake. The lift-to-drag ratio in this case settles to a value of 3.3.

Figure 7 shows the viscous flow past a supported aerofoil, with a support of length $\ell = 0.12$ connected to the aerofoil at $S_1=1/3$ and $S_2=2/3$. The flow parameters are the same as those in Fig. 6. For $\mathrm{{Re}}=1.25\times 10^5$, which corresponds to $u_\infty =4\,\hbox {m}\,\hbox {s}^{-1}$, we find that, unlike the unsupported case, the boundary layer remains attached up to the trailing edge, reducing the oscillations in the lift-to-drag ratio. The lift-to-drag ratio approaches the value 3.7, which is significantly higher than that of the unsupported aerofoil. For $\mathrm{{Re}} = 2.5\times 10^5$, which corresponds to $u_\infty =8\,\hbox {m}\,\hbox {s}^{-1}$, the lift-to-drag ratio increases further, reaching a value of 7.1, which is more than twice the value for the unsupported aerofoil. This is comparable to the value of $C_\mathrm{{L}}/C_\mathrm{{D}}\approx 10$ obtained by Simpson [4] for more complex inflatable aerofoil designs.

Fig. 8

The numerically computed dimensionless transmural pressure $\varDelta P \equiv (p-p_i)L^3/E_\mathrm{{B}}$ given by (16) for the supported aerofoil with parameters $U_\infty =5$, $\alpha =6^\circ$, $\beta = \pi /6$, $P=0$, $\ell =0.12$, $S_1 = 1/3$ and $S_2 = 2/3$, as depicted in Fig. 7. The solid line depicts the pressure for an inviscid flow computed using the boundary integral method and the dashed line depicts the pressure for the viscous flow with $\mathrm{{Re}} = 2.5\times 10^5$ computed using Gerris

To assess the validity of the inviscid approximation used to obtain the equilibria in Sect. 2, we compare in Fig. 8 the inviscid fluid pressure obtained using the boundary integral method to that computed for $\mathrm{{Re}} = 2.5\times 10^5$ for the aerofoil previously shown in Fig. 7. The fluid pressure of the inviscid fluid is found to provide a good approximation of the viscous flow for this aerodynamic aerofoil shape, which suggests that the aerofoil remains in near-equilibrium in the viscous flow.

We have thus shown that with a simple internal support the aerofoil can maintain a good aerodynamic shape in realistic flow conditions, with significantly improved aerodynamic characteristics over an unsupported aerofoil.

4 Summary

We have presented a novel method to compute the deformation of a simple elastic aerofoil. We have investigated the aerodynamic viability of a simple inflatable aerofoil design. We have presented an iterative boundary integral method which we used to obtain equilibrium aerofoil shapes both in a static fluid and in an inviscid fluid flow. Using a combination of boundary layer calculations and full DNS using the software package Gerris [8, 9], we have analysed the aerodynamic properties of the aerofoil.

We have focused on an aerofoil with a trailing edge angle of $\beta = \pi /6$ and a single support of dimensionless length $\ell = 0.12$, which were found to provide a good aerodynamic shape. For inviscid flow the aerofoil does not significantly deform at low flow speeds and the lift depends almost linearly on the angle of attack $\alpha$ as it would for a rigid aerofoil. At higher flow speeds more substantial deformation occurs, particularly toward the trailing edge, and this results in a significant loss in lift. The loss in lift can be reduced by increasing the inflation pressure, but at the expense of an increase in drag as the aerofoil bulges into a less aerodynamic shape. By computing the viscous flow past the deformed aerofoils we found that the presence of an internal support delays the boundary layer separation at the trailing edge, reducing the viscous wake and significantly improving the lift-to-drag ratio of the aerofoil.

We have restricted our study to two-dimensional aerofoils, with an assumed invariance of the aerofoil deformation and fluid flow in the spanwise direction. It would be informative to expand our method to allow for deformation of the aerofoil in the spanwise direction to model wing bending and three-dimensional effects such as wrinkling. Moreover, while our model allows us to model a uniformly distributed load by a suitable tuning of the wing material density, incorporating a more realistic model of the load distribution including the main body of the aircraft would require an extension of the current model to include three-dimensional effects. All of these issues are left for future work.

We have presented results for a particular configuration of the internal support, chosen to demonstrate the improvement on the aerodynamic behaviour of the inflatable aerofoil under steady cruise conditions. Some inflatable aerofoils have a single support as considered here [7], but more complex aerofoils with multiple supports also exist [5] and our method can be easily adapted to cater for this. In either case the framework we have provided could be used as a basis to investigate how to optimise performance under different flight conditions depending on the intended application.