A simple model for desulphurisation of flue gas using reactive filters

Abstract

Desulphurisation of flue gas is essential before it can be released safely into the atmosphere. One way of removing sulphur dioxide is to use a purification device incorporating a reactive filter, in which the flue gas stream passes in front of a porous-catalyst-filled structure which converts the gaseous sulphur dioxide into liquid sulphuric acid. In this paper, we build and solve a simple mathematical model to describe the operation of a paradigm reactive filter. Our model captures the transport of sulphur dioxide through the device via advection in the main “outer” flow and diffusion through the catalyst structure along with the production of sulphuric acid. This sulphuric acid gradually accumulates in the filter rendering it less efficient. We determine the clogging time for an individual channel (that is, the time at which the entrance to the channel becomes completely filled with liquid) and explore how the concentrations of sulphur dioxide and oxygen and the thickness of the sulphuric acid layer change as the key dimensionless parameters are varied, comparing numerical and asymptotic results where appropriate. We then turn our attention to the device scale and solve our model numerically to determine the overall lifetime of the device. We vary the key dimensionless parameters and explore how they affect the efficiency of the device. In the physically relevant parameter regime, we find an explicit solution to the outer flow problem which agrees well with numerical solutions and provides a formula for the lifetime of the device. Finally, we propose a formula for determining the catalyst reaction rate, given data on the concentration of sulphur dioxide exiting the device.

1 Introduction

In the drive to protect the environment, reducing the concentrations of harmful chemicals that are released into the atmosphere has become a priority for industry. One key example is the removal of sulphur dioxide ($\hbox {SO}_2$) from flue gas. $\hbox {SO}_2$ is formed in vast quantities in industrial processes and power plants as a by-product of processing raw materials, such as crude oil and various ores [1,2,3]. Furthermore, it is a highly toxic gas that can cause acid rain and is linked to respiratory illnesses [3, 4]. In order to decrease the concentration of sulphur dioxide in flue gas to be released into the atmosphere, various techniques are used, including “gas scrubbing” (both wet and dry) [5,6,7], membrane gas absorption [8], packed-bed absorption [9], and reactive filtering using catalysts [10]. However, the majority of these methods require high input power and a specifically situated operation site. Furthermore, they produce a lot of waste, such as gypsum containing a variable amount of impurities in the case of gas scrubbing, that needs to be disposed [2].

Our interest is in the use of reactive filters, since these are less costly than the other options in terms of maintenance, are easy to install in a factory, and do not generate toxic waste. These filters also produce sulphuric acid which can be easily captured, stored, and used for other purposes; the sulphuric acid also acts as a natural cleanser for the device. The filters are often made from stackable modules, each of which consists of a series of porous sheets containing catalyst material. Flue gas flows in front of these sheets from one end of the device to the other and diffuses into the porous sheets. When sulphur dioxide, oxygen ($\hbox {O}_2$), and water vapour come into contact with the catalyst-covered surfaces of the pores, liquid sulphuric acid ($\hbox {H}_2\hbox {SO}_4$) is produced, as indicated in Fig. 1. In reality, there are multiple intermediate reactions that take place on the catalyst surface before acid is produced (see, for example, [11, 12]), but the overall reaction is given by

$$\begin{aligned} 2\,\hbox {SO}_{2(\mathrm{g})} + 2\,\hbox {H}_{2}\hbox {O}_{(\mathrm{g})} + \hbox {O}_{2(\mathrm{g})} \mathop {\xrightarrow {\mathrm{carbon~catalyst}}}\limits _{r} 2\,\hbox {H}_{2}\hbox {SO}_{4\mathrm{(l)}}, \end{aligned}$$

(1)

where r is the effective reaction rate taking into account all intermediate steps.

Fig. 1

Schematic showing the generation of sulphuric acid inside a reactive filter

As the chemical reaction proceeds, liquid sulphuric acid accumulates in the pores and inhibits the transport of sulphur dioxide, which results in a reduction in device efficiency over time. The evolution of the sulphuric acid layers near the surface of the sheets results in the formation of surface droplets. When these droplets become sufficiently large, they run down the surface under gravity and accumulate at the bottom of the device. Our aim is to understand the transport of sulphur dioxide and oxygen in the device in order to gain insight into its operation and to determine how the control parameters alter device efficiency and longevity.

Although various models exist for other purification methods, including gas scrubbing [5, 6, 13, 14] and absorption [15, 16], reactive filters are less well studied. In [12], the removal of sulphur dioxide using activated carbon fibres, and the production of sulphuric acid, is studied. They develop a power-law model to describe the steady-state concentration of sulphur dioxide at the outlet of the device and find that this concentration is proportional to the weight of the catalyst and to a specific power of the initial concentrations of sulphur dioxide, oxygen, and water vapour. Furthermore, a detailed kinetic model for the evolution of the concentration of sulphur dioxide in an activated carbon fibre reactor is presented in [17]. They observe that increasing the inlet concentration of sulphur dioxide increases the outlet concentration, whereas increasing the concentrations of either oxygen or water vapour decreases it. Their model is based on a particular functional form for the concentration of sulphur dioxide in the fibre pores and, in addition, the governing equations make use of an effective uptake of sulphur dioxide and are derived from a simple averaging over the pore domain. Neither model involves the evolution of the liquid sulphuric acid produced by the catalytic reaction. In [18], a more sophisticated model for the operation of a catalytic device is derived for the case where spherical catalyst pellets are embedded in a porous matrix. Homogenisation techniques are used to upscale a model for the physical and chemical processes occurring on the pellet scale to one that is relevant for describing device operation. The model is used to predict the device-scale behaviour up until the point when the porous matrix becomes saturated near the inlet. A summary of models describing the related area of break-through-time predictions for gas removal using catalysts can be found in [19].

In this paper, we will build a simple mathematical model for the operation of a reactive filter device. We will assume the simplest possible geometry for the filter, namely a set of finite-length, thin, parallel, channels where the walls have been covered with catalyst material. In Sect. 2, we will derive a mathematical model for the device, which will incorporate an “outer” gas flow coupled with diffusion of sulphur dioxide and oxygen into the reactive channels and the consequent build up of sulphuric acid. In Sect. 3, we will nondimensionalise the model and determine the key dimensionless parameters that control the process. In Sect. 4, we will look at the physically relevant thin-catalyst-channel limit of the problem, which will enable us to reduce the complexity of the model. In Sect. 5, we focus our attention on the catalyst channel at the top of the device, and we will solve (numerically) for the sulphur dioxide concentration and thickness of the sulphuric acid layer in the channels. We will explore how the system behaves at the entrance to the channel and use asymptotic reductions to provide explicit expressions for some of the key variables. We will also consider a reduced model in the case when the liquid layer is very thin. In Sect. 6, we will solve the whole-device model which incorporates the “outer” gas transport as well as the activity in the channels. Finally, in Sect. 7, we will draw our conclusions and discuss extensions.

2 Mathematical model for the purification device

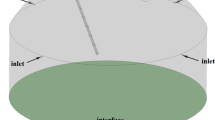
We focus on the simple two-dimensional device shown in the schematic in Fig. 2, where the flue gas flows along the outer region at the left-hand side of the device and diffuses into the catalyst-lined channels on the right. We neglect the transport of water vapour (assuming it is abundant) and also the hygroscopic effect of sulphuric acid (see [20]), and focus instead on the transport of sulphur dioxide and oxygen.

Fig. 2

Schematic showing the idealised reactive filter

2.1 Model for the outer region

We let S(z, t) and C(z, t) denote the concentrations (measured in mol m$^{-3}$) of $\hbox {SO}_2$ and $\hbox {O}_2$ in the gas in the outer region, respectively, where z denotes distance from the bottom of the device and t is the time. We assume that the device has length H and that the gas is transported in the outer flow by convection with constant speed U. Appealing to conservation of mass for $\hbox {SO}_2$ and $\hbox {O}_2$, and assuming a priori that this outer flow is advection dominated, we write

$$\begin{aligned} l\dfrac{\partial S}{\partial t} + lU\dfrac{\partial S}{\partial z} = Q_s, \qquad l \dfrac{\partial C}{\partial t} + l U\dfrac{\partial C}{\partial z} = Q_c, \end{aligned}$$

(2)

where $Q_s(z,t)$ and $Q_c(z,t)$ represent the flux (per unit depth, measured in mol m$^{-2}$ s$^{-1}$) of $\hbox {SO}_2$ and $\hbox {O}_2$ entering the porous structure, respectively, and l is the width of the outer region. We suppose that $\hbox {SO}_2$ and $\hbox {O}_2$ are supplied with a constant concentration at the inlet located at $z=0$, and so we impose the boundary conditions:

$$\begin{aligned} S = S^*, \qquad C =C^*\qquad \text{ at } \qquad z=0. \end{aligned}$$

(3)

Finally, we assume that there is no gas in the outer region initially, so we write

$$\begin{aligned} S=0, \qquad C=0\qquad \text{ at }\qquad t=0. \end{aligned}$$

(4)

2.2 Channel-scale model

As mentioned earlier, we assume for simplicity that the filter comprises numerous small parallel catalyst channels aligned perpendicularly to the direction of the outer gas flow. We focus on a single channel with the aim of determining the fluxes $Q_s$ and $Q_c$ of $\hbox {SO}_2$ and $\hbox {O}_2$ drawn out of the gas stream in the outer region. The geometry under consideration is shown schematically in Fig. 3. We assume that the surfaces of the catalyst channel are located at $y=0$ and $y=2W$ and that the centres of the channels are a constant distance ${{{\mathcal {L}}}}$ apart. We use the coordinate x to denote distance into the filter, with the surface open to the gas flow located at $x=0$ and the back of the filter located at $x=L$. We denote the concentration of $\hbox {SO}_2$ and $\hbox {O}_2$ inside the flue gas in the channels by s(x, y, z, t) and c(x, y, z, t), respectively and, assuming that the gas transport in the channel is diffusion dominated, we write

$$\begin{aligned} \dfrac{\partial s}{\partial t} = D_s^\mathrm{{g}}\left( \dfrac{\partial ^{2}s}{\partial x ^{2}}+\dfrac{\partial ^{2}s}{\partial y ^{2}}\right) , \qquad \dfrac{\partial c}{\partial t} = D_c^\mathrm{{g}}\left( \dfrac{\partial ^{2}c}{\partial x^{2}}+\dfrac{\partial ^{2}c}{\partial y^{2}}\right) , \end{aligned}$$

(5)

where $D_s^\mathrm{{g}}$ and $D_c^\mathrm{{g}}$ are the diffusivities of $\hbox {SO}_2$ and $\hbox {O}_2$ in the flue gas, respectively.

Fig. 3

Schematic showing microscale geometry inside the reactive filter

We suppose that the concentrations of $\hbox {SO}_2$ and $\hbox {O}_2$ are prescribed (by the outer region model) at the front of the filter, and that there is no flux of either species through the back of the filter. Thus, we write

$$\begin{aligned}&s=S(z,t),\quad c=C(z,t) \qquad \text{ at }\qquad x=0, \end{aligned}$$

(6)

$$\begin{aligned}&\frac{\partial s}{\partial x}=\frac{\partial c}{\partial x}=0 \qquad \text{ at }\qquad x=L. \end{aligned}$$

(7)

At the surface of the channel, the reaction turns the gaseous sulphur dioxide, oxygen, and water vapour into liquid sulphuric acid. Assuming that the water vapour is present in excess and, for simplicity¹, that the reaction follows the law of mass action, the velocity $v^*$ of the sulphuric acid produced at the surface is

$$\begin{aligned} v^*= 2 \lambda r {{\mathcal {S}}}^2 {{\mathcal {C}}}|_{y=0}, \end{aligned}$$

(8)

where the concentrations of $\hbox {SO}_2$ and $\hbox {O}_2$ in the liquid layer that forms above the surface are denoted by ${{\mathcal {S}}}(x,y,z,t)$ and ${{\mathcal {C}}}(x,y,z,t)$, respectively, $\lambda$ (measured in m$^3/$mol) is the molar volume of sulphuric acid, r (measured in m$^7/$mol$^2$ s) is the reaction constant, and the factor of two reflects that two molecules of $\hbox {H}_2\hbox {SO}_4$ are produced in the reaction.

The concentrations of $\hbox {SO}_2$ and $\hbox {O}_2$ dissolved in the liquid $\hbox {H}_2\hbox {SO}_4$ layer evolve according to

$$\begin{aligned} \dfrac{\partial {{\mathcal {S}}}}{\partial t} +u\frac{\partial {{\mathcal {S}}}}{\partial x}+v\frac{\partial {{\mathcal {S}}}}{\partial y}= D_s^\mathrm{{l}}\left( \dfrac{\partial ^{2}{{\mathcal {S}}}}{\partial x ^{2}}+\dfrac{\partial ^{2}{{\mathcal {S}}}}{\partial y ^{2}}\right) , \qquad \dfrac{\partial {{\mathcal {C}}}}{\partial t} +u\frac{\partial {{\mathcal {C}}}}{\partial x}+v\frac{\partial {{\mathcal {C}}}}{\partial y}= D_c^\mathrm{{l}}\left( \dfrac{\partial ^{2}{{\mathcal {C}}}}{\partial x^{2}}+\dfrac{\partial ^{2}{{\mathcal {C}}}}{\partial y^{2}}\right) , \end{aligned}$$

(9)

where $D_s^\mathrm{{l}}$ and $D_c^\mathrm{{l}}$ are the diffusivities of $\hbox {SO}_2$ and $\hbox {O}_2$ in the liquid, respectively, and u and v are the liquid velocities along the channel and across the channel, respectively. Appealing again to the law of mass action, the fluxes of dissolved $\hbox {SO}_2$ and $\hbox {O}_2$ removed from the liquid layer at the surface of the channels are

$$\begin{aligned} -D_s^\mathrm{{l}}\frac{\partial {{\mathcal {S}}}}{\partial y}=-2 r {{\mathcal {S}}}^2 {{\mathcal {C}}},\qquad -D_c^\mathrm{{l}}\frac{\partial {{\mathcal {C}}}}{\partial y}=-r{{\mathcal {S}}}^2{{\mathcal {C}}}\qquad \text{ on } \qquad y=0. \end{aligned}$$

(10)

At the moving interface, h(x, z, t), between the gas and the liquid $\hbox {H}_2\hbox {SO}_4$, we impose continuity of flux of $\hbox {SO}_2$ and $\hbox {O}_2$, namely

$$\begin{aligned}&-D_s^\mathrm{{g}} \frac{\partial s}{\partial n}+s (\mathbf{u}\cdot \mathbf{n}-V_n)=-D_s^\mathrm{{l}} \frac{\partial {{\mathcal {S}}}}{\partial n}+ {{\mathcal {S}}}(\mathbf{u}\cdot \mathbf{n}-V_n),\nonumber \\&-D_c^\mathrm{{g}} \frac{\partial c}{\partial n}+c (\mathbf{u}\cdot \mathbf{n}-V_n)=-D_c^\mathrm{{l}} \frac{\partial {{\mathcal {C}}}}{\partial n}+ {{\mathcal {C}}} (\mathbf{u}\cdot \mathbf{n}-V_n), \end{aligned}$$

(11)

where $\mathbf{u}=(u,v)$, $\mathbf{n}$ is the normal to the interface, $\partial /\partial n$ is shorthand for $\mathbf{n}\cdot \nabla$, and $V_n$ is the velocity of the interface. We also apply Henry’s law, which states

$$\begin{aligned} s=\beta _s {{\mathcal {S}}},\qquad c=\beta _c {{\mathcal {C}}}, \end{aligned}$$

(12)

and comes from assuming that the chemical potentials for each species are in equilibrium at the interface. Here, $\beta _s$ and $\beta _c$ are partition coefficients for sulphur dioxide and oxygen, respectively. We further assume that no $\hbox {H}_2\hbox {SO}_4$ molecules pass through the gas–liquid interface, and so the interface satisfies the kinematic condition $\mathbf{u}\cdot \mathbf{n}=V_n$, which can be written as:

$$\begin{aligned} v=\frac{\partial h}{\partial t}+u\frac{\partial h}{\partial x}. \end{aligned}$$

(13)

We note that (11) simplifies considerably under this assumption and reduces to conservation of diffusive flux across the interface.

The liquid flow in the sulphuric acid layer is influenced by the (non-uniform) production of $\hbox {H}_2\hbox {SO}_4$ at the channel surface and the surface tension of the air–liquid interface. To fully capture the motion, we would need to solve a model such as that presented in [21]. In this paper, however, our focus is on species transport, and so we use the simplest possible model for the liquid motion, in which we assume that there is no flow in the x direction, i.e., we set $u=0$. With this assumption, conservation of mass requires that v is independent of y, and thus, using (8) and (13), we find that

$$\begin{aligned} \frac{\partial h}{\partial t}=v=v^*=2 \lambda r {{\mathcal {S}}}^2 {{\mathcal {C}}}|_{y=0}. \end{aligned}$$

(14)

Equation (14) holds true until $h=W$, which we anticipate first occurs at the entrance to the catalyst channel. Subsequently, the channel entrance becomes blocked with liquid and the $\hbox {SO}_2$ extraction pathway switches to be solely through the liquid layer. We will discuss this further in Sect. 2.3. We assume symmetry at the centre of the channel, and so we write

$$\begin{aligned} \frac{\partial s}{\partial y}=\frac{\partial c}{\partial y}=0 \qquad \text{ at } \qquad y=W. \end{aligned}$$

(15)

Finally, we assume that there is no gas in the channels and no liquid layer present at the start, so that we write

$$\begin{aligned} c=s={{\mathcal {C}}}={{\mathcal {S}}}=h=0 \qquad \text{ at }\qquad t=0. \end{aligned}$$

(16)

2.3 Flux drawn out of the outer gas flow

We relate the fluxes, $Q_s$ and $Q_c$, of $\hbox {SO}_2$ and $\hbox {O}_2$ drawn out of the outer gas flow to the activity inside the filter by writing

$$\begin{aligned} Q_s=\chi _0 D_s^\mathrm{{g}} \left( 1-\frac{h}{W}\right) ^+\left. \frac{\partial s}{\partial x}\right| _{x=0},\qquad Q_c=\chi _0 D_c^\mathrm{{g}} \left( 1-\frac{h}{W}\right) ^+\left. \frac{\partial c}{\partial x}\right| _{x=0}, \end{aligned}$$

(17)

where $\chi _0=2W/{{\mathcal {L}}}$ is the void fraction at the surface of the filter. Once the entrances to the channels become blocked (i.e. $h(0,z,t)=W$), the dominant $\hbox {SO}_2$ and $\hbox {O}_2$ transport route switches to being through the liquid. Given the differences in the diffusivities and the solubilities given later in Table 1, we anticipate that it is much more difficult for $\hbox {SO}_2$ and $\hbox {O}_2$ to diffuse through the liquid layer spanning the channel entrance than to diffuse into a channel that is not blocked with liquid. Thus, once $h=W$ at $x=0$ for some z, we stop solving for s, c, ${{\mathcal {S}}}$, ${{\mathcal {C}}}$, and h at that z location and instead simply set the fluxes $Q_s$ and $Q_c$ to zero. This is represented in (17) by

$$\begin{aligned} \left( 1-\frac{h}{W}\right) ^+ {:= \,\text {max}\left\{ \left( 1-\frac{h}{W}\right) ,0\right\} } \end{aligned}$$

(18)

3 Nondimensionalisation

We are interested in the behaviour of the device on the timescale over which the liquid $\hbox {H}_2\hbox {SO}_4$ layer has grown sufficiently that it is of the same order of magnitude as the thickness of the catalyst channels, found by balancing the terms in (14) when $h\sim W$.² We scale distance along the device with the device length, distance along the channel with the channel length, and distance across the channel with the half the channel width, which we also use as the scaling for the thickness of the sulphuric acid layer. We scale the gaseous concentrations of sulphur dioxide and oxygen with their initial concentrations, and the concentrations in the sulphuric acid layer with the concentrations that are in chemical equilibrium with those in the gas. We thus use the following scalings:

$$\begin{aligned}&t=\frac{W \beta _s^2 \beta _c}{\lambda r {S^*}^2 C^*} t', \qquad z = Hz', \qquad x=Lx', \qquad y=Wy',\qquad h=W h',\end{aligned}$$

(19)

$$\begin{aligned}&S=S^* S',\qquad C=C^* C', \qquad s=S^* S',\qquad c=C^* c',\qquad {{\mathcal {S}}}=\frac{S^*}{\beta _s} {{\mathcal {S}}}',\qquad {{\mathcal {C}}}=\frac{C^*}{\beta _c} {{\mathcal {C}}}'. \end{aligned}$$

(20)

The dimensionless model reads, dropping the primes,

$$\begin{aligned}&\frac{\delta {{\mathcal {R}}}}{\text{ Pe }}\frac{\partial S}{\partial t}+\frac{\partial S}{\partial z}=\chi _0\frac{\epsilon ^2 \gamma D_2}{Pe} (1-h)^+\left. \frac{\partial s}{\partial x}\right| _{x=0},\qquad \frac{\delta {{\mathcal {R}}}}{\mathrm {Pe}}\frac{\partial C}{\partial t}+\frac{\partial C}{\partial z}=\chi _0\frac{\epsilon ^2\gamma D_2}{{\mathrm {Pe}} D_1} (1-h)^+\left. \frac{\partial c}{\partial x}\right| _{x=0},\end{aligned}$$

(21)

$$\begin{aligned}&\frac{\delta {{\mathcal {R}}}}{D_2}\frac{\partial s}{\partial t}=\epsilon ^2 \frac{\partial ^2 s}{\partial x^2}+\frac{\partial ^2 s}{\partial y^2},\qquad \frac{\delta {{\mathcal {R}}} D_1}{D_2}\frac{\partial c}{\partial t}=\epsilon ^2 \frac{\partial ^2 c}{\partial x^2}+\frac{\partial ^2 c}{\partial y^2}, \end{aligned}$$

(22)

$$\begin{aligned}&\delta {{\mathcal {R}}}\left( \frac{\partial {{\mathcal {S}}}}{\partial t}+2 \left. \left( {{\mathcal {S}}}^2{{\mathcal {C}}}\right) \right| _{y=0}\frac{\partial S}{\partial y}\right) =\epsilon ^2 \frac{\partial ^2 {{\mathcal {S}}}}{\partial x^2}+\frac{\partial ^2 {{\mathcal {S}}}}{\partial y^2},\end{aligned}$$

(23)

$$\begin{aligned}&\delta {{\mathcal {R}}}\frac{D_3}{ D_2}\left( \frac{\partial {{\mathcal {C}}}}{\partial t}+2 \left. \left( {{\mathcal {S}}}^2{{\mathcal {C}}}\right) \right| _{y=0}\frac{\partial C}{\partial y}\right) =\epsilon ^2 \frac{\partial ^2 {{\mathcal {C}}}}{\partial x^2}+\frac{\partial ^2 {{\mathcal {C}}}}{\partial y^2}, \end{aligned}$$

(24)

$$\begin{aligned}&\frac{\partial h}{\partial t}=2\left( {{\mathcal {S}}}^2{{\mathcal {C}}}\right) |_{y=0}, \end{aligned}$$

(25)

with boundary conditions

$$\begin{aligned}&S=1, C=1 \quad \text{ at }\quad z=0, \end{aligned}$$

(26)

$$\begin{aligned}&s=S, c=C\quad \text{ at }\quad x=0, \end{aligned}$$

(27)

$$\begin{aligned}&\frac{\partial s}{\partial x}=\frac{\partial c}{\partial x}=0 \quad \text{ at }\quad x=1, \end{aligned}$$

(28)

$$\begin{aligned}&\frac{\partial s}{\partial y}=\frac{\partial c}{\partial y}=0 \quad \text{ at }\quad y=1, \end{aligned}$$

(29)

$$\begin{aligned}&s={{\mathcal {S}}}, c={{\mathcal {C}}} \quad \text{ on }\quad y=h, \end{aligned}$$

(30)

$$\begin{aligned}&\frac{\partial s}{\partial y}- \epsilon ^2 \frac{\partial h}{\partial x}\frac{\partial s}{\partial x}=\frac{1}{\beta _s D_2}\left( \frac{\partial {{\mathcal {S}}}}{\partial y}-\epsilon ^2 \frac{\partial h}{\partial x}\frac{\partial {{\mathcal {S}}}}{\partial x}\right) \quad \text{ on }\quad y= h, \end{aligned}$$

(31)

$$\begin{aligned}&\frac{\partial c}{\partial y}- \epsilon ^2 \frac{\partial h}{\partial x}\frac{\partial c}{\partial x}=\frac{D_1}{\beta _c D_3}\left( \frac{\partial {{\mathcal {C}}}}{\partial y}- \epsilon ^2 \frac{\partial h}{\partial x}\frac{\partial {{\mathcal {C}}}}{\partial x}\right) \quad \text{ on }\quad y=h,\end{aligned}$$

(32)

$$\begin{aligned}&\frac{\partial {{\mathcal {S}}}}{\partial y}=2 {{\mathcal {R}}} {{\mathcal {S}}}^2{{\mathcal {C}}},\quad \frac{\partial {{\mathcal {C}}}}{\partial y}={{\mathcal {R}}}\alpha \frac{\beta _c D_3}{\beta _s D_2} {{\mathcal {S}}}^2{{\mathcal {C}}} \quad \text{ at }\quad y=0, \end{aligned}$$

(33)

and initial conditions

$$\begin{aligned} S=C=s=c=h=0 \qquad \text{ at }\qquad t=0. \end{aligned}$$

(34)

We have introduced nine fundamental dimensionless parameters: $\gamma$ is the ratio of the width of the outer channel to the length of the catalyst channels, $\epsilon$ is the aspect ratio of the catalyst channels, $\text{ Pe }$ is the Péclet number associated with transport in the outer region, ${{\mathcal {R}}}$ is the dimensionless reaction constant, $\alpha$ is the ratio of the inlet concentrations of $\hbox {O}_2$ and $\hbox {SO}_2$, $\delta$ is the fraction of the molar volume of sulphuric acid realised by the local concentration of $\hbox {SO}_2$ that is related to the input concentration, and the $D_i$ are diffusivity ratios. These are given by

$$\begin{aligned}&\gamma =\frac{L}{l},\quad \epsilon =\frac{W}{L},\quad Pe=\frac{W^2 U}{D_s^\mathrm{{l}} H}, \quad {{\mathcal {R}}}=\frac{r {S^*}{C^*} W}{\beta _s \beta _c D_s^\mathrm{{l}}},\quad \alpha =\frac{S^*}{C^*},\end{aligned}$$

(35)

$$\begin{aligned}&\delta = \frac{\lambda S^*}{\beta _s},\quad D_1=\frac{D_s^\mathrm{{g}}}{D_c^\mathrm{{g}}},\quad D_2=\frac{D_s^\mathrm{{g}}}{D_s^\mathrm{{l}}},\quad D_3=\frac{D_s^\mathrm{{g}}}{D_c^\mathrm{{l}}}. \end{aligned}$$

(36)

We present the sizes of the physical parameters for a typical operating situation in Table 1, along with the dimensions and operating parameters of a typical device. We note that we do not know the size of the reaction constant r. However, we infer r by noting that it takes a few days for droplets of $\hbox {H}_2\hbox {SO}_4$ to appear on the front of the filter and use our scaling for t and the other parameters to calculate an estimate. The corresponding dimensionless parameters are shown in Table 2.

Table 1 Table showing typical dimensional parameter values for the process

Table 2 Table showing typical dimensionless parameter values for the process

We see that the model depends on various combinations of the fundamental dimensionless groupings, namely

$$\begin{aligned}&\delta {{\mathcal {R}}}\approx 2\times 10^{-5},\qquad \frac{\delta {{\mathcal {R}}}}{Pe}\approx 1\times 10^{-6},\qquad \frac{\epsilon ^2 \gamma D_2}{Pe}\approx 0.8,\qquad \frac{\epsilon ^2 \gamma D_2}{Pe D_1}\approx 1.2, \nonumber \\&\frac{\delta {{\mathcal {R}}}}{D_2}\approx 3\times 10^{-9},\qquad \frac{\delta {{\mathcal {R}}} D_1}{D_2}\approx 2\times 10^{-9},\qquad \frac{\delta {{\mathcal {R}}}D_3}{D_2}\approx 3\times 10^{-5}, \nonumber \\&\frac{1}{\beta _s D_2}\approx 4\times 10^{-3},\qquad \frac{D_1}{\beta _c D_3}\approx 2\times 10^{-6}, \qquad \frac{{{\mathcal {R}}} \alpha \beta _c D_3}{\beta _s D_2}\approx 40,\qquad \epsilon ^2\approx 1\times 10^{-2} . \end{aligned}$$

(37)

We immediately see that, in normal operation, we may drop the time derivatives everywhere except in the equation for the evolution of the sulphuric acid layer (25), and we do this henceforth. Further, the parameters associated with flux transfer across the gas–liquid interface in (31)–(32) are all small, which motivates us to simplify the problem further.

4 Reduction of the model in the catalyst channel

Exploiting the fact that the square of the aspect ratio of the catalyst channel, $\epsilon ^2 \ll 1$, we reduce the complexity of the model by looking for asymptotic solutions for the dependent variables of the form $X\sim X_0+\epsilon ^2 X_1+\cdots$. We work in the richest asymptotic limit of the remaining parameters, namely

$$\begin{aligned}&{{\mathcal {B}}}_1:=\frac{\epsilon ^2 \gamma D_2}{Pe}{=\frac{H D_s^\mathrm{{g}}}{lLU}}, \qquad {{\mathcal {B}}}_2:=\frac{1}{\beta _s D_2\epsilon ^2}{=\frac{D_s^\mathrm{{l}} L^2}{\beta _s D_s^\mathrm{{g}} W^2}},\qquad {{\mathcal {B}}}_3:=\frac{\alpha \beta _c D_3}{2\beta _s D_2}{=\frac{\beta _c D_s^\mathrm{{l}} S^*}{2 \beta _s D_c^\mathrm{{l}} C^*}} , \nonumber \\&{{\mathcal {B}}}_4:=\frac{D_1}{\beta _c D_3\epsilon ^4}{=\frac{D_c^\mathrm{{l}} L^4}{\beta _c D_c^\mathrm{{g}} W^4}}, \end{aligned}$$

(38)

along with $D_1,\chi _0$, are all O(1). Here, ${{\mathcal {B}}}_1$ is the ratio of the diffusive flux of sulphur dioxide entering a catalyst channel to the convective flux of sulphur dioxide passing the channel entrance and indicates how easy it is for sulphur dioxide to enter the channel, ${{\mathcal {B}}}_2$ is the ratio of the diffusive flux of sulphur dioxide through the liquid sulphuric acid to the diffusive flux of sulphur dioxide through the gas, multiplied by the inverse of the square of the aspect ratio and indicates how easy it is for sulphur dioxide to pass across the gas–liquid interface, ${{\mathcal {B}}}_3$ is the ratio of the diffusive fluxes of sulphur dioxide to oxygen reaching the catalyst surface and indicates how oxygen is depleted at the catalyst surface, and ${{\mathcal {B}}}_4$ is the ratio of the diffusive flux of oxygen through the liquid sulphuric acid to the diffusive flux of oxygen through the gas, multiplied by the inverse of the fourth power of the aspect ratio and indicates how easy it is for oxygen to pass across the gas–liquid interface. We will present their sizes, based on the values in Table 2, in (95) in Sect. 6. Given that we are unsure about the precise size of r, we proceed assuming further that the dimensionless reaction rate ${{\mathcal {R}}}=O(1)$.

4.1 Solution in the liquid layer

In this limit, diffusion dominates across the liquid layer, and the relevant leading-order (in $\epsilon ^2$) versions of (23)–(25) and boundary conditions (30)–(33) are

$$\begin{aligned}&\frac{\partial ^2 {{\mathcal {S}}}}{\partial y^2}=0,\qquad \frac{\partial ^2 {{\mathcal {C}}}}{\partial y^2}=0,\qquad \frac{\partial h}{\partial t}=2\left( {{{\mathcal {S}}}}^2{{\mathcal {C}}}\right) |_{y=0}, \end{aligned}$$

(39)

$$\begin{aligned}&{{\mathcal {S}}}=s, \quad {{\mathcal {C}}}=c\quad \qquad \text{ on }\qquad y=h, \end{aligned}$$

(40)

$$\begin{aligned}&\frac{\partial {{\mathcal {S}}}}{\partial y}=2 {{\mathcal {R}}} {{{\mathcal {S}}}}^2{{\mathcal {C}}},\quad \frac{\partial {{\mathcal {C}}}}{\partial y}=2{{\mathcal {R}}}{{\mathcal {B}}}_3 {{{\mathcal {S}}}}^2{{\mathcal {C}}}\qquad \text{ at }\qquad y=0. \end{aligned}$$

(41)

Writing ${{\mathcal {P}}}={{\mathcal {B}}}_3{{\mathcal {S}}}-{{\mathcal {C}}}$, we solve the resulting (trivial) system for ${{\mathcal {P}}}$ to find that ${{\mathcal {P}}}$ is independent of y, and thus

$$\begin{aligned} {{\mathcal {C}}}=c|_h+{{\mathcal {B}}}_3\left( {{\mathcal {S}}}-s|_h\right) , \end{aligned}$$

(42)

where $s|_{h}:=s(x,y=h,z,t)$ (and equivalently for $c|_{h}$). We solve (39) and (42) to find that

$$\begin{aligned} {{\mathcal {S}}}= b+ \left( \frac{s|_{h}-b}{h}\right) y,\qquad {{\mathcal {C}}}= c|_{h}+{{\mathcal {B}}}_3\left( b-s|_{h}\right) \left( 1-\frac{y}{{h}}\right) , \end{aligned}$$

(43)

where $b=\left. {{\mathcal {S}}}\right| _{y=0}$ and substitute (43) in to (41) to find that b satisfies

$$\begin{aligned} s|_{h}-b=\frac{2 {{\mathcal {R}}} b^2 h \,c|_{h}}{1+2 {{\mathcal {R}}}{{\mathcal {B}}}_3 b^2 h}. \end{aligned}$$

(44)

Thus, h satisfies

$$\begin{aligned} \frac{\partial h}{\partial t}=2 b^2 \left( c|_h+{{\mathcal {B}}}_3\left( b-s|_h\right) \right) ,\qquad h(x,z,0)=0. \end{aligned}$$

(45)

We use the solution for ${{\mathcal {S}}}$ and ${{\mathcal {C}}}$ to replace the flux conservation boundary conditions (31) and (32) on $y=h$ with

$$\begin{aligned} \frac{\partial s}{\partial y}-\epsilon ^2\frac{\partial h}{\partial x}\frac{\partial s}{\partial x}= & {} 2 \epsilon ^2{{\mathcal {R}}}{{\mathcal {B}}}_2 b^2\left( c+{{\mathcal {B}}}_3\left( b-s\right) \right) , \end{aligned}$$

(46)

$$\begin{aligned} \frac{\partial c}{\partial y}-\epsilon ^2\frac{\partial h}{\partial x}\frac{\partial c}{\partial x}= & {} \epsilon ^4 {{\mathcal {R}}}{{\mathcal {B}}}_4 b^2\left( c+{{\mathcal {B}}}_3\left( b-s\right) \right) , \end{aligned}$$

(47)

which we can then use to determine the gas flow in the catalyst channels without having to further consider the transport problem in the liquid layer. We note that, in this limit, the right-hand side of (47) is $O(\epsilon ^4)$, and thus we do not expect much $\hbox {O}_2$ to be removed from the gas by this process.

4.2 Solution in the gas in the catalyst channel

In the region of the catalyst channel filled by gas, diffusion across the channel again dominates. Remembering the limit we are working in (given by (38)), we can easily see that $s^{(0)}=s^{(0)}(x,z,t)$ and $c^{(0)}=c^{(0)}(x,z,t)$, and thus the gas concentrations do not vary across the channel. In order to close the model, we need to go to $O(\epsilon ^2)$ in the equations and boundary conditions. The relevant parts are

$$\begin{aligned} \frac{\partial ^2 s^{(1)}}{\partial y^2}+\frac{\partial ^2 s^{(0)}}{\partial x^2}=0,\qquad \frac{\partial ^2 c^{(1)}}{\partial y^2}+\frac{\partial ^2 c^{(0)}}{\partial x^2}=0, \end{aligned}$$

(48)

with

$$\begin{aligned} \frac{\partial s^{(1)}}{\partial y}=0,\qquad \frac{\partial c^{(1)}}{\partial y}=0\qquad \text{ on }\qquad y=1, \end{aligned}$$

(49)

while (46) and (47) become

$$\begin{aligned} \frac{\partial s^{(1)}}{\partial y}-\frac{\partial h^{(0)}}{\partial x}\frac{\partial s^{(0)}}{\partial x}= & {} 2 {{\mathcal {R}}} {{\mathcal {B}}}_2 {b^{(0)}}^2\left( c^{(0)}+{{\mathcal {B}}}_3\left( b^{(0)}-s^{(0)}\right) \right) \qquad \text{ on }\qquad y=h^{(0)},\end{aligned}$$

(50)

$$\begin{aligned} \frac{\partial c^{(1)}}{\partial y}-\frac{\partial h^{(0)}}{\partial x}\frac{\partial c^{(0)}}{\partial x}= & {} 0\qquad \text{ on }\qquad y=h^{(0)}, \end{aligned}$$

(51)

and we remember that the lateral conditions are

$$\begin{aligned} s^{(0)}= & {} S^{(0)}, c^{(0)}=C^{(0)} \qquad \text{ at }\qquad x=0,\end{aligned}$$

(52)

$$\begin{aligned} \frac{\partial s^{(0)}}{\partial x}= & {} \frac{\partial c^{(0)}}{\partial x}=0 \qquad \text{ at }\qquad x=1. \end{aligned}$$

(53)

We first consider the $\hbox {O}_2$ problem. Integrating (48) across the layer, applying (49) and (51), integrating along the layer and applying (52) and (53), we find that

$$\begin{aligned} c^{(0)}=C^{(0)}, \end{aligned}$$

(54)

i.e. oxygen is present in such a high concentration that the reaction does not reduce the leading-order amount of $\hbox {O}_2$ present in the catalyst channels. Turning our attention to the $\hbox {SO}_2$ problem, performing similar integration across the layer we find that, dropping the zeros, s satisfies

$$\begin{aligned} \frac{\partial }{\partial x}\left( \left( 1-h\right) \frac{\partial s}{\partial x}\right) =2 {{\mathcal {R}}}{{\mathcal {B}}}_2 b^2\left( C+{{\mathcal {B}}}_3\left( b-s\right) \right) , \end{aligned}$$

(55)

which, in summary, must be solved alongside

$$\begin{aligned}&\frac{\partial h}{\partial t}=2 b^2 \left( C+{{\mathcal {B}}}_3\left( b-s\right) \right) , \end{aligned}$$

(56)

$$\begin{aligned}&s-b=\frac{2 {{\mathcal {R}}} b^2 h \,C}{1+2 {{\mathcal {R}}}{{\mathcal {B}}}_3 b^2 h}, \end{aligned}$$

(57)

with

$$\begin{aligned}&s=S \qquad \text{ at }\qquad x=0,\qquad \frac{\partial s}{\partial x}=0\qquad \text{ at } \qquad x=1, \end{aligned}$$

(58)

$$\begin{aligned}&h=0 \qquad \text{ at } \qquad t=0. \end{aligned}$$

(59)

The behaviour of the channel model is governed by the three parameters ${{\mathcal {B}}}_2$, ${{\mathcal {B}}}_3$, and ${{\mathcal {R}}}$ and is influenced by the concentrations of $\hbox {SO}_2$ and $\hbox {O}_2$ at the inlet to the channel. Of these parameters, once the device is manufactured, ${{\mathcal {B}}}_2$ is fixed by the chemistry and the geometry, while ${{\mathcal {B}}}_3$ and ${{\mathcal {R}}}$ alter depending on the amount of $\hbox {SO}_2$ supplied.

Fig. 4

Graph showing how s (left) and h (right) vary with x, for $t=0$, 0.1, 0.345 (blue), 1, 1.4, and 1.544 (red). The solid black lines are for $t<0.345$ and the dashed black lines are for $t>0.345$. The parameters are $S=C={{\mathcal {R}}}={{\mathcal {B}}}_2={{\mathcal {B}}}_3=1$

5 Solution to the catalyst-channel model at the entrance to the device

We focus on the channel at the entrance to the device, where $S=1$ and $C=1$ (we will see in Sect. 6 that, in fact, $C=1$ everywhere), since here the behaviour of the catalyst channel decouples from the behaviour of the outer flow. Our aim is to explore the model behaviour and to determine the clogging time for the catalyst-channel entrance. We solve (55)–(59) numerically and, in Fig. 4, we show how s and h vary with x, at various times, assuming all the parameters are set to 1. We see that $\hbox {SO}_2$ adsorption along the surface of the channel causes the $\hbox {SO}_2$ concentration to decrease into the filter, as expected, but that the behaviour at a particular x value is non-monotonic as t increases, with the concentration increasing everywhere in (0, 1] until $t=0.345$, after which it starts to decrease. We also see that the thickness of the sulphuric acid layer is largest at the inlet and decreases monotonically into the filter. However, in contrast to the $\hbox {SO}_2$ concentration, the thickness of the layer increases monotonically with time until the channel clogs at the inlet at $t=t_{{\mathrm{clog}}}=1.544$.

In order to understand why the concentration changes non-monotonically with time, we consider the case where ${{\mathcal {R}}}\gg 1$ and ${{\mathcal {B}}}_3>1$. We scale $t={{\mathcal {R}}} T$ and write the system of equations as:

$$\begin{aligned}&\frac{\partial }{\partial x}\left( \left( 1-h\right) \frac{\partial s}{\partial x}\right) =2 {{\mathcal {R}}}{{\mathcal {B}}}_2 b^2(1+{{\mathcal {B}}}_3 (b-s)=\frac{{{\mathcal {B}}}_2 (s-b)}{h},\end{aligned}$$

(60)

$$\begin{aligned}&\frac{\partial h}{\partial T}=2 {{\mathcal {R}}} b^2(1+{{\mathcal {B}}}_3 (b-s))=\frac{ (s-b)}{h},\end{aligned}$$

(61)

$$\begin{aligned}&s-b=2 {{\mathcal {R}}} b^2 h (1+{{\mathcal {B}}}_3 (b-s))=\frac{2 {{\mathcal {R}}} b^2 h}{1+2 {{\mathcal {R}}}{{\mathcal {B}}}_3 b^2 h}, \end{aligned}$$

(62)

with

$$\begin{aligned} h=0\quad \text{ at }\quad T=0, \qquad s=1 \quad \text{ at }\quad x=0, \qquad \frac{\partial s}{\partial x}=0 \quad \text{ at }\quad x=1. \end{aligned}$$

(63)

Numerical solutions in this limit suggest that $b^2(1+{{\mathcal {B}}}_3 (b-s))=O(1/{{\mathcal {R}}})$ everywhere. We focus on the situation where $b\sim O(1)$ everywhere in the domain, and thus $s-b=1/{{\mathcal {B}}}_3$. We are then able to solve the leading-order-in-$1/{{\mathcal {R}}}$ system, which reads

$$\begin{aligned} \frac{\partial }{\partial x}\left( (1-h)\frac{\partial s}{\partial x}\right) =\frac{{{\mathcal {B}}}_2}{{{\mathcal {B}}}_3 h},\qquad \frac{\partial h}{\partial T}=\frac{1}{{{\mathcal {B}}}_3 h}, \end{aligned}$$

(64)

to find that³

$$\begin{aligned} h=\sqrt{\frac{2 T}{{{\mathcal {B}}}_3}},\qquad s=\frac{{{\mathcal {B}}}_2 x\left( x-2\right) }{2{{\mathcal {B}}}_3 h(1-h)}+1,\qquad b=\frac{{{\mathcal {B}}}_2 x\left( x-2\right) }{2{{\mathcal {B}}}_3 h(1-h)}+1-\frac{1}{{{\mathcal {B}}}_3}. \end{aligned}$$

(65)

Thus, differentiating s given by (65) and using $\partial h/\partial T$ given by (64), we find that

$$\begin{aligned} \frac{\partial s}{\partial T}=-\frac{{{\mathcal {B}}}_2x(2-x)}{2{{\mathcal {B}}}_3^2 h}\left( \frac{1}{(1-h)^2}-\frac{1}{h^2}\right) , \end{aligned}$$

(66)

which is positive for all $x\in (0,1]$ if $h<1/2$, i.e. if $T<{{\mathcal {B}}}_3/8$, and negative if $h>1/2$, i.e. if $T>{{\mathcal {B}}}_3/8$. Thus, we conclude that (in this limit) s initially rises, then falls, as seen in Fig. 4 (albeit for O(1) parameters) and that this is caused by the interplay between the thinning gaseous layer (the $(1-h)$ factor in (64)) and the weakening of the effect of the reaction as the liquid layer grows (the (1/h) factor in (64)).

5.1 Behaviour at $x=0$

The main quantities of importance from the channel model for the operation of the device are the flux q of sulphur dioxide removed from the outer flow by the catalyst channels, defined by

$$\begin{aligned} q=-(1-h)^+\left. \frac{\partial s}{\partial x}\right| _{x=0}, \end{aligned}$$

(67)

and the evolution of the thickness of the liquid layer at the channel entrance, h(0, 0, t). In Fig. 5, we show how these quantities vary with time. We see that the thickness of the liquid layer increases monotonically, and that the flux decreases monotonically, as t increases, with a very rapid switch off near the clogging time.

Fig. 5

Graph showing how the flux, q, of $\hbox {SO}_2$ removed from the outer flow (dashed line), and the thickness h(0, 0, t) of the liquid layer at the entrance to the catalyst channel (solid line) vary with t. The parameters are set to 1

We now explore in more detail the behaviour of the system at $x=0$ in order to make predictions for the clogging time $t_{{\mathrm{clog}}}$. At $x=0$, Eqs. (44) and (45) are

$$\begin{aligned}&1-b_0=2 {{\mathcal {R}}} b_0^2 h_0\left( 1+{{\mathcal {B}}}_3(b_0-1)\right) ,\end{aligned}$$

(68)

$$\begin{aligned}&\frac{\partial h_0}{\partial t}=2 b_0^2\left( 1+{{\mathcal {B}}}_3(b_0-1)\right) , \end{aligned}$$

(69)

where we use the notation $b_0(t)$ and $h_0(t)$ here to indicate values of b and h at $x=0$. We are interested in solving (68) and (69) until the entrance to the channel clogs; the time at which this occurs is given by $t_{{\mathrm{clog}}}$ such that $h_0\left( t_{{\mathrm{clog}}}\right) =1$. Before proceeding, we immediately note that ${{\mathcal {B}}}_2$ cannot influence the clogging behaviour since it does not appear in either (68) or (69). We first scale t and h to remove the ${{\mathcal {R}}}$ dependence from (68) and (69) using $\tau ={{\mathcal {R}}} t$ and ${\bar{h}}_0={{\mathcal {R}}} h_0$, and note that the definition of the clogging time now depends on ${{\mathcal {R}}}$ since ${\bar{h}}_0\left( \tau _{{\mathrm{clog}}}\right) ={{\mathcal {R}}}$. We rearrange (68) to write ${\bar{h}}_0$ as a function of $b_0$ and we then differentiate and substitute into (69) to find that $b_0$ satisfies

$$\begin{aligned} \frac{\partial b_0}{\partial \tau }= \frac{4 b_0^5\left( 1+{{\mathcal {B}}}_3(b_0-1)\right) ^3}{2 {{\mathcal {B}}}_3(1-b_0)^2+b_0-2}. \end{aligned}$$

(70)

Equation (70) may be solved to get an implicit formula for $b_0$, which then gives ${\bar{h}}_0$ through (68). However, it is just as informative to solve (69) and (70) numerically. In either case, we use the initial condition ${\bar{h}}_0(0)=0$ along with $b_0(0)=1$, since this is the solution to (68) when $t=0$.

In Fig. 6, we show how the evolution of $b_0$ and ${\bar{h}}_0$ depends on ${{\mathcal {B}}}_3$ (we recall that ${{\mathcal {B}}}_3$ depends on the ratio $S^*/C^*$, and thus altering ${{\mathcal {B}}}_3$ corresponds to varying the ratio of the concentrations of sulphur dioxide to oxygen in the gas flow). We see in Fig. 6 (left) that $b_0$ decreases as $\tau$ increases and, for ${{\mathcal {B}}}_3>1$, the solution approaches the steady state $b_0=1-1/{{\mathcal {B}}}_3$ while, for ${{\mathcal {B}}}_3\le 1$, the solution tends to zero as $\tau \rightarrow \infty$. The approach to zero is relatively slow; for example, solving the ${{\mathcal {B}}}_3=1$ case, we find that

$$\begin{aligned} b_0\sim \left( \frac{1}{8\tau }\right) ^{\frac{1}{6}}\qquad \text{ as }\qquad \tau \rightarrow \infty \end{aligned}$$

(71)

We also show the value of $b_0$ for which ${\bar{h}}_0={{\mathcal {R}}}$ for ${{\mathcal {R}}}=1$ (red dots) and ${{\mathcal {R}}}=5$ (blue dots). We see that increasing ${{\mathcal {R}}}$ moves the dots to the right in Fig. 6 (left), with consequence that, as ${{\mathcal {R}}}$ increases, $b_0$ becomes increasingly close to its steady-state value. In Fig. 6 (right), we also see that increasing ${{\mathcal {B}}}_3$ slows the rate of increase of ${\bar{h}}_0$, and that the clogging time, for a particular value of ${{\mathcal {R}}}$, increases as ${{\mathcal {B}}}_3$ increases.

Fig. 6

Graph showing how $b_0$ (left) and ${\bar{h}}_0$ (right) vary with $\tau$ for ${{\mathcal {B}}}_3=0$, 0.5 (left only), 1, 2, 3, 5, 10, and 25. The arrow indicates the direction of increasing ${{\mathcal {B}}}_3$. The dots in the left-hand picture show the values of $b_0$ when $h_0$=1, for ${{\mathcal {R}}}=1$ (red) and ${{\mathcal {R}}}=5$ (blue). These are also indicated in the right-hand plot

In order to see the trends in the clogging time as we vary the parameters, we first recall that the time scaling in our nondimensionalisation includes the parameters r and $S^*$. In order to assess the influence of varying r and $S^*$, we remove this hidden dependence by considering $t_{{\mathrm{clog}}}/{{\mathcal {R}}}{{\mathcal {B}}}_3$. We show how $t_{{\mathrm{clog}}}/{{\mathcal {R}}}{{\mathcal {B}}}_3$ varies with ${{\mathcal {B}}}_3$ for ${{\mathcal {R}}}=1$, 10, and 100 in Fig. 7 (left). We see that increasing ${{\mathcal {B}}}_3$ decreases the scaled clogging time, and that, for large ${{\mathcal {B}}}_3$, this behaviour is independent of ${{\mathcal {R}}}$. To find this behaviour, we make the anzatz

$$\begin{aligned} b_0=1-\frac{b_0^{(1)}}{{{\mathcal {B}}}_3}-\frac{b_0^{(2)}}{{{{\mathcal {B}}}_3}^2},\qquad h_0=h_0^{(0)}+\frac{h_0^{(1)}}{{{\mathcal {B}}}_3}, \end{aligned}$$

(72)

for ${{\mathcal {B}}}_3\gg 1$ and scale $t={{\mathcal {B}}}_3 \tau$. Substituting into (68) and (69) we find that, at leading order, both equations are satisfied by $b_0^{(1)}=1$. The $O(1/{{\mathcal {B}}}_3)$ versions of (68) and (69) read

$$\begin{aligned} b_0^{(2)}=-\frac{1}{2{{\mathcal {R}}} h_0^{(0)}},\qquad \frac{\partial h_0^{(0)}}{\partial \tau }=-2 b_0^{(2)}, \end{aligned}$$

(73)

respectively, which we solve to find that

$$\begin{aligned} h_0^{(0)}=\sqrt{\frac{2t}{{{\mathcal {R}}}{{\mathcal {B}}}_3}}. \end{aligned}$$

(74)

Therefore, we conclude that

$$\begin{aligned} \frac{t_{{\mathrm{clog}}}}{{{\mathcal {R}}}{{\mathcal {B}}}_3}\sim \frac{1}{2}\qquad \text{ as }\qquad {{\mathcal {B}}}_3 \rightarrow \infty , \end{aligned}$$

(75)

which we see in Fig. 7 (left) is in excellent agreement with the numerical results. Conversely, when ${{\mathcal {B}}}_3\ll 1$, we find that the leading-order solution to (68) and (70), written in original variables, is

$$\begin{aligned} \frac{6 b_0^4}{3-2b_0}=\frac{6}{24 {{\mathcal {R}}} t+1},\qquad h_0=\frac{1-b_0}{2 {{\mathcal {R}}} b_0^2}. \end{aligned}$$

(76)

Thus, at $t=t_{{\mathrm{clog}}}$, we find that

$$\begin{aligned} b_{{\mathrm{clog}}}=\frac{\sqrt{1+8 {{\mathcal {R}}}}-1}{4{{\mathcal {R}}}},\qquad t_{{\mathrm{clog}}}=\frac{16 {{{\mathcal {R}}}}^2}{3}\left( \frac{6{{\mathcal {R}}}-\left( \sqrt{1+8 {{\mathcal {R}}}}-1\right) }{\left( \sqrt{1+8 {{\mathcal {R}}}}-1\right) ^4}-\frac{1}{128 {{{\mathcal {R}}}}^3}\right) . \end{aligned}$$

(77)

Again, we see excellent agreement between the asymptotic predictions and the numerical results, for all three values of ${{\mathcal {R}}}$ shown in Fig. 7 (left).

Fig. 7

(Left) Graph showing how $t_{{\mathrm{clog}}}/{{\mathcal {R}}}{{\mathcal {B}}}_3$ varies with ${{\mathcal {B}}}_3$ for ${{\mathcal {R}}}=1$, 10, and 100. The dotted line is the asymptotic behaviour as ${{\mathcal {B}}}_3\rightarrow \infty$, while the dashed lines are the asymptotic behaviour as ${{\mathcal {B}}}_3\rightarrow 0$. (Right) Graph showing how $t_{{\mathrm{clog}}}/{{\mathcal {R}}}{{\mathcal {B}}}_3$ varies with ${{\mathcal {R}}}$ for ${{\mathcal {B}}}_3=1$, 10, and 100. The dotted lines are the asymptotic behaviour for large ${{\mathcal {B}}}_3$ while the dashed lines are the asymptotic behaviour for ${{\mathcal {R}}}\rightarrow 0$. The inserts show the corresponding behaviour of $t_{{\mathrm{clog}}}/{{\mathcal {R}}}$; the right-hand insert also shows the plot for ${{\mathcal {B}}}_3=0$

In Fig. 7 (right), we explore how $t_{{\mathrm{clog}}}/{{\mathcal {R}}}{{\mathcal {B}}}_3$ varies as we alter ${{\mathcal {R}}}$, for various values of ${{\mathcal {B}}}_3$. We see that the scaled clogging time decreases as ${{\mathcal {R}}}$ increases, as expected, since an increase in the reaction rate generates more liquid which means that the inlet clogs more quickly. We show the small-${{\mathcal {R}}}$ asymptotic solution (which we will establish in the appendix) as dashed lines and we see excellent agreement. Moreover, we note that the small-${{\mathcal {R}}}$ limit holds over the whole domain for large values of ${{\mathcal {B}}}_3$, as shown in Fig. 7 (right) where we see that the asymptotic line lies on top of the ${{\mathcal {B}}}_3=100$ line. We also show the large-${{\mathcal {B}}}_3$ asymptotic solutions as dotted line and also see excellent agreement there too. In the inset to Fig. 7 (right),⁴ we show the behaviour of $t_{{\mathrm{clog}}}/{{\mathcal {R}}}$ versus ${{\mathcal {R}}}$ and include the curve for ${{\mathcal {B}}}_3=0$. We see that this follows the ${{\mathcal {B}}}_3=1$ curve reasonably closely, and that $t_{{\mathrm{clog}}}/{{\mathcal {R}}}\rightarrow 0$ as ${{\mathcal {R}}}\rightarrow \infty$ for both ${{\mathcal {B}}}_3=0$ and 1. We note that, when ${{\mathcal {B}}}_3\ll 1$, (77) holds over the whole domain and provides an exact formula for $t_{{\mathrm{clog}}}$ when ${{\mathcal {B}}}_3=0$. Similarly, we find that, when ${{\mathcal {B}}}_3=1$,

$$\begin{aligned}&b_{{\mathrm{clog}}}=\frac{1}{6^{1/3}\sqrt{{{\mathcal {R}}}}}\left( \frac{\left( 9\sqrt{{{\mathcal {R}}}}+\sqrt{3}\sqrt{2+27 {{\mathcal {R}}}}\right) ^{1/3}}{6^{1/3}}-\frac{1}{\left( 9 \sqrt{{{\mathcal {R}}}}+\sqrt{3}\sqrt{2+27{{\mathcal {R}}}}\right) ^{1/3}}\right) , \nonumber \\&t_{{\mathrm{clog}}}=\frac{1}{40{{\mathcal {R}}}}\left( \frac{5-4b_{{\mathrm{clog}}}}{b_{{\mathrm{clog}}}^6}-1\right) . \end{aligned}$$

(78)

We note that the behaviour of $t_{{\mathrm{clog}}}$ given by (77) and (78) are identical to the numerical results and are not shown separately in Fig. 7.

5.2 Varying the parameters

We now vary the parameters to determine their influence on the flux, q, of sulphur dioxide drawn into the catalyst channel. In Fig. 8, we show the effect of varying ${{\mathcal {B}}}_2$ (this is analagous to altering the aspect ratio of the channels), ${{\mathcal {B}}}_3$ (this is analagous to altering the ratio of the concentration of sulphur dioxide to oxygen), and ${{\mathcal {R}}}$. We see that increasing all these parameters increases the flux of sulphur dioxide drawn into the catalyst channel, although we note that increasing ${{\mathcal {R}}}$ decreases the actual clogging time, as can be seen in the inset to Fig. 8 (right).

Fig. 8

Graph showing how the flux varies with time for (left) ${{\mathcal {B}}}_2=0.1$, 1, and 10, (middle) ${{\mathcal {B}}}_3=0.1$, 1, and 10, and (right) ${{\mathcal {R}}}=0.1$, 1, and 10. In each case, the other parameters are all set to 1. The inset shows the same data plotted against $t/{{\mathcal {R}}}$

In Fig. 9, we show how the total amount of $\hbox {SO}_2$ extracted by the channel before it clogs , given by $-\int _0^{t_{{\mathrm{clog}}}} q\, \text{ d }t$, varies with ${{\mathcal {R}}}{{\mathcal {B}}}_2$. We see that the total amount of $\hbox {SO}_2$ removed increases with ${{\mathcal {R}}}{{\mathcal {B}}}_2$ and that the behaviour scales like ${{\mathcal {R}}}{{\mathcal {B}}}_2$ when ${{\mathcal {R}}}{{\mathcal {B}}}_2\ll 1$ and like $\sqrt{{{\mathcal {R}}}{{\mathcal {B}}}_2}$ when ${{\mathcal {R}}}{{\mathcal {B}}}_2\gg 1$. We note that it is possible to obtain an asymptotic solution to (55)–(59) in the case when ${{\mathcal {R}}}\ll 1$; we present this solution and compare it with a numerical solution for ${{\mathcal {R}}}$ small, in the Appendix.

Fig. 9

Graph showing how the total amount of sulphur dioxide removed from the gas stream by the channel before clogging as a function of ${{\mathcal {R}}}{{\mathcal {B}}}_2$. The other parameters are set to 1

5.3 The thin-liquid-layer (small-time) approximation

For small time, we expect the thickness of the layer of liquid sulphuric acid to be small compared with the width of the catalyst channels. When $h\ll 1$, $h=\varepsilon {{\mathcal {H}}}$ say, Eq. (57) reduces to $s=b$, and thus (55) and (56) reduce to

$$\begin{aligned}&\dfrac{\partial ^{2}s}{\partial x^{2}}=2 {{\mathcal {R}}} {{\mathcal {B}}}_2 s^2, \end{aligned}$$

(79)

$$\begin{aligned}&\frac{\partial {{\mathcal {H}}}}{\partial {{\mathcal {T}}}}=2 s^2, \end{aligned}$$

(80)

where ${{\mathcal {T}}}=t/\varepsilon$. We note that ${{\mathcal {R}}}{{\mathcal {B}}}_2$, and thus, the solution, only depends on the solubilities, and not the diffusivities, of $\hbox {SO}_2$ and $\hbox {O}_2$ in the $\hbox {H}_2\hbox {SO}_4$ layer. We integrate (79) to find that s satisfies

$$\begin{aligned} \frac{\partial s}{\partial x}=-2 \sqrt{\frac{{{\mathcal {R}}} {{\mathcal {B}}}_2}{3}} \sqrt{s^3-s_\mathrm{{e}}^3}, \end{aligned}$$

(81)

where $s_\mathrm{{e}}=s(1)$ and we have picked the negative gradient on physical grounds. In the thin-liquid-layer limit, the flux $q\approx -\partial s/\partial x|_{x=0}$. Unfortunately, the flux given by (81), evaluated at $x=0$, depends on $s_\mathrm{{e}}$, and thus, we have to calculate $s_\mathrm{{e}}$. In principle, we could integrate (81) to give an implicit formula for $s_\mathrm{{e}}$, but it is just as instructive to solve (79) with boundary conditions (58) numerically. We show the resulting concentration profiles from a numerical simulation in Fig. 10 (left) for various values of ${{\mathcal {R}}} {{\mathcal {B}}}_2$.

Fig. 10

(left) Graph showing how the concentration s in the channels varies with x, for ${{\mathcal {R}}} {{\mathcal {B}}}_2=1$, 2.5, 5, 10, 25, 50, 100. (right) Log–Log graph showing how the (modulus of the) flux into the channel varies with ${{\mathcal {R}}}{{\mathcal {B}}}_2$. The dots are taken from numerical simulations while the dotted line comes from (85)

We see that increasing ${{\mathcal {R}}} {{\mathcal {B}}}_2$ decreases the concentration of $\hbox {SO}_2$ in the channel and increases the flux of $\hbox {SO}_2$ drawn out from the gas. In order to quantify the affect of altering ${{\mathcal {R}}}{{\mathcal {B}}}_2$, we rescale (79) and (58) using $x=\xi /\sqrt{{{\mathcal {R}}}{{\mathcal {B}}}_2}$, and write the model as the first-order system

$$\begin{aligned} \frac{\partial s}{\partial \xi }=p,\qquad \frac{\partial p}{\partial \xi }=2 s^2, \end{aligned}$$

(82)

with

$$\begin{aligned} s = 1&\qquad \text{ at }\qquad&\xi =0 , \end{aligned}$$

(83)

$$\begin{aligned} p =0&\text{ at }&\xi =\xi _e=\sqrt{{{\mathcal {R}}}{{\mathcal {B}}}_2}. \end{aligned}$$

(84)

Remembering that we expect p to be negative, we show in Fig. 11 (left) the phase plane for (82), for various values of p(0). The trajectories split into two sets. For $p(0)>-2/\sqrt{3}$, the solutions reach zero slope at some finite value of s and at some finite value of $\xi$ and represent the set of realisable solutions. For $p(0)<-2/\sqrt{3}$, the solutions reach $s=0$ at some finite slope; we reject these as unphysical since they do not reach $p=0$. We show the dividing trajectory as a red-dashed line. This trajectory has $s,p\rightarrow 0$ as $\xi \rightarrow \infty$ and, thus, corresponds to $p(0)=-2/\sqrt{3}$; this is in line with an appropriately scaled (81) with $s_\mathrm{{e}}=0$. We solve (82)–(84) for a given value of p(0) and calculate $\xi _e$, backing out the relationship between $\xi _e$ and $-p(0)$, which we plot in Fig. 11 (right). We see that, as $\xi _e$ increases, the flux increases (agreeing with (121) for small $\xi _e$) and then tends to $2/\sqrt{3}$ for large $\xi _e$, in keeping with the results presented in Fig. 10 (right) which we will describe on the next page.

Fig. 11

(Left) Phase plane for (82)–(84). The black curves have $p(0)=-1.3$, $-1.2$, $-1.16$, $-1.15$, and $-1.1$, then every 0.1 until $p(0)=-0.1$. The red-dashed trajectory is the dividing trajectory with $p(0)=-2/\sqrt{3}$. The grey lines show the direction of the solutions. (Right) Graph showing the relationship between q and $\xi _e$. The dots represent the data from the feasible solutions in the phase-plane diagram. The dotted line is the limiting value $p(0)=-2/\sqrt{3}$. The dashed line is the flux given by the leading-order version of (121)

Returning to Fig. 10 (left), we also see that the value of $s_\mathrm{{e}}$ decreases as the value of ${{\mathcal {R}}} {{\mathcal {B}}}_2$ increases. We can, thus, find an approximation for the flux of $\hbox {SO}_2$ entering the channel by assuming that $s_\mathrm{{e}}^3\ll 1$. Neglecting $s_\mathrm{{e}}^3$ in (81), we arrive at the simple formula

$$\begin{aligned} \frac{\partial s}{\partial x}=-2 \sqrt{\frac{{{\mathcal {R}}} {{\mathcal {B}}}_2}{3}} s^{3/2}. \end{aligned}$$

(85)

We show how q varies with ${{\mathcal {R}}}{{\mathcal {B}}}_2$ in Fig. 10 (right); our numerical results are presented as dots and the asymptotic results from (85) as a dotted line. We see excellent agreement between our simple formula and the numerically calculated flux, even for ${{\mathcal {R}}}{{\mathcal {B}}}_2=O(1)$. We also note that $q\sim \sqrt{{{\mathcal {R}}}{{\mathcal {B}}}_2}$ for large ${{\mathcal {R}}}{{\mathcal {B}}}_2$, as previously seen in Fig. 9 albeit for the total $\hbox {SO}_2$ removed. The solution to (85) with boundary condition (58) (left) is

$$\begin{aligned} s=\frac{1}{\left( 1+\sqrt{{{\mathcal {R}}}{{\mathcal {B}}}_2/3}\,x\right) ^2}. \end{aligned}$$

(86)

This solution does not satisfy the boundary condition at $x=1$. In fact, there will be a region near $x=1$ where the terms involving $s_\mathrm{{e}}$ that we have previously neglected are important. However, since the flux at $x=0$ is accurately captured, we do not worry about this further.

We next show how the (very thin) layer of liquid evolves. In Fig. 12 (Left), we show the spatial variation of the rate of increase of the thickness for various values of ${{\mathcal {R}}} {{\mathcal {B}}}_2$. We see that increasing ${{\mathcal {R}}} {{\mathcal {B}}}_2$ localises the rate of film growth, and hence the liquid, near the entrance to the channel, as we might expect. Finally, we investigate how the flux into the catalyst channels behaves in the thin-layer case as we move along the device, i.e. as we alter S, remembering that we expect it to be directly proportional to $S^{3/2}$ in cases where we can neglect $s_\mathrm{{e}}$. We show the resulting behaviour as we alter S in Fig. 12, for ${{\mathcal {R}}}{{\mathcal {B}}}_2=1$ and ${{\mathcal {R}}} {{\mathcal {B}}}_2=10$. We see that the flux decreases as the inlet concentration decreases. We further see excellent agreement between the approximate solution given by (85) and the numerical solution when ${{\mathcal {R}}} {{\mathcal {B}}}_2=10$, and reasonable agreement even when ${{\mathcal {R}}} {{\mathcal {B}}}_2=1$. We note that (85) provides a very simple non-linear relationship between the flux of $\hbox {SO}_2$ removed from the gas stream and concentration of $\hbox {SO}_2$ in the gas stream that would have been difficult to predict had we not considered the catalyst-channel-scale model. We will use this relationship in Sect. 6.2, where we propose a simple method for determining r.

Fig. 12

(Left) Graph showing the spatial variation of the liquid layer growth rate, for ${{\mathcal {R}}} {{\mathcal {B}}}_2=1$, 5, 10, 25, 50, and 100 .(Right) Graph showing how the flux into the channel varies with S in the cases where ${{\mathcal {R}}}{{\mathcal {B}}}_2=1$ (dashed) and ${{\mathcal {R}}} {{\mathcal {B}}}_2=10$ (dotted). The dots are taken from numerical experiments while the dashed line is from the approximation presented in (85)

6 Device operation

We now consider how the device operates by coupling the transport of gas through the device with the removal of sulphur dioxide by the filter. As we have seen in Sect. 4.2, the leading-order concentration of oxygen in the catalyst channel does not vary in the channel, and thus, there is no leading-order flux of oxygen into the channel. Thus, we see from (21) that the device does not extract sufficient oxygen to make a significant change to its concentration as the gas passes through, and hence $C=1$ everywhere.

The model for sulphur dioxide removal can be summarised as follows:

$$\begin{aligned}&\frac{\partial S}{\partial z}=\chi _0{{\mathcal {B}}}_1 (1-h)^+\left. \frac{\partial s}{\partial x}\right| _{x=0}, \end{aligned}$$

(87)

$$\begin{aligned}&\frac{\partial }{\partial x}\left( \left( 1-h\right) \frac{\partial s}{\partial x}\right) = 2 {{\mathcal {R}}}{{\mathcal {B}}}_2 b^2\left( 1+{{\mathcal {B}}}_3(b-s)\right) , \end{aligned}$$

(88)

$$\begin{aligned}&\frac{\partial h}{\partial t}=2 b^2\left( 1+ {{\mathcal {B}}}_3(b-s)\right) , \end{aligned}$$

(89)

$$\begin{aligned}&s-b=2 {{\mathcal {R}}} b^2 h\left( 1+{{\mathcal {B}}}_3(b-s)\right) . \end{aligned}$$

(90)

and we note that, in practice, we solve (88) and (89) until $h(0,z,t)=1$, after which we simply hold $h=1$ at that z location and do not solve (88) and (89) further. The relevant boundary and initial conditions are

$$\begin{aligned} S=1\qquad&\text{ at }&\qquad z=0, \end{aligned}$$

(91)

$$\begin{aligned} s=S\qquad&\text{ at }&\qquad x=0,\end{aligned}$$

(92)

$$\begin{aligned} \frac{\partial s}{\partial x}=0 \qquad&\text{ at }&\qquad x=1,\end{aligned}$$

(93)

$$\begin{aligned} h=0\qquad&\text{ at }&\qquad t=0. \end{aligned}$$

(94)

Using the data in Table 2, we calculate that the physically relevant parameter values are

$$\begin{aligned}&{{\mathcal {B}}}_1=\frac{\epsilon ^2 \gamma D_2}{Pe}=\frac{H D_s^\mathrm{{g}}}{lLU}\approx 8,\qquad {{\mathcal {B}}}_2=\frac{1}{\beta _s D_2 \epsilon ^2}=\frac{D_s^\mathrm{{l}} L^2}{\beta _s D_s^\mathrm{{g}} W^2}\approx 0.4, \nonumber \\&{{\mathcal {B}}}_3=\alpha \frac{\beta _c D_3}{2\beta _s D_2}=\frac{\beta _c D_s^\mathrm{{l}} S^*}{2 \beta _s D_c^\mathrm{{l}} C^*}\approx 0.14, \end{aligned}$$

(95)

and we (arbitrarily) pick $\chi _0=0.5$ in order to estimate the size of the parameters under normal operation. We recall that ${{\mathcal {R}}}=150$ (but that it depends on the unknown r). We note that we can control U, the speed of the gas flow, and possibly H, the length of the device (by adding additional filter modules in series) once the system has been built, and that $S^*$ and $C^*$ can vary depending on the gas fed into the filter. Thus, the main controllable parameters in the system are ${{\mathcal {B}}}_1$, ${{\mathcal {B}}}_3$, and ${{\mathcal {R}}}$, while ${{\mathcal {B}}}_2$ remains constant and known once the device has been built.

We solve (87)–(94) numerically using an explicit Euler scheme for (87), (89), (91), and (94) along with Newton iterations for the non-linear algebraic problem (90) and boundary value problem (88), (92), and (93), discretised using a central finite-difference scheme. We implemented the scheme in MATLAB using 800 grid points for x and z (beyond which altering the step size did not appreciably alter the solution), with the parameters given in (95) and show in Fig. 13 how S and $h|_{x=0}$ vary with z, for various values of t. We see that S and $h|_{x=0}$ decrease along the device, with both S and $h|_{x=0}$ initially confined to a region close to to the upper surface, and that both increase monotonically with time. We see that, once $h|_{x=0}=1$ at $z=0$, a front, located at $z=G(t)$ say, propagates down the device behind which $S=1$ and $h|_{x=0}=1$. In Fig. 14 (left), we show how the concentration of $\hbox {SO}_2$ remaining in the gas stream at the outlet of the device varies with time,⁵ while in Fig. 14 (right), we show how the front $z=G(t)$ propagates. We see that the concentration of $\hbox {SO}_2$ exiting the device (for release into the atmosphere) remains low (less than 10% of the input amount) until about $t\approx 100$, which is the equivalent of 296 days, and then increases linearly until just before the time at which the device completely stops working, which we call the device lifetime, $t_\mathrm{{L}}$. Thus, we conclude that the device becomes less efficient as time progresses. For this particular set of parameters, we find that $t_\mathrm{{L}}=264.3$, which is equivalent to 2.1 years. We also see that $G=0$ up until $t_{{\mathrm{clog}}}$, since in this period, the liquid layer thickness is less than one everywhere in the device (as can be seen in Fig. 13 (right)). After $t=t_{{\mathrm{clog}}}$, we see that G moves linearly through the device.

Fig. 13

Graph showing how S (left) and $h|_{x=0}$ (right) vary with z, for $t=1$, 10, 100, 200, 250, and 264.3. The parameters are given in (95)

Fig. 14

Graph showing how (left) the concentration of $\hbox {SO}_2$ exiting the device and (right) the front position vary with t. The inset highlights the non-smooth behaviour of the solution caused by having a finite discretisation. The parameters are given in (95)

We now look at the effect of varying the key parameters on the amount of $\hbox {SO}_2$ exiting the device. In each case, we compare solutions in which we use the parameters in (95) with ones in which we halve, or double, the relevant parameter(s). In order to ensure that we compare like-with-like, we plot the dependence against $t/{{\mathcal {R}}}{{\mathcal {B}}}_3$, to account for the hidden r and $S^*$ in our nondimensionalisation for time. In Fig. 15, we vary ${{\mathcal {B}}}_1$; ${{\mathcal {B}}}_1$ is directly proportional to the length of the device H and inversely proportional to the gas speed U and the width of the outer channel l. In Fig. 15 (left), we see that increasing ${{\mathcal {B}}}_1$ increases the device lifetime, as expected, since this corresponds to increasing the length of the device, or decreasing the gas speed or the width of the outer channel (these both reduce the flux of $\hbox {SO}_2$ passing through the device). We also note that there is a slight kink in the curve for ${{\mathcal {B}}}_1=4$; this occurs at $t=t_{{\mathrm{clog}}}$ and is associated with the switching off of growth at the inlet and the transition to travelling wave behaviour. The kink is, in fact, present in all the curves, but decreases in magnitude as ${{\mathcal {B}}}_1$ increases. In Fig. 15 (right), we see that the time at which G starts to move is the same for each curve, as expected, since $t_{{\mathrm{clog}}}$ does not depend on ${{\mathcal {B}}}_1$. After $t=t_{{\mathrm{clog}}}$, we see that G(t) is linear in all three cases, and that increasing ${{\mathcal {B}}}_1$ decreases the slope ${\dot{G}}$.

Fig. 15

Graphs showing how (left) the concentration of $\hbox {SO}_2$ leaving the device and (right) the front position vary with $t/{{\mathcal {R}}}{{\mathcal {B}}}_3$, for ${{\mathcal {B}}}_1=4$, 8, and 16. The arrows indicate increasing ${{\mathcal {B}}}_1$. The other parameters are as presented in (95)

Fig. 16

Graphs showing (left) how the concentration of $\hbox {SO}_2$ leaving the device and (right) how the filter availability in the device vary with $t/{{\mathcal {R}}}{{\mathcal {B}}}_3$, for $({{\mathcal {R}}},{{\mathcal {B}}}_3)=(75,0.07)$, (150, 0.14), and (300, 0.28), simulating changing the dimensional concentration of $\hbox {SO}_2$, $S^*$, at the entrance to the device. The arrows indicate increasing $S^*$. The red dots are the predictions for $t_{{\mathrm{clog}}}$ given by (96). The other parameters are as presented in (95)

We next present, in Fig. 16, the effect of varying the inlet $\hbox {SO}_2$ concentration $S^*$ (which results in scaling ${{\mathcal {B}}}_3$ and ${{\mathcal {R}}}$ simultaneously; both are doubled or halved) on the concentration of $\hbox {SO}_2$ leaving the device and the front position. We note that we have scaled the vertical axis in Fig. 16 (left) artificially so that a concentration of 1 corresponds with the normal value of $S^*$. We see that increasing the inlet concentration increases the outlet concentration, as found in [17], and consequently reduces $t_\mathrm{{L}}$. This is to be expected, since increasing $S^*$ increases the amount of $\hbox {SO}_2$ passing through the device (per unit time) and, thus, increases the amount of $\hbox {SO}_2$ entering the catalyst channels. In Fig. 16 (right), we see that the front starts propagating earlier as $S^*$ is increased, in keeping with the fact that $t_{{\mathrm{clog}}}$ varies with both ${{\mathcal {R}}}$ and ${{\mathcal {B}}}_3$. We note that ${{\mathcal {B}}}_3\ll 1$ and ${{\mathcal {R}}}\gg 1$ for all three parameter sets in Fig. 17 (and, indeed, for all the results, we are presenting), so $t_{{\mathrm{clog}}}$ can be approximated by taking the large ${{\mathcal {R}}}$ limit of (77), yielding

$$\begin{aligned} \frac{t_{{\mathrm{clog}}}}{{{\mathcal {R}}}{{\mathcal {B}}}_3}\sim \frac{1}{2{{\mathcal {B}}}_3}+\frac{\sqrt{2}}{3 {{\mathcal {B}}}_3\sqrt{{{\mathcal {R}}}}}+O\left( \frac{1}{{{\mathcal {R}}}}\right) . \end{aligned}$$

(96)

We see that the predictions from (96) are in good agreement with the numerical behaviour seen in Fig. 16. After $t_{{\mathrm{clog}}}$, we see that the front propagates linearly through the device for all three choices of parameters, and that the slope increases as $S^*$ increases, in keeping with our intuition that a higher concentration of $\hbox {SO}_2$ at the inlet results in faster film growth throughout the device.

Fig. 17

Graph showing (left) how the concentration of $\hbox {SO}_2$ leaving the device and (right) how the filter availability in the device vary with $t/{{\mathcal {R}}}{{\mathcal {B}}}_3$, for ${{\mathcal {R}}}=15$, 75, 150, 300, and 1500. The arrows indicate increasing ${{\mathcal {R}}}$. The other parameters are as presented in (95)

Fig. 18

Graph showing (left) how the concentration of $\hbox {SO}_2$ leaving the device and (right) how the filter availability in the device vary $t/{{\mathcal {R}}}{{\mathcal {B}}}_3$ as ${{\mathcal {B}}}_1$ and ${{\mathcal {B}}}_2$, as a proxy for the length of the catalyst channels, L, are varied. The parameters are $({{\mathcal {B}}}_1,{{\mathcal {B}}}_2)=(16,0.1),(8,0.4),(4,1.6)$ The other parameters are as presented in (95)

Next we look at how varying the dimensionless reaction rate alters the behaviour of the device. Since we do not know r, we look at five different ${{\mathcal {R}}}$ values to assess inaccuracy in r of two orders of magnitude. We show how the outlet concentration varies as we change ${{\mathcal {R}}}$ in Fig. 17 (left). We see that increasing ${{\mathcal {R}}}$ results in less $\hbox {SO}_2$ being released into the atmosphere at early time (until $t/{{\mathcal {R}}}{{\mathcal {B}}}_3\approx 7$, and then increasing ${{\mathcal {R}}}$ increases the amount of $\hbox {SO}_2$ released, resulting in a decrease in $t_\mathrm{{L}}$. This behaviour can be explained as follows: at early time, increasing ${{\mathcal {R}}}$ results in more $\hbox {SO}_2$ extracted by the catalyst channels close to the inlet and, thus, lower levels of $\hbox {SO}_2$ at the outlet. However, a higher rate of $\hbox {SO}_2$ removal causes faster growth of the $\hbox {H}_2\hbox {SO}_4$ layers and, thus, faster clogging of individual catalyst channels and a corresponding increase in $\hbox {SO}_2$ reaching the outlet. In Fig. 17 (right), we see a small change in the clogging time as ${{\mathcal {R}}}$ increases, in keeping with (96). We also see that, after $t_{{\mathrm{clog}}}$, the fronts propagate linearly through the device, except for ${{\mathcal {R}}}=15$, where the speed increases slightly as the propagation progresses. We also see that the speed of propagation increases slightly as ${{\mathcal {R}}}$ increases. The decrease in $t_\mathrm{{L}}$ is about 14% for an increase in the reaction rate of two orders of magnitude, suggesting that device operation is not so sensitive to the reaction rate. Further, given that the slopes of G are approximately constant (for ${{\mathcal {R}}}>75$), the change in $t_\mathrm{{L}}$ is in line with the change in $t_{{\mathrm{clog}}}$, which (when ${{\mathcal {B}}}_3=0$) alters by 20% as ${{\mathcal {R}}}$ changes from 15 to 1500.

Finally, in Fig. 18, we show the effect of varying the length L of the catalyst channels (via altering both ${{\mathcal {B}}}_1$ and ${{\mathcal {B}}}_2$ appropriately; ${{\mathcal {B}}}_1\sqrt{{{\mathcal {B}}}_2}$ remains constant). We see that increasing L increases the lifetime of the device, but the rate of increase decreases as L increases. We explore this behaviour further by considering the case where ${{\mathcal {R}}}{{\mathcal {B}}}_2\gg 1$. In this case, we scale $x=1/\sqrt{{{\mathcal {R}}}{{\mathcal {B}}}_2}\xi$, and the modified parts of (87)–(94) are

$$\begin{aligned} \frac{\partial S}{\partial z}=\chi _0{{\mathcal {B}}}_1 \sqrt{{{\mathcal {R}}}{{\mathcal {B}}}_2}(1-h)^+\left. \frac{\partial s}{\partial \xi }\right| _{\xi =0},\qquad \frac{\partial }{\partial \xi }\left( \left( 1-h\right) \frac{\partial s}{\partial \xi }\right) = 2 b^2\left( 1+{{\mathcal {B}}}_3(b-s)\right) , \end{aligned}$$

(97)

and

$$\begin{aligned} \frac{\partial s}{\partial \xi }=0 \qquad \text{ at }\qquad \xi =\sqrt{{{\mathcal {R}}}{{\mathcal {B}}}_2}, \end{aligned}$$

(98)

while the problems for b and h remain unchanged. In the scaled coordinates, we see that increasing ${{\mathcal {R}}}{{\mathcal {B}}}_2$ increases the device length, and we anticipate that, as we saw in Fig. 11 (right) for the single-channel-no-liquid case, the scaled flux p will become constant even for moderate values of ${{\mathcal {R}}}{{\mathcal {B}}}_2$. Since ${{\mathcal {B}}}_1\sqrt{{{\mathcal {B}}}_2}$ is independent of L, we expect that the device operation will be completely independent of L for ${{\mathcal {R}}}{{\mathcal {B}}}_2\gg 1$. To illustrate this behaviour, in Fig. 19, we show how $t_\mathrm{{L}}/{{\mathcal {R}}}{{\mathcal {B}}}_3$ varies with ${{\mathcal {B}}}_2$ (${{\mathcal {R}}}=150$ throughout). We see that, above ${{\mathcal {B}}}_2\approx 2$, the device lifetime does not appreciably change. Thus, we calculate that there is no point making the filter thicker than $L=2.2$ mm, for the operating parameters presented in Table 1.

Fig. 19

Graph showing how $t_\mathrm{{L}}/{{\mathcal {R}}}{{\mathcal {B}}}_3$ varies with ${{\mathcal {B}}}_2$ (${{\mathcal {B}}}_1$ was altered to keep ${{\mathcal {B}}}_1\sqrt{{{\mathcal {B}}}_2}$ constant). The other parameters are presented in (95)

6.1 The physically relevant parameter regime ${{\mathcal {R}}}\gg 1$, ${{\mathcal {B}}}_1\gg 1$, ${{\mathcal {B}}}_2\ll 1$, ${{\mathcal {B}}}_3\ll 1$

From (95) and the value of ${{\mathcal {R}}}$ in Table 2, we see that ${{\mathcal {R}}}\gg 1$, ${{\mathcal {B}}}_1\gg 1$, ${{\mathcal {B}}}_2\ll 1$, ${{\mathcal {B}}}_3\ll 1$ during normal device operation, and so we now explore that limit. We first note that ${{\mathcal {B}}}_3\ll 1$ and so neglect all ${{\mathcal {B}}}_3$ terms in (88)–(90). We then solve (90) to find that

$$\begin{aligned} b=\frac{\sqrt{1+8 {{\mathcal {R}}} h s}-1}{4 {{\mathcal {R}}} h}. \end{aligned}$$

(99)

Thus, scaling $t={{\mathcal {R}}} T$, we write (88) and (89) as

$$\begin{aligned}&\frac{\partial }{\partial x}\left( \left( 1-h\right) \frac{\partial s}{\partial x}\right) ={{\mathcal {B}}}_2 \left( \frac{s}{h}+\frac{1-\sqrt{1+8 {{\mathcal {R}}} h s}}{4 {{\mathcal {R}}} h^2}\right) ,\end{aligned}$$

(100)

$$\begin{aligned}&\frac{\partial h}{\partial T}=\frac{s}{h}+\frac{1-\sqrt{1+8 {{\mathcal {R}}} h s}}{4 {{{\mathcal {R}}}} h^2}. \end{aligned}$$

(101)

We now assume that ${{\mathcal {R}}}\gg 1$, so that we may neglect the terms of $O(\sqrt{{{\mathcal {R}}}})$ in (100) and (101), and look for an asymptotic solution of the form $X=X^{(0)}+{{\mathcal {B}}}_2 X^{(1)}+\cdots$, for small ${{\mathcal {B}}}_2$. The solution to the leading-order version of (100) with boundary conditions (92) and (93) is $s^{(0)}=S^{(0)}$, and thus, $s^{(0)}$ does not vary with x. The leading-order version of (101) is

$$\begin{aligned} \frac{\partial h^{(0)}}{\partial T}=\frac{S^{(0)}}{h^{(0)}}, \end{aligned}$$

(102)

and we see that $h^{(0)}$ also does not depend on x. Proceeding to the next order in (100), integrating, applying (93), and evaluating at $x=0$, we find that

$$\begin{aligned} \left. \left( 1-h^{(0)}\right) \frac{\partial s^{(1)}}{\partial x}\right| _{x=0}=-\frac{S^{(0)}}{h^{(0)}}. \end{aligned}$$

(103)

We use the flux given by (103) and the relationship (102) to write (87) as a single partial differential equation for $h^{(0)}$, namely

$$\begin{aligned} \frac{\partial ^2 {h^{(0)}}^2}{\partial z\,\partial T}=-2 \chi _0 {{\mathcal {B}}}_1 {{\mathcal {B}}}_2 \frac{\partial h^{(0)}}{\partial T} \,\varTheta [1-h^{(0)}], \end{aligned}$$

(104)

where $\varTheta [.]$ is the Heaviside function. We immediately see that $h=1$ is a solution to (104). When $h<1$, we integrate (104) with respect to T to find

$$\begin{aligned} \frac{\partial h^{(0)}}{\partial z}=-\chi _0 {{\mathcal {B}}}_1{{\mathcal {B}}}_2, \end{aligned}$$

(105)

where we have used the fact that $h^{(0)}=0$ at $T=0$. The solution to (105) is

$$\begin{aligned} h^{(0)}=f(T)-\chi _0 {{\mathcal {B}}}_1{{\mathcal {B}}}_2 z. \end{aligned}$$

(106)

To determine f(T), we first consider $T\le T_{{\mathrm{clog}}}:=t_{{\mathrm{clog}}}/{{\mathcal {R}}}$. In this case, we solve (102) at $z=0$, where $S^{(0)}=1$, to find that

$$\begin{aligned} h^{(0)}(0,T)=f(T)=\sqrt{2T}, \end{aligned}$$

(107)

in line with (77) expanded for ${{\mathcal {R}}}\gg 1$.

For $T_{{\mathrm{clog}}}<T<T_\mathrm{{L}}:=T_\mathrm{{L}}/{{\mathcal {R}}}$, we have $h^{(0)}=1$ for $z\le G(T)$. We apply the boundary conditions $A^{(0)}=1$ and $S^{(0)}=1$ at $z=G(T)$ to find that

$$\begin{aligned} f(T)=1+T-T_{{\mathrm{clog}}},\qquad G(T)=\frac{T-T_{{\mathrm{clog}}}}{\chi _0{{\mathcal {B}}}_1{{\mathcal {B}}}_2}. \end{aligned}$$

(108)

Thus, the leading-order solution is

$$\begin{aligned} h^{(0)}=\left\{ \begin{array}{ll} \sqrt{\frac{2t}{{{\mathcal {R}}}}}-\chi _0{{\mathcal {B}}}_1{{\mathcal {B}}}_2 z &{}\qquad \text{ for } \qquad t<t _{{\mathrm{clog}}}\left( =\frac{{{\mathcal {R}}}}{2}\right) ,\\ \\ 1 \qquad &{}\qquad \text{ for }\qquad z<\frac{t-t_{{\mathrm{clog}}}}{\chi _0{{\mathcal {R}}}{{\mathcal {B}}}_1{{\mathcal {B}}}_2}, \quad t> t_ {{\mathrm{clog}}},\\ \\ 1-\chi _0{{\mathcal {B}}}_1{{\mathcal {B}}}_2 z+\frac{t-t_{{\mathrm{clog}}}}{{{\mathcal {R}}}}\qquad &{}\qquad \text{ for } \qquad z>\frac{t-t_{{\mathrm{clog}}}}{\chi _0{{\mathcal {R}}}{{\mathcal {B}}}_1{{\mathcal {B}}}_2},\quad t>t_{{\mathrm{clog}}}. \end{array}\right. \end{aligned}$$

(109)

with $S^{(0)}$ found by solving (102) to give

$$\begin{aligned} S^{(0)}=\left\{ \begin{array}{ll} 1-\chi _0{{\mathcal {B}}}_1{{\mathcal {B}}}_2 z \sqrt{\frac{{{\mathcal {R}}}}{2t}} &{}\qquad \text{ for } \qquad t<t _{{\mathrm{clog}}},\\ \\ 1 \qquad &{}\qquad \text{ for }\qquad z<\frac{t-t_ {{\mathrm{clog}}}}{\chi _0{{\mathcal {R}}}{{\mathcal {B}}}_1{{\mathcal {B}}}_2}, \quad t> t_ {{\mathrm{clog}}},\\ \\ 1-\chi _0{{\mathcal {B}}}_1{{\mathcal {B}}}_2 z+\frac{t-t_{{\mathrm{clog}}}}{{{\mathcal {R}}}}\qquad &{}\qquad \text{ for } \qquad z>\frac{t-t_{{\mathrm{clog}}}}{\chi _0{{\mathcal {R}}}{{\mathcal {B}}}_1{{\mathcal {B}}}_2},\quad t>t_{{\mathrm{clog}}};\end{array}\right. \end{aligned}$$

(110)

we note that the solutions for $h^{(0)}$ and $S^{(0)}$ are identical for $t>t_{{\mathrm{clog}}}$. We use (109) to predict that the (leading-order) device lifetime, $T_\mathrm{{L}}$, is given by

$$\begin{aligned} T_\mathrm{{L}}= t_{{\mathrm{clog}}}+\chi _0 {{\mathcal {R}}}{{\mathcal {B}}}_1{{\mathcal {B}}}_2 \end{aligned}$$

(111)

i.e.

$$\begin{aligned} t_\mathrm{{dim},L}= t_{\mathrm{{dim}},{\mathrm{clog}}}\left( 1+2\chi _0\frac{L H {D_s^\mathrm{{l}}}}{\beta _s l U W^2}\right) \qquad \text{ where }\qquad t_{\mathrm{{dim}},{\mathrm{clog}}}=\frac{\beta _s W^2}{2\lambda S^*D_s^\mathrm{{l}}} \end{aligned}$$

(112)

We see from (112), in this limit and to leading order, that neither the dimensional device lifetime, $t_\mathrm{{dim},L}$, nor the dimensional clogging time, $t_{\mathrm{{dim}},{\mathrm{clog}}}$, depends on the reaction rate. This might seem counter intuitive, but we explain it as follows. While Eqs. (10) and (14) each depend on the reaction rate, if we combine them we find that

$$\begin{aligned} \frac{\partial h}{\partial t}=D\lambda \left. \frac{\partial S}{\partial y}\right| _{y=0}, \end{aligned}$$

(113)

which does not depend on the reaction rate r. From Sect. 4.1, we know that the concentration of $\hbox {SO}_2$ varies linearly across the $\hbox {H}_2\hbox {SO}_4$ layer, and (12) tells us that the concentration of $\hbox {SO}_2$ in the liquid is $1/\beta _s$ times the concentration in the gas. Thus, at the entrance to the catalyst channel at the inlet of the device, we estimate the liquid layer thickness, $h_\mathrm{{d}}$, produced in a given time, $t_\mathrm{{d}}$, from (113) as follows:

$$\begin{aligned} \frac{h_\mathrm{{d}}}{t_\mathrm{{d}}}\sim \frac{D_s^\mathrm{{l}} \lambda S^*}{\beta _s h_\mathrm{{d}}}\qquad \implies \qquad h_\mathrm{{d}} \sim \sqrt{\frac{D_s^\mathrm{{l}} \lambda S^* t_\mathrm{{d}}}{\beta _s}}. \end{aligned}$$

(114)

Thus, the scaling for the dimensional clogging time⁶ is given by setting $h_\mathrm{{d}}=W$, which results in $t_{{\mathrm{clog}}}\sim \beta _s W^2/\lambda S^*D_s^\mathrm{{l}}$, and does not depend on r. We recall from (96), however that the next term in the asymptotic expansion for $t_{{\mathrm{clog}}}/{{\mathcal {R}}}{{\mathcal {B}}}_3$ (and thus, its dimensional equivalent) does depend on the reaction rate. We conclude that, with this particular choice of parameter sizes, the device is diffusion limited rather than reaction limited at leading order and weakly varies with the reaction rate. The second term in the expression for $t_\mathrm{{dim},L}$ given in (112) is the ratio of the moles of sulphuric acid needed to fill the whole void space ($=2 W L (H/{{\mathcal {L}}})/\lambda$) to the flux of sulphur dioxide supplied (=$S^* l U$) and, thus, represents the time it takes to supply the device with the amount of suphur dioxide required to produce the amount of sulphuric acid needed to completely fill the void space. We do not proceed further with our asymptotic expansion, since terms of $O({{\mathcal {B}}}_2)$, $O({{\mathcal {B}}}_3)$, $O(1/{{\mathcal {B}}}_1)$, and $O(1/\sqrt{{{\mathcal {R}}}})$ are all likely to come in at the same time. Instead, in Fig. 20, we present a comparison between our asymptotic solution and a numerical solution where we take ${{\mathcal {B}}}_2=0.01$ and ${{\mathcal {R}}}=$ 10,000. We see excellent agreement between the numerical results and the asymptotic predictions, except where $S^{(0)}$ is small.

Fig. 20

Graphs showing how $h^{(0)}$ (left) and $S^{(0)}$ (middle) vary with z, for $T=0.01$, 0.1, 0.3, 0.5, 0.7, and 0.754. (Right) Graph showing how G varies with T. We have used ${{\mathcal {B}}}_1=50.6$, ${{\mathcal {B}}}_2=0.01$, ${{\mathcal {B}}}_3=0.14$, and ${{\mathcal {R}}}=$ 10,000

6.2 Determining the unknown parameter r

Our model can be used to estimate the value for the (dimensional) reaction rate r by using the solution to the thin-liquid-layer problem given in (85) and applying it in the device-scale model at early time. As we have seen in Sect. 5.3, when the liquid layer is thin, the flux of sulphur dioxide removed by the catalyst channels is given by (85), evaluated at $x=0$. Thus, we can replace (87) with

$$\begin{aligned} \frac{\partial S}{\partial Z}=-2 {{\mathcal {B}}}_1 \sqrt{\frac{{{\mathcal {R}}}{{\mathcal {B}}}_2}{3}}S^{3/2}, \end{aligned}$$

(115)

which must be solved along with boundary condition (91). The solution is analagous to (86), and the redimensionalised version reads

$$\begin{aligned} S(z)=\frac{S^*}{\left( 1+\chi _0{{\mathcal {B}}}_1 \sqrt{\frac{{{\mathcal {R}}}{{\mathcal {B}}}_2}{3}}\frac{z}{H}\right) ^2}. \end{aligned}$$

(116)

We can, thus, back out that

$$\begin{aligned} r=3\frac{l^2U^2\beta _s^2\beta _c W}{\chi _0^2 H^2 S^* C^* D_s^\mathrm{{g}}}\left( \sqrt{\frac{S^*}{S(H)}}-1\right) ^2, \end{aligned}$$

(117)

which provides a simple formula for working out r given the physical parameters of the model and an early-time experiment to determine S(H).

7 Discussion

In this paper, we have built a simple model to describe the operation of a filtration device for removing sulphur dioxide from flue gas. Our model incorporates diffusive transport along small catalyst channels where, on the surface, the sulphur dioxide is converted into liquid sulphuric acid, and coupled this with the outer flow of the flue gas which is to be cleaned. We took account of transport through the liquid sulphuric acid layers. We identified the key dimensionless parameter groups that governed the behaviour of the device, and we took advantage of the size of some of these parameters, in particular, the aspect ratio of the catalyst channels, in order to simplify the problem. We solved the catalyst-channel model numerically and found that the sulphur dioxide concentration decreased along the channel, with corresponding maximum growth of the sulphuric acid layer occurring at the channel entrance. We found some interesting non-monotonic (in time) behaviour for the sulphur dioxide concentration, which we explained in a particular parameter regime. We studied the behaviour of the system at the inlet to the catalyst channels and determined the clogging time (that is, the time at which the entrance to the channel first completely filled with liquid sulphuric acid). We varied the parameters and saw how the behaviour altered. We further reduced the model in the case where the thickness of the layer of sulphuric acid was very small compared with the width of the catalyst channel. We solved the resulting problem numerically but were also able to obtain a simple formula for the flux of sulphur dioxide removed from the gas flow in this limit.

We then coupled the activity in the catalyst channels with the outer gas stream. We solved the problem numerically to find that, with the physically relevant parameters, the device operated efficiently until about 296 days (we define efficiency via the concentration of $\hbox {SO}_2$ released into the atmosphere), and then the efficiency decreases until the device completely stops working, at about 2.1 years. Varying the parameters, we saw that increasing the length of the device or reducing the flux of $\hbox {SO}_2$ entering the device resulted in increasing the device lifetime, while increasing the reaction rate decreased the device lifetime. We do not know the value of the reaction rate precisely, and we showed that a change in reaction rate of two orders of magnitude only altered the device lifetime by a factor of 14%. We found that the device was particularly sensitive to changes in the concentration of $\hbox {SO}_2$ that were passed through it; increasing the concentration significantly reduced the device lifetime. Further, we explored the behaviour of the device as we altered the depth of the catalyst channels. We found that the device lifetime plateaued above $L=2.2$ mm (for the operating parameters presented in Table 1), indicating that there is not much point building a device with filter thicker than this value. We then explored the physically relevant parameter regime, solved the appropriate asymptotic limit of the model explicitly, and found excellent agreement between the asymptotic solutions and numerical simulations, although we had to make ${{\mathcal {B}}}_2$ and ${{\mathcal {R}}}$ smaller and bigger, respectively, than their physically relevant sizes to show convergence. We were also able to derive an explicit formula for the device lifetime. Finally, we used the small-liquid-layer approximation in order to provide a formula for determining the catalyst reaction rate, given some data on the concentration of sulphur dioxide exiting the device.

In summary, we conclude that the device lifetime can be increased by making the device longer, decreasing the speed of the flow, and increasing the length of the catalyst channels (up to a certain length). Moreover, the device should be tailored to specific gas concentrations, to avoid the large changes seen as $S^*$ is varied. We also conclude that the device is not particularly sensitive to the uncertainty in the reaction rate.

There are numerous limitations with our model that need refining. For example, we have assumed that the catalyst channels stop taking in sulphur dioxide once the sulphuric acid layer spans the catalyst channel. However, in practice, sulphur dioxide will diffuse through this layer to replenish the trapped gas behind this blocked region, and the sulphuric acid layer will continue to grow, albeit even more slowly than previously. Extending our model to include the fully saturated region is our obvious next step. Another key step will be to compare our model to experimental data in order to fit the value of the reaction rate and to give predictive power. We have used a simplified one-step reaction in our model but, in reality, there is a multi-step process. Extending our model to include multiple reactions would be useful. Finally, sulphuric acid is hygroscopic and, thus, draws in water vapour which results in accelerated growth of the liquid layer. Since water vapour is also present in the gaseous phase, extending our model to incorporate transport and absorption of water vapour, using a model such as in [20], would also enhance our model’s predictive power.

Fig. 21

(Top row) Graphs showing the behaviour of s versus x (left) and h versus x (right) for $t=0.0$, 0.1, 0.2, 0.3, 0.4, and (right) 0.5. (Bottom row) Graphs showing $h|_{x=0}$ versus t (left) and flux versus t (right) in the small ${{\mathcal {R}}}$ limit. The black lines are the numerical results with ${{\mathcal {R}}}=10^{-3}$ and the red-dashed lines are the asymptotic results. Here, ${{\mathcal {B}}}_2=1$ and ${{\mathcal {B}}}_3=1$

Our overarching aim is to improve the understanding of reactive filters, and this simple model provides a stepping stone in that direction.

Appendix: The limit of small \({{\mathcal {R}}}\) in the channel model

We find an approximate solution to (55)–(59) in the case when ${{\mathcal {R}}}$ is small. We expand each of the dependent variables as an asymptotic series of the form $X=X^{(0)}+{{\mathcal {R}}} X^{(1)}+{{{\mathcal {R}}}}^2 X^{(2)}+\cdots$. The expansion is regular, and we find that, correct to $O({{\mathcal {R}}})$, s, b, and h satisfy

$$\begin{aligned}&s\sim 1+{{\mathcal {B}}}_2{{\mathcal {R}}}\left( \frac{x^2-2x}{1-2t}\right) ,\qquad b\sim 1+{{\mathcal {R}}}\left( {{\mathcal {B}}}_2\left( \frac{x^2-2x}{1-2t}\right) -4t\right) ,\end{aligned}$$

(118)

$$\begin{aligned}&h\sim 2t-{{\mathcal {R}}}\left( 4(2+{{\mathcal {B}}}_3)t^2+2 {{\mathcal {B}}}_2(x^2-2x)\log (1-2t)\right) . \end{aligned}$$

(119)

Since $s^{(0)}=1$, the leading-order flux of sulphur dioxide into the channel is zero, and we find that the $O({{\mathcal {R}}})$ flux is constant. We proceed to $O({{{\mathcal {R}}}}^2)$ and find that the flux satisfies

$$\begin{aligned} -(1-h)\frac{\partial s}{\partial x}\sim 2 {{\mathcal {R}}} {{\mathcal {B}}}_2-8{{\mathcal {B}}}_2 {{{\mathcal {R}}}}^2\left( \frac{{{\mathcal {B}}}_2}{1-2t}\left( \frac{x^3}{6}-\frac{x^2}{2}\right) -({{\mathcal {B}}}_3+2) t\, x +\frac{{{\mathcal {B}}}_2}{3(1-2t)}+({{\mathcal {B}}}_3+2)t\right) , \end{aligned}$$

(120)

and thus,

$$\begin{aligned} q=-(1-h)\left. \frac{\partial s}{\partial x}\right| _{x=0}\sim 2 {{\mathcal {R}}}{{\mathcal {B}}}_2-8{{\mathcal {B}}}_2 {{{\mathcal {R}}}}^2\left( \frac{{{\mathcal {B}}}_2}{3(1-2t)}+({{\mathcal {B}}}_3+2)t\right) , \end{aligned}$$

(121)

which we see scales like ${{\mathcal {R}}}{{\mathcal {B}}}_2$, as seen previously in Fig. 9 for the total $\hbox {SO}_2$ removed in the small ${{\mathcal {R}}}{{\mathcal {B}}}_2$ limit. We use (119) to find an expression for the clogging time, $t_{{\mathrm{clog}}}$, namely

$$\begin{aligned} t_{{\mathrm{clog}}}\sim \frac{1}{2}+\left( 1+\frac{{{\mathcal {B}}}_3}{2}\right) {{\mathcal {R}}}. \end{aligned}$$

(122)

In Fig. 21, we compare our asymptotic solution to the numerical solutions for ${{\mathcal {R}}}=0.001$, ${{\mathcal {B}}}_2=1$, and ${{\mathcal {B}}}_3=1$. We see excellent agreement between the two solutions, even near the clogging time.