Instabilities at a sheared interface over a liquid laden with soluble surfactant

Abstract

The linear stability of a semi-infinite fluid undergoing a shearing motion over a fluid layer that is laden with soluble surfactant and that is bounded below by a plane wall is investigated under conditions of Stokes flow. While it is known that this configuration is unstable in the presence of an insoluble surfactant, it is shown via a linear stability analysis that surfactant solubility has a stabilising effect on the flow. As the solubility increases, large-wavelength perturbations are stabilised first, leaving open the possibility of mid-wave instability for moderate surfactant solubilities, and the flow is fully stabilised when the solubility exceeds a threshold value. The predictions of the linear stability analysis are supported by an energy budget analysis which is also used to determine the key physical effects responsible for the (de)stabilisation. Asymptotic expansions performed for long-wavelength perturbations turn out to be non-uniform in the insoluble surfactant limit. In keeping with the findings for insoluble surfactant obtained by Pozrikidis & Hill (IMA J Appl Math 76:859–875, 2011), the presence of the wall is found to be a crucial factor in the instability.

Introduction

It is well known that an insoluble surfactant can destabilise the interface between two fluids subjected to a shear flow, even if the fluids are stably stratified and have no inertia (which is essential for the development of interfacial instabilities in shear flows devoid of surfactant [1] [2,3,4]). The onset of this surfactant-induced instability depends crucially on the presence of a wall bounding one of the fluids [5]: with no wall and two semi-infinite fluids, the flow is stable. However, if a second wall is also present, as is the case for channel flow, then instability is not always possible. For example, [2] showed that when the interface lies in the middle of the channel, the flow is stable. Generally speaking inertia exacerbates any instability, but may have a stabilising influence under some conditions [6,7,8].

Recently the present authors showed that for the inertialess channel flow problem, the ability of the surfactant to dissolve in one of the fluids can either enhance or suppress interfacial instability for certain fluids and/or surfactant properties [9, 10]. Studies of the related problem of film flow down an inclined substrate have found surfactant solubility to have a destabilising effect [11,12,13]. It has been suggested that the destabilisation due to solubility is connected to a phase shift between the interfacial disturbance and the surfactant mass flux onto/off the interface: this allows a redistribution of surfactant at the interface and it thereby mitigates the Marangoni force that is helping to stabilise the flow [13]. A similar explanation was provided for the stabilisation of the flow-induced Marangoni instability found in a vertically falling film loaded with insoluble surfactant in [14].

In this work, we consider a sheared interface separating a semi-infinite fluid and a liquid layer of different viscosity that is loaded with surfactant and that is bounded below by a solid wall. Our main aim is to investigate the influence of surfactant solubility on the linear stability of the flow. The effects of inertia and gravity are ignored. Instability at the interface is induced due to the underlying shear flow and the disparity in fluid viscosities (which results in a velocity jump at the perturbed interface), as well as the Marangoni forces generated because of the presence of surfactant at the interface that leads to local surface tension gradients [15]. Here, the surfactant can be transferred into the liquid layer via a kinetic flux driving the adsorption and desorption of molecules to and from the bulk fluid [16]. A linear stability analysis is carried out and an eigenvalue problem for the complex wave speed is formulated and solved numerically. An asymptotic approximation valid for perturbations of large wavelength is also examined to provide leading-order approximations for the growth rates. Moreover, an energy budget analysis in the manner of [17] is used to tease out the important physical effects driving the instability. A brief discussion of the case of two semi-infinite fluids, which is obtained when the wall is removed, is also presented and supported by analytical and numerical results.

The outline of the rest of the paper is as follows: in Sect. 2, the full non-linear system governing the dynamics of the flow is provided and is later linearised via an energy budget analysis. The disturbances are then written in a normal mode form to obtain a linearised eigenvalue system for the growth rate. A long-wave approximation of the growth rate is also presented. In Sect. 3, growth rate curves are provided as well as data based on energy budget analysis. The stability of the unbounded problem is also discussed. A summary of the main results is given in Sect. 4.

Linear stability analysis

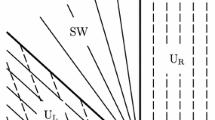
We consider the evolution of an interface between an incompressible liquid of viscosity $\mu _1$ and density $\rho$, which is laden with surfactant and which is confined below by a wall, and a semi-infinite fluid above of the same density and viscosity $\mu _2$, as shown in Fig. 1. The bulk surfactant concentration is assumed to not exceed the critical micelle concentration. At equilibrium, the film has a uniform thickness $h_0$ and a steady shear flow is imposed. The problem is cast in non-dimensional form by scaling lengths with $h_0$, surface tension with the clean value $\gamma _0$ that prevails in the absence of surfactant, velocities with $\gamma _0/\mu _1$, time with $h_0\mu _1/\gamma _0$, pressures with $\gamma _0/h_0$, the interface surfactant concentration by the maximum packing $\varGamma _\infty$, the bulk concentration with $\varGamma _\infty /h_0$, and the mass flux by $\varGamma _{\infty }\gamma _0/h_0\mu _1$.

Fig. 1

Setup of the problem: a surfactant-laden liquid is coated on a horizontal wall and its thickness defines the location of the interface which separates it from a second, semi-infinite fluid. Both fluids undergo a shear flow. The dashed line indicates the location of the undisturbed interface

The flow in each fluid region is described by equations for the conservation of mass and momentum. In this study the aim is to focus on the effect of surfactant solubility on the stability of the flow; since the two fluids are assumed to have the same density, the effect of gravity is negligible. The Reynolds number in each layer is defined by $Re_i=\rho \gamma _0h_0/\mu _i^2$, where $i=1,2$ is used to label the fluids (see Fig. 1), and is assumed to be small. Consequently the flow is governed by the Stokes momentum equation and the continuity equation,

$$\begin{aligned} 0 = - \nabla p_i + m_i\nabla ^2{\varvec{u}}_i, \qquad \nabla \cdot {\varvec{u}}_i = 0, \end{aligned}$$

(1)

where $p_i$, ${\varvec{u}}_i=(u_i,v_i)$, $i=1,2$, are the pressure and velocity fields in the two fluids, the gradient operator is defined in the cartesian coordinate system shown in Fig. 1 by $\nabla =(\partial _x,\partial _y)$, and $m_i = 1+(m-1)(i-1)$, with m the viscosity ratio (defined later in (7)). The evolution of the interface at $y=h(x,t)$ is governed by the kinematic condition

$$\begin{aligned} h_t = v_1 - u_1h_x. \end{aligned}$$

(2)

Subscripts will be used through this paper to either denote variables in the respective fluid (if variable $i=1,2$ is used) or partial derivatives with respect to the shown variable (where t is time).

The no-slip and no-penetration conditions, respectively, require that ${\varvec{u}}_1=(0,0)$ at the wall, and that velocity in the upper fluid ${\varvec{u}}_2$ is bounded in the far-field as $y\rightarrow \infty$. Continuity of velocity, requiring that ${\varvec{u}}_1={\varvec{u}}_2$, is imposed at the interface $y=h(x,t)$ together with the continuity of normal and tangential stresses

$$\begin{aligned}&\left[ -p_i\left( 1+h_x^2\right) + 2m_i\left( h_x^2 u_{ix} + v_{iy} - h_x\left( u_{iy}+v_{ix}\right) \right) \right] _2^1 = \gamma \frac{h_{xx}}{H}, \end{aligned}$$

(3a)

$$\begin{aligned}&\left[ 4m_ih_x u_{ix} + m_j\left( h_x^2-1\right) \left( u_{iy} + v_{jx}\right) \right] _2^1 = -\gamma _xH, \end{aligned}$$

(3b)

where $H=\sqrt{1+h_x^2}$ and the notation $[F_i]^1_2=F_1-F_2$ is used. The surface tension in conditions (3) is given by the Langmuir equation of state which is $\gamma = 1 + Ma\ln \left( 1-\varGamma \right)$ [16, 18] and is seen to depend on the interfacial surfactant concentration $\varGamma$, the evolution of which is described by the convection–diffusion equation [10, 19]

$$\begin{aligned} \frac{1}{H}\Biggl [ \left( H\varGamma \right) _t&+ \left( Hu_I\varGamma \right) _x - \frac{1}{Pe_s}\left( \frac{\varGamma _x}{H} \right) _x \Biggr ] - J_b = 0, \end{aligned}$$

(4)

with $u_I=u_1(x,y=h(x,t),t)$. Here, the adsorption/desorption flux $J_b$ is defined by [9]

$$\begin{aligned} J_b = B\Bigl (R_bC(1-\varGamma ) - \varGamma \Bigr ), \end{aligned}$$

(5)

where the bulk concentration C is evaluated immediately below the interface at $y=h^-$. A positive/negative value of $J_b$ corresponds to adsorption/desorption of surfactant onto/from the interface. In the film the transport of surfactant molecules is governed by the advection–diffusion equation and associated boundary conditions,

$$\begin{aligned} C_t + {\varvec{u}}_1\cdot \nabla C&= \frac{1}{Pe_b}\nabla ^2C, \quad \; C_y\Big |_{y=0} = 0, \quad \; \frac{h_xC_x-C_y}{H}\Big |_{y=h} = Pe_bJ_b. \end{aligned}$$

(6)

The two boundary conditions ensure that there is no flux of surfactant through the wall and that the flux of surfactant onto the interface matches the adsorption/desorption flux $J_b$ defined in (5).

The non-dimensional parameters that appear in the equations above are the viscosity ratio, the Marangoni, Biot, and Péclet numbers (surface and bulk), as well as a solubility parameter, respectively, defined by

$$\begin{aligned} m = \frac{\mu _2}{\mu _1},&\quad Ma= \frac{\mathcal {R}\mathcal {T}\varGamma _\infty }{\gamma _0}, \quad B= \frac{k_dh_0\mu _1}{\gamma _0}, \quad Pe_{s,b} = \frac{\gamma _0h_0}{\mu _1{\mathscr {D}}_{s,b}}, \quad R_b = \frac{k_a}{h_0k_d}, \end{aligned}$$

(7)

where $k_a$, $k_d$ are the adsorption/desorption kinetic rates, respectively, ${\mathscr {D}}_{s,b}$ are the surface and bulk diffusivities, $\mathcal {R}$ is the ideal gas constant, and $\mathcal {T}$ is the absolute temperature. We note that the case of an insoluble surfactant is recovered in one of the limits $B\rightarrow 0$ or $R_b\rightarrow \infty$.

Energy budgets

The flow is disturbed by introducing perturbations to the steady state of the form $f(x,y,t) = {\bar{f}}(y) + {\hat{f}}(x,y,t)$, where the steady state is denoted by the overbar notation and the perturbations are assumed to be small, ${\hat{f}}\ll {\bar{f}}$. Here, f stands for the various variables involved in the problem, i.e. ${\varvec{u}}_i$, $p_i$, h, $\varGamma$, C. The steady horizontal velocity is linear in each fluid and given by

$$\begin{aligned} {\bar{u}}_1(y) = sy, \qquad {\bar{u}}_2(y) = \frac{s}{m}(y + m - 1), \end{aligned}$$

(8)

where s is the shear rate at the interface, while the vertical velocities and pressures are constant in both fluids, ${\bar{v}}_{1,2}(y)=0$, ${\bar{p}}_{1,2}(y)=p_0$. The equilibrium state for the surfactant can be found by setting $J_b=0$ in (5) and is given by uniform concentrations $0<\bar{\varGamma }<1$ and

$$\begin{aligned} {\bar{C}} = \frac{\bar{\varGamma }}{R_b(1-\bar{\varGamma })}. \end{aligned}$$

(9)

The corresponding equilibrium surface tension is $\bar{\gamma } = 1 + Ma\ln \left( 1-\bar{\varGamma }\right)$. We note that normally the interfacial concentration $\bar{\varGamma }$ is prescribed in computations.

To assess the stability properties of the flow and identify the dominant mechanism responsible for interfacial instability, we perform an energy budget analysis. Since the Reynolds number is zero in the present study, the equation for the kinetic energy of the flow does not offer insight into the instability mechanism, but we nevertheless provide it for completeness in Appendix A. Insight can be obtained, however, by examining an equation for the energy of concentration perturbations. To derive this, the linearised convection–diffusion equation for the concentration in the film is multiplied by the perturbation ${\hat{C}}$ and integrated over the film flow region $y\in [0,1]$. The entire equation is then integrated in one horizontal wavelength $x\in [0,\Lambda ]$, where $\Lambda =2\pi /k$ and k is the wavenumber, and spatial periodicity is assumed. Invoking the flux conditions at the wall and interface in (6), the energy budget equation takes the form

$$\begin{aligned} \text {ENC}= \text {DIFC + FLXC} \end{aligned}$$

(10a)

where

$$\begin{aligned} \text {ENC}&= \frac{\mathrm{d}}{\mathrm{d}t} \int _0^\Lambda \int _0^{1} \frac{1}{2}{\hat{C}}^2 \,\mathrm{d} y\,\mathrm{d} x, \nonumber \\ \text {DIFC}&= - \frac{1}{Pe_b}\int _0^\Lambda \int _0^{1} \left( {\hat{C}}_x^2 + {\hat{C}}_y^2 \right) \,\mathrm{d} y\,\mathrm{d} x, \nonumber \\ \text {FLXC}&= - B\int _0^\Lambda \biggl (R_b(1-\bar{\varGamma }){\hat{C}}(1) - \frac{\hat{\varGamma }}{(1-\bar{\varGamma })} \biggr ){\hat{C}}(1) \,\mathrm{d} x. \end{aligned}$$

(10b)

Equation (10b) offers insight into the growth of concentration perturbations and it can be used to identify an instability in Stokes flow [20]. Instability is indicated by a positive value of the ENC term. The diffusion term DIFC is always negative, while the term FLXC is associated with surfactant flux between the bulk and the interface; if the latter effect is sufficiently strong then instability occurs.

Following a similar procedure for the corresponding surfactant transport equation at the interface, but now integrating in the x direction only, the energy equation for the interfacial concentration is found to be

$$\begin{aligned} \text {ENG} = \text {GSH + GU1 + DIFG + FLXG}, \end{aligned}$$

(11a)

where

$$\begin{aligned} \text {ENG}&= \frac{\mathrm{d}}{\mathrm{d}t} \int _0^\Lambda \frac{1}{2}\hat{\varGamma }^2 \,\mathrm{d} x, \nonumber \\ \text {GSH}&= - s\bar{\varGamma }\int _0^\Lambda {\hat{h}}_x\hat{\varGamma } \,\mathrm{d} x, \nonumber \\ \text {GU1}&= - \bar{\varGamma }\int _0^\Lambda {\hat{u}}_{1x}(1)\hat{\varGamma } \,\mathrm{d} x, \nonumber \\ \text {DIFG}&= - \frac{1}{Pe_s}\int _0^\Lambda \hat{\varGamma }_x^2 \,\mathrm{d} x, \nonumber \\ \text {FLXG}&= B\int _0^\Lambda \biggl (R_b(1-\bar{\varGamma }){\hat{C}}(1) - \frac{\hat{\varGamma }}{(1-\bar{\varGamma })}\biggr ) \hat{\varGamma } \,\mathrm{d} x. \end{aligned}$$

(11b)

Instability is present if the term ENG is positive. On the right-hand side in (11b), the term GSH plays a role only in the presence of the background shear, the GU1 term supplies energy due to the perturbed horizontal velocity gradient at the interface, while the term DIFG captures the dampening effect of interfacial diffusion and is always negative. A positive/negative value of FLXG corresponds to a net adsorption/desorption of surfactant onto/from the interface.

The relative sizes of the various terms in (10b) and (11b) can offer insight into the dominant physical mechanisms that provoke instability. Where terms are positive/negative their effect is destabilising/stabilising.

Normal modes

To perform a normal mode analysis it is convenient to introduce the streamfunctions $\psi _i$, defined so that $u_i=\partial \psi _i/\partial y$ and $v_i=-\partial \psi _i/\partial x$. We represent all of the disturbance quantities in the normal mode form ${\hat{f}}(x,y,t) = {\tilde{f}}(y)\mathrm{e}^{ik(x-ct)}$, where k is the real wavenumber to be specified, c is the complex wave speed to be found, and the tilde-decorated variables are eigenfunctions to be determined. The stability of the flow is controlled by the sign of the growth rate $\lambda \equiv k\mathfrak {I}(c)$; in particular, instability occurs if $\lambda >0$.

Substituting the normal mode forms into the governing equations (1)–(6) and linearising, we obtain an eigenvalue problem for the complex wave speed c. The streamfunctions satisfy the ordinary differential equation

$$\begin{aligned} {\tilde{\psi }}_{1,2}''''(y) - 2k^2 {\tilde{\psi }}_{1,2}''(y) + k^4{\tilde{\psi }}_{1,2}(y) = 0, \end{aligned}$$

(12a)

with the boundary conditions

$$\begin{aligned}&{\tilde{\psi }}_1(0)={\tilde{\psi }}_1'(0)=0, \qquad {\tilde{\psi }}_2\Big |_{y\rightarrow \infty }={\tilde{\psi }}_2'\Big |_{y\rightarrow \infty }=0, \end{aligned}$$

(12b)

$$\begin{aligned}&{\tilde{\psi }}_1(1) = {\tilde{\psi }}_2(1), \qquad {\tilde{\psi }}_1'(1)-{\tilde{\psi }}_2'(1) = \left( \frac{1}{m}-1\right) \frac{s}{{\tilde{c}}}{\tilde{\psi }}_1(1), \end{aligned}$$

(12c)

where ${\tilde{c}} = c - {\bar{u}}_1(1)$ is the perturbed wave speed. The jump term in condition (12c) arises due to viscosity stratification. The linearised forms of the normal and tangential interfacial stress balances (3) are

$$\begin{aligned}&\left( m{\tilde{\psi }}_2'''(1)-{\tilde{\psi }}_1'''(1)\right) - 3k^2\left( m{\tilde{\psi }}_2'(1)-{\tilde{\psi }}_1'(1)\right) = -\mathrm{i}\bar{\gamma }k^3\frac{{\tilde{\psi }}_1(1)}{{\tilde{c}}}, \end{aligned}$$

(12d)

$$\begin{aligned}&\left( m{\tilde{\psi }}_2''(1)-{\tilde{\psi }}_1''(1)\right) + k^2\left( m{\tilde{\psi }}_2(1)-{\tilde{\psi }}_1(1)\right) = \frac{\mathrm{i}Mak}{(1-\bar{\varGamma })}{\tilde{\varGamma }}. \end{aligned}$$

(12e)

The surfactant concentration perturbation in the bulk satisfies

$$\begin{aligned}&{\tilde{C}}''(y) - k^2{\tilde{C}}(y) - \mathrm{i}kPe_b(sy-c){\tilde{C}}(y) = 0, \end{aligned}$$

(12f)

$$\begin{aligned}&{\tilde{C}}'(0) = 0, \qquad {\tilde{C}}'(1) + Pe_bBR_b(1-\bar{\varGamma }){\tilde{C}}(1) = \frac{Pe_bB}{(1-\bar{\varGamma })}{\tilde{\varGamma }}, \end{aligned}$$

(12g)

and the linearised form of the interfacial surfactant concentration equation (4) is

$$\begin{aligned} \left( -\mathrm{i}k{\tilde{c}} + \frac{k^2}{Pe_s} + \frac{B}{(1-\bar{\varGamma })} \right) {\tilde{\varGamma }} - BR_b(1-\bar{\varGamma }){\tilde{C}}(1) + \mathrm{i}k\bar{\varGamma }\left( \frac{s}{{\tilde{c}}}{\tilde{\psi }}_1(1) + {\tilde{\psi }}_1'(1) \right) = 0. \end{aligned}$$

(12h)

The general solution for the perturbation streamfunctions satisfying Eq. (12a) is

$$\begin{aligned} {\tilde{\psi }}_i(y) = \alpha _{1,i}\,\mathrm{e}^{ky} + \alpha _{2,i}\,y\,\mathrm{e}^{ky} + \alpha _{3,i}\,\mathrm{e}^{-ky} + \alpha _{4,i}\,y\,\mathrm{e}^{-ky}, \end{aligned}$$

(13)

for coefficients $\alpha _{j,i}$, $j=1,2,3,4$, $i=1,2$, to be determined. The far-field conditions in (12b) yield $\alpha _{1,2} = \alpha _{2,2} = 0$. The general solution for the bulk concentration equation (12f) is

$$\begin{aligned} {\tilde{C}}(y) = b_1\,\mathrm{Ai}(\zeta ) + b_2\,\mathrm{Bi}(\zeta ), \qquad \zeta = (\mathrm{i}ksPe_b)^{1/3}\Bigl (y-\frac{c}{s}-\frac{\mathrm{i}k}{sPe_b}\Bigr ), \end{aligned}$$

(14)

where ${\mathrm{Ai}}$ and ${\mathrm{Bi}}$ are the linearly independent solutions of the Airy equation, and $b_{1,2}$ are arbitrary constants. Given the exact solutions (13), (14), conditions (12) may be assembled to form the linear system

$$\begin{aligned} {\varvec{M}}\cdot {\varvec{x}} = {\varvec{0}}, \end{aligned}$$

(15)

where the coefficient matrix ${\varvec{M}}$ depends on c and the vector of unknowns is ${\varvec{x}}=(\alpha _{1,1},\alpha _{2,1},\alpha _{3,1},\alpha _{4,1},\alpha _{3,2},\alpha _{4,2},b_1, b_2,{\tilde{\varGamma }})^\mathrm{T}$. Non-trivial solutions are obtained if $\det ({\varvec{M}})=0$; owing to the presence of the Airy functions in Equation (14), this gives a transcendental equation for the complex wave speed c that in general yields an infinite number of normal modes and which must be solved numerically. In the insoluble limit attained either by taking $B\rightarrow 0$ or $R_b\rightarrow \infty$, the equation $\det ({\varvec{M}})=0$ reduces to a quadratic equation for c corresponding to just two normal modes [5].

Long-wave approximation

Useful insight into the behaviour of the complex wave speed can be gained by considering perturbations of large wavelength. Assuming that $k \ll 1$, we introduce the expansion for the complex wave speed

$$\begin{aligned} c = c_0 + kc_1 + \cdots , \end{aligned}$$

(16)

substitute it into the transcendental equation $\det ({\varvec{M}})=0$, and solve at successive orders in k to determine $c_0$, $c_1$, etc. In doing so we identify two modes which we term the primary modes, for each of which $c_0$ is real. The two corresponding values of $c_1$ are both purely imaginary and yield the leading-order approximation to the growth rate $\lambda \approx k^2\mathfrak {I}(c_1)$.

Besides the two normal modes that are captured by the expansion (16) there is an infinite number of other modes, which we term secondary modes, whose existence may be attributed to the freedom of the bulk surfactant concentration to disperse in the liquid film. These secondary modes satisfy long-wave expansions different to (16); and, notably, $\mathfrak {I}(c)<0$ at $k=0$.

One of the two primary modes is always stable and satisfies

$$\begin{aligned} \mathfrak {I}\big (c_1^{(1)}\big ) = -MaR_b\bar{\varGamma }(1-\bar{\varGamma }) < 0. \end{aligned}$$

(17)

The first-order contribution to the second primary mode has imaginary part

$$\begin{aligned} \mathfrak {I}(c_1^{(2)}) = \frac{A_4R_b^4 + A_3R_b^3 + A_2R_b^2 + A_1R_b+ A_0}{120Pe_sPe_b\left( 1+(1-\bar{\varGamma })^2R_b\right) ^3}, \end{aligned}$$

(18a)

where

$$\begin{aligned}&A_4 = 120(1-\bar{\varGamma })^7\bar{\varGamma }MaPe_sPe_b, \nonumber \\&A_3 = 120(1-\bar{\varGamma })^5\big ( 2\bar{\varGamma }MaPe_s-(1-\bar{\varGamma }) \big )Pe_b, \nonumber \\&A_2 = 8(1-\bar{\varGamma })^3\Bigl ( 15MaPe_sPe_b\bar{\varGamma }- (1-\bar{\varGamma })\big ( 2s^2Pe_sPe_b^2 + 30Pe_b + 15Pe_s \big ) \Bigr ), \nonumber \\&A_1 = -(1-\bar{\varGamma })^2\Bigl ( \big ( 7s^2Pe_sPe_b^2+120Pe_b+240Pe_s \big ) + \frac{30(1-\bar{\varGamma })s^2Pe_sPe_b}{B}\Bigr ), \nonumber \\&A_0 = -(s^2Pe_b^2+120)Pe_s, \end{aligned}$$

(18b)

and it is either stable or unstable depending on the parameters. In particular, noting that the denominator in (18b) is positive, the Descartes’ rule of signs implies that there is exactly one positive value of $R_b$ at which the numerator, viewed as a polynomial in $R_b$, changes sign and therefore the flow changes stability. For sufficiently large $R_b$ we find that $\mathfrak {I}\big (c_1^{(2)}\big )>0$ so that this mode is unstable in the case of weak solubility, which is qualitatively consistent with established results for insoluble surfactant [3, 5]. Since

$$\begin{aligned} \mathfrak {I}\big (c_1^{(2)}\big ) \rightarrow - \frac{(s^2Pe_b^2+120)}{120Pe_b} < 0 \quad \text {as } R_b\rightarrow 0, \end{aligned}$$

(19)

the second primary mode is evidently stable in the strong solubility limit $R_b\rightarrow 0$. We conclude that surfactant solubility has a stabilising influence on the flow.

The fact that neither of the two leading-order expressions for the growth rate in (17) and (18b) depend on the viscosity ratio m is striking but it is in line with similar long-wave calculations for insoluble surfactant (e.g. for channel flow [3]). It is intriguing to note that

$$\begin{aligned} \mathfrak {I}\big (c_1^{(2)}\big ) \rightarrow -\infty \quad \hbox { as}\ B\rightarrow 0, \qquad \mathfrak {I}\big (c_1^{(2)}\big ) \rightarrow \infty \quad \hbox { as}\ R_b\rightarrow \infty , \end{aligned}$$

(20)

and hence, curiously, neither of the leading-order growth rates of the two primary modes are consistent with the growth rates presented by Pozrikidis & Hill [5] for insoluble surfactant in the limit $B\rightarrow 0$ or $R_b\rightarrow \infty$. This apparent contradiction may be resolved by noting that the expansion (16) breaks down in either of the limits $B\rightarrow 0$ or $R_b\rightarrow \infty$; instead the correct expansion should proceed in powers of $k^{1/2}$.

The situation is reminiscent of the non-uniformity in the long-wave expansion that has been identified in the limits $s\rightarrow 0$, $Ma\rightarrow \infty$, $m\rightarrow 1$, and $R_b\rightarrow R_b^*$, where $R_b^*$ is a certain finite value, for the similar flow in a channel (see [4, 9]). We emphasise that the failure to achieve consistency with the results for insoluble surfactant in the limit $B\rightarrow 0$ or $R_b\rightarrow \infty$ is a facet of the current long-wave approach; taking either of these limits in the solution to the full transcendental equation $\det ({\varvec{M}})=0$ stemming from (15) recovers the growth of [5], as is discussed in Appendix B.

Results and discussion

We seek numerical solutions for the complex wave speed that satisfies system (15) by solving the linear eigenvalue problem (12) numerically using a Chebyshev collocation method [9, 21]. In practice, it is convenient to solve the problem in a channel of large aspect ratio $0\le y \le n$ for a suitably large value of n and impose no-slip and no-flux conditions at the upper wall. We map each fluid region to the canonical domain $Y\in [-1,1]$ by taking

$$\begin{aligned}&Y = 1 - 2y \quad \text {for } y\in [0,1], \end{aligned}$$

(21a)

$$\begin{aligned}&\text {and}\nonumber \\&Y = -1 + \frac{2(y-1)}{(n-1)} \quad \text {for } y\in [1,n]. \end{aligned}$$

(21b)

The interface is therefore located at $Y=-1$, found by setting $y=1$ in each fluid region. In our computations to be presented below we take $n=100$, which we found to be sufficiently large for the presence of the upper wall to have a negligible effect on the results.

Fig. 2

Comparison of the numerically computed growth rates (lines) with the long-wave analysis (symbols), for $s=1$, $m=0.5$, $Ma=1$, $\bar{\varGamma }=0.5$, $Pe_s=10^8$, $Pe_b=100$, $R_b=1$. The black thick lines correspond to the “insoluble” limit with $B=0.01$, while the blue thin lines and symbols correspond to $B=1$. The symbols represent the asymptotic results found analytically for long waves

Unless specified otherwise, the results presented in this section will take the following parameter values: $s=1$, $m=0.5$, $Ma=0.1$, $\bar{\varGamma }=0.5$, $Pe_s=10^8$, $Pe_b=100$ (the surface Péclet number is taken to be large due to the small surface diffusion rate ${\mathscr {D}}_s$ which is normally found in practice). The two parameters that control the surfactant solubility will typically assume values in the ranges $0\le B\le 1$ and $0<R_b<\infty$ and will be altered accordingly in order to investigate the impact of the solubility on interfacial stability. We begin by comparing the numerically computed growth rates to the leading-order long-wave approximations presented in Sect. 2.3 for the two primary modes. In Fig. 2 the first few modes calculated using the Chebyshev method are shown with solid lines for two $B$ values and $R_b=1$, and the long-wave predictions for the largest value of $B$ are shown with symbols (circles for mode 1 in Eq. (17) and squares for mode 2 in Eq. (18b)). The thin lines indicate growth rates for $B=0.01$ so that the surfactant is almost insoluble, while the thick lines are for soluble surfactant with $B=1$. The long-wave predictions for $B=1$ are in excellent agreement with the numerically obtained growth rates for small values of k.

We note that only two modes pass through the origin at $k=0$ in Fig. 2, namely the primary modes identified in Sect. 2.3, and it is these that are responsible for any instability. The remaining modes are secondary modes for which $\mathfrak {I}(c)<0$ at $k=0$ and they are stable over the entire wave number range. In fact, the secondary modes were found to be stable at all k for all parameter sets that we examined; in Appendix C, we prove the stability of these modes in the case of $B=0$.

Figure 3 demonstrates the effect of varying the Biot number B on the growth rates. The dominant mode for the insoluble case ($B=0$) is unstable over the range $0\le k\le k_c$ for $k_c\approx 1.4$, but is stabilised for any $B>0$ at sufficiently small wavenumbers. For weakly soluble surfactant, that is sufficiently small B, mid-wave instability occurs over a window of wavenumbers away from zero (this type of instability has also been found in similar systems, see for example [9, 20, 22]). For larger values of the Biot number such as $B=0.1$, the system is stable over the entire wavenumber range. Figure 4 illustrates how a similar stabilisation occurs by instead decreasing the solubility parameter $R_b$, in which case the maximum value of the growth rate is seen to monotonically decrease for decreasing values of $R_b$. Here the system is unstable for large enough $R_b$ and is completely stabilised when $R_b$ drops below the threshold value $R_b\approx 2.4$ and the surfactant solubility is sufficiently strong.

Fig. 3

Growth rate curves for increasing values of $B$ and fixed $R_b=1$, $Ma=0.1$, with all other parameter values remaining the same as in Fig. 2

Fig. 4

Growth rate curves for decreasing values of $R_b$ and fixed $B=1$, $Ma=0.1$, with all other parameter values remaining the same as in Fig. 2

Figure 5 shows the interface concentration energy budget (11b) for the case examined in Fig. 3. The eigenfunctions are calculated by solving the linear system (12) using the Chebyshev method and applying the normal mode form of the disturbances into the energy equations (10b) and (11b). All of the terms in (11b) have been normalised with the magnitude of the diffusive term DIFC in (10b) (note that DIFG is very small owing to the large Péclet number $Pe_s$ and as such is not suitable for the normalisation). For the case $B=0.01$ instability occurs when ENG switches sign at $k\approx 0.19$, consistent with Fig. 3; the flow is stable for $B=0.1$ (notice also that the terms presented for $B=0.1$ are approximately five times smaller in amplitude than those for $B=0.01$). The flux term FLXG is everywhere negative in both cases: surfactant is overall desorbed from the interface with a stabilising effect on the flow. Evidently the GSH term is both positive and larger in amplitude than the rest of the terms in the energy equation (11b), indicating that it is the underlying shear that is driving the instability. Note that as expected the term ENC in the bulk energy budget (10b) becomes positive when ENG becomes positive, but this is not shown.

Unbounded flow

The unbounded problem with two semi-infinite fluids separated by an interface was first investigated by [23] in the absence of surfactant. They found that instability only occurs in the presence of inertia and/or unstable density stratification. For Stokes flow with equal-density fluids, [5] showed that the flow is stable in the presence of an insoluble surfactant. Exactly two normal modes exist in this case—a hydrodynamic mode and a Marangoni mode—both of which can be found in a closed form.

The unbounded case of two semi-infinite fluids is effectively attained in the present formulation by considering a perturbation of sufficiently short wavelength. There are then only two length scales in the problem provided by the groupings ${\mathscr {D}}_s\mu _1/\gamma _0$ and ${\mathscr {D}}_b\mu _1/\gamma _0$, the latter associated with surfactant solubility. Thus for insoluble surfactant with negligible surface diffusivity, ${\mathscr {D}}_s=0$, there is no natural length scale and the growth rates are independent of the wave number. Even with negligible surface diffusivity (in our calculations we have assumed $Pe_s=10^8\gg 1$), the growth rates for the soluble unbounded problem do depend on the wavenumber underscoring the importance of the length scale ${\mathscr {D}}_b\mu _1/\gamma _0$. We note that the hydrodynamic mode is identical to that obtained in the case of a clean flow.

For two semi-infinite fluids, the coefficient $b_2$ in (14) must vanish to ensure a bounded concentration in the far-field. Looking at the form of $\zeta$ in (14) suggests the scaling $c\sim k^{-1/3}$ in order to retain solubility effects in the analysis. We can then expand the wave speed as $c=c_0k^{-1/3} + \cdots$ in the transcendental equation, and we find that to satisfy the equation at leading order we need

$$\begin{aligned} \mathrm{Ai}'(z)=0 \quad \text {with} \quad z = (-\mathrm{i}sPe_b)^{1/3}s^{-1}c_0. \end{aligned}$$

(22)

It is known that the derivative of the Airy function $\mathrm{Ai}'(z)$ only has zeros on the negative real axis and there are an infinite number of them [24]. Consider this infinite set of roots $z_n=-\xi _n<0$, $n=1,2,\ldots$, with $\xi _n>0$. The leading-order wave speed $c_0$ can then be written as $c_0=-A\xi _n\mathrm{e}^{\mathrm{i}\pi /6}$, where coefficient $A=s^{2/3}Pe_b^{-1/3}$ is a positive constant. Hence any solution for $c_0$ lies on a line in the third quadrant, at an angle of $30^\circ$ with the negative real axis. The leading-order growth rate is therefore stable since $\mathfrak {I}(c_0)=-A\xi _n/2<0$ for all values of n.

We have provided above some analytical evidence that the growth rates of an unbounded flow are stable for small values of k. For arbitrary values of k, the stability of the growth rates is supported by the numerical results presented earlier that correspond to a semi-infinite flow. In particular, it has been demonstrated that all growth rates are stable for sufficiently short waves (this is also true for Fig. 2 at larger k not shown in the plot).

Fig. 5

Variation of the energy budgets of interfacial surfactant from Eq. (11b), for the same parameter set as in Fig. 3 and $B=0.01$ (left) or $B=0.1$ (right). All quantities are normalised by the diffusion in the bulk, DIFC

Conclusions

We have investigated the linear stability of an interface between two sheared viscous fluids above a flat wall, in the case when the thinner fluid layer is filled with a soluble surfactant. In particular, we have found that a soluble surfactant has a stabilising impact on the flow. We performed a linear stability analysis for Stokes flow and analysed the behaviour of the growth rates for different surfactant solubilities. According to Pozrikidis & Hill [5], in the case of insoluble surfactant the flow is always unstable to some perturbation of finite wavelength. We have found that the flow is completely stabilised when the surfactant is sufficiently soluble. Long-wave disturbances are stabilised by a relatively low level of solubility, but mid-wave instability is supported for weakly soluble surfactant; that is, perturbations of moderate wavelengths may be unstable.

The results discussed above were obtained numerically for disturbances of arbitrary wavelength by solving a linear eigenvalue problem for the wave speed of the perturbations. We have also examined the linear system analytically in the case of large-wavelength disturbances using an asymptotic approach. Somewhat unexpectedly, the leading-order forms of the dominant growth rates do not reduce to those found for an insoluble surfactant when the appropriate limits are applied, a discrepancy that we attribute to a non-uniformity in the relevant asymptotic expansion.

We have also carried out an energy budget analysis which provided insight into which of the terms in the surfactant transport equation are key for (de)stabilisation when this is supported. Specifically, we have demonstrated that a term proportional to the shear rate at the interface dominates over all other terms and hence, in keeping with previous studies with insoluble surfactant, it is shear that provides the key component to drive the instability.

It is interesting to contrast the results of this study with those in [12, 13] for a film flow down an inclined substrate, where it was found that solubility has a destabilising effect. Therefore different flow fields disrupt the uniform surfactant distribution at the interface in different ways, leading to Marangoni stresses that may be stabilising (gravity-driven film flow with inertia) or destabilising (shear-driven film flow, as here). However, in both cases the effect of increasing solubility is to mitigate the respective trend, i.e. the stabilising/destabilising effect becomes weaker.

Finally, we have examined the importance of the wall in determining the stability of the flow. In common with the findings of Pozrikidis & Hill [5] for insoluble surfactant, we have found that the presence of the wall is necessary for interfacial instability when the surfactant is soluble. This outcome is suggested by our numerical and analytical results (based on asymptotic analysis for long-wave perturbations) for an unbounded flow. The physical role played by the wall in destabilising the flow remains an open question and is the subject of our current investigations.

Appendices

Appendix A: Kinetic energy budget

To obtain an equation for the kinetic energy, the linearised momentum equations (with $Re\ne 0$)

$$\begin{aligned} Re\bigl ( \hat{{\varvec{u}}}_{it} + \bar{{\varvec{u}}}_i\cdot \nabla \hat{{\varvec{u}}}_i + \hat{{\varvec{u}}}_i\cdot \nabla \bar{{\varvec{u}}}_i \bigr ) = - \nabla {\hat{p}}_i + m_i\nabla ^2\hat{{\varvec{u}}}_i, \qquad \nabla \cdot \hat{{\varvec{u}}}_i = 0, \end{aligned}$$

(23)

are multiplied by the perturbation velocities, ${\hat{u}}_i$ and ${\hat{v}}_i$, respectively, and are then integrated over the respective flow regions and added together. In particular, the vertical integration spans the height of each fluid for $y\in [a_i, b_i]$, $i=1,2$, where $a_1=0$, $b_1=1$ and $a_2=1$, $b_2=\infty$, while integration in the horizontal direction takes place in a wavelength $[0, \Lambda ]$, with $\Lambda =2\pi /k$ and k is the wavenumber (horizontal periodicity is assumed). The pressure terms are then eliminated by using the boundary conditions on the wall, the velocity continuity condition at the interface, and the linearised stress balance equations at the interface. The continuity equation is also applied and the resulting energy budget equation is the following:

$$\begin{aligned} \text {KIN + REY} = \text {DIS + TEN + TAN + MAR}, \end{aligned}$$

(24a)

where

$$\begin{aligned}&\text {KIN} = \sum _{i=1}^2 Re\frac{\mathrm{d}}{\mathrm{d}t} \int _0^\Lambda \int _{a_i}^{b_i} \frac{1}{2}\Bigl ({\hat{u}}_i^2 + {\hat{v}}_i^2\Bigr ) \,\mathrm{d} y\,\mathrm{d} x, \nonumber \\&\text {REY} = \sum _{i=1}^2 Re\int _0^\Lambda \int _{a_i}^{b_i} {\bar{u}}'_i{\hat{u}}_i{\hat{v}}_i \,\mathrm{d} y\,\mathrm{d} x, \nonumber \\&\text {DIS} = - \sum _{i=1}^2 m_i \int _0^\Lambda \int _{a_i}^{b_i} \Bigl ( 2{\hat{u}}_{ix}^2 + 2{\hat{v}}_{iy}^2 + ({\hat{u}}_{iy}+{\hat{v}}_{ix})^2 \Bigr )\,\mathrm{d} y\,\mathrm{d} x, \nonumber \\&\text {TEN} = \bar{\gamma }\int _0^\Lambda {\hat{h}}_{xx}{\hat{v}}_1 \Big |_{y=1} \,\mathrm{d} x, \nonumber \\&\text {TAN} = \int _0^\Lambda ({\hat{u}}_1-{\hat{u}}_2)({\hat{u}}_{1y}+{\hat{v}}_{1x}) \Big |_{y=1} \,\mathrm{d} x, \nonumber \\&\text {MAR}= - \frac{Ma}{(1-\bar{\varGamma })}\int _0^\Lambda \hat{\varGamma }_x{\hat{u}}_2 \Big |_{y=1} \,\mathrm{d} x, \end{aligned}$$

(24b)

cf. [25,26,27]. The first term on the left-hand side, KIN, is the spatially averaged rate of change of the kinetic energy of the disturbances (and is proportional to the growth rate, [17]), while the second term, REY, is the energy transfer from the basic flow to the disturbances via the Reynolds stresses [25]. Both of these terms are proportional to the Reynolds number in the film, which is minuscule due to the small fluid thickness; while these terms are left in the energy budget for completeness, in practice they are both zero for the problem considered here and so Eq. (24b) cannot be used to determine whether the flow is stable or unstable. The terms on the right-hand side are explained as follows: term DIS is viscous dissipation and is always negative; term TEN represents the rate of work done against the interfacial tension in deforming the interface [17, 26] (a term involving the hydrostatic pressure gradient would also be added here had the effect of density stratification been also considered); term TAN represents the transfer of energy from the basic flow to the perturbed flow at the interface [23]—this term is non-zero since the viscosities are unequal, $m\ne 1$; and finally, term MAR is due to the Marangoni stresses at the interface.

Appendix B: Insoluble surfactant limits

Limit $B\rightarrow 0$

In this limit the mass flux $J_b$ tends to zero and the adsorption/desorption process to/from the interface is suspended. The two normal modes obtained via linear stability analysis are the same as those coming from the insoluble surfactant case, as expected. Now there is an infinite number of additional modes that are always stable; the origin of these modes is from the bulk equation, which is now decoupled from the rest of the system and is solved with homogeneous boundary conditions ${\tilde{C}}'(0)={\tilde{C}}'(1)=0$.

Limit $R_b\rightarrow \infty$

In this case, the linearised interfacial flux becomes

$$\begin{aligned} {\tilde{J}}_b = B\left( R_b{\tilde{C}}(1)(1-\bar{\varGamma }) - \frac{{\tilde{\varGamma }}}{(1-\bar{\varGamma })} \right) \sim BR_b(1-\bar{\varGamma }){\tilde{C}}(1) \quad \text {as } R_b\rightarrow \infty . \end{aligned}$$

(25)

The second boundary condition in (12g) then becomes ${\tilde{C}}'(1) + Pe_bBR_b(1-\bar{\varGamma }){\tilde{C}}(1) = 0$, hence in the limit $R_b\rightarrow \infty$ the condition simplifies to ${\tilde{C}}(1)=0$. Consequently, none of the flux terms will remain in the linearised transport equation for the surfactant at the interface (since the only surviving term, seen in Eq. (25), is ${\tilde{C}}(1)=0$ as found above), and hence the interfacial equation is reduced to that for insoluble surfactant. Finally, we note that the bulk equation is again decoupled from the rest of the system but is now solved with boundary conditions ${\tilde{C}}'(0)={\tilde{C}}(1)=0$, in which case all modes found numerically are seen to not pass through the origin $k=0$.

Appendix C: Normal modes of the bulk equation for $B=0$

In the case of insoluble surfactant obtained by setting $B=0$, the linearised bulk equation (12f) is solved with homogeneous boundary conditions ${\tilde{C}}'(0)={\tilde{C}}'(1)=0$. We will show that all modes originating from the bulk concentration system are stable. Multiplying (12f) by the complex conjugate ${\tilde{C}}^*$, integrating over the vertical fluid domain [0, 1], applying integration by parts, and using the boundary conditions, result in

$$\begin{aligned} - \int _0^1 |{\tilde{C}}'(y)|^2\,\mathrm{d}y - \int _0^1 \Bigl [k^2 + \mathrm{i}kPe_bsy - \mathrm{i}kPe_bc\Bigr ]|{\tilde{C}}(y)|^2\,\mathrm{d}y = 0. \end{aligned}$$

(26)

Solving for the wave speed gives

$$\begin{aligned} c = s\frac{\int _0^1 y|{\tilde{C}}(y)|^2\,\mathrm{d}y}{\int _0^1 |{\tilde{C}}(y)|^2\,\mathrm{d}y} - \frac{1}{kPe_b}\left( \frac{\int _0^1 |{\tilde{C}}'(y)|^2\,\mathrm{d}y}{\int _0^1 |{\tilde{C}}(y)|^2\,\mathrm{d}y} + k^2 \right) \mathrm{i}, \end{aligned}$$

(27)

therefore it is clear that $\mathfrak {R}(c)>0$ and $\mathfrak {I}(c)<0$, and hence the growth rates have the property $\lambda =k\,\mathfrak {I}(c)\le 0$ for all $k\ge 0$.