Abstract
The study here is concerned with a thin solid body passing through a boundary layer or channel flow and interacting with the flow. Relevant new features from modelling, analysis and computation are presented along with comparisons. Three scenarios of such fluid-body interactive evolution in two-dimensional settings are considered in turn, namely a long body translating upstream or downstream, a long body with little or no translation and a short body with or without translation. The main progress and findings concern predictions of the time taken by the body to traverse the flow and impact upon the underlying wall, the delicate behaviour at the onset of impact, the dependence on parameters such as the initial conditions and the mass and shape of the body, and the influence of streamwise translation of the body in the surrounding fluid flow.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The background for the present work mainly concerns aircraft flight safety [1,2,3,4] in the presence of ice-crystal impacts, ice-lump and other particle impacts, and storms. Bodies (particles) of various sizes approach the aircraft surface at many different angles and, in the case of ice crystals, can adhere partially or fully to the surface and thereby have an adverse effect on the aerodynamics. The shapes of such bodies vary enormously as well. Industrial interest lies in pursuing relatively fast, reliable, versatile means to predict representative body trajectories including the passage through the external boundary layer on the vehicle. Internal flows such as channel flow are also of concern because of the potential application for bodies entering an engine intake. Road vehicles and ships face similar hazards in the presence of impacts. There are also possible biomedical and environmental applications as well as interests in sports and industrial cleaning.
Previous work of relevance includes analytical studies of dynamic fluid-body interaction for a variety of body lengths, shapes and positions [5,6,7,8,9], although not all possible lengths, shapes or positions are necessarily significant. The typical Reynolds number of real interest is large. A feature common to the recent investigations in [8,9,10,11,12,13,14] for boundary layer and channel flows and to the study herein is that the fluid-flow vorticity is non-zero, contrasting with the cases considered in [5,6,7]. Moreover interactions between a body and the surrounding fluid flow near a solid fixed wall are generally quite different from the well-known interplay provoked by a bump on a wall in view of, first, the presence of a gap between the body and the wall; second, the subtle adjustments of flow near the upstream and downstream ends of the body and third, the increased number of substantial flow regions that become present. Other background work includes direct numerical simulations, various types of modelling and experiments in [15,16,17,18,19,20,21,22,23,24].
This paper addresses for the most part the interactive effects associated with a thin body that is free to move in a boundary layer. The channel-flow scenario tends to be similar as we shall see. Special attention is given analytically to the effects of streamwise upstream or downstream translation of the body, corresponding to varying the angle of incidence of the body passing through the boundary layer. Inviscid and viscous influences are to be described, and we note the interest also in flow separations at the wall or on the body surface. The flow predictions here which are based on asymptotic arguments are used to determine the major forces acting on a body and, hence, deduce the scaled lift and moment, denoted \(C_L\) and \(C_M\), respectively, in order to derive the body motion. The latter motion in turn alters the fluid motion via two-way coupling. As in previous works, only thin bodies at small incidence are investigated in the present study, but, on the other hand, links with practical application in terms of numerical prediction are discussed and identified by [8, 11, 12], while there is an interesting potential complementarity between simulations, analysis and asymptotic reasoning.
The novelties in the current study predominantly surround the effects of streamwise translation of the body, the influence of incident vorticity and fluid viscosity, and the behaviour at impact. The progress to be highlighted, relative to previous work of relevance, concerns quantification of the above (translation, vorticity, viscosity, impact) together with enlargement of understanding on the effects of different body lengths, shapes and positions as well as a comparison between reduced-equation modelling and direct numerical simulations.
We consider a rigid body moving in the boundary layer of a much larger body or airfoil, and model the flow as two-dimensional and incompressible. Non-dimensional variables are taken throughout and are defined by \( ({\hat{x}},{\hat{y}}) = {\hat{l}}(x,y),\ ({\hat{u}},{\hat{v}}) = {\hat{U}}(u,v), \ {\hat{p}} = {\hat{\rho }}_F {\hat{U}}^2 p,\ {\hat{t}} = {\hat{l}}t/{\hat{U}} \), where \(\ \hat{{}}\ \) represents a dimensional quantity and \({\hat{l}}\) is the boundary-layer length, \({\hat{U}}\) is a typical boundary-layer velocity and \({\hat{\rho }}_F\) is the constant fluid density. Here, (x, y) are Cartesian coordinates, t is time, (u(x, y, t), v(x, y, t)) are the corresponding components of the fluid velocity vector field, p(x, y, t) is the pressure field of the fluid. This leads to the non-dimensional incompressible Navier–Stokes equations:
where \(\mathrm {Re}\) is the Reynolds number of the flow, \(\mathrm {Re} = {\hat{U}}{\hat{l}}/{\hat{\nu }}\) and \({\hat{\nu }}\) is the kinematic viscosity of the fluid.
We also have the boundary conditions of (1) no slip at \(y = 0\) (the wall) and at \(y = f^{\pm }\), where \(y = f^{\pm }(x,t)\) are the curves of the upper (+) and lower (−) surfaces of the body and (2) a pressure condition at the trailing edge of the body, inter alia. The condition at the body’s trailing edge is in effect the Kutta condition ensuring that the velocity is finite at the trailing edge, at \(x=L\) (where L is the body length since we choose the leading edge to be at \(x=0\)).
The assumption of the Kutta condition at the trailing edge appears justifiable in most of the modelling here despite it being a sensitive issue in unsteady and viscous-fluid flows as described in [25, 26]. Although the fluid-body interactions being analysed are unsteady, the flows themselves are quasi-steady and so the Kutta condition applies generally for a thin body at least in the absence of separation [26]. In addition, agreement is found with the results of direct numerical simulations where no such trailing edge condition is imposed, both for separating and non-separating flows. The reason for the quasi-steadiness here is that the body is taken to be significantly heavier than the fluid, as in the example of an ice particle passing through air, and the dynamic movement of the body dictates the evolution.
The layout of the paper is as follows. Section 2 describes the motion of a thin heavy body passing through, and interacting with, a boundary layer; the body is long compared with the boundary-layer thickness, and the body is translating upstream or downstream relative to the wall. The modelling and nonlinear analysis in this section are founded on predominantly inviscid rotational flow of the fluid. Various incidence angles are considered, and impact of the body on to the wall is found to arise in many cases. Then Sect. 3 considers the non-translating situation where considerable viscous/inviscid interplay occurs even for a very thin long body. Linear and nonlinear responses are notable in that configuration. This is followed by Sect. 4 which is on the nonlinear fluid-body interaction taking place when a short body is initially positioned very close to the wall whether in a boundary layer or channel flow. Impacts of the body on the wall can again occur. Conclusions are given in Sect. 5 together with the prime connections between the previous sections.
2 Thin heavy body translating in a boundary layer
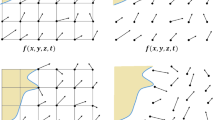
We focus on the region of fluid flow between the wall and the lower surface of the body, \(0 \le y \le f^-(x,t)\), motivated by the fact that the pressure above the body is identically zero at leading order (by identification with the local free-stream). See Fig. 1. We will assume that \(\mathrm {Re} \gg 1\) and that the body is thin such that its non-dimensional thickness is \(O(\Delta = \mathrm {Re}^{-1/2})\) for a given boundary-layer thickness \(\Delta \). The length of the body is taken to be much smaller than the boundary layer length but much larger than its thickness; so the non-dimensional body length L satisfies \(\Delta \ll L \ll 1\). We use the rescaled coordinates \( x = LX, \ y = \Delta Y, \ t = \sigma T, \) where \(\sigma \) is the time scale of body motion. Incompressibility also enforces \(v(x,y,t) = (\Delta /L)V(X,Y,T)\). Defining \(\varepsilon = L/\sigma \), Eq. (1.1) becomes
to leading order, and hence, the pressure \(p = p(X,T)\) is independent of Y. The boundary conditions are
with \(f^-(x,t) = \Delta F(X,T).\) In order for the Kutta condition on p(1, T) to be enforced, we require, by virtue of upstream influence, the existence of a short Euler region surrounding the leading edge, in which the pressure and velocity change dramatically. The flow can be modelled as steady in this region [27, 28], so governed by the nonlinear Euler equations, and Bernoulli’s theorem holds there. Letting \(u = u_0(Y)\) be the incoming unidirectional velocity profile but now measured relative to the translational velocity of the body, the incoming velocity can be related to the post-Euler velocity by \( u_0(Y_0)^2/2 = u(0^+,Y,T)^2/2+p(0^+,T), \) where \(Y_0\) is the Y-coordinate of the relevant streamline in the pre-Euler region. Given \(u_0(0) = - u_c\), we consider first the negative-\(u_c\) scenario.
Diagram showing the set-up for Sect. 2: a thin body translates with speed \(u_c\) in the boundary layer of a much larger body, which acts as a stationary wall. The distance of the body’s centre of mass (CoM) from the x-axis is h and the angle its chord line makes with that axis is \(\theta \). The incoming velocity profile (due to the motion of the larger body) is \(u = u_0(y)\)
We also have the equations of motion of the body. The body centre of mass is at a distance \(\Delta {\hat{h}}({\hat{t}}) = {\hat{l}}\Delta h(t)\) from the x-axis and the angle that its chord line makes with that axis is \((\Delta /L) \theta \). We allow the body to have arbitrary shape, with underbody shape given by \(Y = F_u(X)\). Since we have taken the angle to be small, the equation of the underbody curve for each time is
where \(\beta \) is the X-coordinate of the centre of mass. To determine the body motion equations, we neglect gravity and note that the main force driving the body motion is the pressure force due to the fluid. Then, in our non-dimensional, scaled coordinates,
where \(M = \Delta {\hat{M}}/(L\sigma ^2{\hat{\rho }}_F {\hat{l}}^2)\) and \(I = \Delta {\hat{I}}/(L^3\sigma ^2{\hat{\rho }}_F {\hat{l}}^4)\) are the scaled non-dimensional mass and moment of inertia of the body. Here, \({\hat{M}}\) and \({\hat{I}}\) are their dimensional equivalents, given by \({\hat{M}} = {\hat{\rho }}_B{\hat{l}}^2L\Delta \) and \({\hat{I}} = {\hat{\rho }}_B{\hat{l}}^4L^3\Delta \), where \({\hat{\rho }}_B\) is the constant density of the body. We may then find the body motion time scale since we expect the terms in (2.4) to remain of order unity, which yields \( \varepsilon \sim L(\Delta {\hat{M}}/L{\hat{l}}^2{\hat{\rho }}_F)^{-1/2} = (L/\Delta )\left( {\hat{\rho }}_F/{\hat{\rho }}_B\right) ^{1/2}. \) Thus, \(\varepsilon \ll 1\) provided we take the assumption that \({\hat{\rho }}_F / {\hat{\rho }}_B \ll (\Delta /L)^2\). For an ice particle in air, the density ratio is around \(10^{-3}\); hence, there exists a range of aspect ratios for which this assumption is reasonable. This reduces the fluid flow to quasi-steady form for at least a substantial part of the flow evolution, due to (2.1). We are left with the system:
subject to
for the fluid, with F given by (2.3), and Eq. (2.4) for the body. Since the flow is quasi-steady, Bernoulli’s theorem now holds for the whole flow; hence also,
on a streamline given by \(Y = Y(X)\). Dependence on T is implicit. Here M, I, \(u_0(Y)\) and \(F_u(X)\) are treated as given, and we intend to solve for the behaviour of the body, i.e. h and \(\theta \).
2.1 First temporal stage
Numerical solutions of h and \(\theta \) for a body with \(M=1,\ I=0.2\) are shown in solid blue, with incoming flow profile \(u_0 = 2-\exp (-Y)\). Initial conditions were \(h(0) = 1,\ \theta (0) = 0.2,\ h_T(0) = -0.1,\ \theta _T(0) = 0\). The dashed red curves vary as \((T_0-T)^{4/5}\) with the end points fixed to match the corresponding h or \(\theta \) value there
To solve for h and \(\theta \) in (2.4), we require a relation between the pressure p and the moving underbody shape F(X, T). Note first that the Y coordinate at an arbitrary point is related to the corresponding coordinate at \(X=1\) on its streamline via
We will, for the purposes of this study, assume exclusively forward flow such that \(u \ge 0\) everywhere, and hence, every streamline passes through both the pre-Euler region and through the position \(X=1\). From (2.7), we have that \(u_0(Y_0) = u(1,Y_1)\), where \(Y_0\) is the Y-coordinate of a given streamline in the pre-Euler region, and thus, by (2.8), \(\mathrm{{d}}Y_0/\mathrm{{d}}Y_1 = 1.\) Since \(Y_0\) and \(Y_1\) are both zero at the wall, \(Y_0=Y_1\) and thus, the velocity profile at the trailing edge is identical to the incoming velocity profile, \(u(1,Y) = u_0(Y)\). The equivalent relation for an arbitrary point (X, Y) is \(dY/dY_1 = u_0(Y_1)/u(X,Y) = u_0(Y_1)/(u_0(Y_1)^2-2p(X))^{1/2}\). Choosing the streamline along the underside of the body, we obtain the pressure–shape relation
Coupling this to the body motion equations allows them to be solved numerically. The results given in Fig. 2 show that the body will clash with (impact on) the wall in finite time (given suitable initial conditions). The asymptotic dependency of h and \(\theta \) on time can be determined by first assuming that \(F(X,T) = O(T_0-T)^N,\ N>0\) as the clash is approached, in the X range \(X = X_0+O(T_0-T)^{N/2}\), with the clash occurring at some \((X_0,T_0)\). From (2.9), \(p \sim F^{-2}\) as \(F\rightarrow 0\), and so \(p = O(T_0-T)^{-2N}\). The body motion equations, thus, yield \(N = 4/5\). This value shows very good agreement with numerical results for the behaviour of h and \(\theta \) in the limit of a clash (see Fig. 2), and the results suggest little dependency on the incoming profile.
2.2 Second temporal stage
A diagram showing the outer and inner regions described in Sect. 2.2. The solid lines show the body undercurve and the wall, while the dashed line shows a streamline which begins in the left outer region at \((0,Y_0)\), passes through the inner region (a small area surrounding the contact point \(X=X_0\)), and ends at \((1,Y_1)\) in the right outer region. Integration along such a streamline leads to an extra term in the Bernoulli equation because velocity is large enough in the inner region to make an O(1) contribution to velocity potential
At the end of the first stage, the body speed \(h_T =O(T_0-T)^{-1/5}\) tends to infinity, and thus, we anticipate the need for a second time stage. There is now an inner region, given by \(X-X_0 = O(T_0-T)^{2/5}\), and an outer region where \(X-X_0\) is O(1). See Fig. 3. Defining the order-unity time coordinate \(s = (T-T_0)/\tau \) for the unknown time scale \(\tau \), the rescaled variables for the inner region, informed by the results of Sect. 2.1, are \( \tau ^{2/5}\xi = X-X_0, \ \tau ^{4/5}\eta = Y, \ \tau ^{-4/5}{\tilde{u}} = u, \ \tau ^{-2/5}{\tilde{v}} = V, \ \tau ^{-8/5}{\tilde{p}}(\xi ,s) = p, \ \tau ^{4/5}\phi (\xi ,s) = F(X,T), \ \tau ^{4/5}({\tilde{h}},{\tilde{\theta }}) = (h-h_0,\theta -\theta _0). \) Hence, we find the new governing equations
and boundary conditions
The time derivatives have coefficient \(\varepsilon \tau ^{1/5}\) and so remain small for the current time scale. The horizontal velocity \({\tilde{u}}\) is effectively independent of \(\eta \) because the vorticity \(-u_Y\) is conserved to leading order on streamlines (by the vorticity equation), and so must remain O(1) in the inner region as in the outer region, leading to \({\tilde{u}}_\eta = O(\tau ^{8/5})\). Hence, \({\tilde{u}}\) and \({\tilde{p}}\) are expressible in terms of the volume flux q(s),
The underbody curve in the inner region can be approximated as \(\phi (\xi ,s) = \alpha \xi ^2/2+{\tilde{h}}(s)+(X_0-\beta ){\tilde{\theta }}(s), \) where we have defined \(\alpha = F_u''(X_0)\).
In the outer region, the velocity and pressure are of order unity. The \(Vu_Y\) term is not negligible here; so instead we rewrite the X-momentum equation in (2.1) in the form \( {\mathbf {u}}\cdot \nabla (u^2/2+p) = -\varepsilon \tau ^{-1}uu_t \) which becomes
where we have used \(\mathrm{{d}}s' = \mathrm{{d}}X/u\). Here, \(s'\) parameterises streamlines. If we integrate from the left outer region to the right outer region, i.e. over the inner region, the integral on the RHS (right-hand side) of (2.13) is dominated by this inner contribution, which is of O(1) for \(\tau = \varepsilon ^{5/7}\), thus determining the present time scale.
Then integrating from 0 to some point on the left gives
where \(u_L\) and \(p_L\) are the u and p values at the chosen point in the left region, with streamlines coming from \(Y = Y_0\) in the pre-Euler region, while integrating from 0 to some point on the right gives
with \(u_R\) and \(p_R\) defined analogously to \(u_L\) and \(p_L\). In particular, \( u(1,Y_1,t)^2/2 = u_0(Y_0)^2/2-\int _{-\infty }^{\infty } {\tilde{u}}_s\ \mathrm{{d}}\xi . \) Recall that from (2.10), \({\tilde{u}}\) is known in terms of \(\phi \) and the volume flux q(s). The system can be closed as follows. Let \(F_E(s)\) be the Y value of the continuation of the body streamline into the pre-Euler region. Then,
Using the modified Bernoulli relation (2.15) and integrating \(\mathrm{{d}}Y_1/\mathrm{{d}}Y_0 = u_0(Y_0)/u_1(Y_1)\) from the wall to the body, we have
The coupled system of (2.17) with (2.16) amounts to an ODE for q for each h and \(\theta \). Then (2.12) yields a pressure-shape relation which, coupled with (2.4), can then be solved numerically (as in the previous section). The results of the numerical integration are shown in Fig. 4. As \(s \rightarrow 0\), \(\int _{-\infty }^{\infty } {\tilde{u}}_s\ \mathrm{{d}}\xi \) cannot become large or else the integral becomes complex (we can rule out large negative values of the integral as this would correspond to small inner velocity but large outer velocity which contradicts volume flux conservation). Assuming \(\phi (\xi ,s) = O(|s|^N_1)\) as \(s \rightarrow 0\) for \(\xi = O(|s|^{N_1/2})\) and setting these large terms to zero at leading order shows that \(q = O(|s|^{N_1/2})\). This leads to the conclusion that \(N_1\) must be 1 by considering the body motion equations. This value is confirmed by numerical results (see Fig. 4). The body now collides with finite impact speed. This is in line with the result of [6] which investigates a similar scenario in the absence of incoming vorticity, and overall the present work indicates that the qualitative behaviour of the body in the event of impact is largely independent of the detailed incoming flow profile, even if certain features depend on the details.
The numerical solutions of \({\tilde{h}}\) and \({\tilde{\theta }}\) for a body with \(M = 1,\ I=0.2\) and incoming profile \(u_0 = 2-\exp (-Y)\) are shown in solid blue. For initial conditions, we took \({\tilde{h}}, {\tilde{\theta }}\) large (10 and − 10 respectively) and \({\tilde{h}}_s, {\tilde{\theta }}_s\) small to match with the first stage. The dashed red curves vary as \(|s|^{4/5}\) with the starting points fixed to match the initial conditions, and the dot-dashed yellow curves vary as |s| with the end points similarly fixed
3 Body with small or zero translation
Here, we reconsider the boundary-layer setting, followed by the channel-flow setting, but with little or no streamwise translation of the body taking place. The smallness of such translation leads to a distinct kind of interaction between the thin-body motion and the fluid motion including substantial viscous and inviscid effects. Steady flow is addressed at the start but with unsteady properties being discussed in a final subsection. The length of the body here lies between that of the typical viscous development of the oncoming boundary layer or channel flow and the conventional viscous-inviscid interactive length (namely triple-deck [9] for a boundary layer and 1/7th power of the Reynolds number [12] for a channel flow).
For a boundary layer, the typical viscous development length is O(1) since the boundary-layer thickness increases or decreases substantially on that length scale. By contrast, the conventional viscous-inviscid interactive length \(L_p\) is \(O(\mathrm {Re}^{-3/8})\) because of the triple-deck structure. This scale is due to the pressure in a viscous near-wall sublayer (lower deck) being of order \(L_p^{2/3}\) while the pressure just outside the boundary layer (upper deck) is of order \(\mathrm {Re}^{-1/2}L_p^{-2/3}\), implying that the two interact when \(L_p\) is as in the previous sentence. For a channel flow where the Reynolds number based on channel width and characteristic oncoming flow speed is \(R_2\) say a similar argument holds but founded on the lateral pressure gradient becoming significant and this yields a length scale of \(O(R_2^{1/7})\) much greater than the channel width of unity in non-dimensional terms. See background in [29,30,31,32,33,34,35].
3.1 Boundary-layer setting
The body length \(L_1\) and the body thickness \(H_1\) are assumed to be in the range \( \mathrm {Re}^{-3/8} \ll L_1 \ll 1,\quad H_1 = O(\mathrm {Re}^{-1/2}L_1^{1/3}),\) corresponding, respectively, to lying between the development and interactive lengths described in the previous paragraph and to being comparable with the representative viscous thickness. The main governing equations of concern [9] then describe the flow solution in the nonlinear wall layer where the expansion
applies in (1.1), leading to the interactive viscous-inviscid system
Here, \(X_1\) is scaled on \(L_1\), \(Y_1\) on \(\mathrm {Re}^{-1/2}L_1^{1/3}\) and the unknown pressure P is independent of \(Y_1\). Further, we take the body as non-translating for now and the oncoming velocity profile \(u_0(Y)\) in the boundary layer as having slope \(du_0/dY = \lambda \) at the wall where \(\lambda \) is a given positive constant and again Y is scaled on \(\mathrm {Re}^{-1/2}\). The appropriate boundary conditions (see also Sect. 2) for the interval \(0< X_1 < 1\) are then
These represent in turn the no-slip requirement at the wall, the matching requirement with the core region between the wall layer and the body where inviscid properties hold, and the requirements at the trailing edge where \(P, P_{X_1}\) must vanish. The function \(F_u\) is the prescribed shape of the underbody, while \(K(T_1)\) is an unknown mass flux factor to be determined and time (\(T_1\)) dependence is highlighted in readiness for Sect. 3.3, with \(h_1,\ \theta _1\) denoting the lateral displacement and rotation angle, respectively. The factor \(K(T_1)\) is needed because we do not know in advance how much fluid will pass under the body and how much over it. A nonlinear problem similar to that of (3.2)–(3.3) is addressed in [10]. Jumps in the pressure and velocity across the leading edge station similar to those described in the previous section are also involved in the present configuration.
A linearised solution for small \(O({\hat{\varepsilon }})\) values of \(h_1,\ \theta _1,\ F_u\) is now sought, where \({\hat{\varepsilon }}\) denotes the typical size of the initial displacement, rotation and corresponding velocities as well as the underbody shape function. Thus, we have the expressions
producing on substitution into (3.2)–(3.3) a linear system with K of \(O({\hat{\varepsilon }})\). Proceeding as in [9, 12] we take an \(X_1\)-wise Fourier transform of the linearised version of (3.2a), (3.2b), apply the conditions (3.3a), (3.3b) to the solution and then invert the transform. In consequence, we find for the flat-plate case of zero \(F_u\) that the pressure solution takes the form
where \(\gamma \) is a known positive constant and \(a_0\) is an unknown function of \(T_1\). The condition (3.3c) has considerable effect here as it requires both \( P_1 = 0\text { and }P_{1X_1} = 0\text { at }X_1 = 1^{-}. \) Hence from (3.5) we obtain the relations
determining the relative mass flux in the gap and the amount of upstream influence in terms of the angle \(\theta _1\): a plot of the pressure (3.5) is presented in Fig. 5. It follows also that there is significant growth of the flow perturbations as the leading edge is approached. This growth is provoked by the trailing edge requirements, and it implies there is more subtle interaction close to the leading edge through triple-deck and Euler regions.
The pressure solution (3.5) in a boundary layer
The Euler problem takes a linear form, namely
The boundary conditions of tangential flow at the solid surfaces, assuming there is no significant separation [5,6,7,8,9,10,11,12,13,14], are
where \(w(T_1)\) acts as a given positive constant. The form (3.7a, 3.7b) coupled with appropriate far-field conditions represents a rather basic problem. A conformal mapping \(\pi z/w = - \log (z_2)+z_2/2 + \log (2)-1 + \mathrm{{i}}\pi \) can be used to transform the flow region \(z = x_1+iY\) to an upper half plane \(z_2 = x_2 + iy_2\). For the example of a body relatively close to the wall, such that w is small, the oncoming velocity profile is \(u_0(Y) = \lambda Y\) to leading order and the solution of (3.7a), (3.7b) is
locally. Here, (3.8) produces a pressure variation decaying like the inverse of distance from the origin. On the other hand, there is an outer region where the complete profile \(u_0(Y)\) has influence and so may adjust the pressure variation. The far field beyond that needs further consideration.
3.2 Channel flow setting
As stated at the start of this section, similar reasoning holds for flow in a channel of unit width [5,6,7,8,9, 12], where the expansion parameter is the Reynolds number \(R_2\) based on the channel width, while the non-dimensional body length \(L_2\) and width \(H_2\) satisfy \( R_2^{1/7} \ll L_2 \ll R_2,\quad H_2 = O(R_2^{-1/3}L_2^{1/3}). \) The governing equations in the linearised scenario are identical with those leading to (3.5) and so the behaviour (3.6) holds exactly [9, 12].
Closer to the leading edge, however, the channel flow has a viscous-inviscid interaction over the streamwise length scale \(R_2^{1/7}\), with pressure and velocity jumps across that edge. The smoothing-out of the \(X_1^{-2/3}\) effect appearing in (3.5) occurs over this length scale because of the action of the lateral pressure gradient \(\partial p/\partial y\) as in [12, 34, 35]. Given the eigenfunction behaviour of displacement upstream of the leading edge and the comparative smallness of displacement immediately thereafter, the scaled pressure downstream is given by the formula [12]:
where \(\kappa \) is a known positive constant. Specifically \(\kappa = ( 6 \mathrm {{Ai}}^{\prime }(0)/ J)^{3/7} \lambda ^{5/7}\) with J being the integral of \(u_0^2(Y)\) with respect to Y across the channel from 0 to 1 and the positive constant \(\lambda \) being the scaled wall shear stress of the incident velocity profile \(u_0(Y)\); here \(\lambda = 1\) in the case \(u_0(Y) = Y(1 - Y)\) of oncoming Poiseuille flow. The pressure \(P_2\) is finite at \(X_2 = 0^+\) and decays like \(X_2^{-2/3}\) as \(X_2 \rightarrow \infty \) downstream, consistent with (3.5). See Fig. 6. (A similar smoothing-out takes place in the case of the boundary layer.) The earlier-mentioned jumps across the leading edge are smoothed out by an Euler region in which (3.7a), (3.7b) hold along with
Here, \(x_1\) is now identical with x, while (3.10b), (3.10c) provide consistency with (3.7b), (3.10a) and boundedness in the far field. Moreover \({\hat{\psi }}, {\hat{p}}\) denote the main perturbations which can be as large as the order \(R_2^{-2/7}\) for the limit case where \(L_2\) tends to \(O(R_2^{ 1/7})\) and \({\hat{\varepsilon }}\) tends nominally to O(1), with \({\hat{p}}\) given by
Here, \({\hat{p}} \rightarrow 0\) exponentially in the far field, thus, allowing a match with the pressure over the longer \(R_2^{1/7}\) scale, and \({\hat{p}}\rightarrow 0\) at each of the channel walls, where there is a significant inviscid sublayer. The sublayer width \(O(R_2^{-2/7})\) and length O(1) join the upstream and downstream parts of the viscous-inviscid interactive solution mentioned above. The sublayer velocity profiles far upstream and downstream are different from each other since the flow solution in the Euler region allows a difference in displacement because of (3.10c) but the integral connection between the two profiles is similar to that described in the Sect. 2, and hence, the jumps in pressure and displacement are determined. These jumps match with those of [12] in the linearised case.
A computational solution of the Euler problem (3.7a), (3.7b), (3.10a)–(3.10c) is presented in Fig. 7. This includes plots of the pressures \({\hat{p}}\) acting on the body, with \(p_{\text {ABOVE}},\ p_{\text {BELOW}}\) denoting \({\hat{p}}\) evaluated at Y equal to \(w^+,\ w^-\) in turn. A significant property here is that this pressure \({\hat{p}}\) acting locally to the leading edge gives a contribution to the lift \(C_L\) which can be as large as the order \(R_2^{-2/7}\) for the limit case, thereby outweighing the contribution of order \(R_2^{-2/3}L_2^{5/3}\) (approximately) from the remainder of the body, for a range of body lengths. This is abetted by the moment \(C_M\) likewise being susceptible to domination by \({\hat{p}}\) rather than by the pressure effects from elsewhere on the body surface.
3.3 Free movement of the body
Concerning the evolution of the fluid flow and body motion when the body is free to move, the scaled lift \(C_L\) and moment \(C_M\) clearly play crucial roles because of the relevant body-balance equations which are as in (2.4) essentially.
In channel flow, the dominant contributions to the lift and moment can stem from the vicinity of the leading edge by virtue of the pressure in (3.10d). This reaction is such that when the body inclination \(\theta _1\) is positive, then due to the viscous effect on mass flux, the corresponding \(C_M\) turns out to be positive. Thus, in Fig. 7 where the normalised flux is unity, the pressure perturbation \({\hat{p}}\) is positive on top but negative underneath the body and so yields a positive moment (and negative lift) on the body, an aspect which makes physical sense. Hence, the angular acceleration is positive owing to (2.4). It follows that the fluid–body interaction here is unstable over the present time scale.
In the boundary–layer setting, a similar phenomenon may well arise. This is not fully clear as yet because of the nature of the Euler region and the necessity of matching with the viscous-inviscid solution over the \(\mathrm {Re}^{-3/8}\) length scale upstream and downstream. The flow structures for the boundary-layer and channel-flow cases are fairly similar, but the exponential decay of pressure found in the channel-flow setting is unlikely to apply for the boundary layer, while algebraic decay as mentioned in Sect. 3.1 leads to a divergent integral for the local lift and moment. This in turn suggests that the surface pressure on the remainder of the body plays a pivotal part in the evolution.
Altogether we can expect the overall fluid-body interaction for boundary layers, wall jets and pipe or channel flows to be linearly unstable over the time scale of interest. This makes physical sense in the context of flow at high Reynolds number past a thin body at incidence although we note that the novel time scale is that of the body motion rather than that of a high-frequency instability for instance. The work tends to confirm a trend towards a blockage effect even though viscosity is included; nevertheless stabilising measures are possible as described by [9, 11]. As far as body translation is concerned, we can also expect a match with the properties in Sect. 2 when the present streamwise body speed is increased from zero to a size \(\gg L_1^{1/3}\) (see (3.1)) as discussed in [8, 10] for the boundary-layer setting and likewise for the channel flow.
4 Near-wall body with or without translation
This section concerns an elliptical body near the wall where uniform-shear flow is present with an incident velocity gradient \({\hat{\lambda }}\), as in [11, 13] where a flat-plate configuration is studied. The local Reynolds number is R. Direct numerical solutions of the Navier–Stokes equations are described below for the elliptical body being on the verge of impact. The major axis of the elliptical body is 1 and the minor axis is 0.1.
The body is translating upstream or downstream relative to the wall at a velocity comparable with the flow velocity u such that \(u_w\) (the given wall velocity relative to the body) is generally of order unity. The translational velocity of the body relative to the wall may be zero (Fig. 8a), positive (Fig. 8b), or negative (Fig. 8c). The body’s location is fixed at a normal distance from the wall with the leading edge gap denoted \(\beta _1\) and trailing edge gap \(\beta _2\). The task is to solve numerically the system in (1.1) with R replacing \(\mathrm {Re}\) and zero time dependence. The boundary conditions are:
Thus, (4.1) imposes the conditions of no relative slip at the wall, while (4.2) represents the no-slip requirement on the respective upper and lower surfaces \(f^+, f^-\) of the body. Here, (4.3) applies at large distances, including the incident shear effect far upstream and downstream.
Similar to the method outlined in [13], direct numerical simulations were carried out in OpenFOAM version 1812 using the built in solver simpleFoam to calculate the fluid flow about the body [36, 37].
Velocity profiles underneath and on top of the body taken at various points for \(u_w = 0.1\). Flow reversal is seen along the body as the leading edge gap \(\beta _1\) decreases. Top row, left: \(\beta _1 = 0.1\) and \(\beta _2 = 0.2\), Top row, right: \(\beta _1 = 0.05\) and \(\beta _2 = 0.15\). Bottom row, left: \(\beta _1 = 0.1\) and \(\beta _2 = 0.15\), Bottom row, right \(\beta _1 = 0.05\) and \(\beta _2 = 0.1\) (right)
Velocity profiles underneath and on top of the body taken at various points for \(u_w = -0.1\). Flow reversal becomes more prominent further along the body as the leading edge gap \(\beta _1\) decreases. An eddy is also forming ahead of the leading edge in most cases. Top row, left: \(\beta _1 = 0.1\) and \(\beta _2 = 0.2\), Top row, right: \(\beta _1 = 0.05\) and \(\beta _2 = 0.15\). Bottom row, left: \(\beta _1 = 0.1\) and \(\beta _2 = 0.15\), Bottom row, right \(\beta _1 = 0.05\) and \(\beta _2 = 0.1 \) (right)
4.1 Numerical results
Profiles of the pressure along the length of the wall for \(u_w = 0.1\). Top row, left: \(\beta _1 = 0.1\) and \(\beta _2 = 0.2\), Top row, right: \(\beta _1 = 0.05\) and \(\beta _2 = 0.15\). Bottom row, left: \(\beta _1 = 0.1\) and \(\beta _2 = 0.15\), Bottom row, right \(\beta _1 = 0.05\) and \(\beta _2 = 0.1 \) (right)
Profiles of the pressure along the length of the wall for \(u_w = -0.1\). Top row, left: \(\beta _1 = 0.1\) and \(\beta _2 = 0.2\), Top row, right: \(\beta _1 = 0.05\) and \(\beta _2 = 0.15\). Bottom row, left: \(\beta _1 = 0.1\) and \(\beta _2 = 0.15\), Bottom row, right \(\beta _1 = 0.05\) and \(\beta _2 = 0.1 \) (right)
Eight different scenarios are studied here in which the leading edge gap is varied (\(\beta _1 = 0.1\) and 0.05), the trailing edge gap varied relative to \(\beta _1\) (\(\beta _2 = \beta _1 + 0.1\) and \(\beta _2 = \beta _1 + 0.05\)) and \(u_w\) is either positive or negative (\(u_w = 0.1\) and \(-0.1\)). For each case, the local Reynolds number R is 10.
Velocity profiles across the body are presented in Figs. 9 and 10. In Fig. 9, where \(u_w = 0.1\), for \(\beta _1 = 0.1\) (the first column), there is no flow reversal. However, as \(\beta _1\) decreases, flow reversal is seen in both \(\beta _2\) cases in the gap between the body and the wall, close to the trailing edge. This separation is induced by the closing of the gap between the wall and body which begins to cut off the mass flux beneath the body. For decreased inclination (\(\beta _2 = \beta _1 + 0.05\)), reversal is also seen at a second location close to the leading edge. With the reduced inclination the location of the smallest gap moves towards the centre of the body and, due to the body’s elliptical shape, also decreases in size. The incoming flow is thus squeezed by the diminishing gap and begins to turn when the gap becomes insufficiently wide along the curve of the body, starting to cut off the fluid flux below the body.
For \(u_w = -0.1\), the velocity profiles in Fig. 10 are markedly different. Concerning when flow reversal occurs in these scenarios, note that the free-stream velocity has \(u \le 0\) for \(y \le 0.1\) and \(u > 0\) for \(y > 0.1\). Starting with the top left plot, the leading edge of the body is stationed at the cusp of the change in velocity direction, \(\beta _1 = 0.1\). For \(\beta _2 = \beta _1 + 0.1\), flow separation is seen under the body, close to the trailing edge with the velocity remaining negative for values of \(y > 0.1\). As \(\beta _1\) decreases (top, right), flow reversal of a different nature is seen at several points under the body with the velocity becoming positive for \(y \le 0.1\) and ahead of the body (above the leading edge). Thus, eddies are forming at the leading and trailing edges. A similar trend is seen for the \(\beta _2 = \beta _1 + 0.05\) cases. The notable differences are that slight flow reversal exists ahead of the body even for larger \(\beta _1\) (bottom, left) and that with decreasing \(\beta _1\), there is flow reversal at the leading edge both above and below (with the velocity becoming positive in the gap).
To examine the system further, plots for the wall pressure are presented in Fig. 11 for \(u_w = 0.1\) and Fig. 12 for \(u_w = -0.1\). Qualitatively, the results are remarkably similar (up to a difference in sign), and several features stand out. Concerning flow separation, the magnitude and sign of the pressure gradient are important. In Figs. 11 and 12, there is an initial localised jump in pressure towards the leading edge, producing an adverse pressure gradient (given the velocity direction), which indicates the possibility of flow reversal ahead of the body. After this jump, the pressure gradient becomes favourable, until around the body mid-point where it becomes adverse once again, continuing through to the trailing edge and levelling out as the far field is approached. These results show that as the leading edge of the body becomes closer to the wall (right-hand columns), the amplitudes in pressure are far greater than the equivalent larger gap scenarios (left-hand columns), indicating an increased likelihood of flow reversal with the body’s proximity to the wall. Likewise, in the scenarios with decreased inclination (bottom rows), the magnitudes of the gradients are larger throughout the domain than their increased inclination counterparts; hence, the onset of flow reversal is more likely in both the upstream and downstream regions for the less inclined bodies. These results are consistent with the dynamics and trends previously seen in Figs. 9 and 10 and in the analysis elsewhere in the paper. They also help to establish a trend in the expected dynamics as the gap size and inclination change.
4.2 Comments
In Sect. 4.1, the effect of distance between the body and the wall has been of chief concern as impact is neared. The increased likelihood of the occurrence of significant flow reversal beneath the body (with decreased wall gap) and ahead of the body (for decreased inclination) is notable. The position and magnitude of the separation are highly dependent on the inclination of the body, with a more parallel formation producing significant reversal ahead of and behind the body. It is expected that the results of [13] concerning the effects (on upstream influence and separation) of different Reynolds numbers and different magnitudes of wall velocities for a flat plate will also hold in this scenario. Agreement with reduced-system analysis for a flat plate is found in [14].
The reduced-system analysis also applies when the ellipse is sufficiently close to the wall for large Reynolds numbers, with the interactive boundary-layer equations (3.2a, 3.2b) again describing the flow around the body. Unsteadiness due to the ellipse motion leads to the response in Fig. 13 obtained from numerical time marching. Flow reversals near the leading and trailing edges appear eventually, with the underbody shear changing sign. The results point to a mid-chord impact different from those observed for a flat body [13, 14]. The latest-time plot in Fig. 13b is tentative because of the severe numerical challenge near termination, which accentuates the desirability of further analysis.
5 Final discussion and conclusions
The present study has largely been on the analysis and related computation of dynamic fluid–body interactions taking place in a boundary layer. Aspects of channel flow have also been addressed. The work has accommodated in particular the influence of the substantial vorticity present in the oncoming flow, whether for comparatively long bodies as in Sects. 2, 3 or for a shorter body as discussed in Sect. 4. In all cases, the evolution of the system is due mostly to the dynamic movement of the body and this makes physical sense in the setting of a body passing through air, for example, since it corresponds to the density of the body being much larger than that of the surrounding fluid. Among other connections between the cases studied are the features that the predominant forces acting on the bodies are from the fluid-flow pressures and that both the so-called Euler region and the trailing edge conditions associated with the ends of the body play considerable parts in determining the interactive motion. Clashing, i.e. impact on the wall, occurs commonly in the configurations of Sects. 2, 4 and admits interesting short-time analysis.
The main progress and findings here are the clashes (along with associated properties) and accompanying analyses, the typical time scales to impact, the dependence on parameters such as those governing body mass and shape as well as initial conditions, the dependence also on the streamwise translation of the body relative to the solid wall and the basis provided for further progress.
Discussing certain details of the cases examined in Sects. 2–4 in turn, we observe that the typical body in Sect. 2 has a lateral span which is an order-unity portion of the boundary layer or channel flow whereas the body in Sect. 3 spans only a small portion in the middle and the body of Sect. 4 spans only a relatively thin near-wall layer. These differences are associated firstly with inviscid interaction taking place in the first case, as distinct from viscous–inviscid interaction in the other two cases, and secondly with the important effects of streamwise translation of the body, the match between translating and non-translating scenarios having been described in [8]. The working for the long body of Sect. 2 is focussed on there being an upstream movement of the body relative to the wall, but in principle, the non-translating case is also covered formally by means of a change in square-root choice whenever flow reversal occurs [10] and a similar comment holds in the presence of downstream movements of the body. Alternatively, when viscous forces enter the reckoning, as found in Sect. 3, a thinner body positioned in the middle of the boundary layer or channel is able to provoke nonlinear viscous–inviscid interactions especially at the wall, including flow separations, when the translation is zero or sufficiently small. Likewise a comparatively thin and short body much closer to the wall can induce nonlinear separating flow through viscous–inviscid effects according to Sect. 4; related work is in [13, 14] for thin straight bodies.
Significant issues that arise include the fact that if the body is long enough, then nonlinear viscous–inviscid interaction fills the whole boundary-layer width or channel because of the scaling arguments given in Sects. 2, 3. This represents an intriguing situation. Furthermore in Sect. 3 the property that for channel flow, the dominant pressure force is dependent on the lateral positioning of the body near its leading edge supplements the suggestion in [9]. Effects of lateral positioning are in fact evident for all the boundary-layer configurations of Sects. 2–4, with in particular three main positions of the leading edge in the long body case of Sect. 3 corresponding to the three regions of the triple-deck structure. The Euler region in a sense plays a much more significant part in Sect. 3 than in Sect. 2, despite being nonlinear in the latter but only linear in the former. Body shape can also be very important in many cases. Practical implications are discussed fully in references [8, 11,12,13,14].
The above issues and further ones lead to some suggested future studies. These include the following in summary: continued examination of reversed flow and separation [10, 14]; the question of what happens after impact; the influence of fluid-body interaction on boundary-layer transition [8, 9]; three-dimensional interactions based on extending the two-dimensional ones already studied; laminar and turbulent flow modelling; the influence of flexibility due to droplets and elastic surfaces; the extension to many-body problems [5, 7]; the applications to other areas of interest such as in biomedicine and the environment.
References
Gent RW, Dart NP, Cansdale JT (2000) Aircraft icing. Philos Trans R Soc Lond Ser A: Math Phys Eng Sci 358(1776):2873–2911
Purvis R, Smith FT (2016) Improving aircraft safety in icing conditions. In: UK success stories in industrial mathematics. Springer, Berlin, pp 145–151
Norde E (2017) Eulerian method for ice crystal icing in turbofan engines. PhD thesis, University of Twente
Palmer R, Roberts I, Moser R, Hatch C, Smith F (2018) Non-spherical particle trajectory modelling for ice crystal conditions. In: Proceedings of SAE conference
Smith FT, Ellis AS (2010) On interaction between falling bodies and the surrounding fluid. Mathematika 56(1):140–168
Smith FT, Wilson PL (2011) Fluid-body interactions: clashing, skimming, bouncing. Philos Trans R Soc A 369:3007–3024
Smith FT, Balta S, Liu K, Johnson ER (2019) On dynamic interactions between body motion and fluid motion. In: Mathematics applied to engineering, modelling, and social issues. Springer, Berlin, pp 45–89
Smith FT, Johnson ER (2016) Movement of a finite body in channel flow. Proc R Soc A: Math Phys Eng Sci 472(2191):20160164
Smith FT (2017) Free motion of a body in a boundary layer or channel flow. J Fluid Mech 813:279–300
Smith FT, Palmer R (2019) A freely moving body in a boundary layer: nonlinear separated-flow effects. Appl Ocean Res 85:107–118
Palmer RA, Smith FT (2019) When a small body enters a viscous wall layer. Eur J Appl Math 31:1002–1028
Smith FT, Servini P (2019) Channel flow past a near-wall body. Q J Mech Appl Math 72:359–385
Palmer RA, Smith FT (2021) A body in nonlinear near-wall shear flow: Numerical results for a flat plate. J Fluid Mech 915:A35. https://doi.org/10.1017/jfm.2021.92
Palmer RA, Smith FT (2020b) A body in nonlinear near-wall shear flow: impacts, analysis and comparisons. J Fluid Mech 902:A32
Wang C, Eldredge JD (2015) Strongly coupled dynamics of fluids and rigid-body systems with the immersed boundary projection method. J Comput Phys 295:87–113
Wu K, Yang D, Wright N, Khan A (2018) An integrated particle model for fluid-particle-structure interaction problems with free-surface flow and structural failure. J Fluids Struct 76:166–184
Shao Y, Raupach MR, Findlater PA (1993) Effect of saltation bombardment on the entrainment of dust by wind. J Geophys Res: Atmos 98(D7):12719–12726
Foucaut JM, Stanislas M (1997) Experimental study of saltating particle trajectories. Exp Fluids 22(4):321–326
Diplas P, Dancey CL, Celik AO, Valyrakis M, Greer K, Akar T (2008) The role of impulse on the initiation of particle movement under turbulent flow conditions. Science 322(5902):717–720
Ladd AJC (1994) Numerical simulations of particulate suspensions via a discretized Boltzmann equation. Part 2. Numerical results. J Fluid Mech 271:311–339
Willetts B (1998) Aeolian and fluvial grain transport. Philos Trans R Soc Lond Ser A: Math Phys Eng Sci 356(1747):2497–2513
Loisel V, Abbas M, Masbernat O, Climent E (2013) The effect of neutrally buoyant finite-size particles on channel flows in the laminar-turbulent transition regime. Phys Fluids 25(12):123304
Schmidt C, Young TM, Benard EP (2010) The effect of a particle travelling through a laminar boundary layer on transition. In: Seventh IUTAM symposium on laminar-turbulent transition. Springer, pp 561–564
Labraga L, Kahissim G, Keirsbulck L, Beaubert F (2007) An experimental investigation of the separation points on a circular rotating cylinder in cross flow. J Fluids Eng 129(9):1203–1211
Daniels PG (1978) On the unsteady Kutta condition. Q J Mech Appl Maths 31:49–75
Smith FT (1983) Interacting flow theory and trailing edge separation no stall. J Fluid Mech 131:219–249
Smith FT, Ovenden NC, Franke PT, Doorly DJ (2003) What happens to pressure when a flow enters a side branch? J Fluid Mech 479:231–258
Jones MA, Smith F (2003) Fluid motion for car undertrays in ground effect. J Eng Math 45(3–4):309–334
Neiland VY (1969) Theory of laminar boundary layer separation in supersonic flow. Fluid Dyn 4:33–35
Stewartson K, Williams PG (1969) Self-induced separation. Proc R Soc A 312:181–206
Messiter AF (1970) Boundary-layer flow near the trailing edge of a flat plate. SIAM J Appl Math 18:241–257
Stewartson K (1974) Multistructured boundary layers on flat plates and related bodies. Adv Appl Mech 14:145–239
Sychev VV, Ruban AI, Sychev VV, Korolev GL, Maroko EV (1997) Asymptotic theory of separated flows. Cambridge University Press, Cambridge
Smith FT (2016) Fluid and solid mechanics: Chap internal fluid dynamics. World Scientific Press, Singapore
Sobey I (2001) Introduction to interactive boundary layer theory. Oxford University Press, Oxford
Patankashar S (1980) Numerical heat transfer and fluid flow. CRC Press, Boca Raton
Patankar SV, Spalding DB (1972) A calculation procedure for heat, mass and momentum transfer in three-dimensional parabolic flows. Int J Heat Mass Transf 15(10):1787–1806
Acknowledgements
Our thanks go to Colin Hatch, Richard Moser and Ian Roberts of AeroTex UK for numerous helpful discussions and to EPSRC and UCL for financial support of EJ and RP (through IAA and grants EP/R511638/1, GR/T11364/01, EP/G501831/1, EP/H501665/1, EP/K032208/1). Helpful comments from the reviewers are acknowledged gratefully.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Jolley, E. ., Palmer, R.A. & Smith, F.T. Particle movement in a boundary layer. J Eng Math 128, 6 (2021). https://doi.org/10.1007/s10665-021-10121-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10665-021-10121-7