Abstract
The high-speed impact of a droplet onto a flexible substrate is a highly non-linear process of practical importance, which poses formidable modelling challenges in the context of fluid–structure interaction. We present two approaches aimed at investigating the canonical system of a droplet impacting onto a rigid plate supported by a spring and a dashpot: matched asymptotic expansions and direct numerical simulation (DNS). In the former, we derive a generalisation of inviscid Wagner theory to approximate the flow behaviour during the early stages of the impact. In the latter, we perform detailed DNS designed to validate the analytical framework, as well as provide insight into later times beyond the reach of the proposed analytical model. Drawing from both methods, we observe the strong influence that the mass of the plate, resistance of the dashpot, and stiffness of the spring have on the motion of the solid, which undergo forced damped oscillations. Furthermore, we examine how the plate motion affects the dynamics of the droplet, predominantly through altering its internal hydrodynamic pressure distribution. We build on the interplay between these techniques, demonstrating that a hybrid approach leads to improved model and computational development, as well as result interpretation, across multiple length and time scales.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Droplet impacts are a rich and ubiquitous phenomenon in both nature and industry, from inkjet printing [1] to pesticide spray deposition [2] and estimating the early stages of oily aerosol dispersal in the atmosphere after large-scale spills [3]. The dynamics of these processes are governed by the complex flow physics of the droplet and the surrounding gas, as well as the properties of the substrate, such as wettability [4] and roughness [5]. An additional layer of complexity is added to the system if the substrate is deformable, meaning that the force of the impactor causes the substrate to move or change shape. A common example of droplet impact onto deformable substrates is that of rainfall onto leaves [6]. Previous theoretical and experimental studies of this class of systems include droplet impact onto cantilever beams [7], silicone gels [8] and elastic membranes [9].
Recent developments in experimental imaging techniques, improving in both frame rate and spatial resolution, have reinvigorated investigative efforts in high-speed impact [10], revealing previously inaccessible features due to the small, rapidly developing regions upon impact, such as the impingement of micro-drops [11] and early azimuthal instabilities of the ejecta [12]. Similarly, the increase in high-performance computing resources has allowed increasingly efficient direct numerical simulations (DNS) of these systems to be performed [13,14,15], which are intensive due to the rapidly evolving interfaces, multi-scale flow features and high density and viscosity ratios present. These experimental and computational difficulties mean that rigorous mathematical modelling of such flows is of key importance to any comprehensive investigation, as analytical approximations to the flow can provide insight into the underlying physical processes, greatly enhance predictive capabilities in regimes otherwise difficult to examine, and save computational resources required for numerical simulations. In all cases, the deformability of the substrate makes studying these systems even more complex, from the difficulty in observing small deformations experimentally to the additional degrees of freedom required for numerical study.
Studies of droplet impact usually focus on a specific timescale, as examining the rapidly evolving interfaces makes universal investigations challenging. Shortly before impact, the cushioning effect of the gas layer between the droplet and the substrate leads to high pressures which cause the bottom of the droplet to dimple. This interfacial deformation results in a gas bubble being entrapped inside the droplet upon impact, which has been widely observed experimentally [16], as well as reproduced in numerical studies [15], and modelled analytically [17]. At early stages of the impact, close to the points of contact, the free surface rapidly turns over and begins to spread across the substrate. During this timescale, instabilities in the free surface can cause micro-droplets to be rapidly expelled, which has been observed experimentally using high-speed photography [18]. Numerical schemes with adaptive mesh refinement [19, 20] allow for the computational study of this early timescale by concentrating resources in the small region close to the substrate [13, 15, 21]. Analytical approaches adapt Wagner theory [22,23,24,25], an inviscid fluid model for solid–liquid impact inspired by the study of aircraft landing on water and ship slamming. Later in the impact process, once the droplet begins to fully spread across the substrate, viscosity and surface tension, as well as the chemistry of the substrate, tend to play a more significant role. Various physical parameters determine whether the droplet retracts, rebounds or splashes; see [10] for an extensive review on the experimental studies on late impact. Quantities of interest at this timescale include the minimum thickness and the maximum diameter of the droplet as it spreads, and in particular, how these depend on the physical properties of the liquid and the substrate have been the focus of previous theoretical studies [26, 27].
Experimental work focused on droplet impact onto elastic substrates is much less common. Recent investigations have examined the impact of droplets onto the end of cantilever beams [7, 28], drawing close parallels to the impact onto leaves. In both cases, the impact of the droplet excited oscillations at the end of the beam, with characteristic time periods of the order of the late impact timescale. Different length beams were considered in order to show how stiffer beams resulted in oscillations with higher frequencies. Other studies concerning droplet impact onto elastic membranes [9] and silicone gels [8] show that the compliance of the substrate strongly affects the splashing threshold (regarded here as the minimum velocity necessary to observe splashing), which is significantly increased when the stiffness of the substrate is reduced.
Fluid–structure interaction problems are notoriously difficult to study numerically and allowing the substrate to deform only exacerbates this. If the substrate only exhibits translational motion (without accounting for bending), then the problem can be simplified by considering a moving frame of reference, centred on the substrate [29], whereas substrates which exhibit bending need to be considered using more complex techniques such as the immersed boundary method [30]. Two-phase flow systems with immersed boundaries have not been studied extensively, with only a few noticeable exceptions [31, 32]. Despite considering complex moving boundaries (such as a twin screw kneader), the motion of the boundaries was prescribed rather than resulting from fluid–structure interaction, although the proposed methods could in principle be extended to consider this. More recently, the impact of droplets in capillary-dominated regimes onto a flexible substrate has been modelled using the Lattice-Boltzmann method [33], focusing on the spreading and rebound of the droplets and how the contact time is affected by the bending stiffness. The late-time spreading and rebound dynamics of an undamped plate-spring system have recently been studied numerically [34], inspired by the feathers of kingfishers. It was found that springs with certain stiffness values can shorten the length of time the droplet is in contact with the substrate, as well as increase the speed the droplet rebounds after impact.
Analytical models for a liquid impacting a deformable substrate (or vice versa), on the other hand, have been proposed for over half a century. One of the earliest models investigated a droplet impacting onto an elastic half-space by imposing a constant uniform pressure over a circle whose radius increased in proportion to the square root of time [35]. The full hydroelastic problem of the impact of a two-dimensional wave onto an Euler-Bernoulli beam has previously been studied using Wagner theory [36], and more recently this analytical model has been extended to study the axisymmetric impact of a droplet onto an elastic plate, where the elastic plate has a radius much smaller than the droplet and its deflection governed by thin-plate theory [37]. A thorough parameter study was conducted for different types of plate, and regimes where the elasticity of the plate could cause splashing of the droplet at early times, defined as the detachment of the splash sheet from the surface of the plate, have been identified.
To the best of our knowledge, a comprehensive study considering the fluid–structure interaction between an impacting droplet and a compliant substrate that systematically compares accurate numerical results to analytical or experimental counterparts has yet to materialise. One of the simplest types of deformable substrate systems which exhibits both elastic and damping effects is a rigid plate suspended by a Hookean spring and a linear dashpot, where the force of the impacting droplet causes the spring to compress, with the dashpot damping the motion. Here, we present both a new analytical model extended from Wagner theory, as well as a direct numerical simulation platform for a droplet impacting onto a rigid plate supported by a spring and a dashpot. Our focus is on scenarios in which the inertial effects of the impact are dominant, and hence, the derived analytical model neglects the effects of viscosity, surface tension, gravity, and surrounding gas, while these effects are retained in the DNS. Our comprehensive investigation, thus, benefits from a dual-method approach, where the assumptions behind the analytical model are rigorously tested by directly comparing its predictions for a variety of relevant parameters with the results from the numerical simulations. The system is used as a validation testbed for the two approaches, as well as a framework for an extensive parametric study focused on the effect of surface compliance on the ensuing drop dynamics in this challenging regime. We observe systematically how the influence of the substrate properties (mass, spring stiffness and damping factor) affects the fluid–structure interaction, emphasising how the resulting motion of the plate substantially alters the pressure field of the droplet, and, in turn, the hydrodynamic force exerted onto the plate, revealing a rich coupling of the different forces at play in the system.
The rest of this paper is structured as follows. We outline the system geometry and general mathematical framework, as well as discuss assumptions at the level of the analytical and numerical models in Sect. 2. In Sect. 3, we present the analytical model, deriving the leading-order composite solution for the pressure along the plate and the resulting hydrodynamic force. We describe the computational setup required for the direct numerical simulations and the specific algorithm we use to model the fluid–structure interaction in Sect. 4. The solutions from the analytical and numerical models are presented in Sect. 5, where they are compared for a range of parameters of the plate-spring-dashpot system. We conclude by summarising our results and discussing the implications of this study and possible future extensions in Sect. 6.
2 Problem formulation
We consider the vertical impact of a droplet of incompressible, Newtonian liquid onto a rigid, planar, circular plate supported by a Hookean spring and linear dashpot. The droplet is initially spherical with radius \(R_d^*\) and travelling uniformly downwards with speed \(V^*\), surrounded by an incompressible gas. Throughout this study, dimensional quantities are denoted with a superscript \(^*\). The plate has radius \(R^*_p\), and the plate-spring-dashpot system is initially in equilibrium. The bottom of the droplet is introduced at a height \(\delta ^* > 0\) above the plate. A Cartesian coordinate system \((x^*, y^*, z^*)\) is defined such that the surface of the plate lies in the \(z^* = 0\) plane, the droplet falls along the \(z^* > 0\) axis, and the bottom of the droplet is given by \((x^*, y^*, z^*) = (0, 0, \delta ^*)\) at the onset of the dynamics, as illustrated in Fig. 1.
The system is initialised at a time \(t^* = t^*_0 = -\delta ^* / V^*\). If the gas was absent, then the plate would experience a zero net force until the droplet makes contact and would, therefore, remain in equilibrium. In this case, the droplet would make contact with the plate at \(t^* = 0\) with the plate stationary for \(t^* < 0\). However, the presence of the gas means that there will be a pressure build-up prior to the impact [17, 38], resulting in a net force that causes the plate to accelerate downwards so the droplet will make contact at a time \(t^*_c > 0\).
The liquid comprising the droplet and the surrounding gas have densities \(\rho ^*_l\), \(\rho ^*_g\) and viscosities \(\mu ^*_l\), \(\mu ^*_g\), respectively. The surface tension coefficient between the liquid and the gas is denoted by \(\sigma ^*\) (taken to be constant), and the acceleration due to gravity is \(\mathbf{g} ^* = g^* \hat{\mathbf{n }}_z\), where \(\hat{\mathbf{n }}_z\) is the unit vector in the \(z^*\) direction. The vertical position of the plate at time \(t^*\) is \(z^* = -s^*(t^*)\), where \(s^*(t^*)\) is referred to as the plate displacement.
Denoting the variables in the liquid and gas with a subscript l and g, respectively, the Navier–Stokes equations are assumed to hold in each fluid,
where \(i = l, g\), \(\mathbf{u} ^*_i\) is the velocity vector and \(p^*_i\) represents the pressure in each fluid.
The impermeability condition on the plate states that the fluid velocity must match the velocity of the plate along its surface:
where the overdot denotes differentiation with respect to time.
The kinematic condition at the multivalued free surface \(z^* = h^*(x^*, y^*, t^*)\) is
where \(\hat{\mathbf{n }}\) is the unit outward-pointing normal vector to the free surface and \(v^*_n\) is the normal speed of the free surface. Continuity of velocity and normal stress across the free surface are given by
where \(\mathcal {T}^*_i\) is the Cauchy stress tensor in each fluid and \(\kappa ^* = - \varvec{\nabla }\cdot \hat{\mathbf{n }}\) is the curvature of the free surface.
Initially, at \(t^* = t^*_0\), the liquid has a uniform downwards velocity \(V^*\),
while the centre of the droplet is initially at \(z^* = \delta ^* + R_d^*\), meaning that the free surface \(h^*(x^*, y^*, t^*_0)\) satisfies
The pressure \(p^*_i\) is initially hydrostatic in each fluid, equal to \(p^*_i = p^*_{\text {atm}} - \rho ^*_i g^* z^*\), where \(p^*_{\text {atm}}\) denotes atmospheric pressure. The gas far from the impact remains undisturbed for all times, so that
The plate, which has total mass \(M^*\), is supported by a Hookean spring with spring constant \(k^*\), and a dashpot with damping factor \(c^*\). At \(t^* = t^*_0\), the plate is in equilibrium. Hence by Newton’s third law, the force due to the compression of the spring balances the weight of the plate. Denoting the net hydrodynamic force applied to the plate in the downwards direction \(-\hat{\mathbf{n }}_z\) as \(F^*(t^*)\), the displacement of the plate from this equilibrium is governed by
The net hydrodynamic force \(F^*(t^*)\) is equal to the sum of the contributions from the hydrodynamic pressure and viscous stress above and below the plate. Assuming that the gas below the plate is at a constant pressure \(p^*_{\text {atm}}\) and exerts a negligible amount of force due to viscous stress, then
where \(p^* = p^*_l\), \(\mu ^* = \mu ^*_l\), \(u^*_z = u^*_{l, z}\) where the plate is wetted and \(p^* = p^*_g\), \(\mu ^* = \mu ^*_g\), \(u^*_z = u^*_{g, z}\) where the plate is unwetted.
2.1 Non-dimensionalisation
We take the initial droplet radius, \(R_d^*\), and speed, \(V^*\), as the characteristic length and velocity scales, respectively. Then, choosing the advective and inertial time and pressure scales, we non-dimensionalise by setting
where \(R_p\) is referred to as the dimensionless plate radius.
Under these scalings, the plate displacement equation (9) becomes
where
The ratio between the mass of the plate and the mass of the droplet is equal to \(3 \alpha / 4\pi \), hence \(\alpha \) is referred to as the mass ratio. The damping factor, \(\beta \), measures the strength of the resistance to motion due to the damping from the dashpot, and the stiffness factor, \(\gamma \), measures the strength of the restoring force due to elastic compression of the spring.
The relevant dimensionless parameters describing the flow dynamics are the Reynolds, Weber and Froude numbers, defined respectively by
Finally, the ratios between the densities and the viscosities of the gas and the liquid are given by
2.2 Modelling assumptions
In both Sects. 3 and 4, scenarios where the inertial effects of the impact are more significant than the effects of viscosity, surface tension and gravity are considered. Hence, we assume throughout that the values of Re, We and Fr\(^2\) are large. As an illustrative example, consider the impact of a droplet of water with radius \(R_d^* = 1\) mm and velocity \(V^* = 5\) m/s, surrounded by air under atmospheric conditions. This gives
and we make the assumption that they remain large throughout the early stages of impact. Furthermore, the density and viscosity ratios for the air-water scenario are
which provides support for neglecting the effects of the gas phase in the analytical model (but not in the DNS).
As the system is initially radially symmetric about the z-axis, we assume that this symmetry remains in place throughout the impact and consider an axisymmetric coordinate system (r, z), where \(r^2 = x^2 + y^2\). This assumption restricts the applicability of the model away from systems that involve fully three-dimensional effects, such as prompt splashing [18] and azimuthal instabilities of the ejecta sheet [12].
3 Analytical model
The analytical model focuses on the dynamics shortly after the time of impact. The model follows the structure of previous works on axisymmetric Wagner theory, and the reader is directed to [21,22,23, 39, 40] for more details on the general methodology for impact involving stationary substrates. Based on the assumptions made in Sect. 2.2, the analytical model neglects the influence of the liquid viscosity, surface tension, gravity and the surrounding gas. As the gas phase is ignored, all expressed quantities are in the liquid, and the subscript l is dropped for brevity. In this context, the droplet impacts the plate at \(t = 0\), where the displacement and velocity of the plate are both zero at \(t = 0\).
3.1 Governing equations
Under these assumptions, the flow is irrotational for \(t < 0\) and hence by Kelvin’s circulation theorem will remain irrotational for \(t > 0\). Therefore, a velocity potential \(\phi \) can be introduced, such that \(\mathbf{u} = \varvec{\nabla }{\phi }\). The dimensional continuity equation (2) transforms to Laplace’s equation for \(\phi \),
and the dimensional momentum equation (1) results in the unsteady Bernoulli equation for \(\phi \) and p,
for some C(t). The absence of viscosity and surface tension means that the continuity of normal stress boundary condition (5) reduces to specifying that \(p = 0\) at the free surface. Finally, by neglecting the gas phase and liquid viscosity, the net hydrodynamic force (10) is just equal to the integral of the pressure p across the wetted part of the plate. Hence, the governing equations are a set of non-linear equations for the velocity potential \(\phi \), pressure p, free surface location h and plate displacement s.
3.2 Asymptotic structure
Following the structure of previous analytical models for droplet impact [22], we identify that for \(t \ll 1\), the radial extent of the penetration region (where the droplet would be below the r axis were the plate not present) is \(O(\sqrt{t})\). Given this, we introduce an arbitrarily small parameter \(0 < \epsilon \ll 1\) and rescale time
where \(\hat{t} = O(1)\) as \(\epsilon \rightarrow 0\). With the plate present, the free surface is violently displaced and the liquid is ejected along the plate in a splash sheet. The curve at which the free surface is vertical is called the turnover curve, and for small times, we assume that its radial extent is close to that of the penetration region, meaning that
where the turnover curve \(\hat{d}(\hat{t}) = O(1)\) as \(\epsilon \rightarrow 0\). The bottom of the penetration region is at \(z = - \epsilon ^2 \hat{t}\), so if we assume that the plate acts to decelerate the vertical motion of the droplet at early times, then the plate position \(z = - s(t) > - \epsilon ^2 \hat{t}\), which motivates the rescaling
where \(\hat{s}(\hat{t}) = O(1)\) as \(\epsilon \rightarrow 0\). For brevity, the hat notation for \(\hat{t}, \hat{d}\) and \(\hat{s}\) is dropped for the rest of Sect. 3.
As \(\epsilon \rightarrow 0\), the problem breaks down into four distinct spatial regions, as depicted in Fig. 2. In the outer–outer region, for which \((r, z) = O(1) \times O(1)\), the bulk of the droplet is unaffected by the plate to leading order and is hence spherical and moving downwards with unit speed. This is sufficient to give us \(C(t) = 1/2\) to leading order in the Bernoulli equation (19), and we shall not need to consider its higher-order corrections in the present analysis. The \(O(\epsilon ) \times O(\epsilon )\) region close to the centre of the plate is referred to as the outer region, and here, the splash sheet is neglected and the boundary conditions are linearised onto the undisturbed plate location. This solution breaks down close to the turnover curve where the velocity and pressure become singular, which is corrected by introducing an inner region of size \(O(\epsilon ^3) \times O(\epsilon ^3)\) in which the free surface turns over, ejecting fluid into the splash sheet. The thin, fast-moving splash sheet region is of size \(O(\epsilon ) \times O(\epsilon ^3)\), emanating across the surface of the plate from the inner region. In the following derivation, we assume that the splash jet does not detach from the plate.
In the present analysis, we shall consider the outer, inner and splash sheet regions in detail; however, we forgo an analysis for the outer–outer region as it does not contribute to the leading-order hydrodynamic force on the plate.
3.3 Outer region
Guided by a well-known scaling argument [22], in the outer region, we set
and expand \((\hat{\phi }, \, \hat{h}, \, \hat{p}, \, d, \, s) = (\hat{\phi }_0, \, \hat{h}_0, \, \hat{p}_0, \, d_0, \, s_0) + o(1)\) as \(\epsilon \rightarrow 0\). The resulting governing equations in the outer region are
where (23) is Laplace’s equation for \(\hat{\phi }_0\), (24) is the kinematic boundary condition on the plate, (25) is the kinematic boundary condition at the free surface and (26) is the dynamic boundary condition at the free surface, where (26) is found by integrating the leading-order Bernoulli equation (19) with respect to time and applying the initial condition for \(\hat{\phi }_0\).
The far-field conditions as we tend towards the outer–outer region state that, to leading order, the flow is travelling downwards with unit speed and the free surface is parabolic in \(\hat{r}\), such that
with subsequent initial conditions
In addition, the so-called Wagner condition is needed in order to match to the inner solution:
which states that, at leading order, the free surface meets the plate at the turnover curve [23]. Finally, matching with the inner region reveals that \(\hat{\phi }_0 = O(\sqrt{d_0(t) - \hat{r}})\) as \(\hat{r}\rightarrow d_0(t)^-\), as in the classical Wagner regime [23].
Following [41], it is useful to consider the variational formulation of the axisymmetric problem by introducing the leading-order displacement potential, \(\varUpsilon _0\), as follows:
which is governed by the equations
such that the displacement potential is \(\varUpsilon _0 = O((d_0(t) -\hat{r}))^{3/2})\) as \(\hat{r}\rightarrow d_0(t)^-\). The far-field condition for \(\hat{\phi }_0\) (27) implies that \(\varUpsilon _0\) is bounded as \(\sqrt{\hat{r}^2 + \hat{z}^2} \rightarrow \infty \), which means a separable solution for \(\varUpsilon _0\) can be found via
where \(J_0\) is a Bessel function of the first kind and \(\nu (\lambda , t)\) is a coefficient function found by solving the dual-integral equations necessary to satisfy (32) and (34), namely
We refer to previous studies [39, 42] for further details.
Evaluating (35) along the plate and expanding as \(\hat{r}\rightarrow d_0(t)^-\), we find
Hence, to enforce \(\varUpsilon _0 = O((d_0(t) - \hat{r})^{3/2})\) as \(\hat{r}\rightarrow d_0(t)^-\) means that we must have
Note that if the plate is stationary, \(s_0(t) \equiv 0\) and we recover the classical Wagner solution \(d_0(t) = \sqrt{3t}\) [43]. Clearly, when the plate is compliant, the displacement of the plate is expected to slow down the spreading of the droplet, at least for times early enough that \(s_0(t) > 0\). It is well known that the Wagner problem is unstable under time reversal [23], which means the solution breaks down if \(\dot{d}_0(t) \le 0\). We, therefore, assume that \(\dot{s}_0(t) < 1\) in order for the velocity of the turnover curve, \(\dot{d}_0(t) = \sqrt{3} (1 - \dot{s}_0(t)) / (2 \sqrt{t - s_0(t)})\), to remain positive.
Finally, since it is necessary to calculate the hydrodynamic force on the plate F(t), we use the leading-order form of the Bernoulli equation (19) to find the pressure on the plate
where \(d_0(t)\) is given in terms of \(s_0(t)\) in (38). Note that this solution diverges as \(\hat{r}\rightarrow d_0(t)\).
3.4 Inner region
Since the pressure is locally singular, there is an inner region moving with the turnover curve at \(r = \epsilon d(t)\) and the surface of the plate at \(z = - \epsilon ^2 s(t)\). The appropriate scalings are given by [23]
Under these scalings, it is straightforward to show that to leading-order, the plate is stationary in the inner region. Hence, as described in detail in [39], the leading-order inner problem is quasi-two-dimensional in each plane perpendicular to it, and is given by
subject to appropriate matching conditions into the outer region,
and towards the splash sheet
where J(t) is referred to as the asymptotic sheet thickness.
The solution to this problem is well known [25], and given parametrically by
where \(\zeta \in \mathbb {C}\), \(\mathfrak {I}(\zeta ) > 0\), \(a(t) \in \mathbb {C}\) is an arbitrary function of time, the branch cuts for \(\log (\zeta )\) and \(\sqrt{\zeta }\) are taken along \(\mathfrak {R}(\zeta ) < 0, \mathfrak {I}(\zeta ) = 0\) and \(\mathfrak {R}\), \(\mathfrak {I}\) denote the real and imaginary parts of a complex number.
To match with the leading-order outer solution, we take \(|\zeta | \rightarrow \infty \) in (47), which yields
Thus, comparing (48) with (37) gives the leading-order sheet thickness
Again note that as \(d_0(t) = \sqrt{3(t - s_0(t))}\), the displacement of the plate slows the spreading of the droplet, which leads to a thinner splash sheet. This is consistent with the findings of [8], who showed that soft substrates inhibit splashing. Note that the derivative of the sheet thickness \(\dot{J}(t) = \sqrt{3} (1 - \dot{s}_0(t))\sqrt{t - s_0(t)} / \pi \) is positive for all t, so the sheet thickness will still increase for all time within the Wagner model.
The leading-order pressure in the inner region is
Along the surface of the plate, where \(\tilde{z}= 0\), this solution is given parametrically by
where \(d_0(t)\) and J(t) are given in terms of \(s_0(t)\) in (38) and (49), respectively.
3.5 Splash sheet region
Upon impact, the fluid is ejected from the inner region into a thin, fast-moving sheet of fluid attached to the plate. In this region, we rescale
As described in detail by [40], the leading-order splash sheet problem for the radial velocity \(\bar{u}_0 = \partial \bar{\phi }_0 / \partial \bar{r}\) and free surface height \(\bar{h}_0\) reduces to the zero-gravity shallow-water equations. These equations can be solved using the method of characteristics, and the solution is, as derived in [39, 40],
where \(0< \tau < t\).
The subsequent solution for the pressure in the splash sheet region is found by differentiating the Bernoulli equation (19) with respect to z, expressing in the splash sheet variables, and expanding to leading-order, such that
Integrating with respect to \(\bar{z}\) and noting that \(\bar{p}_0 = 0\) at \(\bar{z}= \bar{h}_0\) means the leading-order pressure along the plate is
It is worth noting that in the classical case of a stationary plate, where \(s_0(t) \equiv 0\), the leading-order pressure (55) would be zero and instead \(\bar{p}= O(\epsilon ^2)\). Therefore, the velocity \(\dot{s}_0(t)\) and acceleration \(\ddot{s}_0(t)\) of the plate increase the magnitude of the pressure in the splash sheet region. In particular, if \(\dot{s}_0(t) \partial \bar{u}_0 / \partial \bar{r}- \ddot{s}_0(t) < 0\), the leading-order pressure would be below atmospheric pressure, which could provide a possible mechanism for splash sheet detachment. However, the contribution the pressure in the splash sheet region makes to the leading-order force is still \(O(\epsilon ^3)\), which is lower in magnitude than the contributions from the outer and inner regions, so we shall neglect it henceforth in this analysis.
3.6 Composite pressure
Classically, the hydrodynamic force is determined by integrating only the outer pressure (39) for \(0 \le \hat{r}< d_0(t)\) [40]. However, as will be discussed in Sect. 6, we find better agreement with the numerical simulations at later times by using the composite expansion between the outer and inner regions. Van Dyke’s matching principle [44] is used to find the overlap function between the outer and inner solutions for \(r < \epsilon d_0(t)\). By evaluating the time derivatives in (39), the one-term-outer pressure is
Expressing this in the inner variables and expanding to leading order give the overlap pressure
Therefore, the composite expansion for p(r, 0, t) is
where H is the Heaviside step function, \(\hat{p}_0\) is given by (39) and \(\tilde{p}_0\) by (51).
Analytical solutions for the pressure for \(\epsilon = 0.1\) at \(t = 5\), with the left-hand side black lines showing the stationary plate case, \(s_0(t) = 0\) (mirrored about the line \(r = 0\)), and the right-hand side grey lines the moving plate case, \(s_0(t) = 0.02 t^2\). The outer solution for the pressure (39) is shown by the dashed lines, the inner solution (51) by the dotted lines and the composite solution (58) by the solid lines. The thin vertical dashed lines show the location of the turnover curve \(r = \epsilon d_0(t)\)
The composite pressure profile (58) depends on the plate displacement \(s_0(t)\), which is solved for in Sect. 3.8 once the hydrodynamic force is determined. However, in order to illustrate the effects of a moving substrate on the pressure, we compare its value in the case where the plate is stationary (\(s_0(t) \equiv 0\)) to that of a prescribed moving plate case where \(s_0(t) = 0.02 t^2\). Note that this value for \(s_0(t)\) is chosen for illustrative purposes and is not a solution to (12) and only satisfies the assumption that \(\dot{s}_0(t) < 1\) for \(t < 25\).
We compare the solutions at \(t=5\) in Fig. 3, where the left-hand-side black lines show the outer, inner and composite solutions to the pressure for the stationary plate case (mirrored about the line \(r = 0\)), and the right-hand side grey lines show the corresponding values for the moving plate case. The vertical dashed lines show the location of the turnover curve at \(r = \epsilon d_0(t)\), and it can be seen that that the turnover curve in the moving plate case has advanced less than in the stationary plate case, as according to (38). The pressure in the moving plate case is significantly lower overall than in the stationary plate case. This shows how the downwards motion of the plate does not only slow the spreading, but also decreases the hydrodynamic pressure inside the droplet. Also noteworthy is that the inner solution under-estimates the solution away from the turnover curve in the stationary plate case, but over-estimates it in the moving plate case.
3.7 Hydrodynamic force
In order to solve (12) for the displacement of the plate s(t), the value of the hydrodynamic force, F(t), needs to be determined to leading order. We approximate the force by integrating the composite expansion to the pressure (58) across the outer and inner regions. The composite expansion for the force is, hence,
where \(\eta _0(t)\) is defined implicitly by
where the detailed derivation can be found in Appendix A.
We highlight that the composite force \(F_{\text {comp}}(t)\) differs from the force on a stationary plate if and only if the turnover curve \(d_0(t)\) or sheet thickness J(t) differs from their corresponding stationary plate values.
3.8 Plate displacement solution
The remaining unknown from Sect. 3.3 to 3.7 is the leading-order plate displacement \(s_0(t)\), where \(s_0(t)\) appears in the solution (38) for the turnover curve \(d_0(t)\) and in the solution (49) for the jet thickness J(t). The plate displacement is found by solving the second-order ordinary differential equation (12), approximating the force term F(t) by the composite force \(F_{\text {comp}}(t)\) (59). The resulting equation is non-linear and implicit and is solved using MATLAB’s ode15i solver in conjunction with the fsolve solver to find \(\eta _0(t)\) via (60) at each timestep. As the value of \(\dot{d}_0(t)\) diverges at \(t = 0\), the numerical scheme is initialised at a time \(t = t_i = 10^{-9}\), with zero initial guesses for \(s_0(t_i) = \dot{s}_0(t_i) = \ddot{s}_0(t_i) = 0\). A small-time asymptotic analysis of the plate displacement reveals that \(s_0(t) = O(t^{5/2})\) as \(t \rightarrow 0\), so the problem is regular and we are hence justified in taking zero initial guesses. The results will be discussed in comparison to the full DNS in Sect. 5.
For \(\epsilon = 0.1\), the numerical solution for \(s_0(t)\) is found for \(0 \le t \le 100\) on 1 CPU in approximately 10 s. In comparison, the DNS results in Sect. 5 required approximately 24 CPU hours for the same dimensionless timescale, hence finding a numerical approximation to the analytical solution is significantly less computationally expensive than the DNS and a valuable first incursion into the parameter space, providing much-needed direction for the heavier numerical machinery.
4 Direct numerical simulations
We build on the open-source, volume-of-fluid package Basilisk [20] to implement this complex multi-phase system, retaining effects due to viscosity and density in both the liquid and the gas, as well as surface tension and gravity. Basilisk, and its predecessor Gerris [19], have been used extensively to study interfacial flows, and in particular droplet impact, with great success over the past two decades, cross-fertilising investigative efforts within experimental, analytical and computational communities alike [13,14,15, 21, 27].
4.1 Moving frame coordinates
In order to avoid including an embedded boundary in the quadtree-structured computational domain, we transfer the flow into a frame moving with the plate, fixing the plate along the bottom computational boundary. The dimensionless moving frame coordinates are defined by \(\mathbf{x} ' = (x', y', z') = \mathbf{x} + \mathbf{s} (t)\), \(\mathbf{u} ' = \mathbf{u} + \dot{\mathbf{s }}(t)\), where \(\mathbf{s} (t) = (0, 0, s(t))\), and the prime \('\) decorates all quantities in the moving frame. Introducing the dimensionless variable density \(\rho '(\mathbf{x} ', t)\) and viscosity \(\mu '(\mathbf{x} ', t)\), such that, following notation from Sect. 2.1, \(\rho ' = 1\), \(\mu ' = 1\) in the liquid and \(\rho ' = \rho _R\), \(\mu ' = \mu _R\) in the gas, the dimensionless governing equations in the moving frame are given by
where \(\kappa '\) is the radius of curvature of the free surface, \(\delta _s'\) is a Dirac distribution centred on the liquid-gas free surface and \(\hat{\mathbf{n }}'\) is the unit normal to the interface. Note that the kinematic condition (63) is that of a stationary plate, and the problem in the moving frame is equivalent to a droplet impacting onto a stationary plate, with the liquid and gas under additional forcing equal to \(\rho ' \ddot{\mathbf{s }}(t)\). In the far field, we assume that the pressure tends to 0 (neglecting variations due to gravity) and the vertical velocity tends to \(\mathbf{u} ' \rightarrow \dot{\mathbf{s }}(t)\). The prime notation is dropped for the remainder of this section for brevity.
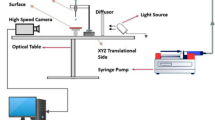
4.2 Computational setup
In all our simulations, we consider a droplet with dimensional radius \(R^*_d = 1\) mm initially travelling vertically downwards at speed \(V^* = 5\) m/s, where the values of Re, We and Fr\(^2\), \(\rho _R\), \(\mu _R\), are given in Sect. 2.2. The radius of the plate is taken to be twice the initial radius of the droplet, so that \(R_p = 2\), and the initial separation between the bottom of the droplet and top of the plate is \(\delta ^* = 0.125 R^*_d = 0.125\) mm. The values of the mass ratio \(\alpha \), damping factor \(\beta \) and stiffness factor \(\gamma \) are varied across different parametric studies.
Direct numerical simulation setup at \(t = t_0 = -0.125\), for a droplet of (non-dimensional) unit radius, separated from the plate by a distance of 0.125 and travelling with a vertical velocity \(-\,1\). The inset shows a snapshot of a simulation at \(t = 0.045\) close to the surface, in the region indicated by the grey rectangle. The colour map illustrates the adaptive mesh refinement strategy, while the black line depicts the location of the interface
The dimensionless governing equations (61)–(62) are solved using Basilisk within an axisymmetric domain, where the droplet initially has unit dimensionless radius, travelling with uniform vertical velocity \(-1\). The axisymmetric computational domain for the simulations is shown in Fig. 4. The domain is given by a square box, with the r axis along the bottom boundary and the z axis along the left boundary. The side length of the domain is set to \(L = 6\), which is sufficiently large so that far-field conditions do not artificially alter the target dynamics. Neumann conditions \(\partial _n \mathbf{u} = 0\) are specified along the top and right boundaries, where \(\partial _n\) is the partial derivative in the normal direction to the boundary. The vertical velocity along the right boundary is specified as \(u_z = \dot{s}(t)\), to reflect the far-field velocity condition. The appropriate symmetry conditions are applied along the left boundary. A mixed boundary condition is specified along \(z = 0\), with \(u_z = 0\) for \(r \le R_p\) and \(u_z = \dot{s}(t)\) for \(r > R_p\), the former representing the kinematic condition along the plate (63) and the latter representing the far-field condition. The no-slip condition \(u_r = 0\) and a 90\(^{\circ }\) contact angle are applied along the bottom boundary. Finally, the pressure p in the gas is set to to be zero along the top and right boundaries in line with the far-field condition (8).
The quadtree grid construction features in Basilisk allow for a high grid resolution in areas of interest, varying from levels 5 to 13, where level n corresponds to \(2^n\) square cells per dimension, if the grid was uniform. In this case, the largest cell has side length \(6 / 2^5\), corresponding to 0.188 mm in dimensional terms. The smallest cell has side length \(6 / 2^{13}\), corresponding to \(0.732\,\upmu \)m. In order to accurately calculate the force on the plate, a region along the bottom boundary for \(0 \le r \le R_p\) of height \(24/2^{13}\) (\(\approx \) 2.93 \(\upmu \)m in dimensional terms) is held at level 13, such that the bottom four grid cells in this region are at maximum level. This avoids numerical errors induced by multi-grid interpolation in a region which requires particular care due to the delicate fluid–structure interaction calculations outlined below. Adaptive mesh refinement is also used to refine the domain in regions where the velocities and interface location are rapidly changing. An example of the typical grid structure is shown in the inset of Fig. 4.
At regular timesteps \(\varDelta t = 10^{-4}\) (corresponding to 20 ns in dimensional terms), the hydrodynamic force applied to the surface of the plate, F(t), is determined by numerically integrating the pressure, p, and the viscous stress, \(-2 \mu \partial u_z/\partial z\), along the bottom boundary for \(0 \le r \le R_p\). This value of the force is then used to solve the dimensionless plate displacement equation (12) using a second-order finite difference scheme, giving \(s(t), \dot{s}(t)\) and \(\ddot{s}(t)\). The boundary conditions are then updated with the new value of \(\dot{s}(t)\), and the vertical acceleration in all of the cells is incremented by \(\rho \ddot{s}(t)\).
Several computational details are noteworthy in terms of ensuring a robust fluid–structure interaction calculation procedure. As observed in other studies on droplet impact [21], numerical instabilities in the projection solver used for the resulting Poisson equation within Basilisk may cause the calculated pressure values to fluctuate between timesteps, thus, causing the resulting force values to vary artificially. These pressure spikes lead to artefacts in the finite difference scheme, which can ultimately result in the simulation breaking down due to diverging acceleration terms. To prevent this, we use a peak-detection algorithm [45] to identify numerical spikes and smooth out the resulting force. Spatial filtering is also used to manage the contrast in density and viscosity between the liquid and gas phases. Furthermore, any small gas bubbles or liquid drops that have a diameter smaller than sixteen level 13 cells (corresponding to \(\approx \) 10 \(\mu \)m in dimensional terms) are deemed unphysical and dynamically removed, with the exception of the entrapped gas bubble centred at \(r = z = 0\).
The simulations span 0.8 dimensionless time units, corresponding to 0.2 ms in dimensional time. During this timescale, the end of the splash sheet typically reaches \(r \approx 1.9\), close to the edge of the plate, and the turnover curve reaches \(r \approx 1.3\). The early impact stage can be considered over long before the turnover curve surpasses the initial droplet radius; hence, we also capture timescales beyond when we expect the analytical results to be valid. Each individual simulation consisted in approximately 60, 000 (dynamically adapted) degrees of freedom and was executed in parallel on 4–8 CPUs, for approximately 24 CPU hours on local high-performance computing facilities.
4.3 Numerical validation
As will be demonstrated in the following section, the excellent agreement between analytical and numerical results gives us encouragement that the simulations are converging to the correct solution. However, in order to ensure computational robustness, we have also conducted a comprehensive validation study, confirming that the results in Sect. 5 are mesh independent at the selected refinement level, as well as insensitive to further increases in the computational domain size, adjustment of the initial droplet height or width of the plate, where the reader is directed to Appendix B for details. We concluded that taking a maximum level of 13 was sufficient and insensitive to further refinement. We are, thus, confident in proceeding with a comprehensive parametric study, exploring the solution space with both analytical and computational approaches.
5 Results and comparisons
The aim of this section is twofold: first, to systematically compare the predictions of the analytical model from Sect. 3 to the results of the numerical simulations from Sect. 4, identifying timescales during which good agreement is observed and, second, to provide insight into the physical mechanisms introduced once substrate motion is allowed, systematically showing how the mass ratio \(\alpha \), damping factor \(\beta \) and stiffness factor \(\gamma \) affect the dynamics of the system. To facilitate the comparison of the analytical and numerical results, we re-express all quantities into the original non-dimensional variables from Sect. 2.1, transforming from the asymptotic variables \(t = \epsilon ^2 \hat{t}\) in Sect. 3.1 and the primed moving frame variables in Sect. 4.1. All simulations were conducted for \(-\,0.125 \le t \le 0.675\).
(Top) Comparison of the hydrodynamic force F(t) between the stationary plate case (black) and a moving plate (grey) with mass ratio \(\alpha = 2\), damping factor \(\beta = 0\), stiffness factor \(\gamma = 500\), with a dashed line for the analytical solution from (59) and a solid line for the corresponding numerical value. (Middle) Displacement of the moving plate case s(t), with the dashed line showing the analytical solution to (12) and the solid line depicting the corresponding numerical results. (Lower panels) DNS-calculated pressure p comparison between the stationary plate case (left) and the moving plate case (right) at times labelled 1–4 in the plots above. An animation of the pressure fields shown in the lower panels is provided as electronic supplementary material, shown alongside the corresponding analytical results for the pressure along the plate \(p(r, -s(t), t)\) and plate displacement s(t)
5.1 Stationary plate comparison
In order to understand the influence the motion of the plate has on the system, we must compare to the case where the plate is held in a stationary position. In particular, we wish to find where the hydrodynamic force on the plate F(t) differs from the corresponding value for the stationary plate case, allowing us to identify where the plate motion has a strong influence on the dynamics of the droplet.
The analytical and numerical predictions for the hydrodynamic force F(t) and the plate displacement s(t) for \(\alpha = 2, \beta = 0, \gamma = 500\) are shown in Fig. 5, alongside the corresponding analytical and numerical predictions for the stationary plate case. Under no damping or hydrodynamic forcing, the plate displacement s(t) in (12) would oscillate about \(s(t) = 0\) with a natural time period \(T = 2 \pi \sqrt{\alpha /\gamma } \approx 0.397\). The parameters \(\alpha \) and \(\gamma \) are chosen so T is of the same order of magnitude as the timescale of the simulation \(-0.125 \le t \le 0.675\). In dimensional terms, this system corresponds to an aluminium plate of radius 2 mm, thickness \(\approx \) 0.06 mm and spring constant \(k^*\approx \) 12.5 N/m. In Fig. 5, snapshots of the simulations at the points in time labelled 1–4 in the graphs are shown in the panels, with the left-hand panels showing the stationary plate case, the right-hand panels showing the moving plate case and the colour map showing the pressure distribution in each. The computed value of the viscous stress along the plate in the DNS was typically < 0.1% of the pressure; hence, the dominant contribution to the numerical results for the force F(t) was due to the pressure itself. Supplementary video material depicting both analytical and computational results for this test case has also been made available.
Point 1 (\(t = 0.015\)) in Fig. 5 is shortly after the impact of the droplet. Here, the value of F(t) for the moving plate is close to that of the stationary plate, as the plate has only deformed to within a distance of \(O(10^{-3})\) of its initial location, and it can be seen in the panels in Fig. 5 that the pressure distribution for both cases is similar. The plate displaces downwards until around \(t = 0.25\), at which point the strength of the elastic restoring force, \(\gamma s(t)\), causes the plate to recoil. Shortly after this, at point 2 (\(t = 0.295\)), the graphs in Fig. 5 show that the hydrodynamic force in the moving plate case is greater than the stationary plate case, due to the stronger pressure that can be seen in the panels. The plate subsequently moves upwards into the droplet until around \(t =0.5\), when the elastic force balances with the hydrodynamic force and the plate begins to accelerate downwards again. The hydrodynamic force reaches a local minimum at point 3 (\(t = 0.535\)). Point 4 (\(t = 0.675\)) marks the end point of the simulations, but it can be extrapolated from the graphs in Fig. 5 that this oscillatory behaviour would continue for later times.
The analytical solutions in Fig. 5 show excellent agreement with the numerical results up until close to point 2 at \(t = 0.295\). This is remarkable, as the analytical model makes the assumption that \(t \ll 1\), and that the radius of the turnover curve remains small compared to the droplet radius; however, the panels show that the turnover curve at point 2 is close to \(r = 0.75\).
Both the value of the plate displacement s(t) and the difference in the location of the fluid interfaces in the graphs and snapshots shown in Fig. 5 are small in comparison to the size of the droplet. Hence, upon experimental observation, the physical system may not appear different to the stationary plate case. However, the oscillations in the hydrodynamic force and the pressure differences in the snapshots show that flow inside the droplet is being significantly affected by the motion of the plate. This shows that just introducing substrate motion due to linear elasticity results in a substantial change in the dynamics of the droplet.
5.2 Plate parameter comparisons
In Sect. 5.1, we showed in detail how the system behaves for specific values of the mass ratio \(\alpha \), damping factor \(\beta \) and stiffness factor \(\gamma \). In the following, we aim to study physical mechanisms represented by these parameters individually.
In order to systematically observe the effects of these physical mechanisms, we conducted a series of simulations for \(-0.125 \le t \le 0.675\) with varying values of \(\alpha \), \(\beta \) and \(\gamma \). The hydrodynamic force F(t) was calculated regularly and is shown by the solid grey-scale lines in Fig. 6, where darker lines correspond to higher values of \(\alpha \), \(\beta \) or \(\gamma \). For comparison, the solid black line and dashed line correspond to the numerical and analytical hydrodynamic force for the stationary plate case. Analytical solutions for the rest of the cases are not shown for visual clarity on the plots; however, an analysis similar to that presented in Sect. 5.1 could be conducted for all each value of \(\alpha \), \(\beta \) and \(\gamma \).
Numerical results for the hydrodynamic force on the plate F(t) computed via DNS, with solid grey lines showing moving plate cases with varying values of the mass ratio \(\alpha \), damping factor \(\beta \) and stiffness factor \(\gamma \), and solid black lines showing the stationary plate case. The black dashed lines indicate the analytical solution to F(t) for a stationary plate given by (59). a \(\beta \) = \(\gamma \) = 0, and \(\alpha \) ranges from 1 to 100. b \(\alpha \) = 2, \(\gamma = 100\) and \(\beta = 0\), \(0.25 \beta _c\), \(\beta _c\) and \(5 \beta _c\), with critical damping value \(\beta _c = 2 \sqrt{\alpha \gamma } \approx 28.28\). c \(\alpha = 2\), \(\beta = 0\) and \(\gamma \) ranges from 0 to 1000
The mass ratio \(\alpha = M^* / \rho ^*_l {R_d^*}^3\) represents (up to a constant) the ratio between the mass of the plate \(M^*\) and the mass of the droplet \(4 \pi \rho ^*_l {R_d^*}^3 / 3\). Upon impact, the pressure of the droplet exerts a hydrodynamic force onto the plate, causing it to accelerate downwards. The downwards motion of the plate causes the pressure at the surface of the plate to decrease, in turn decreasing the hydrodynamic force. For lighter plates (smaller \(\alpha \)), this downwards motion will be faster, and hence, we expect that the hydrodynamic force will be lower in lighter plates than for heavier ones. The mass ratio \(\alpha \) is varied from 1 to 100 in Fig. 6a, with \(\beta = \gamma = 0\). In these cases, the only force acting on the plate is the hydrodynamic force of the droplet from above; hence, the plate accelerates downwards at a rate depending on the mass ratio \(\alpha \). It can be seen from Fig. 6a that increasing \(\alpha \) causes the overall force to increase, tending towards the stationary plate value for large values of \(\alpha \). In addition, the time at which the hydrodynamic force reaches a maximum increases as \(\alpha \) increases, which happens once the plate has accelerated to its maximum velocity, resulting in a lower hydrodynamic force. It takes longer for this to happen the heavier the plate is; hence, the time at which the maximum is reached increases as \(\alpha \) increases.
The damping factor \(\beta \) determines the amount of resistance to motion the dashpot exerts. We note that the ODE for the plate displacement (12) under no external forcing has a critical damping value of \(\beta = \beta _c = 2 \sqrt{\alpha \gamma }\). If this unforced system was displaced from its equilibrium position and released, the undamped system (\(\beta = 0\)) would experience oscillations of a fixed amplitude about the equilibrium point. For \(0< \beta < \beta _c\), the system would be underdamped, and the amplitude of the oscillations would decay at a rate increasing with \(\beta \). If \(\beta > \beta _c\), the system would be overdamped and would exponentially return to equilibrium, returning more slowly with increasing \(\beta \). Finally, if \(\beta = \beta _c\), the system would be critically damped and would return to the equilibrium in the fastest time. However, inclusion of the hydrodynamic forcing will alter these dynamics, and, in particular, we expect that higher values of \(\beta \) would lead to smaller displacements from equilibrium due to the resistance to motion. In Fig. 6b, the mass ratio and stiffness factor are fixed at \(\alpha = 2\), \(\gamma = 100\) such that the critical damping value is \(\beta _c = 20 \sqrt{2} \approx 28.28\). The grey-scale lines show the values of force for \(\beta = 0\), \(0.25 \beta _c\), \(\beta _c\) and \(5 \beta _c\). For \(\beta = 0\), we can clearly see oscillations in the force, and the amplitude of these oscillations decreases when the system is underdamped for \(\beta = 0.25 \beta _c\). These oscillations are suppressed in the case of critical damping \(\beta = \beta _c\), where the force follows a trend that is initially lower than the stationary plate value, whereas the force approaches the stationary plate value for the overdamped case \(\beta = 5 \beta _c\). Since the force depends predominantly on the hydrodynamic pressure in the droplet, the fact that the force follows the same behaviour of under-, over- and critical damping shows the strong influence the dashpot has on the behaviour of the droplet.
The strength of the elastic force from the compression of the spring is represented by the stiffness factor \(\gamma \). In the absence of damping and external forcing, the solution of (12) for s(t) would oscillate with a dimensionless time period \(T = 2 \pi \sqrt{\alpha /\gamma }\); hence, an increase in the stiffness factor results in the oscillations having a shorter time period. The spring does work on the droplet via a vertical force equal to \(\gamma s(t)\), so the droplet loses kinetic energy depending on how far below the z axis the plate is displaced. Unlike damping, the elastic force is conservative, meaning the loss of kinetic energy from the droplet due to the elasticity is converted into potential energy in the spring, which is then in turn converted into kinetic energy via oscillations. Figure 6c shows the hydrodynamic forces in systems for mass ratio and damping factor \(\alpha = 2\) and \(\beta = 0\), with stiffness factor \(\gamma \) varying from 0 to 1000. As expected, we observe that the time periods of the oscillations decrease as \(\gamma \) increases in Fig. 6c. For the two highest \(\gamma \) values (500 and 1000), it can be seen that the values of F(t) oscillate centred on the force value for the stationary plate case. This suggests that as \(\gamma \) increases, although the frequency of oscillations increases, the amplitude of the oscillations would decrease and eventually the force would tend to the stationary plate value.
Although the analytical solution was only shown for the stationary plate case in Fig. 6, it is worth noting the good agreement that this solution has with the numerical values at early times for the majority of the moving plate cases shown. At early times, the velocity of the plate is still small; hence, it does not significantly alter the hydrodynamic force. It is only once the plate has been accelerated that its motion affects the hydrodynamic force by doing work on the liquid.
5.3 Pressure along the plate
In the previous subsections, we highlighted how the dominant contribution to the force on the plate F(t) in the simulations shown in Fig. 6 was from the pressure along the plate \(p(r, -s(t), t)\), with the viscous stress only contributing \(\approx \) 1%. Hence, in order to better understand the contributing factors to the force, we now focus on the dynamics of the pressure along the plate.
As mentioned in Sect. 4, the projection solver used by Basilisk to determine the pressure is prone to numerical instabilities localised in time, making it occasionally difficult to accurately represent certain quantities such as the pressure at a particular point in the domain over long periods of time without noise, a behaviour also noted in previous studies of droplet impact (see, e.g. the appendix of [21]). Other quantities that are used extensively in the analytical solution, such as the turnover curve d(t) and jet thickness J(t), are also difficult to extract at early times when the contract region spans a small number of computational grid cells. These quantities are readily solved for using the analytical model; hence, we will use the analytical solutions derived in Sect. 3 in the following subsection to study quantities that would otherwise be difficult to obtain from the DNS at very early times.
As an example, we select three sets of parameters shown in Fig. 6 with \(\alpha = 2\): \((\beta , \gamma ) = (0, 0)\), \((\beta , \gamma ) = (0, 100)\) and \((\beta , \gamma ) = (28.28, 100)\), with the first representing a case without elasticity or damping, the second an oscillatory case without damping and finally a critically damped case. To gain insight into the evolution of the pressure, we use the composite expansion (58) to determine the pressure at the centre of the plate \(p(0, -s(t), t)\) and the maximum pressure along the plate \(p_{\text {max}}(t)\), and plot these alongside the plate displacement s(t) from (12) and the turnover curve d(t) from (38) in Fig. 7a for the three parameter cases and the stationary plate case. It can be seen that the pressure evolution is substantially different between the cases, with a notable reduction in pressure for the case \((\beta , \gamma ) = (0, 0)\), as well as clear oscillations in the pressure at the centre of the plate for the case \((\beta , \gamma ) = (0, 100)\).
Analytical predictions for the pressure at the centre of the plate \(p(0, -s(t), t)\), the maximum pressure \(p_{\text {max}}(t)\), the plate displacement s(t) and the turnover curve d(t) according to (58), (12) and (38) for various parameter values. The stationary plate case is plotted in solid lines, cases with mass ratio \(\alpha = 2\) are plotted in row (a) and cases with mass ratio \(\alpha = 0.1\) are plotted in row (b). The grey boxes in (b) indicate the temporal region shown in Fig. 8
From the comparison between the analytical and numerical solutions in Fig. 5, we expect the analytical solution to be most accurate for early times, and in particular for \(t \lesssim 0.1\). The differences between the cases shown in Fig. 7a are most apparent after this time, so we now instead focus on a set of parameters where the differences are visible on this early timescale. To achieve this, we choose a small value of the mass ratio \(\alpha = 0.1\) with \((\beta , \gamma ) = (0, 0)\), \((\beta , \gamma ) = (0, 25)\) and \((\beta , \gamma ) = (3.16, 25)\), which again correspond to a case without elasticity or damping, an oscillatory case without damping and a critically damped case. The same quantities as before are plotted for these cases in Fig. 7b. The smaller mass ratio results in the pressure being significantly reduced in all cases, with it even becoming less than zero for the \((\beta , \gamma ) = 0\) case. This results in a substantial plate displacement s(t), which is again most pronounced in the \((\beta , \gamma ) = (0, 0)\) case. In all three cases, the turnover curve at \(r = d(t)\) evolves more slowly when compared to its stationary plate counterpart, showing that the plate motion hinders the spread of the droplet.
The grey boxes on the \(p(0, -s(t), t)\) and \(p_{\text {max}}(t)\) graphs of Fig. 7b show the timescale from \(t = 0\) to \(t = 0.1\). The full pressure along the plate, \(p(r, -s(t), t)\) from (58) for this timescale for all the \(\alpha = 0.1\) cases is shown in Fig. 8. The lines are plotted at regular time intervals from \(t = 0.001\) to 0.1, with the left-hand sides showing the stationary plate case mirrored about \(r = 0\) and the right-hand sides showing the \((\beta , \gamma ) = (0, 0)\), \((\beta , \gamma ) = (0, 25)\) and \((\beta , \gamma ) = (3.16, 25)\) cases. The vertical dashed lines indicate the position of the turnover curve at \(r = d(t)\) and the arrow indicates increasing time. The figure shows that the reduction in pressure due to plate motion occurs across the whole plate, not just at the origin and the maximum point as shown in Fig. 7b. It is also clearly visible how much the droplet spreading is slowed in comparison to the stationary plate case, most pronounced for the \((\beta , \gamma ) = (0, 0)\) case.
Analytical predictions for the pressure along the plate \(p(r, -s(t), t)\) according to (58), plotted at regular time intervals from \(t = 0.001\) to 0.1, with the arrow indicating increasing time and the vertical dashed lines showing the location of the turnover curve at \(r = d(t)\), given by (38). Left-hand sides: Predictions for the stationary plate case where \(s(t) \equiv 0\), mirrored about \(r = 0\). Right-hand sides: Predictions for mass ratio \(\alpha = 0.1\) and a selection of values for damping factor \(\beta \) and stiffness factor \(\gamma \)
We observe in Figs. 7 and 8 that the motion of the plate can cause a significant reduction in the pressure in the droplet. Not only this, but it can also slow down the spreading of the droplet, as seen by a decrease in the value of d(t). The combination of these factors gives insight into the evolution of the value of the computationally determined force F(t) shown for various parameters in Fig. 6, as the dominant contribution to F(t) in the simulations was the integral of \(p(r, -s(t), t)\) across the plate surface. In particular, small values of F(t) could either be due to a reduction of the pressure, a slowing of the turnover curve d(t), or a combination of both.
We underline that in all of the investigated cases, the evolution of the turnover curve at \(r = d(t)\) was slower than the corresponding stationary plate scenario. The consequence of this fact is that the plate motion always acts to slow the spread of the droplet, as opposed to accelerating the spread. This means any case shown in Fig. 6 where the the value of F(t) was greater than the stationary plate case would be due to an increase in the pressure, as opposed to a faster spread across the surface of the plate.
In this section, we have shown the rich variety in behaviours that the system exhibits as a result of the individual physical contributions due to the mass of the plate, strength of the dashpot and stiffness of the spring. These physical mechanisms result in previously unreported changes in the droplet dynamics, such as pressure oscillations which can be suppressed by energy losses due to damping, a reduction in the overall pressure along the plate and a slowing of the droplet spreading. Although the magnitude of the plate displacement is small in comparison to the length scale of the droplet in all cases, the strong coupling observed between the plate displacement s(t) and the hydrodynamic force F(t) justify making use of models where the fluid–structure interaction is retained in order to accurately predict the dynamics of the droplet over these timescales.
6 Summary and discussion
In this paper, we have presented two models for the vertical impact of a droplet onto a plate supported by a spring and a dashpot: an analytical model using matched asymptotic expansions and a full computational framework based on DNS. Although droplet impact onto elastic beams has been considered previously [37], the analytical model we present is the first to consider the Wagner theory formulation where the substrate experiences both elastic forcing and damping. As opposed to previous axisymmetric models [37, 40], we approximate the hydrodynamic force on the substrate using the leading-order composite expansion of the pressure between the outer and inner region (rather than just the outer region). Significantly, we found that the composite force shown in Fig. 5 is within 10% of the numerical solution up to \(t \approx 0.2\), in contrast to the force contribution due to the outer region only remains within 10% of the numerical solution up to \(t \approx 0.04\), which justifies considering the contributions from the inner region in order to extend the timescale in which such analytical models are valid more generally. Previous numerical investigations involving a plate-spring system [34] do not take into account forcing due to damping, and focus on the late-time dynamics of spreading and rebound, whereas we focus on the influence the plate motion has on the delicate early stages of impact in a high-speed context. Finally, the response of an elastic substrate on an impacting droplet has very recently been modelled using an effective boundary condition on the pressure in order to consider a stationary computational domain [8]. By contrast, in our model, the substrate motion is resolved by using a moving frame of reference centred on the surface of the substrate, fully representing the fluid–structure interaction.
The two proposed methodologies are distinct in their approach to understanding the system, and yet they are stronger in combination. In a problem with such violent topological changes over short scales, it is vital to have analytical results to both validate and inform our DNS platform. The analytical model provides guidance into key quantities, such as the location of the turnover curve, which can be used as a prediction for the simulation duration and refinement strategy. In addition, the analytical model can be used to rapidly search for parameters where interesting coupling between the droplet and plate can be observed, rather than spending considerable computational resources searching for these regimes numerically. However, the analytical model relies on a series of assumptions, such as neglecting viscosity, surface tension and gravity, and is limited to early impact times. On its own, it is impossible to assess the consequence of these assumptions, and where they break down. By systematically comparing the analytical predictions to the numerical model, we can identify the regimes where these assumptions are valid and support the use of the analytical model as opposed to the costly DNS. If desired, the DNS can then be used to go beyond those regimes and study timescales inaccessible to the analytical model. It is only when used in conjunction that the predictive power and robustness of these models reach their full potential.
Not only have the methods presented in this paper extended existing analytical and numerical models, but they have also allowed us to provide physical insight into the dynamics of a novel, complex multi-phase system. We recognise that the displacement of the plate and perturbation of the free surface of the droplet are small; hence, these models provide insight into a physical regime that would otherwise be very difficult to study experimentally. In particular, in Fig. 5, 7 and 8 we observed significant alterations of the pressure inside the droplet due to the motion of the plate both numerically and analytically – a quantity which would be difficult to measure experimentally. Through an extensive parameter study, we identified the influence that the mass ratio \(\alpha \), damping factor \(\beta \) and stiffness factor \(\gamma \) have on the hydrodynamic force exerted by the droplet. In particular, we found that lighter plates (smaller \(\alpha \)) result in a lower value of the force; stiffer springs (higher \(\gamma \)) result in oscillations of higher frequency and that resistive dashpots (higher \(\beta \)) suppress the oscillations due to the elasticity from the spring.
The plate-spring-dashpot system is one of the simplest models for a flexible substrate, as it only allows for vertical motion. Droplet impact onto the end of a cantilever, such as a leaf, is more complex as the bending of the beam breaks the axisymmetry. However, as considered in [7], the deflection of the end of the beam can be modelled using the second-order differential equation (12) when the deflection is small (hence negligible bending). Therefore, the model for the substrate motion considered in this paper could provide insight into the early time dynamics of droplet impact onto the end of cantilever beams. In addition, there is much scope to extend these models to more complex substrates, such as elastic membranes under tension, as previously studied experimentally [9], further guided by recent analytical [37] and computational [31, 32] progress. In conclusion, we believe that the proposed mathematical framework embodies productive co-development and investigative interplay between rigorous state-of-the-art methodologies, providing a general and highly efficient route to studying complex systems involving fluid–structure interaction in the future.
References
Hoath SD (2016) Fundamentals of inkjet printing, 1st edn. Wiley, Weinheim
Smith DB, Askew SD, Morris WH, Shaw DR, Boyette M (2000) Droplet size and leaf morphology effects on pesticide spray deposition. Trans Am Soc Agric Eng 43(2):255–259
Murphy DW, Li C, D’Albignac V, Morra D, Katz J (2015) Splash behaviour and oily marine aerosol production by raindrops impacting oil slicks. J Fluid Mech 780:536–577
Antonini C, Amirfazli A, Marengo M (2012) Drop impact and wettability: from hydrophilic to superhydrophobic surfaces. Phys Fluids 24(10):102104
Ellis AS, Smith FT, White AH (2011) Droplet impact on to a rough surface. Q J Mech Appl Math 64(2):107–139
Gilet T, Bourouiba L (2014) Rain-induced ejection of pathogens from leaves: revisiting the hypothesis of splash-on-film using high-speed visualization. Integr Comp Biol 54(6):974–984
Gart S, Mates JE, Megaridis CM, Jung S (2015) Droplet impacting a cantilever: a leaf-raindrop system. Phys Rev Appl 3(4):044019
Howland CJ, Antkowiak A, Castrejón-Pita JR, Howison SD, Oliver JM, Style RW, Castrejón-Pita AA (2016) It’s harder to splash on soft solids. Phys Rev Lett 117(18):184502
Pepper RE, Courbin L, Stone HA (2008) Splashing on elastic membranes: the importance of early-time dynamics. Phys Fluids 20(8):082103
Josserand C, Thoroddsen S (2016) Drop impact on a solid surface. Annu Rev Fluid Mech 48(1):365–391
Visser CW, Frommhold PE, Wildeman S, Mettin R, Lohse D, Sun C (2015) Dynamics of high-speed micro-drop impact: numerical simulations and experiments at frame-to-frame times below 100 ns. Soft Matter 11(9):1708–1722
Li EQ, Thoraval MJ, Marston JO, Thoroddsen ST (2018) Early azimuthal instability during drop impact. J Fluid Mech 848:821–835
Cimpeanu R, Moore MR (2018) Early-time jet formation in liquid–liquid impact problems: theory and simulations. J Fluid Mech 856:764–796
López-Herrera JM, Popinet S, Castrejón-Pita AA (2019) An adaptive solver for viscoelastic incompressible two-phase problems applied to the study of the splashing of weakly viscoelastic droplets. J Non-Newtonian Fluid Mech 264:144–158
Thoraval MJ, Takehara K, Etoh TG, Popinet S, Ray P, Josserand C, Zaleski S, Thoroddsen ST (2012) Von Kármán vortex street within an impacting drop. Phys Rev Lett 108(26):264506
Thoroddsen ST, Etoh TG, Takehara K, Ootsuka N, Hatsuki Y (2005) The air bubble entrapped under a drop impacting on a solid surface. J Fluid Mech 545(–1):203–212
Hicks PD, Purvis R (2010) Air cushioning and bubble entrapment in three-dimensional droplet impacts. J Fluid Mech 649:135–163
Thoroddsen ST, Takehara K, Etoh TG (2012) Micro-splashing by drop impacts. J Fluid Mech 706:560–570
Popinet S (2003) Gerris: a tree-based adaptive solver for the incompressible Euler equations in complex geometries. J Comput Phys 190(2):572–600
Popinet S (2015) A quadtree-adaptive multigrid solver for the Serre–Green–Naghdi equations. J Comput Phys 302:336–358
Philippi J, Lagrée PY, Antkowiak A (2016) Drop impact on a solid surface: short-time self-similarity. J Fluid Mech 795:96–135
Howison SD, Ockendon JR, Oliver JM, Purvis R, Smith FT (2005) Droplet impact on a thin fluid layer. J Fluid Mech 542:1–23
Howison SD, Ockendon JR, Wilson SK (1991) Incompressible water-entry problems at small deadrise angles. J Fluid Mech 222(–1):215–230
Scolan YM, Korobkin AA (2001) Three-dimensional theory of water impact. Part 1. Inverse Wagner problem. J Fluid Mech 440:293–326
Wagner H (1932) Über Stoß- und Gleitvorgänge an der Oberfläche von Flüssigkeiten. Z Angew Math Mech (ZAMM) 12(4):193–215
Eggers J, Fontelos MA, Josserand C, Zaleski S (2010) Drop dynamics after impact on a solid wall: theory and simulations. Phys Fluids 22(6):062101
Wildeman S, Visser CW, Sun C, Lohse D (2016) On the spreading of impacting drops. J Fluid Mech 805:636–655
Weisensee PB, Tian J, Miljkovic N, King WP (2016) Water droplet impact on elastic superhydrophobic surfaces. Sci Rep 6(1):30328
Li L, Sherwin SJ, Bearman PW (2002) A moving frame of reference algorithm for fluid/structure interaction of rotating and translating bodies. Int J Numer Methods Fluids 38(2):187–206
Peskin CS (2002) The immersed boundary method. Acta Numer 11(January 2002):479–517
Patel HV, Das S, Kuipers JA, Padding JT, Peters EA (2017) A coupled volume of fluid and immersed boundary method for simulating 3D multiphase flows with contact line dynamics in complex geometries. Chem Eng Sci 166:28–41
Sun X, Sakai M (2016) Numerical simulation of two-phase flows in complex geometries by using the volume-of-fluid/immersed-boundary method. Chem Eng Sci 139:221–240
Xiong Y, Huang H, Lu XY (2020) Numerical study of droplet impact on a flexible substrate. Phys Rev E 101(5):1–15
Zhang C, Wu Z, Shen C, Zheng Y, Yang L, Liu Y, Ren L (2020) Effects of eigen and actual frequencies of soft elastic surfaces on droplet rebound from stationary flexible feather vanes. Soft Matter 16(21):5020–5031
Blowers RM (1969) On the response of an elastic solid to droplet impact. IMA J Appl Math 5(2):167–193
Korobkin AA (1998) Wave impact on the center of an Euler beam. J Appl Mech Tech Phys 39(5):770–781
Pegg M, Purvis R, Korobkin A (2018) Droplet impact onto an elastic plate: a new mechanism for splashing. J Fluid Mech 839:561–593
Wilson SK (1991) A mathematical model for the initial stages of fluid impact in the presence of a cushioning fluid layer. J Eng Math 25(3):265–285
Moore MR (2014) New mathematical models for splash dynamics. PhD thesis, University of Oxford
Oliver JM (2002) Water entry and related problems. Thesis, Oxford University, p 150
Korobkin AA (1982) Formulation of penetration problem as a variational inequality. Din Sploshnoi Sredy 58:73–79
Sneddon IN (1966) Mixed boundary value problems in potential theory. North-Holland, Amsterdam
Wilson SK (1989) The mathematics of ship slamming. PhD thesis, University of Oxford
Van Dyke M (1975) Perturbation methods in fluid mechanics. Parabolic Press, Stanford
van Brakel JP (2014) Robust peak detection algorithm (using z-scores). https://stackoverflow.com/questions/22583391/peak-signal-detection-in-realtime-timeseries-data
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Below is the link to the electronic supplementary material.
Supplementary material 1 (mp4 1636 KB)
Appendices
Appendix A: Composite hydrodynamic force
For the analytical model, the hydrodynamic force is determined by integrating the pressure p across the surface of the plate. As the leading-order solution in the outer region (39) diverges at the turnover curve, the force contribution close to the turnover curve must be an over-estimate. Hence, the leading-order composite pressure between the outer and the inner regions was found in Sect. 3.6 in order to determine the resulting composite force, where the force contribution from the splash sheet region was determined to be negligible. When viscosity is neglected, the dimensionless hydrodynamic force on the plate (10) is given by
The composite force is found by integrating the composite pressure (58) along the surface of the plate, which is determined by splitting the range of the integral across the respective asymptotic regions,
where \(F_{\text {outer}}(t)\) and \(F_{\text {inner}}(t)\) are the result of integrating the leading-order outer pressure (39) and inner pressure (51), respectively, and \(F_{\text {overlap}}(t)\) is the result of integrating the overlap pressure (57). The resulting force due to the outer region is, hence,
For \(F_{\text {inner}}(t)\), the integration variable is changed to the parameter \(\eta \) from (51). Then, \(\eta _0(t)\) is defined such that \(r = 0\) for \(\eta = \eta _0(t)\), i.e.
where \(\eta _0(t)\) must be solved for numerically for each t. Note that \(\eta \rightarrow -\infty \) as \(r \rightarrow \infty \), where \(\tilde{p}_0\) decays exponentially. Hence, we take the upper limit of the integral to be \(r = \infty \), which introduces exponentially small errors. The resulting force due to the inner region is, hence,
Finally the overlap force is
Combining (66), (68) and (69), the composite force is
where \(d_0(t)\) and J(t) are given by (38) and (49), respectively.
Appendix B: Direct numerical simulation validation
Given the complexity of our computational framework, prior to the comparisons and excellent agreement between the analytical and numerical results shown in Sect. 5, we have made significant efforts to ensure the robustness and mesh independence of our output. This is particularly important in the context of the numerical approach retaining effects that are neglected in the analytical model, such as the action of the surrounding gas.
A key quantity in our analysis is the force on the plate, F(t), and here, we show the convergence of the results as the maximum grid refinement level is varied. We discuss two specific parametric cases: the stationary plate case (where \(s(t) \equiv 0\)), and a representative moving plate case where \(\alpha = 2\), \(\beta = 7.07\) and \(\gamma = 100\). For all cases, the force F(t) was extracted at regular intervals of \(\varDelta t = 10^{-4}\), running from non-dimensional \(t = -0.125\) to \(t = 0.675\), giving a total of 8001 data points. We recall that a cell at spatial refinement level m has width equal to \(\varDelta r = L / 2^m\), where \(L = 6\) is the width of the computational domain. For each case, five simulations were studied, varying the maximum refinement level from \(m = 10\) (with \(\varDelta r \approx 5.86 \times 10^{-3}\)) to \(m = 14\) (with \(\varDelta r \approx 3.66 \times 10^{-4}\)). For reference, if the grids were uniform at level m, then \(m = 10\) would introduce \(\approx \) 171 cells per droplet radius, whereas \(m = 14\) would have \(\approx \) 2731 cells per droplet radius. Thus, even our lowest level setting contains considerable detail, while the most stringent grid refinement scenario ensures significant resources are deployed to capture the target impact dynamics. The associated results are summarised in Fig. 9a and b, respectively.
Numerical solutions for the force on the plate \(F_m(t)\) at maximum refinement level m varied between 10 and 14 for two cases: (left) stationary plate and (right) a moving plate setup. The insets illustrate the \(L_2\)-norm of the difference between solutions with maximum level m and the reference maximum level 14 results across the entire simulation timescale, with the discrete \(L_2\)-norm is defined in (71)
Due to the complexity of these scenarios and the absence of an analytical solution incorporating full non-linearity, the influence of the surrounding gas and topological changes such as entrapped bubble formation, we measure how close the results of the simulations align to the most refined case with maximum level 14 as a benchmark. Hence, we define the discrete \(L_2\)-norm of the difference between cases with maximum level m and the reference level 14 scenario across the full simulation timescale to be
where \(t_n\) is the discretised time value and \(N = 8001\) is the total number of timesteps, such that \(t_N = t_{\text {max}}\). The \(L_2\)-norm for each case is shown in the insets of Fig. 9a and b. As can be seen, the \(L_2\)-norm rapidly decreases, with diminishing returns after a maximum level of 12. We are hence confident that the scheme has converged and opted to keep the a maximum level of 13 throughout Sect. 5, which includes a variety of parametric studies. We believe this to be a viable balance between the capability to explore our problem space in detail and computational cost. For context, each level increase in the maximum allowed refinement level results in a roughly fourfold increase in the number of degrees of freedom (roughly due to the advantages of using mesh adaptivity), as well as a halving of the associated timestep in order to ensure stability of the underlying numerical scheme.
We have have also conducted similar analyses for the width of the computational domain, initial height of the droplet and width of the plate, and concluded that the scheme is insensitive to further changes in these values. These studies ultimately contributed to a systematically constructed and thoroughly validated numerical framework, which was essential to furthering our understanding of this challenging fluid–structure interaction problem.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Negus, M.J., Moore, M.R., Oliver, J.M. et al. Droplet impact onto a spring-supported plate: analysis and simulations. J Eng Math 128, 3 (2021). https://doi.org/10.1007/s10665-021-10107-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10665-021-10107-5