1 Introduction

We investigate the propagation and interaction of weakly nonlinear elastic plane waves in transversely isotropic media. Our aim is to reveal the difference in the shear waves’ behaviour in anisotropic versus isotropic materials. We are interested in weakly nonlinear effects. It is known that a quadratic nonlinearity is present only in quasi-longitudinal waves when we restrict ourselves to isotropic materials [1]. The “weakest” type of nonlinearity which is manifested by shear waves propagation is cubic in such materials [2, 3]. However, anisotropy and in particular the presence of fibres changes this situation. The coupling of shear waves on a quadratically nonlinear level is possible when a special direction of propagation in anisotropic materials is chosen [3,4,5]. Here, we demonstrate that the quadratic nonlinearity may show up even for a single shear wave propagation due to the presence of fibres. It seems that this fact has not been discussed before. To show the appearance of the quadratic nonlinearity for shear waves propagating in anisotropic materials, we use a weakly nonlinear asymptotics method. We analyse particularly simple models of transversely isotropic materials. We study fibre-reinforced materials in which the strain energy function decouples into the part representing a matrix material and the other part which represents the properties of reinforcing fibres that are embedded in the matrix. For simplicity, we choose models in which the anisotropic part of the energy function depends on only one strain invariant. This is the so-called standard reinforcing model [6], some properties of which were discussed in [7].

The paper is organized as follows. In the next section, we display the explicit forms of the stored energy function for our model. Section 3 is devoted to the equations of elastodynamics. We describe plane waves as solutions of the first-order quasilinear system of partial differential equations. We present stored energy functions for plane waves with nonlinear terms up to the third order. This is sufficient to capture the quadratically nonlinear effect in elastic waves’ interactions.

In the following section, we determine the eigensystem for the linearised equations of plane waves. The obtained eigenvectors are then used in Sect. 5 to define three-wave interaction coefficients. These are calculated to reveal the difference between the isotropic and transversely isotropic models.

In Sect. 6, we apply the method of weakly nonlinear asymptotics [5] in order to derive the evolution equation for a single quasi-shear wave for our model of transversely isotropic materials. It turns out that for almost all range of parameters, we obtain the inviscid Burgers’ equation. This result is in total contrast to the isotropic case, where the equation with quadratic nonlinearity cannot describe any shear wave propagation. We finish the section with an example of numerical solutions for the obtained evolution equation. The paper is ended with concluding remarks.

2 Hyperelastic material model

In this section, we define hyperelastic material models considered in the next part of the article. Firstly, we discuss an isotropic model which is a generalization of well-known Ciarlet model [8]. It states a simple example of a model with a polyconvex stored energy function. Secondly, a transversely isotropic model is presented as an extension of the isotropic one. The resulting stored energy function also fulfils the polyconvexity condition.

2.1 Isotropic material model

A stored energy function \(W\) of a hyperelastic material model should satisfy certain mathematical conditions [9]. One of them is polyconvexity, which means that there exists a convex function \({\mathcal {W}}\) such that

$$\begin{aligned} W({\mathbf {F}})={\mathcal {W}}({\mathbf {F}},\text {Cof}\,{\mathbf {F}},\det {{\mathbf {F}}}), \end{aligned}$$
(1)

where \({\mathbf {F}}\) is a deformation gradient and ‘Cof’ stands for cofactor. In the special case of isotropy [10], polyconvex potentials of hyperelasticity may be constructed as a sum of convex functions \({\hat{W}}_i(I_i),\quad i=1,2,3\)

$$\begin{aligned} W({\mathbf {F}})={\hat{W}}(I_1,I_2,I_3)={\hat{W}}_1(I_1)+{\hat{W}}_2(I_2)+{\hat{W}}_3(I_3), \end{aligned}$$
(2)

where \(I_i\) are the basic invariants of the right Cauchy–Green deformation tensor \({\mathbf {C}}={\mathbf {F}}^\mathrm{{T}}{\mathbf {F}}\)

$$\begin{aligned} I_{1}=\mathrm {tr}\left( {\mathbf {C}}\right) ,\quad I_{2}=\frac{1}{2}\left( I_{1}^{2}-\mathrm {tr}\left( {\mathbf {C}}^2\right) \right) ,\quad J=\sqrt{I_{3}}=\det {{\mathbf {F}}}. \end{aligned}$$
(3)

One of the simplest polyconvex stored energy function which also meets certain growth conditions is a potential proposed by Ciarlet in the form

$$\begin{aligned} {\hat{W}}(I_1,I_2,J)=aI_{1}+bI_{2}+cJ^2-d\ln {J}-(3a+3b+c) \end{aligned}$$
(4)

with positive constants. In the article, we consider a generalized model such that [11]

$$\begin{aligned} W_{\mathrm{{iso}}}\left( I_{1},I_{2},J \right) =a\left( I_{1}-3\right) +b\left( I_{2}-3\right) +c\left( I_{1}-3\right) ^2+\alpha (J) \end{aligned}$$
(5)

with a convex function \(\alpha \) satisfying

$$\begin{aligned} \frac{\partial \alpha (J)}{\partial J}\Bigr |_{J=1}=-2a-4b. \end{aligned}$$
(6)

The model provides a richer description considering a shear deformation in comparison to the Ciarlet one. A particular choice of the convex function is given by

$$\begin{aligned} \alpha (J)=d (J^2-1)-2(a+2b+d)\ln {J}. \end{aligned}$$
(7)

To ensure the polyconvexity of the model, we assume that the parameters satisfy the following conditions: \(a,b,d>0,c\ge 0.\)

2.2 Transversely isotropic material model

We assume that the stored energy function \(W\) for transversely isotropic models consists of two separate isotropic and anisotropic parts [12]

$$\begin{aligned} W=(1-p)W_\mathrm{{iso}}\left( I_{1},I_{2},J \right) +p W_{fib}\left( I_{4} \right) . \end{aligned}$$
(8)

Here \(p\in (0,1)\) stands for the volume fraction of the fibre family in a unit of a material volume. The invariant \(I_4\) is given by

$$\begin{aligned} I_{4}=\mathrm {tr}\left( {\mathbf {M}}{\mathbf {C}}\right) \end{aligned}$$
(9)

with \({\mathbf {M}}={\mathbf {m}}\otimes {\mathbf {m}}\), where \({\mathbf {m}}\) defines a direction of a fibre family in a reference configuration. We are particularly interested in the following special form of the anisotropic part

$$\begin{aligned} W_{fib}\left( I_{4} \right) =\frac{E_{z}}{4}\left( I_{4}-1\right) ^2 \end{aligned}$$
(10)

together with the isotropic part defined by (5). Parameter \(E_{z}>0\) is interpreted as the initial Young’s modulus of the fibre family. Additionally, the quadratic approximation of the stored energy function (5) shows that the bulk initial modulus and the first Lamé constant of the isotropic matrix are given by

$$\begin{aligned} K_{0}=\frac{4}{3}(a+4b+6c+3d),\quad \lambda _{0}=4(b+2c+d). \end{aligned}$$
(11)

The function (8), defined with a help of (5) and (10), is polyconvex because of the fact that it is constructed as a sum of the convex functions as follows:

$$\begin{aligned} {\hat{W}}(I_1,I_2,I_3,I_4)={\hat{W}}_1(I_1)+{\hat{W}}_2(I_2)+{\hat{W}}_3(I_3)+{\hat{W}}_4(I_4), \end{aligned}$$
(12)

and \(I_4\) is convex with respect to \({\mathbf {F}}\) [13]. We emphasize that the quadratic approximation of (8) with respect to the Lagrangian strain tensor \({\mathbf {E}}\) does not lead to the Hooke’s law of transversely isotropic model with five independent constants [14] because of the lack of \(I_1I_4\) term. Such case does not result in a polyconvex stored energy function so it is not considered here.

Transversely isotropic models are widely applied in modelling textile membrane structures as well as soft tissues [15]. The theory of finite deformations of elastic materials reinforced by fibres was mainly developed by Spencer [16] and extended among others by Spencer and Soldatos in [17].

A model of the form similar to (8) is discussed in [18,19,20] in terms of loss of ellipticity, see also [21]. However, our model contains the additional parameter \(p\), which controls the volumetric content of fibres in the material.

3 Dynamics of elastic materials

In this section, we present the equations of elastodynamics. Our aim is to study propagation of weakly nonlinear waves in models with the stored energy function defined in Sect. 2. The dynamics of hyperelastic solids is governed by the equation of motion which written in the Lagrangian coordinates has the form

$$\begin{aligned} \rho _{0}\frac{\partial {\mathbf {u}}^2}{\partial t^2}=\text {Div}\,{\mathbf {S}}. \end{aligned}$$
(13)

Here \(\rho _0\) is a mass density in the reference configuration, \({\mathbf {u}}={\mathbf {u}}\left( t,{\mathbf {X}}\right) \) is a displacement vector, \({\mathbf {S}}\) is the first Piola–Kirchhoff stress tensor. In hyperelasticity, the existence of stored energy function \(W\) is assumed. Then, \({\mathbf {S}}\) can be expressed in terms of \(W\) as

$$\begin{aligned} {\mathbf {S}}=\frac{\partial W}{\partial {\mathbf {F}}}, \end{aligned}$$
(14)

where \({\mathbf {F}}\) is the deformation gradient.

The assumption of polyconvexity implies in particular that equations of elastodynamics are hyperbolic [1]. It means that the elastic waves propagate with finite, real speeds.

3.1 First-order system for plane waves

It is convenient to transform the elastodynamics equations into a first-order system to analyse their mathematical properties

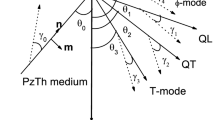
$$\begin{aligned} \rho _{0}\frac{\partial {\mathbf {v}}}{\partial t}=\text {Div}\,{\mathbf {S}},\quad \frac{\partial {\mathbf {F}}}{\partial t}=\text {Grad}\,{\mathbf {v}}. \end{aligned}$$
(15)

Here \({\mathbf {v}}\) is the velocity vector. We have 12 equations with 12 unknowns which are components of the velocity vector and the deformation gradient. We are interested in plane waves so we reduce the equations to a \(6\times 6\) system for such waves. Let \({\mathbf {n}}\) be an arbitrary given unit vector. We consider the motion of the form

$$\begin{aligned} {\mathbf {x}}={\mathbf {X}}+{\mathbf {u}}\left( t,x \right) , \end{aligned}$$
(16)

where \({\mathbf {x}}\) denotes the Eulerian and \({\mathbf {X}}\) the Lagrangian position vector with \(x=~{\mathbf {n}}\cdot {\mathbf {X}}\). Let us define the displacement gradient vector as

$$\begin{aligned} {\mathbf {g}}\left( t,x \right) =\frac{\partial {\mathbf {u}}\left( t,x \right) }{\partial x}. \end{aligned}$$
(17)

Since \({\mathbf {F}}=\partial {{\mathbf {x}}}/\partial {{\mathbf {X}}}\), differentiating (9) with respect to \({\mathbf {X}}\) and taking into account (17), we get

$$\begin{aligned} {\mathbf {F}}={\mathbf {I}}+{\mathbf {g}}\otimes {\mathbf {n}}. \end{aligned}$$
(18)

Now, we reduce the system (15) for plane motion (9)

$$\begin{aligned} \text {Div}\,{\mathbf {S}}=\frac{\partial {\mathbf {S}}}{\partial x}{\mathbf {n}},\quad \text {Grad}\,{\mathbf {v}}=\frac{\partial {\mathbf {v}}}{\partial x}\otimes {\mathbf {n}},\quad \frac{\partial {\mathbf {F}}}{\partial t}=\frac{\partial {\mathbf {g}}}{\partial t}\otimes {\mathbf {n}}. \end{aligned}$$
(19)

Next, we define the reduced stress vector by

$$\begin{aligned} {\mathbf {s}}({\mathbf {g}})={\mathbf {S}}({\mathbf {F}}){\mathbf {n}}={\mathbf {S}}({\mathbf {I}}+{\mathbf {g}}\otimes {\mathbf {n}}){\mathbf {n}}. \end{aligned}$$
(20)

Then, taking into account (19), we obtain from (15) the plane waves system

$$\begin{aligned} \rho _{0}\frac{\partial {\mathbf {v}}}{\partial t}=\frac{\partial {\mathbf {s}}({\mathbf {g}})}{\partial x},\quad \frac{\partial {\mathbf {g}} }{\partial t}=\frac{\partial {\mathbf {v}}}{\partial x}. \end{aligned}$$
(21)

In parallel with the definition of the reduced stress vector, we define the reduced stored energy function as

$$\begin{aligned} V({\mathbf {g}})=W({\mathbf {F}})=W({\mathbf {I}}+{\mathbf {g}}\otimes {\mathbf {n}}). \end{aligned}$$
(22)

Using this definition and (14), we can now write the system (21) as

$$\begin{aligned} \rho _{0}\frac{\partial {\mathbf {v}}}{\partial t}=\frac{\partial }{\partial x}\left( \frac{\partial V}{\partial {\mathbf {g}}}\right) ,\quad \frac{\partial {\mathbf {g}} }{\partial t}=\frac{\partial {\mathbf {v}}}{\partial x}. \end{aligned}$$
(23)

3.2 Quasilinear hyperbolic system

The system (23) may be written in the quasilinear form as

$$\begin{aligned} \frac{\partial {\mathbf {w}}}{\partial t}+{\mathbf {A}}({\mathbf {w}})\frac{\partial {\mathbf {w}}}{\partial x}={\mathbf {0}}, \end{aligned}$$
(24)

where

$$\begin{aligned} {\mathbf {w}}=\begin{bmatrix} {\mathbf {v}}(t,x) \\ {\mathbf {g}}(t,x)\end{bmatrix}, \quad {\mathbf {A}}({\mathbf {w}})=-\begin{bmatrix} {\mathbf {0}} &{} \frac{1}{\rho _{0}}{\mathbf {G}}({\mathbf {g}})\\ {\mathbf {I}} &{} {\mathbf {0}} \end{bmatrix}. \end{aligned}$$
(25)

The symmetric acoustic tensor

$$\begin{aligned} {\mathbf {G}}=\frac{\partial {\mathbf {s}}}{\partial {\mathbf {g}}}=\frac{\partial ^2 V}{\partial {\mathbf {g}}\otimes \partial {\mathbf {g}}} \end{aligned}$$
(26)

has components in the Cartesian coordinates of the form

$$\begin{aligned} G_{ij}=\frac{\partial ^2 V}{\partial g_i \partial g_j}, \quad i,j=1,2,3. \end{aligned}$$
(27)

In the case of isotropy with \({\mathbf {n}}=[1,0,0]^\mathrm{{T}}\), the explicit form of the reduced stored energy function (22) is given by

$$\begin{aligned} {\hat{V}}({\mathbf {g}})=(a+b)(2g_{1}+\Vert {\mathbf {g}}\Vert ^2)+b(2g_{1}+g_{1}^2)+4cg_1(g_{1}+\Vert {\mathbf {g}}\Vert ^2)+{\hat{\alpha }}\left( g_{1}\right) , \end{aligned}$$
(28)

where \(\Vert \cdot \Vert \) denotes the Euclidean norm and we restrict ourselves to at most cubic terms. Here \({\hat{\alpha }}\) function is a cubic approximation of \(\alpha \). Hence, a representation of acoustic tensor \({\mathbf {G}}({\mathbf {0}})\) contains at most linear terms

$$\begin{aligned} {\mathbf {G}}({\mathbf {g}})=\begin{bmatrix} 2 a+4 b+24 c g_1+{\hat{\alpha }}''(g_1) &{} 8cg_2 &{} 8cg_3 \\ 8cg_2 &{} 2 (a+b+4cg_1) &{} 0 \\ 8cg_3 &{} 0 &{} 2 (a+b+4cg_1) \\ \end{bmatrix}. \end{aligned}$$
(29)

In the case of transversely isotropic model under assumptions \({\mathbf {m}}=[\cos \phi ,\sin \phi ,0]^{T}\) and \({\mathbf {n}}=[1,0,0]^{T}\), the stored energy function yields

$$\begin{aligned} \begin{aligned} {\hat{V}}({\mathbf {g}})&=(1-p)\left[ (a+b)(2g_{1}+\Vert {\mathbf {g}}\Vert ^2)+b(2g_{1}+g_{1}^2)+4cg_1(g_{1}+\Vert {\mathbf {g}}\Vert ^2)+{\hat{\alpha }}\left( g_{1}\right) \right] \\ {}&+pE_z \cos {\phi } (g_1 \cos {\phi }+g_2 \sin {\phi })^2 \left[ (1+g_1) \cos {\phi }+g_2 \sin {\phi }\right] . \end{aligned} \end{aligned}$$
(30)

Here the components of \({\mathbf {G}}({\mathbf {g}})\) are expressed by

$$\begin{aligned} \begin{aligned} G_{11}&=2\left( 1-p\right) \left[ a+2b+4c+12cg_1+{\hat{\alpha }}''\left( g_1\right) \right] +\,2E_{z}p\cos ^3\phi \left[ \left( 1+3g_1\right) \cos \phi +3g_2\sin \phi \right] ,\\ G_{22}&=2\left( 1-p\right) \left( a+b+4cg_1\right) +\,E_{z}p\left[ \left( 1+3g_1\right) \left( 1-\cos 4\phi \right) +3g_2\left( 2\sin 2\phi -3\sin 4\phi \right) \right] ,\\ G_{33}&=2\left( 1-p\right) \left( a+b+4cg_1\right) ,\\ G_{12}&=G_{21}=8\left( 1-p\right) cg_2+2E_{z}p\cos ^2\phi \sin \phi \left[ \left( 1+3g_1\right) \cos \phi +3g_2\sin \phi \right] ,\\ G_{13}&=G_{31}=8\left( 1-p\right) cg_3,\\ G_{23}&=G_{32}=0. \end{aligned} \end{aligned}$$
(31)

It is worth pointing out that the initial polyconvexity assumption is satisfied in a subset of admissible deformations if at most cubic terms of \({\mathbf {g}}\) are considered as it is in (28) or (30).

4 The eigensystem of matrix \({\mathbf {G}}(0)\)

From now on, we assume for simplicity that \(\rho _0=1\). In the following part of the article, we consider the eigenvalue problem for isotropic and transversely isotropic material models. Instead of analysing \({\mathbf {A}}({\mathbf {0}})\) from (25), it suffices to restrict ourselves to \({\mathbf {G}}({\mathbf {0}})\). We can use lemma 5.11 from [1] which states that the pairs \((\lambda _i,{\mathbf {r}}_i)\), i.e eigenvalues and eigenvectors of \({\mathbf {A}}\), are related to the pairs \((\kappa _i,{\mathbf {q}}_i)\) corresponding to \({\mathbf {G}}\) as Follows:

$$\begin{aligned} \lambda _1=-\sqrt{\kappa _1}=-\lambda _2,\quad \lambda _3=-\sqrt{\kappa _2}=-\lambda _4,\quad \lambda _5=-\sqrt{\kappa _3}=-\lambda _6 \end{aligned}$$
(32)

and

$$\begin{aligned} \begin{matrix} {\mathbf {r}}_1=\begin{bmatrix} \sqrt{\kappa _1}{\mathbf {q}}_1 \\ {\mathbf {q}}_1 \end{bmatrix},\\ \ \\ {\mathbf {r}}_2=\begin{bmatrix} -\sqrt{\kappa _1}{\mathbf {q}}_1 \\ {\mathbf {q}}_1 \end{bmatrix}, \end{matrix}\qquad \begin{matrix} {\mathbf {r}}_3=\begin{bmatrix} \sqrt{\kappa _2}{\mathbf {q}}_2 \\ {\mathbf {q}}_2 \end{bmatrix},\\ \ \\ {\mathbf {r}}_4=\begin{bmatrix} -\sqrt{\kappa _2}{\mathbf {q}}_2 \\ {\mathbf {q}}_2 \end{bmatrix}, \end{matrix}\qquad \begin{matrix} {\mathbf {r}}_5=\begin{bmatrix} \sqrt{\kappa _3}{\mathbf {q}}_3 \\ {\mathbf {q}}_3 \end{bmatrix},\\ \ \\ {\mathbf {r}}_6=\begin{bmatrix} -\sqrt{\kappa _3}{\mathbf {q}}_3 \\ {\mathbf {q}}_3 \end{bmatrix}. \end{matrix} \end{aligned}$$
(33)

The pair \((\kappa _1, {\mathbf {q}}_1)\) characterizes the quasi-longitudinal waves in terms of the speeds \(\pm \lambda _1\) and polarizations \({\mathbf {r}}_1, {\mathbf {r}}_2\). The second pair \((\kappa _2, {\mathbf {q}}_2)\) corresponds to the quasi-shear waves propagating with the speeds \(\pm \lambda _3\) and polarizations \({\mathbf {r}}_3,{\mathbf {r}}_4\). Finally, the third pair \((\kappa _3, {\mathbf {q}}_3)\) concerns the pure shear waves propagating with the speeds \(\pm \lambda _5\) and polarizations \({\mathbf {r}}_5, {\mathbf {r}}_6\).

4.1 Isotropic material model

Substituting \(p=0\) into (31), we obtain a representation of the acoustic tensor for the isotropic material model

$$\begin{aligned} {\mathbf {G}}({\mathbf {0}})=\begin{bmatrix} 2 a+4 b+8 c+{\hat{\alpha }}''(1) &{} 0 &{} 0 \\ 0 &{} 2 (a+b) &{} 0 \\ 0 &{} 0 &{} 2 (a+b) \\ \end{bmatrix}. \end{aligned}$$
(34)

The eigenvalue problem for \({\mathbf {G}}\left( {\mathbf {0}}\right) \) yields

$$\begin{aligned} \kappa _1= 2 a+4 b+8 c+{\hat{\alpha }}''(1)=4(a+2b+2c+d),\quad \kappa _2= \kappa _3=2 (a+b) \end{aligned}$$
(35)

with the corresponding eigenvectors

$$\begin{aligned} {\mathbf {q}}_1=\begin{bmatrix} 1 \\ 0\\ 0\end{bmatrix}, \quad {\mathbf {q}}_2=\begin{bmatrix} 0 \\ 1\\ 0\end{bmatrix}, \quad {\mathbf {q}}_3=\begin{bmatrix} 0 \\ 0\\ 1\end{bmatrix}. \end{aligned}$$
(36)

We emphasize that the result \(\kappa _2= \kappa _3\) is characteristic for isotropy [1] where quasi-shear and pure shear waves propagate with the same speed.

4.2 Transversely isotropic material model

For a treatment of a more general case, we consider the transversely isotropic material model given by (30). It yields

$$\begin{aligned} {\mathbf {G}}({\mathbf {0}})=\begin{bmatrix} G_{11} &{} 2 p E_z \sin {\phi } \cos ^3{\phi } &{} 0 \\ 2 p E_z \sin {\phi } \cos ^3{\phi } &{} G_{22} &{} 0 \\ 0 &{} 0 &{} 2(1-p)(a+b) \\ \end{bmatrix}, \end{aligned}$$
(37)

where

$$\begin{aligned} G_{11}= & {} 4(1-p)(a+2b+2c+d)+2 p E_z\cos ^4{\phi },\nonumber \\ G_{22}= & {} 2(1-p) (a+b)+\frac{1}{4}pE_z(1-\cos {4\phi }). \end{aligned}$$
(38)

Here, the eigenvalues of \({\mathbf {G}}({\mathbf {0}})\) are given by

$$\begin{aligned} \begin{aligned} \kappa _1&=\frac{1}{2}\left[ (1-p)\gamma +pE_{z}\left( 1+\cos {2 \phi }\right) +\sqrt{\delta }\right] ,\\ \kappa _2&=\frac{1}{2}\left[ (1-p)\gamma +pE_{z}\left( 1+\cos {2 \phi }\right) -\sqrt{\delta }\right] ,\\ \kappa _3&=2 (1-p) (a+b),\\ \delta&=4 \beta ^2-2 p \beta (4 \beta -E_{z})+p^2 \left( 4 \beta ^2+E_{z}^2-2 \beta E_{z}\right) \\ {}&\quad +\,E_{z} p \left[ 2 \cos {2 \phi } (2\beta +p (E_{z}-2 \beta ))+E_{z} p \cos ^2{2 \phi }-2 \beta (p-1) \cos {4 \phi }\right] ,\\ \beta&=a+3 b+4 c+2 d, \quad \gamma =6 a+10 b+8 c+4 d \end{aligned} \end{aligned}$$
(39)

with the corresponding eigenvectors

$$\begin{aligned} {\mathbf {q}}_1&=\begin{bmatrix} \dfrac{\zeta _{1}}{\sqrt{1+(\zeta _{1})^2}}\\ \dfrac{1}{\sqrt{1+(\zeta _{1})^2}}\\ 0\end{bmatrix}, \quad {\mathbf {q}}_2=\begin{bmatrix} \dfrac{\zeta _{2}}{\sqrt{1+(\zeta _{2})^2}} \\ \dfrac{1}{\sqrt{1+(\zeta _{2})^2}} \\ 0\end{bmatrix}, \quad {\mathbf {q}}_3=\begin{bmatrix} 0 \\ 0\\ 1\end{bmatrix} \end{aligned}$$
(40)

together with

$$\begin{aligned} \zeta _i=\dfrac{1}{2pE_z\cos {\phi }\sin ^3{\phi }}\left[ (1-p)\beta +\dfrac{1}{4}pE_z(1+2\cos {2\phi }+\cos {4\phi })+\dfrac{(-1)^{i+1}}{2}\sqrt{\delta }\right] . \end{aligned}$$
(41)

One may verify that \(\lim _{\phi \rightarrow 0^+}{\zeta _1}=+\infty \) and \(\lim _{\phi \rightarrow 0^+}{\zeta _2}=0\). Thus, it is worth to investigate the eigenvalues for characteristic values of \(\phi \) in terms of the fibre direction:

  • for \(\phi =0\) (wave propagation parallel to the fibre direction)

    $$\begin{aligned} \begin{aligned} \kappa _1&=(1-p) \left( 2 a+4 b+8 c+{\hat{\alpha }} ''(1)\right) +2pE_z,\\ \kappa _2&=\kappa _3=2(1-p)(a+b), \end{aligned} \end{aligned}$$
    (42)

  • for \(\phi =\frac{\pi }{2}\) (wave propagation perpendicular to the fibre direction)

    $$\begin{aligned} \kappa _1=(1-p) \left( 2 a+4 b+8 c+{\hat{\alpha }} ''(1)\right) , \quad \kappa _2=\kappa _3=2(1-p)(a+b) \end{aligned}$$
    (43)

    with the eigenvectors for both cases

    $$\begin{aligned} {\mathbf {q}}_1=\begin{bmatrix} 1 \\ 0\\ 0\end{bmatrix}, \quad {\mathbf {q}}_2=\begin{bmatrix} 0 \\ 1\\ 0\end{bmatrix}, \quad {\mathbf {q}}_3=\begin{bmatrix} 0 \\ 0\\ 1\end{bmatrix}. \end{aligned}$$
    (44)

We see that in the latter case the eigenvalues are equal up to the multiplier \( (1-p)\) to the eigenvalues for isotropy (35). It means that for this special direction the anisotropic part does not influence the eigenvalues. It is worth to notice that only three different wave speeds occur for a propagation along the principal axes.

5 Wave interaction coefficients

In this section, we are interested in revealing the difference between our isotropic and anisotropic models as far as the quadratic nonlinear interaction of plane waves is concerned. To measure this effect, we define (after [22]) wave interaction coefficients as follows:

$$\begin{aligned} \varGamma _{pq}^{j}={\mathbf {l}}_{j}\cdot \left( D_{{\mathbf {w}}}\mathbf {A({\mathbf {w}})r}_{p} \right) {\mathbf {r}}_q \vert _{{\mathbf {w}}={\mathbf {0}}}, \end{aligned}$$
(45)

where \({\mathbf {A}}\left( {\mathbf {w}}\right) \) is defined by (25) with \(\rho _0=1\), while \(\lambda _j,{\mathbf {l}}_j,{\mathbf {r}}_j\) are eigenvalues, and left and right eigenvectors of \({\mathbf {A}}({\mathbf {0}})\), respectively. These coefficients measure the strength of the interaction of \(p\) and \(q\) waves on the produced \(j\) wave. In particular, if \( j = p = q\), we obtain a self-interaction coefficient as \(\varGamma _{j}\equiv \varGamma _{jj}^{j}\). Next, we display a graphical representation of calculated coefficients in the figures below. This representation can be interpreted as follows. Each colour in the table \(\varGamma _{pq}^{j}\) denotes the nonzero value of the interaction coefficient which describes the strength of the interaction of \(p\) wave with \(q\) wave to produce \(j\) wave. For each new wave \(j= 1,2,\ldots ,6 \), we present a \(6\times 6\) table of interaction coefficients. The hyperelasticity assumption implies that \(\varGamma _{pq}^{j}=\varGamma _{qp}^{j}\) for all \(j,p,q=1,2,\ldots ,6\). Besides, the structure of the elastodynamics equations implies that \(\varGamma _{pq}^{j}=-\varGamma _{pq}^{j+1}\). Therefore, we display only the tables of coefficients \(\varGamma _{pq}^{j}\) with \(j = 1,3,5\) and \(p,q=1,2,\ldots ,6\).

5.1 Isotropy

In the case of isotropy, it is known [2] that there are only three different, nonzero values of the interaction coefficients. We calculate them explicitly, and the analytical formulae are as follows:

$$\begin{aligned}&\varGamma _1=-\varGamma _2=\frac{{\hat{\alpha }}^{'''}(1)+24 c}{2 \sqrt{{\hat{\alpha }}^{''}(1)+2 a+4 b+8 c}}, \end{aligned}$$
(46)
$$\begin{aligned}&\varGamma ^{1}_{33}=\frac{4 c}{\sqrt{{\hat{\alpha }}^{''}(1)+2 a+4 b+8 c}},\quad \varGamma ^{3}_{13}=\frac{2 \sqrt{2} c}{\sqrt{a+b}}. \end{aligned}$$
(47)

Apart from this, the following symmetry relations hold:

$$\begin{aligned} \begin{aligned} \varGamma ^{1}_{11}&=\varGamma ^{1}_{12}=\varGamma ^{1}_{21}=\varGamma ^{1}_{22}=-\varGamma ^{2}_{11}=-\varGamma ^{2}_{12}=-\varGamma ^{2}_{21}=-\varGamma ^{2}_{22},\\ \varGamma ^{1}_{33}&=\varGamma ^{1}_{34}=\varGamma ^{1}_{43}=\varGamma ^{1}_{44}=-\varGamma ^{2}_{33}=-\varGamma ^{2}_{34}=-\varGamma ^{2}_{43}=-\varGamma ^{2}_{44}\\&=\varGamma ^{1}_{55}=\varGamma ^{1}_{56}=\varGamma ^{1}_{65}=\varGamma ^{1}_{66}=-\varGamma ^{2}_{55}=-\varGamma ^{2}_{56}=-\varGamma ^{2}_{65}=-\varGamma ^{2}_{66},\\ \varGamma ^{3}_{13}&=\varGamma ^{3}_{14}=\varGamma ^{3}_{23}=\varGamma ^{3}_{24}=-\varGamma ^{4}_{13}=-\varGamma ^{4}_{14}=-\varGamma ^{4}_{23}=-\varGamma ^{4}_{24}\\&=\varGamma ^{3}_{31}=\varGamma ^{3}_{41}=\varGamma ^{3}_{32}=\varGamma ^{3}_{42}=-\varGamma ^{4}_{31}=-\varGamma ^{4}_{41}=-\varGamma ^{4}_{32}=-\varGamma ^{4}_{42}\\&=\varGamma ^{5}_{15}=\varGamma ^{5}_{16}=\varGamma ^{5}_{25}=\varGamma ^{5}_{26}=-\varGamma ^{6}_{15}=-\varGamma ^{6}_{16}=-\varGamma ^{6}_{25}=-\varGamma ^{6}_{26}\\&=\varGamma ^{5}_{51}=\varGamma ^{5}_{61}=\varGamma ^{5}_{52}=\varGamma ^{5}_{62}=-\varGamma ^{6}_{51}=-\varGamma ^{6}_{61}=-\varGamma ^{6}_{52}=-\varGamma ^{6}_{62}. \end{aligned} \end{aligned}$$
(48)

These relations between nonzero coefficients are shown in the form of tables in Figs. 1, 2, 3, where

(49)

We recall that numbers 1, 2 correspond to quasi-longitudinal waves, 3 and 4 to quasi-shear waves, and 5, 6 to pure shear waves. Since \(\varGamma _{5}=\varGamma _{6}=0\), there is no self-interaction between pure and quasi-shear waves for isotropy.

Fig. 1
figure 1

Interaction coefficients \(\varGamma _{pq}^1\) with \(p,q=1,2,\ldots ,6\) for quasi-longitudinal waves 1. Each colour in the table denotes a different nonzero value of the interaction coefficient. (Color figure online)

Full size image
Fig. 2
figure 2

Interaction coefficients \(\varGamma _{pq}^3\) with \(p,q=1,2,\ldots ,6\) for quasi-shear waves 3. The blue colour in the table denotes a nonzero value of the interaction coefficient. (Color figure online)

Full size image
Fig. 3
figure 3

Interaction coefficients \(\varGamma _{pq}^5\) with \(p,q=1,2,\ldots ,6\) for pure shear waves 5. The blue colour in the table denotes a nonzero value of the interaction coefficient. (Color figure online)

Full size image

It follows from Fig. 1 that interactions of waves from the same family only influence quasi-longitudinal waves. On the other hand, from Figs. 2 and 3 it is visible that interactions of quasi-longitudinal with quasi-shear waves, and quasi-longitudinal with pure shear waves only influence quasi-shear and pure shear waves, respectively.

5.2 Transverse isotropy

In the case of transverse isotropy we get ten different, nonzero interaction coefficients

$$\begin{aligned} \varGamma ^{i}_{11}, \quad \varGamma ^{i}_{33}, \quad \varGamma ^{i}_{13},\ \varGamma ^{i}_{55}, \quad \varGamma ^{5}_{15}, \quad \varGamma ^{5}_{35},\quad i=1,3. \end{aligned}$$
(50)

The other nonzero coefficients are related by the symmetry relations

$$\begin{aligned} \begin{aligned} \varGamma ^{i}_{11}&=\varGamma ^{i}_{12}=\varGamma ^{i}_{21}=\varGamma ^{i}_{22}=-\varGamma ^{i+1}_{11}=-\varGamma ^{i+1}_{12}=-\varGamma ^{i+1}_{21}=-\varGamma ^{i+1}_{22},\\ \varGamma ^{i}_{33}&=\varGamma ^{i}_{34}=\varGamma ^{i}_{43}=\varGamma ^{i}_{44}=-\varGamma ^{2}_{33}=-\varGamma ^{2}_{34}=-\varGamma ^{2}_{43}=-\varGamma ^{2}_{44},\\ \varGamma ^{i}_{55}&=\varGamma ^{i}_{56}=\varGamma ^{i}_{65}=\varGamma ^{i}_{66}=-\varGamma ^{i+1}_{55}=-\varGamma ^{i+1}_{56}=-\varGamma ^{i+1}_{65}=-\varGamma ^{i+1}_{66},\\ \varGamma ^{i}_{13}&=\varGamma ^{i}_{31}=\varGamma ^{i}_{14}=\varGamma ^{i}_{41}=-\varGamma ^{i+1}_{13}=-\varGamma ^{i+1}_{31}=-\varGamma ^{2}_{14}=-\varGamma ^{i+1}_{41}\\&=\varGamma ^{i}_{23}=\varGamma ^{i}_{32}=\varGamma ^{i}_{24}=\varGamma ^{i}_{42}=-\varGamma ^{i+1}_{23}=-\varGamma ^{i+1}_{32}=-\varGamma ^{i+1}_{24}=-\varGamma ^{i+1}_{42},\\ \varGamma ^{5}_{15}&=\varGamma ^{5}_{16}=\varGamma ^{5}_{25}=\varGamma ^{5}_{26}=-\varGamma ^{6}_{15}=-\varGamma ^{6}_{16}=-\varGamma ^{6}_{25}=-\varGamma ^{6}_{26}\\&=\varGamma ^{5}_{51}=\varGamma ^{5}_{61}=\varGamma ^{5}_{52}=\varGamma ^{5}_{62}=-\varGamma ^{6}_{51}=-\varGamma ^{6}_{61}=-\varGamma ^{6}_{52}=-\varGamma ^{6}_{62},\\ \varGamma ^{5}_{35}&=\varGamma ^{5}_{36}=\varGamma ^{5}_{45}=\varGamma ^{5}_{46}=-\varGamma ^{6}_{35}=-\varGamma ^{6}_{36}=-\varGamma ^{6}_{45}=-\varGamma ^{6}_{46}\\&=\varGamma ^{5}_{53}=\varGamma ^{5}_{63}=\varGamma ^{5}_{54}=\varGamma ^{5}_{64}=-\varGamma ^{6}_{53}=-\varGamma ^{6}_{63}=-\varGamma ^{6}_{54}=-\varGamma ^{6}_{64} \end{aligned} \end{aligned}$$
(51)

for \(i=1,3\).

In the following part of the article, we present tables of the nonzero interaction coefficients, similarly to the isotropic case, where

(52)

It turns out that the fibre-reinforcing model admits a much richer waves’ interaction in comparison to the isotropic model judging by Figs. 4, 5, and 6.

Fig. 4
figure 4

Interaction coefficients \(\varGamma _{pq}^1\) with \(p,q=1,2,\ldots ,6\) for quasi-longitudinal waves 1. Each colour in the table denotes a different nonzero value of the interaction coefficient. (Color figure online)

Full size image
Fig. 5
figure 5

Interaction coefficients \(\varGamma _{pq}^3\) with \(p,q=1,2,\ldots ,6\) for quasi-shear waves 3. Each colour in the table denotes a different nonzero value of the interaction coefficient. (Color figure online)

Full size image
Fig. 6
figure 6

Interaction coefficients \(\varGamma _{pq}^5\) with \(p,q=1,2,\ldots ,6\) for pure shear waves 5. Each colour in the table denotes a different nonzero value of the interaction coefficient. (Color figure online)

Full size image

We do not provide analytical formulae for the coefficients (51) as they are fairly complicated. In order to show some properties of them, we plot the values of selected coefficients as functions of the fibre orientation angle \(\phi \) in Figs. 7, 8, 9, 10 and 11.

We want to emphasize that the self-interaction of quasi-shear waves is possible on the quadratically nonlinear level for our transversely isotropic models in contrary to the isotropic case, see Fig. 7. This follows from the fact that \(\varGamma _3\) does not equal to zero for a wide range of parameters. Actually, it vanishes only for \(\phi =0\), \(\phi =\frac{\pi }{2}\) and \(\phi ^* \in \left( 0,\frac{\pi }{2}\right) \), where it continuously changes the sign from the negative to the positive one. On the other hand, the self-interaction of pure shear waves is not possible because of \(\varGamma _5=0\), similarly to the isotropic case.

Fig. 7
figure 7

Self-interaction coefficients \(\varGamma _1,\ \varGamma _3\) for \(a=b=c=d=E_z=1, \quad (\mathbf{a} ) \ p=\frac{1}{4}, \quad (\mathbf{b} )\ p=\frac{99}{100}\)

Full size image
Fig. 8
figure 8

Interaction coefficients \(\varGamma _{33}^1,\ \varGamma _{55}^1\) for \(a=b=c=d=E_z=1, \quad (\mathbf{a} )\ p=\frac{1}{4}, \quad (\mathbf{b} )\ p=\frac{99}{100}\)

Full size image
Fig. 9
figure 9

Interaction coefficients \(\varGamma _{11}^3,\ \varGamma _{55}^3\) for \(a=b=c=d=E_z=1, \quad (\mathbf{a} )\ p=\frac{1}{4}, \quad (\mathbf{b} )\ p=\frac{99}{100}\)

Full size image
Fig. 10
figure 10

Interaction coefficients \(\varGamma _{15}^5,\ \varGamma _{13}^3\) for \(a=b=c=d=E_z=1, \quad (\mathbf{a} )\ p=\frac{1}{4}, \quad (\mathbf{b} )\ p=\frac{99}{100}\)

Full size image
Fig. 11
figure 11

Interaction coefficients \(\varGamma _{35}^5,\ \varGamma _{13}^1\) for \(a=b=c=d=E_z=1, \quad (\mathbf{a} )\ p=\frac{1}{4}, \quad (\mathbf{b} )\ p=\frac{99}{100}\)

Full size image

6 Weakly nonlinear asymptotics

To illustrate differences between our isotropic and transversely isotropic models, we apply the method of weakly nonlinear asymptotics [1] to the plane waves system. Looking for a single wave asymptotic solution to the initial value problem, as a result, we obtain the evolution equation for waves amplitudes.

6.1 Cauchy problem with perturbed initial data

We analyse the following Cauchy problem for our system (45) with slightly perturbed initial data

$$\begin{aligned} \dfrac{\partial {\mathbf {w}}^{\varepsilon }}{\partial t}+{\mathbf {A}}\left( {\mathbf {w}}^{\varepsilon }\right) \dfrac{\partial {\mathbf {w}}^{\varepsilon }}{\partial x}={\mathbf {0}}, \quad {\mathbf {w}}^{\varepsilon }\left( 0,{\mathbf {x}}\right) =\varepsilon {\mathbf {w}}_1(0,x), \end{aligned}$$
(53)

where \(\varepsilon \) is a sufficiently small parameter. We assume Taylor expansion

$$\begin{aligned} {\mathbf {A}}( {\mathbf {w}}^{\varepsilon })={\mathbf {A}}\left( \varepsilon {{\tilde{\mathbf{w}}}}\right) ={\mathbf {A}}\left( {\mathbf {0}}\right) +\varepsilon {\mathbf {B}}\tilde{{\mathbf {w}}}+\frac{1}{2}\varepsilon ^2{\mathbf {C}}\tilde{{\mathbf {w}}}\tilde{{\mathbf {w}}}+{\mathcal {O}}(\varepsilon ^3) \end{aligned}$$
(54)

with

$$\begin{aligned} \begin{aligned}&\tilde{{\mathbf {w}}}={\mathbf {w}}_1+\varepsilon {\mathbf {w}}_2+\cdots ,\\&{\mathbf {B}}\tilde{{\mathbf {w}}}=\left[ \partial _{{\mathbf {w}}}{\mathbf {A}}\left( {\mathbf {w}}\right) \vert _{{\mathbf {w}}={\mathbf {0}}}\right] \tilde{{\mathbf {w}}},\\&{\mathbf {C}}\tilde{{\mathbf {w}}}\tilde{{\mathbf {w}}}=\left[ \partial _{{\mathbf {w}}}{\mathbf {B}}\left( {\mathbf {w}}\right) \vert _{{\mathbf {w}}={\mathbf {0}}}\right] \tilde{{\mathbf {w}}}\tilde{{\mathbf {w}}}. \end{aligned} \end{aligned}$$
(55)

6.2 Evolution equation for an amplitude of single wave

We express the Cauchy problem (53) in terms of the new independent variables \(\eta =x-\lambda t\) and \(\tau =\varepsilon t\) with \(\lambda \)—an eigenvalue of \({\mathbf {A}}({\mathbf {0}})\), and \(\varepsilon \)—a small parameter. We have

$$\begin{aligned} \begin{aligned} \frac{\partial {\mathbf {w}}^{\varepsilon }}{\partial t}&=\varepsilon \left( \frac{\partial {\mathbf {w}}_1}{\partial \tau }\frac{\partial \tau }{\partial t}+\frac{\partial {\mathbf {w}}_1}{\partial \eta }\frac{\partial \eta }{\partial t}\right) +\varepsilon ^2\left( \frac{\partial {\mathbf {w}}_2}{\partial \tau }\frac{\partial \tau }{\partial t}+\frac{\partial {\mathbf {w}}_2}{\partial \eta }\frac{\partial \eta }{\partial t}\right) \\&=\varepsilon \left( \varepsilon \frac{\partial {\mathbf {w}}_1}{\partial \tau }-\lambda \frac{\partial {\mathbf {w}}_1}{\partial \eta }\right) +\varepsilon ^2\left( \varepsilon \frac{\partial {\mathbf {w}}_2}{\partial \tau }-\lambda \frac{\partial {\mathbf {w}}_2}{\partial \eta }\right) . \end{aligned} \end{aligned}$$
(56)

Hence

$$\begin{aligned} \frac{\partial {\mathbf {w}}^{\varepsilon }}{\partial t}=-\varepsilon \lambda \frac{\partial {\mathbf {w}}_1}{\partial \eta }+\varepsilon ^2\left( \frac{\partial {\mathbf {w}}_1}{\partial \tau }-\lambda \frac{\partial {\mathbf {w}}_2}{\partial \eta }\right) +\cdots . \end{aligned}$$
(57)

Similarly, we have

$$\begin{aligned} \frac{\partial {\mathbf {w}}^{\varepsilon }}{\partial x}=\varepsilon \frac{\partial {\mathbf {w}}_1}{\partial \eta }+\varepsilon ^2\frac{\partial {\mathbf {w}}_2}{\partial \eta }. \end{aligned}$$
(58)

Therefore, it holds

$$\begin{aligned} \begin{aligned} \frac{\partial {\mathbf {w}}^{\varepsilon }}{\partial t}+{\mathbf {A}}\left( \mathbf {w^{\varepsilon }}\right) \frac{\partial {\mathbf {w}}^{\varepsilon }}{\partial x}&=\varepsilon \left( {\mathbf {A}}\left( {\mathbf {0}}\right) -\lambda {\mathbf {I}}\right) \frac{\partial {\mathbf {w}}_1}{\partial \eta } +\,\varepsilon ^2\left[ \frac{\partial {\mathbf {w}}_1}{\partial \tau }+{\mathbf {B}}\left( {\mathbf {0}}\right) {\mathbf {w}}_1\frac{\partial {\mathbf {w}}_1}{\partial \eta }+\left( {\mathbf {A}}\left( {\mathbf {0}}\right) -\lambda {\mathbf {I}}\right) \frac{\partial {\mathbf {w}}_2}{\partial \eta }\right] . \end{aligned} \end{aligned}$$
(59)

Next, we equate to zero the consecutive terms. The condition requiring \(\varepsilon \)-order terms to vanish implies

$$\begin{aligned} \left( {\mathbf {A}}\left( {\mathbf {0}}\right) -\lambda {\mathbf {I}}\right) \frac{\partial {\mathbf {w}}_1}{\partial \eta }={\mathbf {0}}. \end{aligned}$$
(60)
Fig. 12
figure 12

Plot of the solution to (66) for \(\varGamma =\frac{1}{10}\)

Full size image
Fig. 13
figure 13

Plot of the solution to (66) for \( \varGamma =-\frac{1}{10}\)

Full size image

Hence, we obtain

$$\begin{aligned} {\mathbf {w}}_1=a{\mathbf {r}}, \end{aligned}$$
(61)

where \({\mathbf {r}}\) is the eigenvector corresponding to the eigenvalue \(\lambda \) and \(a=a\left( \tau ,\eta \right) \) is an unknown amplitude. Next, equating to zero the \(\varepsilon ^2\)-order terms imply that

$$\begin{aligned} \left( {\mathbf {A}}\left( {\mathbf {0}}\right) -\lambda {\mathbf {I}})\right) \frac{\partial {\mathbf {w}}_2}{\partial \eta }=-\frac{\partial {\mathbf {w}}_1}{\partial \tau }-{\mathbf {B}}\left( {\mathbf {0}}\right) {\mathbf {w}}_1\frac{\partial {\mathbf {w}}_1}{\partial \eta }. \end{aligned}$$
(62)

Denoting by \(\varvec{{\mathcal {F}}}\left( \tau ,\eta \right) \ \)the right-hand side of (62), we claim that the above nonhomogeneous equation has a nonzero solution iff

$$\begin{aligned} {\mathbf {l}}\cdot \varvec{{{\mathcal {F}}}}\left( \tau ,\eta \right) =0, \end{aligned}$$
(63)

where \({\mathbf {l}}\) is the left eigenvector of \({\mathbf {A}}\left( {\mathbf {0}}\right) \) corresponding to the eigenvalue \(\lambda \). Substituting (61) into (63) and taking into account that \({\mathbf {l}}\cdot {\mathbf {r}}=1\), we obtain an evolution equation for the amplitude of a wave

$$\begin{aligned} \frac{\partial a}{\partial \tau }+\varGamma a \frac{\partial a}{\partial \eta }=0 \end{aligned}$$
(64)

with the self-interaction coefficient

$$\begin{aligned} \varGamma ={\mathbf {l}}\cdot {\mathbf {B}}{\mathbf {r}}{\mathbf {r}}. \end{aligned}$$
(65)

In the previous section, it is shown that \(\varGamma \equiv \varGamma _3\ne 0\) for most of the values of parameters characterizing our models in the transversely isotropic case. Hence, equation (64) with a nonzero self-interaction coefficient \(\varGamma _3\) may represent the evolution equation for a quasi-shear wave propagation. This is in contradiction with the isotropic case, where \(\varGamma _3=0\), which implies that the quadratic self-interaction is impossible in the isotropic case.

Equation (64) also describes a quasi-longitudinal wave propagation if \(\varGamma \equiv \varGamma _1\). For considered models \(\varGamma _1\) takes on only positive values, see Fig. 7.

6.3 Example

In order to illustrate basic properties of the evolution equation (64), which is recognized as the inviscid Burgers’ equation, we present numerical solutions to the initial-boundary value problem given by

$$\begin{aligned} {\left\{ \begin{array}{ll} \dfrac{\partial a}{\partial \tau }+\varGamma a \dfrac{\partial a}{\partial \eta }=0, \\ a\left( \eta ,0\right) =\sin \left( \pi \eta \right) , \quad \eta \in \left( 0,1\right) ,\\ a\left( 0,\tau \right) =a\left( 1,\tau \right) =0, \quad \tau \in \left( 0,3\right) . \end{array}\right. } \end{aligned}$$
(66)

Since \(\varGamma _3\) may take on positive as well as negative values, the problem is solved for \(\varGamma =\frac{1}{10}\) and \(\varGamma =-\frac{1}{10}\). Solutions are obtained with the help of a Mathematica software [23] using ‘NDSolve’ solver.

One may notice that the plots of the solutions in Figs. 12 and 13 are symmetric with respect to plane \(\eta =0.5\) at least for the considered range of \(\tau \).

7 Concluding remarks

The aim of this paper is to demonstrate the difference between isotropic and transversely isotropic models with respect to the propagation and interaction of weakly nonlinear elastic waves. We are interested in investigating the “weakest” quadratically nonlinear effects. We analyse a simple modification of a polyconvex isotropic model. It turns out that the addition of a single term depending on one invariant \(I_4\) only with one fibre direction, already brings the difference. Contrary to the isotropic case, the quadratically nonlinear effect appears in quasi-shear waves’ self-interaction for the fibre-reinforcing model. We also investigate the interaction of weakly nonlinear elastic waves by analysing the interaction coefficients in both isotropic and transversely isotropic models. It turns out that the fibre-reinforcing model admits a much richer type of the quadratically nonlinear interaction in comparison to the isotropic model. The details are collected in the table of coefficients included in Sect. 5.