Numerical study on the instability of localized buckling modes in the axially compressed strut on a distributed-spring elastic foundation with softening quadratic nonlinearity

Abstract

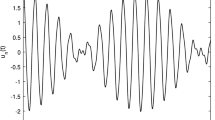
Localized buckling modes in the axially compressed strut on a distributed-spring elastic foundation with a softening quadratic nonlinearity are numerically calculated based on a modified Petviashvili method in the spatial frequency domain. As the load decreases (increases), the maximum displacement of the corresponding localized buckling mode increases (decreases) and its width decreases (increases). Then, under the influence of longitudinal and transverse perturbations, stabilities of these localized buckling modes are numerically investigated. The adopted numerical method is the spatial Fourier transform in space and the finite difference method in time. For initial positive longitudinal perturbations, localized buckling modes are unstable showing focusing-type finite-time blowup singularities. For initial negative perturbations, localized buckling modes are unstable and become dispersed showing small-amplitude oscillations. For initial transverse perturbations, localized buckling modes are unstable and are transformed into three-dimensional locally confined modes, finally showing finite-time blowup singularities.

Appendix

The nonlinear algebraic equation to be solved is Eq. (17).

$$\begin{aligned} {\hat{u}}(k)=D(k) \left\{ {{\hat{u}}(k) *{\hat{u}}(k)} \right\} . \end{aligned}$$

(A.1)

Here, the convolution terms can be re-expressed using a matrix-vector multiplication. In this case, for the column vector ${\hat{\eta }}=(c_0, c_1, c_2, \ldots ,c_{n-1})^\mathrm{T}$ (where T means the transpose), the circular convolution term for this finite-length vector is equal to

$$\begin{aligned} {\hat{u}} *{\hat{u}} = \begin{bmatrix} c_0 &{}\quad c_{n-1} &{}\quad c_{n-2} &{}\quad \cdots &{}\quad c_1 \\ c_1 &{}\quad c_0 &{}\quad c_{n-1} &{}\quad \ddots &{}\quad \vdots \\ c_2 &{}\quad c_1 &{}\quad \ddots &{}\quad \ddots &{}\quad c_{n-2} \\ \vdots &{}\quad \vdots &{}\quad \ddots &{}\quad \ddots &{}\quad c_{n-1}\\ c_{n-1} &{}\quad c_{n-2} &{}\quad \cdots &{}\quad c_1 &{}\quad c_0 \\ \end{bmatrix} \begin{bmatrix} c_0 \\ c_1 \\ c_2 \\ \vdots \\ c_{n-1} \end{bmatrix} \equiv {\mathbf {C}}({\hat{u}}){\hat{u}}. \end{aligned}$$

(A.2)

In addition, $D=(d_0, d_1, d_2, \ldots ,d_{n-1})^\mathrm{T}$ in Eq. (A.1) can be expressed as a diagonal matrix, then, the original equation, Eq. (A.1) becomes the following nonlinear matrix problem:

$$\begin{aligned} {\hat{u}}= \begin{bmatrix} d_0 &{}\quad 0 &{}\quad 0 &{}\quad \cdots &{}\quad 0 \\ 0 &{}\quad d_1 &{}\quad 0 &{}\quad \ddots &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad d_2 &{}\quad \ddots &{}\quad \vdots \\ \vdots &{}\quad \ddots &{}\quad \ddots &{}\quad \ddots &{}\quad 0\\ 0 &{}\quad 0 &{}\quad \cdots &{}\quad 0 &{}\quad d_{n-1} \\ \end{bmatrix} \begin{bmatrix} c_0 &{}\quad c_{n-1} &{}\quad c_{n-2} &{}\quad \cdots &{}\quad c_1 \\ c_1 &{}\quad c_0 &{}\quad c_{n-1} &{}\quad \ddots &{}\quad \vdots \\ c_2 &{}\quad c_1 &{}\quad \ddots &{}\quad \ddots &{}\quad c_{n-2} \\ \vdots &{}\quad \vdots &{}\quad \ddots &{}\quad \ddots &{}\quad c_{n-1}\\ c_{n-1} &{}\quad c_{n-2} &{}\quad \cdots &{}\quad c_1 &{}\quad c_0 \\ \end{bmatrix} \begin{bmatrix} c_0 \\ c_1 \\ c_2 \\ \vdots \\ c_{n-1} \end{bmatrix} \equiv \mathbf {DC}({\hat{u}}){\hat{u}} \equiv {\mathbf {A}}({\hat{u}}){\hat{u}}. \end{aligned}$$

(A.3)

For a symmetric buckling mode solution, the matrix ${\mathbf {C}} ({\hat{u}})$ is a symmetric circulant Toeplitz matrix, and ${\mathbf {D}}$ is a symmetric diagonal matrix. Therefore, the resultant matrix ${\mathbf {A}}$ in Eq. (A.3) is diagonalizable. Like in the linear matrix eigenvalue problem, if the diagonalizable square matrix ${\mathbf {A}}$ with a size $n \times n$ has a dominant eigenvalue with a corresponding dominant eigenvector, then one can choose an initial approximation of a nonzero vector ${\hat{\mathbf {u}}}_{\mathbf {0}}$ with a size $n \times 1$ to perform the following numerical sequence with a proper stabilizing factor, assuming the sequence to be convergent. In other words,

$$\begin{aligned} \begin{aligned} {\hat{\mathbf {u}}}_{\mathbf {1}}&= (1/S_1) \mathbf {A_0} {\hat{\mathbf {u}}}_{\mathbf {0}}, \\ {\hat{\mathbf {u}}}_{\mathbf {2}}&= (1/S_2) \mathbf {A_1} {\hat{\mathbf {u}}}_{\mathbf {1}}= (1/S_2S_1) \mathbf {A_1A_0} {\hat{\mathbf {u}}}_{\mathbf {0}}, \\ {\hat{\mathbf {u}}}_{\mathbf {3}}&= (1/S_3) \mathbf {A_2} {\hat{\mathbf {u}}}_{\mathbf {2}}= (1/S_3S_2S_1) \mathbf {A_2A_1A_0} {\hat{\mathbf {u}}}_{\mathbf {0}}, \\&~~~~~~~~~~~~~~\vdots \\ {\hat{\mathbf {u}}}_{\mathbf {k}}&= (1/S_k) \mathbf {A_{k-1}} {\hat{\mathbf {u}}}_{\mathbf {k-1}}= (1/S_kS_{k-1} \cdots S_3S_2S_1) (\mathbf {A_{k-1} \cdots A_2A_1A_0}){\hat{\mathbf {u}}}_{\mathbf {0}}. \end{aligned} \end{aligned}$$

(A.4)

Since all the matrices in Eq. (A.3) are diagonalizable, one can assume that the matrix $\mathbf {A_i}$ ($i=0,1,2,3, \ldots ,k$ ) has a set of eigenvectors $\{ {\mathbf {x_0^{(i)}, x_1^{(i)}, \ldots , x_{n-1}^{(i)}}} \}$ and a set of associated eigenvalues $\{ {\lambda _0^{(i)},\lambda _1^{(i)}, \ldots , \lambda _{n-1}^{(i)}} \}$ with descending orders of their absolute magnitudes $\big ( {\big | {\lambda _0^{(i)}} \big | > \big | {\lambda _1^{(i)}} \big |} \ge \cdots \ge \big | {\lambda _{n-1}^{(i)}} \big | \big )$ at each iteration step. To begin with, the initial vector ${\hat{\mathbf {u}}}_{\mathbf {0}}$ can be expressed as a linear combination of the eigenvectors of $\mathbf {A_0}$ as follows:

$$\begin{aligned} {\hat{\mathbf {u}}}_{\mathbf {0}}=\sum _{j=0}^{n-1} c_j^{(0)} {\mathbf {x}}_j^{\mathbf {(0)}} . \end{aligned}$$

(A.5)

Here, $c_j^{(0)}~(j=0,1, \ldots , n-1)$ are coefficients in the linear combination. In the first iterative step, ${\hat{\mathbf {u}}}_{\mathbf {1}}$ in Eq. (A.4) can be expressed using Eq. (A.5) as follows:

$$\begin{aligned} \begin{aligned} {\hat{\mathbf {u}}}_{\mathbf {1}} = (1/S_1) \mathbf {A_0} {\hat{\mathbf {u}}}_{\mathbf {0}} = (1/S_1) \mathbf {A_0} \sum _{j=0}^{n-1} c_j^{(0)} {\mathbf {x}}_j^{\mathbf {(0)}} = (1/S_1) \sum _{j=0}^{n-1} c_j^{(0)} \lambda _j^{(0)} {\mathbf {x}}_j^{\mathbf {(0)}} \sim \frac{\lambda _0^{(0)} }{S_1}\left( {\mathbf {x_0^{(0)}} + \sum _{j=1}^{n-1} \frac{\lambda _j^{(0)}}{\lambda _0^{(0)}}} {\mathbf {x}}_j^{\mathbf {(0)}} \right) . \end{aligned} \end{aligned}$$

(A.6)

In the second iterative step,

$$\begin{aligned} {\hat{\mathbf {u}}}_{\mathbf {2}} = (1/S_2) \mathbf {A_1} {\hat{\mathbf {u}}}_{\mathbf {1}} = (1/S_2S_1) \mathbf {A_1} \sum _{j=0}^{n-1} c_j^{(0)} \lambda _j^{(0)} {\mathbf {x}}_j^{\mathbf {(0)}} . \end{aligned}$$

(A.7)

Since ${\mathbf {x}}_j^{(0)}~(j=0,1, \ldots ,n-1)$ can be expressed as a linear combination of ${\mathbf {x}}_j^{(1)}~(j=0,1, \ldots ,n-1)$, say,

$$\begin{aligned} \mathbf {x_0^{(0)}}= \sum _{i=0}^{n-1}C_i^{(1)} \mathbf {x_i^{(1)}}, \, \mathbf {x_1^{(0)}}= \sum _{i=0}^{n-1}D_i^{(1)} \mathbf {x_i^{(1)}}, \, \ldots , \, \mathbf {x_{n-1}^{(0)}}= \sum _{i=0}^{n-1}E_i^{(1)} \mathbf {x_i^{(1)}}. \end{aligned}$$

(A.8)

Then, by substituting Eq. (A.8) into Eq. (A.7),

$$\begin{aligned} \begin{aligned} {\hat{\mathbf {u}}}_{\mathbf {2}}&= \frac{1}{S_1S_2} \mathbf {A_1} \left( { c_0^{(0)}\lambda _0^{(0)} \sum _{i=0}^{n-1}C_i^{(1)}\mathbf {x_i^{(1)}} + c_1^{(0)}\lambda _1^{(0)} \sum _{i=0}^{n-1}D_i^{(1)}\mathbf {x_i^{(1)}} + \cdots + c_{n-1}^{(0)}\lambda _{n-1}^{(0)} \sum _{i=0}^{n-1}E_i^{(1)}\mathbf {x_i^{(1)}} } \right) \\&= \frac{1}{S_1S_2} \left( { c_0^{(0)}\lambda _0^{(0)} \sum _{i=0}^{n-1}C_i^{(1)}\lambda _i^{(1)}\mathbf {x_i^{(1)}} +c_1^{(0)}\lambda _1^{(0)} \sum _{i=0}^{n-1}D_i^{(1)}\lambda _i^{(1)}\mathbf {x_i^{(1)}} + \cdots + c_{n-1}^{(0)}\lambda _{n-1}^{(0)} \sum _{i=0}^{n-1}E_i^{(1)}\lambda _i^{(1)}\mathbf {x_i^{(1)}} } \right) \\&\sim \frac{\lambda _0^{(1)} \lambda _0^{(0)}}{S_1S_2} \left( { \mathbf {x_0^{(1)}} + \sum _{j=1}^{n-1} \frac{\lambda _j^{(1)}}{\lambda _0^{(1)}} \frac{\lambda _j^{(0)}}{\lambda _0^{(0)}} {\mathbf {x}}_j^{(1)}} \right) . \end{aligned} \end{aligned}$$

(A.9)

Similarly, in the third iterative step,

$$\begin{aligned} {\hat{\mathbf {u}}}_{\mathbf {3}} \sim \frac{\lambda _0^{(2)}\lambda _0^{(1)}\lambda _0^{(0)}}{S_3S_2S_1} \left( {{\mathbf {x}}_{{\mathbf {0}}}^{(2)} +\sum _{j=1}^{n-1} \frac{\lambda _j^{(2)}}{\lambda _0^{(2)}} \frac{\lambda _j^{(1)}}{\lambda _0^{(1)}}\frac{\lambda _j^{(0)}}{\lambda _0^{(0)}} {\mathbf {x}}_{j}^{(2)} } \right) . \end{aligned}$$

(A.10)

Deductively, in the kth iterative step,

$$\begin{aligned} {\hat{\mathbf {u}}}_{\mathbf {k}} \sim \frac{\lambda _0^{(k-1)} \cdots \lambda _0^{(2)}\lambda _0^{(1)}\lambda _0^{(0)}}{S_k \cdots S_3S_2S_1} \left( {{\mathbf {x}}_{{\mathbf {0}}}^{(k-1)} +\sum _{j=1}^{n-1} \left( {\frac{\lambda _j^{(k-1)}}{\lambda _0^{(k-1)}} \cdots \frac{\lambda _j^{(2)}}{\lambda _0^{(2)}} \frac{\lambda _j^{(1)}}{\lambda _0^{(1)}}\frac{\lambda _j^{(0)}}{\lambda _0^{(0)}}} \right) {\mathbf {x}}_{j}^{(k-1)} } \right) . \end{aligned}$$

(A.11)

Depending on the relative magnitude ratio, $\left| {\lambda _1^{(i)}\big /\lambda _0^{(i)}} \right| <1$, which affects the convergence rate, the above sequence is expected to converge to an intermediate state where the sets of eigenvector and eigenvalue become almost constant. Including and after the jth step, let’s assume that the sets of eigenvectors and eigenvalues become almost equal to $\mathbf {\{ {x_0, x_1, x_2, \ldots , x_{n-1}} \}}$ and $\{ {\lambda _0, \lambda _1, \lambda _2, \ldots , \lambda _{n-1}} \}$, where $( \left| {\lambda _0} \right| > \left| {\lambda _1} \right| \ge \cdots \ge \left| {\lambda _{n-1}} \right| )$, respectively. Based on these eigenvectors, Eq. (A.11) is re-expressed as

$$\begin{aligned} {\hat{\mathbf {u}}}_{\mathbf {k}} = c_0\mathbf {x_0} + c_1\mathbf {x_1}+c_2\mathbf {x_2}+\cdots +c_{n-1}\mathbf {x_{n-1}} . \end{aligned}$$

(A.12)

For the next m sequences, assuming $\mathbf {A_k \approx A_{k+1} \approx \cdots \approx A_{k+m}}$

$$\begin{aligned} {\hat{\mathbf {u}}}_{\mathbf {k+1}}= & {} \mathbf {A_k} {\hat{\mathbf {u}}}_{\mathbf {k}} = \mathbf {A_k} \left( { c_0 \mathbf {x_0}+c_1 \mathbf {x_1}+c_2 \mathbf {x_2}+\cdots +c_{n-1} \mathbf {x_{n-1}} } \right) \nonumber \\= & {} c_0\lambda _0\mathbf {x_0} + c_1\lambda _1\mathbf {x_1} + c_2\lambda _2\mathbf {x_2} + \cdots + c_{n-1}\lambda _{n-1}\mathbf {x_{n-1}},\nonumber \\ {\hat{\mathbf {u}}}_{\mathbf {k+2}}= & {} \mathbf {A_{k+1}} {\hat{\mathbf {u}}}_{\mathbf {k+1}} \approx \mathbf {A_{k}} {\hat{\mathbf {u}}}_{\mathbf {k+1}} \nonumber \\\approx & {} c_0{(\lambda _0)}^2 \mathbf {x_0} + c_1{(\lambda _1)}^2 \mathbf {x_1} + c_2{(\lambda _2)}^2 \mathbf {x_2} + \cdots + c_{n-1}{(\lambda _{n-1})}^2 \mathbf {x_{n-1}}, \nonumber \\&~~~~\vdots \nonumber \\ {\hat{\mathbf {u}}}_{\mathbf {k+m}}\approx & {} c_0{(\lambda _0)}^m \mathbf {x_0} + c_1{(\lambda _1)}^m \mathbf {x_1} + c_2{(\lambda _2)}^m \mathbf {x_2} + \cdots + c_{n-1}{(\lambda _{n-1})}^m \mathbf {x_{n-1}} \nonumber \\= & {} {(\lambda _0)}^m \left( { c_0\mathbf {x_0} + c_1{\left( {\frac{\lambda _1}{\lambda _0}} \right) }^m \mathbf {x_1} + c_2{\left( {\frac{\lambda _2}{\lambda _0}} \right) }^m \mathbf {x_2} + \cdots + c_{n-1}{\left( {\frac{\lambda _{n-1}}{\lambda _0}} \right) }^m \mathbf {x_{n-1}} } \right) . \end{aligned}$$

(A.13)

From Eq. (A.13), ${\hat{\mathbf {u}}}_{\mathbf {k+m}} \approx (\lambda _0)^m c_0 \mathbf {x_0}$ as m approaches infinity (practically, some finite numbers) due to the existence of the dominant eigenvalue $\lambda _0~( \left| {\lambda _0} \right| > \left| {\lambda _1} \right| \ge \cdots \ge \left| {\lambda _{n-1}} \right| )$. In other words, the final nonlinear solitary wave solution in the physical domain is equal to a multiple of the inverse Fourier transform of the dominant eigenvector $\mathbf {x_0}$ in the wavenumber domain.