A scalar prototype problem of deep abrasive drilling with an infinite free boundary: an asymptotic modeling study

Abstract

A vanishing at infinity solution of the three-dimensional Laplace equation is sought in an a priori unknown domain with overdetermined boundary conditions, the right-hand sides of which depend on the unit normal to the free boundary. A perturbation analysis of the nonstandard free boundary problem that models deep abrasive drilling has been performed under the assumption that the free boundary is close to the surface of a given semi-infinite cylinder, the longitudinal position of which depends on the boundary data, and the leading-order asymptotic solution has been developed.

1 Introduction

Free and moving boundary problems [1, 2], where the problem domain is a priori unknown are encountered in different areas of science and engineering [3], including laser drilling of metals [4, 5], crack propagation and delamination in composite materials [6, 7], in Hele–Shaw flow [8, 9], and elastic and plastic torsion [10, 11].

An example of stationary free boundary problem for a harmonic function u can be formulated as an overdetermined problem with two boundary conditions:

$$\begin{aligned} u\bigr \vert _\varGamma =g,\quad \frac{\partial u}{\partial n}\biggr \vert _\varGamma =h, \end{aligned}$$

(1)

on a free boundary $\varGamma$.

A number of approaches for numerical solution of stationary free boundary value problems have been developed, in particular, using trial methods [12, 13], shape optimization [14], cost functional minimization [15], Newton’s method [16], and level set techniques [17].

We note that the so-called Serrin-type overdetermined boundary value problems for Poisson’s equation with the boundary conditions (1) with constant right-hand sides have been studied for both interior [18, 19] and exterior [20, 21] domains. It has been established that if $g=\mathrm const$ and $h=\mathrm const$, then $\varGamma$ is a sphere and u is radially symmetric about the center of the sphere.

The case of a Bernoulli problem with non-constant gradient boundary constraint, that is (instead of the second boundary condition (1))

$$\begin{aligned} \vert \nabla u\vert \Bigr \vert _\varGamma =h, \end{aligned}$$

(2)

was studied in [22] under the assumption that its right-hand side depends on the unit normal to the unknown boundary.

In the present paper, we consider one nonstandard free boundary problem, where the right-hand sides of Eqs. (1) depend both on the unit normal vector to the surface $\varGamma$ and its position. The problem was motivated by recent mathematical modeling studies [23, 24] of deep drilling mechanics. Since the deep drilling problem considered in [23] is strongly nonlinear, we formulate its scalar prototype to highlight the novelty of the free boundary formulation. The term “abrasive” refers to the Neumann boundary condition (1)$_2$, whereas the direct analogy with the deep drilling problem [23, 24], which has been formulated in the framework of linear elasticity, implies the use of the Bernoulli boundary condition (2). We note that the Neumann boundary condition (1)$_2$ with a constant right-hand side models a nearly constant contact pressure distribution achieved in stationary abrasive wear according to Archard’s law (see, e.g., [25, 26]). Note also that confusion should be avoided with the term “free boundary” that is usually used to refer to traction-free boundary in solid mechanics.

An important feature of the deep drilling problem is that the free boundary $\varGamma$ is assumed to be infinite and, in a sense, close to the surface of a semi-infinite cylinder, representing the drilling bit. To the best of the authors’ knowledge, no published work, outside the works of Mikhailov and Namestnikova [23, 24, 27], has attempted to study an overdetermined boundary value problem with the Dirichlet boundary data defined as the sign distance to a given surface.

Another novelty of the deep abrasive problem is that the Dirichlet boundary condition, which is imposed on a proper subset of $\varGamma$, additionally contains a scalar parameter, $\delta$, value of which depends on the Neumann boundary data via the unknown function u.

The rest of the paper is organized as follows. In Sect. 2, we formulate the scalar problem of deep abrasive drilling. Its perturbation analysis has been given in Sect. 3 under the assumption that the free boundary is close to the bit surface in some displaced position, corresponding to the level of imposed external loading. In Sect. 4, we linearize the free boundary problem and present the leading order asymptotic solution. A simple example, where some analytical results can be derived based on the known solutions, is considered in Sect. 5. Finally, in Sect. 6, we outline the discussion of the presented analysis.

2 Free boundary problem formulation

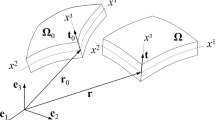
We consider stationary abrasive drilling of a semi-infinite bore-hole ${\mathbb {R}}^3\setminus {{\bar{\varOmega }}}$, spreading to $x_3=+\infty$ in an infinite space ${\mathbb {R}}^3$ (see Fig. 1). Let the $x_3$-axis of the Cartesian coordinate system $\mathbf{x}=(x_1,x_2,x_3)$ coincide with the bore-hole axis. For simplicity, we may assume that the bit is axially symmetric and, therefore, the domain outside the bore-hole $\varOmega$ is axially symmetric as well. Let B denote the domain occupied by the bit in the unloaded state. We assume that the bit’s boundary $\partial B$ is semi-infinite and is composed of two parts: a vertical cylindrical surface $\partial B_\Vert$ and a curvilinear bottom surface $\partial B_\cup$.

Fig. 1

Undeformed configuration. Bore-hole boundary partition

Fig. 2

Deformed configuration. Bit boundary partition

In the loaded state, the bit is moved into contact with the bore-hole surface. Let $\delta >0$ be the bit’s vertical displacement in the opposite direction of the $x_3$-axis, so that $B^\delta$ and $\partial B^\delta =\partial B^\delta _\Vert \cup \partial B^\delta _\cup$ will denote the domain occupied by the displaced bit and its boundary (see Fig. 2). Further, in the loaded state, the bit’s bottom surface $\partial B^\delta _\cup$ represents the rupture front $\partial \varOmega ^\delta _\cup$, which is characterized by the boundary condition

$$\begin{aligned} -\mu \frac{\partial u}{\partial n}(\mathbf{x})=p,\quad \mathbf{x}\in \partial \varOmega _\cup . \end{aligned}$$

(3)

Here, $\mathbf{n}(\mathbf{x})$ is a unit outward (i.e., directed inward the bore-hole) normal vector, $\mu$ and p are positive constants. Note that at the center of coordinates (denoted as point O), we have $\mathbf{n}(O)=1$.

For the sake of simplicity, we assume that in the loaded state, the vertical bore-hole surface $\partial \varOmega _\Vert =\partial \varOmega {\setminus }\partial \varOmega _\cup$ comes into full contact with the bit’s vertical surface $\partial B^\delta _\Vert$, i.e., $\partial \varOmega ^\delta _\Vert =\partial B^\delta _\Vert$, and the contact is stress- and damage-free, so that

$$\begin{aligned} \frac{\partial u}{\partial n}(\mathbf{x})=0,\quad \mathbf{x}\in \partial \varOmega _\Vert . \end{aligned}$$

(4)

In the loaded state, the bore-hole surface $\partial \varOmega ^\delta$ coincides with the bit surface $\partial B^\delta$, whereas in the unloaded state, there is a gap between the surfaces $\partial \varOmega$ and $\partial B$. Hence, let $g(\mathbf{x})$ denote the gap measured along the normal to the boundary $\partial \varOmega$ in the inward direction with respect to the bore-hole. It is clear that the gap between the lateral surfaces $\partial \varOmega _\Vert$ and $\partial B_\Vert$ is invariant with regard to any downward vertical translation of the cylindrical bit surface $\partial B_\Vert$, while the gap between the bottom surfaces $\partial \varOmega _\cup$ and $\partial B^\delta _\cup$ will be, respectively, affected. So, let the gap between the surfaces $\partial \varOmega _\cup$ and $\partial B^\delta _\cup$ be denoted by $g^\delta (\mathbf{x})$.

The unknown function $u(\mathbf{x})$ is required to satisfy the Laplace equation inside the domain $\varOmega$, i.e.,

$$\begin{aligned} -\mu \varDelta _x u(\mathbf{x})=0,\quad \mathbf{x}\in \varOmega , \end{aligned}$$

(5)

and to vanish at infinity,

$$\begin{aligned} u(\mathbf{x})=o(1),\quad \vert \mathbf{x}\vert \rightarrow \infty ; \end{aligned}$$

(6)

however, the problem domain itself is supposed to be unknown.

To complete the problem statement, we impose the second boundary condition on each of the boundary parts $\partial \varOmega _\cup$ and $\partial \varOmega _\Vert$ as follows:

$$\begin{aligned} u(\mathbf{x})= & {} g^\delta (\mathbf{x}),\quad \mathbf{x}\in \partial \varOmega _\cup , \end{aligned}$$

(7)

$$\begin{aligned} u(\mathbf{x})= & {} g(\mathbf{x}),\quad \mathbf{x}\in \partial \varOmega _\Vert . \end{aligned}$$

(8)

Observe that by analogy with contact problems, one may additionally impose the so-called equilibrium condition

$$\begin{aligned} -\mu \iint \limits _{\partial \varOmega _\cup } \frac{\partial u}{\partial n}(\mathbf{x})n_3(\mathbf{x})\,\mathrm{{d}}S_x=P \end{aligned}$$

(9)

with a constant P that, in view of Eq. (3), should be related to p. Indeed, the substitution of (3) into Eq. (9) leads to the relation

$$\begin{aligned} P=p\vert \omega _\cup \vert , \end{aligned}$$

(10)

where $\vert \omega _\cup \vert$ is the area of the projection $\omega _\cup$ of the surface $\partial \varOmega _\cup$ on the plane $x_3=0$.

Further, we note that there is some ambiguity in the definition of the bit surface $\partial B$ in the unloaded state. Here we will follow the convention usually used in contact problems that the surfaces $\partial B_\cup$ and $\partial \varOmega _\cup$ coincide at a single point O lying on the vertical $x_3$-axis. So, using the arbitrariness in the vertical position of the center of coordinates, we will assume that

$$\begin{aligned} g(O)=0, \end{aligned}$$

(11)

as the point O has been chosen as the coordinate center.

Equation (11) immediately implies that

$$\begin{aligned} g^\delta (O)=-\,\delta , \end{aligned}$$

(12)

where $\delta$ is the bit displacement. To simplify the calculations of the displaced gap function $g^\delta$ under the assumption of relatively small displacement $\delta$, the following approximation can be utilized:

$$\begin{aligned} g^\delta (\mathbf{x})\simeq g(\mathbf{x})-\delta n_3(\mathbf{x}),\quad \mathbf{x}\in \partial \varOmega _\cup . \end{aligned}$$

(13)

Finally, the partition of the bore-hole boundary $\partial \varOmega$ into two parts $\partial \varOmega _\cup$ and $\partial \varOmega _\Vert$ will be determined by the conditions

$$\begin{aligned} 0<n_3(\mathbf{x}),\quad \mathbf{x}\in \partial \varOmega _\cup ; \qquad n_3(\mathbf{x})\le 0,\quad \mathbf{x}\in \partial \varOmega _\Vert , \end{aligned}$$

(14)

so that the contribution to the total contact force P [see Eq. (9)] from the surface loading p, as it is specified by Eq. (3), will be positive on the entire rupture front $\partial \varOmega _\cup$.

Equations (3)–(14) constitute a free boundary problem, where positions of the surfaces $\partial \varOmega _\cup$ and $\partial \varOmega _\Vert$ must be determined in the process of solution.

Remark 1

Let ${{\mathcal {H}}}(x)$ be the Heaviside function, that is $\mathcal{H}(x)=1$ if $x>0$, and ${{\mathcal {H}}}(x)=0$ if $x\le 0$. Then, in view of (13) and (14), the boundary conditions (3), (4) and (7), (8) can be represented in the form (1) as follows:

$$\begin{aligned} -\mu \frac{\partial u}{\partial n}(\mathbf{x})= & {} p{{\mathcal {H}}}\bigl (n_3(\mathbf{x})\bigr ),\quad \mathbf{x}\in \varGamma , \end{aligned}$$

(15)

$$\begin{aligned} u(\mathbf{x})= & {} g(\mathbf{x})-\delta n_3(\mathbf{x}){{\mathcal {H}}}\bigl (n_3(\mathbf{x})\bigr ),\quad \mathbf{x}\in \varGamma . \end{aligned}$$

(16)

Here, $\varGamma =\partial \varOmega$ is the entire boundary of the hole.

3 Perturbation analysis of the free boundary problem

We assume that the unknown bore-hole surface $\partial \varOmega$ is close to the bit surface $\partial B_\cup$, so that the gap $g(\mathbf{x})$ is relatively small compared to the radius of the cylindrical surface $\partial B_\Vert$.

Now, by applying a perturbation technique [28], we will move the boundary conditions from the surface $\partial \varOmega$ to the surface $\partial B$. With this aim, we introduce a local orthogonal curvilinear coordinate system on $\partial B$, denoted as $\varvec{\alpha }=(\alpha _1,\alpha _2)$ with the Lamé coefficients $A_1(\varvec{\alpha })$ and $A_2(\varvec{\alpha })$, and a unit outward (with respect to the bit domain B) vector $\varvec{\nu }(\varvec{\alpha })$ (it is assumed that $\varvec{\nu }=\mathbf{e}_1\times \mathbf{e}_2$). Let also $\gamma (\varvec{\alpha })$ denote the gap between the surfaces $\partial B$ and $\partial \varOmega$ measured from the surface $\partial B$ to the surface $\partial \varOmega$ in the direction of the vector $\varvec{\nu }(\varvec{\alpha })$. Then, in the local coordinate system $(\alpha _1,\alpha _2,\nu )$, the unknown surface $\partial \varOmega$ can be parameterized as follows:

$$\begin{aligned} \nu =\gamma (\alpha _1,\alpha _2). \end{aligned}$$

(17)

By accounting only for the first-order perturbation effects, we can replace the boundary condition (8) with the following:

$$\begin{aligned} u\bigl (\varvec{\alpha }+\gamma (\varvec{\alpha })\varvec{\nu }\bigr )= \gamma (\varvec{\alpha }),\quad \varvec{\alpha }\in \partial B_\Vert . \end{aligned}$$

(18)

Thus, by approximating the left-hand side of Eq. (18) as

$$\begin{aligned} u\bigl (\varvec{\alpha }+\gamma (\varvec{\alpha })\varvec{\nu }\bigr )= u(\varvec{\alpha })+\gamma (\varvec{\alpha })\frac{\partial u}{\partial \nu }(\varvec{\alpha })+\ldots , \end{aligned}$$

we linearize Eq. (18) as follows:

$$\begin{aligned} \gamma (\varvec{\alpha })\Bigl ( 1-\frac{\partial u}{\partial \nu }(\varvec{\alpha }) \Bigr )=u(\varvec{\alpha }),\quad \varvec{\alpha }\in \partial B_\Vert . \end{aligned}$$

(19)

Now, we can parameterize the surface $\partial \varOmega _\Vert$ by using the radius-vector $\mathbf{r}(\varvec{\alpha })$ of the surface $\partial B_\Vert$ as follows:

$$\begin{aligned} \mathbf{R}(\varvec{\alpha })=\mathbf{r}(\varvec{\alpha })+\gamma (\varvec{\alpha })\varvec{\nu }. \end{aligned}$$

Differentiating the radius-vector $\mathbf{R}(\varvec{\alpha })$ with respect to the curvilinear coordinates and making use of the Rodrigues theorem, we obtain

$$\begin{aligned} \frac{\partial \mathbf{R}}{\partial \alpha _i}=A_i\Bigl (1+\frac{\gamma }{R_i}\Bigr )\mathbf{e}_i +\frac{\partial \gamma }{\partial \alpha _i}\varvec{\nu }\quad (i=1,2), \end{aligned}$$

(20)

where $R_1$ and $R_2$ are the two principal curvature radii, $\mathbf{e}_1$ and $\mathbf{e}_2$ denote the unit coordinate vectors of the coordinate system $(\alpha _1,\alpha _2)$.

Then, the gradient of a scalar field $\phi$ in the orthogonal coordinate system $(\alpha _1,\alpha _2,\nu )$ is defined by the formula

$$\begin{aligned} \nabla _x\phi =\frac{\mathbf{e}_1}{A_1(\varvec{\alpha })} \Bigl (1+\frac{\nu }{R_1(\varvec{\alpha })}\Bigr )^{-1}\frac{\partial \phi }{\partial \alpha _1} +\frac{\mathbf{e}_2}{A_2(\varvec{\alpha })} \Bigl (1+\frac{\nu }{R_2(\varvec{\alpha })}\Bigr )^{-1}\frac{\partial \phi }{\partial \alpha _2} +\varvec{\nu }\frac{\partial \phi }{\partial \nu }. \end{aligned}$$

(21)

Correspondingly, the Laplacian of a scalar field $\phi$ is defined as follows:

$$\begin{aligned} \nabla _x^2\phi =\frac{1}{h_1 h_2}\biggl \{ \frac{\partial }{\partial \alpha _1} \Bigl (\frac{h_2}{h_1}\frac{\partial \phi }{\partial \alpha _1}\Bigr ) +\frac{\partial }{\partial \alpha _2} \Bigl (\frac{h_1}{h_2}\frac{\partial \phi }{\partial \alpha _2}\Bigr ) +\frac{\partial }{\partial \nu } \Bigl (h_1 h_2\frac{\partial \phi }{\partial \nu }\Bigr )\biggr \}. \end{aligned}$$

(22)

Here, $h_1$, $h_2$, and $h_3=1$ are the Lamé coefficients of the coordinate system $(\alpha _1,\alpha _2,\nu )$, i.e.,

$$\begin{aligned} h_1=A_1\Bigl (1+\frac{\nu }{R_1}\Bigr ),\quad h_2=A_2\Bigl (1+\frac{\nu }{R_2}\Bigr ). \end{aligned}$$

Observe also that formula (21) in the vicinity of the base surface $\partial B$ can be approximated as

$$\begin{aligned} \nabla _x\simeq \nabla _\alpha -\sum _{i=1,2} \frac{\nu }{A_i R_i}\mathbf{e}_i\frac{\partial }{\partial \alpha _i} +\varvec{\nu }\frac{\partial }{\partial \nu }, \quad \nabla _\alpha =\frac{\mathbf{e}_1}{A_1}\frac{\partial }{\partial \alpha _1} +\frac{\mathbf{e}_2}{A_2}\frac{\partial }{\partial \alpha _2}, \end{aligned}$$

(23)

where $\nabla _\alpha$ is the gradient operator in the curvilinear coordinate system on $\partial B$.

Since the two vectors (20) ($i=1,2$) are tangent vectors to the surface $\partial \varOmega _\Vert$, we can define the limit normal vector to the surface $\partial \varOmega _\Vert$ as follows:

$$\begin{aligned} \mathbf{n}=-\frac{\mathbf{N}}{\vert \mathbf{N}\vert },\quad \mathbf{N}=\frac{\partial \mathbf{R}}{\partial \alpha _1}\times \frac{\partial \mathbf{R}}{\partial \alpha _2}. \end{aligned}$$

(24)

Recall that the normal vector $\mathbf{n}$ has been defined previously to be directed inward the bore-hole, i.e., in the opposite direction with respect to the normal vector $\varvec{\nu }$.

Substituting (20) ($i=1,2$) into the second equation (24) and making use of the assumptions $\vert \gamma \vert \ll \min \{R_1,R_2\}$ and $\vert \partial \gamma /\partial \alpha _i\vert \ll 1$ ($i=1,2$), we derive the second-order approximation

$$\begin{aligned} \mathbf{n}\simeq \frac{1}{A_1}\frac{\partial \gamma }{\partial \alpha _1}{} \mathbf{e}_1 +\frac{1}{A_2}\frac{\partial \gamma }{\partial \alpha _2}{} \mathbf{e}_2 -\varvec{\nu }. \end{aligned}$$

(25)

Now, we are in a position to move the boundary condition (4) from the surface $\partial \varOmega _\Vert$ to the surface $\partial B_\Vert$. First, by definition, we have

$$\begin{aligned} \frac{\partial u}{\partial n}\biggr \vert _{\partial \varOmega _\Vert } =\mathbf{n}\cdot \nabla _x u\bigl (\mathbf{r}(\varvec{\alpha }) +\nu \varvec{\nu }(\varvec{\alpha })\bigr ) \Bigr \vert _{\nu =\gamma (\varvec{\alpha })}, \end{aligned}$$

(26)

where the gradient operator $\nabla _x$ is defined by (21).

Second, by utilized formulas (23), we readily obtain

$$\begin{aligned} \nabla _x u(\mathbf{r}+\nu \varvec{\nu })\Bigr \vert _{\nu =\gamma } \simeq \nabla _\alpha u(\mathbf{r}+\nu \varvec{\nu }) +\varvec{\nu }\frac{\partial u}{\partial \nu }(\mathbf{r}+\nu \varvec{\nu }) \biggr \vert _{\nu =\gamma } -\sum _{i=1,2} \frac{\gamma }{A_i R_i}{} \mathbf{e}_i\frac{\partial u(\mathbf{r})}{\partial \alpha _i}, \end{aligned}$$

and the subsequent application of the Maclaurin approximation yields

$$\begin{aligned} \nabla _x u\bigr \vert _{\partial \varOmega _\Vert } \simeq \Bigl (\nabla _\alpha +\varvec{\nu }\frac{\partial u}{\partial \nu } \Bigr )\biggr \vert _{\partial B_\Vert } +\gamma \biggl (\nabla _\alpha \frac{\partial u}{\partial \nu }+ \varvec{\nu }\frac{\partial ^2 u}{\partial \nu ^2} \biggr )\biggr \vert _{\partial B_\Vert } -\gamma \biggl ( \frac{\mathbf{e}_1}{A_1 R_1}\frac{\partial u}{\partial \alpha _1} +\frac{\mathbf{e}_2}{A_2 R_2}\frac{\partial u}{\partial \alpha _2} \biggr )\biggr \vert _{\partial B_\Vert }. \end{aligned}$$

(27)

Third, substituting the first-order approximations (25) and (27) into Eq. (26), we find

$$\begin{aligned} \frac{\partial u}{\partial n}\biggr \vert _{\partial \varOmega _\Vert } \simeq -\frac{\partial u}{\partial \nu } -\gamma \frac{\partial ^2 u}{\partial \nu ^2} +\nabla _\alpha \gamma \cdot \nabla _\alpha u\,\biggr \vert _{\partial B_\Vert }. \end{aligned}$$

(28)

Thus, the boundary condition (4) can be linearized as follows:

$$\begin{aligned} \frac{\partial u}{\partial \nu }\biggr \vert _{\partial B_\Vert } =-\gamma \frac{\partial ^2 u}{\partial \nu ^2} +\nabla _\alpha \gamma \cdot \nabla _\alpha u\,\biggr \vert _{\partial B_\Vert }. \end{aligned}$$

(29)

In the same way, we replace the boundary condition (3), which is imposed on the surface $\partial \varOmega _\cup$, with the following one on the bit bottom surface:

$$\begin{aligned} \frac{\partial u}{\partial \nu }\biggr \vert _{\partial B_\cup } =\frac{p}{\mu }-\gamma \frac{\partial ^2 u}{\partial \nu ^2} +\nabla _\alpha \gamma \cdot \nabla _\alpha u\,\biggr \vert _{\partial B_\cup }. \end{aligned}$$

(30)

It is to emphasize here that p and $\mu$ are constants.

Finally, let $\gamma ^\delta (\varvec{\alpha })$ denote the gap between the surfaces $\partial B_\cup ^\delta$ and $\partial \varOmega _\cup$ measured from the surface $\partial B_\cup ^\delta$ in the direction of the vector $\varvec{\nu }(\varvec{\alpha })$. Then, in the framework of the first-order approximation, we replace the boundary condition (7) on the free boundary $\partial \varOmega _\cup$ with the following, which is imposed on the bit bottom surface in the unloaded state:

$$\begin{aligned} u\bigl (\varvec{\alpha }+\gamma (\varvec{\alpha })\varvec{\nu }\bigr )= \gamma ^\delta (\varvec{\alpha }),\quad \varvec{\alpha }\in \partial B_\cup . \end{aligned}$$

(31)

Now, the application of the perturbation method to Eq. (31) yields the linearized boundary condition

$$\begin{aligned} \gamma ^\delta -\gamma \frac{\partial u}{\partial \nu }\biggr \vert _{\partial B_\cup } =u\bigr \vert _{\partial B_\cup }. \end{aligned}$$

(32)

Thus, on each part of the known boundary $\partial B$, we again have two boundary conditions, one of which should be used for determination of the gap function.

4 Solution of the linearized free boundary problem

First of all, we emphasize that Eqs. (19), (29), (30), and (32) have been derived by neglecting second-order terms. Therefore, by making use of Eqs. (29) and (30), and staying within the limits of their accuracy, we can simplify Eqs. (19) and (32), respectively, as follows:

$$\begin{aligned} \gamma \bigr \vert _{\partial B_\Vert }= & {} u\bigr \vert _{\partial B_\Vert }, \end{aligned}$$

(33)

$$\begin{aligned} \gamma ^\delta -\frac{p}{\mu }\gamma \biggr \vert _{\partial B_\cup }= & {} u\bigr \vert _{\partial B_\cup }. \end{aligned}$$

(34)

The second leading-order solution of the linearized free boundary problem, which is composed by the Laplace equation

$$\begin{aligned} -\mu \varDelta _x u_0(\mathbf{x})=0,\quad \mathbf{x}\in {\mathbb {R}}^3\setminus \bar{B}, \end{aligned}$$

(35)

and the boundary conditions (29), (30), (33), and (34), can be constructed by satisfying the limit forms of Eqs. (29) and (30), that are

$$\begin{aligned} \frac{\partial u_0}{\partial \nu }\biggr \vert _{\partial B_\cup }=\frac{p}{\mu },\quad \frac{\partial u_0}{\partial \nu }\biggr \vert _{\partial B_\Vert }=0. \end{aligned}$$

(36)

The boundary value problem (35), (36) has a unique solution satisfying the following asymptotic condition:

$$\begin{aligned} u_0(\mathbf{x})=o(1),\quad \vert \mathbf{x}\vert \rightarrow \infty . \end{aligned}$$

(37)

At the same time, the leading-order approximations for the gap functions on the surfaces $\partial B_\Vert$ and $\partial B_\cup$, in light of Eqs. (33) and (34) are given by

$$\begin{aligned} \gamma _0\bigr \vert _{\partial B_\Vert } =u_0\bigr \vert _{\partial B_\Vert }, \end{aligned}$$

(38)

$$\begin{aligned} \gamma _0^\delta \bigr \vert _{\partial B_\cup } =u_0\bigr \vert _{\partial B_\cup }, \end{aligned}$$

(39)

where the right-hand sides are known from the solution $u_0(\mathbf{x})$ of the Neumann problem (35)–(37).

Some comment is necessary on the use of Eq. (39) instead of Eq. (34). Observe that Eqs. (35) and (36) are linear, and, therefore, the function $u_0(\mathbf{x})$ will be proportional to the dimensionless ratio $p/\mu$. On the other hand, Eq. (38) has been derived under the assumption that $\gamma _0$ is relatively small (which turns out to be of the same order as $u_0$). Therefore, when considering the leading-order approximation, the second term on the left-hand side of Eq. (34) can be neglected.

As can be seen from Eq. (39), there arises a difficulty in determining the gap function $\gamma _0$ on the bit bottom surface $\partial B_\cup$. This problem can be solved as follows.

First, by recollecting Eqs. (11) and (12), we can write

$$\begin{aligned} \gamma _0(O)=0,\quad \gamma ^\delta (O)=-\delta _0. \end{aligned}$$

(40)

Therefore, Eqs. (39) and (40) yield

$$\begin{aligned} \delta _0=-u_0(O), \end{aligned}$$

(41)

where $\delta _0$ is the leading-order approximation for the bit displacement.

Let $\mathbf{r}(\alpha _1,\alpha _2)$ be the radius-vector of the surface $\partial B_\cup$. Then, the displaced surface $\partial B_\cup ^\delta$ can be defined by the radius-vector $\mathbf{r}(\alpha _1,\alpha _2)-\delta \mathbf{i}_3$, where $\mathbf{i}_3$ is the $x_3$-axis unit vector. It is to emphasize that, because $\partial B_\cup ^\delta$ is obtained from $\partial B_\cup$ by translation along the vertical, the normal vector $\varvec{\nu }(\alpha _1,\alpha _2)$ of the surface $\partial B_\cup$ will serve as the normal vector for the surface $\partial B_\cup ^\delta$ as well. Therefore, the unknown surface $\partial \varOmega _\cup$ can be approximated by the radius vector

$$\begin{aligned} \mathbf{R}=\mathbf{r}(\varvec{\alpha })-\delta _0\mathbf{i}_3+\varvec{\nu }(\varvec{\alpha }) \gamma _0^\delta (\varvec{\alpha }), \end{aligned}$$

(42)

where $\delta _0$ and $\gamma _0^\delta (\varvec{\alpha })$ are given by Eqs. (41) and (39), respectively.

Thus, since the parametrization (42) is known, the gap $\gamma _0^\delta (\varvec{\alpha })$ between the surface $\partial B_\cup$ and the surface defined by Eq. (42), which is measured from the surface $\partial B_\cup$ in the direction of the vector $\varvec{\nu }(\varvec{\alpha })$ can be determined by direct calculations.

Finally, the first-order approximation can be obtained by solving the boundary value problem

$$\begin{aligned} -\mu \varDelta _x u_1(\mathbf{x})= & {} 0,\quad \mathbf{x}\in {\mathbb {R}}^3\setminus \bar{B}, \end{aligned}$$

(43)

$$\begin{aligned} \frac{\partial u_1}{\partial \nu }\biggr \vert _{\partial B_\Vert }= & {} -\gamma _0\frac{\partial ^2 u_0}{\partial \nu ^2} +\nabla _\alpha \gamma _0\cdot \nabla _\alpha u_0\,\biggr \vert _{\partial B_\Vert }, \end{aligned}$$

(44)

$$\begin{aligned} \frac{\partial u_1}{\partial \nu }\biggr \vert _{\partial B_\cup }= & {} \frac{p}{\mu }-\gamma _0\frac{\partial ^2 u_0}{\partial \nu ^2} +\nabla _\alpha \gamma _0\cdot \nabla _\alpha u_0\,\biggr \vert _{\partial B_\cup }, \end{aligned}$$

(45)

$$\begin{aligned} u_1(\mathbf{x})= & {} o(1),\quad \vert \mathbf{x}\vert \rightarrow \infty , \end{aligned}$$

(46)

and using the equations

$$\begin{aligned} \gamma _1\bigr \vert _{\partial B_\Vert }= & {} \Bigl (1-\frac{\partial u_0}{\partial \nu }\Bigr )^{-1} u_1\biggr \vert _{\partial B_\Vert }, \end{aligned}$$

(47)

$$\begin{aligned} \gamma _1^\delta \bigr \vert _{\partial B_\cup }= & {} \frac{p}{\mu }\gamma _0+u_1\biggr \vert _{\partial B_\cup }, \end{aligned}$$

(48)

where the zero index refers to the leading-order approximations.

5 Example of cylindrical bit

Let B be a semi-infinite circular cylinder of unit radius, so that the surface $\partial B_\cup$ coincide with the circular part $0\le r\le 1$ of the plane $z=0$. For this bit configuration, the leading-order approximation problem (35)–(37) represents a special case of the external Neumann problem for a semi-infinite cylinder studied in [29], i.e.,

$$\begin{aligned} \frac{1}{r}\frac{\partial }{\partial r}\Bigl (r\frac{\partial U_0}{\partial r}\Bigr ) +\frac{\partial ^2 U_0}{\partial z^2}=0,\quad \frac{\partial U_0}{\partial z}\biggr \vert _{z=0,\ r<1}=f_0,\quad \frac{\partial U_0}{\partial r}\biggr \vert _{r=1,\ z>0}=0, \end{aligned}$$

where $f_0$ is a constant,

$$\begin{aligned} f_0=1. \end{aligned}$$

(49)

The function $U_0(r,z)$ is represented as follows [29]:

$$\begin{aligned} U_0(r,z)= & {} \int \limits _0^\infty A_0(\lambda )J_0(\lambda r)\mathrm{{e}}^{\lambda z}\mathrm{{d}}\lambda ,\quad z<0,\quad 0\le r<\infty , \end{aligned}$$

(50)

$$\begin{aligned} U_0(r,z)= & {} \int \limits _0^\infty B_0(\lambda )\mathrm{Im}\left\{ \frac{H_0^{(1)}(\lambda r)}{\bigl [H_0^{(1)}(\lambda r) \bigr ]^\prime }\right\} \mathrm{{e}}^{-\lambda z}\mathrm{{d}}\lambda ,\quad z>0,\quad r>1. \end{aligned}$$

(51)

Here, $J_0(x)$ and $H_0^{(1)}(x)$ are Bessel functions of the first and third kind.

In turn, the functions $A_0(\lambda )$ and $B_0(\lambda )$ depend on the solution $\omega _0(x)$ of the integral equation

$$\begin{aligned} \omega _0(x)=\frac{I_1(x)}{2K_1(x)}e^{-2x}\left\{ \frac{2(x+1)}{x^2}-\int \limits _0^\infty \frac{\omega _0(y)}{x+y}\,\mathrm{{d}}y\right\} \end{aligned}$$

(52)

via the function

$$\begin{aligned} D_0(\lambda )=\frac{\mathrm{{i}}}{\pi }\mathrm{{e}}^{\mathrm{{i}}\lambda }\left\{ 2\frac{(i\lambda -1)}{\lambda ^2}+\int \limits _0^\infty \frac{\omega _0(x)\,\mathrm{{d}}x}{\mathrm{{i}}\lambda -x}\right\} \end{aligned}$$

(53)

as follows:

$$\begin{aligned} A_0(\lambda )=\mathrm{Re\,}D_0(\lambda ),\quad B_0(\lambda )=-\mathrm{Im}\bigl \{ \bigl [H_0^{(2)}(\lambda )\bigr ]^\prime D_0(\lambda ) \bigr \}. \end{aligned}$$

(54)

Here, $I_1(x)$ and $K_1(x)$ are modified Bessel functions of the first and second kind, $\mathrm{Re}$ and $\mathrm{Im}$ denote the real part and the imaginary part.

Let us rewrite Eq. (52) in the form

$$\begin{aligned} \omega _0(x)=f(x)-F(x)\int \limits _0^\infty \frac{\omega _0(y)\,\mathrm{{d}}y}{x+y}, \end{aligned}$$

(55)

where we have introduced the notation

$$\begin{aligned} f(x)=\frac{2(x+1)}{x^2}F(x),\quad F(x)=\frac{I_1(x)}{2K_1(x)}\mathrm{{e}}^{-2x}. \end{aligned}$$

Then, the use of Taylor and asymptotic expansions of the modified Bessel functions yields

$$\begin{aligned} F(x)\simeq x^2,\quad x\rightarrow 0,\quad F(x)=\frac{1}{2\pi }+O\Bigl (\frac{1}{x}\Bigr ),\quad x\rightarrow \infty . \end{aligned}$$

(56)

Observe that the solvability of singular integral equations (55) of type (56) was studied in detail in [30, 31].

To solve Eq. (55), we use the Bubnov–Galerkin method and look for the solution in the form of the expansion

$$\begin{aligned} \omega _0(x)=\sum _{n=0}^\infty a_n\varphi _n(x), \end{aligned}$$

(57)

where

$$\begin{aligned} \varphi _n(x)=\mathrm{e}^{-x/2}L_n(x), \end{aligned}$$

and $L_n(x)$ are the Laguerre polynomials defined as

$$\begin{aligned} L_n(x)=\sum _{k=0}^n \frac{(-1)^k}{k!}C_n^k x^k,\quad C_n^k=\frac{n!}{k!(n-k)!}. \end{aligned}$$

The substitution of (57) into Eq. (55) results in the infinite system of linear algebraic equations

$$\begin{aligned} a_n=b_n-\sum _{k=0}^\infty M_{nk}a_k, \end{aligned}$$

(58)

where

$$\begin{aligned} b_n=\int \limits _0^\infty f(x)\varphi _n(x)\,\mathrm{{d}}x,\quad M_{nk}=\int \limits _0^\infty \varphi _n(x)F(x)\,\mathrm{{d}}x \int \limits _0^\infty \frac{\varphi _k(y)}{x+y}\,\mathrm{{d}}y. \end{aligned}$$

(59)

In view of (56), all integrals (59) are convergent. The infinite system (58) is then solved by truncation. Observe that by means of formula (3.353.5) from [32] the iterated improper integral (59)$_2$ can be evaluated as follows:

$$\begin{aligned} M_{nk}=\int \limits _0^\infty \varphi _n(x)F(x) \sum _{m=0}^k\frac{C_k^m}{m!}\biggl ( -x^m \mathrm{{e}}^{x/2}\mathrm{Ei}\Bigl (-\frac{x}{2}\Bigr ) +\sum _{l=1}^m (-1)^l 2^l (l-1)! x^{m-l}\biggr )\mathrm{{d}}x. \end{aligned}$$

Here, $\mathrm{Ei}(x)$ is the exponential integral. We note also that the substitution of (57) into (53) leads to the integrals $\int _0^\infty x^m \mathrm{{e}}^{-px}(\lambda ^2+x^2)^{-1}\,\mathrm{{d}}x$, which can be evaluated in terms of the sine and cosine integrals $\mathrm{Si}(x)$ and $\mathrm{Ci}(x)$.

In the problem under consideration, the following quantities are of interest:

$$\begin{aligned} U_0(r,0)=\int \limits _0^\infty A_0(\lambda )J_0(\lambda r)\,\mathrm{{d}}\lambda ,\quad 0\le r\le 1, \end{aligned}$$

(60)

$$\begin{aligned} U_0(1,z)=-\frac{2}{\pi }\int \limits _0^\infty \frac{B_0(\lambda )\mathrm{{e}}^{-\lambda z}\mathrm{{d}}\lambda }{ \lambda \bigl [J_1^2(\lambda )+Y_1^2(\lambda )\bigr ]},\quad 0\le z<\infty . \end{aligned}$$

(61)

Here, according to Eqs. (53) and (54), we have

$$\begin{aligned} A_0(\lambda )= & {} \frac{2}{\pi \lambda ^2}(\sin \lambda -\lambda \cos \lambda ) +\frac{\sin \lambda }{\pi }\int \limits _0^\infty \frac{\omega _0(x)x}{\lambda ^2+x^2}\,\mathrm{{d}}x +\frac{\lambda \cos \lambda }{\pi }\int \limits _0^\infty \frac{\omega _0(x)\,\mathrm{{d}}x}{\lambda ^2+x^2}, \end{aligned}$$

(62)

$$\begin{aligned} B_0(\lambda )= & {} -\frac{2J_1(\lambda )}{\pi \lambda ^2}(\lambda \sin \lambda +\cos \lambda ) -\frac{2Y_1(\lambda )}{\pi \lambda ^2}(\sin \lambda -\lambda \cos \lambda ) -\frac{1}{\pi }\bigl [J_1(\lambda )\cos \lambda +Y_1(\lambda )\sin \lambda \bigr ] \int \limits _0^\infty \frac{\omega _0(x)x}{\lambda ^2+x^2}\,\mathrm{{d}}x \nonumber \\&+\frac{\lambda }{\pi }\bigl [J_1(\lambda )\sin \lambda -Y_1(\lambda )\cos \lambda \bigr ] \int \limits _0^\infty \frac{\omega _0(x)\,\mathrm{{d}}x}{\lambda ^2+x^2}. \end{aligned}$$

(63)

Note that in the derivation of formula (63), we made use of the known relations $H_0^{(2)}(\lambda )=J_0(\lambda )-\mathrm{{i}} Y_0(\lambda )$ and $\bigl [H_0^{(2)}(\lambda )\bigr ]^\prime =-J_1(\lambda )+\mathrm{{i}} Y_1(\lambda )$.

Fig. 3

Gap functions on the rupture front in the case of a flat-ended cylindrical bit

The results for the leading-order approximations for the relative displaced gap function ${\bar{\gamma }}^\delta =(\mu /p)\gamma ^\delta$ and the relative gap function ${\bar{\gamma }}=(\mu /p)\gamma$ under the bit’s base are shown in Fig. 3. It is interesting to observe that, since $\mathbf{n}=\mathbf{e}_3$ and $\varvec{\nu }=-\mathbf{e}_3$, the bottom surface $\partial \varOmega _\cup$ of the bore-hole is concave (i.e., curving inward).

6 Discussion

Let us comment on the derivation of the linearized free boundary problem (35)–(37), and in particular to answer the question of why we have chosen the boundary conditions (36). Consider, first, the lateral boundary $\partial B_\Vert$, where we have got two equations (29) and (33). By excluding the unknown function $\gamma$, we arrive at the equation

$$\begin{aligned} \frac{\partial u}{\partial \nu } +u\frac{\partial ^2 u}{\partial \nu ^2} -\nabla _\alpha u\cdot \nabla _\alpha u\biggr \vert _{\partial B_\Vert }=0. \end{aligned}$$

(64)

Now, by accounting for Eq. (5) and the formula

$$\begin{aligned} \nabla _x^2\bigr \vert _{\partial B_\Vert }= \nabla _\alpha ^2+2H\frac{\partial }{\partial \nu } +\frac{\partial ^2}{\partial \nu ^2}, \end{aligned}$$

where $H=\bigl (R_1^{-1}+R_2^{-1}\bigr )/2$ is the mean curvature, and

$$\begin{aligned} \nabla _\alpha ^2=\frac{1}{A_1 A_2}\biggl \{ \frac{\partial }{\partial \alpha _1}\Bigl ( \frac{A_2}{A_1}\frac{\partial }{\partial \alpha _1}\Bigr ) +\frac{\partial }{\partial \alpha _2}\Bigl ( \frac{A_1}{A_2}\frac{\partial }{\partial \alpha _2}\Bigr ) \biggr \}, \end{aligned}$$

we can rewrite Eq. (64) as follows:

$$\begin{aligned} \frac{\partial u}{\partial \nu } -u\nabla _\alpha ^2 u-2H u\frac{\partial u}{\partial \nu } -\nabla _\alpha u\cdot \nabla _\alpha u\biggr \vert _{\partial B_\Vert }=0. \end{aligned}$$

(65)

Thus, it is readily seen that the second equation (36) has been obtained as a linearization of Eq. (65).

Further, the derivation of the nonlinear boundary condition from Eqs. (30) and (32) has been complicated by the presence of $\gamma ^\delta$ along with $\gamma$. For shallow surfaces, one can make use of the approximation $\gamma ^\delta \simeq \gamma +\delta \varvec{\nu }\cdot \mathbf{i}_3$ and the equations $\gamma ^\delta =u$ and $\gamma ^\delta (O)=-\delta$ to obtain $\gamma \simeq u+u(O)\nu _3$. The latter equation allows us to rewrite Eq. (30) in the form

$$\begin{aligned} \frac{\partial u}{\partial \nu } -(u+u(O)\nu _3)\Bigl (\nabla _\alpha ^2 u +2H\frac{\partial u}{\partial \nu }\Bigr ) -\nabla _\alpha (u+u(O)\nu _3)\cdot \nabla _\alpha u\biggr \vert _{\partial B_\cup } =\frac{p}{\mu }. \end{aligned}$$

(66)

Again, the linearization of Eq. (66) leads to the corresponding boundary condition (see Eq. (36)$_1$) for the leading-order approximation.

By analogy with the contact problem of drilling, which was formulated in [27], we can consider the following rupture front equation instead of Eq. (3):

$$\begin{aligned} \Bigl (\frac{\partial u}{\partial n}\Bigr )^2 +\vert \nabla _s u\vert ^2\biggr \vert _{\partial \varOmega _\cup } =\Bigl (\frac{\sigma _c}{\mu }\Bigr )^2. \end{aligned}$$

(67)

Here, $\nabla _s u$ is the gradient of the function u in the local orthogonal curvilinear coordinate system $\mathbf{s}=(s_1,s_2)$ on the surface $\partial \varOmega _\cup$, $\sigma _c$ is a positive constant.

The boundary condition (67) should be supplemented by the inequality

$$\begin{aligned} \frac{\partial u}{\partial n}\biggr \vert _{\partial \varOmega _\cup }<0, \end{aligned}$$

(68)

which ensures the load transfer from the bit to the bore-hole surface.

Hence, in light of (68), Eq. (67) can be rewritten as follows:

$$\begin{aligned} -\frac{\partial u}{\partial n}\biggr \vert _{\partial \varOmega _\cup } =\sqrt{\frac{\sigma _c^2}{\mu ^2}-\vert \nabla _s u\vert ^2} \biggr \vert _{\partial \varOmega _\cup }. \end{aligned}$$

(69)

The boundary condition (69) can be moved from the surface $\partial \varOmega _\cup$ to the surface $\partial B_\cup$, and in the light of leading-order approximation one can arrive at the following result:

$$\begin{aligned} \frac{\partial u_0}{\partial \nu }\biggr \vert _{\partial B_\cup } =\sqrt{\frac{\sigma _c^2}{\mu ^2}-\vert \nabla _\alpha u_0\vert ^2} \biggr \vert _{\partial B_\cup }. \end{aligned}$$

(70)

Observe that the nonlinearity of Eq. (70) is due to the intrinsic nonlinearity of the boundary condition (67). Note that the solvability of the so-called exterior gravitational problem has been studied in [33, 34].

Another modification of the considered problem formulation that can be introduced by analogy with the deep drilling problem [27] is the assumption that only the bore-hole bottom surface $\partial \varOmega _\cup$ is a free boundary, whereas the lateral surface $\partial \varOmega _\Vert$ is assumed to be cylindrical with the radius determined by the homogeneous Neumann boundary condition (4) and the continuity with the adjacent part of the surface $\partial \varOmega _\cup$. In this case, it can be shown that the linearized problem equations (35)–(38), (40), and (41) still hold. Note also that, by employing the terminology used in [35], such free boundary problem can be termed as partially overdetermined.

Finally, in the same way as it was done in Sect. 3, it can be shown that the boundary conditions from the free boundary $\varGamma$ can be moved onto any nearby surface $\varGamma _j$. This simple idea, together with a approximate rule for iteration of the boundary, forms the basis of numerical methods for free boundary problems. Assuming that $u_j(\mathbf{x})$ solves the Neumann problem with the boundary condition

$$\begin{aligned} -\mu \frac{\partial u_j}{\partial n}(\mathbf{x})=p\mathcal{H}\bigl (n_3^j(\mathbf{x})\bigr ),\quad \mathbf{x}\in \varGamma _j, \end{aligned}$$

the new surface $\varGamma _{j+1}$ can be found (see, e.g., [36]) by moving $\varGamma _j$ in its normal direction $\mathbf{n}^j$ so that

$$\begin{aligned} u_j\big (\mathbf{x}^{j+1}\big )\approx u_j\big (\mathbf{x}^j\big )+\frac{\partial u_j}{\partial n}\big (\mathbf{x}^j\big )d_j\big (\mathbf{x}^j\big ), \end{aligned}$$

where $\mathbf{x}^{j+1}=\mathbf{x}^j+\mathbf{n}^j d_j(\mathbf{x}^j)$, and the distance $d_j(\mathbf{x}^j)$ is determined by the requirement that $\mathbf{x}^{j+1}$ equals the right-hand side of the Dirichlet boundary condition (16). In a similar way, we can derive the $j+1$-th approximation ($j=0,1,\ldots$) for the gap function

$$\begin{aligned} \gamma _{j+1}(\varvec{\alpha })=u^j_0(\varvec{\alpha })+u^j_0(O)\nu _3^j(\varvec{\alpha })\mathcal{H}\bigl (-\nu _3^j(\varvec{\alpha })\bigr ). \end{aligned}$$

(71)

In the iterative algorithm (72), the linearized free boundary problem (35)–(37) in the exterior of the surface $\varGamma _j$ can be solved on each iteration starting from $\varGamma _0=\partial B$.

It should be emphasized that the function $\gamma _{j+1}$ denotes the gap between the surfaces $\varGamma _j$ and $\varGamma$ measured from the surfaces $\varGamma _j$ in the direction of the normal vector $\varvec{\nu }^j$, and the difference between the gaps $\gamma _{j+1}$ and $g_{j+1}$, which is measured from the corresponding point on the surface $\varGamma$, was tentatively assumed to be small. At the same time under the latter assumption, the gap function $g^\delta$, which enters the boundary condition (7), can be interpreted in terms of the distance function from $\partial B^\delta _\cup$ to $\varGamma$. Indeed, let $\mathbf{x}\in \varGamma$ and $\varvec{\alpha }\in \partial B^\delta _\cup$, where $\varvec{\alpha }=(\alpha _1,\alpha _2)$ are the local curvilinear coordinates on $\partial B$, such that $\mathbf{r}(\varvec{\alpha })=\mathbf{x}+g^\delta (\mathbf{x})\mathbf{n}(\mathbf{x})$. Then, we have $g^\delta (\mathbf{x})=\mathrm{dist}\bigl (\mathbf{r}(\varvec{\alpha }),\varGamma \bigr )$ and, therefore, the solution $u_0(\mathbf{x})$ of the Neumann problem (35)–(37) yields $g^\delta _0(\mathbf{x})=u_0\bigl (\mathbf{r}(\varvec{\alpha })\bigr )$, where $\varvec{\alpha }\in \partial B^\delta _\cup$. Thus, the iterative scheme (72) can be modified accordingly.

However, by using the specificity of the present problem, the new boundary iteration procedure can be formulated as follows. Given the j-th gap $g_j(\mathbf{x})$ for $\mathbf{x}\in \varGamma _j$, one can find $\varvec{\alpha }^{j+1}(\mathbf{x})\in \partial B$ such that $\mathbf{r}(\varvec{\alpha }^{j+1})=\mathbf{x}+g_j(\mathbf{x})\mathbf{n}^j(\mathbf{x})$, thereby parameterizing the surface $\partial B$. Taking into account that for any $\mathbf{x}\in \partial \varOmega _\cup ^j$, the boundary condition (7) applied on the boundary $\varGamma _j$ yields $g_j^\delta (\mathbf{x})$ and $\delta _j=-u_j(O)$. Now, the new surface $\partial \varOmega _\cup ^{j+1}$ can be determined so that

$$\begin{aligned} u_j(\mathbf{x})-u_j(O)n_3^j(\mathbf{x})=\mathrm{dist}\bigl (\mathbf{r}(\varvec{\alpha }^{j+1}(\mathbf{x})), \partial \varOmega _\cup ^{j+1}\bigr ), \end{aligned}$$

(72)

and the final extension of the surface $\partial \varOmega _\cup ^{j+1}$ is determined by reinforcing the first boundary condition (14). We note that Eq. (72) determines the surface $\partial \varOmega _\cup ^{j+1}$ by incorporating the geometry of Huygens’ principle (see, e.g., [37]).

Here, for consistency’s sake, we complement this discussion by taking a physical point of view with respect to the gradient boundary condition (3). Namely, in considering the scalar prototype problem, which is a simpler version of the elasticity problem that was introduced earlier in [23, 24], we may interpret the normal derivative $\partial u_0/\partial \nu$ as the normal pressure and the tangential gradient $\nabla _\alpha u_0$ as the tangential stress vector. In this way, one can introduce the following generalized fracture criterion:

$$\begin{aligned} \biggl (\frac{\mu }{\sigma _c} \frac{\partial u_0}{\partial \nu }\biggr )^\alpha +\lambda \biggl (\frac{\mu }{\sigma _c}\vert \nabla _\alpha u_0\vert \biggr )^\beta =1. \end{aligned}$$

(73)

Here, $\alpha$, $\beta$, and $\lambda$ are dimensionless positive constants.

Thus, depending on its value, which is supposed to be determined experimentally, the parameter $\lambda$ can be regarded as either small or large. This opens new possibilities for asymptotic analysis of the scalar prototype problem of deep percussive drilling.