Abstract
Although various forms for the Hashin–Shtrikman bounds on the effective elastic properties of inhomogeneous materials have been written down over the last few decades, it is often unclear how to construct and compute such bounds when the material is not of simple type (e.g. isotropic spheres inside an isotropic host phase). Here, we show how to construct, in a straightforward manner, the Hashin–Shtrikman bounds for generally transversely isotropic two-phase particulate composites where the inclusion phase is spheroidal, and its distribution is governed by spheroidal statistics. Note that this case covers a multitude of composites used in applications by taking various limits of the spheroid, including both layered media and long unidirectional composites. Of specific interest in this case is the fact that the corresponding Eshelby and Hill tensors can be derived analytically. That the shape of the inclusions and their distribution can be specified independently is of great utility in composite design. We exhibit the implementation of the computations with several examples.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Fibre-reinforced composites (FRCs) are commonly employed in numerous applications in science and engineering, one of their main uses being to provide improved tensile strength. It is therefore of great interest to possess knowledge of the overall (effective) properties of such materials; of specific interest in this article will be their effective linear elastic properties and the ability to determine useful bounds on these for a variety of fibre microstructures. FRCs typically occur as one of two types: long unidirectional fibre materials where the fibres are aligned (parallel) to some common axis and they are so long that end effects can be neglected, or short fibre materials where the short fibres may or may not be aligned, depending upon the application. Such FRCs are frequently then used as ply phases in order to build up layered composites, see e.g. Tsai [1]. Furthermore, such layered and FRC materials have the potential to be of great use in modern metamaterial applications as was described by Torrent and Sanchez-Dehesa [2] and Amirkhizi et al. [3] for example. The main objective of this article is to pull together ideas relating to FRCs from a variety of diverse publications, placing particular emphasis on the explicit construction and computation of the Hashin–Shtrikman bounds on effective elastic constants, including information regarding the two-point correlation functions associated with the distribution of inclusion phases.
From a mathematical viewpoint, modelling inhomogeneous materials such as FRCs, which possess a microstructure (i.e. a lengthscale that is much smaller than the characteristic lengthscale of loading, e.g. a propagating wavelength) is difficult, because the partial differential equations that arise possess rapidly varying coefficients (in space). Before the early 1960s, there was a paucity of theoretical work regarding the prediction of the effective behaviour of elastic composite materials, i.e. elastic materials composed of two or more so-called phases that are mixed together in order to improve and/or optimize the overall material behaviour in some sense. In particular, very limited information was available regarding the prediction of the fourth-order effective linear elastic modulus tensor \(\mathbf {C}^*\). Key results were those of Voigt [4] and Reuss [5] in 1889 and 1929, respectively, whose approximations of uniform strain and stress (respectively) throughout the composite are straightforwardly identified as upper and lower bounds (respectively) on the effective elastic properties. For a composite with phases labelled \(r=0,\ldots ,n\) and with associated elastic modulus tensors \(\mathbf {C}^r\), these bounds are written
Here the bounds are interpreted component-wise and the Reuss (lower) bound \(\mathbf {C}^R\) is defined by
where \(\phi _r\) is the volume fraction of the \(r\)th phase, and \(\mathbf {I}\) is the fourth-order identity tensor with components \(I_{ijk\ell }=(\delta _{ik}\delta _{j\ell }+\delta _{i\ell }\delta _{jk})/2\). We have used \(\mathbf{A}^{-1}\) to denote the inverse of the tensor \(\mathbf{A}\). Later, we discuss technical aspects for the inversion of transversely isotropic tensors. Finally, the Voigt (upper) bound \(\mathbf {C}^V\) is defined by
In addition to these bounds, there also existed Eshelby’s dilute estimate for particulate composites derived in his seminal paper of 1957 [6]. Such dilute estimates are only valid for small volume fractions \(\phi _r\) (asymptotically correct to \({\mathcal O}(\phi _r)\)) and furthermore, although the establishment of the Reuss/Voigt bounds was an important step, in many cases, the distance between these bounds can be large, meaning that little can be inferred as regards the effective elastic properties themselves.
Numerous important contributions to the subject occurred in the early 1960s, the main motivation being the understanding of the overall behaviour of FRCs. At that time, such materials were used in a variety of applications but principally within the aerospace industry because of their high strength-to-weight ratio compared with more conventional structural materials. In particular, Hashin and Shtrikman [7] established a variational principle for elastostatics which they subsequently applied to multiphase (macroscopically isotropic) composites [8]. The resulting bounds on the effective bulk and shear moduli are the celebrated Hashin–Shtrikman bounds. Hashin [9] extended the principle in order to derive bounds for long FRCs where the macroscopic anisotropy is that of transverse isotropy and phases are isotropic. Hashin [10] also derived results for fibre reinforced composites where phases are transversely isotropic but not via the classical Hashin–Shtrikman variational scheme. Derivations of the Hashin–Shtrikman bounds have been improved and revised by many authors since they were originally devised. In particular, we note the works [11] and [12–16]. The analogous problem for nonlinear heterogeneous media has been treated less frequently. In this regard, we can refer to Willis [17] where the approach of Hill [18] was applied to nonlinear dielectrics, and Talbot and Willis [19] where theoretical aspects of the extension of the Hashin–Shtrikman variational principles to nonlinear heterogeneous systems were formulated. Other variational structures for nonlinear media, based on comparisons with linear homogeneous media that allow the estimation of the effective energy function of nonlinear composites, in terms of the corresponding properties for linear problems with the same microscopic distribution, were obtained by Ponte Castañeda [20, 21].
The articles just described were instrumental in enabling general forms of the Hashin–Shtrikman bounds to be written down for arbitrarily anisotropic composites.
Working in Cartesian coordinates \(x_1, x_2, x_3\), let us denote differentiation of a second-order tensor \(\varvec{\sigma }=\varvec{\sigma }(x_1,x_2,x_3)\) with respect to \(x_k\) by \(\varvec{\sigma }_{\!,k}\), and we adopt the Einstein summation convention for summation over repeated indices. We also introduce the notation \(\mathbf{x}=(x_1,x_2,x_3)\). The key step in a most succinct derivation of the Hashin–Shtrikman bounds in the structure developed by Willis [12] is to write the standard governing equations of elastostatics for an inhomogeneous material in an alternative form. Upon neglecting body forces and supposing that the elastic modulus tensor of the inhomogeneous material is \(\mathbf {C}=\mathbf {C}(\mathbf{x})\), the equations of elastostatics are
where \(\varvec{\sigma }\) is the Cauchy stress tensor, \(\mathrm{div}\) is the divergence operator, \(\mathbf {e}\) is the linear strain tensor, and the superscript \(\mathrm{T}\) here denotes transpose. In common with much of the existing literature, we use notation \(\mathbf{A}\mathbf{B}\) to denote contraction over the final two and first two indices of the tensors \(\mathbf{A}\) and \(\mathbf{B}\), respectively. This is rather convenient as it can be applied to tensors of arbitrary order. Here the \(ij\)th component of \(\mathbf{C}\mathbf{e}\) is therefore \(C_{ijk\ell }e_{\ell k}=C_{ijk\ell }e_{k\ell }\) and also later, we will use this notation extensively for the contraction of two fourth-order tensors \(\mathbf{A}\) and \(\mathbf{B}\) so that the \(ijk\ell \)th component of \(\mathbf{A}\mathbf{B}\) is \(A_{ijmn}B_{nmk\ell }\).
The alternative form of (1.2) used by Willis is derived by writing Hooke’s law as \(\varvec{\sigma } = \mathbf {C}^c\mathbf {e} + \varvec{\tau }(\mathbf {x})\) where \(\mathbf {C}^c\) is a homogeneous linear elastic comparison material (the choice of which will be discussed shortly), and \(\varvec{\tau }\) is the so-called polarization stress, which is necessarily spatially dependent. The equations of elastostatics thus reduce to
where \(\varvec{\sigma }^c=\mathbf {C}^c\mathbf {e}\). The divergence of the polarization stress can therefore be interpreted as a spatial distribution of body forces in a homogeneous medium with elastic modulus tensor \(\mathbf{C}^c\). Upon introducing the second-order elastostatic Green’s tensor \(\mathbf{G}^c\) associated with the (anisotropic) comparison material, a variational principle on the strain energy is then found in terms of the polarization stress \(\varvec{\tau }(\mathbf{x})\) [12, 16]. Next, we choose the polarization stress to be piecewise uniform (uniform in each phase), usually written as \(\varvec{\tau }(\mathbf{x})=\sum _{k=0}^N\chi _k(\mathbf{x})\varvec{\tau }^r\) where \(\chi _k(\mathbf{x})\) is unity when \(\mathbf{x}\) resides in the \(k\)th phase and is zero otherwise, and each component of \({\varvec{\tau }}^r\) is constant.
Optimizing with respect to \(\varvec{\tau }^r\) and choosing the distribution function to have the same spheroidal statistics as the shape of the corresponding inclusion phase, we are led to the classical (and much quoted) form of the Hashin–Shtrikman bounds ((3.13) below) derived by Willis [12]. This form can also be deduced from the more general formulation (3.8) developed by Ponte Castañeda and Willis [16] which allows for more general distributions. The key advantage of the Hashin–Shtrikman bounds over the Reuss–Voigt bounds is that the former uses information about the macroscopic anisotropy; this permits an improvement over the Reuss–Voigt bounds in almost all cases.
It is worth noting at this point that improved bounds, using more general polarizations leading to higher-order statistics, can also be derived [22–24]. However, it is often the case that such higher-order statistical correlation information for a given material is not known or difficult to determine accurately.
Although the general form for the Hashin–Shtrikman bounds applicable to arbitrarily anisotropic composites can be derived in a straightforward manner in some cases, only very recently have explicit bounds for generally transversely isotropic materials been written down [25]. Furthermore, as far as the authors are aware, works concerning the construction and computation of such bounds for a given material, using tensor bases (thus permitting fast implementation), are not available. Indeed it appears that the Hashin–Shtrikman bounds have often taken on a mysterious air in the literature. These bounds always appear to be merely stated (not derived constructively) and almost no information can be found in the literature regarding bounds on the effective properties of composites that are not simply either macroscopically isotropic or transversely isotropic of the long FRC variety. Therefore, the step taken in [25] was a useful and important one since explicit bounds were stated and compared with numerous homogenization and micromechanical methods. However, in [25], very little discussion of the required tensor-basis for transverse isotropy was given, and furthermore the uniformity of the so-called \(\mathbf {P}\)-tensor (directly related to the Eshelby tensor and sometimes known as the Hill tensor in the literature) was not exploited fully since expressions for the \(\mathbf {P}\)-tensor were given in integral form, rather than explicit expressions which have been previously derived for spheroidal inclusions and distributions.
For all of the reasons above, the construction and computation of the Hashin–Shtrikman bounds for those “not in the know” are far from straightforward. This is important specifically for engineers, materials scientists and industrialists who may wish to construct the Hashin–Shtrikman bounds for a variety of such media. They are often restricted from doing so by lack of information regarding the detail of the construction. It would be convenient to have a systematic and prescriptive way of constructing the Hashin–Shtrikman bounds from the first principles. That is, given the volume fractions, elastic properties, shapes of phases of the composite and their spatial distribution, it would be convenient to have a mechanism by which the Hashin–Shtrikman bounds could be constructed in a straightforward manner using the correct tensor basis set and the appropriate expressions for the Eshelby (\(\mathbf {S}\)) tensors and/or Hill (\(\mathbf {P}\)) tensors. In particular in this respect, it appears that although knowledge of explicit bounds is very useful, we would argue that it is less important than being able to construct the bounds from the first principles.
The principal objective of this article is therefore the discussion of such a construction and computation of the Hashin–Shtrikman bounds for transversely isotropic composites restricting attention to two-phase fibre-reinforced media. We consider cases that incorporate separately the influence of the fibre (or “inclusion”) phase and the distribution of these inclusions. Initially, we shall consider the general case of an arbitrary number of phases, but considering general statistics makes the study of media with more then one inclusion phase more complicated, and therefore that case shall be considered in a follow-up article.
The paper is organized as follows. In Sect. 2, we introduce notation and the basics concerning Hill’s tensor. In Sect. 3, we describe the general formulation of the Hashin–Shtrikman bounds, initially for the general multiphase case before restricting attention to two phases, the primary concern of this article. We specialize in Sect. 4 to the case of macroscopically transversely isotropic materials. This specialization therefore motivates the discussion of transversely isotropic fourth-order tensors in Sect. 5 and in particular we describe a convenient basis set for such tensors which was introduced in this context by Hill [26]. In Sect. 6, we describe how such a basis set, together with knowledge of the appropriate Hill and Eshelby tensors (stated in the appendices), allows us to construct the Hashin–Shtrikman bounds in a straightforward, procedural manner. We discuss the specific limiting cases of layered and long cylindrical fibre-reinforced media in Sect. 7 before illustrating the implementation of the construction via some examples in Sect. 8. The main focus is the illustration of the simple implementation via the basis set employed as well as the study of distributions of inclusions that have a different spheroidal spread to their shape, the latter being associated with the appropriate Hill tensor. We conclude in Sect. 9 indicating required areas for future study.
2 Notation and preliminaries
Let us first define some language: we shall say that a tensor is uniform if all of its components are constant (and these components can be different constants of course). In this article, we speak generally at first with regard to multi-phase particulate composite materials occupying the domain \(\varOmega \) with closed boundary \(\partial \varOmega \) and with \(n\) types of inclusion phase that could be chosen independently of their spatial distribution [16]. We denote the elastic modulus tensor of the \(r\)th inclusion phase by \(\mathbf{C}^r\!, r=1,\ldots ,n\). Inclusion phases are embedded inside a host phase with elastic modulus tensor \(\mathbf{C}^0\). Although results can in principle be obtained for ellipsoidal inclusions, let us restrict attention to the case of spheroidal inclusions; this is convenient for reasons that will become clear shortly. We note that this case is extremely useful since many composites are of this class (including the limiting cases of long FRCs and layered media). Let us denote \(\varOmega ^r\) as the total domain of the \(r\)th phase, i.e. it is the collection of all spheroidal inclusions which constitute that phase, each aligned and having the shape defined by a domain \(V^r\). Each spheroid constituting the \(r\)th phase is located at a different point in space; in terms of the computation of the Hashin–Shtrikman bounds, only their shape and distribution is important. The total volume fraction of this phase is therefore \(\phi _r=|\varOmega ^r|/|\varOmega |\) where \(|\cdot |\) denotes a volume. The volume fraction of the host phase is therefore \(\phi _0=1-\sum _{r=1}^n\phi _r\).
In micromechanics and homogenization, a specific tensor known as the \(\mathbf {P}\)-tensor frequently arises [13]. This fourth-order tensor, also often known as Hill’s polarization tensor, has components defined by
being linked with the free-space Green’s tensor having components \(G^c_{ij}(\mathbf{x}-\mathbf{y})\), i.e. that associated with the linear comparison phase having elastic modulus tensor \(\mathbf {C}^c\). We note that the integral in (2.1) is over the domain of a spheroid in the \(r\)th phase, i.e. \(V_r\) (hence the superscript \(r\) on \(\mathbf{P}\)) and dependent only on the ratio of semi-axes, and not the size of the spheroid. It is also independent of the material properties of the inclusion so that in the particular case where all inclusion phases are of the same shape, the \(\mathbf {P}\)-tensor considered here is identical for any phase. The notation \(|_{(ij),(k\ell )}\) indicates symmetrization with respect to these indices, i.e. for a tensor \(Q_{ijk\ell }\) such a symmetrization would be
If the domain \(V_r\) is spheroidal as here (ellipsoidal even) then the \(\mathbf {P}\)-tensor defined in (2.1) is uniform (i.e. each component is constant) [6, 27, 28]. Note that \(P_{ijk\ell }^c\), Hill’s tensor associated with the comparison phase, is related to the Eshelby tensor \(S^c_{ijk\ell }\) via the expression
where the second equality is due to the inclusions being ellipsoids so that \(S^r_{ijmn}=S^r_{jimn}\).
The \(\mathbf {P}\)-tensor associated with an ellipsoidal inclusion of the \(k\)th phase, say \(V_{k}= \{\mathbf {x}:\, |\mathbf {A}^{(k)}_s \mathbf {x}|^2<1\}\), for some second-order tensor \(\mathbf{A}_s^{(k)}\) (which is usually diagonal with diagonal components corresponding to the semi-axes of the ellipsoid) may be computed from the expression
where \(S^2\) is the unit sphere and \(\bar{\varvec{\xi }}\) is a unit vector pointing from the centre of \(S^2\) to a point on its surface. Furthermore,
For spheroidal inclusions, explicit forms may be obtained as is detailed in Appendix B. The subscript ‘s’ is associated with shape, to distinguish it from an analogous quantity (with subscript \(d\)) that we will encounter shortly associated with distributions.
3 The Hashin–Shtrikman variational principle
In his paper of 1977, Willis [12] developed a variational structure to derive the Hashin–Shtrikman bounds. Introducing a polarization stress relative to a so-called comparison material, both the inclusion shape and their distribution (from integrals of the associated two-point correlation functions) are incorporated through appropriate influence tensors. The distribution tensors were assumed to be the same as the associated shape tensor for simplicity. Later, Ponte Castañeda and Willis [16] generalized the structure of Willis [12, 14], whereby the derived bounds contain general distribution tensors. It makes use of the alternative variational representation for the effective energy function given by Talbot and Willis [19], which also applies for nonlinear composites.
Let us now consider the linear composite described above whose stress–strain constitutive relation is given by
Under homogeneous boundary conditions, the fourth-order-effective moduli tensor \(\mathbf {C}^*\) can be defined as
and the average strain energy density (see [29]) is determined as
Following [7, 11], a comparison material is introduced with uniform modulus \( \mathbf {C}^c\) and a polarization field is defined by \(\varvec{\tau }(\mathbf {x})=(\mathbf {C}(\mathbf {x})-\mathbf {C}^c)\mathbf {e}\). Next assume that \( \mathbf {C}^c\le \min _{0\le r\le n} \mathbf {C}^r (\ge \max _{0\le r\le n} \mathbf {C}^r)\), in the sense that \(\mathbf {e} ( \mathbf {C}^c- \mathbf {C}^r) \mathbf {e}\le (\ge ) \,0\), \(r = 0,\ldots , n\). Certainly, choosing \(\mathbf {C}^c- \mathbf {C}^r\le (\ge ) \,0\) componentwise achieves this. Finally select a piecewise constant polarization stress
Such an assumption subsequently yields at most two-point statistics regarding phase distribution. Under the hypothesis of ellipsoidal symmetry for the distribution of the inclusions (possibly with a different ellipsoidal shape to the shape of the inclusion), the following bounds on the effective energy are derived in [16]:
where
is the average of the so-called optimal polarizations \(\varvec{\tau }_k^*\).
By linearity, using (3.1), the following expression for the optimal bounds is derived from (3.2):
where \(\le \) is here interpreted componentwise, and where \(\mathbf {C}^B=\mathbf {C}^+\) refers to an upper bound and \(\mathbf {C}^B=\mathbf {C}^-\) to a lower bound. These bounds depend on the choice of comparison modulus tensor and the optimal polarizations which satisfy the relations:
The tensor parameters \(\mathbf{M}^{(k\ell )}\) in (3.4) depend on \(\mathbf {C}^0\) and on the microstructure. They can be shown to be symmetric and to have the form (see [16]):
Here \(\mathbf {P}^k_s\) is the \(\mathbf {P}\)-tensor associated with the shape of the inclusion in the \(k\)th phase as introduced in (3.6). On the other hand, the notation \(\mathbf {P}_d^{(k\ell )}\) is the (uniform) \(\mathbf {P}\)-tensor associated with the ellipsoidal distribution tensor concerning interaction between the \(k\)th and \(\ell \)th phases. It is associated with the ellipsoid \(V_d^{(k\ell )}= \{\mathbf {x}:|\mathbf {A}^{(k\ell )}_d \mathbf {x}|^2<1\}\) for some symmetric matrix \(\mathbf {A}^{(k\ell )}_d\) and may be computed from the expression:
Recall that the subscripts \(s\) and \(d\) refer to the shape and distribution of inclusions, respectively. By definition, we have \(\mathbf {P}_d^{(k\ell )}=\mathbf {P}_d^{(\ell k)}\), and for conciseness, we will write \(\mathbf {P}_d^{k}\), to denote \(\mathbf {P}_d^{(kk)}\), \(k=0, \ldots ,n.\)
Given the above, let us therefore recall the Hashin–Shtrikman variational principle which states the following regarding the choice of the elastic modulus tensor \(\mathbf {C}^c\) of the comparison material and the way that this leads to bounds, denoted by \(\mathbf {C}^B=\mathbf {C}^+\) for the upper and \(\mathbf {C}^B=\mathbf {C}^-\) for the lower bounds. The theorem that we state has been stated in a number of different ways depending upon the context and application. See e.g. [16].
Theorem 1
Given the linear elastic comparison material with elastic modulus tensor \(\mathbf {C}^c\), let us choose
meaning that we choose the maximal value of each component in the tensor \(\mathbf {C}^r\). Then, using this choice of \(\mathbf {C}^c\) in \(\mathbf {C}^B\), we find that \(\mathbf {C}^B=\mathbf {C}^+\) is an upper bound on the effective modulus tensor, i.e.
where we remind the reader that \(\le \) is interpreted componentwise.
Alternatively, let us choose
meaning that we choose the minimal value of each component in the tensor \(\mathbf {C}^r\). Then, using this choice of \(\mathbf {C}^c\) in \(\mathbf {C}^B\) we find that \(\mathbf {C}^B=\mathbf {C}^-\), is a lower bound on the effective modulus tensor, i.e.
The Hashin–Shtrikman bounds are thus
Therefore, the lower bound \(\mathbf {C}^B\) in (3.7) is given whenever \(\mathbf {C}^r-\mathbf {C}^c\) is positive semi-definite for all \(r=0,\ldots ,n\). If \(\mathbf {C}^r-\mathbf {C}^c\) is negative semi-definite, the upper bound is given.
In some instances, instead of obtaining bounds, authors have chosen to obtain an approximation to the effective properties by choosing \(\mathbf {C}^c=\mathbf {C}^0\), the host elastic modulus tensor, regardless of its relationship to other moduli [16]. Let us consider this case first.
3.1 The Hashin–Shtrikman estimates
Let us take \(\mathbf {C}^c=\mathbf {C}^0\). This immediately yields \(\varvec{\tau }_0^*=0\) and due to the form of (3.4), we are able to write down a simple system for the polarizations, i.e. for \(k=1,2,\ldots ,n\), we have
and for this general case, one simply has to solve this linear system for the optimal polarizations, which are then fed into the expression for \(\mathbf {C}^B=\mathbf {C}^*\) to obtain an estimate (note that it is not a bound unless \(\mathbf {C}^0\) is either minimal or maximal over all phase modulus tensors).
Various cases enable clean simplifications and explicit expressions. Firstly suppose that although we allow the shape and elastic moduli to vary between phases, the distributions are the same for all so that \(\mathbf {P}_d^{(k\ell )}=\mathbf {P}_d\), \(k,\,\ell =1,\ldots ,n\). It is then straightforward to show that the estimate simplifies to
where
A little work enables the form (3.8) to be written as
If all of the inclusions have the same shape, then \(\mathbf {P}^r_s=\mathbf {P}_s\) and furthermore, if it transpires that \(\mathbf {P}_s=\mathbf {P}_d\), then the form (3.9) simplifies significantly to
3.2 The Hashin–Shtrikman bounds
As the title suggests we shall restrict attention to two-phase particulate media so that there is a single inclusion phase. The bounding technique for greater than one inclusion phase is not well established. Suppose that the inclusion phase is a distribution of (possibly different sized) aligned spheroids but where each spheroid has the same aspect ratio \(\delta =a_3/a\) and where the long/short axis (same direction as the semi-axis \(a_3\) of the spheroid) is aligned with \(x_3\). Note that this spheroidal shape is taken into account thanks to the tensor \(\mathbf {P}_s\). Their distribution is accounted for by virtue of the tensor \(\mathbf {P}_d\) which we shall consider to be governed by spheroidal statistics, of aspect ratio \(\epsilon \). We shall consider this notion further shortly. Let us first consider the case when the comparison phase can be chosen as either the host or inclusion phase. Note that this may not always be possible, however.
3.2.1 Comparison phase can be identified as either host or inclusion phase
Let us first suppose that we are able to identify \(\mathbf {C}^c=\mathbf {C}^0\). In this case, \(\varvec{\tau }^0=0\) and it is straightforward to determine that
and this forms the lower bound if \(\mathbf {C}^0\le \mathbf {C}^1\) or the upper bound if \(\mathbf {C}^0\ge \mathbf {C}^1\).
Analogously, if we are able to identify \(\mathbf {C}^c=\mathbf {C}^1\), then \(\varvec{\tau }^1=0\) and
where
The quantity \(\mathbf {C}^B\) forms the lower bound if \(\mathbf {C}^1\le \mathbf {C}^0\) or the upper bound if \(\mathbf {C}^1\ge \mathbf {C}^0\).
Of course, it may not always be the case that the comparison material can be identified as exactly one of the inclusion phases. As such, it is instructive to determine general bounds in terms of the comparison modulus tensor.
3.2.2 Comparison phase cannot be identified as either host or inclusion phase
In this case, both polarization stresses have non-zero components. As such, the linear system is
which we shall conveniently write as
so that we can solve to find that
Other forms can also be found.
3.2.3 The distribution \(\mathbf {P}\)-tensor is identical to the shape \(\mathbf {P}\)-tensor
If \(\mathbf {P}_s=\mathbf {P}_d=\mathbf {P}\), one can write down a clean form involving the comparison phase. We have
This also generalizes to the multi-phase case, so that we can write
3.3 Distribution \(\mathbf {P}\)-tensor
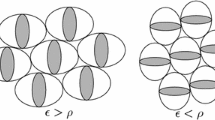
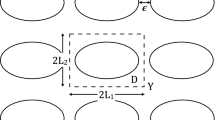
Let us now consider the \(\mathbf {P}\)-tensor \(\mathbf {P}_d\) which as noted above is associated with a spheroid of aspect ratio \(\epsilon \) whose long or short axis is in the \(x_3\) direction. We must consider the relation between the aspect ratio of the inclusions \(\delta \) and that of \(\mathbf {P}_d\), i.e. \(\epsilon \). Let us refer to Fig. 1) where we note that the distribution spheroid is a safety spheroid, containing a single spheroidal inclusion and which is not intersected by any other security spheroid (hence the terminology). The details of the distribution tensors for more than one inclusion phase become quite complex and will be discussed in a future article. Here we focus on a single inclusion phase.
Assuming that \(\mathbf {P}_s\) and \(\mathbf {P}_d\) are given, this construction of the composite means that there is a maximal volume fraction associated with how much of the inclusion can fit into the security spheroid. This depends on whether \(\delta >\epsilon \) or \(\delta <\epsilon \) (see Fig. 1). Simple calculations show that when \(\delta >\epsilon \), we have
whereas if \(\delta <\epsilon \), we have
Alternatively, consider that the inclusion aspect ratio \(\delta \) is fixed as well as the volume fraction. This then gives a condition on the maximum \(\epsilon \) permitted. In particular, when \(\epsilon <\delta \), we can determine that \(0\le \epsilon \le \delta \sqrt{\phi }\le \delta \) whereas when \(\epsilon >\delta \), we have \(\delta \le \epsilon \le \delta /\phi \). A special case is the example when inclusions are spherical so that \(\delta =1\), when \(\phi _\mathrm{max}=1\).
4 Transversely isotropic composites
We have spoken of a general construction of bounds in terms of the elastic modulus tensors \(\mathbf{C}^r\). Of course, above when it comes to implementation, one must consider a specific form and in general, this can cause great difficulty, particularly for anisotropic phases. Let us now restrict attention to two-phase composites where phases are (at most) transversely isotropic (TI), all with \(x_3\) as the axis of transverse symmetry so that the \(x_1x_2\) plane is the plane of isotropy. This is a very commonly occurring case in practice. Many fibre-reinforced media are of this type with fibres being TI in order to provide high tensile strength. Elastic modulus tensors that are TI are in fact symmetric TI tensors, a concept that we will discuss shortly. Therefore, in the \(r\)th phase, the Cauchy stress \(\varvec{\sigma }^r\) is linked to the linear elastic strain \(\mathbf {e}^r\) via \(\varvec{\sigma }^r=\mathbf {C}^r\mathbf {e}^r\) where \(\mathbf {C}^r\) is (symmetrically) transversely isostropic. We use the following notation (following Hill [26]) in component form:
Here \(k_r\) and \(m_r\) are known as the in-plane bulk and shear moduli of phase \(r=1,0\), respectively, and \(p_r\) is the anti-plane (or longitudinal) shear modulus. We note here that \(C^r_{1111}=k_r+m_r, C^r_{1133}=\ell _r, C^r_{3333}=n_r, C_{1122}^r=k_r-m_r\), \(C^r_{1313}=p_r\) and \(C^r_{1212}=(C^r_{1111}-C^r_{1122})/2 = m_r\). Finally, we note that the engineering notation for the elastic modulus tensor is often used, which expresses stress in terms of strain via multiplication by a six by six matrix \(C^r_{ij}\). The coefficients of this matrix are related to the elastic modulus tensor by the expressions \(C^r_{1111}=C^r_{11}, C^r_{1133}=C^r_{13}, C^r_{3333}=C^r_{33}, C^r_{1212}=C^r_{66}, C^r_{1313}=C^r_{55}\).
Note that in the above, we have worked with the elastic modulus tensor and the Hill notation for this. We also note the following strain–stress relationship in terms of the so-called engineering constants
where \(E^\mathrm{T}\) and \(E^A\) are the transverse and axial Young’s moduli and \(\nu ^\mathrm{T}\) and \(\nu ^A\) are the transverse and axial Poisson ratios, respectively. In particular, \(\nu ^A=\nu ^{31}\) corresponds to the lateral contraction when a force is applied in the axial direction, and we note the relationship \(\nu ^A_{31}/E_A=\nu ^A_{13}/E_T\). Note also that there are still only five independent constants due to the relationship \(E^\mathrm{T}_r = 2m_r(1+\nu ^\mathrm{T}_r)\). The relationships between the Engineering moduli and the constants appearing in the Hill notation of the elastic modulus tensor are given in appendix.
As detailed above, we restrict attention to inclusions (and distributions) that are spheroidal and with the axis of TI of the phases being the \(x_3\) axis. This yields macroscopically TI materials. Note that the limits \(\delta \rightarrow \infty \) and \(\delta \rightarrow 0\) correspond to the long cylindrical fibre and layer (or penny-shape) limits, respectively.
The macroscopic stress–strain law associated with the effective material will be that in (4.1)–(4.3) with \(r\) replaced by \(*\) everywhere (denoting the effective material). In what follows then we shall describe how to construct the Hashin–Shtrikman bounds on the effective elastic properties \(k_*, \ell _*, n_*, m_*\) and \(p_*\) and subsequently on the Engineering moduli \(E^\mathrm{T}*, E^A_*, \nu ^\mathrm{T}_*\) and \(\nu ^A_*\).
5 Transversely isotropic tensors
A fourth-order isotropic tensor can be defined with respect to the tensor basis set \(\{I_{ijk\ell }^{(1)},I_{ijk\ell }^{(2)}\}\) where
Therefore, a fourth-order isotropic tensor \(H_{ijk\ell }\) can be written as
Given the basis set (5.1), an isotropic tensor \(H_{ijk\ell }\) may therefore be specified by a list of two parameters, in short-hand notation: \(\mathbf {H}=(X_1,X_2)\). In order to specify an isotropic elastic modulus tensor \(C_{ijk\ell }\), frequently the short-hand notation \(\mathbf {C}=(3\kappa ,2\mu )=(X_1,X_2)\) is adopted where \(\kappa =\lambda +2\mu /3\) corresponds to the bulk modulus and \(\mu \) to the shear modulus. The parameters \(\lambda \) and \(\mu \) are the Lamé constants of the material.
Analogously, suppose now that instead of isotropy we consider the case of transverse isotropy, where the axis of transverse symmetry is the \(x_3\) axis. In this case, a transversely isotropic (TI) tensor \(H_{ijk\ell }\) can also be defined with respect to a tensor basis set. Several of these have been proposed; all slight variants of each other, see for example [30, 31]. However we shall use the basis associated with the notation introduced for TI tensors by Hill [26] since this is a frequently used notation in the composite materials community, particularly when the Hashin–Shtrikman bounds are discussed. Although it does not appear that Hill wrote down this specific basis set, it is clear that this was what his notation referred to. This basis set enables a TI tensor \(H_{ijk\ell }\) to be written in the form:
where \(X_n\) are constants and the basis tensors \(\mathcal {H}^{(n)}_{ijk\ell }\) are defined by
where \(\varTheta _{ij} = \delta _{ij}-\delta _{i3}\delta _{j3}\). The notation \(\mathcal {H}\) has been used to signify the Hill basis.
The set of symmetric TI tensors (\(H_{ijk\ell }=H_{k\ell ij}\)) is defined by setting \(X_2=X_3\) (e.g. a TI elastic modulus tensor falls into this class). The set of symmetric TI tensors is not closed under multiplication in the sense that if we take two symmetric TI tensors \(A_{ijk\ell }\) and \(B_{ijk\ell }\) and perform the double contraction \(A_{ijmn}B_{nmk\ell }=D_{ijk\ell }\), the resulting tensor \(D_{ijk\ell }\) is not symmetric TI because \(D_{3311}\ne D_{1133}\), and so \(X_2\ne X_3\) in this case; see Eq. (5.8) below. Hence in general, when considering transversely isotropic tensors, we must consider them with respect to the six basis tensors \(\mathcal {H}_{ijk\ell }^{(n)}\) defined above; this basis set is closed with respect to double contraction. Note this important difference between transversely isotropic tensors and symmetric transversely isotropic tensors. For more discussion of this point, see [32], although the terminology symmetric TI tensors is specific to this article.
Analogous to the short-hand notation introduced for isotropic tensors above, in order to specify a TI tensor \(H_{ijk\ell }\), the shorthand notation \(\mathbf {H}=(2k_H,\ell _H,\ell '_H,n_H,2m_H,2p_H)=(X_1,X_2,X_3,X_4,X_5,X_6)\) is adopted, i.e. the tensor is defined by these six constants (a symmetric TI tensor corresponds to \(\ell _H'=\ell _H\)). This notation is motivated by the fact that Hooke’s law with respect to this basis (4.1)–(4.3) links stress to strain via the (symmetric) transversely isotropic tensor \(C_{ijk\ell }\) which in short-hand notation is written \(\mathbf {C}=(2k,\ell ,\ell ',n,2m,2p)\) with \(\ell '=\ell \). Before we proceed, let us define the shorthand notation:
for contraction between the basis tensors defined in (5.3)–(5.5). The contractions defined in (5.6) are summarized in Table 1.
With the notation above, using the contractions in Table 1, we can therefore write down the operations of addition and contraction (in short-hand notation) on the two TI tensors \(H_{ijk\ell }^1\) and \(H_{ijk\ell }^2\) defined in short-hand notation by \(\mathbf {H}^1=(2k_1,\ell _1,\ell _1',n_1,2m_1,2p_1)\) and \(\mathbf {H}^2=(2k_2,\ell _2,\ell _2',n_2,2m_2,2p_2)\), respectively. We define the operation of addition \(H_{ijk\ell }=H_{ijk\ell }^1+H_{ijk\ell }^2\) in short-hand notation by
and the operation of double contraction \(H_{ijk\ell }=H^1_{ijmn}H^2_{nmk\ell }\) by
Note that even if \(\ell '_1=\ell _1\) and \(\ell '_2=\ell _2\) (corresponding to symmetric TI tensors \(\mathbf {H}^1\) and \(\mathbf {H}^2\)), the second and third elements on the right-hand side of (5.8) are not equal in general, i.e. contraction between two symmetric TI tensors produces a non-symmetric TI tensor in general. This is why we must write out the theory for the evaluation of the Hashin–Shtrikman bounds for TI materials by using the general TI tensor basis set. We note that (5.8) is a correction to the typographical error in the corresponding expression in Appendix A of [25].
The fourth-order identity tensor \(I_{ijk\ell }\) and isotropic basis tensors \(I^{(1)}_{ijk\ell }\) and \(I_{ijk\ell }^{(2)}\), written with respect to this TI basis are
Finally the inverse of the tensor \(\mathbf {H}^1=(2k_1,\ell _1,\ell _1',n_1,2m_1,2p_1)\) is
6 Construction and computation of the bounds
Here we describe the procedure for constructing the Hashin–Shtrikman bounds for TI composites of the type considered above. This procedure can be easily coded in any standard mathematical package or alternatively in widely used programming languages, in a straightforward manner. In particular, we have described the construction in a way that should be simple to implement in such languages, by defining functions that represent the operations of taking the inverse and double contraction of TI tensors.
The construction is achieved by using the short-hand notation for TI tensors described in the previous section. In particular, we specify a TI tensor by writing this short-hand list of six constants as a 6-vector \((2k,\ell ,\ell ',n,2m,2p)\), with symmetric transverse isotropy if \(\ell '=\ell \). We then exploit the properties of the Hill basis defined above by defining the appropriate tensor operations of contraction and inversion as in (5.8) and (5.10). This vector notation is particularly convenient for computational implementation of the computation of the HS bounds.
First we define the (symmetric TI) elastic modulus tensor:
We also define the fourth-order identity tensor and isotropic basis tensors in 6-vector forms as in (5.9). Two TI comparison materials are defined (as 6-vectors) as in Remark 1:
This means that we take the minimal and maximal elements over all of the phases. For a multi-phase material therefore, it could be that the comparison phase does not correspond to any of the specific phases constituting the composite, since, for example, the modulus \(m_1\) of phase 1 may be maximal but the modulus \(n_2\) of phase 2 could be maximal.
We now define the operations of double contraction and inversion in terms of the 6-vector notation introduced here. With reference to (5.8) and (5.10), we introduce the functions \(\mathbb {C}[\mathbf {H}^1,\mathbf {H}^0]:\mathbb {R}^6\times \mathbb {R}^6\rightarrow \mathbb {R}^6\) and \(\mathcal {\mathbb {I}}[\mathbf {H}^1]:\mathbb {R}^6\rightarrow \mathbb {R}^6\) operating on the 6-vectors \(\mathbf {H}^1=(2k_1,\ell _1,\ell _1',n_1,2m_1,2p_1)\) and \(\mathbf {H}^0=(2k_0,\ell _0,\ell _0',n_0,2m_0,2p_0)\) in the following way:
Such operations can therefore be straightforwardly coded by introducing such functions with arguments as 6-vectors.
Therefore, given the (non-symmetric) TI Eshelby tensor (defined in Appendix A) corresponding to the appropriate comparison phase, written in 6-vector form as \(\mathbf {S}^{\delta }=(2k_{\delta },\ell _{\delta },\ell _{\delta }^{\prime },n_{\delta },2m_{\delta },2p_{\delta })\) the super or subscript \(\delta \) (or \(\epsilon \)) refers to the aspect ratio of the spheroid in question involved in the Eshelby tensor. The \(\mathbf {P}\)-tensor (also written as a 6-vector) can thus be defined via (2.2) as
and we note that \(\mathbf {P}^c\) is a symmetric transversely isotropic tensor. We also recall that the \(\mathbf{P}\) tensor is associated with the comparison material.
Let us now consider the different computations, according to the choice of comparison material. Suppose first that we are able to choose the comparison material as either the host or inclusion as in Sect. 3.2.1.
6.1 Construction when comparison phase is host or inclusion phase
Start by letting \(\mathbf {N}=\mathbb {I}[\mathbf {C}^1-\mathbf {C}^0]\). In the case when \(\mathbf {C}^c=\mathbf {C}^0\), define
and then we have
which is a lower bound if \(\mathbf {C}^1-\mathbf {C}^0\) is positive semi-definite, or an upper bound if \(\mathbf {C}^1-\mathbf {C}^0\) is negative semi-definite.
Similarly, in the case when \(\mathbf {C}^c=\mathbf {C}^1\) then we define
and then we have
which is a lower bound if \(\mathbf {C}^0-\mathbf {C}^1\) is positive semi-definite or an upper bound if \(\mathbf {C}^0-\mathbf {C}^1\) is negative semi-definite.
If we have \(\mathbf {P}_d=\mathbf {P}_s=\mathbf {P}\), then one can simply use this in the procedure above, or alternatively one could use the contraction and inversion procedures to code up the approach written down in Sect. 3.2.3. In this two phase case (a single inclusion phase), re-writing in this manner is no more advantageous. However, in the multi-phase case, this alternative approach does make the construction more simple because we may exploit the form (3.13). We will describe this further in future work.
Since we can write the effective elastic modulus tensor in the short-hand notation form
we have therefore constructed the bounds on each of the properties, i.e. from (3.7) and (6.5), we have
As regards the Engineering constants, we can follow Hill [26] who noted the expression
where
Therefore according as to whether \(\mathcal {P}\) is positive or negative we can derive bounds on \(\nu ^A_*\) and \(E^A_*\) from the bounds on \(k_*\) in (6.6). Furthermore from [10], we can then use their expressions to state the following bounds on the transverse properties:
where
6.2 Construction in the general case
Let us now consider the most general case when the host or inclusion phases cannot be identified as the comparison material. Let us take into account the formulation in Sect. 3.2.2 and using the contractions and inversion operations described in (6.2) and (6.3), we introduce the following fourth-order tensors:
Having defined (6.7), from (3.3) we can therefore write
This provides lower (upper) bound whenever \(\mathbf {C}^r-\mathbf {C}^c\), \(r=0,\,1\) is positive (negative) semi-definite.
7 Limiting cases of transversely isotropic composites
We note that the two limits \(\delta =\epsilon \rightarrow 0\) and \(\delta =\epsilon \rightarrow \infty \) correspond to a layered medium and a long fibre-reinforced medium, respectively. As regards the former, the effective properties of such media are known exactly. They are the well-known [33] results, which for a material with TI phases, of the type considered here take the form:
where the superscript \(L\) denotes a layered medium.
It is straightforward (but time consuming) to derive the results (7.1)–(7.3) analytically using the construction of the Hashin–Shtrikman bounds in the form (3.13). In this specific limiting case, the Hashin–Shtrikman bounds coincide for all five effective properties of course, thus giving the exact results (7.1)–(7.3) for a layered medium (or a medium consisting of aligned uniformly distributed penny-shaped inclusions).
In the limit \(\delta \rightarrow \infty \), the Hashin–Shtrikman bounds do not coincide; they become the form of bounds given in [9] on long FRCs for \(k_*, m_*\) and \(p_*\). Bounds on \(n_*\) and \(\ell _*\) were not given in [9] but they may be determined by appealing to the so-called universal properties of composites [18]). In [9], Hashin dealt with only isotropic phases, although since he wrote the paper in terms of (de-coupled) in-plane and anti-plane problems and wrote the expressions in terms of shear moduli and in-plane bulk moduli, it is straightforward to derive the bounds for TI phases by simple replacement of the corresponding moduli with their TI counterparts. As in the layered medium case above, it is straightforward to derive these bounds analytically in this limiting case using the details regarding transversely isotropic tensors in Sect. 5 (once again noting the use of (5.8) and (5.10) in particular) in the construction of the Hashin–Shtrikman bounds described above, together with the exact form of the Eshelby tensor in this limit (given in 1). These results for an \(n\) phase composite of the type considered in this article are the following, in terms of \(k^B, \ell ^B, n^B, m^B\) and \(p^B\), specified in terms of the comparison phase:
and therefore lower (upper) bounds follow from setting the comparison material equal to the smallest (largest) moduli, as described above. Therefore in this limit we are not as fortunate as the layered case where the bounds coincide. Many theories have been proposed to model the effective elastic properties of long FRC materials and a first check on the efficacy such theories is that the prediction sits within the bounds (7.4)–(7.8).
8 Implementation
We now implement the construction above in various scenarios. Table 2 states the phase properties (taken from [25]). In particular, note that traditionally the Hashin–Shtrikman bounds are plotted as a function of volume fraction \(\phi =\phi _1\) of the inclusion phase, for a fixed aspect ratio \(\delta \) of inclusion. Here we not only plot this case, but also consider the bounds plotted as a function of \(\delta \) for a fixed volume fraction of inclusion. This was also done in [25] but note that here the \(\mathbf {P}\)-tensor is computed analytically, and therefore it is easy to plot such results for a wide range of \(\delta \) (we plot results for a logarithmic scale in \(\delta \)). Moreover, here we also study the dependence of the bounds on the distribution aspect ratio (\(\epsilon \)). Such plots are very informative particularly since the Reuss–Voigt bounds are independent of \(\delta \) and \(\epsilon \) and so they cannot give this information.
8.1 Example 1: Isotropic glass inclusions in the isotropic epoxy host phase
Let us here suppose that \(\mathbf {P}_s=\mathbf {P}_d\) so that \(\epsilon =\delta \). Consider the example of isotropic glass inclusions uniformly distributed in the epoxy host phase. First we consider the case of spherical glass inclusions, and therefore the effective material is isotropic. In Fig. 2, we plot bounds on the effective bulk modulus \(\kappa _*\) and shear modulus \(\mu _*\) of the composite material. In particular, we plot the Reuss (lower) and Voigt (upper) bounds on these effective properties together with the Hashin–Shtrikman bounds. Note the improvement of the Hashin–Shtrikman bounds over the Reuss/Voigt bounds.
Plots of bounds on the effective bulk modulus \(\kappa _*\) and effective shear modulus \(\mu _*\) for a glass/epoxy composite with spherical (\(\delta =1\)) glass inclusions. The effective material is isotropic. We plot the Reuss (lower) and Voigt (upper) bounds (dashed lines) and the Hashin–Shtrikman bounds (solid lines). Note the improvement of the Hashin–Shtrikman bounds over the Reuss–Voigt bounds
Alternatively, we can consider the case of spheroidal glass inclusions with general aspect ratio \(\delta \) so that the effective material is transversely isotropic. In Fig. 3, we plot the Hashin–Shtrikman bounds on the effective shear moduli \(m_*/m_0\) and \(p_*/p_0\). Note that the bounds coincide in the (layered) limit when \(\delta \rightarrow 0\). In the case of the in-plane shear modulus, the bounds become equal to the Voigt bound, whereas in the anti-plane shear modulus they become equal to the Reuss bound; this can be seen from the exact results in (7.3). Note also that the anti-plane shear modulus does not change significantly when we increase \(\delta \) from \(\delta =1\) to the \(\delta \rightarrow \infty \) limit. This can also be seen on the right of Fig. 6 where we plot the bounds on the effective shear moduli as a function of \(\delta \) for \(\phi =0.3\). In Fig. 4, we plot the effective properties \(k_*/k_0\) and \(n_*/n_0\), noting that the layered limit bounds coincide. We also note that in this instance, the bounds on \(n_*/n_0\) for \(\delta \rightarrow \infty \) are very tight. The different regimes of \(\ell _*/\ell _0\) are plotted in Fig. 5.
Plots of the Hashin–Shtrikman bounds on the effective shear moduli of a glass/epoxy composite with spheroidal glass inclusions of aspect ratio \(\delta \). On the left is the in-plane shear modulus \(m_*/m_0\), and on the right is the anti-plane shear modulus \(p_*/p_0\). In both plots: \(\delta =1\) (solid line), \(\delta \rightarrow \infty \) (dotted line), \(\delta =0.1\) (dashed line) and \(\delta \rightarrow 0\) (dot-dashed line). In the last case, the bounds coincide as can also be seen clearly in Fig. 6. These correspond to the Voigt (\(m_*\)) and Reuss (\(p_*\)) bounds in those cases
Plots of the Hashin–Shtrikman bounds on the effective moduli of a glass/epoxy composite with spheroidal glass inclusions of aspect ratio \(\delta \). On the left is the in-plane bulk modulus \(k_*/k_0\) and on the right is the longitudinal property \(n_*/n_0\). In both plots: \(\delta =1\) (solid line), \(\delta \rightarrow \infty \) (dotted line), \(\delta =0.4\) (dashed line) and \(\delta \rightarrow 0\) (dot-dashed line). In the last case, the bounds coincide as can be seen clearly in Fig. 6
Plots of the Hashin–Shtrikman bounds on the effective modulus \(\ell _*/\ell _0\) of a glass/epoxy composite with spheroidal glass inclusions of aspect ratio \(\delta \). On the left, we plot \(\delta =1\) (solid line), \(\delta =0.1\) (dashed line) and the \(\delta \rightarrow 0\) limit (dot-dashed line). On the right, we plot \(\delta =1\) (solid line), \(\delta =5\) (dashed line) and the \(\delta \rightarrow \infty \) limit (dotted line)
Plots of the upper and lower Hashin–Shtrikman bounds on the effective material properties of a glass/epoxy composite as a function of glass inclusion of aspect ratio \(\delta \) for fixed volume fraction \(\phi =0.5\) of the inclusion phase. Left plot \(k_*/k_0\) (dot-dash line), \(\ell _*/\ell _0\) (dashed line), \(n_*/n_0\) (dotted line). Right plot \(m_*/m_0\) (dot-dash line), \(p_*/p_0\) (dotted line). The plotted discs indicate the limiting values as \(\delta \rightarrow 0\) and \(\delta \rightarrow \infty \) of the Hashin–Shtrikman bounds and concur with the values of the Backus expressions and classical Hashin–Shtrikman bounds on long fibre-reinforced composites, respectively
In Fig. 6, we illustrate the dependence of the bounds as a function of \(\delta \) for fixed volume fraction \(\phi =0.5\). In particular, we note the recovery of the (exact) layered expressions (7.1)–(7.3) as \(\delta \rightarrow 0\) (denoted by disks) and also the recovery of the classical Hashin–Shtrikman bounds (7.4)–(7.8) for long FRCs when \(\delta \rightarrow \infty \) (also denoted by disks). Note in particular that the fibres do not have to be particularly long before they reach this limit: \(\delta = \mathcal{O}(10)\) suffices for this limit to be reached, with the exception of \(n_*\) which requires a larger \(\delta \), perhaps \(\delta = \mathcal{O}(100)\).
8.2 Example 2: Transversely isotropic PZT-7A inclusions in the isotropic Epoxy II host phase
Let us once again suppose that \(\mathbf {P}_s=\mathbf {P}_d\) so that \(\epsilon =\delta \), but now consider the effect of a TI inclusion phase (PZT-7A). We shall embed such inclusions in an epoxy phase with properties designated as Epoxy II in Table 2. We plot Hashin–Shtrikman bounds as a function of \(\phi \), the inclusion volume fraction in Figs. 7, 8 and 9 for different values of \(\delta \), the inclusion aspect ratio. In Fig. 10, we plot the bounds as a function of \(\delta \) for a fixed volume fraction, \(\phi =0.3\).
Plots of the Hashin–Shtrikman bounds on the effective shear moduli of a PZT-7A/Epoxy II composite with spheroidal PZT-7A inclusions of aspect ratio \(\delta \). On the left is the in-plane shear modulus \(m_*/m_0\) and on the right is the anti-plane shear modulus \(p_*/p_0\). In both plots: \(\delta =1\) (solid line), \(\delta \rightarrow \infty \) (dotted line), \(\delta =0.1\) (dashed line) and \(\delta \rightarrow 0\) (dot-dashed line). In the last case, the bounds coincide as can be seen clearly in Fig. 10. These correspond to the Voigt (\(m_*\)) and Reuss (\(p_*\)) bounds in those cases. Note the high contrast in effective shear moduli (particularly the in-plane shear modulus) as we increase the inclusion volume fraction
Plots of the Hashin–Shtrikman bounds on the effective moduli of a PZT-7A/Epoxy II composite with spheroidal PZT-7A inclusions of aspect ratio \(\delta \). On the left is the in-plane bulk modulus \(k_*/k_0\) and on the right is the longitudinal property \(n_*/n_0\). In both plots: \(\delta =1\) (solid line), \(\delta \rightarrow \infty \) (dotted line), \(\delta =0.5\) (dashed line) and \(\delta \rightarrow 0\) (dot-dashed line). For the \(k_*/k_0\) case, we have only plotted the upper bound for the \(\delta =1\) case since \(\delta \) has to be extremely small before it departs from this significantly. This can be seen in Fig. 10. In the case when \(\delta \rightarrow 0\), the bounds coincide as can also be seen clearly in Fig. 10
Plots of the Hashin–Shtrikman bounds on the effective modulus \(\ell _*/\ell _0\) of a PZT-7A/Epoxy II composite with spheroidal PZT-7A inclusions of aspect ratio \(\delta \). On the left, we plot \(\delta =1\) (solid line), \(\delta =0.1\) (dashed line) and the \(\delta \rightarrow 0\) limit (dot-dashed line). On the right, we plot \(\delta =1\) (solid line) and the \(\delta \rightarrow \infty \) limit (dotted line). Any value of \(\delta \) between \(1\) and the long fibre limit sits between these two latter sets of bounds
Plots of the upper and lower Hashin–Shtrikman bounds on the effective material properties of a PZT-7A/Epoxy II composite with spheroidal PZT-7A inclusions of aspect ratio \(\delta \) for fixed volume fraction \(\phi =0.3\) of the inclusion phase. Left plot: \(k_*/k_0\) (dot-dash line), \(\ell _*/\ell _0\) (dashed line), \(n_*/n_0\) (solid line). Right plot: \(m_*/m_0\) (dot-dash line), \(p_*/p_0\) (solid line). The plotted discs indicate the limiting values as \(\delta \rightarrow 0\) and \(\delta \rightarrow \infty \) of the Hashin–Shtrikman bounds and concur with the values of the Backus expressions and classical Hashin–Shtrikman bounds on long fibre-reinforced composites, respectively
In Fig. 7, we plot the bounds on the effective shear moduli of this composite. Note in particular the high contrast achieved by addition of the inclusion phase (particularly the in-plane shear modulus). As in example 1, the effective shear moduli are not affected greatly by increasing \(\delta \) from unity, particularly the anti-plane shear modulus. This is also seen in the plot on the right of Fig. 10. In Fig. 8, we plot corresponding bounds on \(k_*/k_0\) and \(n_*/n_0\). For \(k_*/k_0\), we plot only the upper bound for \(\delta =1\) since this does not change significantly until \(\delta \) is very small, when the upper and lower bounds coincide in the layered limit as can be seen in the plot on the left. This can also be seen in Fig. 10 (noting the logarithmic scale for \(\delta \)). As in the isotropic case, bounds on \(n_*/n_0\) become relatively tight in the long cylindrical fibre limit, \(\delta \rightarrow \infty \). In Fig. 9, we plot \(\ell _*/\ell _0\), on the left as we decrease \(\delta \) below unity and on the right as we increase \(\delta \) above unity. On the left, we see that bounds become progressively tighter as \(\delta \) is decreased until the layered limit is reached. On the right, we see that the bounds do not become modified greatly by increasing \(\delta \) above unity.
For all properties, as \(\delta \rightarrow 0\), the layered limit is achieved, as should be expected. We note from Fig. 10 that this limit is not reached as quickly as in the isotropic phase case in example 1. In particular even for \(\delta =10^{-3}\), this limit has not yet been reached for the in-plane shear modulus \(m_*/m_0\).
8.3 Example 3: Spheroidal glass inclusions with spheroidal distribution in the epoxy host phase
Let us now consider a case when the distribution spheroid has a different shape to that of the inclusion phase. Let us first take spherical glass inclusions (\(\delta =1\)) and consider both prolate (\(\epsilon >1\)) and oblate (\(\epsilon <1\)) distributions, referring to Fig. 1. We shall take the case of the isotropic epoxy host phase. Following the discussion in Sect. 3.3 for a given volume fraction, we take the distribution spheroid to be \(\epsilon =\sqrt{\phi }<1\) in the oblate case and \(\epsilon =1/\phi \) in the prolate case and plot the resulting bounds in Figs. 11 and 12, noting how tight the Hashin–Shtrikman bounds are in these cases and that the distribution has an apparently greater effect on \(m_*\) and \(n_*\) than on \(p_*\) and \(\ell _*\). Of course, each point on these curves represents a different type of composite in the sense that the distribution has different spheroidal distribution statistics. If we were to fix \(\epsilon \) (i.e. fix the type of distribution), then we would have a maximum volume fraction \(\phi _\mathrm{max}<1\). As an example, in Fig. 13, we therefore take \(\epsilon =1/\sqrt{2}, 1, 2\) and plot bounds on the shear moduli up to a maximal (in the non-spherical distribution cases) volume fraction of \(\phi =0.5\). Bounds on the in-plane shear modulus \(m_*\) are very tight, particularly in the case of the case \(\epsilon =1/\sqrt{2}\). The bounds for \(m_*\) tend to shift upwards with a decrease in \(\epsilon \) and vice versa, whereas with \(p_*\), the bounds move down with a decrease in \(\epsilon \).
On the left: Hashin–Shtrikman bounds for the effective in-plane shear modulus \(m_*/m_0\) (effective anti-plane shear modulus \(p_*/p_0\) on the right resp.) of a glass/epoxy composite with spherical inclusions (\(\delta =1\)) and spheroidal symmetry with ratio \(\epsilon =\sqrt{\phi }\le 1\) (dot-dashed line) for the oblate case and ratio \(\epsilon =1/{\phi }\ge 1\) for the prolate one (dashed line). Voigt–Reuss bounds (solid lines) are also represented
On the left: Hashin–Shtrikman bounds of the longitudinal property \(n_*/n_0\) (effective modulus \(\ell _*/\ell _0\) on the right resp.) for a glass/epoxy composite with spherical inclusions (\(\delta =1\)) and spheroidal symmetry with ratio \(\epsilon =\sqrt{\phi }\le 1\) (dot-dashed line) for the oblate case and ratio \(\epsilon =1/{\phi }\ge 1\) (dashed line) for the prolate one. Voigt–Reuss bounds (solid lines) are also represented. Analogous to previous case, note the improvement of (6.8) bounds over the Voigt–Reuss bounds
Bounds on the effective in-plane shear modulus \(m/m_0\) (left) and effective anti-plane shear modulus \(p /p_0\) (right) for a glass/epoxy composite with spheroidal inclusions with a spheroidal distribution. We plot Hashin–Shtrikman with \(\epsilon \)= 2 (dashed lines) and \(\epsilon =1/\sqrt{2}\) (dotted lines) and additionally for spherical distributions, \(\epsilon =1\) (dot-dashed lines). Voigt–Reuss bounds (solid lines) are also represented. The maximum volume fraction in the spheroidal distribution cases is \(\phi =0.5\)
Plots of the upper and lower Hashin–Shtrikman bounds on the effective material properties of a glass/epoxy composite as a function of glass inclusion of aspect ratio \(\delta \) for fixed volume fraction \(\phi =0.5\) of the inclusion phase. We plot two sets of curves: one set corresponding to the results in Fig. 6 associated with a spheroidal distribution with the same aspect ratio as that of the inclusion (and same line styles), i.e. \(\epsilon =\delta \) and another where the distribution spheroid has aspect ratio \(\epsilon =\delta \sqrt{\phi }=\delta /\sqrt{2}\) (the associated solid curves). Left plot \(k_*/k_0\) (dot-dash line), \(\ell _*/\ell _0\) (dashed line), \(n_*/n_0\) (dotted line). Right plot \(m_*/m_0\) (dot-dash line), \(p_*/p_0\) (dotted line). The plotted discs indicate the limiting values as \(\delta \rightarrow 0\) and \(\delta \rightarrow \infty \) of the Hashin–Shtrikman bounds and concur with the values of the Backus expressions and classical Hashin–Shtrikman bounds on long fibre-reinforced composites, respectively, which still hold for the alternative spheroidal distribution
Hashin–Shtrikman bounds for the in-plane shear modulus \(m_*/m_0\) (dashed lines) and the anti-plane shear modulus \(p_*/p_0\) (solid lines) for a two-phase glass/epoxy composite with volume fraction \(\phi =0.2\) of glass inclusions, plotted as a function of spheroidal distribution aspect ratio \(\epsilon \). Top left \(\delta =1.5\), top right \(\delta =1\) (spheres), bottom left \(\delta =0.6\) and bottom right \(\delta =0.2\)
Let us now consider the effect when the inclusion becomes a spheroid with aspect ratio \(\delta \) possibly distinct from \(\epsilon \) the aspect ratio of the spheroidal distribution. In particular, we refer to Fig. 14 where we consider the modification to the plot in Fig. 6 when the spheroidal distribution is \(\epsilon =\delta \sqrt{\phi }=\delta /\sqrt{2}<\delta \). Note that the plot has log-linear scaling and as should be expected, the most significant effect is felt away from the limiting cases when \(\delta \rightarrow 0\) and \(\delta \rightarrow \infty \) corresponding to the layer and long fibre limits.
Finally with reference to Fig. 15, we study the glass/epoxy composite with fixed volume fraction \(\phi =0.2\) of glass inclusions. We then fix the inclusion aspect ratio and study the dependence of the shear moduli \(m_*/m_0\) and \(p_*/p_0\) on the spheroidal distribution aspect ratio \(\epsilon \). In particular, we present results for the four values \(\delta =1.5, 1\) (spheres), \(\delta =0.6\) and \(0.2\). In plotting the range of \(\epsilon \), we take into account the inequalities given in Sect. 3.3. In particular from subfigure to subfigure, we see the shift in bounds as \(\delta \) is decreased. Note in particular that there is little variation in the bounds as \(\epsilon \) increases above unity. More variation is seen for \(\epsilon <1\).
9 Concluding remarks
We have shown how to construct, in a straightforward manner, the Hashin–Shtrikman bounds for transversely isotropic composites focusing in particular on the case of two-phase FRCs. The shape of the inclusion phase and their corresponding distributions can be chosen independently by use of the appropriate Hill and Eshelby tensors and TI tensor basis set. Note in particular that for TI materials, the Eshelby tensor can be derived analytically, and we summarized its various forms for spheroids in the Appendix. We implemented different computations for two specific composite materials, exhibiting the improvement of the Hashin–Shtrikman bounds over the Reuss–Voigt bounds, also showing how bounds behave for different inclusion (\(\delta \)) and distribution (\(\epsilon \)) aspect ratios, including the limiting cases of layered media (\(\delta \rightarrow 0\)) where bounds coincide, agreeing with the Backus expressions [33] and also long fibre-reinforced media (\(\delta \rightarrow \infty \)) where the bounds are then the classical Hashin–Shtrikman bounds (some of which were derived by Hashin [9]) for such media. Entirely analogous approaches may be followed for phases and materials of arbitrary anisotropy, although in general, the corresponding Green’s tensor (and hence \(\mathbf {P}\)-tensor) cannot be derived analytically.
Future work needs to consider the construction and computation of the Hashin–Shtrikman bounds for multi-phase composites, a case that has not been studied sufficiently in the literature.
Notes
This latter point does not appear to have been recognized in the original papers on this subject, e.g. [34]. An example of a transversely isotropic material for which \(v_2=\overline{v_1}\in \mathbb {C}\) is zinc with (all in GPa) \(k=80, \ell =33, n=50, m=63, p=40\), for which \(v_1\) = 1.1284 + 0.6465i to four digits of precision.
References
Tsai SW (1992) Theory of composite design. Think Composites, Dayton, Ohio
Torrent D, Sanchez-Dehesa J (2008) Acoustic cloaking in two dimensions: a feasible approach. New J Phys 10:063015
Amirkhizi AV, Tehranian A, Nemat-Nasser S (2010) Stress-wave energy management through material anisotropy. Wave Motion 47:519–536
Voigt W (1889) Ueber die Beziehung zwischeden beiden Elasticitätsconstanten. Annalen der Physik 38:573–587
Reuss A (1929) Calculation of the flow limits of mixed crystals on the basis of the plasticity of mono-crystals. Z Angew Math Mech 9:49–58
Eshelby JD (1957) The determination of the elastic field of an ellipsoidal inclusion. Proc R Soc Lond A 241:376–396
Hashin Z, Shtrikman S (1962) On some variational principles in anisotropic and non-homogeneous elasticity. J Mech Phys Solids 10:335–342
Hashin Z, Shtrikman S (1963) A variational approach to the theory of the elastic behaviour of multiphase materials. J Mech Phys Solids 11:127–140
Hashin Z (1965) On the elastic behaviour of fibre reinforced materials of arbitrary transverse phase geometry. J Mech Phys Solids 13:119–134
Hashin Z (1979) Analysis of properties of fiber composites with anisotropic constituents. J Appl Mech 46:543–550
Walpole LJ (1966) On bounds for the overall elastic moduli of inhomogeneous systems-I. J Mech Phys Solids 14:151–162
Willis JR (1977) Bounds and self-consistent estimates for the overall moduli of anisotropic composites. J Mech Phys Solids 25:185–202
Willis JR (1981) Variational and related methods for the overall properties of composites. Adv Appl Mech 21:1–78
Willis JR (1982) Theory elasticity, of composites mechanics of solids, the Rodney Hill 60th anniversary volume. In: Hopkins HG, Sewell MJ (eds) Pergamon, Oxford, pp 653–686
Willis JR, Bounds on the overall properties of anisotropic composites. In: Mura T, Koya T (eds) Variational methods in mechanics, chap. 21. Oxford University Press, Oxford
Ponte Castañeda P, Willis JR (1995) The effect of spatial distribution on the effective behaviour of composite materials and cracked media. J Mech Phys Solids 43:1919–1951
Willis JR (1986) Variational estimates for the overall response of an inhomogeneous nonlinear dielectric. In: Ericksen JL (ed) Homogenization and effective moduli of materials and media. Springer, New York, pp 247–263
Hill R (1963) Elastic properties of reinforced solids: some theoretical principles. J Mech Phys Solids 11:357–372
Talbot DRS, Willis JR (1985) Variational principles for inhomogeneous nonlinear media. IMA J Appl Math 35(1):39–54
Ponte Castañeda P (1862) The overall constitutive behaviour of nonlinearly elastic composites. Proc R Soc Lond Ser A 422(1989):147–171
Ponte Castañeda P (1992) A new variational principle and its application to nonlinear heterogeneous systems. SIAM J Appl Math 52:1321–1341
Beran MJ, Molyneux J (1966) Use of classical variational principles to determine bounds for the effective bulk modulus in heterogeneous media. Q Appl Math 24:107–118
Milton GW, Phan-Thien N (1982) New bounds on the effective moduli of two-component materials. Proc R Soc Lond A 380:305–331
Torquato S (1991) Random heterogeneous media: microstructure and improved bounds on effective properties. Appl Mech Rev 44:37–76
Rodrígues-Ramos R, Guinovart-Díaz R, Bravo-Castillero J, Sabina FJ, Berger H, Kari S, Gabbert U (2009) Variational bounds for anisotropic elastic multiphase composites with different shapes of inclusions. Arch Appl Mech 79:695–708
Hill R (1964) Theory of mechanical properties of fibre-strengthened materials: I. Elastic behaviour. J Mech Phys Solids 12:199–212
Liu LP (2008) Solutions to the Eshelby conjectures. Proc R Soc Lond A 464:573–594
Kang H, Milton GW (2008) Solutions to the Polya Szego conjecture and the weak Eshelby conjecture. Arch Ration Mech Anal 188:93–116
Hill R (1952) The elastic behavior of a crystalline aggregate. Proc Phys Soc Lond Sect A 65:349
Sevostianov I, Yilmaz N, Kushch V, Levin VM (2005) Effective elastic properties of matrix composites with transversely isotropic phases. Int J Solids Struct 42:455–476
Kanaun SK, Levin VM (2008) Self-consistent methods for composites. Volume 1-static problems. Springer, Dordrecht
Walpole LJ (1984) Fourth-rank tensors of the thirty two crystal classes: multiplication tables. Proc R Soc Lond A 391:149–179
Backus G (1962) Long-wave elastic anisotropy produced by horizontal layering. J Geophys Res 67:4427–4440
Withers PJ (1989) The determination of the elastic field of an ellipsoidal inclusion in a transversely isotropic medium and its relevance to composite materials. Phil Mag A 59:759–781
Mura T (1991) Micromechanics of defects in solids. Kluwer, Dordrecht
Acknowledgments
The authors thank Prof. I.D. Abrahams (University of Manchester, UK) for helpful discussions, Prof. P.A. Martin (Colorado School of Mines, USA) for reading through an early draft, and Prof. A.N. Norris (Rutgers University, USA) for providing useful references on tensor bases. This work has been partially supported by the project MTM 2011-24457 of the “Ministerio de Ciencia e Innovación” of Spain and the research group FQM-309 of the “Junta de Andalucía”.
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
1.1 Relationships between elastic and engineering moduli
Here we note the relationships between the moduli \(k,\ell ,n,m\) and the Engineering moduli:
and
1.2 The Eshelby (\(\mathbf {S}\)) tensor and the Hill (\(\mathbf {P}\)) tensor
We discuss these tensors for spheroids of aspect ratio \(\delta \), and thus we refer to the shape tensors, i.e. \(\mathbf {S}_s\) and \(\mathbf {P}_s\). However, we merely change \(\delta \) to \(\epsilon \) to obtain the associated distribution tensors, i.e. \(\mathbf {S}_d\) and \(\mathbf {P}_d\). Thus, consider the case of a spheroidal inclusion with semi-axes \(a_1=a_2\ne a_3\), embedded inside a transversely isotropic (TI) comparison phase with axis of symmetry along \(x_3\) and with elastic modulus tensor \(\mathbf {C}^c\). In short-hand notation, we write this as \(\mathbf {C}^c=(2k_c,\ell _c,\ell _c,n_c,2m_c,2p_c)\). The resulting Eshelby tensor \(\mathbf {S}_s\) is TI (but not symmetric in general), and in the short-hand notation, it may be written
where
Let us define the parameters:
where \(\hat{\ell }_c=(n_c(k_c+m_c))^{1/2}\). We note that for elastic materials \(v_3\in \mathbb {R}\) but \(v_1,v_2\in \mathbb {C}\) in general with \(v_2=\overline{v_1}\), where an overbar denotes the complex conjugate.Footnote 1 For \(v_i\in \mathbb {R}\), define
whereas when \(v_i\in \mathbb {C}\), either of the expressions in (10.4) can be used since they are merely an analytic continuation of the function (of \(v_i\)) into the complex \(v_i\)-plane.
We note that in the case of isotropy, \(\ell _c=\lambda _c=\ell _c'\), \(p_c=m_c=\mu _c\), \(\hat{\ell }_c=n_c=k_c+m_c=\lambda _c+2\mu _c\) (where \(\lambda _c\) and \(\mu _c\) are the Lamé moduli of the comparison phase) and thus \(v_1=v_2=v_3=1\). We introduce the notation \(I_1=I_1(1)\) for the isotropic case.
1.2.1 Eshelby tensor for an isotropic comparison phase
For an isotropic comparison phase defined by the Lamé moduli \(\lambda _c\) and \(\mu _c\), \(S_{ijk\ell }^c\) takes the form (see [6, 35], although note the slightly different notation involving the \(I_{ij}\)):
where \(A = [8\pi (1-\nu _c)]^{-1}, B = (1-2\nu _c)A\), and \(\nu _c=\lambda _c/(2(\lambda _c+\mu _c))\) is Poisson’s ratio of the comparison medium. We have defined
and thus the Eshelby tensor for the isotropic case is defined purely in terms of \(I_1=I_1(1)\) from (10.4). In the limiting case of an isotropic (\(v_i=1\)) sphere (\(\delta =1\)), the appropriate limit of (10.4) gives \(I_1=4\pi /3\) which completely defines the Eshelby tensor via (10.5)–(10.9). Only in this spherical, isotropic case does \(S_{1133}=S_{3311}\).
1.2.2 Eshelby tensor for a transversely isotropic comparison phase
For a TI comparison phase defined by elastic properties \(k_c, \ell _c, n_c, m_c\) and \(p_c\), the components \(S_{ijk\ell }\) take the form [34] (although note some typographical errors there that are corrected here):
where
Note that we have used the notation \(I_3(v_i)=-2I_1(v_i)+4\pi /v_i\) in (10.10)–(10.15) whereas [34] used \(I_2(v_i)\) instead of \(I_3(v_i)\) in the corresponding equations. This is to preserve the symmetry with the isotropic case above. Finally, let us define two very useful limits of the Eshelby tensor for TI comparison materials.
1.2.3 Layer (penny-shaped) limit (strongly oblate)
If we take the limit as \(\delta \rightarrow 0\), we find that
1.2.4 Long cylindrical fibre limit (strongly prolate)
If we take the limit as \(\delta \rightarrow \infty \), we find that
1.2.5 The \(\mathbf {P}\)-tensor
The \(\mathbf {P}\)-tensor is defined from (2.1), (2.2) and (6.4) and is a symmetric transversely isotropic tensor, which we write in short-hand notation as
for that associated with the shape of the inclusion (aspect ratio \(\delta \))—for the distribution \(\mathbf {P}\)-tensor \(\mathbf {P}_d\) replace \(\delta \) with \(\epsilon \).
Given an isotropic comparison phase with bulk modulus \(\kappa _c=\lambda _c+2\mu _c/3\) and shear modulus \(\mu _c\), we have
and given that we can write the tensors \(I^1\) and \(I^2\) in the form in (5.9), we can thus write
The \(\mathbf {P}\)-tensor then follows as in (6.4) by contracting \(\mathbf {S}^c\) for the isotropic comparison phase case as defined in 1 with this \((\mathbf {C}^c)^{-1}\).
For a transversely isotropic comparison phase \(\mathbf {C}^c=(2k_c,\ell _c,\ell _c,n_c,2m_c,2p_c)\) with inverse
the \(\mathbf {P}\)-tensor then follows as in (6.4) by contracting \(\mathbf {S}^c\) for the TI comparison phase case as defined in 1 with this \((\mathbf {C}^c)^{-1}\). Given that we have defined the Eshelby tensor components explicitly in Sect. 1, it is best written in terms of these components as
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
About this article
Cite this article
Parnell, W.J., Calvo-Jurado, C. On the computation of the Hashin–Shtrikman bounds for transversely isotropic two-phase linear elastic fibre-reinforced composites. J Eng Math 95, 295–323 (2015). https://doi.org/10.1007/s10665-014-9777-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10665-014-9777-3