Temperature distribution and heat flow around a crack of arbitrary orientation in a functionally graded medium

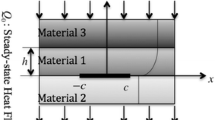
Abstract

This paper investigates the heat transfer problem of an infinite functionally graded medium containing an arbitrarily oriented crack under uniform remote heat flux. In the mathematical treatment the crack is approximated as a perfectly insulating cut. By using Fourier transformation, the mixed boundary value problem is reduced to a Cauchy-type singular integral equation for an unknown density function. The singular integral equation is then solved by representing the density function with a Chebyshev polynomial-based series and solving the resulting linear equation using a collocation technique. The temperature field in the vicinity of the crack and the crack-tip heat flux intensity factor are presented to quantify the effect of crack orientation and grading inhomogeneity on the heat flow around the crack.

Appendix: Solution for homogeneous medium

The density function $\psi (t)$ that satisfies Eq. (2.25) can be expressed as

$$\begin{aligned} \psi (t)=\frac{-2\cos \theta }{\sqrt{1-t^{2}}}. \end{aligned}$$

(7.1)

The temperature distribution along the crack surface planes are given by

$$\begin{aligned} \bar{{T}}_2 (\bar{{s}},0^{+})&= \left\{ {{\begin{array}{l@{\qquad }ll} \cos \theta \cos (\sin ^{-1}\bar{{s}})&{}\,\left| {\bar{{s}}} \right| <1, \\ 0&{}\,\left| {\bar{{s}}} \right| >1, \\ \end{array} }} \right. \end{aligned}$$

(7.2)

$$\begin{aligned} \bar{{T}}_2 (\bar{{s}},0^{-})&= \left\{ {{\begin{array}{l@{\quad }ll} -\cos \theta \cos (\sin ^{-1}\bar{{s}}) &{} \left| {\bar{{s}}} \right| <1, \\ 0&{}\left| {\bar{{s}}} \right| >1. \\ \end{array} }} \right. \end{aligned}$$

(7.3)

Substituting $\theta =0^{\circ }$ into Eqs. (7.2) and (7.3), the temperature solutions reduce to the solutions given in [8].