Skip to main content
SpringerLink
Log in

Applicability of the method of fundamental solutions to 3-D wave–body interaction with fully nonlinear free surface

  • Published:
Journal of Engineering Mathematics Aims and scope Submit manuscript

Abstract

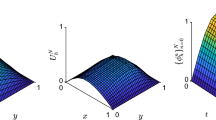
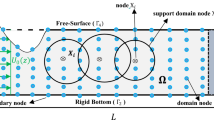
A numerical model for three-dimensional fully nonlinear free-surface waves is developed by applying a boundary-type meshless approach with a leap-frog time-marching scheme. Adopting Gaussian Radial Basis Functions to fit the free surface, a non-iterative approach to discretize the nonlinear free-surface boundary is formulated. Using the fundamental solutions of the Laplace equation as the solution form of the velocity potential, free-surface wave problems can be solved by collocations at only a few boundary points since the governing equation is automatically satisfied. The accuracy of the present method is verified by comparing the simulated propagation of a solitary wave with an exact solution. The applicability of the present model is illustrated by applying it to the problem of a solitary wave running up on a vertical surface-piercing cylinder and the problem of wave generation in infinite water depth by a submerged moving object.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Longuet-Higgins HS, Cokelet ED (1976) The deformation of steep waves on water, I, a numerical method of computation. Proc R Soc Lond A 350: 1–26. doi:10.1098/rspa.1976.0092

    Article  MATH  ADS  MathSciNet  Google Scholar 

  2. Issacson M (1982) Nonlinear wave effects on fixed and floating bodies. J Fluid Mech 120: 267–281. doi:10.1017/S0022112082002766

    Article  ADS  Google Scholar 

  3. Dommermuth DG, Yue DKP (1987) Numerical simulations of nonlinear axisymmetric flows with a free surface. J Fluid Mech 178: 195–219. doi:10.1017/S0022112087001186

    Article  MATH  ADS  Google Scholar 

  4. Grilli ST, Skourup J, Svendsen IA (1989) An efficient boundary element method for nonlinear water waves. Eng Anal Bound Elem 6: 97–107. doi:10.1016/0955-7997(89)90005-2

    Article  Google Scholar 

  5. Cooker MJ, Peregrine DH, Skovggard O (1990) The interaction between a solitary wave and a submerged semicircular cylinder. J Fluid Mech 215: 1–22. doi:10.1017/S002211209000252X

    Article  MATH  ADS  MathSciNet  Google Scholar 

  6. Ohyama T, Nadaoka K (1991) Development of a numerical wave tank for analysis of nonlinear and irregular wave field. Fluid Dyn Res 8: 231–251. doi:10.1016/0169-5983(91)90045-K

    Article  Google Scholar 

  7. Grilli ST, Guyenne P, Dias F (2001) A fully nonlinear model for three-dimensional overturning waves over an arbitrary bottom. Int J Numer Methods Fluids 35: 829–867 doi:10.1002/1097-0363(20010415)35:7 < 829::AID-FLD115 > 3.0.CO;2-2

    Article  MATH  Google Scholar 

  8. Tsai WT, Yue DKP (1996) Computation of nonlinear free-surface flows. Annu Rev Fluid Mech 28: 249–278

    ADS  MathSciNet  Google Scholar 

  9. Rokhlin V (1985) Rapid solution of integral equations of classical potential theory. J Comput Phys 60: 187–207. doi:10.1016/0021-9991(85)90002-6

    Article  MATH  ADS  MathSciNet  Google Scholar 

  10. Hackbusch W, Nowak ZP (1989) On the fast matrix multiplication in the boundary element method by panel clustering. Numer Math 54: 463–491. doi:10.1007/BF01396324

    Article  MATH  MathSciNet  Google Scholar 

  11. Beylkin G, Coifman R, Rokhlin V (1991) Fast wavelet transforms and numerical algorithms I. Commun Pure Appl Math 44: 141–183. doi:10.1002/cpa.3160440202

    Article  MATH  MathSciNet  Google Scholar 

  12. Cao YS, Schultz WW, Beck RF (1991) 3-dimensional desingularized boundary integral methods for potential problems. Int J Numer Methods Fluids 12: 785–803. doi:10.1002/fld.1650120807

    Article  MATH  MathSciNet  Google Scholar 

  13. Lalli F (1997) On the accuracy of the desingularized boundary integral method in free surface flow problems. Int J Numer Methods Fluids 25: 1163–1184 doi:10.1002/(SICI)1097-0363(19971130)25:10 < 1163::AID-FLD614 > 3.0.CO;2-5

    Article  MATH  MathSciNet  Google Scholar 

  14. Wang QX (2005) Unstructured MEL modeling of nonlinear unsteady ship waves. J Comput Phys 210: 368–385. doi:10.1016/j.jcp.2005.04.012

    Article  MATH  ADS  Google Scholar 

  15. Hardy RL (1971) Multiquadric equations of topography and other irregular surfaces. J Geophys Res 76: 1905–1915. doi:10.1029/JB076i008p01905

    Article  ADS  Google Scholar 

  16. Franke C (1982) Scattered data interpolation: test of some methods. Math Comput 38: 181–200. doi:10.2307/2007474

    Article  MATH  MathSciNet  Google Scholar 

  17. Moody J, Darken C (1989) Fast-learning in networks of local tuned processing units. Neural Comput 1: 281–294. doi:10.1162/neco.1989.1.2.281

    Article  Google Scholar 

  18. Kansa JE (1990) Multiquadrics—a scattered data approximation scheme with applications to computational fluid dynamics—II, Solutions to parabolic, hyperbolic and elliptic partial differential equations. Comput Math Appl 19: 127–145. doi:10.1016/0898-1221(90)90270-T

    Article  MATH  MathSciNet  Google Scholar 

  19. Du CJ (1999) Finite-point simulation of steady shallow water flows. J Hydraul Eng 125: 621–630. doi:10.1061/(ASCE)0733-9429(1999)125:6(621)

    Article  Google Scholar 

  20. Du CJ (2000) An element-free Galerkin method for simulation of stationary two-dimensional shallow water flows in rivers. Comput Methods Appl Mech Eng 182: 89–107. doi:10.1016/S0045-7825(99)00087-0

    Article  MATH  Google Scholar 

  21. Zhou X, Hon YC, Cheung KF (2004) A grid-free, nonlinear shallow-water model with moving boundary. Eng Anal Bound Elem 28: 967–973. doi:10.1016/S0955-7997(03)00124-3

    Article  MATH  Google Scholar 

  22. Young DL, Jane SJ, Lin CY, Chiu CL, Chen KC (2004) Solution of 2D and 3D Stokes law using multiquadratics method. Eng Anal Bound Elem 28: 1233–1243. doi:10.1016/j.enganabound.2003.04.002

    Article  MATH  Google Scholar 

  23. Ata R, Soulaimani A (2005) A stabilized SPH method for inviscid shallow water flows. Int J Numer Methods Fluids 47: 139–159. doi:10.1002/fld.801

    Article  MATH  MathSciNet  Google Scholar 

  24. Ma Q (2005) Meshless local Petrov–Galerkin method for two-dimensional nonlinear water wave problems. J Comput Phys 205: 611–625. doi:10.1016/j.jcp.2004.11.010

    Article  MATH  ADS  MathSciNet  Google Scholar 

  25. Golberg MA, Chen CS (1998) The method of fundamental solutions for potential, Helmholtz and diffusion problems. In: Golberg MA (ed) Boundary integral methods-numerical and mathematical aspects. Computational Mechanics Publications, pp.103–176

  26. Young DL, Chen KH, Lee CW (2005) Novel meshless method for solving the potential problems with arbitrary domain. J Comput Phys 209: 290–321. doi:10.1016/j.jcp.2005.03.007

    Article  MATH  ADS  Google Scholar 

  27. Wu NJ, Tsay TK, Young DL (2006) Meshless simulation for fully nonlinear water waves. Int J Numer Methods Fluids 50: 219–234. doi:10.1002/fld.1051

    Article  MATH  Google Scholar 

  28. Wu NJ, Tsay TK, Young DL (2008) Computation of nonlinear free-surface flows by a meshless numerical method. J Waterw Port Coast Ocean Eng 134: 97–103. doi:10.1061/(ASCE)0733-950X(2008)134:2(97)

    Article  Google Scholar 

  29. Grimshaw R (1971) The solitary wave in water of variable depth, part 2. J Fluid Mech 9: 611–622. doi:10.1017/S0022112071000739

    Article  ADS  Google Scholar 

  30. Ambrosi D, Quartapelle L (1998) A Taylor–Galerkin method for simulation nonlinear dispersive waves. J Comput Phys 146: 546–569. doi:10.1006/jcph.1998.6027

    Article  MATH  ADS  MathSciNet  Google Scholar 

  31. Peregrine DH (1967) Long waves on beach. J Fluid Mech 27: 815–827. doi:10.1017/S0022112067002605

    Article  MATH  ADS  Google Scholar 

  32. Nwogu O (1993) An alternative form of Boussinesq equations for near shore wave propagation. J Waterw Port Coast Ocean Eng 119: 618–638. doi:10.1061/(ASCE)0733-950X(1993)119:6(618)

    Article  Google Scholar 

  33. Wei G, Kirby JT, Grilli ST, Subramanya R (1995) Time-dependent numerical code for extended Boussinesq equations. J Fluid Mech 294: 71–92. doi:10.1017/S0022112095002813

    Article  MATH  ADS  MathSciNet  Google Scholar 

  34. Gobbi MF, Kirby JT (1999) Wave evolution over submerged sills: tests of a high order Boussinesq model. Coast Eng 37: 57–96. doi:10.1016/S0378-3839(99)00015-0

    Article  Google Scholar 

  35. Berkhoff JCW (1972) Computation of combined refraction–diffraction. In: Proc. 13th conf. eng., ASCE, Vancouver; pp. 471–490

  36. Liu PLF, Tasy TK (1984) Refraction–diffraction model for weakly nonlinear water waves. J Fluid Mech 136: 453–466

    Google Scholar 

  37. Tang Y, Ouellet Y (1996) A new kind of nonlinear mild-slope equation for combined refraction–diffraction of multi-frequency waves. J Coast Eng 31: 3–36. doi:10.1016/S0378-3839(96)00050-6

    Article  Google Scholar 

  38. Chen MY, Mei CC (2006) Second-order refraction and diffraction of surface water waves. J Fluid Mech 552: 137–166. doi:10.1017/S0022112005008530

    Article  MATH  ADS  MathSciNet  Google Scholar 

  39. Havelock TH (1931) The wave resistance of a spheroid. Proc R Soc Lond, A 131: 275–285. doi:10.1098/rspa.1931.0052

    Article  MATH  ADS  Google Scholar 

  40. Farell C (1973) On the wave resistance of a submerged spheroid. J Ship Res 17: 1–11

    Google Scholar 

  41. Doctors LJ, Beck RF (1987) Convergence properties of the Neumann–Kelvin problem for a submerged body. J Ship Res 31: 227–234

    Google Scholar 

  42. Bertram V, Schultz WW, Cao Y, Beck RF (1991) Nonlinear computations for wave drag, lift and moment of a submerged spheroid. Ship Technol Res 38: 3–5

    Google Scholar 

  43. Cao Y (1991) Computations of nonlinear gravity waves by a desingularised boundary integral method. Ph.D. dissertation, Department of Naval Architecture and Marine Engineering, The University of Michigan

  44. Scullen DC (1998) Accurate computation of steady nonlinear free-surface flows. Ph.D. dissertation, Department of Applied Mathematics, The University of Adelaide

  45. Tuck EO, Scullen DC (2002) A comparison of linear and nonlinear computations of waves made by slender submerged bodies. J Eng Math 42: 255–264. doi:10.1023/A:1016131128042

    Article  MATH  MathSciNet  Google Scholar 

  46. Kent CP, Choi W (2007) An explicit formulation for the evolution of nonlinear surface waves interacting with a submerged body. Int J Numer Methods Fluids 55: 1019–1038. doi:10.1002/fld.1504

    Article  MATH  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Civil Engineering, National Taiwan University, 1 Roosevelt Rd., Sec. 4, Taipei City, 10617, Taiwan

    Nan-Jing Wu & Ting-Kuei Tsay

Authors
  1. Nan-Jing Wu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Ting-Kuei Tsay
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Ting-Kuei Tsay.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Wu, NJ., Tsay, TK. Applicability of the method of fundamental solutions to 3-D wave–body interaction with fully nonlinear free surface. J Eng Math 63, 61–78 (2009). https://doi.org/10.1007/s10665-008-9250-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10665-008-9250-2

Keywords

Search

Navigation