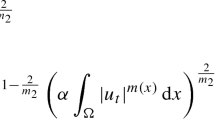Skip to main content
SpringerLink
Log in

Nonlinear wave equation with Dirichlet and Acoustic boundary conditions: theoretical analysis and numerical simulation

  • Published:
Computational and Applied Mathematics Aims and scope Submit manuscript

Abstract

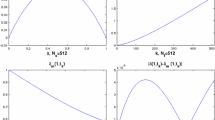
We investigate some theoretical and numerical aspects of a nonlinear wave equation with variable coefficient and Dirichlet and Acoustic boundary conditions. The existence and uniqueness of the solution are obtained applying the Faedo-Galerkin method with some compactness results and energy method. In addition, we prove the uniform stability of the energy. For numerical simulation, firstly we use the Crank–Nicolson Galerkin method, in which it consists of applying the finite element method in the spatial variable and the Crank–Nicolson method over time. Subsequently, in the resulting nonlinear algebraic system, for each discrete time, we apply the Newton’s method without losing the convergence order. Moreover, are presented figures of the numerical solutions for the two-dimensional case, tables with error and convergence order and the numerical energy decay. These results justify the consistency between the theoretical and numerical results.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3

Similar content being viewed by others

References

  • Alcântara AA, Clark HR, Rincon MA (2018) Theoretical analysis and numerical simulation for a hyperbolic equation with dirichlet and acoustic boundary conditions. Comput Appl Math 37(4):4772–4792

    Article  MathSciNet  Google Scholar 

  • Baker GA (1976) Error estimates for finite element methods for second order hyperbolic equations. SIAM J Numer Anal 13:564–576

    Article  MathSciNet  Google Scholar 

  • Basson M, van Rensburg NFJ (2013) Galerkin finite element approximation of general linear second order hyperbolic equations. Numer Funct Anal Optim 34(9):976–1000

    Article  MathSciNet  Google Scholar 

  • Beale JT (1976) Spectral properties of an acoustic boundary condition. Indiana Univ Math J 25(9):895–917

    Article  MathSciNet  Google Scholar 

  • Beale JT (1977) Acoustic scattering from locally reacting surfaces. Indiana Univ Math J 26(2):199–222

    Article  MathSciNet  Google Scholar 

  • Beale JT, Rosencrans SI (1974) Acoustic boundary conditions. Bull Am Math Soc 80(6):1276–1278

    Article  MathSciNet  Google Scholar 

  • Carmo BA, Clark HR, Guardia RR, Rincon MA (2018) Mathematical analysis and numerical simulation of a nonlinear thermoelastic system. Numer Funct Anal Optim pp 1–29

  • Cavalcanti MM, Domingos Cavalcanti VN, Frota CL, Vicente A (2020) Stability for semilinear wave equation in an inhomogeneous medium with frictional localized damping and acoustic boundary conditions. SIAM J Control Optim 58(4):2411–2445

    Article  MathSciNet  Google Scholar 

  • Cavalcanti M SJ Domingos Cavalcanti V (2006) Global Solvability and Asymptotic Stability for the Wave Equation with Nonlinear Boundary Damping and Source Term, Birkhäuser Basel, pp 161–184

  • Chen G (1979) Energy decay estimates and exact boundary-value controllability for the wave equation in a bounded domain’’. Journal de Mathématiques Pures et Appliquées 58:249–273

    MathSciNet  MATH  Google Scholar 

  • Chen Y, Huang Y (1998) The full-discrete mixed finite element methods for nonlinear hyperbolic equations. Commun Nonlinear Sci Numer Simul 3(3):152–155

    Article  MathSciNet  Google Scholar 

  • Chrysafinos K, Hou LS (2017) Semi-discrete error estimates of the evolutionary stokes equations with inhomogeneous dirichlet boundary data. Comput Math Appl 73(8):1684–1696

    Article  MathSciNet  Google Scholar 

  • Ciarlet PG (2002) The finite element method for elliptic problems. SIAM

  • Clark H, Jutuca LSG, Miranda MM (1998) On a mixed problem for a linear coupled system with variable coefficients. Eletron J Differ Equ 1(4):1–20

    MATH  Google Scholar 

  • Cousin AT, Frota CL, Larkin NA (2004) On a system of klein-gordon type equations with acoustic boundary conditions. J Math Anal Appl 293(1):293–309

    Article  MathSciNet  Google Scholar 

  • Dupont T (1973) \({L}^2\)-estimates for galerkin methods for second order hyperbolic equations. SIAM J Numer Anal 10(5):880–889

    Article  MathSciNet  Google Scholar 

  • Frigeri S (2010) Attractors for semilinear damped wave equations with an acoustic boundary condition. J Evol Equ 10(1):29–58

    Article  MathSciNet  Google Scholar 

  • Frota C, Medeiros L, Vicente A et al (2011) Wave equation in domains with non-locally reacting boundary. Differ Integr Equ 24(11/12):1001–1020

    MathSciNet  MATH  Google Scholar 

  • Frota CL, Goldstein JA (2000) Some nonlinear wave equations with acoustic boundary conditions. J Differ Equ 164(1):92–109

    Article  MathSciNet  Google Scholar 

  • Frota CL, Larkin NA (2005) Uniform stabilization for a hyperbolic equation with acoustic boundary conditions in simple connected domains. In: Contributions to nonlinear analysis, Springer, pp 297–312

  • Graber PJ (2012) Uniform boundary stabilization of a wave equation with nonlinear acoustic boundary conditions and nonlinear boundary damping. J Evol Equ 12(1):141–164

    Article  MathSciNet  Google Scholar 

  • Gunzburger M, Hou S (1992) Treating inhomogeneous essential boundary conditions in finite element methods and the calculation of boundary stresses. SIAM J Numer Anal 29(2):390–424

    Article  MathSciNet  Google Scholar 

  • Ha TG (2016) General decay estimates for the wave equation with acoustic boundary conditions in domains with nonlocally reacting boundary. Appl Math Lett 60:43–49

    Article  MathSciNet  Google Scholar 

  • Hipp D, Kovács B (2020) Finite element error analysis of wave equations with dynamic boundary conditions: L2 estimates. IMA J Numer Anal 41(1):638–728

    Article  Google Scholar 

  • Hipp D, Hochbruck M, Stohrer C (2018) Unified error analysis for non-conforming space discretizations of wave-type equations. IMA J Numer Anal 39(2):1206–1245

    MATH  Google Scholar 

  • Karaa S (2011) Finite element o-schemes for the acoustic wave equation. Adv Appl Math Mech 3(1):181–203

    Article  MathSciNet  Google Scholar 

  • Kashiwabara T, Colciago C, Dedè L, Quarteroni A (2015) Well-posedness, regularity, and convergence analysis of the finite element approximation of a generalized robin boundary value problem. SIAM J Numer Anal 53(1):105–126

    Article  MathSciNet  Google Scholar 

  • Kobayashi Y, Tanaka N (2008) An application of semigroups of locally lipschitz operators to carrier equations with acoustic boundary conditions. J Math Anal Appl 338(2):852–872

    Article  MathSciNet  Google Scholar 

  • Komornik V, Zuazua E (1990) A direct method for boundary stabilization of the wave equation. J Math Pure et Appl 69:33–54

    MathSciNet  MATH  Google Scholar 

  • Lee MJ, Kang JR (2021) Blow-up results for a quasilinear von karman equation of memory type with acoustic boundary conditions. Appl Math Lett 112

  • Límaco J, Clark HR, Frota CL, Medeiros LA (2011) On an evolution equation with acoustic boundary conditions. Math Methods Appl Sci 34(16):2047–2059

    Article  MathSciNet  Google Scholar 

  • Lions JL (1969) Quelques méthodes de résolution des problemes aux limites non linéaires, vol 31. Dunod Paris

  • Medeiros LA, Miranda MM (1996) On a boundary value problem for wave equations: Existence, uniqueness-asymptotic behavior. Revista de Matemáticas Aplicadas, Universidade do Chile 17:47–73

    MathSciNet  MATH  Google Scholar 

  • Mugnolo D (2006) Abstract wave equations with acoustic boundary conditions. Math Nachr 279(3):299–318

    Article  MathSciNet  Google Scholar 

  • Shi D, Li Z (2008) Superconvergence analysis of the finite element method for nonlinear hyperbolic equations with nonlinear boundary condition. Appl Math J Chin Univ 23(3):455–462

    Article  MathSciNet  Google Scholar 

  • Silva PB, Clark H, Frota C (2017) On a nonlinear coupled system of thermoelastic type with acoustic boundary conditions. Comput Appl Math 36(1):397–414

    Article  MathSciNet  Google Scholar 

  • Verfürth R (1994) A posteriori error estimation and adaptive mesh-refinement techniques. J Comput Appl Math 50(1):67–83

    Article  MathSciNet  Google Scholar 

  • Vicente A, Frota C (2013) Nonlinear wave equation with weak dissipative term in domains with non-locally reacting boundary. Wave Motion 50(2):162–169

    Article  MathSciNet  Google Scholar 

  • Vicente A, Frota C (2013) On a mixed problem with a nonlinear acoustic boundary condition for a non-locally reacting boundaries. J Math Anal Appl 407(2):328–338

    Article  MathSciNet  Google Scholar 

  • Wheeler MF (1973) \(l_{\infty }\) estimates of optimal orders for galerkin methods for one-dimensional second order parabolic and hyperbolic equations. SIAM J Numer Anal 10(5):908–913

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

Adriano A. Alcântara and Bruno A. Carmo were partially supported by CAPES-Brazil. Mauro A. Rincon was partially supported by CNPq-Brazil.

Author information

Authors and Affiliations

  1. Institute of Computing, Federal University of Rio de Janeiro, Rio de Janeiro, RJ, Brazil

    Adriano A. Alcântara, Bruno A. Carmo & Mauro A. Rincon

  2. Department of Mathematics, Federal University of the Delta do Parnaíba, Parnaíba, PI, Brazil

    Haroldo R. Clark

  3. Institute of Mathematics and Statistics, State University of Rio de Janeiro, Rio de Janeiro, RJ, Brazil

    Ronald R. Guardia

Authors
  1. Adriano A. Alcântara
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Bruno A. Carmo
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Haroldo R. Clark
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Ronald R. Guardia
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Mauro A. Rincon
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Adriano A. Alcântara.

Additional information

Communicated by Abdellah Hadjadj.

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Alcântara, A.A., Carmo, B.A., Clark, H.R. et al. Nonlinear wave equation with Dirichlet and Acoustic boundary conditions: theoretical analysis and numerical simulation. Comp. Appl. Math. 41, 141 (2022). https://doi.org/10.1007/s40314-022-01822-5

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s40314-022-01822-5

Keywords

Mathematics Subject Classification

Search

Navigation