Mastering uncertainty in performance estimations of configurable software systems

Abstract

Understanding the influence of configuration options on the performance of a software system is key for finding optimal system configurations, system understanding, and performance debugging. In the literature, a number of performance-influence modeling approaches have been proposed, which model a configuration option’s influence and a configuration’s performance as a scalar value. However, these point estimates falsely imply a certainty regarding an option’s influence that neglects several sources of uncertainty within the assessment process, such as (1) measurement bias, choices of model representation and learning process, and incomplete data. This leads to the situation that different approaches and even different learning runs assign different scalar performance values to options and interactions among them. The true influence is uncertain, though. There is no way to quantify this uncertainty with state-of-the-art performance modeling approaches.

We propose a novel approach, P4, which is based on probabilistic programming, that explicitly models uncertainty for option influences and consequently provides a confidence interval for each prediction alongside a scalar. This way, we can explain, for the first time, why predictions may be erroneous and which option’s influence may be unreliable. An evaluation on 13 real-world subject systems shows that P4’s accuracy is in line with the state of the art while providing reliable confidence intervals, in addition to scalar predictions. We qualitatively explain how uncertain influences of individual options and interactions cause inaccurate predictions.

1 Introduction

Most software systems, such as database management systems, video trans-coders, and compilers, exhibit configuration options so that users can tailor these systems’ functionality to a specific use case. Moreover, these configuration options also affect performance, i.e., non-functional properties such as energy consumption, response time, and throughput. The task of (optimally) configuring a software system is of paramount importance because (1) many systems are shipped with a sub-optimal default configuration (Aken et al. 2017; Herodotou et al. 2011), (2) manually exploring configurations does not scale (Xu et al. 2015), and (3) fine-grained tuning can improve performance up to several orders of magnitude (Jamshidi and Casale 2016; Zhu et al. 2017). This is why certain disciplines have whole branches of parameter optimization (Bergstra et al. 2011) or algorithm selection (Rice 1976), but with substantially smaller and usually unconstrained configuration spaces.

Domain engineers often have tight non-functional constraints, for which they need to find a satisfying configuration, for example, when a binary footprint of a system needs to fit on a given flash size, or one seeks to minimize the energy consumed when running the system. In these cases, we must understand an option’s influence on performance to find a proper combination of options. Different approaches have been proposed to model the influence of options and interactions among options on performance, including rule-based decision trees (Guo et al. 2013), symbolic regression (Siegmund et al. 2012b), and neural networks (Ha and Zhang 2019a; Cheng et al. 2022). These performance-influence models require a set of configurations that is sampled from the software system’s configuration space and whose performance is subsequently measured. These data are then fed into a learning algorithm, which yields a model that allows stakeholders to estimate a single performance value for a given configuration. Since these models treat option influences as having fixed, but unknown values, we refer to them as frequentist models. Unfortunately, the scalar prediction value of frequentist models falsely implies a certainty in its estimates which neglects several sources of uncertainty in the modeling process: (1) measurement bias, (2) choices of model representation and learning process, and (3) incomplete data (e.g., due to sampling bias) (Smith 2013).

Without a proper uncertainty measure, application engineers may be led to unfavorable decisions as there is no available information about how certain a learned option’s influence or estimated performance is. For example, a domain engineer may rely on a frequentist model to configure a database management system such that it has a large number of features but still allows a battery life of 10 hours of the mobile platform onto which it will be deployed. In this case, the domain engineer cannot judge how much fault tolerance to leave in the case the frequentist model is wrong and has to resort to trial and error. Figure 1 illustrates the scalar influence of an exemplary option as a vertical bar. The different bars exemplify that different learning approaches lead to different fitted scalar influences, and even a single approach can produce substantially different values arising from different runs and different hyper-parameter settings. That is, looking at Fig. 1, it is unclear which actual effect the option has on the system’s energy consumption, and there is no way to quantify this uncertainty with state-of-the-art frequentist performance-influence modeling approaches for configurable systems. When configuring a database management system with a battery life constraint, a frequentist model will guide a domain engineer to a single configuration while there may be better configurations that the model misjudged due to unconsidered uncertainties.

Fig. 1

An exemplary option’s energy consumption influence modeled by different scalar regression models (bars), which are contrasted by P4’s probability density prediction (blue curve)

We set out to address this issue and propose an approach, called P4, that accounts for uncertainty about the true influences of individual options and their interactions on performance, which may arise from measurement bias, the learning procedure, and incompleteness of data (Trubiani and Apel 2019). By making uncertainty explicit across the whole modeling process, using a Bayesian rather than a frequentist approach, we foster model understanding, provide clear expectation boundaries for performance estimates, and offer a means to quantify when and where a learned model is inaccurate (e.g., due to missing data). All these pieces of information are absent in current approaches, which harms trust in the models and transfer into practice. In contrast, P4 allows users to rely on the expectation boundaries of our approach to avoid trial and error while configuring a database management system under battery life constraints.

To illustrate P4, let us compare the probability distribution (in blue) in Fig. 1 against the scalars of the different frequentist learning approaches. Considering the distribution as a whole, we can derive how likely the influence of an option or interaction falls into a value range. The spread of the distribution indicates how certain the model is about the option’s actual influence and whether additional data for this option might be necessary. It also gives confidence intervals for predictions and performance optimizations. This way, users are not only aware of uncertain predictions, but they can also find out which option is not well enough understood by the model to inflate the predicted uncertainty.

Our approach frames the problem of performance-influence modeling in a Bayesian setting with probabilistic programming (Salvatier et al. 2016). This requires the specification of three key components: likelihood, prior, and observations. The likelihood expresses a generative model of how the observations (i.e., measured configurations) are distributed. The prior encodes the belief (or expectation) about each option’s and interaction’s influence on performance. This is usually expressed as a distribution over a specific value range (e.g., a uniform distribution between 40 and 65 s). However, the domain knowledge to specify this distribution is not always available. As a remedy, P4 includes an automated prior estimation algorithm as a key element, which can be used to learn accurate Bayesian performance-influence models without domain knowledge.

This work extends an existing conference paper (Dorn et al. 2020): As part of the conference version, we propose an approach for performance-influence modeling that incorporates and quantifies the uncertainty of influences of configuration options and interactions on performance. A key ingredient is an automatic prior estimation algorithm that takes the burden of guessing priors from the user. We conduct an evaluation of the reliability of the uncertainty estimates of inferred models and compare the accuracy of our approach to a state-of-the-art frequentist model. In this journal extension, we furthermore study the distribution of uncertainty within learned models and qualitatively investigate whether we can trace inaccurate predictions back to uncertain influences, which enables future work on active learning in this direction.

We make the following contributions:

• P4, a probabilistic modeling approach for performance-influence modeling of configurable software systems,

• a data preprocessing pipeline to avoid inference failures and to improve model interpretability,

• an open-source implementation of P4,

• an evaluation of its prediction accuracy,

• an evaluation of the reliability of the uncertainty measures of inferred models,

• an analysis of the distribution of uncertainty measures of inferred models, and

• a qualitative root-cause analysis for highly uncertain predictions

With our approach, we add to the important trend on explainability and interpretability of machine-learning models. We believe that this is especially important in domains such as software engineering, in which machine-learning models must provide insights and explanations to help improving the field.

2 Modeling Uncertainty

Performance-influence modeling entails different kinds of uncertainty, of which we consider aleatoric and epistemic uncertainty in our work, similar to Kendall and Gal (2017) and Kiureghian and Ditlevsen (2008). Aleatoric uncertainty results from errors inherent to the measurements of the training set, epistemic uncertainty expresses doubt in the model’s parameters. Both can be be integrated into a Bayesian performance model, for which we explain the basics in Section 2.3.

2.1 Aleatoric Uncertainty

Performance-influence models describe a system’s performance in terms of influences of its configuration options and interactions (Siegmund et al. 2015). A configuration is a set of assignments to all available options from a certain domain (e.g., binary or numeric), that is $c = \{o_{1}, o_{2}, \dots , o_{n} \}$, where n is the number of options and o_i is the value assigned to the i-th option. We denote the assigned value of an option o in a given configuration c with the predicate of the option’s name, o(c).

We measure the performance of a configuration by configuring a software system, and executing a workload. Formally, we denote a configuration’s performance π as a function that maps a configuration c from the set of valid configurations $\mathcal {C}$ to its corresponding scalar performance value: $\pi : C \mapsto \mathbb {R}$. For a DBMS, we could choose energy consumption as a performance metric, run a benchmark, and query an external power meter to determine the energy needed. However, there are two notable sources of error arising from measurement, which introduce uncertainty: measurement error and representation error.

2.1.1 Measurement Error

Typically, the measurement process has an inherent error ε, which is typically either absolute or relative (Taylor 1997). Absolute errors ε_abs affect all measurements equally:

$$ \hat{\pi}(c) \in \Big[\pi(c) - \varepsilon_{\mathit{abs}}, \pi(c) + \varepsilon_{\mathit{abs}} \Big] $$

(1)

By contrast, relative errors ε_rel are given in percent and affect higher values more severely:

$$ \hat{\pi}(c) \in \left[ \pi(c) \cdot \frac{100 - \varepsilon_{\mathit{rel}}}{100}, \pi(c) \cdot \frac{100 + \varepsilon_{\mathit{rel}}}{100} \right] $$

(2)

Note that, depending on the context, this interval, called confidence interval, can be defined to span all possible measurements for $\hat {\pi }$ or, alternatively, to contain $\hat {\pi }$ only in a fraction of cases (e.g. 95%). Unfortunately, this information is rarely available to the user.

The confidence interval of the measurement error constitutes an uncertainty that can be reduced by aggregating repeated measurements, but it is fixed at modeling time (i.e., the time when we fit the model). Moreover, absolute and relative errors are examples for homoscedastic and heteroscedastic aleatoric uncertainty, respectively. This means that, in the case of relative measurement error, the variance of uncertainty depends on the individual sample (heteroscedastic), whereas it is constant for the absolute measurement error (homoscedastic).

2.1.2 Representation Error

Representation of measurement data requires discretization for storage and processing. We assume a decimal representation for simplicity, as the precision of floating-point representations is more complicated¹. Discretization can happen on the sensor side before we store the data. For example, an energy meter returning only integer Watt-hour (Wh) values may cause a representation error of ± 0.5Wh, while storing the execution time of a benchmark in seconds with two decimals may yield a representation error of ± 5ms.

$$ \bar{\pi}(c) \in \big[\hat{\pi}(c) - u, \hat{\pi}(c) + u \big] $$

(3)

That is, in the general case, the performance value at modeling time lies around the measured performance $\hat {\pi }(c)$ within ± u, the unit length of the discretization. Depending on the use case, the representation error can induce substantial uncertainty.

2.2 Epistemic Uncertainty

Models, in general, and performance-influence models, in particular, never match reality perfectly. While, in our case, aleatoric uncertainty arises from the training data samples, epistemic uncertainty stems from the model chosen and the amount of data provided. Let us assume a linear performance model π(c) for a configurable software system with n options:

$$ \pi(c) = \beta_{0} + \beta_{1} \cdot o_{1}(c) + {\dots} + \beta_{n} \cdot o_{n}(c) $$

(4)

Here, o_i returns the value for the i-th option of configuration c; these values are multiplied with the model parameters β, where β₀ is the base performance of the system. However, we can assign different values to β to model π as a one-point estimate.

A typical use case in practice are linear regression models, which can be fitted to minimize different objective functions. Lasso (Tibshirani 1996) and Ridge (Hoerl and Kennard 1970) regression are alternatives to Ordinary Least Squares regression, which can be combined into an Elastic Net (Zou and Hastie 2017). Their objectives differ in their way of computing the learning error (L1 and L2 normalization). A tuning parameter changes Elastic Net’s error computation function such that there is no single right way to fit a linear model. As Fig. 1 shows, we obtain different values for the same coefficient β_i when applying Lasso, Ridge, and Ordinary Least Squares. Hence, the fitted value for β_i is uncertain, as the blue curve in Fig. 1 illustrates.

Another reason why β can take different values lies in the training data used. Different samples of configurations — sampled according to different sampling strategies (Kaltenecker et al. 2020) — lead to different β values, even with the same error function, as the literature on sampling approaches has demonstrated (Kaltenecker et al. 2019; Henard et al. 2015; Siegmund et al. 2012b). Yet, even different hyperparameter settings can result in different coefficients depending on how strong we penalize the learning error. In addition, unless a training set contains all valid samples, we are uncertain whether β is a good fit, since increasing the training set size usually improves the prediction accuracy of a regression model by refining β and also reduces uncertainty about β. Note that although adding samples to the training set reduces uncertainty, each sample itself is still subject to aleatoric uncertainty.

Instead of specifying the model’s weights as a real-valued vector $\boldsymbol {\beta } \in \mathbb {R}^{n}$, we can formally incorporate uncertainty into β by changing it to a probability vector $\hat {\boldsymbol {\beta }}$. This way, each model weight becomes a probability density function that specifies which values for β are more probable than others representing the best fit. Thus, for Gaussian-distributed uncertainty, we can specify

$$ \boldsymbol{\hat{\beta}} \sim \mathcal{N}(\boldsymbol{\mu}, \boldsymbol{\sigma}), $$

(5)

as a probability vector, with $\boldsymbol {\mu }, \boldsymbol {\sigma } \in \mathbb {R}^{n}$. We do not know, though, whether uncertainty is Gaussian-distributed for real-valued configurable systems and what are the settings for μ,σ. To determine this distribution, we need probabilistic programming.

2.3 Probabilistic Programming

Framing the problem of performance modeling in a Bayesian setting can be done via probabilistic programming (Salvatier et al. 2016). Users of this paradigm must specify three key components with a probabilistic programming language (PPL): likelihood, prior, and observations. With these, the PPL takes care of Bayesian inference according to Bayes’ according to Bayes’ theorem:

$$ \overbrace{\mathbb{P}(A\!\mid\!B)}^{\text{Posterior}} = \frac{ \overbrace{\mathbb{P}(B\!\mid\!A)}^{\text{Likelihood}}\cdot \overbrace{\mathbb{P}(A)}^{\text{Prior}}} {\mathbb{P}(B)} $$

(6)

We refrain from explaining Bayesian statistics from scratch, but explain in what follows the necessary components for inference. If we assume that A and B are distinct events, then $\mathbb {P}(\cdot )$ maps an event to its probability to occur, $\mathbb {P}(\cdot \!\mid \!\cdot )$ gives the conditional probability of an event A given that another event B occurs. In the context of probabilistic programming, A is a vector of random variables that represents model parameters, whereas B represents observations. A Probability Density Function (PDF) is a function of a random variable whose integral over an interval represents the probability of the random variable’s value to lie within this interval. Accordingly, $\mathbb {P}(\cdot )$ maps a random variable to its PDF, and $\mathbb {P}(\cdot \!\mid \!\cdot )$ returns the conditional PDF of a random variable given that another random variable has a certain PDF. With these definitions, we next explain the components of Bayes’ theorem that are relevant for probabilistic programming.

Likelihood

$\big (\mathbb {P}(B\!\mid \!A)\big )$ The likelihood specifies the distribution of observations B assuming that the PDFs for model parameters A are true. With probabilistic programming, the likelihood is typically specified as a generative model that incorporates random variables. Imagine an example in which we repeatedly toss a coin to find out whether and how it is biased. We can represent the probabilities of the possible outcomes, heads and tails, with a Bernoulli distribution $\mathbb {B}(\cdot )$, whose parameter p ∈ [0,1] defines the probability of heads. Formally, we first let A be a Bernoulli-distributed random variable and then define the likelihood $\mathbb {P}(B\!\mid \!A)$ to be determined by A:

$$ \begin{array}{@{}rcl@{}} A &\sim & \mathbb{B}(p) \\ B\!\mid\!A &\sim & A \end{array} $$

While this model has only one random variable, more complex models are possible; however, the inference may not be analytically solvable, requiring approximations such as Monte Carlo Markov Chain (MCMC) sampling (Neal 1993). Such a generative model can make predictions that are PDFs (i.e., posterior distributions) themselves.

Prior

$\big (\mathbb {P}(A)\big )$ Priors define our belief about the distribution of our random variables before seeing any training data. Choosing priors naturally requires domain knowledge and is comparable to selecting an optimization starting point. An uninformed prior for the coin-toss example is

$$ A \sim \mathbb{B}(0.5)\text{,} $$

which assumes that both heads and tails are equally probable.

Posterior

$\big (\mathbb {P}(A\!\mid \!B)\big )$ from Observations B Given a likelihood, we can finally update our prior beliefs with observations. From a machine-learning stance, observations form the training set. In case of the coin-toss example, running Bayesian inference with 5 observed heads will yield an updated generative model, the posterior, which will give heads a higher probability.

3 Bayesian Performance Modeling

In this section, we describe our approach of incorporating uncertainty into performance-influence models. Figure 2 provides an overview of all steps involved. In a nutshell, we perform the following tasks: First, we preprocess a given set of measured configurations (i.e., the training set) to ensure that inference

• (i) does not break and that it

• (ii) finishes in a reasonable time, and

• (iii) yields interpretable models.

Second, we apply probabilistic programming to build a Bayesian model for a selection of options and interactions thereof. It is key for scalability that this selection comprises the actual set of influencing options and interactions. Third, we estimate the priors for the model’s random variables (i.e., options and interactions) and compute a fitted model with Bayesian inference.

Fig. 2

Workflow of P4: First, we preprocess data to evade multicollinearity. Second, we compose model from options and interactions based on the information a sample set can provide using Lasso selection. Third, we estimate priors for random variables based on weights of linear models trained on the sample set. Fourth, we infer a Bayesian performance-influence model using probabilistic programming

3.1 Data Preprocessing

Our approach relies on a training set consisting of a number of sampled configurations that are attributed with their performance. Thus, our approach can be combined with any sampling strategy, such as feature-wise, t-wise (Johansen et al. 2012), or random sampling (Gogate and Dechter 2006). However, it is important to process the sample set to avoid inference failures and to promote interpretability, as we explain next.

Similar to Ordinary Least Squares, Bayesian inference is prone to failure if multicollinearity exists in the training set, which occurs when the values of independent variables are intercorrelated (Hill and Adkins 2007; Farrar and Glauber 1967). Let us consider the following training set for an exemplary software system with options X, Y, Z, and M, illustrating multicollinearity:

B	X	Y	Z	M	π(⋅)
1	1	0	0	1	10
1	0	1	0	1	20
1	0	0	1	1	30

Option B is mandatory. It represents the base functionality of the system, which results from configuration-independent parts of the code. Options X, Y, and Z form an alternative group, that is, the system’s constraints enforce that exactly one of them is active in each configuration. An important insight is that an alternative group introduces multicollinearity to a training set because the selection of any single option is determined by the remaining options, for example: Z = 1 −X −Y. Multicollinearity not only hinders inference, but also interpretability. Considering the training set above, we see that the following performance-influence models are accurate with respect to the measurements, but assigning different contributions of individual options:

$$ \begin{array}{@{}rcl@{}} \pi(c) &=& {\kern5pt}0 \cdot c(\textsf{B}) + 10 \cdot c(\textsf{X}) + 20 \cdot c(\textsf{Y}) + 30 \cdot c(\textsf{Z}) \\ \pi(c) &=& {\kern5pt}5 \cdot c(\textsf{B}) + {\kern7pt}5 \cdot c(\textsf{X}) + 15 \cdot c(\textsf{Y}) + 25 \cdot c(\textsf{Z}) \\ \pi(c) &=& 10 \cdot c(\textsf{B}) + {\kern7pt}0 \cdot c\textsf{(X}) + 10 \cdot c(\textsf{Y}) + 20 \cdot c(\textsf{Z}) \end{array} $$

Because exactly one option of the alternative group is active in each configuration, the base performance of a software system can be attributed to the base functionality B and the options of an alternative with any ratio. For example, option X can have an influence of 10, 5, or none, depending on how we assign the performance to the system’s base functionality. Therefore, performance influence models for such systems are difficult to compare and interpret. Here, we do not even know whether an option (e.g., X) is influential at all. This is a problem that related approaches share (Siegmund et al. 2012a; Guo et al. 2013).

Choosing a default configuration provides remedy for multicollinearity inference failures and interpretability problems. That is, we select a default option for each alternative group using domain knowledge or at random. We then remove these options from the training set to achieve the following effects:

• Default options’ performance influences are set to 0.

• Multicollinearity arising from alternative groups is reduced, since the selection of a single remaining option of an alternative group cannot be determined without the removed default option (i.e., Z = 1 −X −Y does not hold anymore if any of these options is removed from the training set).

Mandatory options, which must be selected in each configuration, introduce a special case of multicollinearity. Option M is mandatory and therefore present in each configuration and indistinguishable from the base influence. Similar to alternative groups, a model can split the base influence between mandatory options and the base influence with any ratio.

Moreover, we can see that such an option does not contribute any information to the model by computing the Shannon information entropy (Shannon 1948):

$$ H(o) = - \sum\limits_{x = 0}^{1} P_{o} (x ) \cdot \log_{2} \big( P_{o} (x ) \big) $$

(7)

As M is selected in each configuration, its only selection value is 1, with selection probability P_M(1) = 1. We see that, therefore, the information entropy of M is 0:

$$ \begin{array}{@{}rcl@{}} H (\textsf{M} ) & =& - P_{\textsf{M}}(1) \cdot \log_{2} \big( P_{\textsf{M}}(1) \big) - P_{\textsf{M}}(0) \cdot \log_{2} \big( P_{\textsf{M}}(0) \big) \\ & =& -1 \cdot \log_{2} 1 - 0 \cdot \log_{2} 0 = 0 \end{array} $$

(8)

For that reason, we can safely remove mandatory options from the training set. The same applies for dead options, which are never active.

Note that options may only appear to be dead or mandatory as an artifact of the sampling process. That is, it is insufficient to query only the system’s variability model for its constraints to detect mandatory or dead options. Hence, we perform constraint mining on the sample set rather than the whole system to overcome this problem. We use the Shannon information entropy in (7) as a means to determine dead options and scan the set of options for combinations that appear to be alternative groups.

3.2 Model Composition

To build a Bayesian model with probabilistic programming, we first need to specify which options and interactions are present in the model. Subsequently, we create random variables from this model structure to account for epistemic and aleatoric uncertainty.

3.2.1 Option and Interaction Filtering

Composing a model from all options and all potential interactions, whose number is exponential in the number of options, is impractical for large software systems, because models with high numbers of parameters are difficult to interpret and, more importantly, inference may become computationally infeasible (Gareth et al. 2013). Therefore, we apply model selection to constrain the number of parameters. In particular, we use a subset selection approach (Alan 2002), because it yields a subset of unaltered options from a parent set, which is not the case for other approaches, such as dimensionality reduction (Maaten et al. 2009). We build the parent set of available options $\mathcal {S}$ from all options $\mathcal {O}$ of the system in question as well as all pair-wise interactions $\mathcal {I}$ with $\mathcal {S} = \mathcal {O} \cup \mathcal {I}$. We map each pair-wise interaction i to a virtual option with respect to its constituting options o_r and o_s:

$$ c(o_{n + p}) = c(o_{r}) \cdot c(o_{s}) \quad \text{with} \quad 1 \leq p \leq | \mathcal{I} | ~ \wedge ~ r \neq s $$

(9)

Compared to higher-order interactions, pair-wise interactions have been found to frequently influence performance (Siegmund et al. 2012a) and to be the most common kind of interaction (Kolesnikov et al. 2019). However, we acknowledge that considering higher-order interactions may improve the accuracy of our approach (Siegmund et al. 2012a), at the cost of possibly leading to computationally intractable models. The explicit modeling of interactions introduces non-linearity to the otherwise linear model structure.

Subset selection approaches define a filter function $F: \mathcal {S} \mapsto \left \{0,1 \right \}$, which yield 1 if an option or interaction of the parent set $\mathcal {S}$ should be considered by the model, and 0, otherwise. The result of subset selection consists of filtered options and interactions:

$$ \mathcal{V} = \big\{ s | \forall s \in \mathcal{S} \text{ and } F(s) = 1 \big\} $$

(10)

Similar to previous work (Ha and Zhang 2019b), we apply Lasso regression (Tibshirani 1996) on the preprocessed training set. As a result, Lasso assigns zero performance influence to less- and non-influential options and interactions, and it distributes the NFP influence among the remaining elements in $\mathcal {V}$. Our Lasso filter selects $v_{l} \in \mathcal {V}$, whose NFP influence $I_{\pi _{\textit {Lasso}}}(v_{l})$ is non-zero according to Lasso regression:

$$ F_{\textit{Lasso}}(v_{l}) = \left\{\begin{array}{ll} 0 & ~~~ I_{\pi_{\textit{Lasso}}}(v_{l}) = 0 \\ 1 & ~~~ I_{\pi_{\textit{Lasso}}}(v_{l}) \neq 0 \end{array}\right. $$

(11)

3.2.2 Applied Probabilistic Programming

We follow related approaches for performance modeling of configurable software systems and choose an additive model to make the uncertainty of the options’ and interactions’ performance influence explicit. We start with a model that takes the form of (4) (which represents the state of the art) with two differences:

• 1. Instead of scalar influences $\boldsymbol {\beta } \in \mathbb {R}^{n}$, we use a probability vector $\hat {\boldsymbol {\beta }}$, whose elements each have a PDF and form the coefficients as explained in Section 2.2.

• 2. We use the filtered options and interactions $\mathcal {V}$ from Section 3.2.1 and thus enable our model to capture non-linear performance influence:

  $$ \begin{array}{@{}rcl@{}} \pi_{\mathit{ep}}(c) = \hat{\beta}_{0} & +& \hat{\beta}_{1} \cdot c(o_{1}) + {\dots} + \hat{\beta}_{n} \cdot c(o_{n}) \\ & + &\hat{\beta}_{n+1} \cdot c(o_{n+1}) + {\dots} + \hat{\beta}_{n+| \mathcal{I} | } \cdot c(o_{n+| \mathcal{I} | }) \end{array} $$

  (12)

To infer the distribution of an option, we need to specify a prior distribution for the probability vector $\hat {\boldsymbol {\beta }}$. This distribution should be continuous (i.e., defined over all $\beta \in \mathbb {R}$) and have non-zero mass for any $\beta \in \mathbb {R}$, not to exclude certain values entirely. For performance modeling, we choose the normal distribution $\mathcal {N}(\mu , \sigma )$. It has a mode that, other than the uniform distribution, lets us encode an influence area of high probability. That is, an option’s or interaction’s influence has a normally distributed probability to fall into an interval to be inferred by probabilistic programming. Note that, even if a normal distribution is not the best fit for all random variables, Bayesian inference can adjust them. We describe how to determine the parameters for chosen prior distributions, such as the mean μ and the standard deviation σ for the normal distribution $\mathcal {N}(\mu , \sigma )$, in Section 3.3.

At this point, we have constructed π_ep, a model that incorporates epistemic uncertainty in $\boldsymbol {\hat {\beta }}$. To account for aleatoric uncertainty (i.e., the uncertainty in the training set), we use two different models, one for homoscedastic (constant variance) and heteroscedastic (variance depending on true performance) aleatoric uncertainty. These models build on π_ep. We adopt the common prior of a normal distribution for both models.

Homoscedastic Model

If we assume that the variance of uncertainty is equal for all training set samples, we can complete our Bayesian model with a normal distribution around π_ep(c):

$$ \pi_{\mathit{ho}}(c) = \mathcal{N}(\pi_{\mathit{ep}}(c),\sigma) $$

(13)

This normal distribution is modeled as an additional random variable, whose σ parameter captures the variance of absolute errors in training set samples.

Heteroscedastic Model

To account for errors in the training set that are relative to the training set sample performance, we introduce σ_rel, a random variable that captures uncertainty about the error ratio. As an error ratio is in $\mathbb {R}_{>0}$ (i.e., a continuous, positive variable), we choose the Gamma distribution as prior for σ_rel. The Gamma distribution with a shape parameter a and a spread parameter b can take a (possibly skewed) bell shape with non-negative values:

$$ \sigma_{\mathit{rel}} = \mathcal{G}(a, b) $$

(14)

Similar to the homoscedastic model, we define the heteroscedastic model as a normal distribution around π_ep(c), but with the product of the epistemic performance prediction and the relative error ratio σ_rel as standard deviation:

$$ \pi_{\mathit{he}}(c) = \mathcal{N}(\pi_{\mathit{ep}}(c), \pi_{\mathit{ep}}(c) \cdot \sigma_{\mathit{rel}}) $$

(15)

3.3 Prior Estimation

Regular Bayesian inference requires the user to estimate prior distributions for the model’s random variables from domain knowledge or personal experience. Distributions that are too uninformative (i.e., very wide) can lead to a hold of the inference, whereas distributions that are too informative will also slow down inference if they are imprecise (Salvatier et al. 2016). Our approach automatically chooses which options and interactions are modeled as random variables, such that the user does not need to know which random variables need priors beforehand. For that reason, we employ an automatic prior estimation following the empirical Bayes approach (Robbins 1956), which differs from the regular Bayesian approach in that it estimates priors from the training data. As a result, every aspect of Bayesian modeling is automated for the user.

3.3.1 Epistemic Uncertainty Priors

We capture epistemic uncertainty in our Bayesian model in random variables for the base influence and the influences for options and interactions, whose assumed normally distributed priors rely on means μ and standard deviations σ.

We propose a prior estimation algorithm that uses the influence values of other additive models to estimate priors. As models, we use instances of Elastic Net (Zou and Hastie 2017) with r evenly distributed ratios of l₁ ∈ [0,1]. For l₁ = 1, Elastic Net behaves like Lasso, for l₁ = 0 it behaves like Ridge regression and it interpolates the error functions of both approaches for 0 < l₁ < 1. We fit 50 Elastic Nets with evenly distributed l₁ parameter on the training set. This way, we obtain a set of 50 models ${\mathscr{M}}$ with different performance influences I(⋅) for the previously selected options and interactions. In initial experiments, increasing the number of Elastic Nets did not improve accuracy of Bayesian models. Next, we determine the empirical distribution of influences for each option and interaction:

$$ \boldsymbol{\hat{I}}_{\mathcal{M}}(v_{l}) = \left\{ I_{m}(v_{l}) | \forall m \in \mathcal{M} \right\} $$

(16)

We could use the mean and standard deviation of $\boldsymbol {\hat {I}}_{{\mathscr{M}}}$ as prior μ and σ for each option and interaction. However, not all models in ${\mathscr{M}}$ will fit the training data well. To reduce the influence for unfit models, we weigh each model according to its average error on the training set $\bar {\varepsilon }(\cdot )$:

$$ \boldsymbol{w} = \left\{ \frac{-\bar{\varepsilon}(m_{i})}{{\sum}_{i=1}^{\|\mathcal{M}\|}{-\bar{\varepsilon}(m_{i})}} \forall m_{i} \in \mathcal{M} \right\} $$

(17)

We compute the weighted mean μ_w(t) and weighted standard deviation σ_w(t) for a specific option or interaction t as follows:

$$ \mu_{w}(t) = \frac{1}{{\sum}_{i=1}^{\|\boldsymbol{w}\|} w_{i}^{\gamma} } \sum\limits_{\forall i \in \hat{I}_{\mathcal{M}}(t)}{w_{i}^{\gamma} i} $$

(18)

$$ \sigma_{w}(t) = \sqrt{ \frac{1}{{\sum}_{i=1}^{\|\boldsymbol{w}\|} w_{i}^{\gamma} } \sum\limits_{\forall i \in \hat{I}_{\mathcal{M}}(t)}{w_{i}^{\gamma} ( \mu_{w}(t) - i )^{2}} } $$

(19)

We added the tuning parameter γ to enable polynomial weighting. That is, the influence of models with the lowest average error $\bar {\varepsilon }$ is increased for γ > 1. In a pre-study, we empirically evaluated different values for γ and found that γ = 3 yields accurate priors.

3.3.2 Aleatoric Uncertainty Priors

We model aleatoric uncertainty (i.e., uncertainty in each training set sample) as a normal distribution for the homoscedastic model π_ho and as a gamma distribution as the relative uncertainty in the heteroscedastic model π_he. We build the set of all absolute prediction errors for all models $m \in {\mathscr{M}}$ over the samples in the training set and fit a normal distribution using maximum likelihood estimation to estimate a prior for the aleatoric uncertainty in π_ho. Likewise, we estimate a prior for the gamma distribution in π_ho, but we compute relative prediction errors, instead, to model the error ratio (cf. (15)).

3.4 Bayesian Inference and Prediction

As discussed in Section 2.3, Bayesian inference uses prior assumptions on PDFs of random variables that form a generative model, called likelihood, to compute a posterior, that is, an updated belief about the random variable’s PDFs. Unfortunately, the posterior to many Bayesian inference problems cannot be computed directly, so recent research in this field has developed algorithms that can estimate the posterior approximately. Two notable classes of inference algorithms are variational inference and Markov chain Monte Carlo (Murphy 2012).

Variational inference algorithms tune the prior distribution’s parameters without changing the types of the distributions (i.e., a prior normal distribution stays a normal distribution) (Roeder and Yuhuai 2017). This method is preferred for quick results that do not need to be precise.

Markov chain Monte Carlo (MCMC) algorithms draw samples from the posterior distributions and are able to estimate arbitrary posterior distributions in theory (a prior normal distribution may by transformed to a skewed distribution). MCMC algorithms are considered more precise, but also slower than variational inference.

We follow a combined approach by first estimating an approximate solution with variational inference (Roeder and Yuhuai 2017) and subsequently fine-tune with the No-U-Turn Sampler (NUTS) (Hoffman and Gelman 2014), an MCMC algorithm. We allow 200,000 iterations for variational inference, but abort on convergence. Initialized with the intermediate result of variational inference, NUTS first draws 3,000 samples for initial tuning and then acquires 12,000 of each random variable’s posterior distribution. The number of posterior samples determines the granularity of subsequent analyses. For example, a number of 100 posterior samples bounds the granularity of computed confidence intervals to 1%, at best. To facilitate fine-granular confidence intervals covering low-probability values for which MCMC draws fewer posterior samples, such as a 95%-confidence interval, we need more posterior samples. While we acquire a large number 12,000 posterior samples, a lower number of MCMC samples in the order of 1000 may be a more economic choice.

Prediction

To predict the performance of a configuration c, we insert c’s option selection values into $o_{1}(c), \dots , o_{n}(c)$ and determine active interactions according to (9). We can now draw a number of posterior samples to approximate the distribution for the prediction. Increasing the number of posterior samples makes the approximation more accurate, but also slows down prediction. We draw 1000 posterior samples to yield a good approximation. With this approximation, we can make different kinds of predictions, for which we introduce individual notations. The most informative kind of prediction is the sampled approximation itself ($\widetilde {\pi }$). Using $\widetilde {\pi }$, we can compute a confidence interval for a desired confidence $\alpha _{\mathit {ci}} \in \left [0 \%, 100 \% \right ]$ ($\bar {\pi }_{\alpha }$). This yields the interval around the mode of prediction over which the predicted distribution integrates to α_ci. We use $\bar {\pi }$ to indicate the 95%-confidence interval by default. The mode of the approximation also serves as a single-point estimate prediction ($\dot {\pi }$).

Figure 3 illustrates P4’s predictions process. For an Apache configuration with seven active options, it shows that two options (ECDSA and TLS) have an individual influence in addition to the core influence, which is always present. One option (ComprLvl9) increases energy consumption when it interacts with the other two options (ECDSA and TLS). Each influence’s marginal posterior distribution propagates into a predictive distribution displaying a wide 95%-confidence interval.

Fig. 3

Prediction of the performance of Apache with options ECDSA, TLS, and ComprLvl set to 9. The probability distributions represent P4’s inferred influences for the chosen options and two interactions thereof. At the bottom, the prediction, as well as its shaded 95%-confidence interval, are the result of propagating the individual influences’ uncertainties and considering the inferred absolute error (not shown here)

4 Subject Systems

For our experiments, we use 13 real-world configurable software systems that have been used in the literature, as presented in Table 1. We use measured execution time as performance for 10 subject systems from Kaltenecker et al. (2019). For VPXENC, LLVM, and x264, we have additionally measured energy consumption with a different workload. A further description of the systems including the used benchmarks is given at our supplementary Web site². In addition, we consider energy consumption for three further subject systems: Apache, PostgreSQL (short PSQL), and HSQLDB (Werner 2019). Following the state of the art (Kaltenecker et al. 2019), we measure each configuration’s performance five times. We repeat the measurement five more times if the coefficient of variation (i.e., the standard deviation divided by the mean) of the first 5 measurements was was above 10%.

We adopt the procedure of extracting training and test sets from each system’s measurement data from Kaltenecker et al. (2019). That is, we apply t-wise sampling with t ∈{1,2,3} to obtain three training test sets, $\mathcal {T}_{1}, \mathcal {T}_{2}, \mathcal {T}_{3}$, of different sizes. Apache poses an exception as its $\mathcal {T}_{1}$ size of 2 configurations breaks P4’s inference. We therefore discard $\mathcal {T}_{1}$ for Apache. Each system’s whole population (i.e., all measurements) form its test set. Table 1 lists the sizes of all training and test sets.

Table 1 Overview of the subject systems with domain, number of valid configurations $| \mathcal {C} |$, number of options $| \mathcal {O} |$, the size of training sets $\mathcal {T}_{1}$, $\mathcal {T}_{2}$, $\mathcal {T}_{3}$, and the performance metric

5 Evaluation

To evaluate our approach, we state three research questions that are in line with related work and are also concerned with the new possibilities of obtaining a confidence interval for performance predictions. Specifically, we answer the following research questions:

This research question places our approach in relation to a state-of-the-art approach that resorts only to a scalar value. Although this is not the main usage scenario, we evaluate whether our approach has a comparable accuracy.

RQ₂ refers to the ability that users can specify a confidence interval of predictions. This can substantially affect prediction accuracy and evaluates the strength of our approach.

The third research questions aims at providing a deeper understanding of confidence intervals and incorporated uncertainties in our approach. In contrast to RQ₂, RQ₃ is not concerned with prediction accuracy. Instead, we evaluate whether predicted intervals with higher confidence contain the correct value more often and, hence, truly capture the uncertainty in the predictions.

In addition to the research questions answered in this articles’ preceding conference paper (Dorn et al. 2020), we aim at explaining the occurrence of high prediction errors by studying the distribution of uncertainty within P4 models. To this end, we first analyze the nature of posterior influence distributions and then analyze the cause for inaccurate predictions, answering two further research questions:

With this research question, we study whether Gaussian prior distributions are the right choice to model option and interaction influences. Although our experiments in Section 5 use Gaussian priors, the inferred posteriors may be distributed differently. Changing the prior distribution is possible since we use the Markov chain Monte Carlo algorithm for inference.

As the lack of training data is one source of epistemic uncertainty, we expect that building P4 models on a larger portion of the configuration space will reduce epistemic uncertainty. However, since we compose the performance-influence model in step 2 in an automated way using Lasso regression, increasing the training data might automatically increase model complexity such that even more training data might be needed. With RQ₅, we investigate which effect prevails for real-world software systems.

RQ₆ focuses on epistemic uncertainty, which captures the uncertainty of the individual option and interaction influences. For some software systems, all options and interaction influences may be similarly uncertain. However, P4 may reveal instances where uncertainty of a single or few unreliable options and interactions overshadows the rest, which can indicate an unbalanced training set or highly non-deterministic option behavior. As a result, predictions for configurations containing such an unreliable option or interaction will be substantially more uncertain. With RQ₆, we answer if there are unreliable options and study their cause.

5.1 General Experiment Setup

We implement our approach with the PyMC3 (Salvatier et al. 2016) framework. PyMC3 offers implementations for MCMC, variational inference, as well as confidence interval computation for model parameters β and predictions. For maximum likelihood prior estimations, we rely on SciPy (Virtanen et al. 2020).

To answer our research questions, we infer Bayesian models with absolute and relative error with P4 for the chosen subject systems using three training sets $\mathcal {T}_{1}, \mathcal {T}_{2}, \mathcal {T}_{3}$ on a cluster of machines with Intel Xeon E5-2690v2 CPU and 64GB memory. For the ten subject systems by Kaltenecker et al. (2019), we use the training sets provided at their supplementary Web site. For the remaining subject systems, we sample new training sets with SPL Conqueror (Siegmund et al. 2012b).

For t = 1, t-wise sampling equals option-wise sampling, which yields $n \leq | \mathcal {O} |$ samples. Since we want to evaluate our approach also for learning interactions among options, creating $n+| \mathcal {I} |$ random variables leads to a modeling problem with more variables than observations. We avoid this situation by excluding interactions from our model for $\mathcal {T}_{1}$. This might affect prediction accuracy especially compared to other approaches that do not exclude interactions. We will discuss this in RQ₁.

To account for stochastic elements in MCMC, we run the inference for each system’s training set with 5 repetitions for the purpose of our experiments. Nonetheless, these repetitions are not necessary to use P4 in practice, as an individual run already quantifies uncertainty based on the priors and the training data. The average fitting time over all experiments was $8 \min \limits$. Although in the worst case, π_he needs $245.8 \min \limits$ to fit VP9’s $\mathcal {T}_{3}$ training set, overall, 80% of all models were fitted within $6 \min \limits$. The models for the $\mathcal {T}_{1}$ and $\mathcal {T}_{2}$ training sets were fitted in only $3 \min \limits$ and $5 \min \limits$ on average. They also contained fewer options and interactions than the models for the $\mathcal {T}_{3}$ training sets. However, models with more options and interactions do not always require more fitting time as we observe only a moderate Kendall rank correlation (Kendall 1938) (τ = 0.52) between the number of options and interactions in a model and its fitting time. We detail the fitting times in our experiments on our supplementary website. As explained in Section 3.4, we recommend an order of magnitude less inference samples, which also aids the reduction of fitting time.

5.2 RQ₁: Accuracy of Scalar Predictions

P4 is designed to both predict confidence intervals and point estimates. To assess the accuracy of the point estimates, we compare P4 to state-of-the-art models, which can only predict point estimates. RQ₁ is concerned with whether P4 is competitive even for point estimates and, thus, can replace traditional models. In this scenario, we neglect P4’s capability to predict confidence intervals as P4 is, to the best of our knowledge, the first approach to model uncertainty of performance prediction. Hence, there is no baseline to compare to.

5.2.1 Setup

We chose SPL Conqueror for comparison because it shares the additive model structure with our approach and is used as baseline in the literature (Kaltenecker et al. 2019; Oh et al. 2017). For comparison, we rely on accuracies of SPL Conqueror as reported by Kaltenecker et al. (2019). That is, we consider for RQ₁ the ten subject systems that the original authors have used. Another benefit is that Kaltenecker et al. provided raw measurements of the whole population, so we have a reliable ground truth.

We use the inferred performance-influence models to predict the performance of the whole populations of our subject systems. We adopt the Mean Absolute Percentage Error (MAPE) from previous work (Kaltenecker et al. 2019) to quantify prediction accuracy. That is, we first compute the absolute percentage error (APE) for each configuration $c \in \mathcal {C}$ with the measured performance π_true(c) and predicted scalar performance $\dot {\pi }(c)$ for our models π_ho and π_he:

$$ \text{APE}(c) = \frac{ \left | \pi_{\mathit{true}}(c) - \dot{\pi}(c) \right |}{\pi_{\mathit{true}}(c)} $$

(20)

We then compute the MAPE as the average over all APEs:

$$ \text{MAPE}(\mathcal{C}) = \frac{{\sum}_{c \in \mathcal{C}} \text{APE}(c)}{| \mathcal{C} |} $$

(21)

5.2.2 Results

As Fig. 4 shows, P4 achieves MAPE scores comparable to SPL Conqueror. Table 2 allows for a more fine-grained view. We see that the overall accuracy is higher when using SPL Conqueror, which is to be expected as only the mode is taken from the performance distribution provided as predictions by our approach. Nevertheless, we observe that, for many systems, especially when using π_he, the model with relative error, we obtain a similar or even better prediction indicated by underscored values. The mean error is, thus, distorted by some larger outliers, such as HIPA^cc and VP9. These systems have many alternative options such that there is a larger uncertainty involved and since we are not using the provided confidence interval, we deprive our approach of its strength.

Fig. 4

Scalar Mean Absolute Percentage Error (MAPE) of SPL Conqueror compared to the MAPE and interval predictions MAPE (MAPE_CI) for confidence levels 50% and 95% of P4 with relative error (π_he) for t-wise sampled training sets. Vertical bars represent the standard deviation over experiment repetitions. For each subject system’s training set, we specify P4’ s model size in terms of number modeled options (o) and interactions (i) below the system’s name

Interestingly, compared to $\mathcal {T}_{1}$, for some subject systems P4 performs worse on $\mathcal {T}_{2}$. The reason is that the increased number of random variables in P4, due to the additional modeling of interactions, requires more measurements as provided by $\mathcal {T}_{2}$ to effectively infer performance distributions. Moreover, we see a clear trend that, with an increasing number of measurements, P4 closes the gap in prediction accuracy with SPL Conqueror and even outperforms it for $\mathcal {T}_{3}$ and π_he for 7 out of 10 systems.

Table 2 Scalar Mean Absolute Percentage Error (MAPE) of SPL Conqueror (short SPLC) compared to the MAPE and confidence interval predictions MAPE (MAPE_CI 95%) of P4, with absolute error (π_ho) and relative error (π_he) for t-wise sampled training sets

5.3 RQ₂: Accuracy of Confidence Intervals

One of P4’ s key novelties is the ability to predict confidence intervals. With RQ₂, we ask how accurate P4’ s predicted confidence intervals are. However, due to the lack of a baseline, we cannot compare P4 to any other approach. Instead, we adopt the error metric from RQ₁ to confidence intervals instead of scalars.

5.3.1 Setup

Confidence intervals with confidence α_CI ∈ [0%, 100%] specify a range in which a given PDF integrates to α_CI. For predictions, a 95% confidence interval specifies a performance range for which the model is 95% confident that it contains the true performance value of the corresponding configuration. Consequently, we can expect the true performance to lie outside the 95% confidence interval in 5% of predictions. Although we can expect to always capture the true performance with a 100% confidence interval, such an interval will likely approach $[-\infty , +\infty ]$ for PDFs that are defined over $\mathbb {R}$.

Similar to RQ₁, we use a relative error metric to answer RQ₂. However, for RQ₂, we use P4 to predict confidence intervals as prediction, which is the actual strength and novel feature of our approach. Instead of using the APE of a scalar prediction, we compute the confidence interval’s APE_CI with relation to the closest endpoint of the confidence interval $\bar {\Pi }_{\alpha }$ for an outlying true performance; we define APE_CI = 0 for an α confidence interval that includes the measured performance:

$$ \text{APE}_{\mathit{CI}}(c) = \frac{\min_{\forall \pi \in \bar{\pi}_{\alpha}(c)} {\big | \pi_{\mathit{true}}(c) - \pi \big |}}{\pi_{\mathit{true}}(c)} $$

(22)

Hence, the MAPE_CI is the average over all APE_CI, similar to Equation 21. For our models π_ho and π_he, we report the MAPE_CI for predicted confidence intervals with α_CI = 95% for highly confident predictions and α_CI = 50% for less confident predictions, for which we expect a narrower interval and, consequently, a higher error.

5.3.2 Results

The dotted lines in Fig. 4 illustrate a substantial decrease in prediction error when using a confidence interval rather than a scalar prediction. Note that we report in Fig. 4 only MAPE_CI’s for π_he; we provide similar results for π_ho at our supplementary Web site. Table 2 provides further data for π_ho. It reveals that the predicted confidence intervals for 7z, BDB-C, lrzip, and x264 contain all measured performance values when training the absolute model π_ho on $\mathcal {T}_{3}$.

Table 3 Five most uncertain features measured by the mean relative confidence interval $\beta ^{?_{j}}$ according to (25), of models trained on $\mathcal {T}_{1}$

We illustrate how more training samples allow P4 to decrease uncertainty in internal parameters to achieve better prediction accuracy using the variance inflation factor (VIF). The VIF is an indicator for multicollinearity, which can be computed for the activation values of an option o_j in the training set $\mathcal {T}$. It is based on the coefficient of determination R². To determine R² for an option o_j, we fit a linear regression function f_j to predict whether o_j is active in a configuration c ∖ o_j with the remaining options as predictors.

We compute the VIF as follows:

$$ \begin{array}{@{}rcl@{}} \text{VIF}_{j} & =& \frac{1}{1-{R^{2}_{j}}} \end{array} $$

(23)

$$ \begin{array}{@{}rcl@{}} {R^{2}_{j}} & =& 1- \frac{\sum\limits_{\forall c \in \mathcal{T}} \big(c(o_{j}) - \bar{c}(o_{j})\big)^{2}}{\sum\limits_{\forall c \in \mathcal{T}}^{} \big(c(o_{j}) - f_{j}(c \setminus o_{j})\big)^{2}} \end{array} $$

(24)

A VIF of 0 indicates an option with no multicollinearity in the training set, while higher values mark increasingly problematic multicollinearity. We adopt the thresholds of 5 and 10 (O’Brien 2007; Wooldridge 2012) to indicate moderate and highly problematic multicollinearity, respectively.

Although we could use the VIF as a filter for feature selection (cf. Section 3.3) to remove options with high multicollinearity in the training set, the computational effort required to calculate all ${R^{2}_{j}}$ makes it infeasible in practice. Hence, we compute the VIF only for the 5 most uncertain options in $\mathcal {T}_{1}$ to analyze whether multicollinearity is a possible cause for uncertainty of options’ influences. To compute the uncertainty of an option influence βj?, we use its confidence interval $\bar {\beta }_{j}$ and point estimate $\dot {\beta }_{j}$. To remove the influence of differing influence scales between software systems, we determine the scaled confidence interval width as the ratio of the absolute confidence interval width $| \bar {\beta }_{j} |$ and the point estimate:

$$ \beta^?_{j} = \frac{| \bar{\beta}_{j} |}{\dot{\beta}_{j}} $$

(25)

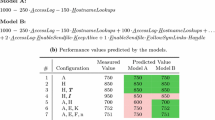
Looking at Table 3, we see that all five options exhibit either a moderate or even a high VIF for the training set $\mathcal {T}_{1}$. This points to a situation in which the learning procedure cannot safely assign a performance ratio to the specific option. Investigating this closer, four options are part of an alternative group despite our efforts to avoid multicollinearity by removing one alternative from each alternative group. For option threads_4, we found that it was active in almost every configuration (13 out of 16), reducing the contained information according to (7).

To further confirm our hypothesis that multicollinearity can be a possible cause, we show in Table 3 the uncertainty βj? and the VIF for these five options using the larger training set $\mathcal {T}_{3}$. We see a substantial reduction in uncertainty for three options in line with the reduction of the VIF. This strongly indicates that a reduced multicollinearity reduces also the uncertainty of an option’s influence on performance. Options Files_30 and BlockSize_1024 have no uncertainty as they were chosen by P4 to be removed from the alternative group in $\mathcal {T}_{3}$.

Overall, π_ho yields better results than π_he in most cases, but both approaches always show substantially lower relative errors than scalar predictions. Of course, it would be easy for a model to predict all performance values correctly with a sufficiently large confidence interval. However, our findings for RQ₃ demonstrate that P4’s prediction confidence intervals are reliable, as we will discuss in Section 5.4.

5.4 RQ₃: Reliability of Prediction Confidence Intervals

Contrary to RQ₂, RQ₃ is not concerned with the distance of predicted confidence intervals to the measured performance intervals. Instead, we are interested whether P4 judges the predicted uncertainty correctly and when predicted confidence intervals may be too wide or too narrow. If P4 finds the sweet spot between too wide and too narrow predictions, we call its prediction confidence intervals reliable.

5.4.1 Setup

As predictions, our approach can yield confidence intervals with any given confidence level $\alpha _{\mathit {CI}} \in \left [0 \%,100 \%\right ]$. We call a model’s predicted confidence intervals reliable if predictions with an α_CI confidence interval contain the measured performance with a similar observed frequency α_obs (i.e., $\alpha _{\textit {obs}}\left (\alpha _{\mathit {CI}}\right ) \approx \alpha _{\mathit {CI}}$). To compute the observed frequency α_obs(α_CI) for an α_CI confidence interval, we first define the function within, which returns 1 if the measured performance π_true(c) lies in a predicted confidence interval $\bar {\pi }(c)$, and 0, otherwise:

$$ \text{within} \big( \pi_{\mathit{true}}(c), \bar{\pi}(c) \big) = \begin{cases} 1 & \pi_{\mathit{true}}(c) \in \bar{\pi}(c) \\ 0 & \text{else} \end{cases} $$

(26)

Second, the observed frequency is computed as the average of within over all configurations of a subject system and their measured performance π_true(c):

$$ \alpha_{obs}(\alpha_{CI}) = \frac{ {\sum}_{c \in \mathcal{C}} \text{within}\left( \pi_{\mathit{true}}(c), \bar{\pi}(c) \right ) }{\left | \mathcal{C} \right |} $$

(27)

If $\alpha _{\mathit {CI}} \gg \alpha _{\textit {obs}}\left (\alpha _{\mathit {CI}}\right )$, the predicted confidence interval is inaccurate more often than we expect and should have been broader; conversely, the predicted confidence interval should be more narrow and thus more informative if $\alpha _{\mathit {CI}} \ll \alpha _{\textit {obs}}\left (\alpha _{\mathit {CI}}\right )$. Since using confidence intervals for performance predictions is novel, we have no baseline to which we can compare. Hence, we report the observed frequencies for confidence levels α_CI from 5% to 95% in steps of 5% as well as the average error in percentage to answer RQ₃. In addition, we report the MAPE_CI for all confidence intervals.

5.4.2 Results

Figure 5 shows a calibration plot that compares α_CI with α_obs using dashed lines. A model with α_CI = α_obs for all α_CI would yield values along the dashed gray diagonal. Values above the diagonal indicate too broad confidence intervals (i.e., our predictions are more accurate than they should be), values below it signal confidence intervals that are too narrow.

Fig. 5

MAPE_CI depending on model confidence (solid) versus uncertainty calibration (dashed) for t-wise training set aggregated over all subject systems. Gray dashed line indicates ideal calibration

The solid lines in Fig. 5 show the mean MAPE_CI over all subject systems for both the relative and the absolute model. The shaded area around it constitutes a 95% confidence interval.

When analyzing the dashed lines, we see that using the absolute error π_ho yields intervals that are closer to the diagonal than when using the relative error π_he. Moreover, there is a clear trend that, when using more measurements, the intervals become either nearly perfectly aligned or are underestimating the models prediction accuracy. Hence, we see a picture that resembles the picture when using the mode for scalar performance prediction: The approach requires a certain number of measurements to become accurate, but then works robustly.

We can make a further interesting observation when comparing the confidence intervals (dashed lines) with the MAPE_CI (solid lines). First and most importantly, we see that using confidence intervals of varying sizes has a clear monotonic relationship with the prediction error. That is, increasing the interval decreases the error. Second, the errors fall rapidly, especially for $\mathcal {T}_{2}$ and $\mathcal {T}_{3}$, already when using a narrow interval, such as 25%. This is good news as this clearly indicates that narrow confidence intervals yield accurate predictions. Third, we observe that (for the solid lines) the uncertainty is higher with fewer measurements, as indicated by the colored area. That is, the model is aware that the measurements are insufficient to actually make trustworthy predictions. This is a feature missing in all scalar prediction approaches. For example, for SPL Conqueror, there is no way to determine whether the model is confident with a certain prediction. With P4, we have a means to quantify this confidence.

5.5 RQ₄: Distribution of P4’ s Posteriors

P4 uses a normal distribution as the default prior distribution for term influences. Variational inference—the first step in P4’s inference—uses these priors as an initial guess. Hence, the priors naturally influence the outcome of the inference. Therefore, we are interested in whether the posteriors inferred with P4 in our experiments challenge our choice of the default prior.

5.5.1 Setup

As the result of MCMC sampling, the influence of each term is inferred as the marginal posterior π^β, which is represented as a set of 12,000 MCMC samples.

Across the set of all models π that were inferred in our previous experiments, including both π_ho and π_he, we first obtain the set of all marginal posteriors π^β:

$$ {\Pi}^{\beta} = \left\{ \pi^{\beta} | \forall \beta \in \pi, \forall \pi \in {\Pi} \right\} $$

(28)

To test for normality, we apply a Shapiro-Wilk (Shapiro and Wilk 1965) test and refute the h₀ hypothesis of π^β being normally distributed for α < 0.05. For non-normal posterior distributions, we detect multi-modality with the dip test for uni-modality (Hartigan and Hartigan 1985). In addition, we compute the standardized skewness and the excess kurtosis (Zwillinger and Kokoska 1999) to quantify the effect size of non-normality for non-normal uni-modal posteriors. For skewness values outside [− 0.5,0.5], a distribution is considered skewed. In this case, the distribution has considerably more weight on one tail than the other. The excess kurtosis measures how the weight of a distribution’s tails deviates from those of a normal distribution. For positive excess kurtosis, the distribution has heavier tails than anticipated by the prior. Conversely, the distribution has thinner tails if the excess kurtosis is negative. Posterior distributions with heavy tails, such as the Cauchy distribution, may be problematic for the computation of confidence intervals because outliers of confident intervals approach $\pm \infty$ quickly. This property makes confidence intervals of heavy-tailed distributions less useful and can lead to wildly varying single-point predictions; nevertheless, knowing the kurtosis can alarm a domain engineer, who would be otherwise ignorant of the inherent uncertainty given only a scalar influence of a traditional performance-influence model.

To evaluate the choice of normal-distributed marginal priors in an unbiased experiment setting, we replicate our previous experiments using flat marginal priors instead of normal-distributed ones. Flat priors have a probability of 0 for any possible influence. Thus, they avoid any bias through the choice of prior, but will result in more uncertainty in the marginal posteriors. We apply a Shapiro-Wilk test to determine the number of normal-distributed marginal posteriors after inference.

5.5.2 Results

When P4 uses flat priors instead of normal-distributed priors, 83% of all inferred marginal posterior distributions are normal-distributed using the $\mathcal {T}_{1}$ training set. Because we do not consider interactions for $\mathcal {T}_{1}$, P4 has enough training data to change the shape of the influence of the limited number of terms. Figure 6 shows that 48% and 55% of the flat priors are inferred normal-distributed with $\mathcal {T}_{2}$ and $\mathcal {T}_{3}$, even though the P4 models are more complex and require more training data to change the shape of the marginal priors. Our results indicate that, with enough training data, even flat priors are inferred normal-distributed.

Fig. 6

Ratio of normal-distributed influences per training set and marginal prior shape

When P4 regularly uses normal-distributed priors, 82% of all inferred posterior distributions are normal-distributed, confirming the appropriateness of the choice of a normal-distributed prior. Still, 18% of posterior distributions are non-normal, for different reasons. Firstly, 35% of non-normal distributions are multi-modal. That is, these influences have two or more distinct value ranges of high probability. For these influences, P4 allows us to consider more than one probable influence value, while traditional performance-influence models consider only one. Secondly, 15% of non-normal distributions are skewed. This means that, for these distributions, P4’s scalar prediction will not be in the center of it’s confidence interval prediction. For skewed distributions, P4 therefore provides the information that, with respect to the most likely value, other likely values will be either higher or lower. Thirdly, we observe higher absolute kurtosis values for non-normal distributions, which is to be expected because normal distributions by definition have a excess kurtosis close to 0 whereas non-normal distributions may deviate. However, as Fig. 7 shows, there are distributions with kurtosis values as high as 160. This option Ref_9 of x264, which is inferred with the maximum kurtosis for $\mathcal {T}_{1}$ training data, sets the number of reference video frames to 9. It is part of an alternative group of other reference frame numbers. Due to P4’s pre-processing, we avoid multicollinearity problems such that Ref_9 has an unproblematic VIF of only 1.6 in $\mathcal {T}_{1}$ despite its membership in an alternative group. Hence, we conjecture that $\mathcal {T}_{1}$ may be too small to allow inference with low uncertainty in this case.

Fig. 7

Comparison of the distribution of kurtosis values of inferred term influences. Normal-distributed influences (orange) are close to 0, while non-normal influences (blue) have a larger variance and reach values as large as 160

Interestingly, Fig. 6 reveals that there are fewer non-normal marginal posteriors with increasing training set size. Increasing the training set size from $\mathcal {T}_{1}$ and $\mathcal {T}_{2}$ allows P4 to learn interactions and produces the largest decrease of normal-distributed marginal posteriors. We argue therefore that non-normality among marginal posteriors is partly an artifact of an undersized training set and an under-complex model structure (e.g., when no interactions are modeled). For example, P4 infers a non-zero distribution for only a single option (and the base influence) with BDB-C’s $\mathcal {T}_{1}$ training set, which consequently is inferred as non-normal. By contrast, P4 infers eight influential terms using $\mathcal {T}_{2}$. Overall, our results emphasize the limitations of regular point-estimate models and show that P4 provides fine-grained information on option and interaction influences. Moreover, by explicitly modeling uncertainty, we can, for the first time, rationalize about the size of the training set and its implications on the suitable model complexity.

5.6 RQ₅: The Effect of More Training Data on Uncertainty

In theory, increasing the training set size of a model should decrease its epistemic uncertainty. However, this expectation may hold only when we keep the model complexity (i.e., the number of terms) constant. We designed P4 such that, with more training data, P4 can build models with more terms. This way, the prediction uncertainty may increase despite lower uncertainty for individual terms, because adding up a large number of uncertainties may counteract that the uncertainties are smaller. Consequently, we take both the uncertainty within learned internal influences as well as the uncertainty in predictions into account. Studying this relationship of prediction uncertainty and uncertainty of model terms is of practical interest since increasing the complexity of the model with an increasing training set size is sensible (e.g., fitting a quadratic curve with a linear function will not work no matter how many training points we supply). So, there might be a fine line in the relation of the growth of the training set size and in the growth of model complexity. As mentioned in Section 3.2.1, we use Lasso to naturally limit the growth of the model complexity. RQ₅ helps also answering whether Lasso is too restrictive or too lax in this sense.

5.6.1 Setup

To study the effect of increasing the training data set size, we analyze P4 models trained on the $\mathcal {T}_{2}$ and $\mathcal {T}_{3}$ data sets. We exclude $\mathcal {T}_{1}$ data sets as P4 does not learn interaction influences on them. We quantify the uncertainty of P4 with two metrics: mean term-influence uncertainty and mean prediction uncertainty.

Mean term-influence uncertainty

The mean term-influence uncertainty $\bar {\pi }_{95 \%}^{\bar {\beta }}$ captures the uncertainty within the inferred influences of P4 models. We compute it by averaging the 95%-confidence interval widths $W(\bar {\pi }_{95 \%}^{\beta })$ of all terms $\beta \in \mathcal {I}$ inside a given model π:

$$ \bar{\pi}_{95 \%}^{\bar{\beta}} = \frac{{\sum}_{\beta \in \mathcal{I}} W(\bar{\pi}_{95 \%}^{\beta})}{| \mathcal{I} | } $$

(29)

Mean prediction uncertainty

The mean prediction uncertainty $\overline {\bar {\pi }_{\mathit {rel}}}(c)$ captures the uncertainty in P4’s predictions. Similar to the MAPE, the mean prediction uncertainty is relative to the mode (i.e., the most likely value) of the prediction. However, instead of computing a prediction error in an evaluation setting where the target value is known, the mean prediction uncertainty relies solely on the predicted uncertainty. It is based on the scaled confidence interval width $\bar {\pi }_{\mathit {rel}}(c)$ for a given configuration $c \in \mathcal {C}$, which we compute by dividing the 95%-confidence interval width $W(\bar {\pi }_{95 \%}(c) )$ by the prediction’s mode $\dot {\pi }(c)$:

$$ \bar{\pi}_{\mathit{rel}}(c) = \frac{W( \bar{\pi}_{95 \%}(c) )}{\dot{\pi}(c)} $$

(30)

Consequently, the mean prediction uncertainty $\overline {\bar {\pi }_{\mathit {rel}}}$ is the average across the $\bar {\pi }_{\mathit {rel}}$ of all valid configurations:

$$ \overline{\bar{\pi}_{\mathit{rel}}} = \frac{{\sum}_{c \in \mathcal{C}} \bar{\pi}_{\mathit{rel}}(c)}{ | \mathcal{C} | } $$

(31)

Aggregation

For a given software system, attribute, training set, and model type (π_ho and π_he), there are 5 models corresponding to the 5 repetitions we perform in our experiments. To report a difference between $\mathcal {T}_{2}$ and $\mathcal {T}_{3}$, we take the median of a metric for the P4 models resulting from the 5 repetitions. We choose the median because it is more robust against outlier repetitions compared to the mean.

5.6.2 Results

Mean term-influence uncertainty

The median differences in uncertainty of using $\mathcal {T}_{2}$ versus $\mathcal {T}_{3}$ are detailed in Fig. 8 for all subject systems and attributes. Here, each bar shows the difference between the median $\overline {\bar {\pi }_{\mathit {rel}}}$ of the 5 repetitions for $\mathcal {T}_{2}$ versus $\mathcal {T}_{3}$. Across all subject systems and attributes, we observe that P4 infers less uncertain influences using $\mathcal {T}_{3}$ with the notable exception of x264 (Energy) with π_he. In this instance, the median term-influence uncertainty increases by over 100% using $\mathcal {T}_{3}$ compared to $\mathcal {T}_{2}$. Moreover, one of the two inference failures in our experiments occurred for a repetition of the experiment using $\mathcal {T}_{3}$, while the other occurred for a repetition of the corresponding experiment using $\mathcal {T}_{2}$. We discuss possible reasons for this effect in Section 5.7. Excluding the π_ho result for x264 (Energy) with $\mathcal {T}_{3}$, the remaining term influence confidence intervals are 34% smaller in π_ho models and 45% smaller in π_he models trained on $\mathcal {T}_{3}$ in comparison to $\mathcal {T}_{2}$.

Fig. 8

Median term-influence uncertainty difference of $\mathcal {T}_{2}$ versus $\mathcal {T}_{3}$ per software system and per attribute

We present a more detailed view of individual term-influence uncertainty difference for two experiments³ on the left of Fig. 9. Here, each column color-encodes a term influence confidence interval width for P4 trained on $\mathcal {T}_{2}$ (upper row) and $\mathcal {T}_{3}$ (lower row), sorted in descending order for $\mathcal {T}_{3}$. Figure 9a shows that, for LLVM (Energy), influences inferred with $\mathcal {T}_{2}$ become less uncertain (less saturated) when using $\mathcal {T}_{3}$. P4 adds new terms with $\mathcal {T}_{3}$, which all are less uncertain than the most uncertain terms of $\mathcal {T}_{2}$.

Fig. 9

Term influence and prediction confidence interval width comparison for $\mathcal {T}_{2}$ versus $\mathcal {T}_{3}$. Each bar represents the width of the confidence interval for a single term (on the left) of a single prediction (on the right). Matching terms are aligned for comparison. We sort all bars in descending order according to the largest interval width of $\mathcal {T}_{3}$ from left to right. Terms that were present only in $\mathcal {T}_{3}$ models are shown gray in the $\mathcal {T}_{2}$ row and vice versa

However, this observation is not consistent across all experiments. For example, we see in Fig. 9 that not all $\bar {\pi }_{95 \%}^{\beta }$ become smaller for BerkeleyDBC (Time). We observe that most options that were more uncertain with $\mathcal {T}_{2}$ remain more uncertain with $\mathcal {T}_{3}$. The interaction between HAVE_CRYPTO and PS32K, the most uncertain term with $\mathcal {T}_{2}$, becomes considerably less uncertain with $\mathcal {T}_{2}$, whereas HAVE_CRYPTO, the most uncertain term with $\mathcal {T}_{3}$, was far less uncertain with $\mathcal {T}_{2}$. In this case, P4 selects too many interactions containing HAVE_CRYPTO, including the second-most uncertain term. We conjecture that $\mathcal {T}_{3}$ does not contain enough data to sufficiently differentiate between the influence of option HAVE_CRYPTO and its interactions. Next, we study whether additional interactions may lead to more uncertain predictions using the mean prediction uncertainty.

Mean prediction uncertainty

P4 achieves decreased mean prediction uncertainty $\overline {\bar {\pi }_{\mathit {rel}}}(c)$ for 4 out of 16 inference settings (software system & attribute) using π_ho and for 10 out of 16 inference settings using π_he. However, this improvement stays behind the reduction in term-influence uncertainty. The highly uncertain term influences of x264 (Energy) with π_he result in the highest increase of mean prediction uncertainty with factor 3870. This increase exceeds the mean term-influence uncertainty because the individual term-influence uncertainties accumulate for all the terms that are active in a predicted configuration. Excluding this inference setting, the mean prediction uncertainty using $\mathcal {T}_{3}$, on average, increases by 37% for π_ho and decreases by 4% for π_he in comparison to $\mathcal {T}_{2}$. Figure 10 visualizes the difference in mean prediction uncertainty of $\mathcal {T}_{3}$ versus $\mathcal {T}_{2}$ and illustrates that π_he performs better than π_ho overall. In particular, we present the prediction uncertainties of two inference settings on the right in Fig. 9. Figure 9b illustrates that π_he consistently increases its energy prediction uncertainty for LLVM configurations using $\mathcal {T}_{3}$. The uniformly distributed values for $\mathcal {T}_{3}$ stem from the uniformly distributed term influences uncertainties displayed in Fig. 9a. Moreover, we show π_ho time predictions for BerkeleyDBC in Fig. 9d. Similar to LLVM, the distribution of prediction uncertainties follows the distribution of its term-influence uncertainties in Fig. 9c. That is, as HAVE_CRYPTO’s uncertainty increases but the uncertainty of the interaction between HAVE_CRYPTO and PS32K decreases with $\mathcal {T}_{3}$, one subset of the most uncertain predictions with $\mathcal {T}_{2}$ becomes less uncertain while the another subset remains among the most uncertain predictions with $\mathcal {T}_{2}$.

Fig. 10

Median prediction uncertainty difference of $\mathcal {T}_{2}$ versus $\mathcal {T}_{3}$ per software system and per attribute

Although the mean prediction uncertainty does not improve for a number of systems and attributes, P4 still improves prediction accuracy in terms of MAPE and MAPE_CI as displayed in Fig. 4. That is, although the 95%-confidence interval width of predicted probability distributions does not become more narrow with $\mathcal {T}_{3}$ in general, its mode is still accurate enough to match the state of the art. Moreover, the uncertainty calibration in Fig. 5 shows that, with $\mathcal {T}_{2}$, both π_ho and π_he were overconfident in their 95%-confidence interval. This means that the correct value was not inside this interval for 95% of all predictions, but in only less than 70% of the cases. P4 improved its calibration with $\mathcal {T}_{3}$, which can be due to improved accuracy or adjusted confidence intervals. Our results contain both effects: P4 became more accurate as measured by the MAPE_CI and it increased predicted confidence interval widths. Moreover, Fig. 5 shows that π_ho becomes under-confident with $\mathcal {T}_{3}$, which means that it predicts confidence intervals that are wider than necessary. This is explainable by the mean prediction uncertainty of π_ho, which increases more than π_he. As both models incorporate the same terms and only differ in the ability to model a relative error, we conjecture that the relative error in π_he can model prediction error more accurately than π_ho given enough training data.

5.7 RQ₆: Unreliable Options and Their Cause

Evaluation of frequentist point-estimate models on a test set cannot provide information about the cause of inaccurate predictions. By contrast, P4 provides a degree of uncertainty for each option and interaction involved in a prediction. This way, we can identify individual options and interactions that are responsible for uncertain predictions. We refer to these terms in a model as unreliable terms. Unreliable terms empower developers to identify code regions associated to these options that may exhibit large variations of performance or are uncertain by nature (e.g., due to non-determinism). Knowing unreliable terms also allows us to improve the composition of a training set by acquiring more samples that add information on the corresponding configuration options or interactions.

5.7.1 Setup

During prediction, P4 performs a convolution on the posteriors of the terms that are active in the given configuration. Hence, extraordinarily uncertain predictions must involve unreliable terms. We call a term unreliable if its influence’s confidence interval is substantially wider than the confidence intervals of the model’s remaining options and interactions. We quantify this property using the scaled confidence interval width $W_{\mathit {rel}}(\bar {\pi }^{\beta })$, which specifies the degree of uncertainty relative to the mean within a model. It results from dividing a term’s 95%-confidence interval width $W(\bar {\pi }_{95 \%}^{\beta })$ by the average 95%-confidence interval width of the model:

$$ W_{\mathit{rel}}(\bar{\pi}^{\beta}) = \frac{W(\bar{\pi}_{95 \%}^{\beta})}{ \frac{1}{| \mathcal{I} |} {\sum}_{\beta \in \mathcal{I}}W(\bar{\pi}_{95 \%}^{\beta})}. $$

(32)

To answer RQ₆, we concentrate on the top 5% terms with the largest scaled confidence interval widths. In what follows, we present the distribution of unreliable terms as well as a qualitative root-cause analysis on the 8 most unreliable terms across all experiments.

5.7.2 Results

Throughout all experiments, P4 identifies a similar number of unreliable options with both the π_ho (i.e., modeling an absolute error) and π_he (i.e., modeling a relative error) model: 541 unreliable terms using π_ho and 491 using π_he. In Fig. 11, we show the number of unreliable terms per subject system and model. Each row depicts the number of unreliable terms in the respective model. With both approaches, BerkeleyDBC, LLVM, PSQLDB, VP9 (Energy), and x264 have less than 30 unreliable terms across all training sets. Moreover, using π_he, P4 infers no unreliable terms for PSQLDB, VP9 (Energy), and x264 (Time). By contrast, using either π_ho or π_he, JavaGC and HIPA^cc have over 60 unreliable terms. This shows that unreliable options are not common for all subject systems and attributes. We see that P4 finds the highest number of unreliable terms for the execution time of JavaGC using π_ho and for the execution time of VP9 using π_he. Both models yield a high number of unreliable terms for HIPA^cc. At the same time, P4 identifies the highest number of terms for JavaGC, VP9, and HIPA^cc, as Fig. 4 illustrates.

Fig. 11

Number of unreliable options for P4 trained on $\mathcal {T}_{1}$, $\mathcal {T}_{2}$, and $\mathcal {T}_{3}$ training sets of different subject systems and attributes

A possible explanation could be that the absolute number of terms for these systems is high, but the relative number of uncertain terms remains moderate. To examine if P4 generally identifies more unreliable options for subject models with more terms, we compute Pearson’s correlation coefficient for the number of unreliable terms and the total number of terms inferred for each model in our experiments. The moderate correlation of r = 0.47 indicates that P4 models with more terms also tend to contain more unreliable terms. Furthermore, we color-coded the training sizes to compare the absolute number of unreliable terms per subject system. Figure 11 shows that many subject systems have fewer unreliable terms using $\mathcal {T}_{1}$ compared to $\mathcal {T}_{2}$ and $\mathcal {T}_{3}$, such as JavaGC and HIPA^cc. By contrast, we find numerous unreliable terms using $\mathcal {T}_{1}$ for x264 (Time), PSQLDB (Energy), and 7z (Time). For these systems, P4 infers a similar number of terms for $\mathcal {T}_{1}$ and $\mathcal {T}_{3}$. This is in line with previous observations that more unreliable terms occur with more terms in a model.

We list the 8 terms with the highest scaled confidence interval width $W_{rel}(\bar {\pi }^{\beta })$ in Table 4. Out of these 8 most unreliable terms, the most common subject systems are x264, JavaGC, and VP9. In what follows, we therefore concentrate on these systems.

Table 4 Most uncertain influences measured by the scaled confidence interval width $W_{\mathit {rel}}(\bar {\pi }^{\beta })$

x264

Compared to the other subject systems, x264 (Energy) has few inferred terms using $\mathcal {T}_{3}$. Although x264 (Energy) matches the previously described trend of higher numbers of unreliable terms with a larger number of terms in a model, it has Ref_9 as the term with the highest overall $W_{\mathit {rel}}(\bar {\pi }^{\beta })$ using π_ho. Ref_9 is part of an alternative group. Its 95%-confidence interval is 14 times as wide as the mean of all intervals in the inferred model and will drastically increase the uncertainty of predictions in which the option is active. In fact, we observed and discussed these highly uncertain predictions in RQ₅. Despite our efforts, the $\mathcal {T}_{3}$ training data still has a highly problematic VIF of over 10 for this option, as well as for Ref_5 (the 7th-most unreliable term). This reduces the amount of information for these options that is present in the training data. As a result, the π_ho model cannot differentiate between the two alternative group options and the base influence (the third-most unreliable term) such that all three are unreliable. In addition, the influences of all three terms are multi-modal. Looking at Ref_9’s marginal posterior distribution in Fig. 12, we can clearly identify three modes at 1.1 kJ, 1.5 kJ, and 2.4 kJ. Thus, P4 has identified several probable value ranges due to remaining multicollinearity and the epistemic uncertainty due to the π_ho model structure. These observations result in an important insight: Alternative options may need individually more measurements to account for the inherent multicollinearity than other options. We are not aware of any existing sampling approach that adds to this insight.

Fig. 12

Multi-modal, non-normal marginal posterior distribution with the highest $W_{\mathit {rel}}(\bar {\pi }^{\beta })$ reported in Table 4

JavaGC

Among the most unreliable terms, we find two pairwise interactions for JavaGC between UseAdaptiveSizePolicy and options of the NewRatio alternative group. The two NewRatio options set the maximum ratio of the young versus the tenured generation in the Java heap to 1:16 (using π_ho) and 1:32 (using π_he), respectively. As the default NewRatio is 2, these values are comparably high and will lead to a small young generation and cause more frequent minor garbage collections. The UseAdaptiveSizePolicy option on its own will automatically adjust the young and the tenured generation size over time. However, activating both options is discouraged and will lead to unexpected program behavior. Figure 13 displays the marginal posterior distribution of the interaction between NewRatio_16 and UseAdaptiveSizePolicy in blue. In comparison to the marginal posterior histogram of the option UseAdaptiveSizePolicy from the same model shown in red, we see that, although both are normal-distributed, the influence of NewRatio_16 is more uncertain by a large margin. Again, this observation produces an insight not seen in related work: Uncertainties of interactions may be traced to external factors, and, henceforth, cannot be reduced by more measurements or a more complex model. P4 is a valuable detector of such scenarios.

Fig. 13

Uni-modal, normal marginal posterior distribution of NewRatio_16× UseAdaptiveSizePolicy with the second highest $W_{\mathit {rel}}(\bar {\pi }^{\beta })$ reported in Table 4 and UseAdaptiveSizePolicy’s (AS) influence with less uncertainty

VP9

VP9’s option cpuUsed_4 is over nine times more uncertain than the other influences in the π_he model trained on $\mathcal {T}_{3}$. This is due to the distance between its two modes at − 22s and − 5s, which are shown in Fig. 14. Similarly to x264’s option Ref_9, we find a highly problematic VIF of 23.7 in the training data for this option, explaining why cpuUsed_4 is unreliable. Interestingly, cpuUsed_4’s uncertainty is tied to the uncertainty of the base influence, which is multi-modal and has a $W_{\mathit {rel}}(\bar {\pi }^{\beta })$ of over 9. In this instance, we did not entirely avoid the multicollinearity of the cpuUsed alternative group which allowed cpuUsed_4’s influence to be partly assigned to the base influence. Therefore, both become uncertain. However, despite sharing the same training data $\mathcal {T}_{3}$, the option cpuUsed_4 is never inferred unreliable in any π_ho model. To investigate this discrepancy, we display the base influence and cpuUsed_4’s influence for both a π_ho and a π_he model in Fig. 14. It shows that the π_ho influences for both terms are inferred uni-modal with the same spread as the individual modes. While the uni-modality of the π_ho model influences provide smaller confidence interval widths, it pushes the influence to more extreme values, which is an undesirable effect of multicollinearity. This effect is not limited to the aforementioned influences, but is present throughout all inferred influences of π_ho. Figure 15 visualizes all inferred influences of π_ho and π_he and shows that the modes of π_ho’s influences go beyond ± 40s with absolute confidence interval widths below 4s. These data do not hint at issues in the training data, whereas π_he’s influences of ± 20s with absolute confidence interval widths of up to 18s certainly do. This indicates that the π_he model is able to signal the uncertainty owing to multi-modality by inferring multiple modes. We therefore recommend π_he when multicollinearity cannot be ruled out entirely.

Fig. 14

Bi-modal, non-normal marginal posterior distributions of π_he (in saturated color) next to normal-shaped distributions of π_ho (in unsaturated color) for cpuUsed_4, the term with the third highest $W_{\mathit {rel}}(\bar {\pi }^{\beta })$ reported in Table 4. The respective base influence takes a similar shape as cpuUsed_4, but mirrored along the y-axis

Fig. 15

Comparison of term confidence interval widths and modes

6 Threats to Validity

Threats to internal validity arise from measurement bias. We reuse a measurement set from a recent paper whose authors controlled for this bias by repeating the measurements several times (Kaltenecker et al. 2019). A threat to construct validity may arise from the model construction process in PyMC3. To this end, we selected probability distributions for the random variables based on typical least squares error distributions and best practices for regression modeling in probabilistic programming. However, since we limit the degree of modeled interactions, our analyzes are limited to the same interaction degree. External validity refers to the generalizability of our approach. Our data set comprises 13 different subject systems of varying domains and sizes. Moreover, we assessed different properties, such as energy consumption and response time. We made similar observations for all systems such that we are convinced that our approach works on a large and practically relevant class of configurable software systems.

7 Related Work

There are numerous approaches to model the performance of configurable software systems. Black-box models only require performance observations of a configurable software system under varying configurations. The modeling task, hence, becomes a regression problem. For example, SPL Conqueror applies multiple linear regression with forward feature selection (Siegmund et al. 2015). Nair et al. achieve accurate ranking of configurations according to their performance to facilitate optimization by training inaccurate models that are inexpensive to fit (Nair et al. 2017b). CART (Guo et al. 2013) and its improved version DECART (Guo et al. 2018) use rule-based models to accurately learn performance models with a small number of samples. FLASH (Nair et al. 2020) is a sequential model-based method that relies on active learning to fit CART (Guo et al. 2013) models more efficiently. A strength of these CART-based approaches is their interpretability as rules for performance behavior are explicit through branches in the decision tree. On the other hand, more complex models can improve accuracy at the cost of interpretability. As such, DeepPerf (Ha and Zhang 2019a) is a deep learning-based approach which uses sparse neural networks for performance estimation (Ha and Zhang 2019a). HINNPerf constructs a hierarchical ensemble of artificial neural networks to infer interactions (Cheng et al. 2022). This approach provides interpretability of their artificial neural networks by adopting the Integrated Gradients method. Zhang et al. (2015) propose a framework to model performance influence with Fourier approximation, whereas Nair et al. employ spectral learning with dimensionality reduction (Nair et al. 2017a). P4 also classifies as a black-box performance model. In contrast, none of the other proposed approaches considers uncertainty in predictions and in the internal representation of influences, producing only scalar estimates.

White-box approaches also consider source code in addition to performance observations. To this end, Velez et al. propose Comprex, an approach that leverages taint analysis to segment the source code by configuration options (Velez et al. 2021). This allows Comprex to learn small models with few samples for each code segment and overall reduce the number of required measurements. ConfigCrusher first conducts a data-flow analysis to determine influential options (Velez et al. 2020). Then, ConfigCrusher measures configurations based on only these influential options to improve data-efficiency. Similarly, Weber et al. propose an approach that uses a coarse-grained profiler to infer a performance-influence model for each method (Weber et al. 2021). Then, they conduct more fine-grained measurements using a fine-grained profiler to improve the worst models, providing a method-level understanding of the configuration influence on performance. Although white-box models can pin-point performance-influences to individual source code regions, these influences currently are still scalar and cannot express uncertainty.

While typical regression models only provide correlative information, recent work has studied causality between performance and environmental variables, such as software configuration. Dubslaff et al. (2022) investigate causality in configurable software systems with counterfactual reasoning (Dubslaff et al. 2022). This way, they find defect causes, estimate option influences and identify interactions thereof. Unicorn builds a causal performance model with causal reasoning (Iqbal et al. 2022). Contrary to Dubslaff et al. (2022), UNICORN also considers intermediate causal mechanisms in addition to software options in order to provide results that are more robust against environmental changes. Causal reasoning has the potential to provide even more useful insights into performance-influences of options than white-box models, but the current methods cannot express how certain the causal relations are.

Notably, the need for incorporating uncertainty in performance modeling of configurable software systems has been argued before by Trubiani and Apel (2019). While there are already considerations in other fields for both epistemic and aleatoric uncertainty, such as for computer vision (Kendall and Gal 2017), for software engineering, there are only approaches that model some kind of epistemic uncertainty. Antonelli et al. have incorporated uncertainty by allowing two parameters of a performance index for cloud computing systems to be uncertain and thus adapt to changing hardware (Antonelli et al. 2020). Another approach by Arcaini et al.transforms a feature model into two Queuing Networks—one each for the two variants with minimal and maximal performance—and thereby represents uncertainty in performance (Arcaini et al. 2020). To the best of our knowledge, we are the first to follow Trubiani and Apel’s call to incorporate both epistemic and aleatoric uncertainty in performance modeling of configurable software systems. However, probabilistic methods have been applied in software engineering on different problems. Elbaum and Rosenblum (2014) discuss the role of aleatoric and epistemic uncertainty in testing. Horcas et al. (2021) use a Monte Carlo tree search to perform automated analyses, such as localizing defective configurations. Mandrioli and Maggio (2021) combine Monte Carlo sampling and extreme value theory as part of scenario theory to provide lower and upper bounds for performance estimations. In contrast to our work, they do not infer probability distributions for individual options and interactions. ConEx employs a Monte Carlo Markov Chain to optimize performance in vast configuration spaces with over 900 options (Krishna et al. 2020). However, it does not yield insights into influences of options and interactions as it does not build a model.

8 Summary

Existing approaches for performance-influence modeling provide only scalar predictions based on modeling influences of options and interactions with scalar values. We argue that these approaches neglect uncertainty arising from the modeling and measurement process. We propose a novel performance-influence modeling approach that incorporates uncertainty explicitly and yields confidence intervals alongside scalar point-estimate predictions. This way, we provide not only a singular number as a performance estimate, but also a posterior distribution and a confidence in which range a performance value lies. Our experiments with 13 real-world software systems show that our implementation, P4, yields scalar prediction accuracies that match the state of the art when provided with a sufficient number of measurements. Further evaluation shows that the confidence intervals provided are reliable and, when used for prediction, achieve competitive accuracies.

The analysis of our trained models indicates that options that are selected in almost every configuration can reduce the amount of information contained in a training set, rendering the option’s influence uncertain. This observation calls for a shift in current sampling strategies by taking the information gain more into account, as compared to coverage or uniformness. P4 showed its potential especially with pairwise and triple-wise sampled training sets. Improving P4 for small training sets, hence, remains an open issue. A possible remedy are P4’s option influence uncertainties, which may be facilitated in an active learning setup to learn more efficiently. In addition to our original findings, we report in this article that a normal distribution is a reasonable choice for P4’s priors as most posteriors are normal-distributed in our experiments. Nevertheless, P4 can also detect multi-modal influences, indicating issues in the training data, such as multicollinearity. In most cases, we find a reduction of uncertainty given more training data for both modeled influence uncertainty as well as prediction uncertainty. For some predictions, however, prediction uncertainty does not decrease as expected. We show that, using P4, it is possible to identify individual unreliable options and interactions thereof that cause particularly uncertain predictions. A qualitative study on the most unreliable options and interactions shows multicollinearity and interactions leading to non-defined program behavior as reasons for unreliability. It motivates research into active sampling using P4 as a driving source.