The dynamic effects of fiscal consolidation episodes on income inequality: evidence for 17 OECD countries over 1978–2013

Abstract

Using an annual data set covering 17 OECD countries over the time period 1978–2013, this paper analyzes the dynamic effects of fiscal consolidation episodes on income inequality in the short- and medium-run. By estimating impulse response functions from local projections, we find that fiscal consolidations typically lead to an increase in income inequality. Baseline results suggest that in the aftermath of the start of a fiscal adjustment episode, the Gini coefficient of disposable income increases by about 0.4% points in the short-run (in year three), and by 0.6% points in the medium-run (in year seven). The impact of fiscal austerity measures on the income distribution is found to be more pronounced (a) when the size of the fiscal consolidation package is large rather than small; (b) when the duration of the adjustment is long instead of short; (c) when the fiscal consolidation is based more on spending cuts than on tax increases; (d) when the consolidation is started in the aftermath of a financial crisis rather than in a non-crisis episode; and (e) when the adjustment falls into a period of low economic growth instead of high growth.

Introduction

In most OECD countries, income inequality has increased markedly since the mid-1980s (e.g. OECD 2015; Atkinson and Morelli 2010). Panel A of Fig. 1 shows the evolution of the Gini coefficient of disposable (post-taxes and post-transfers) income for five selected OECD countries over the time period 1986–2014. It can be seen that income inequality in the US and in the UK has risen by several percentage points, while the trend also points upwards for Germany and Italy, with France being an exception, as inequality in France decreased over the time period covered. Furthermore, Panel B of Fig. 1 plots the evolution of the Gini coefficient of disposable income in a sample of 17 OECD countries; both the unweighted average and the population-weighted average exhibit a general trend of rising inequality. While researchers have found evidence that a growing divide in incomes may cause social cohesion to deteriorate and public health problems to become more significant (Wilkinson and Pickett 2009), recent research has also indicated that economies characterized by an unequal distribution of incomes may be subject to higher financial fragility and macroeconomic instability (e.g. Kapeller and Schütz 2014; Kumhof et al. 2015; Stockhammer 2015). Since the financial crisis of 2008, fiscal consolidation measures have been a central feature of crisis management in several OECD countries, as countries push for government spending cuts and tax increases in order to cut fiscal deficits and bring down public debt (e.g. Lane 2012; Blanchard and Leigh 2014; Alesina et al. 2015a). As the increase in income inequality and high public debt may be seen as two of the most pressing policy problems of our time, the consequences of fiscal consolidation measures on the income distribution are of high relevance. Past research has shown that fiscal policies have an important distributional role to play (e.g. Martinez-Vazquez et al. 2012; International Monetary Fund 2012); hence, well-informed policy-makers should be able to rely on robust estimates about how the income distribution develops in the aftermath of fiscal consolidation episodes. In this context, concerns about the (potential) effects of fiscal austerity on income inequality have grown over recent years (e.g. Rawdanowicz et al. 2013; International Monetary Fund 2014; OECD 2015).

Fig. 1

The evolution of income inequality in the OECD since the mid-1980s. Notes Data: SWIID (Solt 2016); own calculations. Panel B shows an unweighted average of 17 OECD countries (Australia, Austria, Belgium, Canada, Denmark, Finland, France, Germany, Ireland, Italy, Japan, Netherlands, Portugal, Spain, Sweden, the United Kingdom, and the United States of America), which we will also include in the data set for the empirical analysis in the remainder of this paper

While a substantial literature dealing with the effects of fiscal adjustments on economic growth and employment has developed since the outbreak of the global financial crisis (e.g. Holland and Portes 2012; in ’t Veld 2013; Blanchard and Leigh 2014; Guajardo et al. 2014; Alesina et al. 2015a; Yang et al. 2015; Alesina et al. 2015b; Jorda and Taylor 2016; Heimberger 2017), empirical research on the distributional effects of fiscal austerity measures has so far been comparatively underdeveloped. Researchers at the OECD and the IMF have intensified their work on the distributional effects of fiscal policy (Cournède et al. 2013; OECD 2015; International Monetary Fund 2012; Rawdanowicz et al. 2013; Ball et al. 2013; International Monetary Fund 2014; Furceri et al. 2016; Woo et al. 2017), and some peer-reviewed papers from recent years deal with different aspects of the distributional impact of fiscal consolidation measures (Agnello and Sousa 2012, 2014; Schaltegger and Weder 2014; Kaplanoglou et al. 2015; Agnello et al. 2016; Schneider et al. 2017; Woo et al. 2017). However, although Ball et al. (2013) and Furceri et al. (2016) have already done seminal work on the dynamic effects of fiscal consolidation episodes on income inequality, one of the major gaps in the existing literature concerns the lack of a large-scale and long-term analysis of the impact of fiscal consolidations on income inequality that also includes data for the years during and after the most recent global financial crisis. Furthermore, an in-depth investigation of the role played by the size, duration and the composition of fiscal consolidation episodes as well as the occurence of financial crises has so far also been missing when it comes to studying the dynamic effects of fiscal consolidation episodes on income inequality.

This paper contributes to closing this gap in the existing empirical literature on the distributional effects of fiscal austerity. The aim is to formally analyze the dynamic impact of consolidation episodes on income inequality in a broad set of OECD countries over an extended period of time. For this purpose, we make use of an annual data set consisting of 17 OECD countries over the time period 1978–2013. Inspired by Jorda (2005), we estimate impulse response functions from local projections to obtain estimates about how the Gini coefficient (of market and disposable income, respectively) develops within eight years after the start of a fiscal consolidation episode. Our analysis covers data over more than three decades (1978–2013), as we also include data on the years after the outbreak of the global financial crisis. In comparison to past contributions (e.g. Agnello and Sousa 2014; Ball et al. 2013), our analysis delivers novel insights into how the dynamic effects of fiscal austerity on the income distribution depend on the size and duration of fiscal consolidation programs, the economic growth situation, and on whether consolidations are started in the aftermath of financial crises. Over recent years, questions regarding the effects of economic policy decisions on income inequality have gained importance both in the economic research community (e.g. Piketty 2014; Atkinson 2015; Milanovic 2016b) as well as in policy-making circles (e.g. Rawdanowicz et al. 2013; International Monetary Fund 2014; OECD 2015); hence, the results presented in this paper should be of interest both to a wider community of economists working on distributional and macroeconomic issues as well as to policy-makers.

The rest of this paper is structured as follows. Section 2 provides a review on the literature dealing with the macroeconomic effects of fiscal consolidation measures. Section 3 explains the econometric approach used in this paper. Section 4 presents the main empirical results and a number of extensions. Section 5 provides several robustness checks. Section 6 discusses the main results against the background of the existing econometric literature. Section 7 concludes.

Literature review

The financial crisis of 2008 has brought about “the revival of interest in the short-run macroeconomic effects of government spending and tax changes.” (Ramey 2011, p. 673). Fiscal stimulus measures that were implemented in many OECD countries to counteract the crisis (e.g. Khatiwada 2009; Cottarelli et al. 2014) came with the empirical question about the effects of increases in government spending and cuts in taxes on economic growth. On the one hand, stimulus packages in specific OECD countries such as the American Recovery and Reinvestment Act in the US were studied in empirical detail (e.g. Blinder and Zandi 2010; Wilson 2012). On the other hand, a series of papers delivered more general insights into how the size of the fiscal multiplier might change with the business cycle, monetary policy accomodation, the composition of the respective fiscal measures (spending-based vs. tax-based), the initial level of public indebtedness, the exchange-rate regime, the openness of the economy, spillover effects with other economies, and the international business environment (e.g. Christiano et al. 2011; Ramey 2011; Woodford 2011; Barrell et al. 2012; DeLong and Summers 2012; Eggertsson and Krugman 2012; Ilzetzki et al. 2013; Gechert and Rannenberg 2014).

The turn towards fiscal consolidation from 2010 onwards—especially in Europe (e.g. Lane 2012)—triggered the development of a new empirical literature that is specifically concerned with estimating fiscal consolidation multipliers in order to assess the effects of fiscal austerity on growth and employment (Blanchard and Leigh 2014; Guajardo et al. 2014; Alesina et al. 2015a; Yang et al. 2015; Alesina et al. 2015b; Jorda and Taylor 2016; Heimberger 2017). The policy-relevant controversy is about whether consolidation efforts can be ’expansionary’, i.e. have a positive effect on growth – even in the short-run. After Alesina and Ardagna (2010) and some other authors from the “expansionary austerity” strand of the literature had argued that periods of large cuts in government spending can actually have positive growth effects (Blyth 2013; Dellepiane-Avellaneda 2015), a prominent study by Blanchard and Leigh (2014) provided econometric evidence in contradiction to the ’expansionary austerity hypothesis’. Blanchard and Leigh (2014) estimated that for each additional percentage point of fiscal consolidation measures, institutions such as the IMF and the European Commission had underestimated their negative growth effects by about 1% point. The IMF and other institutions had assumed that the multiplier would be about 0.5; hence, the results presented by Blanchard and Leigh (2014) imply that fiscal multipliers during 2010/2011 in their sample of advanced economies stood at about 1.5. Over the last years, researchers have repeatedly taken up the task of assessing the GDP losses caused by fiscal austerity in Europe (e.g. in ’t Veld 2013; Gechert et al. 2015; Heimberger 2017), while other empirical studies have looked at a larger sample of European and non-European OECD countries over a time frame ranging back to the 1970s in order to reassess how growth is being affected in the aftermath of fiscal consolidation episodes—with the main finding that fiscal consolidations are always contractionary, while the highest multipliers are found in periods of economic slack (Guajardo et al. 2014; Yang et al. 2015; Jorda and Taylor 2016).

So far most of the existing studies on the macroeconomic effects of fiscal consolidation measures have focused on the effects of fiscal adjustments on economic growth; the distributional effects of austerity have comparatively enjoyed fewer research efforts. Nevertheless, it has to be recognized that both the IMF and the OECD have over recent years started to gather evidence on how fiscal consolidations affect the income distribution (Cournède et al. 2013; OECD 2015; International Monetary Fund 2012, 2014; Rawdanowicz et al. 2013; Ball et al. 2013; Furceri et al. 2016; Woo et al. 2017). While the IMF has raised concerns that “preventing a significant worsening of the income distribution during the [fiscal] adjustment phase is critical to the sustainability of deficit reduction efforts, as a consolidation that is perceived as being fundamentally unfair will be difficult to maintain” (International Monetary Fund 2012, p. 50), the OECD stresses that fiscal consolidation programs may “undermine long-term growth and exacerbate income inequality. It is therefore important for governments to adopt consolidation strategies that minimise these adverse side-effects.” (Cournède et al. 2013, p. 6) In this context, Rawdanowicz et al. (2013) point out that fiscal consolidations might increase income inequality via several channels. An important channel might be an increase in unemployment that widens the disparities in market incomes; furthermore, cuts in social transfers may affect households in lower parts of the income distribution the most, and a rollback of public programmes benefiting the poor might also increase disposable income inequality.

Table1 presents a summary of the relevant econometric literature on the link between fiscal consolidation measures and income inequality.¹ The main problem for empirical researchers is that obtaining high-quality data on fiscal consolidation measures is fraught with difficulties. As government revenues and spending move with the business cycle, a typical endogeneity problem arises: when it comes to studying various effects of fiscal adjustments, researchers are interested in identifying fiscal measures that are explicitly motivated by the policymakers’ desire to cut the fiscal deficit; and this means that the effect of automatic stabilizers on the budget balance has to be accounted for. There are two main approaches in the macroeconometric literature that deal with this endogeneity problem (Yang et al. 2015). The first approach for identifying the timing and size of fiscal consolidation measures can be called the ’conventional approach’, which is based on calculating changes in cyclically-adjusted fiscal data. Basically, the headline fiscal balance is corrected for the effects of the business cycle on government revenues and expenditures. Institutions such as the IMF and the European Commission perform cyclical adjustments by estimating the fiscal balance that would be obtained if the economy operated at potential output, which requires some model-based measure of potential output. After correcting for the cyclical component of the fiscal balance, one may additionally account for so-called budgetary one-off effects, such as costs that result from bailing-out financial institutions—yielding the ’structural budget balance’ (Mourre et al. 2014). The intensity of fiscal consolidation measures can then be calculated by looking at changes in the estimated cyclically-adjusted fiscal data (e.g. Alesina and Ardagna 2010; Afonso 2010; Blanchard and Leigh 2014). From Table 1, it can be seen that papers 1, 2 and 8 follow the ’conventional approach’ of using cyclically-adjusted fiscal data.

Table 1 Summary of relevant econometric papers on the link between fiscal consolidations and income inequality

However, a typical criticism in the literature is that—due to problems related to estimating the fiscal balance that would be obtained if the economy operated at non-observable potential output (e.g. Perotti 2013; Carnot and de Castro 2015)—changes in cyclically-adjusted fiscal data might not only reflect the policymakers’ desire to cut the fiscal deficit. Therefore, there is a second major strategy in the macroeconometric literature for overcoming the endogeneity problem, which is called the ’narrative approach’. In a seminal paper, Romer and Romer (2010) identify size and timing of fiscal policy measures from budgets, budget documents and policy papers by accounting for the policy-makers’ motivations for implementing the respective measures. By doing so, they construct an “exogenous” measure of fiscal policy, which should be uninfluenced by economic conditions. Considering that the usage of cyclically-adjusted fiscal data can lead to biased estimates on the actual impact of fiscal consolidation programs (e.g. Perotti 2013; Guajardo et al. 2014), it comes as no surprise that nearly all of the recent papers in the relevant macroeconometric literature follow the ’narrative’ approach to identify fiscal adjustment episodes. Table 1 indicates that papers 3, 4, 5, 6, 7 and 9 all use the narrative data on fiscal consolidations in OECD countries collected by IMF economists for the period 1978–2009 (DeVries et al. 2011). Their data focus on discretionary changes in government spending and taxes that were motivated by the policymakers’ desire to reduce the budget deficit—and not by a response to prospective economic conditions. Hence, this ’narrative’ variable should by construction be unburdened by the endogeneity problem.

Using the narrative-approach fiscal consolidation data provided by DeVries et al. (2011), a number of studies find that fiscal consolidations typically lead to an increase in disposable income inequality (Ball et al. 2013; Agnello and Sousa 2014; Furceri et al. 2016; Woo et al. 2017), while Agnello and Sousa (2012)—who use fiscal consolidation data based on the ’conventional approach’—report the reverse result. Schneider et al. (2017) and Schneider et al. (2016) take a different approach to all those papers, as they estimate a parametric Lorenz curve model and then use Gini-like indices of income inequality to assess distributional changes at the top and bottom of the distribution, finding that more drastic fiscal consolidations are associated with a widening in income dispersion, as inequality rises at the top. Schaltegger and Weder (2014) focus on the question of whether increases in inequality that are due to fiscal consolidations depend on the political party or government type. They find that coalition governments do significantly better than single party and minority governments when it comes to addressing distributional concerns. In this context, Kaplanoglou et al. (2015) argue that “fairness in consolidation”—related to measures such as improvements in the targeting of social transfers or higher public outlays on labor market programs—increases the odds of successfullly introducing a fiscal adjustment program. In an earlier study, Mulas-Granados (2005) analyzes the effects which fiscal adjustments with different compositions might have on income inequality. He finds that expenditure-based consolidations perform better in terms of economic growth than revenue-based adjustments, while the former increase income inequality more than the latter. Ball et al. (2013), Furceri et al. (2016) and Agnello and Sousa (2014) also report that spending-based consolidations are more detrimental than tax-based adjustments in terms of their consequences for the income distribution. While Agnello et al. (2016) consistently find that income dispersion increases more with spending cuts, it has to be noted that they focus on the effects of national fiscal adjustments on income inequality in the European regions, with the main finding that fiscal adjustments exacerbate regional disparities in income.

From this review of the relevant econometric literature, it becomes apparent that none of the reviewed papers—with the exception of Schneider et al. (2017)—has considered data for the years from 2010 onwards. Moreover, the literature has so far not studied whether the dynamic effects of fiscal consolidation episodes on income inequality depend on the size and duration of fiscal consolidation measures as well as on the timing of the business cycle. In what follows, this paper contributes to closing existing gaps in the literature.

Empirical study design

We estimate the distributional effects of fiscal consolidation measures over the short- and medium-run. In doing so, we follow the methodology proposed by Jorda (2005), who estimates impulse response functions (IRFs) from local projections. Jorda (2005) shows that the standard linear projection is a direct estimate of the typical impulse response, as derived from a traditional vector autoregression (VAR). In principle, there are other possibilities to measure dynamic effects; in particular, one could estimate a Panel Vector Autoregression (PVAR) or an Autoregressive-Distributed-Lag Model (ARDL). However, in our case both options are inferior to the local projections method. The VAR approach suffers from identification and size-limitation problems, which is not the case for the more flexible local projections method (Gupta et al. 2017, p. 18–19). And the stability of IRFs obtained from an ARDL is undermined by their lag-sensitivity (e.g. Ball et al. 2013). Moreover, Cai and DenHaan (2009) point out that when the dependent variable is very persistent (which is the case for Gini data), statistically significant long-run effects may result from “one-type-of-shock models”²—a problem that does not haunt the local projections method since lagged dependent variables are not used to derive the IRFs, but only enter as controls. Another advantage of the Jorda (2005) method is that the uncertainty around the IRFs can be estimated directly from the standard errors of the estimated coefficients without any need for Monte Carlo simulations.

In the context of estimating the effects of fiscal adjustments on income inequality, we employ the local projections method introduced by Jorda (2005). The empirical investigation in this paper goes beyond previous attempts to study the dynamic effects of fiscal austerity on income inequality. First, we cover a longer time period, as we are able to include data on the crisis years 2010–2013, thereby covering the more extensive time period 1978–2013. Second, we account for a richer set of control variables. Third, we extend our analysis by various relevant aspects, thereby providing new insights into how the distributional effects depend on the size and duration of fiscal adjustments and the timing of the business cycle. Fourth, we employ a comprehensive set of robustness checks.

Econometric strategy

Our regressions are based on the following equation, which is estimated for each future time period k (with $k = 1,\ldots ,8$),³ allowing us to obtain local projections on how income inequality changes following the start of a fiscal consolidation episode:

$$\begin{aligned} G_{i, t+k} - G_{i, t}=\beta _{k} D_{i, t}+\gamma _{k} Z_{i,t}+\sum _{j=1}^{l}\delta _{j}^{k}\Delta G_{i,t-j}+\zeta _{i}^{k}+\eta _{t}^{k}+\epsilon _{i, t}^{k} \end{aligned}$$

(1)

In Eq. 1, G represents our measure of income inequality, i.e. the Gini coefficient of (in most cases: disposable) income, where the data sources used throughout the analysis will be explained below (see Sect. 3.2); $D_{i, t}$ is a dummy variable that takes the value of 1 for the starting year of each fiscal consolidation episode and 0 otherwise. $Z_{i,t}$ is a vector of additional control variables that should be understood as pre-treatment variables (i.e. determined before the treatment of fiscal consolidation starts; see Nakamura and Steinsson (2018)). These pre-treatment controls will be introduced in Sect. 3.2. $\Delta G_{i,t-j}$ are the lags in the change of the measure of income inequality, where we set the number of lags l to two,⁴ although we show later on that the estimation results are robust to different numbers of lags. $\zeta _{i}^{k}$ are country fixed-effects. $\eta _{t}^{k}$ are period fixed-effects. And $\epsilon _{i, t}^{k}$ represents the stochastic residual. Equation 1 is estimated by using the panel-corrected standard error estimator (PCSE). As shown by Beck and Katz (1995), the OLS-PCSE procedure is well-suited for time-series cross-section data, when the number of years covered is not much larger than the number of countries in the cross-sectional dimension of the data. The main reason for the superior performance of the OLS-PCSE estimation strategy—compared to the Parks estimator and other Feasible Generalized Least Squares estimators—is that the method proposed by Beck and Katz (1995) is well-suited to addressing cross-section heteroskedasticity and autocorrelation in the residuals, allowing us to avoid biased standard errors.

Data

As consolidation data from the ’conventional approach’ imply the risk of obtaining biased estimates on the macroeconomic effects of fiscal austerity (e.g. Perotti 2013; Guajardo et al. 2014), the empirical analysis in this paper builds on fiscal consolidation measures that were identified according to the ’narrative approach’. Cyclically-adjusted data based on the ’conventional approach’ used by Afonso (2010) will only be used for the purpose of checking the robustness of our results. The ’narrative’ fiscal consolidation data includes 17 OECD countries (Australia, Austria, Belgium, Canada, Denmark, Finland, France, Germany, Ireland, Italy, Japan, Netherlands, Portugal, Spain, Sweden, the United Kingdom, and the United States of America). The size of the country group and the years that we cover in our data are dictated by data availability on this ’narrative’ fiscal consolidation variable. To identify episodes of cuts in government spending and/or increases in taxes which aim at reducing the budget deficit, we obtained annual data from DeVries et al. (2011) for the time period 1978–2009. By using the same ’narrative methodology’ as DeVries et al. (2011), Alesina et al. (2015a) have extended this dataset for the years 2010–2013. There are 60 consolidation episodes in total, covering 214 years with fiscal consolidations over the time period 1978–2013. The average size of the 60 fiscal consolidation programs amounts to 4.2% of GDP.

Table 2 summarizes the occurrence of fiscal consolidation episodes in our dataset. It can be seen that many fiscal consolidations actually come in the form of packages that span two or more years. The longest adjustment period was started by Canada in 1984 and lasted until 1997. For the period after the financial crisis, it can also be seen that fiscal adjustments were in general bundled into multi-year packages. For example, Ireland’s consolidation lasted from 2009 to 2013, and countries such as Austria, Denmark and Germany consolidated from 2011 to 2013. Table 2 presents the 60 fiscal consolidation episodes (that were bundled into packages of one or several years). The average duration of the fiscal consolidation programmes is 3.5 years.

Table 2 Fiscal consolidation episodes, based on DeVries et al. (2011) and Alesina et al. (2015a)

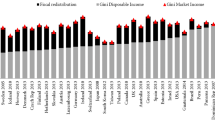
For the measure of income inequality (G), we obtained data on Gini coefficients for market income and disposable income from Version 5.1 of the Standardized World Income Inequality Database SWIID (Solt 2016). Gini coefficients are bounded between 0—each reference unit receives exactly the same share of income—and 100, which would imply that a single reference unit gets all the income. The average Gini of disposable market income in our data set is 28.4, with a minimum of 16.5 and a maximum of 37.6. It has to be noted that the panel data are unbalanced, since Solt (2016) does only provide Gini data for 550 out of 612 possible observations (T = 36; N = 17). In the robustness check section, we will show that results do not change markedly when we interpolate the data in order to balance the panel. In the baseline regressions, however, we take the data from Solt (2016) as they are—without interpolating the missing values.⁵ As we are mainly interested in how income inequality changes after taxes and transfers, the baseline results will be based on net (disposable) Gini data. Figure 2 shows the evolution in the disposable Gini coefficient for the 17 OECD countries in our country sample.

Fig. 2

The evolution of the Gini index of disposable income in 17 OECD countries. Notes Grey bars indicate fiscal consolidation episodes. For details, see Table 2

There are three main advantages of using the SWIID dataset. First, the data ensure that income inequality across countries is measured in a harmonized way. Second, the data include a large group of countries and allow us to obtain long time-series on Gini coefficients of market and disposable income for all the 17 OECD countries in our sample. Third, comparability across countries is enhanced by a transparent procedure of how the data were collected. As a robustness check, we will later on also use the database provided by Milanovic (2016a), who offers an ’All the Ginis’ index for disposable income by merging several data sources.

We control for five additional variables that function as pre-treatment controls (see Vector $Z_{i,t}$ in Eq. 1): First, to consider possible effects of international trade on (future) income inequality, we include the change in trade openness (measured as the sum of imports and exports in relation to GDP), where data were obtained from the European Commission’s AMECO database. Consistent with Woo et al. (2017) and other studies, we use trade-to-GDP as a proxy to control for trade globalization, which might explain parts of the increase in income inequality in developed countries by affecting wages for skilled and low-skilled labor through various channels (e.g. Bensidoun et al. 2011). Second, we control for the change in the average years of schooling (Barro and Lee 2013)—here data come from the International Human Development Indicator—in order to capture possible effects of education on future income inequality. Third, we include GDP growth (AMECO data), as a decrease in economic activity may lead to an increase in the debt-to-GDP ratio via the workings of automatic stabilizers, so that the probability of fiscal consolidation measures might increase. Fourth, we account for the change in the unemployment rate (OECD data), where the rationale is the same as for considering GDP growth. Fifth, we control for the growth rate in Total Factor Productivity as a proxy for capturing the effects of technological change on income inequality (e.g. Acemoglu 2003; Roser and Crespo-Cuaresma 2016), where data were obtained from the AMECO database. These additional regressors are typically considered in the empirical literature on the determinants of income inequality (e.g. Acemoglu 2003; Ball et al. 2013; Roser and Crespo-Cuaresma 2016; Woo et al. 2017). Hence, the model presented in Eq. 1 covers the most relevant control variables from the empirical literature. With another robustness check, we will introduce additional lags for GDP growth and the change in the unemployment rate, since it might be argued that these variables have lagged impacts on the relation between fiscal consolidation and future income inequality.

Results

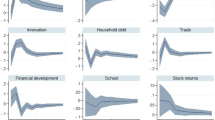
By following the estimation strategy outlined above, we estimate the distributional effects following the start of a fiscal consolidation episode. Since we include country fixed effects in our regressions, the results should be interpreted in comparison to a baseline country-specific trend. By running regressions on Eq. 1, impulse response functions based on local projections can be obtained by plotting the estimated consolidation coefficients $\beta _{k}$ for each future time period k. Grey areas in all the plots below indicate the confidence bands of the impulse response functions, calculated by using one standard error bands of the estimated coefficients; in doing so, we follow Ball et al. (2013) and Furceri et al. (2016) in order to enhance comparability with previous studies. Hence, Fig. 3 graphically depicts the estimated response of income inequality to the shock of a fiscal consolidation episode. The local projection is done from year zero, with the first impact of the shock felt in the first year. The path of the local projection is then constructed to year eight; the figure shows the deviations from the levels in year zero. It can be seen from the plot that fiscal consolidation episodes typically have long-lasting effects on income inequality, as the Gini coefficient increases following the start of a fiscal consolidation episode.

From Panel A of Fig. 3, it can be seen that for Gross (market income) Gini data from Solt (2016), local projections suggest that income inequality increases by 1.07% points (ppts.) in year three, peaking at 1.20 ppts. in year seven. For disposable (after taxes and transfers) Gini data, the increase is 0.35 ppts. in year 3, with a peak of 0.60 ppts. in year 5 (see Panel B of Fig. 3).⁶ The finding that the effect of consolidation episodes on market income is stronger than on disposable (after-taxes, after-transfers) income may be expected if the increase works through the channels of higher (long-term) unemployment—fiscal austerity decreases demand, lowers growth and pushes up unemployment (e.g. Guajardo et al. 2014; Jorda and Taylor 2016) –, skewing the distribution of market incomes (Ball et al. 2013; Furceri et al. 2016). However, the social safety net (consisting of unemployment benefits and other types of social spending) may still be able to bridge parts of the consolidation shock to income inequality. As a first robustness check, we complement our results that are based on a binary fiscal consolidation dummy by running regressions on Eq. 1 with a continuous fiscal consolidation variable ($D_{i, t}$), which expresses the size of fiscal consolidation in % of GDP (DeVries et al. 2011; Alesina et al. 2015a). As can be seen from Panel C and D of Fig. 3, the result that a fiscal consolidation shock pushes up inequality is not sensitive to using the binary or the continuous instrument for fiscal consolidation.

In what follows, we take the local projections results related to the net Gini data and the binary ’narrative’ fiscal consolidation variable as our baseline (Panel B of Fig. 3). We mainly want to focus on how income inequality (post-taxes, post-transfers) changes in the years after a fiscal consolidation episode has started. Moreover, the existing literature has also focused on using a binary consolidation dummy indicating when a fiscal consolidation episode takes place (Ball et al. 2013; Agnello and Sousa 2014; Furceri et al. 2016). Hence, we prefer to use the binary dummy variable for the ’fiscal consolidation treatment’ in order to foster comparability, where starting periods of fiscal consolidations have the value 1, and all other periods are treated as zeroes. However, as indicated by the results in Fig. 3, the precise choice of the instrument variable makes little difference in terms of the overall results.

Fig. 3

Baseline results: Impulse response functions. Notes Grey areas represent one standard error bands around the coefficients. Additional controls: two lags of change in Gini, GDP growth, change in unemployment rate, change in trade openness, change in years of schooling, TFP growth, country fixed effects, time fixed effects

Do size, duration and composition of consolidation programs matter?

As a first extension to our baseline analysis, we consider the characteristics of fiscal consolidation episodes in terms of the size of the fiscal adjustment. The average size of the consolidation programs in our sample is 4.2% of GDP. 17 of the 60 fiscal consolidation programs are larger than the average. In what follows, we construct a new dummy variable for large-sized fiscal consolidations, which takes the value of 1 for the starting period of those fiscal adjustment packages that are larger than the average, and 0 otherwise. Correspondingly, the dummy for small-sized consolidations takes the value of 1 for the starting year of consolidation packages smaller than the average of 4.2%. From Fig. 6, it can be seen that large-sized consolidations have a much more pronounced impact on income inequality, where it is notable that all of the inequality-enhancing impact takes place in the medium-term; in year seven after the start of a large-sized consolidation episode, the Gini has increased by 1.3 ppts. (see Panel A of Fig. 6). In contrast, most of the impact of small-sized consolidations on the income distribution materializes in the short-run; however, it has to be noted that the uncertainty around those estimates is substantial. The medium-term increase in the Gini is significantly less pronounced for small-sized consolidations, coming in at 0.4 ppts. in year five (see Panel B of Fig. 6), which is not even half of the impact of large-sized consolidations in year five.

The duration of the fiscal consolidation episode might also matter. Hence, we distinguish between consolidation episodes longer than the average of 3.5 years, and those shorter than the average. In our dataset, 22 out of 60 episodes are labelled as “long consolidation episodes”. As can be seen from Panel C and Panel D of Fig. 4, adjustments with a long duration had a rather strong impact on inequality; the Gini of disposable income increased by 1.3 ppts. in year seven. For short episodes, in stark contrast, we do not find that the medium-term impact on inequality is different from zero.⁷

Furthermore, we analyze whether the composition of fiscal consolidation measures matters for the effects on income inequality. Our data allows us to distinguish between measures that are based on spending cuts and tax increases. Hence, we are able to estimate Eq. 1 separately for spending- and tax-based adjustments. The results depicted by Fig. 4 suggest that spending-based adjustments have more pronounced effects on income inequality. The standard definition of the consolidation dummies implies a value of 1 whenever a fiscal consolidation episode starts, and 0 otherwise. However, there are concerns that the corresponding results might be biased, because most of the fiscal adjustments in the database involve both spending and tax-based measures. This issue is addressed by using an alternative definition for a) episodes where tax-based consolidations were larger than spending-based adjustments, and b) for episodes where spending-based consolidations were larger than tax-based adjustments.⁸ As can be seen from Fig. 4, results from both the standard and the alternative definition suggest that spending-based adjustments have more pronounced effects on income inequality.

Does the timing of the business cycle matter?

Does it matter whether a country starting a fiscal consolidation episode is doing so from a rather strong or weak position of economic growth? To answer this question, we begin by checking whether the impacts of fiscal adjustments differ in periods of high and low economic growth. For the purpose of characterizing consolidation episodes marked by rather low growth, we construct a dummy variable that takes the value of 1 for all consolidation periods where the real GDP growth rate was lower than 2% at the start—and 0 otherwise. Correspondingly, we construct a fiscal consolidation variable that captures periods of fiscal consolidation that started under relatively high economic growth (> 2%). With this distinction between high- and low-growth episodes, we follow Agnello and Sousa (2014, p. 13). Given this definition, 32 of the 60 consolidation episodes in our sample were started when growth was low. We find that income inequality increases markedly stronger for low-growth fiscal adjustments. As can be seen from Panel A of Fig. 6, the Gini increases by 0.6 ppts. in year three, rising to 0.8 ppts. in the seventh year. Panel B of Fig. 6 shows that, in stark contrast, income inequality is typically less affected if an adjustment episode starts during relatively high growth. This finding suggests that business cycle conditions do not only matter for the size of fiscal multipliers (e.g. DeLong and Summers 2012; Blanchard and Leigh 2014; Gechert and Rannenberg 2014; Qazizada and Stockhammer 2015), but that they may also be important regarding the distributional effects of fiscal consolidations (Fig. 5).

Fig. 4

Do size and duration of consolidation episodes matter? Notes Grey areas represent one standard error bands around the coefficients. Additional controls: two lags of change in Gini, GDP growth, change in unemployment rate, change in trade openness, change in years of schooling, TFP growth, country fixed effects, time fixed effects. See the text on how large vs. small and long vs. short fiscal consolidation episodes are to be distinguished

Fig. 5

Does the composition of consolidation episodes matter? Notes Grey areas represent one standard error bands around the coefficients. Additional controls: two lags of change in Gini, GDP growth, change in unemployment rate, change in trade openness, change in years of schooling, TFP growth, country fixed effects, time fixed effects. See the text for an explanation on how the standard and alternative definitions of adjustment episodes are to be distinguished

It might also make a difference whether the start of a fiscal consolidation episode was preceded by a systemic banking or currency crisis. As Reinhart and Rogoff (2011) have shown by means of long historical time series, sovereign debt crises are typically preceded or coincide with banking crises, which may be due to governments taking on a large pile of debt to ensure that the ailing banking sector does not collapse. As a consequence of sovereign debt crises, governments are regularly forced to implement fiscal consolidation measures in order to bring down fiscal deficits and public debt (e.g. Lane 2012). To investigate whether the impact of fiscal adjustments on income inequality depends on whether or not they were preceded by a systemic crisis, we identify those fiscal consolidation episodes that started within three years after the occurence of a financial crisis, using the data set provided by Valencia and Laeven (2012). 16 of the 60 consolidation episodes in our data set were started in the aftermath of a financial crisis. Comparing Panel C and Panel D of Fig. 6, estimation results suggest that fiscal consolidations that start after financial crises have a stronger impact on income inequality than those episodes that start in non-financial-crisis times. Specifically, in year five after the start of a financial-crisis-related consolidation episode, income inequality has increased by about 1.2 ppts.—compared to a much lower 0.4 ppts. in the non-financial-crisis-related cases.

Fig. 6

Does the timing of the business cycle matter? Notes Grey areas represent one standard error bands around the coefficients. Additional controls: two lags of change in Gini, GDP growth, change in unemployment rate, change in trade openness, change in years of schooling, TFP growth, country fixed effects, time fixed effects

Robustness checks

In order to further test the robustness of the baseline results reported in the previous section, we perform several robustness checks, as we drop and add control variables, consider variations in the disposable Gini data, use alternative fiscal consolidation data, investigate the impact of excluding time- and period-fixed effects, and vary the number of lags of the dependent variable. First, we account for potential concerns that GDP growth and the change in the unemployment rate might have an effect on the relationship between fiscal consolidation and future income inequality only with lags. Panel A and B of Fig. 7 show that including one and two lags of these two additional controls, respectively, does not change the results. Second, we vary data on the Gini of disposable income, by using data from Milanovic (2016a) instead of the SWIID data provided by Solt (2016).⁹ Figure 7 suggests that the results remain broadly unchanged (see panel C of Fig. 7), although it has to be noted that the impacts on inequality are larger when we use the Milanovic data. Third, we investigate whether the 62 missing values out of 612 observations from the Gini data provided by Solt (2016) play a role (see Fig. 2). We use linear interpolation to balance the panel data. Panel D of Fig. 7 shows that the results do not change much in comparison to Panel A of the same Figure: in year three, the increase in the Gini is 0.2 ppts. and in year seven 0.5 ppts.¹⁰

Fig. 7

Robustness checks: variations in Gini data. Notes Grey areas represent one standard error bands around the coefficients. Additional controls: two lags of change in Gini, GDP growth, change in unemployment rate, change in trade openness, change in years of schooling, TFP growth, country fixed effects, time fixed effects

With the fourth step of our robustness analysis, we check whether the results hold when we use the ’conventional approach’ to identifying fiscal consolidation episodes. Specifically, we follow the methodology proposed by Afonso (2010), who documents the start of a fiscal consolidation episode when either the change in the primary cyclically-adjusted budget balance is at least one and a half times the standard deviation in one year (in relation to the whole panel sample), or when the change in the primary cyclically-adjusted budget balance has been at least one standard deviation on average in the last two years.¹¹ From Panel B in Fig. 8, it can be seen that the result that fiscal consolidation episodes push up inequality holds, although the short-term increase is found to be smaller when we use the Afonso (2010) approach, while the medium-term impact is more pronounced.¹²

Fig. 8

Robustness checks: vary fiscal consolidation variable, time FE and country FE. Notes Grey areas represent one standard error bands around the coefficients. Additional controls: two lags of change in Gini, GDP growth, change in unemployment rate, change in trade openness, change in years of schooling, TFP growth. Panel C excludes time fixed effects. Panel D excludes country fixed effects. Otherwise, all estimations include country fixed effects and time fixed effects

Fig. 9

Robustness checks: vary the number of lags of the change in the Gini coefficient. Notes Grey areas represent one standard error bands around the coefficients. Additional controls: GDP growth, change in unemployment rate, change in trade openness, change in years of schooling, TFP growth, country fixed effects, time fixed effects

Fifth, reading Nickell (1981) raises concerns that our estimation results might be biased as we include both a lagged dependent variable and country fixed effects. However, Nickell (1981) points out that the order of bias is 1 / T, and this number is small for our dataset, so that the relatively long time dimension allows us to expect that this concern is not of high importance for our analysis. Additionally, Teulings and Zubanov (2014) point out that local projections might be biased because country-fixed effects may interact with country-specific arrival rates of fiscal consolidation episodes. Panel D of Fig. 8 mitigates the concerns raised by the works of Nickell (1981) and Teulings and Zubanov (2014), as our results do not change markedly when we drop country fixed effects from our regressions, although a temporary spike can be seen in the impulse response function in year 3. Besides from that spike, however, the impact of fiscal consolidation episodes on income inequality is nearly of the same size if one compares the results from excluding country fixed effects to the baseline results that include country fixed effects. As a final robustness check, we analyze whether variations in the number of lags regarding the change in the Gini index G controlled for in Eq. 1 has an impact on the results. Figure 9 shows that the baseline results are robust to varying the number of lags.¹³

Discussion

The results presented in this paper suggest that fiscal consolidation episodes have long-lasting effects on income inequality, measured in terms of the Gini coefficient of disposable household income. Notably, our baseline finding for the short-term impact of austerity on income inequality—an increase in the Gini by 0.35 ppts. in year three after the start of a fiscal consolidation episode—is consistent with earlier findings in the literature. Agnello and Sousa (2014) report that fiscal consolidation episodes lead to an increase in the Gini index of about 0.3 ppts. in the short-run. In comparison, Ball et al. (2013) find that three years after a fiscal adjustment episode, income inequality has increased by a little more than 0.2 ppts. The baseline estimates of Ball et al. (2013) of an increase in the Gini of disposable income by 0.7 ppts. after 7 years also do not deviate much from our 0.57-ppts.-finding. The main difference to the existing literature is that our study includes data on the crisis years 2010–2013, while we also consider a more comprehensive set of additional variables (trade openness, average years of schooling, TFP growth) and provide further extensions and robustness checks. In a nutshell, we confirm results from the earlier literature, which finds that fiscal consolidation measures—identified by the ’narrative approach’ (DeVries et al. 2011)—typically lead to an increase in income inequality in the short- and medium-run. Our finding that spending-based adjustment episodes have a more pronounced effect on inequality than tax-based consolidations is also in line with the previous literature (Mulas-Granados 2005; Ball et al. 2013; Agnello and Sousa 2014; Furceri et al. 2016; Woo et al. 2017). Consistent with Ball et al. (2013) and Furceri et al. (2016), this paper finds that the effects of fiscal consolidations on market income inequality are more pronounced than the effects on the distribution of disposable income (after taxes and transfers). This finding may be expected if the increase works mainly through the channels of higher (long-term) unemployment—fiscal austerity decreases demand, lowers growth and pushes up unemployment (e.g. Jorda and Taylor 2016; Heimberger 2017) –, which may cause a more unequal distribution of market incomes. The social safety net (consisting of unemployment benefits and other types of social spending) seems to be able to deliver some redistribution that compensates at least for parts of the consolidation shock to income inequality. The channels through which fiscal consolidations affect income inequality, however, have to be analyzed more carefully before one can draw substantial conclusions (see below regarding the outlook for future research).

The baseline results discussed here should be interpreted as the average response of income inequality after introducing a fiscal consolidation episode as a shock to the system. The average Gini of disposable income in our data set is 28.4. An increase of 0.35 ppts. in the short-term therefore pushes up income inequality by 1.2% (on average), and a rise of 0.57 ppts. in the medium-term corresponds to an increase by 2.0%. However, our extensions suggest that the effects may depend both on the size, duration and composition of the consolidation—where large-sized, long-lasting and spending-based episodes have more pronounced effects—as well as on the timing of the business cycle, where we find that programs started in the aftermath of financial crises and when growth was low have a more detrimental effect on the income distribution. Notably, our data consist of only four consolidation episodes that were large-sized, of long duration, spending-based and started both in the aftermath of a financial crisis and when growth was low.¹⁴

In what follows, we use a couple of country examples to provide a better intuition about the economic relevance of our findings. Nevertheless, it should be noted that our results only indicate the average response to a fiscal consolidation shock. The experience of a particular country with a specific consolidation episode does not necessarily have to fit this average response. However, the results might still be used to obtain some rough estimate about the economic relevance of the contribution of a fiscal consolidation episode to the evolution of income inequality. We start with Italy’s fiscal consolidation from 1991 to 1998. The Gini increased from 29.4 to 34.0 over this time period, and by using the average response of income inequality to a long-lasting consolidation (see Fig. 4), one can gauge that the consolidation accounts for about 28% of the increase in income inequality in the medium-term (in year seven). In contrast, our results on short adjustment episodes suggest that consolidations such as the one in Austria in 1996–1997¹⁵ or the one in the Netherlands in 2004–2005¹⁶ should not have had a medium-term impact on inequality that can be distinguished from zero. Similarly, the tax-based adjustment in Australia in 1994 should have had milder effects on income inequality than the spending-based adjustment in Denmark that started in 1983. Let’s turn to Finland next. From 1985 to 2000, the Gini of disposable in Finland income increased from 20.5 to 24.9 points. In 1992, the Finish government started a fiscal consolidation program, which was implemented in the aftermath of a systemic banking crisis (Valencia and Laeven 2012). One of the extensions to our baseline results suggests that the average medium-term increase in inequality is more pronounced when an episode is started in conjunction with a financial crisis, with an increase of about 0.9 ppts. in year eight. Against this backdrop, the fiscal consolidation started in 1992 would explain about 23% of the increase in the Gini in year eight after the start of the consolidation episode in 1992.

The results presented in this paper come with limitations; further research on the distributional effects of fiscal austerity would be beneficial. First, it should again be recognized that we estimated the average response of income inequality to a fiscal consolidation shock. The fact that many of the consolidations that started in the aftermath of the global financial-crisis are long in duration and large in size does not mean that they are guaranteed to have a strong medium-term impact on income inequality; other factors might play a role. One would have to study the episode from 2008 onwards in detail to allow for conclusions on the specific distributional effects. For such an analysis, however, one would have to use a different dataset (with more data points after the crisis) and to employ a different econometric method (e.g. Schneider et al. 2017, 2016).¹⁷ However, as our results suggest that the medium-term impact is stronger than in the short-term, it may be seen as prudent to expect that it will take some years before the effects of consolidation measures on income inequality fully materialize. Second, future work could analyze the channels through which consolidation measures have an impact on income inequality in more depth. For example, Ball et al. (2013) and Furceri et al. (2016) have taken a look at how fiscal austerity impacts on the wage (and profit) share as well as on short-term and long-term unemployment—an analysis that could be extended further not only by additionally considering data for the more recent crisis years, but also by including relevant additional controls and by accounting for differences in size and composition of adjustment measures. In particular, the finding of this paper that it takes about four years before the upward-pushing effects of large fiscal consolidations on income inequality start to materialize could be analyzed in the context of the relevant channels through which fiscal consolidations affect income inequality. One possibility for further analysis would be to check whether the resolution of economic downturns is delaying the impact of fiscal consolidation measures (that are motivated by the desire to bring down fiscal deficits) on the income distribution. Another possibility would be to analyze whether the tax and transfer system can mitigate the effect of increases in market income inequality (which are the effect of fiscal consolidation measures) only in the short-term. Third, an important limitation of the papers in the existing literature certainly is that the fiscal consolidation data used do not allow to distinguish between different components of tax increases and spending cuts. However, the effects of retrenchment in transfer payments, different types of tax increases and cuts in public investment on the income distribution might differ substantially. Finally, Rawdanowicz et al. (2013) have rightly pointed out that a comprehensive assessment of the distributional effects of fiscal adjustment programs would not only have to present estimates on the dynamic effects of fiscal adjustments on income inequality, which was the focus of this paper. To arrive at a more global and detailed assessment, one would also have to analyze the effects of austerity on the life-time income distribution, equality of opportunity and interactions with other policies. Until researchers will have figured out how to address these open points, however, the already existing literature on the distributional consequences of fiscal consolidation episodes—to which this paper has contributed—could still help policy-makers to make fiscal policy decisions in a world of high income inequality. Furthermore, in the spirit of Jorda and Taylor (2016), future research could look at different policy specifications.

Conclusions

This paper has analyzed the dynamic effects of fiscal consolidation episodes on income inequality in the short- and medium-run by building on an annual data set covering 17 OECD countries over the time period 1978–2013. We have contributed to the relevant empirical literature by providing the first econometric analysis that includes ’narrative approach’ data for the crisis years from 2010 onwards. Based on the methodology proposed by Jorda (2005), we derived impulse response functions from local projections, where the main finding is that fiscal consolidations typically lead to an increase in income inequality. According to our baseline results, the Gini coefficient of disposable income increases by about 0.4% points in the short-run (in year three after the shock), and by 0.6% points in the medium-run (in year seven)—which is largely consistent with the earlier literature (Ball et al. 2013; Agnello and Sousa 2014; Furceri et al. 2016; Woo et al. 2017). By providing several extensions to our baseline analysis, we are able to paint a more nuanced picture of the dynamic impact of fiscal austerity, as we find that the effects on income inequality are more pronounced (a) when the size of the fiscal consolidation package is large rather than small; (b) when the duration of the adjustment is long instead of short; (c) when the fiscal consolidation is based more on spending cuts than on tax increases; (d) when the consolidation is started in the aftermath of a financial crisis rather than in a non-crisis episode; and (e) when the adjustment falls into a period of low economic growth instead of high growth. The findings that fiscal consolidation policies are an important determinant of income inequality could be taken into account by governments for which introducing measures to counteract high income inequality is a priority.