Labour supply in Austria: an assessment of recent developments and the effects of a tax reform

Abstract

We apply a structural discrete choice framework to estimate income-specific own-wage and cross-wage labour supply elasticities in regard to working hours and participation for married and single males and females in Austria. We use data from the Austrian components of the European Statistics of Income and Living Conditions from 2004 to 2012. Own-wage elasticities are very small for males and slightly higher for females. Cross-wage elasticities are practically zero for males and slightly negative for females. Male and female own-wage elasticities decrease with higher incomes. Over time female labour supply elasticities decrease. Furthermore, we assess the labour supply and fiscal effects of the Austrian tax reform of 2016. We find a total increase in working hours by 0.71%. The labour supply effects are stronger on the intensive margin, for females and for low-income earners. On total the tax reform induces a tax relief of 4.7 billion Euros. The positive effects on tax burden and disposable income increase with the individual income.

1 Introduction

Labour supply elasticities are interesting on their own but also key to answer tax-benefit orientated research questions. To be able to provide valid approximations of changes in the revenue outcome and the distributional effects of tax or benefit reforms it is necessary to know about the labour supply reactions of different socio-economic groups. Unfortunately, the empirical evidence on labour supply elasticities is not unambiguous. Estimates vary tremendously (Blundell and MaCurdy 1999; Evers et al. 2008; Meghir and Phillips 2008; Keane and Rogerson 2012; Bargain and Peichl 2013). This is especially true for female labour supply elasticities.¹

Of course the variation in labour supply elasticities across countries might be simply explained by different labour supply behaviour. Despite of that one has to be aware of a few pitfalls. Bargain et al. (2014) point out the difficulties in comparing labour supply elasticities for different countries: Different studies might use different methodological approaches, the data might suffer from selection bias, and estimates might be derived for different periods of time or with different estimation methods.

To overcome the mentioned problems and to achieve international comparable labour supply elasticities Bargain et al. (2014) collected comparable data for 17 European countries and the United States. Male and female own-wage elasticities are positive in every country, with the female labour supply elasticities being larger.² In every country the cross-wage elasticity is very close to zero for males and slightly negative for females.

Also for a detailed country-specific analysis it is crucial to apply a consistent data base and estimation method to make labour supply elasticities of different socio-economic groups comparable. For Austria we are only aware of a recent study by Wernhart and Winter-Ebmer (2012). They study labour supply elasticities on the intensive and extensive margin for married and never-married males and females between 1987 and 1999. Their main finding is a strong reduction of the labour supply elasticity on the extensive margin for married women during that period.³

Estimating a structural discrete choice model (VanSoest 1995; Hoynes 1996; Blundell et al. 2000) and using the Austrian components of the European Statistics of Income and Living Conditions, EU-SILC, from 2004 to 2012 our contribution to the literature is twofold. First, we follow the research question in Wernhart and Winter-Ebmer (2012) and provide an in-depth country specific analysis of labour supply elasticities for Austria. We enhance their analysis by studying cross-wage elasticities for males and females deciding on their labour supply individually and in a household context.⁴ In addition we estimate income-specific elasticities. Precisely, we estimate static steady-state labour supply elasticities of hours worked (intensive margin) and labour market participation (extensive margin) for single and married males and females for ten different income levels. For single males and females we estimate own-wage elasticities, for married males and females we also estimate cross-wage elasticities.

As a second contribution we simulate the impact of the Austrian tax reform which became effective as of January 1st 2016. We use our derived gender and income-specific elasticities to calculate the changes in hours worked and the labour market participation for males and females at all income levels. Overall the hours worked increase by 0.71% and the participation probability increases by 0.21 percentage points due to the tax reform. On average the reform has a stronger impact on the intensive margin, for females and for low-income earners. For males and females the effects decrease with the income level. Furthermore, we assess the fiscal effects of the tax reform and estimate the aggregate tax relief to 4.7 billion Euros per year. We present first and second round effects and show that the positive effects of the tax reform increase with the income.

The remainder of the paper is organized as follows. Section 2 presents our empirical model and specification within a discrete choice framework. We describe our data in Sect.  3 and present our results in Sect. 4. In Sect. 5 we describe the Austrian tax reform of 2016 and assess the labour supply and fiscal effects. The last section concludes.

2 Model specification in a discrete choice framework

We use a structural discrete choice labour supply model to estimate labour supply elasticities and to assess the labour supply effects of the Austrian tax reform of 2016. To do so we implement the new rules and regulations of the tax reform in the IHS Labour Supply Model for Austria ILSA.⁵

ILSA is a structural discrete choice labour supply model that allows for the estimation of static uncompensated own and cross-wage elasticities at the intensive and extensive margin. The advantage of discrete choice models is that they directly account for the fact that observed hours of work cluster around zero and full-time hours and incorporate both the intensive and extensive margin of labour supply (Bargain et al. 2014). Furthermore, as it is not necessary to specify the entire budget constraint, the discrete choice approach is well suited to the complexities of the tax benefit system and its interplay with means tested benefits given the labour supply of different members of one household. For each hours choice transfer entitlements and take home pay are directly evaluated.⁶

As many micro-simulation models ILSA views labour supply decisions of individuals and couples as an optimal choice from a discrete set of working hours categories (VanSoest 1995; Creedy and Kalb 2005). The observed working hours are interpreted as the result of utility maximisation of households, and therefore represent the trade-off between consumption (income) and leisure. For couple households, the existence of a joint utility function is assumed, that features household income and both partners’ leisure as an argument. This approach allows for the estimation of the structural parameters of the underlying utility function through a multinomial logit model. Based on these estimates the behavioural response to a given change in disposable income can be quantified, such that second round distributional effects can be evaluated on individual as well as aggregate level.

To be more specific, we follow VanSoest (1995) and interpret labour supply as a choice of unitary households n = 1, ..., N from a discrete set of alternatives j = 1,..., J.

Every discrete alternative is a combination of the disposable income of the household $y_{nj}$ and the male $m_{nj}$ and female $f_{nj}$ leisure time. Leisure time is the total time endowment (168 h) minus corresponding hours worked. The gross hourly wage rates are $w_{n}^{m}$ and $w_{n}^{f}$. Thus, the disposable income is a function of the male $h_{nj}^{m}$ and female $h_{nj}^{f}$ working time and the wage rates minus taxes $\tau$:

$$\begin{aligned} y_{nj} = w_{n}^{m}h_{nj}^{m} + w_{n}^{f}h_{nj}^{f} - \tau (w_n^{m}h_{nj}^{m},w_{n}^{f}h_{nj}^{f};Z_{n}). \end{aligned}$$

(1)

The tax-benefit function expresses the individual tax burden. This depends on the male and female gross income as well as on household characteristics $Z_{n}$, e.g. whether a child is living in the household. Non-labour income (e.g. transfers) is included in the disposable income, also influenced by the household characteristics. For the working hours we divide the continuum of possible working hours in six categories and define the median working hours in a group as the discrete alternative. The distribution of working hours within each group differs for males and females, thus we have slightly different discrete alternatives for males and females. The discrete alternatives are given by the medians of the following working hours groups: 0, 1–10, 11–20, 21–30, 31–40, 40+.

The six individual choice alternatives lead to 36 choice alternatives in the household decision model. The gross hourly wages are calculated from our annual data using working hours per week, number of months in employment and the gross yearly income. Wages in the upper and lower 1% percentile are truncated. For these observations and when wages are not observable (e.g. if non-employed) a Heckman model is estimated to correct for sample selection (Heckman 1976, 1979).⁷

The utility of the household is given by a systematic part $V_{nj} = V(y_{nj},m_{nj},f_{nj};Z_{n})$ and a random error following an extreme value distribution of type I: $U_{nj} = V_{nj} + \varepsilon _{nj}, \forall n,j$. For the systematic part we further assume a quadratic form and potential interactions:

$$\begin{aligned} V_{nj} & = \overline{\alpha }_{y}y_{nj} + \overline{\alpha }_{m}m_{nj} + \overline{\alpha }_{f}f_{nj} + \beta _{y2}y_{nj}^{2} + \beta _{m2}m_{nj}^{2} + \beta _{f2}f_{nj}^{2}\nonumber \\& \quad + \beta _{ym}y_{nj}m_{nj} + \beta _{yf}y_{nj}f_{nj} + \beta _{mf}m_{nj}f_{nj}. \end{aligned}$$

(2)

We account for observed heterogeneity among the households through the vectors $\overline{\alpha }_{y}, \overline{\alpha }_{m}$ and $\overline{\alpha }_{f}$. Each of these vectors contains the direct preference and measures the effect of each household characteristic through taste-shifting parameters $\overline{\gamma }_{y}, \overline{\gamma }_{m}$ and $\overline{\gamma }_{f}$:

$$\begin{aligned} \overline{\alpha }_{y}&= \beta _{y} + Z_{n}^{'}\overline{\gamma }_{y}\end{aligned}$$

(3)

$$\begin{aligned} \overline{\alpha }_{m}&= \beta _{m} + Z_{n}^{'}\overline{\gamma }_{m}\end{aligned}$$

(4)

$$\begin{aligned} \overline{\alpha }_{f}&= \beta _{f} + Z_{n}^{'}\overline{\gamma }_{f}. \end{aligned}$$

(5)

As taste-shifting parameters we include age, work experience, education, other household income (e.g. from other members of the household inflexible in their labour supply), number and age of children and whether a person lives in Vienna. The impact of further direct preferences are measured via parameter $\beta _{y}$, $\beta _{m}$ and $\beta _{f}$.

For single males and females the disposable income (1) in the utility function (2) depends only on the net income of the individual plus possible transfers (depending on household characteristics, such as children). Similar taste shifters apply as in the household model, but here we also consider whether the person lives alone.

Using the unitary household model and the individual models for males and females we calculate labour supply elasticities for married and single males and females in Austria. Building on our results we estimate the labour supply effect of the Austrian tax reform of 2016. We present changes at the intensive and extensive margin for ten different income levels.

3 Data

Our analysis bases on the Austrian component of the European Statistics of Income and Living Conditions, EU-SILC. We use the Austrian waves from 2004 to 2012. The EU-SILC is a cross-sectional dataset that retains 75% of all households for re-interviewing in the following year. The employment and income information of each SILC wave refers to income and employment of the previous year. We make use of the SILC’s panel component to merge subsequent SILC waves by assigning income and employment information. As a consequence, we lose a quarter of observations each year—the households which leave the panel. Furthermore, if one member of the household has left the household in the next wave, we drop the entire household to maintain household composition.

Because our objective is to estimate labour supply elasticities, we remove individuals from the sample who are not expected to enter into paid employment. Specifically, we drop all individuals below the age of 15, those who are in full-time education or receive a scholarship, those enrolled in an apprenticeship program, and those serving their military or civilian service. We also drop individuals above the statutory retirement age (60 for females, 65 for males), and those who receive an old-age pension or care allowance before reaching this age. We also exclude females who are not allowed to work because they are under maternity protection (eight weeks before and after giving birth) and anyone receiving income from self-employment.⁸

We treat individuals who are living with inflexible (e.g. self-employed) spouses like single individuals: they maximize their individual utility, determined by their earned income and own leisure. Income of their spouse only enters the optimization problem as a taste shifter variable. In contrast, couples with two flexible spouses are assumed to maximize a household utility function determined by household income and the leisure of both spouses.

This leaves us with a pooled cross sectional sample of 25,702 individual observations including 6993 couples where both spouses are or could be active on the labour market. For each SILC wave we apply the regulations of the Austrian tax-benefit system in place at the time of data collection.

The estimation of the model and the calculation of income elasticities is in real terms, all cross sections are valorised to 2015 Euros. Also, the estimation of the gross hourly wages at the beginning of the microsimulation is done in real terms. However, the tax benefit system contains absolute values (e.g. the thresholds of the tax brackets, the threshold of compulsory insurance, etc.). In order to calculate the correct amount of disposable income given gross income in different working hour categories, the numbers have to be valorised to the year of the tax-benefit rule (i.e. the year of the cross section sample). Therefore, there are three steps of valorisation in the model:

• 1. The cross sections are valorised to 2015 and pooled to estimate gross hourly wages.

• 2. Each cross section is re-valorised in order to run through the tax-benefit system individually.

• 3. All cross sections are valorised to 2015 and pooled in order to estimate the model and calculate the elasticities.

Table 1 shows some descriptive statistics for the sample. The average male and female are very similar in most variables, with the exception of labour market related variables. The average female in our sample is 41 years old, has 17 years of experience, works 25 h a week and earns an hourly wage of 16.93 Euros. Those females who are working work on average for 32 h per week. 32% of all females are high school graduates and 75% are married. The average male is also 41 years old, his work experience is 23 years, he works 39 h a week and earns an hourly wage of 22.93 Euros. Given the high labour market participation rate of males it is not surprising that the working hours conditional on working are just slightly higher. 29% of all males are high school graduates and also 75% are married.

Table 1 Descriptive statistics

4 Results

In a first step we pool all EU-SILC waves for Austria from 2004 to 2012 and apply the described models to derive the log-likelihood functions for the household, if both partners are flexible in their labour supply, and for the individual models for males and females if there is only one flexible person in the household. Table 2 shows the estimated parameters for the household model and Tables 3 and 4 for individual males and females.

In all three tables the main parameters show the expected signs and are highly significant. As previously discussed in Sect.  2 we control for a variety of taste-shifting parameters like age, work experience, education and whether children live within the household. Furthermore, we control for the age of the children and for other household income. Other household income covers all net incomes of all inflexible household members, transfers and capital incomes. In the individual models we control for the fact of actually living alone.

In the household model the household income as well as the male and female leisure increase the household’s utility with a decreasing effect as the level of leisure or income increases. Both partners seem to like to spend time together as the interaction effect between male and female leisure is positive. A higher income is more appreciated in the urban area of Vienna and by males and females with at least a high school diploma.

In the assessment of leisure there are similarities but also some differences between males and females. For both sexes leisure is less appreciated by people who graduated from high school or university. For males the value of leisure decreases with age, for females the utility of leisure increases with age. As indicated through the interaction effects a great difference between males and females occurs in the assessment of leisure while children are present in the household. Despite for very young children there is a negative effect of children on the utility of leisure for males. For females the interaction effect between leisure and having children is positive, and especially pronounced for young children.

Single males and females seem to behave more or less as their married counterparts. In the individual models the sign and size of the effects are confirmed. Still striking is the difference in the assessment of leisure while children are present. In the individual model the interaction effect between having children and leisure for males is negative even in the presence of very small children.

Table 2 Household model estimates

Table 3 Individual model estimates—males

Table 4 Individual model estimates—females

With our approach we are able to predict the observed working hours quite well. Table 5 shows the observed and predicted mean working hours for the different subgroups of our sample.⁹ Although we slightly underestimate the working hours for males and slightly overestimate it for females we come very close to the actually observed working hours.

Table 5 Goodness-of-fit of the model

To show income specific labour supply reactions we calculate unconditional own- and cross-wage elasticities with respect to the working hours and the participation probability at the means of the ten deciles of the wage distribution.

Table 6 shows the own- and cross-wage elasticities for males and females in the household model.¹⁰ The reported deciles are deciles of the hourly wage distribution of males and females, respectively. An increase of 1% in the male wage increases the working hours of males on average by 0.08% and their participation probability by 0.01 percentage points. Both elasticities are higher in the bottom three wage deciles and decrease from there on with higher wages. An increase of 1% in the female wage increases the working hours of females by 0.24% and the participation probability by 0.07 percentage points. The elasticities are higher in the bottom 50 percent of the wage distribution and decrease thereafter. Compared to males, the female own-wage elasticities are higher in all wage deciles.

The cross-wage elasticities for males are very close to zero throughout the wage distribution. Due to an 1% increase in the male wage females decrease their working hours on average by 0.15% and their participation probability by 0.03 percentage points. Throughout the female wage distribution the cross-wage elasticities are negative. Notably, we find especially high negative cross-wage elasticities at the upper end of the female wage distribution.

Table 6 Labour supply elasticities—household model

Table 7 reports the own-wage working hours and participation elasticities for single males and females. A 1% wage increase in male wages leads on average to an increase in working hours by 0.13% and to a 0.04 percentage points increase in participation probability. For females a 1% wage increase leads on average to an increase of working hours by 0.24% and to a 0.08 percentage points increase in participation probability. Compared to the household model the mean own-wage elasticities are much higher for males and about the same for females. For males and females the wage specific pattern is much more pronounced in the individual model: The higher the wage the lower the elasticity.

The above stated differences in the impact of leisure on the utility of males and females when kids are present lead to higher wage elasticities for females in a household. Females without children are more similar to males in terms of labour supply behaviour. Females without children increase their working hours due to a 1% wage increase on average only by 0.19% and their participation by 0.05 percentage points, whereas females with children increase their working hours by 0.29% and their participation by 0.10 percentage points.

Table 7 Own-wage labour supply elasticities—individual model

Overall, our household and individual estimates are in line with literature (Wernhart and Winter-Ebmer 2012; Hanappi and Müllbacher 2013; Bargain et al. 2014).¹¹ However, we find especially smaller participation elasticities for females. Taking into consideration that we use very recent data this finding is in line with the convergence of male and female labour supply in Austria at the end of the 1980s and during the 1990s found by Wernhart and Winter-Ebmer (2012).

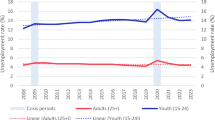
To shed more light on the development of the labour supply of the different groups we estimate labour supply elasticities over time.¹² Thereby we calculate for every year from 2004 to 2012 the mean working hour elasticities and mean participation elasticities for married and single males and females. The evolution of the mean working hours elasticities is shown in Fig. 1 and the evolution of the participation elasticities is shown in Fig. 2.

Fig. 1

Data source EU-SILC 2004–2012, own representation

Mean own-wage elasticities for working hours between 2004 and 2012 in Austria.

Fig. 2

Data source EU-SILC 2004–2012, own representation

Mean own-wage elasticities for participation between 2004 and 2012 in Austria.

The mean own-wage elasticities for working hours of single and married males seem to decrease slightly over time. For females the working hours elasticities vary over time but are in 2012 at about the same level as in 2004. The own-wage participation elasticities for married males seem to be very stable over time. The participation elasticities for females and single males seem to decrease over time a little bit.

5 Labour supply effects of the Austrian tax reform 2016

5.1 The Austrian tax reform

As of January 1^st 2016 an extensive tax reform became effective in Austria. This reform constitutes a major change in the progressive income tax system. The marginal tax rate in the lowest tax bracket (applicable for taxable income of at least 11,000 Euros) dropped significantly from 36.5 to 25%. The before highest marginal tax rate of 50% now starts at a taxable income of 90,000 Euros instead of 60,000 Euros.¹³ Figure 3 shows the marginal tax rates up to an income of 100,000 Euros before and after the tax reform. Next to changes in the progressive tax scale the general tax credit increased from 345 to 400 Euros per year. For people with an income too low to benefit from the tax credit the maximum in-work benefit increased from 110 Euros to 400 Euros per year. For low pensions a payable tax credit of 110 Euros was introduced. In addition, the tax deductible for children doubled to 220 Euros per year and child.

Fig. 3

Source: Own representation

Marginal tax rates before and after the Austrian tax reform of 2016.

5.2 Fiscal effects

Before we study the labour supply effects in detail we take a closer look at the aggregated first and second round effects of the Austrian tax reform of 2016.¹⁴ In the first round the total tax relief adds up to about 4.7 billion Euros a year.¹⁵ Table 8 shows the first round total and mean tax relief per household due to the reform in the ten income deciles (disposable household income). In the first round the tax relief equals the change in the disposable income of the household. The total as well as the mean tax relief per household increases with the income decile. Whereas the 10% with the lowest incomes only benefit from a total tax relief of about 70 million Euros the highest income decile receives a first round relief of about 1 billion Euros. Per household the mean tax relief increases from 153 Euros in the lowest income decile to 2706 Euros in the highest.

Accounting for labour supply adjustments of the households we find slightly moderating effects. To calculate the second round effects we use the labour supply effects which are presented in great detail in the following subsection. Table 9 shows the second round effects of the tax reform. While people in the lowest eight income deciles pay in every income decile more taxes due to adjusting their labour supply, people in the highest two income deciles pay less. Along with the taxes the aggregated disposable income changes in the same pattern. While people with incomes up to the 80% percentile gain in disposable income, people above show a reduction. On total the overall disposable income increases by about 130 million Euros due to second round effects. On the household level most households pay between 13 and 22 Euros more taxes and receive between 70 and 85 Euros more disposable income due to changes in their labour supply.

Table 8 First round fiscal effects of the Austrian tax reform by income decile

Table 9 Second round fiscal effects of the Austrian tax reform by income decile

Table 10 Overall fiscal effects of the Austrian tax reform by income decile

Taking both effects together it is obvious that the first round effects dominate the second round effects. To make a total assessment of the Austrian tax reform of 2016 we present in Table 10 the overall effects (first + second round effects). As one would suspect from the dominating first round effect the overall effect increases with the income. In the lowest decile the aggregated tax relief amounts to only 67 million Euros whereas in the highest decile the tax relief amounts to over one billion Euros. The same pattern is prevalent for the change in disposable income. In the lowest decile it increases on aggregate only by 92 million Euros whereas in the highest decile it increases by about 946 million Euros. On the household level the mean tax relief increases with the income from 145 Euros a year up to 2911 Euros in the highest income decile. Analogously, the mean additional disposable income increases from 200 Euros in the lowest decile to 2545 Euros in the highest decile. Overall, one can state redistributive effects toward high-income earners due to this tax reform. This finding is in line with previous studies on the Austrian tax reform of 2016 (Hofer et al. 2015; Rocha-Akis 2015).

5.3 Labour supply effects

Using the models presented in Sect. 2 we simulate the effect of the Austrian tax reform of 2016 in regard to changes in the labour supply based on the EU-SILC waves from 2004 to 2012 for Austria. For the simulation we use the derived elasticities presented in Sect. 4. We apply the new regulations of the reform and estimate the changes in the working hours elasticity and the participation elasticity due to this reform. We calculate the absolute changes in working hours, full-time equivalents and number of employees. We apply the household model and the individual models (Tables 2, 3 and 4).

Table 11 shows marginal effects of the tax reform on the working hours and on the participation rate. The tax reform has a stronger effect on singles. In response to the tax reform single males increase their working hours on average by 0.61% and increase their participation by 0.17 percentage points. Single females show a stronger response and increase their working hours on average by 1.20%. Their participation increases by 0.32 percentage points. Married males increase their working hours by 0.28% and married females by 0.74%. The participation goes up by 0.10 percentage points for males and 0.24 percentage points for females. These findings are quite as expected, as we saw overall higher labour supply elasticities for single males in the baseline results.

Table 11 Labour supply effects of the Austrian tax reform

Table 12 presents the additional labour supply due to the tax reform. The overall effect is quite substantial. The total labour supply increases by 433,639 working hours which equal 12,675 full time equivalents. Compared to the pre-tax reform level there are 5307 new employees. Hence, the intensive labour supply margin seems to be more pronounced. The total increase in the labour supply is driven slightly more by females than by males. Females increase their working hours in total by 263,655 h which equal 7533 full time equivalents, whereas males increase their working hours by 180,020 h which equal 5142 full time equivalents.

Table 12 Additional labour supply due to the Austrian tax reform

The increased labour supply is not uniformly distributed over the distribution of disposable income before the reform. Although the relative tax relieves are higher for higher incomes we observe that low-income people generally react stronger in their labour supply to financial incentives. Taking both effects together we see especially strong reactions in deciles two to five. The increase of working hours in the bottom half of the wage distribution amounts to 342,335 h whereas in the upper half the additional working hours amount to 101,304 h. In the highest decile the working hours effect is even negative, although the largest part of the reform volume is distributed into this decile. The same pattern can be found in the number of additional full-time equivalents. Notably, in the highest decile the number of new employees is increasing. Whereas the overall effects show a more pronounced increase in the labour supply at the intensive margin these findings point to a pronounced effect at the extensive margin for higher income. Furthermore, the number of new employees in the 9th decile exceeds the number of new full time equivalents (Table 13).

Table 13 Additional working hours due to the Austrian tax reform by income decile

Finally, the question arises whether the Austrian tax reform has a small or large impact on the labour supply, what depends on the specific labour supply elasticities. As shown by Bargain et al. (2014) in an international comparison the Austrian own-wage elasticities of single males and females are rather small, whereas own-wage elasticities for males and especially females in a household are rather high. As most people live in households the own-wage elasticities would point to an above average effect in Austria. But also the cross-wage elasticities of males and females in Austria are rather large in comparison to other countries. So there is a relative strong reduction of the own labour supply as the income of the partner increases—which is the case in such a tax reform. Therefore, in the big picture we would expect that similar reforms in other developed economies would lead to similar effects.

6 Conclusion

We apply a structural discrete choice framework to assess recent developments in the Austrian labour supply behaviour in detail and estimate the effects of the Austrian tax reform of 2016. We use the Austrian part of the EU-SILC waves from 2004 to 2012.

For married and single males we estimate average own-wage elasticities of 0.08% and 0.13% in regard to working hours and 0.01 percentage points and 0.04 percentage points in regard to labour market participation. Cross-wage elasticities are very close to zero for married males. For married and single females the own-wage elasticities are very similar. We estimate 0.24% for both groups in regard to working hours and 0.07 percentage points and 0.08 percentage points in regard to labour market participation. The cross-wage elasticities for married women are slightly negative with $-$0.15% in regard to working hours and 0.03 percentage points in regard to participation. For males and females the own-wage elasticities decrease with the income. We also study labour supply elasticities year by year and find decreasing female labour supply elasticities. All results are in line with previous findings in the literature.

As of 1st of January 2016 a major tax reform became effective in Austria decreasing considerably the marginal tax rates for annual taxable incomes between 11,000 and 90,000 Euros. The first and second round fiscal effects amount to an aggregated tax relief of 4.7 billion Euros. The tax reform relieves higher incomes more than lower deciles, one can state a redistribution in favor of higher incomes. In regard to labour supply we estimate a total effect of 433,639 additional working hours which equals 12,675 full-time equivalents. The tax reform increases especially the labour supply of females and low-income earners. Overall the effects are stronger on the intensive margin.

Appendix

See Tables 14, 15.

Table 14 Labour supply elasticities over time—household model

Table 15 Own-wage labour supply elasticities over time—individual model