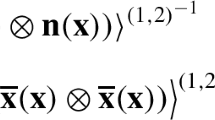The Elastic Properties of Dilute Solid Suspensions with Imperfect Interfacial Bonding: Variational Approximations Versus Full-Field Simulations

Abstract

Approximations for the elastic properties of dilute solid suspensions with imperfect interfacial bonding are derived and assessed. A variational procedure is employed in such a way that the resulting approximations reproduce exact results for weakly anisotropic but otherwise arbitrarily large interfacial compliances. Two approximations are generated which display the exact same format but differ in the way the interfacial compliance is averaged over the interfaces: the first approximation depends on an ‘arithmetic’ mean while the second approximation depends on a ‘harmonic’ mean. Both approximations allow for arbitrary elastic anisotropy of the constitutive phases but are restricted to suspended inclusions of spherical shape. The approximations are applied to a class of isotropic suspensions and confronted to full-field numerical simulations for assessment. Simulations are performed by means of a Fast Fourier Transform algorithm suitably implemented to handle dilute suspensions with imperfect interfaces. Also included in the comparisons are available results for suspensions with extremely anisotropic bondings. Overall, the ‘harmonic’ approximation is found to be much more precise than the ‘arithmetic’ approximation. The finding is of practical relevance given the widespread use of ‘arithmetic’ approximations in existing descriptions based on modified Eshelby tensors.

Appendices

Appendix A: Auxiliary Problem

Consider the displacement field ${\mathbf{v}}({\mathbf{x}})$ that solves the set of equations

$$\begin{aligned} &\nabla \cdot \boldsymbol{\sigma}= {\mathbf{0}}, \quad \boldsymbol{\sigma}= \mathbb{C}^{(1)} \boldsymbol{\varepsilon}+ \chi ^{(2)}({\mathbf{x}})\ \boldsymbol{\tau}^{(2)}, \quad \boldsymbol{\varepsilon}= \overline{\boldsymbol{\varepsilon}}+ \nabla \otimes _{s} {\mathbf{v}}({ \mathbf{x}}) \quad \mbox{in} \quad \varOmega \backslash \varGamma ^{(1,2)}, \end{aligned}$$

(87)

$$\begin{aligned} &[\!\![\boldsymbol{\sigma}]\!\!]{\mathbf{n}}= {\mathbf{0}}, \quad [\!\![{\mathbf{v}}]\!\!]= {\mathbf{d}}({\mathbf{x}}), \quad {\mathbf{d}}({ \mathbf{x}}) = a{\mathbf{D}}^{(1,2)}{\mathbf{n}}({\mathbf{x}}) \quad \quad \mbox{on} \quad \varGamma ^{(1,2)}, \end{aligned}$$

(88)

$$\begin{aligned} &{\mathbf{v}}({\mathbf{x}}) = {\mathbf{0}} \quad \mbox{on} \quad \partial \varOmega , \end{aligned}$$

(89)

for prescribed second-order symmetric tensors $\boldsymbol{\tau}^{(2)}$ and ${\mathbf{D}}^{(1,2)}$. We intend to determine the corresponding strain field within the inclusion phase. To that end, we begin by condensing these equations into

$$\begin{aligned} \nabla \cdot \left [ \mathbb{C}^{(1)} \nabla \otimes _{s} {\mathbf{v}}({ \mathbf{x}}) \right ] + \nabla \cdot \boldsymbol{\tau}({\mathbf{x}}) = { \mathbf{0}} \quad \mbox{in} \quad \varOmega \end{aligned}$$

(90)

with

$$\begin{aligned} \boldsymbol{\tau}({\mathbf{x}}) = \chi ^{(2)}({\mathbf{x}})\ \boldsymbol{\tau}^{(2)} - \delta ^{(1,2)}({\mathbf{x}})\ \mathbb{C}^{(1)} \mathbb{E}\left ({\mathbf{n}}({\mathbf{x}})\right ) {\mathbf{D}}^{(1,2)}, \end{aligned}$$

(91)

which should be understood in the sense of distributions. Here, $\mathbb{E}({\mathbf{n}}) = a\ {\mathbf{I}}\boxtimes ({\mathbf{n}}\otimes {\mathbf{n}})$ and $\delta ^{(1,2)}({\mathbf{x}})$ refers to the Dirac delta function with support on the interface $\varGamma ^{(1,2)}$. Making use of the Radon transform of equation (90) and its inverse we can write the strain field as

$$\begin{aligned} \boldsymbol{\varepsilon}({\mathbf{x}}) = \overline{\boldsymbol{\varepsilon}}+ \frac{1}{8\pi ^{2}} \int _{| \boldsymbol{\xi}|=1} \mathbb{H}(\boldsymbol{\xi})\ \frac{\partial ^{2} \breve{\boldsymbol{\tau}}}{\partial p^{2}}( \boldsymbol{\xi},\boldsymbol{\xi}\cdot {\mathbf{x}})\ {\mathrm{d}} \boldsymbol{\xi} \end{aligned}$$

(92)

with

$$\begin{aligned} \mathbb{H}_{\mathit{ijkl}}(\boldsymbol{\xi}) = \left . K_{ik}^{-1}( \boldsymbol{\xi}) \xi _{j}\xi _{l} \right |_{(ij)(kl)} \quad \mbox{and} \quad K_{ik}(\boldsymbol{\xi}) = \mathbb{C}^{(1)}_{\mathit{ijkl}} \xi _{j} \xi _{l}, \end{aligned}$$

(93)

and the Radon transform of the polarization field $\boldsymbol{\tau}({\mathbf{x}})$ given by

$$\begin{aligned} \breve{\boldsymbol{\tau}}(\boldsymbol{\xi},p) &= \int _{ \mathbb{R}^{3}} \boldsymbol{\tau}({\mathbf{x}})\ \delta ( \boldsymbol{\xi}\cdot {\mathbf{x}}- p)\ {\mathrm{d}}{\mathbf{x}}. \end{aligned}$$

(94)

Given that inclusions are well separated, the strain field within any particular inclusion can be computed by neglecting the presence of all the other inclusions. This amounts to identifying the functions $\chi ^{(2)}({\mathbf{x}})$ and $\delta ^{(1,2)}({\mathbf{x}})$ in (91) with those of a single inclusion centered at the origin of an infinite medium. In that case,

$$\begin{aligned} \breve{\boldsymbol{\tau}}(\boldsymbol{\xi},p) &= - \breve{\mathbb{T}}(\boldsymbol{\xi},p) \boldsymbol{\tau}^{(2)} - \mathbb{C}^{(1)} \breve{\mathbb{E}}(\boldsymbol{\xi},p) {\mathbf{D}}^{(1,2)}, \end{aligned}$$

(95)

where

$$\begin{aligned} \breve{\mathbb{T}}(\boldsymbol{\xi},p) &= \int _{\mathbb{R}^{3}} \chi ^{(2)}({\mathbf{x}})\ \delta (\boldsymbol{\xi}\cdot {\mathbf{x}}- p) \ \mathbb{I}\ {\mathrm{d}}{\mathbf{x}}= \int _{\mathcal{S}( \boldsymbol{\xi},p)} \mathbb{I}\ {\mathrm{d}}{\mathbf{x}}, \end{aligned}$$

(96)

$$\begin{aligned} \breve{\mathbb{E}}(\boldsymbol{\xi},p) &= \int _{\mathbb{R}^{3}} \delta ^{(1,2)}({\mathbf{x}})\ \mathbb{E}\left ({\mathbf{n}}({\mathbf{x}})\right )\ \delta (\boldsymbol{\xi}\cdot {\mathbf{x}}- p)\ {\mathrm{d}}{\mathbf{x}}=\int _{ \mathcal{C}(\boldsymbol{\xi},p)} \frac{\mathbb{E}\left ({\mathbf{n}}({\mathbf{x}})\right )}{\left [1 - (\boldsymbol{\xi}\cdot {\mathbf{n}}({\mathbf{x}}))^{2}\right ]^{1/2}} {\mathrm{d}}{\mathbf{x}}, \end{aligned}$$

(97)

and the sets $\mathcal{S}(\boldsymbol{\xi},p) = \left \{{\mathbf{x}}:\ |{\mathbf{x}}| \leq a \ \mbox{and} \ \boldsymbol{\xi}\cdot {\mathbf{x}}=p \right \}$ and $\mathcal{C}(\boldsymbol{\xi},p) = \left \{{\mathbf{x}}:\ |{\mathbf{x}}| = a \ \mbox{and} \ \boldsymbol{\xi}\cdot {\mathbf{x}}=p \right \}$ are the intersections of a Radon plane with the spherical inclusion and with its surface, respectively; computations give

$$\begin{aligned} \breve{\mathbb{T}}(\boldsymbol{\xi},p) &= \pi \left (a^{2} - p^{2} \right ) \mathbb{I}\ H\left (1 - \frac{|p|}{a}\right ) \quad \mbox{and} \end{aligned}$$

(98)

$$\begin{aligned} \breve{\mathbb{E}}(\boldsymbol{\xi},p) &= 2\pi \left [p^{2} \boldsymbol{\xi}\otimes \boldsymbol{\xi}+ \frac{a^{2} - p^{2}}{2} ({\mathbf{I}}- \boldsymbol{\xi}\otimes \boldsymbol{\xi}) \right ] \boxtimes {\mathbf{I}}\ H\left (1 - \frac{|p|}{a}\right ), \end{aligned}$$

(99)

where $H(\cdot )$ is the Heaviside step function. Introducing these expressions into (92) then gives an expression for the strain field within the spherical inclusion ($|{\mathbf{x}}|< a$) of the form

$$\begin{aligned} \boldsymbol{\varepsilon}({\mathbf{x}}) = \overline{\boldsymbol{\varepsilon}}- \mathbb{P} \boldsymbol{\tau}^{(2)} - (\mathbb{I} - \mathbb{P} \mathbb{C}^{(1)}) {\mathbf{D}}^{(1,2)}, \end{aligned}$$

(100)

where ℙ is a microstructural tensor given by

$$\begin{aligned} \mathbb{P} = \frac{1}{4\pi} \int _{|\boldsymbol{\xi}|=1} \mathbb{H}(\boldsymbol{\xi}) \ {\mathrm{d}}\boldsymbol{\xi}. \end{aligned}$$

(101)

Thus, the strain field within every inclusion of the suspension is uniform and given by expression (100). An equivalent analysis in terms of Green’s functions was originally carried out by Qu [8] but contained an error later amended by Othmani et al. [28]. The above procedure avoids the problem by making use of Radon transforms instead of Green’s functions. The procedure was initially advocated by Willis [10] to study inclusion problems with perfect interfacial bonding.

Appendix B: A Numerical Method Based on the Fast Fourier Transform

2.1 B.1 Method

Following Michel et al. [14] and Hashin [21], the mechanical problem (3) for suspensions with imperfect interfaces is replaced by the mechanical problem

$$\begin{aligned} \widetilde{w}(\overline{\boldsymbol{\varepsilon}}) = \min _{ \boldsymbol{\varepsilon}\in \mathcal{K}( \overline{\boldsymbol{\varepsilon}})} \left [ \sum _{r=1}^{2} c^{(r)} \left \langle \frac{1}{2} \boldsymbol{\varepsilon}\cdot \mathbb{C}^{(r)}\boldsymbol{\varepsilon}\right \rangle ^{(r)} + c^{(1,2)} \Big\langle \frac{1}{2} \boldsymbol{\varepsilon}\cdot \mathbb{C}^{(1,2)}({\mathbf{n}}({\mathbf{x}})) \boldsymbol{\varepsilon} \Big\rangle ^{(1,2)} \right ] \end{aligned}$$

(102)

for suspensions with a thin compliant interphase $\varOmega ^{(1,2)} = \varGamma ^{(1,2)}\times (0,h)$ of finite thickness $h$ coating each inclusion and perfectly bonded to the matrix and inclusion phases. Here, $c^{(1,2)}$ and $\langle \cdot \rangle ^{(1,2)}$ denote —with slight abuse of notation— the volume fraction and the volume average over the interphase $\varOmega ^{(1,2)}$, respectively, and $\mathcal{K}(\overline{\boldsymbol{\varepsilon}})$ is now the set of strain fields of the form $\boldsymbol{\varepsilon}({\mathbf{x}}) = \overline{\boldsymbol{\varepsilon}}+ \nabla \otimes _{s}{\mathbf{v}}({ \mathbf{x}})$ with ${\mathbf{v}}:\varOmega \rightarrow \mathbb{R}^{3}$ square-integrable with compact support. Note that the interphasial elasticity tensor $\mathbb{C}^{(1,2)}({\mathbf{n}})$ is allowed to depend on the unit vector ${\mathbf{n}}({\mathbf{x}}) = {\mathbf{x}}/|{\mathbf{x}}|$ defined by the position vector ${\mathbf{x}}$ relative to the center of each spherical inclusion. By choosing positive-definite tensors $\mathbb{C}_{\mathit{ijkl}}^{(1,2)}({\mathbf{n}})$ such that

$$\begin{aligned} \eta _{ik}^{-1}({\mathbf{n}}) = h^{-1} \mathbb{C}_{\mathit{ijkl}}^{(1,2)}({\mathbf{n}}) n_{j} n_{l} \quad \mbox{and} \quad ||\mathbb{C}^{(1,2)}({\mathbf{n}})|| < < || \mathbb{C}^{(r)}||, \end{aligned}$$

(103)

the mechanical problems (3) and (102) coincide in the limit of vanishing thickness $h \rightarrow 0$.

The mechanical fields in (102) are numerically determined by considering a periodic cubic array of sufficiently small spherical inclusions and solving the Euler-Lagrange equations via an FFT-based algorithm. This FFT-based method has been extensively employed to determine mechanical fields in periodic media with a wide variety of local constitutive responses. When the number of elements/voxels is large —as in this work—, FFT-based methods are faster and require less computer memory than finite element methods (FEM) [29, 30]. In addition, periodic boundary conditions are natural in FFT-based methods while cumbersome and complex in FEM methods. In any event, the presence of a thin interphase in FFT simulations requires special treatment. Standard FFT-based implementations would discretize the spherical inclusion and the interphase into a regular grid of cuboidal voxels with two deleterious consequences. First, the smoothly curved boundaries of the thin interphase are represented in that case by a set of mutually orthogonal planes leading to spurious local stress concentrations and numerical contingencies; this is especially pronounced in the case of soft interphase behavior like the one required in this work. Second, small interphase thickness-to-inclusion radius ratios like the ones required in this work could only be achieved with unreasonably fine grid resolutions in view of the fact that the interphase thickness should contain at least one voxel. These contigencies are circumvented here following the strategy of Zecevic et al. [26], whose central idea is to embed the mechanical problem (102) into a large-deformation formulation with a suitably chosen reference configuration that differs from the initial and deformed configurations in such a way that FFT computations are facilitated. Specifically, a reference configuration is identified here with a square array of aligned cuboidal inclusions. The initial configuration is then generated by first applying the conformal mapping

$$\begin{aligned} x_{1}=X_{1}\sqrt{1-\frac{1}{2}\left (\frac{X_{2}}{a}\right )^{2}- \frac{1}{2}\left (\frac{X_{3}}{a}\right )^{2}+\frac{1}{3}\left ( \frac{X_{2}X_{3}}{a^{2}}\right )^{2}} \\ x_{2}=X_{2}\sqrt{1-\frac{1}{2}\left (\frac{X_{1}}{a}\right )^{2}- \frac{1}{2}\left (\frac{X_{3}}{a}\right )^{2}+\frac{1}{3}\left ( \frac{X_{1}X_{3}}{a^{2}}\right )^{2}} \\ x_{3}=X_{3}\sqrt{1-\frac{1}{2}\left (\frac{X_{1}}{a}\right )^{2}- \frac{1}{2}\left (\frac{X_{2}}{a}\right )^{2}+\frac{1}{3}\left ( \frac{X_{1}X_{2}}{a^{2}}\right )^{2}} \end{aligned}$$

(104)

between reference Cartesian coordinates $X_{i}$ of points belonging to a cuboidal inclusion of edge $2a$ and initial Cartesian coordinates $x_{i}$ of points belonging to a spherical inclusion of radius $a$. Second, the coordinates of two layers of grid points belonging to the interphase in the initial configuration are obtained using an analogous mapping from cubes to spheres with radii $(1+f)a$ and $(1+2f)a$, where $f$ defines the distance between interphase grid points in the initial configuration and the thickness of the interphase. The layer of grid points belonging to the matrix adjacent to the interphase is mapped to a sphere with radius $(1+3f)a$. Finally, the coordinates of the remaining grid points of the matrix domain in the initial configuration are obtained by interpolation with the sides of the unit cell. In doing so, the spacing between matrix coordinates is increased with increasing distance from the inclusion. Corresponding conformal displacements are calculated as ${\mathbf{u}}^{c} = {\mathbf{x}}- {\mathbf{X}}$, and the conformal deformation gradient is given by ${\mathbf{F}}^{c} = {\mathbf{I}}+ \partial {\mathbf{u}}^{c}/\partial {\mathbf{X}}$. A cross section of the resulting initial configuration is shown in Fig. 3b for $f = 0.001$.

Fig. 3

Zoom-in of the y-z cross section, showing upper right quadrant of the inhomogeneity in the (a) reference and (b) initial configurations

Finally, the deformed configuration is generated by composing this stress-free deformation with a small-strain deformation dictated by the equilibrium equations associated with the mechanical problem (102). The latter amount to solving for the Cauchy stress and Eulerian strain rate fields in the current/initial configuration satisfying the equilibrium, compatibility and constitutive equations using periodic Green’s function. The original unit cell, discretized on an irregular grid, is replaced by a reference linear heterogeneous medium in the initial configuration, to which a stress polarization field is applied. The heterogeneity of the reference medium accounts for the distortion of the grid, while the polarization field accounts for the heterogeneity of the unit cell. The stress in the heterogeneous linear reference medium is given by

$$\begin{aligned} \boldsymbol{\sigma}({\mathbf{x}})=\mathbb{L({\mathbf{x}})} \frac{\partial \dot{{\mathbf{u}}}}{\partial {\mathbf{x}}}({\mathbf{x}})+ \boldsymbol{\phi}({\mathbf{x}}), \end{aligned}$$

(105)

where $\mathbb{L}_{\mathit{ijkl}}({\mathbf{x}}) = \mathbb{L}^{\mathit{ref}}_{\mathit{iokp}}F_{\mathit{jo}}({\mathbf{X}}) F_{lp}({ \mathbf{X}})/J({\mathbf{X}})$ is the spatially varying linear viscous stiffness in the current configuration, $\mathbb{L}^{\mathit{ref}}$ is a constant linear viscous stiffness in the reference configuration, $J$ is determinant of the deformation gradient, and $\boldsymbol{\phi}$ is the Cauchy stress polarization field in the current configuration. For a given polarization field, the velocity gradient in the linear reference medium is given by

$$\begin{aligned} \frac{\partial \dot{{\mathbf{u}}}}{\partial {\mathbf{x}}}({\mathbf{x}})&=-\left [ \int _{\varOmega ^{\mathit{ref}}}\mathbb{G}^{\mathit{ref}}({\mathbf{X}}-{\mathbf{X}}')[J({\mathbf{X}}')( \boldsymbol{\phi}({\mathbf{x}}')-\left < \boldsymbol{\phi} \right >){\mathbf{F}}^{-T}({\mathbf{X}}')] d{\mathbf{X}}'\right ]{\mathbf{F}}^{-1}({\mathbf{X}}) \\ &{}+ \frac{\partial \dot{\mathbf{{U}}}}{\partial {\mathbf{X}}}{\mathbf{F}}^{-1}({\mathbf{X}})+ \left < \frac{\partial \dot{{\mathbf{u}}}}{\partial {\mathbf{x}}}\right >, \end{aligned}$$

(106)

where $\mathbb{G}^{\mathit{ref}}$ is the periodic Green’s operator in reference configuration. The above convolution integral is performed over the unit cell in the reference configuration, $\varOmega ^{\mathit{ref}}$, where grid is regular. Therefore, the convolution theorem can be used and the convolution integral is efficiently calculated as a point-wise product in Fourier space. The system of equations given by Eq. (106) is solved using an augmented Lagrangian method [35, 36] modified for the case of large grid distortions [31].

2.2 B.2 Algorithm

In the augmented Lagrangian (AL) method, auxiliary stress and velocity gradient fields, $\boldsymbol{\lambda}$ and $\partial \dot{{\mathbf{u}}}/\partial {\mathbf{x}}$, are introduced and iteratively adjusted until the auxiliary stress and the symmetric part of the auxiliary velocity gradient fields converge to the constitutively related stress and strain rate, respectively. The AL algorithm reads:

• 1. Calculate new guess for the auxiliary velocity gradient field:

  $$\begin{aligned} \frac{\partial \dot{{\mathbf{u}}}}{\partial {\mathbf{x}}}^{i+1}= \frac{\partial \dot{{\mathbf{u}}}}{\partial {\mathbf{x}}}^{i}-\left [ \mathbb{G}^{\mathit{ref}}*(J(\boldsymbol{\lambda}^{i}-\left < \boldsymbol{\lambda}^{i}\right >){\mathbf{F}}^{-T})\right ]{\mathbf{F}}^{-1}+ \frac{\partial \dot{\mathbf{{U}}}}{\partial {\mathbf{X}}}{\mathbf{F}}^{-1}, \end{aligned}$$

  where “∗” represents convolution.

• 2. Calculate new guess for the stress field by solving the residual at each grid point:

  $$\begin{aligned} {\mathbf{R}}(\boldsymbol{\sigma}^{i+1})=\boldsymbol{\sigma}^{i+1}+ \mathbb{L}\dot{\boldsymbol{\varepsilon}}( \boldsymbol{\sigma}^{i+1})-\boldsymbol{\lambda}^{i}- \mathbb{L}\frac{\partial \dot{{\mathbf{u}}}}{\partial {\mathbf{x}}}^{i+1}+ \mathbb{L}[\mathbb{G}^{\mathit{ref}}(\mathbf{0})(J(\boldsymbol{\sigma}^{i+1}- \boldsymbol{\sigma}^{i}){\mathbf{F}}^{-T}){\mathbf{F}}^{-1}]=\mathbf{0}. \end{aligned}$$

• 3. The new guess for the auxiliary stress field is:

  $$\begin{aligned} \boldsymbol{\lambda}^{i+1}=\boldsymbol{\lambda}^{i}+ \mathbb{L}\left (\frac{\partial \dot{{\mathbf{u}}}}{\partial {\mathbf{x}}}^{i+1}- \dot{\boldsymbol{\varepsilon}}^{i+1}\right )= \boldsymbol{\sigma}^{i+1}. \end{aligned}$$

• 4. Convergence test.

In comparison to the original augmented Lagrangian method, the algorithm given above differs in the expression for residual in step 2. The last term in the expression of the residual is introduced, which accounts for the effect of the new guess for stress at each grid point, $\boldsymbol{\sigma}^{i+1}$, on the velocity gradient at the same grid point, $(\partial \dot{{\mathbf{u}}}/\partial {\mathbf{x}})^{i+1}$, through the convolution Eq. (106) [31]. Note that effect of the new guess for stress in the surrounding grid points on the velocity gradient at the current grid point is not considered. Also note that once the fields are converged, $\boldsymbol{\sigma}^{i}\approx \boldsymbol{\sigma}^{i+1}$, and the last term vanishes.

2.3 B.3 Calibration and Verification

Full-field simulations are carried out to determine the effective properties of the isotropic dilute suspensions introduced in Sect. 6. To that end, interphasial elasticity tensors of the form

$$\begin{aligned} \mathbb{C}^{(1,2)}({\mathbf{n}}) = f_{1}\mathbb{E}^{[1]}({\mathbf{n}}) + f_{2} \mathbb{E}^{[2]}({\mathbf{n}}) + f_{3}\mathbb{E}^{[3]}({\mathbf{n}}) + f_{4} \mathbb{E}^{[4]}({\mathbf{n}}) + f_{5}\mathbb{E}^{[5]}({\mathbf{n}}) + f_{6} \mathbb{E}^{[6]}({\mathbf{n}}) \end{aligned}$$

(107)

are employed, where the set $\mathbb{E}^{[b]}({\mathbf{n}})$ ($b=1,\ldots,6$) constitutes Walpole’s basis for transversely isotropic tensors with symmetry axis ${\mathbf{n}}$ [32], and the moduli $f_{b}$ must satisfy the conditions

$$\begin{aligned} f_{1} + f_{2} > 0, \quad f_{1} f_{2} - f_{3}^{2} > 0, \quad f_{5} > 0, \quad f_{6} > 0, \quad f_{3} = f_{4}, \end{aligned}$$

(108)

so that the tensor $\mathbb{C}^{(1,2)}({\mathbf{n}})$ is symmetric and positive-definite. For interfacial compliances of the form (64), condition (103)₁ requires that

$$\begin{aligned} f_{1} = \frac{h}{\eta _{\parallel }} \quad \mbox{and} \quad f_{6} = \frac{2h}{\eta _{\perp}}. \end{aligned}$$

(109)

The remaining moduli can be chosen arbitrarily provided conditions (103)₂ and (108) are satisfied; a convenient choice is

$$\begin{aligned} f_{2} = f_{1}, \quad f_{3} = f_{4} = 0, \quad f_{5} = f_{6}. \end{aligned}$$

(110)

It is recalled that, while mathematically simpler, interphasial elastiticy tensors with isotropic —rather than transversely isotropic— symmetry do not give access to the entire range of possible values for $\eta _{\parallel }$ and $\eta _{\perp}$, as already noted by Hashin [17]. The connection between thin interphases with transversely isotropic elasticity and sharp imperfect interfaces has been recently investigated by Kushch [33]. It should be noted, however, that even though the above choice gives access to a much wider range of interfacial compliances, the range remains constrained by the additional inequality (103)₂. Indeed, noting that for the above choice of interphasial elasticity tensor

$$\begin{aligned} ||\mathbb{C}^{(1,2)}|| \leq \frac{h}{\eta _{\parallel }} ||\mathbb{E}^{[1]} + \mathbb{E}^{[2]}|| + \frac{2h}{\eta _{\perp}} ||\mathbb{E}^{[5]} + \mathbb{E}^{[6]}|| = \frac{\sqrt{2} h}{\eta _{\parallel }} + \frac{4h}{\eta _{\perp}} \end{aligned}$$

(111)

in view of the triangle inequality, and that

$$\begin{aligned} ||\mathbb{C}^{(r)}|| > 2\mu ^{(r)} ||\mathbb{K}|| = 2\sqrt{5} \mu _{*} \end{aligned}$$

(112)

with $\mu _{*} = {\mathrm{min}}\{\mu ^{(1)}, \mu ^{(2)} \}$, it is easy to verify that a sufficient condition for the inequality (103)₂ to hold is

$$\begin{aligned} \eta _{s} >> \frac{h/a}{\sqrt{5}} \left (\frac{\sqrt{2}/2}{1+2\alpha} + \frac{2}{1-\alpha} \right ) a\mu _{*}^{-1}, \end{aligned}$$

(113)

where the interfacial parameters $\eta _{s}$ and $\alpha$ are defined in terms of $\eta _{\parallel }$ and $\eta _{\perp}$ by (79) to provide the alternative representation (78) for the interfacial compliance tensor. Given the smallness of the ratio $h/a$ for the microgeometries of interest in this work, we conclude that the inequality

$$\begin{aligned} \eta _{s} \geq \frac{1}{\sqrt{5}} \left (\frac{\sqrt{2}/2}{1+2\alpha} + \frac{2}{1-\alpha} \right ) a\mu _{*}^{-1} \end{aligned}$$

(114)

warrants admissibility of interfacial parameters. Given that the right-hand side of this inequality is strictly positive, the parameter $\eta _{s}$ cannot vanish. Consequently, the thin interphase model cannot mimic a perfect interface. According to this criterion, when mimicking isotropic interfaces ($\alpha =0$) the model is constrained to $\eta _{s} \gtrsim 1.21\ a \mu _{*}^{-1}$, whereas when mimicking strongly anisotropic interfaces ($\alpha \rightarrow -1/2$ or $\alpha \rightarrow 1$) the model is constrained to imperfect interfaces with large compliances $\eta _{s}$.

In any event, for this choice of local constitutive tensors, the effective bulk modulus of the isotropic suspension can be determined exactly in terms of the interphase thickness $h$ following the strategy of Hashin [20] for concentric shells; the result is

$$\begin{aligned} \widetilde{\kappa} = \kappa ^{(1)} + c \frac{(1+h/a)^{3}}{\displaystyle \frac{1}{\kappa ^{(1,2)} - \kappa ^{(1)}} + \frac{1}{\kappa ^{(1)} + 4\mu ^{(1)}/3}}, \end{aligned}$$

(115)

where

$$\begin{aligned} \kappa ^{(1,2)} = \frac{h}{3\eta _{\parallel }} + \frac{1}{\displaystyle \frac{(1+h/a)^{3}}{\kappa ^{(2)} - h/(3\eta _{\parallel })} + \frac{(1 + h/a )^{3} - 1}{h/\eta _{\parallel }}} \end{aligned}$$

(116)

Central to the derivation of this result are the choices (110)₁ and (110)₂; this class of transversely isotropic elasticity tensors produces the same form of radial displacement fields as their isotropic counterparts. In the limit of sharp imperfect interfaces ($h \rightarrow 0$), expression (115) reduces to (66). This exact result can be exploited for calibration and verification of the numerical simulations. Figure 4a compares the dilute correction factors $\beta _{\kappa }= (\widetilde{\kappa}/\kappa ^{(1)}-1)/c$ predicted by the exact result (115) and the FFT simulations, as a function of the ratio $h/a$, for interfaces with a spherical compliance $\eta_{s} = a/\mu^{(1)}$ and various interfacial anisotropies ($\alpha = -0.25,0,0.75$). The FFT simulations discretize the unit cell into $256^{3}$ voxels such that $92^{3}$ grid points lie within the inclusion, and make use of 2 voxels across the interphase. These settings generate inclusion contents of approximately $c \approx 2.4\times 10^{-3}$, which were found small enough to mimic dilute suspensions. In all simulations a tolerance of $10^{-6}$ for the change in stress/strain-rate fields was required for convergence. Also included in the figure is the limiting value of (66) for sharp imperfect interfaces ($h \rightarrow 0$). Two observations are in order. First, the FFT results are seen to reproduce the exact result for the entire range of interphasial thicknesses considered, thus confirming the validity of the various parameters employed in the simulations. Second, the FFT simulations with the smallest thickness considered ($h/a = 10^{-4}$) are seen to accurately reproduce the exact result for suspensions with sharp imperfect interfaces. This grid size and interphase thickness were therefore chosen to produce reference results for suspensions with sharp imperfect interfaces more generally. As the thickness of the interphase reduces,the interaction between different points within the interphase as defined by the integral equation (106) also reduces due to the decrease in relative volume of the interphase, leading to imperfect interface conditions. The numerical model is further verified by performing a more stringent comparison with the exact local fields within dilute suspensions with imperfect interfaces subject to uniaxial tension derived by Zhong and Meguid [34]. Figure 4b shows the variation of the local tensile stress colinear with the applied tension ($x_{3}$ direction) along its perpendicular direction ($x_{1}$ direction) starting from the center of the inclusion. The Poisson’s ratios and shear moduli of matrix and inclusion phases are $\nu ^{(1)} = 0.35$, $\nu ^{(2)}=0.2$, and $\mu ^{(2)} = 20\mu ^{(1)}$. Three different combinations of interfacial compliances are considered. For simplicity, this particular comparison makes use of isotropic interphasial elasticity tensors, $128^{3}$ voxels such that $48^{3}$ grid points lie within the inclusion, an inclusion content of $c \approx 2.2 \times 10^{-3}$, and a thickness-to-radius ratio of $h/a = 2 \times 10^{-3}$. In all cases, excellent agreement is observed for the entire domain considered, thus confirming the validity of the various parameters employed in the simulations for different loading conditions.

Fig. 4

Comparisons between full-field simulations (FFT) and exact results: a) dilute correction for the bulk modulus of a suspension with thin interfacial coating of thickness $h$, spherical compliance $\eta_{s} = a/\mu^{(1)}$ and various interfacial anisotropies ($\alpha = -0.25,0,0.75$); b) tensile stress distribution in a specimen subject to uniaxial tension for various interfacial compliances [34]