Skip to main content
SpringerLink
Log in

Accretion Mechanics of Nonlinear Elastic Circular Cylindrical Bars Under Finite Torsion

  • Published:
Journal of Elasticity Aims and scope Submit manuscript

Abstract

In this paper we formulate the initial-boundary value problem of accreting circular cylindrical bars under finite torsion. It is assumed that the bar grows as a result of printing stress-free cylindrical layers on its boundary while it is under a time-dependent torque (or a time-dependent twist) and is free to deform axially. In a deforming body, accretion induces eigenstrains, and consequently residual stresses. We formulate the anelasticity problem by first constructing the natural Riemannian metric of the growing bar. This metric explicitly depends on the history of deformation during the accretion process. To simplify the kinematics, we consider incompressible solids. For the example of incompressible neo-Hookean solids, we solve the governing equations numerically. We also linearize the governing equations and compare the linearized solutions with the numerical solutions of the neo-Hookean bars.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

Notes

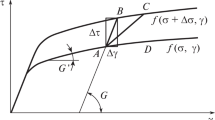
  1. This decomposition is due to Kondaurov and Nikitin [13], Takamizawa and Hayashi [36], Takamizawa and Matsuda [37], and Takamizawa [35]. One can find similar ideas in [39, 40]. This decomposition was popularized in the literature of biomechanics by Rodriguez et al. [26]. For a historical account of this decomposition in different fields see [27, 50].

  2. Growing bodies are non-Euclidean in the sense that their natural configuration is not Euclidean, in general. Non-Euclidean solids—a term that was coined by Henri Poincaré [25]—has been used interchangeably for anelastic bodies in the recent literature [42, 52, 53].

  3. This was first observed in the setting of linear accretion mechanics in the seminal work of Brown and Goodman [5] who studied accreting planets under self-gravity.

  4. The idea of a time of attachment map is due to Metlov [21].

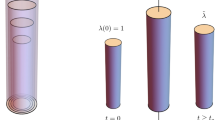
  5. Family 3 deformations are universal for certain inhomogeneous and anisotropic bars as well [44, 47, 48]. In this paper, we restrict our calculations to isotropic and homogeneous bars.

  6. Note that as soon as a layer is deposited it becomes part of the body and participates in the deformation process. If the load is fixed, one would have a classical twist-fit problem (Fig. 1). The time dependence of the load (or twist) makes the natural state of the body (the material metric) inhomogeneous. In other words, after completion of accretion if each cylindrical layer is allowed to relax independently of the rest of the body the collection of relaxed thin cylindrical shells can not be put back together in the Euclidean ambient space without local elastic deformations. This incompatibility of the local rest configurations depends on the state of deformation during accretion and indirectly on the applied load during accretion.

  7. This is identical to what was obtained in [51] in the case of accreting bars under finite extension.

  8. The physical components of the Cauchy stress are defined as \({\bar{\sigma}}^{ab}=\sigma ^{ab}\sqrt{g_{aa}\,g_{bb}}\) (no summation) [41].

  9. This is a simple application of the Leibniz integral rule:

    $$ \hat{k}'_{3}(t)=\frac{d}{dt}\int _{R_{0}}^{s(t)} f(t,R)\,dR =s'(t)\,f(t,s(t))+ \int _{R_{0}}^{s(t)} \frac{\partial f(t,R)}{\partial t}\,dR\,, $$

    where

    $$ f(t,R)=R\int _{R}^{s(t)}\frac{d\xi}{\lambda ^{3}(\tau (\xi ))}\,. $$

    Note that

    $$ f(t,s(t))=s(t) \int _{s(t)}^{s(t)} \frac{d\xi}{\lambda ^{3}(\tau (\xi ))}=0\,,\quad \frac{\partial f(t,R)}{\partial t}=R \,s'(t) \frac{1}{\lambda ^{3}(\tau (s(t)))}=\frac{R\,u_{0}}{\lambda ^{3}(t)} \,. $$

    Thus

    $$ \hat{k}'_{3}(t)=\int _{R_{0}}^{s(t)} \frac{R\,u_{0}}{\lambda ^{3}(t)} \,dR =\frac{u_{0}}{2\lambda ^{3}(t)}\big(s^{2}(t)-R_{0}^{2}\big) \,. $$

References

  1. Abi-Akl, R., Cohen, T.: Surface growth on a deformable spherical substrate. Mech. Res. Commun. 103, 103457 (2020)

    Article  Google Scholar 

  2. Abi-Akl, R., Abeyaratne, R., Cohen, T.: Kinetics of surface growth with coupled diffusion and the emergence of a universal growth path. Proc. R. Soc. A 475(2221), 20180465 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  3. Arutyunyan, N.K., Naumov, V., Radaev, Y.N.: A mathematical model of a dynamically accreted deformable body. Part 1: kinematics and measure of deformation of the growing body. Izv. Akad. Nauk SSSR, Meh. Tverd. Tela 6, 85–96 (1990)

    Google Scholar 

  4. Bergel, G.L., Papadopoulos, P.: A finite element method for modeling surface growth and resorption of deformable solids. Comput. Mech. 68(4), 759–774 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  5. Brown, C., Goodman, L.: Gravitational stresses in accreted bodies. Proc. R. Soc. Lond. A, 276, 571–576 (1963)

    Article  MATH  Google Scholar 

  6. Doyle, T.C., Ericksen, J.L.: Nonlinear elasticity. Adv. Appl. Mech. 4, 53–115 (1956)

    Article  MathSciNet  Google Scholar 

  7. Drozdov, A.D.: Continuous accretion of a composite cylinder. Acta Mech. 128(1) (1998)

  8. Drozdov, A.D.: Viscoelastic Structures: Mechanics of Growth and Aging. Academic Press, San Diego (1998)

    MATH  Google Scholar 

  9. Ericksen, J.L.: Deformations possible in every isotropic, incompressible, perfectly elastic body. Z. Angew. Math. Phys. 5(6), 466–489 (1954)

    Article  MathSciNet  MATH  Google Scholar 

  10. Goodbrake, C., Yavari, A., Goriely, A.: The anelastic Ericksen problem: universal deformations and universal eigenstrains in incompressible nonlinear anelasticity. J. Elast. 142(2), 291–381 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  11. Hodge, N., Papadopoulos, P.: A continuum theory of surface growth. Proc. R. Soc. Lond. A 466(2123), 3135–3152 (2010)

    MathSciNet  MATH  Google Scholar 

  12. Klingbeil, W.W., Shield, R.T.: On a class of solutions in plane finite elasticity. Z. Angew. Math. Phys. 17(4), 489–511 (1966)

    Article  MathSciNet  Google Scholar 

  13. Kondaurov, V., Nikitin, L.: Finite strains of viscoelastic muscle tissue. J. Appl. Math. Mech. 51(3), 346–353 (1987)

    Article  MathSciNet  MATH  Google Scholar 

  14. Lychev, S.: Universal deformations of growing solids. Mech. Solids 46(6), 863–876 (2011)

    Article  Google Scholar 

  15. Lychev, S., Manzhirov, A.: The mathematical theory of growing bodies. Finite deformations. J. Appl. Math. Mech. 77(4), 421–432 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  16. Lychev, S., Manzhirov, A.: Reference configurations of growing bodies. Mech. Solids 48(5), 553–560 (2013)

    Article  Google Scholar 

  17. Lychev, S., Koifman, K., Djuzhev, N.: Incompatible deformations in additively fabricated solids: discrete and continuous approaches. Symmetry 13(12), 2331 (2021)

    Article  Google Scholar 

  18. Manzhirov, A.: The general non-inertial initial-boundaryvalue problem for a viscoelastic ageing solid with piecewise-continuous accretion. J. Appl. Math. Mech. 59(5), 805–816 (1995)

    Article  MathSciNet  MATH  Google Scholar 

  19. Manzhirov, A.V.: Mechanics of growing solids: New track in mechanical engineering. In: ASME 2014 International Mechanical Engineering Congress and Exposition, p. V009T12A039. American Society of Mechanical Engineers, Montreal, Quebec, Canada (2014)

    Google Scholar 

  20. Marsden, J., Hughes, T.: Mathematical Foundations of Elasticity. Dover, New York (1983)

    MATH  Google Scholar 

  21. Metlov, V.: On the accretion of inhomogeneous viscoelastic bodies under finite deformations. J. Appl. Math. Mech. 49(4), 490–498 (1985)

    Article  MATH  Google Scholar 

  22. Naumov, V.E.: Mechanics of growing deformable solids: a review. J. Eng. Mech. 120(2), 207–220 (1994)

    Google Scholar 

  23. Ogden, R.W.: Non-linear Elastic Deformations. Dover, New York (1984)

    MATH  Google Scholar 

  24. Ong, J.J., O’Reilly, O.M.: On the equations of motion for rigid bodies with surface growth. Int. J. Eng. Sci. 42(19), 2159–2174 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  25. Poincaré, H.: Science and Hypothesis. The Walter Scott Publishing Company, New York (1905)

    Google Scholar 

  26. Rodriguez, E.K., Hoger, A., McCulloch, A.D.: Stress-dependent finite growth in soft elastic tissues. J. Biomech. 27(4), 455–467 (1994)

    Article  Google Scholar 

  27. Sadik, S., Yavari, A.: On the origins of the idea of the multiplicative decomposition of the deformation gradient. Math. Mech. Solids 22(4), 771–772 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  28. Simo, J., Marsden, J.: Stress tensors, Riemannian metrics and the alternative descriptions in elasticity. In: Trends and Applications of Pure Mathematics to Mechanics, pp. 369–383. Springer, Berlin (1984)

    Chapter  Google Scholar 

  29. Singh, M., Pipkin, A.C.: Note on Ericksen’s problem. Z. Angew. Math. Phys. 16(5), 706–709 (1965)

    Article  Google Scholar 

  30. Skalak, R., Farrow, D., Hoger, A.: Kinematics of surface growth. J. Math. Biol. 35(8), 869–907 (1997)

    Article  MathSciNet  MATH  Google Scholar 

  31. Southwell, R.: Introduction to the Theory of Elasticity for Engineers and Physicists. Oxford University Press, London (1941)

    Google Scholar 

  32. Sozio, F., Yavari, A.: Nonlinear mechanics of surface growth for cylindrical and spherical elastic bodies. J. Mech. Phys. Solids 98, 12–48 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  33. Sozio, F., Yavari, A.: Nonlinear mechanics of accretion. J. Nonlinear Sci. 29(4), 1813–1863 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  34. Sozio, F., Faghih Shojaei, M., Sadik, S., Yavari, A.: Nonlinear mechanics of thermoelastic accretion. Z. Angew. Math. Phys. 71(3), 1–24 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  35. Takamizawa, K.: Stress-free configuration of a thick-walled cylindrical model of the artery: an application of Riemann geometry to the biomechanics of soft tissues. J. Appl. Mech. 58(3), 840–842 (1991)

    Article  Google Scholar 

  36. Takamizawa, K., Hayashi, K.: Strain energy density function and uniform strain hypothesis for arterial mechanics. J. Biomech. 20(1), 7–17 (1987)

    Article  Google Scholar 

  37. Takamizawa, K., Matsuda, T.: Kinematics for bodies undergoing residual stress and its applications to the left ventricle. J. Appl. Mech. 57(2), 321–329 (1990)

    Article  Google Scholar 

  38. Tomassetti, G., Cohen, T., Abeyaratne, R.: Steady accretion of an elastic body on a hard spherical surface and the notion of a four-dimensional reference space. J. Mech. Phys. Solids 96, 333–352 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  39. Tranquillo, R.T., Murray, J.D.: Continuum model of fibroblast-driven wound contraction: inflammation-mediation. J. Theor. Biol. 158(2), 135–172 (1992)

    Article  Google Scholar 

  40. Tranquillo, R.T., Murray, J.: Mechanistic model of wound contraction. J. Surg. Res. 55(2), 233–247 (1993)

    Article  Google Scholar 

  41. Truesdell, C.: The physical components of vectors and tensors. Z. Angew. Math. Mech. 33(10–11), 345–356 (1953)

    Article  MathSciNet  MATH  Google Scholar 

  42. Truskinovsky, L., Zurlo, G.: Nonlinear elasticity of incompatible surface growth. Phys. Rev. B 99(5), 053001 (2019)

    Article  MathSciNet  Google Scholar 

  43. Yavari, A.: A geometric theory of growth mechanics. J. Nonlinear Sci. 20(6), 781–830 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  44. Yavari, A.: Universal deformations in inhomogeneous isotropic nonlinear elastic solids. Proc. R. Soc. A 477(2253), 20210547 (2021)

    Article  MathSciNet  Google Scholar 

  45. Yavari, A., Goriely, A.: Riemann-Cartan geometry of nonlinear dislocation mechanics. Arch. Ration. Mech. Anal. 205(1), 59–118 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  46. Yavari, A., Goriely, A.: The twist-fit problem: Finite torsional and shear eigenstrains in nonlinear elastic solids. Proc. R. Soc. Lond. A 471(2183) (2015)

  47. Yavari, A., Goriely, A.: Universal deformations in anisotropic nonlinear elastic solids. J. Mech. Phys. Solids 156, 104598 (2021)

    Article  MathSciNet  Google Scholar 

  48. Yavari, A., Goriely, A.: The universal program of nonlinear hyperelasticity. J. Elast., 1–56 (2022)

  49. Yavari, A., Ozakin, A.: Covariance in linearized elasticity. Z. Angew. Math. Phys. 59(6), 1081–1110 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  50. Yavari, A., Sozio, F.: On the direct and reverse multiplicative decompositions of deformation gradient in nonlinear anisotropic anelasticity. J. Mech. Phys. Solids 170, 105101 (2022)

    Article  MathSciNet  Google Scholar 

  51. Yavari, A., Safa, Y., Soleiman Fallah, A.: Finite extension of accreting nonlinear elastic solid circular cylinders (2022)

  52. Zurlo, G., Truskinovsky, L.: Printing non-Euclidean solids. Phys. Rev. Lett. 119(4), 048001 (2017)

    Article  Google Scholar 

  53. Zurlo, G., Truskinovsky, L.: Inelastic surface growth. Mech. Res. Commun. 93, 174–179 (2018)

    Article  Google Scholar 

Download references

Acknowledgement

This research was partially supported by NSF – Grant No. CMMI 1939901, and ARO Grant No. W911NF-18-1-0003.

Author information

Authors and Affiliations

  1. School of Civil and Environmental Engineering, Georgia Institute of Technology, Atlanta, GA, 30332, USA

    Arash Yavari & Satya Prakash Pradhan

  2. The George W. Woodruff School of Mechanical Engineering, Georgia Institute of Technology, Atlanta, GA, 30332, USA

    Arash Yavari

Authors
  1. Arash Yavari
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Satya Prakash Pradhan
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

The authors contributed equally to this paper.

Corresponding author

Correspondence to Arash Yavari.

Ethics declarations

Competing interests

The authors declare no competing interests.

Additional information

Publisher’s Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Yavari, A., Pradhan, S.P. Accretion Mechanics of Nonlinear Elastic Circular Cylindrical Bars Under Finite Torsion. J Elast 152, 29–60 (2022). https://doi.org/10.1007/s10659-022-09957-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10659-022-09957-6

Keywords

Mathematics Subject Classification

Search

Navigation